Допустимая ошибка метода определения это - Решение и исправление самых разных ошибок на TopOshibok.ru

From Wikipedia, the free encyclopedia

Probability densities of polls of different sizes, each color-coded to its 95% confidence interval (below), margin of error (left), and sample size (right). Each interval reflects the range within which one may have 95% confidence that the true percentage may be found, given a reported percentage of 50%. The margin of error is half the confidence interval (also, the radius of the interval). The larger the sample, the smaller the margin of error. Also, the further from 50% the reported percentage, the smaller the margin of error.

The margin of error is a statistic expressing the amount of random sampling error in the results of a survey. The larger the margin of error, the less confidence one should have that a poll result would reflect the result of a census of the entire population. The margin of error will be positive whenever a population is incompletely sampled and the outcome measure has positive variance, which is to say, whenever the measure varies.

The term margin of error is often used in non-survey contexts to indicate observational error in reporting measured quantities.

Concept[edit]

Consider a simple yes/no poll as a sample of respondents drawn from a population $N{\text{, }}(n\ll N)$ reporting the percentage of yes responses. We would like to know how close is to the true result of a survey of the entire population , without having to conduct one. If, hypothetically, we were to conduct poll over subsequent samples of respondents (newly drawn from ), we would expect those subsequent results $p_{1},p_{2},\ldots$ to be normally distributed about $\overline {p}$ , the true but unknown percentage of the population. The margin of error describes the distance within which a specified percentage of these results is expected to vary from $\overline {p}$ .

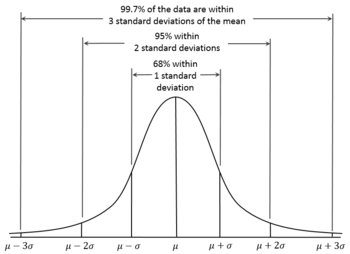
According to the 68-95-99.7 rule, we would expect that 95% of the results $p_{1},p_{2},\ldots$ will fall within about two standard deviations ( $\pm 2\sigma _{P}$ ) either side of the true mean $\overline {p}$ . This interval is called the confidence interval, and the radius (half the interval) is called the margin of error, corresponding to a 95% confidence level.

Generally, at a confidence level $\gamma$ , a sample sized of a population having expected standard deviation $\sigma$ has a margin of error

$MOE_{\gamma }=z_{\gamma }\times {\sqrt {\frac {\sigma ^{2}}{n}}}$

where $z_{\gamma }$ denotes the quantile (also, commonly, a z-score), and ${\sqrt {\frac {\sigma ^{2}}{n}}}$ is the standard error.

Standard deviation and standard error[edit]

We would expect the average of normally distributed values $p_{1},p_{2},\ldots$ to have a standard deviation which somehow varies with . The smaller , the wider the margin. This is called the standard error $\sigma _{\overline {p}}$ .

For the single result from our survey, we assume that $p={\overline {p}}$ , and that all subsequent results $p_{1},p_{2},\ldots$ together would have a variance $\sigma _{P}^{2}=P(1-P)$ .

${\text{Standard error}}=\sigma _{\overline {p}}\approx {\sqrt {\frac {\sigma _{P}^{2}}{n}}}\approx {\sqrt {\frac {p(1-p)}{n}}}$

Note that $p(1-p)$ corresponds to the variance of a Bernoulli distribution.

Maximum margin of error at different confidence levels[edit]

For a confidence level $\gamma$ , there is a corresponding confidence interval about the mean $\mu \pm z_{\gamma }\sigma$ , that is, the interval $[\mu -z_{\gamma }\sigma ,\mu +z_{\gamma }\sigma ]$ within which values of should fall with probability $\gamma$ . Precise values of $z_{\gamma }$ are given by the quantile function of the normal distribution (which the 68-95-99.7 rule approximates).

Note that $z_{\gamma }$ is undefined for $|\gamma |\geq 1$ , that is, $z_{1.00}$ is undefined, as is $z_{1.10}$ .

$\gamma$	$z_{\gamma }$		$\gamma$	$z_{\gamma }$
0.68	0.994457883210	0.999	3.290526731492
0.90	1.644853626951	0.9999	3.890591886413
0.95	1.959963984540	0.99999	4.417173413469
0.98	2.326347874041	0.999999	4.891638475699
0.99	2.575829303549	0.9999999	5.326723886384
0.995	2.807033768344	0.99999999	5.730728868236
0.997	2.967737925342	0.999999999	6.109410204869

Log-log graphs of $MOE_{\gamma }(0.5)$

vs sample size n and confidence level γ. The arrows show that the maximum margin error for a sample size of 1000 is ±3.1% at 95% confidence level, and ±4.1% at 99%.
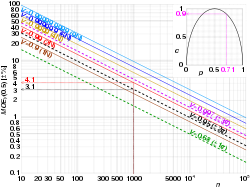
The inset parabola $\sigma _{p}^{2}=p-p^{2}$

illustrates the relationship between $\sigma _{p}^{2}$

at $p=0.71$

and $\sigma _{max}^{2}$

. In the example, MOE₉₅(0.71) ≈ 0.9 × ±3.1% ≈ ±2.8%.

Since $\max \sigma _{P}^{2}=\max P(1-P)=0.25$ at p=0.5 , we can arbitrarily set $p={\overline {p}}=0.5$ , calculate $\sigma _{P}$ , $\sigma _{\overline {p}}$ , and $z_{\gamma }\sigma _{\overline {p}}$ to obtain the maximum margin of error for at a given confidence level $\gamma$ and sample size , even before having actual results. With $p=0.5,n=1013$

$MOE_{95}(0.5)=z_{0.95}\sigma _{\overline {p}}\approx z_{0.95}{\sqrt {\frac {\sigma _{P}^{2}}{n}}}=1.96{\sqrt {\frac {.25}{n}}}=0.98/{\sqrt {n}}=\pm 3.1\%$

$MOE_{99}(0.5)=z_{0.99}\sigma _{\overline {p}}\approx z_{0.99}{\sqrt {\frac {\sigma _{P}^{2}}{n}}}=2.58{\sqrt {\frac {.25}{n}}}=1.29/{\sqrt {n}}=\pm 4.1\%$

Also, usefully, for any reported $MOE_{95}$

$MOE_{99}={\frac {z_{0.99}}{z_{0.95}}}MOE_{95}\approx 1.3\times MOE_{95}$

Specific margins of error[edit]

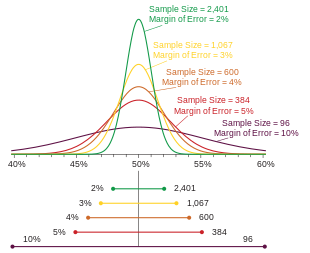
If a poll has multiple percentage results (for example, a poll measuring a single multiple-choice preference), the result closest to 50% will have the highest margin of error. Typically, it is this number that is reported as the margin of error for the entire poll. Imagine poll reports $p_{a},p_{b},p_{c}$ as $71\%,27\%,2\%,n=1013$

$MOE_{95}(P_{a})=z_{0.95}\sigma _{\overline {p_{a}}}\approx 1.96{\sqrt {\frac {p_{a}(1-p_{a})}{n}}}=0.89/{\sqrt {n}}=\pm 2.8\%$

(as in the figure above)

$MOE_{95}(P_{b})=z_{0.95}\sigma _{\overline {p_{b}}}\approx 1.96{\sqrt {\frac {p_{b}(1-p_{b})}{n}}}=0.87/{\sqrt {n}}=\pm 2.7\%$

$MOE_{95}(P_{c})=z_{0.95}\sigma _{\overline {p_{c}}}\approx 1.96{\sqrt {\frac {p_{c}(1-p_{c})}{n}}}=0.27/{\sqrt {n}}=\pm 0.8\%$

As a given percentage approaches the extremes of 0% or 100%, its margin of error approaches ±0%.

Comparing percentages[edit]

Imagine multiple-choice poll reports $p_{a},p_{b},p_{c}$ as $46\%,42\%,12\%,n=1013$ . As described above, the margin of error reported for the poll would typically be $MOE_{95}(P_{a})$ , as $p_{a}$ is closest to 50%. The popular notion of statistical tie or statistical dead heat, however, concerns itself not with the accuracy of the individual results, but with that of the ranking of the results. Which is in first?

If, hypothetically, we were to conduct poll over subsequent samples of respondents (newly drawn from ), and report result $p_{w}=p_{a}-p_{b}$ , we could use the standard error of difference to understand how $p_{w_{1}},p_{w_{2}},p_{w_{3}},\ldots$ is expected to fall about ${\overline {p_{w}}}$ . For this, we need to apply the sum of variances to obtain a new variance, $\sigma _{P_{w}}^{2}$ ,

$\sigma _{P_{w}}^{2}=\sigma _{P_{a}-P_{b}}^{2}=\sigma _{P_{a}}^{2}+\sigma _{P_{b}}^{2}-2\sigma _{P_{a},P_{b}}=p_{a}(1-p_{a})+p_{b}(1-p_{b})+2p_{a}p_{b}$

where $\sigma _{P_{a},P_{b}}=-P_{a}P_{b}$ is the covariance of $P_{a}$ and $P_{b}$ .

Thus (after simplifying),

${\text{Standard error of difference}}=\sigma _{\overline {w}}\approx {\sqrt {\frac {\sigma _{P_{w}}^{2}}{n}}}={\sqrt {\frac {p_{a}+p_{b}-(p_{a}-p_{b})^{2}}{n}}}=0.029,P_{w}=P_{a}-P_{b}$

$MOE_{95}(P_{a})=z_{0.95}\sigma _{\overline {p_{a}}}\approx \pm {3.1\%}$

$MOE_{95}(P_{w})=z_{0.95}\sigma _{\overline {w}}\approx \pm {5.8\%}$

Note that this assumes that $P_{{c}}$ is close to constant, that is, respondents choosing either A or B would almost never chose C (making $P_{a}$ and $P_{b}$ close to perfectly negatively correlated). With three or more choices in closer contention, choosing a correct formula for $\sigma _{P_{w}}^{2}$ becomes more complicated.

Effect of finite population size[edit]

The formulae above for the margin of error assume that there is an infinitely large population and thus do not depend on the size of population , but only on the sample size . According to sampling theory, this assumption is reasonable when the sampling fraction is small. The margin of error for a particular sampling method is essentially the same regardless of whether the population of interest is the size of a school, city, state, or country, as long as the sampling fraction is small.

In cases where the sampling fraction is larger (in practice, greater than 5%), analysts might adjust the margin of error using a finite population correction to account for the added precision gained by sampling a much larger percentage of the population. FPC can be calculated using the formula^[1]

$\operatorname {FPC} ={\sqrt {\frac {N-n}{N-1}}}$

…and so, if poll were conducted over 24% of, say, an electorate of 300,000 voters,

$MOE_{95}(0.5)=z_{0.95}\sigma _{\overline {p}}\approx {\frac {0.98}{\sqrt {72,000}}}=\pm 0.4\%$

$MOE_{95_{FPC}}(0.5)=z_{0.95}\sigma _{\overline {p}}{\sqrt {\frac {N-n}{N-1}}}\approx {\frac {0.98}{\sqrt {72,000}}}{\sqrt {\frac {300,000-72,000}{300,000-1}}}=\pm 0.3\%$

Intuitively, for appropriately large ,

$\lim _{n\to 0}{\sqrt {\frac {N-n}{N-1}}}\approx 1$

$\lim _{n\to N}{\sqrt {\frac {N-n}{N-1}}}=0$

In the former case, is so small as to require no correction. In the latter case, the poll effectively becomes a census and sampling error becomes moot.

References[edit]

^ Isserlis, L. (1918). «On the value of a mean as calculated from a sample». Journal of the Royal Statistical Society. Blackwell Publishing. 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)

Sources[edit]

Sudman, Seymour and Bradburn, Norman (1982). Asking Questions: A Practical Guide to Questionnaire Design. San Francisco: Jossey Bass. ISBN 0-87589-546-8
Wonnacott, T.H.; R.J. Wonnacott (1990). Introductory Statistics (5th ed.). Wiley. ISBN 0-471-61518-8.

External links[edit]

«Errors, theory of», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Weisstein, Eric W. «Margin of Error». MathWorld.

Источник

Определение
допустимых пределов погрешности
результатов лабораторных исследований
преследует цель установить приемлемость
их аналитических качеств для клинических
целей.

Теоретические
основы определения допустимой
аналитической вариации

(случайной
погрешности) базируются на следующем:

1. Определение
аналитической вариации (среднего
квадратического отклонения и коэффициента
вариации) в наиболее квалифицированных
лабораториях. Полезными в этом вопросе
могут быть опыты по межлабораторному

контролю
качества, позволяющие определить
межлабораторную вариацию.

2. Теоретический
расчет аналитической вариации как
фиксированной части биологической
вариации.

Для улучшения
диагностической значимости лабораторных
тестов наиболее существенна не
абсолютная величина аналитической
вариации, а ее соотношение с биологической
вариацией.

Соотношение между
различными видами вариации определяется
следующим уравнением:

S²общ
= S²ан
+ S²биол

где
S²общ
— общая вариация; S²ан
— аналитическая вариация; S²биол
— биологическая вариация.

Аналитическая
вариация, равная 1/4 пределов нормальных
величин в процентах от средней
величины нормы, расширяет их более чем
на 20%, равная 1/8
—
на 10—12%. равная 1/12
—
менее чем на 8%.

Коэффициент
вариации метода не должен превышать
1/8 области нормальных пределов в процентах
от средней величины нормы; при этом
нормальные величины рассматриваются
как совокупность аналитической и
биологической вариаций.

Во всех случаях
при расчете допустимых пределов
погрешности метода индивидуально для
каждого вещества и метода аналитическая
вариация, полученная экспериментально,
должна сопоставляться с теоретически
рассчитанными величинами.

3. Медицински
допустимые пределы погрешности.
Этот способ оценки

допустимых
пределов погрешности основан на опросе
мнений врачей-клиницистов и лабораторных
работников.

Каждое
вещество в конечном счете исследуется
для определенных клинических целей
— установления диагноза, контроля за
лечением, обследования здоровых лиц,
поэтому медицински допустимые пределы
погрешности в различных клинических
ситуациях будут различными. Например,
при повторном анализе теста медицински
допустимые пределы погрешности будут
включать внутрииндивидуальную и
аналитическую вариации изо дня в день.
При массовом обследовании здоровых
наибольшее значение для разделения
нормы и патологии будут иметь
межиндивидуальные колебания. В такой
ситуации требования к точности будут
ниже.

3. Технология оценки результатов лабораторных исследований

Результаты
лабораторных исследований (информация)
— единственный продукт, производимый
лабораторией. При интерпретации
результатов анализов необходимо оценить,
значимы ли обнаруженные отклонения
величин исследуемых параметров от
нормальных показателей (референтных
величин); имеют ли эти отклонения
физиологический характер или они
являются патологическими (то есть нет
ли оснований объяснить их какими-либо
физиологическими или иными, не связанными
с болезнью причинами); насколько
надёжно эти отклонения или их сочетание
позволяют подтвердить диагноз определённой
болезни.

Понятие
референтной
величины

Важнейший этап
оценки результатов лабораторных
исследований — установление отличия
нормы от патологии. Это нетрудно сделать
при явном отклонении показателей от
нормы. Однако большинство результатов
лабораторных анализов непросто
разделить на «норму» и «патологию»,
поскольку они по природе своей не
дихотомические и не имеют отчётливых
разрывов или двух различных пиков, из
которых один соответствовал бы нормальному
результату, а другой — патологическому.
Объясняется это несколькими причинами.

Во-первых, разделение
биологической популяции людей по многим
лабораторным показателям на больных
и здоровых невозможно даже с теоретической
точки зрения. Заболевание может
развиваться незаметно, проявляясь
постепенным переходом от небольших
отклонений показателя к высоким по мере
нарастания дисфункции.

Во-вторых, здоровые
и больные фактически принадлежат к двум
различным популяциям, но когда эти
две популяции перемешаны, распознать
каждую из них в общей массе практически
невозможно, поскольку у различных
больных один и тот же показатель может
принимать различные значения, перекрывая
значения этого показателя у здоровых;
кроме того, количество больных в общей
популяции невелико.

Чтобы
трактовать данные лабораторных
исследований, необходимо сравнивать
их с нормальными величинами, поэтому
важно определить, что такое нормальный
показатель. Нормальные показатели —
показатели, выявляемые у здоровых
людей, однако в группах последних они
могут иметь различные числовые значения.
Это обусловлено индивидуальными
особенностями обмена веществ, гемопоэза,
функционирования тех или иных органов.
Нормальные лабораторные показатели
определяют путём выборочного обследования
здоровой популяции людей, например,
специально отобранных призывников
или студентов, группируемых по возрасту
и полу. При проведении исследований
некоторые факторы должны быть
стандартизованы. Например, при исследовании
крови её необходимо забирать натощак,
способ забора у всех обследуемых должен
быть одинаковым, так же как и метод
определения исследуемых показателей.
Математический анализ результатов,
полученных при таких исследованиях,
позволил выделить два основных класса
параметров биоматериалов здоровых
людей. Одни из них подчиняются закону
Гауссова (нормального) распределения,
другие — биноминальному распределению.

Например,
всем обследуемым определяют концентрацию
глюкозы в крови и строят кривую
распределения. Среднюю величину
рассчитывают делением суммы всех
результатов на их количество.

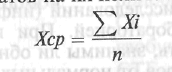
где:
Хср
— средняя величины; n
— количество результатов, Xi
— значение отдельного результата.

Дисперсию
средней величины при распределении
Гаусса можно выразить среднеквадратическим
отклонением (SD),
которое рассчитывают с помощью следующей
формулы.

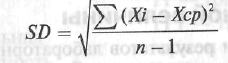
Как
правило, распределение биологических
объектов по степени выраженности
одного из признаков описывает кривая
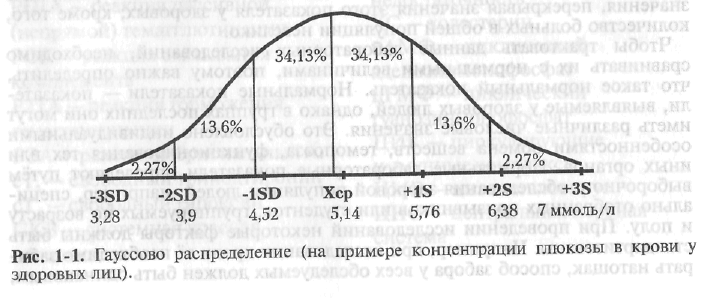
Гаусса (рис. 1-1), это подразумевает, что
в интервал, где величина признака
колеблется в пределах М±2SD
(применительно к концентрации глюкозы
в крови — 3,9-6,38 ммоль/л) попадает более
95% биологических объектов; тем не менее
почти у 5% лиц здоровой популяции
концентрация глюкозы не входит в
интервал М±2SD.
Именно поэтому критерием диагностики
сахарного диабета считают концентрацию
глюкозы в крови 7 ммоль/л и выше, а
пациентов с результатами в пределах
6,38-6,9 ммоль/л относят к группе риска по
данному заболеванию.

Таким
образом, если распределение признака
отвечает закону Гаусса, то нормальные
лабораторные показатели определяют
как среднее значение показателя для
здоровой популяции ±2 стандартных
отклонения (±2SD).

Вместе
с тем у 5% здоровых людей значение
показателя выходит за пределы
указанного диапазона. Приведённой
математической закономерности подчиняется
рапределение значительной части
лабораторных показателей химического
и клеточного состава крови.

Ко второй группе
лабораторных показателей относят
результаты, для которых расчёт средней
величины и среднеквадратичного отклонения
невозможны. Поэтому для таких
показателей вместо наиболее частой
нормальной величины определяют и
указывают пределы нормальных колебаний.
Можно просто указать диапазон полученных
результатов от самой малой до самой
большой величины, но чаще отсекают 3%
первых величин (снизу) и 3% последних
(сверху).

Вместе с тем
нормальные лабораторные показатели
различных веществ, которыми нередко
пользуются в лабораторной диагностике,
включают только общую биологическую
вариацию без учёта отдельных факторов,
что снижает диагностическую ценность
лабораторных тестов. Поэтому на смену
термину «нормальные лабораторные
показатели» приходит концепция
референтных величин. Референтные
величины дают представление о диапазоне,
в котором располагаются нормальные
величины. Смысл этого введения состоит
в том, что результаты лабораторного
исследования сравнивают с референтными
величинами, полученными в чётко
определённых условиях с учётом отдельных
факторов, влияющих на биологическую
вариацию. Референтные величины в
настоящее время установлены для
ограниченного количества показателей
(приблизительно 150). Установление
референтных интервалов колебаний для
каждого лабораторного параметра имеет
существенное значение для всей проблемы
надёжности лабораторной информации,
так как сравнение с ними служит основанием
для принятия диагностических и
лечебных решений.

При оценке
результатов лабораторных исследований
необходимо помнить, что референтные
величины являются статистическими
данными 95% популяции, и отклонения за
пределы диапазона не обязательно
указывают на наличие патологии.

Как правило,
стандартный набор биохимических
исследований, применяемых в обычных
лечебных учреждениях, включает не менее
10-12 тестов. Вероятность того, результаты
всех 12 тестов окажутся нормальными,
невелика. При статистическом анализе
установлено, что при определении 8
показателей результат одного из них
будет «патологическим» приблизительно
у 25% здоровых лиц, а при проведении 20
тестов одно или более отклонений от
нормы выявят у 55%. Приведённые данные
подтверждают мысль о том, что каждое
лабораторное исследование следует
назначать обдуманно, по строгим
показаниям, а перечень скрининговых
тестов должен быть ограниченным.

Таким
образом, приблизительно у 5% здоровых
людей выявляют «ненормальные»
лабораторные показатели, поэтому не
все значения, выходящие за пределы
нормы, следует расценивать как
патологические. И напротив, не всегда
показатель, лежащий в интервале М±2SD,
следует считать нормальным, так как
диапазон многих параметров достаточно
широк. Например, в норме гематокрит
у мужчин варьирует от 42 до 52%. Массивная
кровопотеря может привести к падению
гематокрита от 52 до 42%. Показатель 42% не
вызовет тревоги у врачей, поскольку он
относится к диапазону нормальных
величин, хотя для конкретного пациента
такое снижение может быть клинически
значимым. Поэтому каждый врач должен
помнить об изменчивости нормы,
связанной с внутрииндивидуальными и
межиндивидуальными вариациями. По этой
же причине лучшими референтными
величинами для конкретного пациента
следует считать стабильные результаты
лабораторных исследований, полученные
при его обследовании в течение нескольких
лет.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Допустимая ошибка

Предмет
Бухгалтерский учет и аудит

Разместил

🤓 slepenchuk_2022

👍 Проверено Автор24

максимальный размер ошибки генеральной совокупности, который аудитор считает приемлемой.

Научные статьи на тему «Допустимая ошибка»

Оценка допустимой ошибки (уровня существенности)

Понятие уровня существенности

Определение 1

Уровень существенности – это максимально допустимый…
Поэтому крайне важно понимать, что подразумевается под существенностью или так называемой допустимостью…
ошибки….
Существенность в большей степени зависит от суммы ошибки, значимости статьи, в которой допущена ошибка…
Данный вид ошибка является наиболее существенным.

Статья от экспертов

Актуальные проблемы при производстве осмотра места происшествия

В данной статье рассмотрены ошибки, допущенные лицами, проводящими предварительное расследование по уголовным делам при производстве осмотра места происшествия.

Понятие допустимой ошибки в аудите и уровень существенности

Определение 1

Допустимая ошибка – это максимальный размер ошибки генеральной совокупности, которую…
Материальные ошибки и пропуски, которые влияют на решение аудитора….
отчетности, а потом и общая материальность в целом;
дедуктивный подход – определяется общая величина допустимой…
ошибки и распределяется между статьями отчетности….
Общая допустимая ошибка не должна превышать сумму ошибок по отдельным счетам.

Статья от экспертов

Применение уровня существенности для расчета аудиторской выборки

В статье раскрываются теоретические и практические аспекты применения уровня существенности для определения объема аудиторской выборки, сформированной с помощью случайного отбора, основанного на законах теории вероятностей. Особое внимание уделено теоретическим аспектам применения выборочного метода в аудите, а именно основным трем параметрам: риск выборки, допустимая ошибка, ожидаемая ошибка. Установлено, что аудитор должен определить объем выборки, необходимого для получения требуемой точности результатов с заданной вероятностью, а также возможный предел ошибки репрезентативности, гарантированный с заданной вероятностью, и сравнить его с величиной допустимой погрешности. Автор предлагает формулу расчета статистической аудиторской выборки с применением уровня существенности и производит вычисление объема выборки документов на оприходование животных на выращивании и откорме. В результате обоснована зависимость между уровнем существенности, ожидаемой ошибкой и объемом аудиторской выб…

Повышай знания с онлайн-тренажером от Автор24!

Напиши термин
Выбери определение из предложенных или загрузи свое
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек

Источник

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Ваш е-мэйл

Заполните, если хотите получить ответ

Оцените наш проект

Источник

Concept[edit]

Standard deviation and standard error[edit]

Maximum margin of error at different confidence levels[edit]

Specific margins of error[edit]

Comparing percentages[edit]

Effect of finite population size[edit]

See also[edit]

References[edit]

Sources[edit]

External links[edit]

3. Технология оценки результатов лабораторных исследований

Допустимая ошибка

Научные статьи на тему «Допустимая ошибка»

Оценка допустимой ошибки (уровня существенности)

Актуальные проблемы при производстве осмотра места происшествия

Понятие допустимой ошибки в аудите и уровень существенности

Повышай знания с онлайн-тренажером от Автор24!

Предложите, как улучшить StudyLib