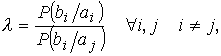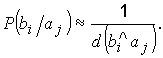Основными
характеристиками помехоустойчивых
кодов являются: длина кода n,
его основание m,
общее число кодовых комбинаций N,
число разрешенных кодовых комбинаций
Nр,
избыточность кода Ки
и минимальное кодовое расстояние dmin.
Длина
кода2
n
– это
число символов в кодовой комбинации.
Например, комбинация 11010 состоит из пяти
символов, следовательно, n=5.
Если все кодовые комбинации содержат
одинаковое число символов, то код
называется равномерным.
В неравномерных
кодах длина кодовых комбинаций может
быть разной.
Основание
кода m
– это число различных символов в коде.
Для двоичных кодов символами являются
1 и 0, поэтому m=2.
Число
кодовых комбинаций
для равномерного кода равно N=mn.
Например, для равномерного двоичного
кода, имеющего длину n=6,
число различных кодовых комбинаций
равно N=26=64.
Число
разрешенных кодовых комбинаций Nр
– это количество кодовых комбинаций
кода, используемых для передачи сообщений.
Для помехоустойчивых кодов Nр<N.
Оставшиеся кодовые комбинации N—Nр
называют запрещенными.
Если Nр=N,
то код является безызбыточным. Для
разделимых кодов Nр=2
k.
Избыточность
кода Ки
в общем случае определяется выражением
.
(5.1)
и
показывает, какая доля длины кодовой
комбинации не используется для передачи
информации, а используется для повышения
помехоустойчивости кода. Для разделимых
кодов
,
(5.2)
где
величина k/n
называется относительной
скоростью кода.
Кодовое
расстояние d(А,В)
– это число позиций, в которых две
кодовые комбинации А
и В
отличаются друг от друга. Например, если
А=01101,
В=10111,то
d(А,В)=3.
Кодовое расстояние между комбинациями
А
и В
может быть найдено в результате сложения
по модулю 2 одноименных разрядов
комбинаций, а именно
,
(5.3)
где
ai
и
bi
– i-е
разряды кодовых комбинаций A
и
B;
символ
обозначает сложение по модулю 2. Например,
чтобы получить кодовое расстояние между
комбинациями 1101011 и 0111101 достаточно
подсчитать число единиц в сумме этих
комбинаций по модулю 2:
Кодовое
расстояние между различными комбинациями
конкретного кода может быть различным.
Так, для первичных кодов (приложения 1,
2) это расстояние для различных пар
кодовых комбинаций может принимать
значения от единицы до величины длины
кода.
Минимальное
кодовое расстояние dmin
–
это минимальное расстояние между
разрешенными кодовыми комбинациями
данного кода. Минимальное кодовое
расстояние является основной
характеристикой корректирующей
способности кода. В первичных
(безызбыточных) кодах все комбинации
являются разрешенными, поэтому минимальное
кодовое расстояние для них равно единице
(dmin
=
1).
Такие коды не способны обнаруживать и
исправлять ошибки. Для того чтобы код
обладал корректирующими способностями,
его минимальное кодовое расстояние
должно быть не менее двух (dmin
2).
Для
обнаружения всех ошибок кратностью3
s
и менее, минимальное кодовое расстояние
должно удовлетворять условию
dmin
s
+1
. (5.4)
Если
код используется для исправления ошибок
кратности не более t,
то минимальное кодовое расстояние
должно иметь значение
dmin
2t
+1
. (5.5)
Например,
из (5.4) и (5.5) следует, что для обнаружения
однократных ошибок (s
=
1) требуется код с dmin
=
2, а для того чтобы исправить такие
ошибки, требуется код с кодовым расстоянием
dmin
=
3.
Для
обнаружения s
ошибок и исправления t
ошибок должно выполняться условие
dmin
s
+ t
+1 . (5.6)
Таким
образом, задача построения кода с
заданной корректирующей способностью
сводится к обеспечению необходимого
кодового расстояния. Увеличение dmin
приводит к росту избыточности кода. При
этом желательно, чтобы число проверочных
символов r
было минимальным. В настоящее время
известен ряд верхних и нижних границ,
которые устанавливают связь между
кодовым расстоянием и числом проверочных
символов. Сведения о границах для
кодового расстояния будут приведены
позже в процессе оценки качества приема
кодированных сообщений.
Соседние файлы в папке Лекции. СИСТЕМЫ И СЕТИ
- #
- #
- #
- #
- #
- #
- #
| 1. /Корректирующие коды в системах передачи информации/POC9_11.DOC 2. /Корректирующие коды в системах передачи информации/POC9_12.DOC 3. /Корректирующие коды в системах передачи информации/POC9_21.DOC 4. /Корректирующие коды в системах передачи информации/POC9_31.DOC 5. /Корректирующие коды в системах передачи информации/POC9_32.DOC 6. /Корректирующие коды в системах передачи информации/POC9_33.DOC 7. /Корректирующие коды в системах передачи информации/POC9_34.DOC 8. /Корректирующие коды в системах передачи информации/POC9_41.DOC 9. /Корректирующие коды в системах передачи информации/POC9_LIT.DOC 10. /Корректирующие коды в системах передачи информации/PИC9_П.DOC |
Г. А. Чернецкий Корректирующие коды в системах передачи информации учебное пособие новосибирск Простейшие корректирующие коды 2 Циклические коды 1 Кодирование циклических кодов 3 Свёрточные коды 1 Свёрточные коды и их свойства 3. 3 Пороговое декодирование свёрточных кодов 3. 4 Итерационные алгоритмы порогового декодирования 3. 5 Реализация пороговых кодеков сверточных кодов 5. 1 Методика статистического анализа канала связи и устройств Учебник для вузов/А. Г. Зюко, Д. Д. Кловский, М. В. Назаров, Л. М. Финк. М.: Радио и связь, 1986. 304 с Приложение 1 Таблица многочленов циклических кодов бчх (TablСycle) |
Министерство Российской Федерации по связи и информатизации
Сибирский государственный университет
телекоммуникаций и информатики
А.А. Макаров
Г.А. Чернецкий
Корректирующие коды
в системах передачи
информации
УЧЕБНОЕ ПОСОБИЕ
Новосибирск
1999
УДК 621.391(075)
Ктн, доцент А.А. Макаров, ктн, доцент Г.А.Чернецкий.
Рассматриваются вопросы построения и применения помехоустойчивых кодов в системах передачи информации, программная реализация кодирующих и декодирующих устройств, методика и некоторые результаты статистических исследований универсальных программных модулей кодеков циклических и свёрточных кодов с пороговым итерационным декодированием. Приводятся таблицы производящих многочленов циклических и свёрточных кодов.
Для студентов, обучающихся по специальностям «Радиосвязь, радиовещание и телевидение», «Радиотехника», «Аудиовизуальная техника», в том числе при курсовом и дипломном проектировании, а также для инженеров и научных работников, занимающихся проектированием и разработкой систем передачи информации с защитой от ошибок.
Каф. РТС
Иллюстраций – , таблиц – , список литературы – 18 названий.
Рецензент: В.П.Петров, Л.В.Бурый
Для специальностей:
200700, 200800, 200900, 20100, 201100, 201200, 201400
Утверждено редакционно-издательским Советом СибГУТИ
в качестве учебного пособия.
© Сибирский государственный университет
телекоммуникаций и информатики, 1999 г
СОДЕРЖАНИЕ
Предисловие 4
1 Корректирующие коды 5
1.1 Основные понятия и определения 5
1.2 Принцип обнаружения и исправления ошибок
корректирующими кодами 7
1.2.1 Коды с обнаружением и исправлением ошибок 7
1.2.2 Кодовое расстояние, избыточность кода 11
1.2.3 Энергетический выигрыш 13
1.3 Простейшие корректирующие коды 15
1.3.1 Код с четным числом единиц 15
1.3.2 Код с код с постоянным весом 15
1.3.4 Инверсный код 16
1.4 Групповые коды 17
1.4.1 Кодирование и декодирование групповых кодов 17
1.4.2 Коды Хэмминга 22
2 Циклические коды 25
2.1 Кодирование циклических кодов 25
2.2 Декодирование циклических кодов 27
2.3 Мажоритарное и порговое декодирование 33
2.4 Универсальный синдромно-матричный кодек циклических кодов 36
3 Свёрточные коды 39
3.1 Свёрточные коды и их свойства 39
3.2 Кодирование и декодирование свёрточных кодов 42
3.2.1 Методы кодирования и декодирования 42
3.2.2 Декодирование по алгоритму Витерби 49
3.3.3 Последовательное декодирование 50
3.3.4 Синдромное декодирование 52
3.3 Пороговое декодирование свёрточных кодов 52
3.4 Итерационные алгоритмы порогового декодирования 65
3.5 Реализация пороговых кодеков сверточных кодов 77
4 Каскадные и итеративные коды 82
5 Статистические исследования 83
5.1 Методика статистического анализа канала связи и устройств
защиты от ошибок на ЭВМ 83
-
Результаты статистических исследований 86
5.2.1 Выбор модели непрерывного канала и определение
характеристик дискретного канала 86
5.2.2 Выбор и статистические испытания УЗО 90
Заключение 95
ПРИЛОЖЕНИЕ 1 96
Приложение 2 97
Список литературы 100
ПРЕДИСЛОВИЕ
В учебном пособии рассматриваются ключевые вопросы помехоустойчивого кодирования в системах передачи информации. Практика создания систем связи различного назначения показала, что эффективным методом повышения достоверности передачи информации дискретными сообщениями является использование корректирующих кодов, предназначенных для обнаружения и исправления ошибок на приёме перед выдачей сообщения получателю.
К.Шеннон в теореме для дискретных каналов связи с помехами показал кардинальную возможность решения задачи надёжной передачи информации путём помехоустойчивого кодирования сообщений перед передачей их по дискретному каналу связи. Теория и практика построения и применения корректирующих кодов получила к настоящему времени широкое развитие, о чём свидетельствуют многочисленные монографии, например, [14]. Однако, в учебной литературе по курсам: Теория электрической связи, Основы радиотехнических систем и др. эти вопросы не получили систематизированного изложения.
Авторы не ставили перед собой задачи фундаментального изложения теории помехоустойчивого кодирования; это и невозможно в обьёме данного пособия. В учебном пособии рассматриваются принципиальные подходы к проблемам обнаружения и исправления ошибок корректирующими кодами, построения простейших корректирующих кодов, основы теории линейных кодов, основные методы их кодирования и декодирования, несколько больше внимания уделено алгоритмам итерационного порогового декодирования свёрточных кодов. Кроме того, рассмотрены вопросы программной реализации кодеков циклических и свёрточных кодов с учётом опыта кафедры по разработке автоматизированного рабочего места (АРМ) исследования систем передачи информации с защитой от ошибок [5], приводится методика и некоторые результаты статистических исследований этих кодеков на моделях каналов связи с различной статистической природой.
В учебном пособии использован многолетний опыт научно- исследовательской работы кафедры радиотехнических систем по разработке систем передачи и обработки информации с применением корректирующих кодов, а также известные по литературным источникам сведения по помехоустойчивому кодированию.
Авторы признательны О.А. Артёмовой за предоставленную возможность использования материалов её диссертационной работы [6] по исследованию итерационных пороговых декодеров свёрточных кодов, что способствовало улучшению содержания учебного пособия.
1 Корректирующие коды
1.1 Основные понятия и определения
Кодами в широком смысле принято называть системы соответствий между элементами сообщения и кодовыми символами, при помощи которых эти сообщения могут быть зафиксированы и при необходимости переданы на расстояние или использованы для дальнейшей обработки.
В соответствии с теоремой Шеннона для дискретных каналов связи (ДКС) с помехами информация в таких каналах может передаваться со сколь угодно высокой степенью достоверности при условии, что скорость передачи информации не превышает пропускной способности канала. Этим фундаментальным положением теории информации Шеннон показал кардинальный путь решения задачи надежной передачи данных путём так называемого помехоустойчивого кодирования сообщений перед передачей их по дискретному каналу связи.
Любая система передачи сообщений (система передачи информации) безусловно включает в себя источник сообщений, устройство преобразования передаваемых сигналов (УПС передачи), линию связи, устройство преобразования принимаемых сигналов (УПС приёма) и получатель сообщений (рисунок 1.1). При передаче дискретных сообщений УПС передачи и приёма содержат кодек (кодер и декодер), в котором может использоваться помехоустойчивый (корректирующий) код, способный обнаруживать и исправлять ошибки, возникающие в канале связи под действием помех.
Ошибки при передаче кодированного сигнала сводятся к тому, что некоторые из переданных кодовых символов из-за влияния помех заменяются другими, в двоичном канале это проявляется в переходах 1 в 0 или 0 в 1.
Если входные и выходные сигналы канала являются дискретными, то и канал называется дискретным. Математическая модель дискретного канала связи требует, как известно, описания следующих параметров:
- алфавитов входных и выходных сообщений;
- скорости передачи элементов алфавита;
- переходных вероятностей.
Диаграмма состояний и переходов для двоичного дискретного канала связи с помехами показана на рисунке 1.2 , где S0, S1 – алфавит источника; y0, y1 – алфавит на выходе канала; p(yi / Sj) – переходные вероятности.
Характеристики непрерывного канала (в том числе характер действия помех в линии связи) проявляются в свойствах переходных вероятностей дискретного канала (ДК). В результате этого ДК могут быть [7]:
- симметричными, когда переходные вероятности p(yi / Sj) одинаковы для всех i j и, соответственно, несимметричными в противном случае ;
- без памяти, когда переходные вероятности p(yi / Sj) не зависят от того, какие символа и с каким качеством передавались до данного символа Sj , и, соответственно, с памятью в противном случае;
- без стирания, когда алфавиты на входе канала и выходе демодулятора (1-ое решающее устроство) совпадают, в канале со стиранием алфавит на выходе демодулятора имеет дополнительный символ стирания, который формируется в том случае, если демодулятор не может с заданной надёжностью опознать переданный символ.
Ошибки в симметричных каналах без памяти независимые и определяются вероятностью ошибки p, примером такого канала является биномиальный канал. В каналах с памятью ошибки пакетируются (группируются), примером такого канала является марковскиий канал.
Прежде всего вспомним, что под помехоустойчивостью систем связи понимают способность её противостоять вредному влиянию помех или, другими словами, это способность системы связи функционировать с заданным (требуемым) качеством в условиях воздействия помех.
При передаче дискретных сообщений воздействие помех на передаваемый сигнал в линии связи будет сопровождаться искажением принимаемого сигнала (по сравнению с передаваемым) и возникновением ошибок в принимаемой дискретной последовательности. Количественной мерой достоверности (мерой качества) передачи дискретных сообщений является вероятность ошибки в принимаемой последовательности.
Из теории помехоустойчивости известно, что вероятность ошибки на приеме зависит от отношения сигнал/шум на входе решающего устройства приемника:
- при неоптимальном приеме — это отношение средней мощности сигнала Pс к средней мощности помехи Pп , тогда
h2 = Pс / Pп ; (1.1)
при этом Pс определяется его амплитудой Um и для гармонического сигнала Pс = U2m /2, а Pп = N0 * fпр , N0 — спектральная плотность мощности помехи (типа белого шума), fпр — полоса пропускания канала связи;
- при оптимальном приеме — это отношение энергии элемента сигнала Eс к спектральной плотности мощности помехи N0, тогда
h20 = Eс / N0 = Pс T/ N0 = U2m T /2 N0 . (1.2)
Эти соотношения указывают энергетический путь повышения достоверности передачи информации, а именно: либо увеличением амплитуды сигнала Um, либо увеличением длительности элемента сигнала T, но за счет уменьшения скорости передачи сообщений (модуляции) V = 1/T. В ряде случаев такой путь оказывается неприемлемым, например, в каналах с принципиально ограниченной энергетикой (гидроакустические, спутниковые каналы связи), в каналах с замираниями и др.
Практика создания систем связи различного назначения показала, что эффективным методом повышения достоверности передачи информации дискретными сообщениями является использование помехоустойчивых (корректирующих) кодов [8]. Помехоустойчивое кодирование основано на введении в передаваемую последовательность двоичных символов 1 и 0 специально организованной избыточности, предназначенной для обнаружения и исправления ошибок на приеме перед выдачей сообщения получателю.
- Принцип обнаружения и исправления ошибок
корректирующими кодами
1.2.1 Коды с обнаружением и исправлением ошибок
Прежде, чем начать рассмотрение специальных корректирующих кодов, следует отметить, что любой код способен обнаруживать и исправлять ошибки, если не все кодовые слова (кодовые комбинации) этого кода используются для передачи сообщений [9,10]. Нагляднее рассмотреть это на примере блочных кодов, у которых последовательность символов на выходе источника разбивается на блоки (кодовые слова, кодовые комбинации), содержащие одинаковое число символов k. При этом для двоичного кода ансамбль сообщений будет иметь объем Nр=2k. При помехоустойчивом кодировании это множество из Nр сообщений отображается на множество N = 2n возможных кодовых слов, такая процедура и называется помехоустойчивым кодированием дискретных сообщений (число n – число символов в кодовом слове после кодирования, иногда его называют длиной кодовых слов или значностью кода).
В общем случае для блочного равномерного кода с основанием код имеет
возможных кодовых слов. Используемые для передачи сообщений кодовые слова из множества
называют разрешенными, остальные кодовые слова из множества
не используются и называются запрещенными (неразрешенными для передачи).
Сущность обнаружения ошибок схематично поясняется на рисунке 1.3, а. Если в результате искажений в канале связи переданное (разрешенное) кодовое слово Ai (i= 1,2, … Nр) превращается в одно из запрещённых Bj (j= 1,2, … Nз), то ошибка обнаруживается, так как такое слово не могло быть передано. Ошибка не обнаруживается только в том случае, когда очередное передаваемое кодовое слово превращается в другое разрешенное, например Aj, которое также могло быть передано.
Рисунок 1.3 Обнаружение и исправление ошибок
Исправление ошибок представляет собой более сложную операцию, так как кроме обнаружения наличия ошибки в принятом кодовом слове необходимо определить и местоположение искаженного кодового символа (а если , то и характер искажения). Для того чтобы рассматриваемый код исправлял ошибки, необходимо часть или всё множество
запрещённых кодовых слов разбить на Nр непересекающихся подмножеств
(i) (i= 1,2, … Nр) по количеству разрешенных кодовых слов. Каждое из подмножеств
(i) в декодере приемника приписывается одному из разрешенных кодовых слов (рисунок 1.3, б).
Способ приема заключается в том, что если принятое кодовое слово принадлежит подмножеству (i), считается переданным
—е разрешенное кодовое слово. Ошибка не может быть исправлена (исправляется неверно), если переданное кодовое слово
в результате искажений превращается в кодовое слово любого другого подмножества
(j), (j i). На рисунке 1.3, б ошибка в запрещенном кодовом слове B1j будет исправлена, так как это слово принадлежит подмножеству
(1), приписанному к переданному разрешенному слову A1; ошибка в кодовых словах B2j или B4j не будет исправлена, так как эти слова относятся к подмножествам, приписанным к другим разрешённым кодовым словам.
Если принятое кодовое слово попадает в подмножество запрещенных слов, не принадлежащих ни к одному из подмножеств (i) (i= 1,2, … Nр), то ошибка только обнаруживается, но не исправляется. Этот признак может быть использован для исправления ошибки другими методами, например, методом переспроса.
Свойства кода по обнаружению и исправлению ошибок характеризуются количественно коэффициентами обнаружения Kоб и исправления ошибок Kис, которые показывают, во сколько раз уменьшается вероятность ошибки после декодирования по сравнению с её величиной на входе приемного устройства (декодера), благодаря обнаружению ошибок или их исправлению соответственно. Ошибки в кодовых словах могут иметь произвольную конфигурацию, что определяется случайным характером помех в канале связи.
Число ошибочных символов в принятом кодовом слове называется кратностью ошибки t, при длине кодового слова из n символов она изменяется в пределах от 0 до n.
Если это вероятность ошибки кратности t 1 в n разрядном кодовом слове на входе декодера, а Pоб — вероятность обнаружения ошибок в декодере, то коэффициент обнаружения определяется следующим выражением
. (1.3)
Коэффициент исправления ошибок будет определяться выражением
, (1.4)
где Pис — вероятность исправления ошибок в декодере.
Последняя численно равна вероятности ошибок в кодовом слове, кратность которых не превышает величины кратности гарантированно исправляемых ошибок tис, то есть Pис = Pвх( tис, n).
Коэффициент исправления кода всегда меньше коэффициента обнаружения, что является общим условием для любых корректирующих кодов.
Для реализации потенциальных возможностей кода, исправляющего ошибки, необходимо учитывать статистический характер ошибок в реальных каналах связи, в которых предполагается применение этого кода. Разбиение неразрешенных комбинаций на подмножества (i) должно выполняться таким образом, чтобы исправлялись ошибки, появление которых наиболее вероятно в данном канале связи.
В общем случае передаваемая кодовая комбинация искажается случайным образом, что определяется случайным характером помех в канале связи. В реальных системах связи при многообразии характера действующих в линии связи помех распределение кратностей ошибок в дискретном канале связи может быть самым различным. Поэтому построению декодера, исправляющего ошибки, должно предшествовать изучение статистических свойств канала связи. В качестве примера, на рисунке 1.4 приведены кривые распределения кратностей ошибок Pn(t) для двух случаев: для двоичного канала с независимыми ошибками в кодовых символах p – кривая 1 (биномиальное распределение)
Pn(t) = Cnt pt(1- p)n-t (1.5)
и кривая 2 для канала, в котором передаваемое кодовое слово с одинаковой вероятностью может превратиться в другое кодовое слово данного кода (из множества N )
Pn(t) = Cnt /mn . (1.6)
Графики соответствуют длине кодового слова .
Рисунок 1.4 Распределение кратностей ошибок
Для приведенных на рисунке 1.3 распределений кратностей ошибок определим величины коэффициентов исправления для корректирующего кода с параметрами: ,
(
),
, исправляющего одиночные ошибки:
.
Вероятность ошибки в передаваемом кодовом слове в канале с распределением кратностей ошибок Pn(t), соответствующим кривой 1(рисунок 1.4), и вероятностью искажения символа кода p = 0,1 равна
Вероятность исправления ошибки (вероятность ошибки с кратностью t =1):
.
Тогда
В канале связи с распределением кратностей ошибок Pn(t), соответствующим кривой 2 (рисунок 1.4), вероятность исправления ошибки (вероятность ошибки с кратностью t =1) равна
где — доля ошибок, кратность которых
ис из общего числа возможных ошибок mn. Тогда коэффициент исправления равен
Таким образом, один и тот же код в первом случае исправляет примерно в четыре раза больше ошибок, чем во втором. Это объясняется тем, что в первом случае наибольшее количество ошибок имеет кратность t =1 и исправляется данным кодом, у которого каждому разрешенному кодовому слову приписывается подмножество ближайших неразрешенных слов, а во втором случае наибольшее количество ошибок имеет кратность t >1, которые не исправляются данным кодом.
Очевидно, что, если в канале связи преобладают ошибки большой кратности, целесообразно к разрешенным кодовым словам приписывать подмножество таких неразрешенных слов, которые удалены от данного разрешенного на расстояние, соответствующее этим ошибкам.
1.2.2 Кодовое расстояние, избыточность кода
Обнаруживающая и исправляющая способность корректирующих кодов тесно связана с расстояниями между разрешенными кодовыми словами. Расстояние между любой парой кодовых слов и
выражает различие между ними
, (1.7)
где ,
— координаты кодовых слов
,
в
-мерном неевклидовом пространстве Ln.
Если код является двоичным, под расстоянием между парой кодовых слов понимается количество символов, в которых они отличаются между собой. Оно определяется сложением двух этих слов по модулю 2 и равно числу единиц в этой сумме. Например:
Знак означает сумму по модулю 2 (сложение по модулю два выполняется по правилу:
,
,
,
).
Напомним, что геометрической моделью -значного двоичного кода является
-мерный куб с ребром, равным единице, каждая вершина которого представляет одно из возможных кодовых слов. Расстояние между словами dij равно числу ребер куба, отделяющих одну вершину от другой. Наименьшее расстояние между любой парой разрешенных слов данного кода называется кодовым расстоянием d = min dij. (1.8)
Так как кратность ошибки в геометрическом представлении является расстоянием между переданной комбинацией и искаженной, то для обнаружения ошибок кратности tоб требуется кодовое расстояние, равное
. (1.9)
Для исправления ошибок кратности tис требуется кодовое расстояние
. (1.10)
Это означает, что для исправления ошибок искаженное кодовое слово должно располагаться ближе всего к соответствующему правильному слову.
Для исправления стираний кратности tст требуется кодовое расстояние
, (1.11)
то есть для исправления стираний требуется такое же кодовое расстояние, как и для обнаружения ошибок.
Способность корректирующих кодов обнаруживать и исправлять ошибки (или стирания) определяется передачей дополнительной (избыточной) информации по каналу связи. Коэффициент избыточности в соответствии с теорией информации, как известно, равен
(1.12)
где — число избыточных кодовых символов в слове (
+
=
).
Для каналов с независимыми ошибками вероятность приёма кодового слова с ошибками определяется очевидным выражением вида
, (1.13)
а вероятность обнаружения ошибки в принятом кодовом слове при декодировании равна
=
. (1.14)
Тогда вероятность необнаружения ошибки при декодировании соответственно равна =
, то есть
=
. (1.15)
Тогда коэффициент обнаружения можно определить следующим образом
. (1.16)
В настоящее время известно большое число корректирующих кодов, отличающихся по помехоустойчивости и способам построения. Применение некоторых из них ограничивается сложностью технической реализации кодирующих и декодирующих устройств.
На рисунке 1.5 приведена классификация наиболее часто используемых корректирующих кодов, в которой отмечаются только семейства кодов без подробной детализации.
Применение корректирующих (помехоустойчивых) кодов является эффективным средством борьбы с ошибками в каналах связи с помехами. Такие коды используются либо только для обнаружения ошибок, либо для обнаружения и исправления ошибок (или ошибок и стираний в каналах со стиранием).
1.2.3 Энергетический выигрыш кода
В заключение рассмотрим энергетический выигрыш от помехоустойчивого кодирования для случая известных (заданных) параметров канала связи и кода. Вероятность ошибки на выходе дискретного канала связи pвых (или вероятность ошибки декодирования pд) является функцией отношения сигнал/шум и качества используемого корректирующего кода. “Выигрыш от кодирования” или “энергетический выигрыш” (ЭВК в дБ), который указывает на улучшение качества системы связи от использования данного способа кодирования или метода защиты от ошибок, определяется выражением

где h12, h22 — отношения сигнал/шум в первой и второй сравниваемых
системах связи при одинаковой вероятности ошибок на выходе;
a — коэффициент, выравнивающий скорость передачи информации
в сравниваемых системах.
Например, если первая система является системой без помехоустойчивого кодирования, а вторая система — с обнаружением ошибок и переспросом, то а = (n/k)×Tср /T; здесь Тср — средняя длительность передачи кодового слова (или символа длительности T ) в системе с переспросом. Для системы c кодом, исправляющим ошибки без переспроса, a=n/k.
Если снять ограничения на длину кодового слова и полосу частот, занимаемую системой связи, то предельный выигрыш от помехоустойчивого кодирования при данной вероятности ошибки в канале связи с гауссовским шумом будет равен [9]

На рисунке 1.6 приведены, для примера, кривые предельных значений ЭВК от кодирования при когерентном и некогерентном приеме сигналов
дискретной частотной модуляции (ЧМ) в зависимости от вероятности ошибки
в дискретном канале связи.
Рисунок 1.6 Предельные значения ЭВК от кодирования при ЧМ
В реальных системах связи длина кода и занимаемая полоса частот ограничены, для этих условий может быть определен асимптотический выигрыш для данного кода. Он зависит только от скорости кода k/n и кодового расстояния.
Для каналов с жёстким решением (на выходе демодулятора двоичныесимволы 1 и 0)
(1.19)
для каналов с мягким решением (на выходе демодулятора многоуровневый сигнал)
(1.20)
Такой выигрыш достигается, когда E/No ®µ. Из этих соотношений видно, что мягкие решения обеспечивают дополнительный выигрыш не более 3 дБ (при E/No ®µ) и существенно меньше при реальных значениях отношения сигнал/шум.
| Обноружение ошибок | ||||
| Исправление ошибок | ||||
| Коррекция ошибок | ||||
| Назад | ||||
Методы обнаружения ошибок
В обычном равномерном непомехоустойчивом коде число разрядов n в кодовых
комбинациях определяется числом сообщений и основанием кода.
Коды, у которых все кодовые комбинации разрешены, называются простыми или
равнодоступными и являются полностью безызбыточными. Безызбыточные коды обладают
большой «чувствительностью» к помехам. Внесение избыточности при использовании
помехоустойчивых кодов связано с увеличением n – числа разрядов кодовой комбинации. Таким
образом, все множество

подмножество разрешенных комбинаций, обладающих определенными признаками, и
подмножество запрещенных комбинаций, этими признаками не обладающих.
Помехоустойчивый код отличается от обычного кода тем, что в канал передаются не все
кодовые комбинации N, которые можно сформировать из имеющегося числа разрядов n, а только
их часть Nk , которая составляет подмножество разрешенных комбинаций. Если при приеме
выясняется, что кодовая комбинация принадлежит к запрещенным, то это свидетельствует о
наличии ошибок в комбинации, т.е. таким образом решается задача обнаружения ошибок. При
этом принятая комбинация не декодируется (не принимается решение о переданном
сообщении). В связи с этим помехоустойчивые коды называют корректирующими кодами.
Корректирующие свойства избыточных кодов зависят от правила их построения, определяющего
структуру кода, и параметров кода (длительности символов, числа разрядов, избыточности и т. п.).
Первые работы по корректирующим кодам принадлежат Хеммингу, который ввел понятие
минимального кодового расстояния dmin и предложил код, позволяющий однозначно указать ту
позицию в кодовой комбинации, где произошла ошибка. К информационным элементам k в коде
Хемминга добавляется m проверочных элементов для автоматического определения
местоположения ошибочного символа. Таким образом, общая длина кодовой комбинации
составляет: n = k + m.
Метричное представление n,k-кодов
В настоящее время наибольшее внимание с точки зрения технических приложений
уделяется двоичным блочным корректирующим кодам. При использовании блочных кодов
цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной
длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга.
Почти все блочные коды относятся к разделимым кодам, кодовые комбинации которых
состоят из двух частей: информационной и проверочной. При общем числе n символов в блоке
число информационных символов равно k, а число проверочных символов:
К основным характеристикам корректирующих кодов относятся:
|
— число разрешенных и запрещенных кодовых комбинаций; |
Для блочных двоичных кодов, с числом символов в блоках, равным n, общее число
возможных кодовых комбинаций определяется значением
Число разрешенных кодовых комбинаций при наличии k информационных разрядов в
первичном коде:
Очевидно, что число запрещенных комбинаций:
а с учетом отношение будет
где m – число избыточных (проверочных) разрядов в блочном коде.
Избыточностью корректирующего кода называют величину
откуда следует:
Эта величина показывает, какую часть общего числа символов кодовой комбинации
составляют информационные символы. В теории кодирования величину Bk называют
относительной скоростью кода. Если производительность источника информации равна H
символов в секунду, то скорость передачи после кодирования этой информации будет
поскольку в закодированной последовательности из каждых n символов только k символов
являются информационными.
Если число ошибок, которые нужно обнаружить или исправить, значительно, то необходимо
иметь код с большим числом проверочных символов. Чтобы при этом скорость передачи
оставалась достаточно высокой, необходимо в каждом кодовом блоке одновременно
увеличивать как общее число символов, так и число информационных символов.
При этом длительность кодовых блоков будет существенно возрастать, что приведет к
задержке информации при передаче и приеме. Чем сложнее кодирование, тем длительнее
временная задержка информации.
Минимальное кодовое расстояние – dmin. Для того чтобы можно было обнаружить и
исправлять ошибки, разрешенная комбинация должна как можно больше отличаться от
запрещенной. Если ошибки в канале связи действуют независимо, то вероятность преобразования
одной кодовой комбинации в другую будет тем меньше, чем большим числом символов они
различаются.
Если интерпретировать кодовые комбинации как точки в пространстве, то отличие
выражается в близости этих точек, т. е. в расстоянии между ними.
Количество разрядов (символов), которыми отличаются две кодовые комбинации, можно
принять за кодовое расстояние между ними. Для определения этого расстояния нужно сложить
две кодовые комбинации «по модулю 2» и подсчитать число единиц в полученной сумме.
Например, две кодовые комбинации xi = 01011 и xj = 10010 имеют расстояние d(xi,xj) , равное 3,
так как:
Здесь под операцией ⊕ понимается сложение «по модулю 2».
Заметим, что кодовое расстояние d(xi,x0) между комбинацией xi и нулевой x0 = 00…0
называют весом W комбинации xi, т.е. вес xi равен числу «1» в ней.
Расстояние между различными комбинациями некоторого конкретного кода могут
существенно отличаться. Так, в частности, в безызбыточном первичном натуральном коде n = k это
расстояние для различных комбинаций может изменяться от единицы до величины n, равной
разрядности кода. Особую важность для характеристики корректирующих свойств кода имеет
минимальное кодовое расстояние dmin, определяемое при попарном сравнении всех кодовых
комбинаций, которое называют расстоянием Хемминга.
В безызбыточном коде все комбинации являются разрешенными и его минимальное
кодовое расстояние равно единице – dmin=1. Поэтому достаточно исказиться одному символу,
чтобы вместо переданной комбинации была принята другая разрешенная комбинация. Чтобы код
обладал корректирующими свойствами, необходимо ввести в него некоторую избыточность,
которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными
комбинациями не менее двух – dmin ≥ 2..
Минимальное кодовое расстояние является важнейшей характеристикой помехоустойчивых
кодов, указывающей на гарантируемое число обнаруживаемых или исправляемых заданным
кодом ошибок.
Число обнаруживаемых или исправляемых ошибок
При применении двоичных кодов учитывают только дискретные искажения, при которых
единица переходит в нуль («1» → «0») или нуль переходит в единицу («0» → «1»). Переход «1» →
«0» или «0» → «1» только в одном элементе кодовой комбинации называют единичной ошибкой
(единичным искажением). В общем случае под кратностью ошибки подразумевают число
позиций кодовой комбинации, на которых под действием помехи одни символы оказались
замененными на другие. Возможны двукратные (g = 2) и многократные (g > 2) искажения
элементов в кодовой комбинации в пределах 0 ≤ g ≤ n.
Минимальное кодовое расстояние является основным параметром, характеризующим
корректирующие способности данного кода. Если код используется только для обнаружения
ошибок кратностью g0, то необходимо и достаточно, чтобы минимальное кодовое расстояние
было равно dmin ≥ g0 + 1.
В этом случае никакая комбинация из go ошибок не может перевести одну разрешенную
кодовую комбинацию в другую разрешенную. Таким образом, условие обнаружения всех ошибок
кратностью g0 можно записать
Чтобы можно было исправить все ошибки кратностью gu и менее, необходимо иметь
минимальное расстояние, удовлетворяющее условию dmin ≥ 2gu
В этом случае любая кодовая комбинация с числом ошибок gu отличается от каждой
разрешенной комбинации не менее чем в gu+1 позициях. Если условие не выполнено,
возможен случай, когда ошибки кратности g исказят переданную комбинацию так, что она станет
ближе к одной из разрешенных комбинаций, чем к переданной или даже перейдет в другую
разрешенную комбинацию. В соответствии с этим, условие исправления всех ошибок кратностью
не более gи можно записать:
Из и
следует, что если код исправляет все ошибки кратностью gu, то число
ошибок, которые он может обнаружить, равно go = 2gu. Следует отметить, что эти соотношения
устанавливают лишь гарантированное минимальное число обнаруживаемых или
исправляемых ошибок при заданном dmin и не ограничивают возможность обнаружения ошибок
большей кратности. Например, простейший код с проверкой на четность с dmin = 2 позволяет
обнаруживать не только одиночные ошибки, но и любое нечетное число ошибок в пределах go < n.
Корректирующие возможности кодов
Вопрос о минимально необходимой избыточности, при которой код обладает нужными
корректирующими свойствами, является одним из важнейших в теории кодирования. Этот вопрос
до сих пор не получил полного решения. В настоящее время получен лишь ряд верхних и нижних
оценок (границ), которые устанавливают связь между максимально возможным минимальным
расстоянием корректирующего кода и его избыточностью.
Коды Хэмминга
Построение кодов Хемминга базируется на принципе проверки на четность веса W (числа
единичных символов «1») в информационной группе кодового блока.
Поясним идею проверки на четность на примере простейшего корректирующего кода,
который так и называется кодом с проверкой на четность или кодом с проверкой по паритету
(равенству).
В таком коде к кодовым комбинациям безызбыточного первичного двоичного k-разрядного
кода добавляется один дополнительный разряд (символ проверки на четность, называемый
проверочным, или контрольным). Если число символов «1» исходной кодовой комбинации
четное, то в дополнительном разряде формируют контрольный символ «0», а если число
символов «1» нечетное, то в дополнительном разряде формируют символ «1». В результате
общее число символов «1» в любой передаваемой кодовой комбинации всегда будет четным.
Таким образом, правило формирования проверочного символа сводится к следующему:
где i – соответствующий информационный символ («0» или «1»); k – общее их число а, под
операцией ⊕ здесь и далее понимается сложение «по модулю 2». Очевидно, что добавление
дополнительного разряда увеличивает общее число возможных комбинаций вдвое по сравнению
с числом комбинаций исходного первичного кода, а условие четности разделяет все комбинации
на разрешенные и неразрешенные. Код с проверкой на четность позволяет обнаруживать
одиночную ошибку при приеме кодовой комбинации, так как такая ошибка нарушает условие
четности, переводя разрешенную комбинацию в запрещенную.
Критерием правильности принятой комбинации является равенство нулю результата S
суммирования «по модулю 2» всех n символов кода, включая проверочный символ m1. При
наличии одиночной ошибки S принимает значение 1:
— ошибок нет,
— однократная ошибка
Этот код является (k+1,k)-кодом, или (n,n–1)-кодом. Минимальное расстояние кода равно
двум (dmin = 2), и, следовательно, никакие ошибки не могут быть исправлены. Простой код с
проверкой на четность может использоваться только для обнаружения (но не исправления)
однократных ошибок.
Увеличивая число дополнительных проверочных разрядов, и формируя по определенным
правилам проверочные символы m, равные «0» или «1», можно усилить корректирующие
свойства кода так, чтобы он позволял не только обнаруживать, но и исправлять ошибки. На этом и
основано построение кодов Хемминга.
Коды Хемминга позволяют исправлять одиночную ошибку, с помощью непосредственного
описания. Для каждого числа проверочных символов m =3, 4, 5… существует классический код
Хемминга с маркировкой
т.е. (7,4), (15,11) (31,26) …
При других значениях числа информационных символов k получаются так называемые
усеченные (укороченные) коды Хемминга. Так для кода имеющего 5 информационных символов,
потребуется использование корректирующего кода (9,5), являющегося усеченным от
классического кода Хемминга (15,11), так как число символов в этом коде уменьшается
(укорачивается) на 6.
Для примера рассмотрим классический код Хемминга (7,4), который можно сформировать и
описать с помощью кодера, представленного на рис. 1 В простейшем варианте при заданных
четырех информационных символах: i1, i2, i3, i4 (k = 4), будем полагать, что они сгруппированы в
начале кодового слова, хотя это и не обязательно. Дополним эти информационные символы
тремя проверочными символами (m = 3), задавая их следующими равенствами проверки на
четность, которые определяются соответствующими алгоритмами, где знак ⊕ означает
сложение «по модулю 2»: r1 = i1 ⊕ i2 ⊕ i3, r2 = i2 ⊕ i3 ⊕ i4, r3 = i1 ⊕ i2 ⊕ i4.
В соответствии с этим алгоритмом определения значений проверочных символов mi, в табл.
1 выписаны все возможные 16 кодовых слов (7,4)-кода Хемминга.
Таблица 1 Кодовые слова (7,4)-кода Хэмминга
|
k=4 |
m=4 |
|
i1 i2 i3 i4 |
r1 r2 r3 |
|
0 0 0 0 |
0 0 0 |
|
0 0 0 1 |
0 1 1 |
|
0 0 1 0 |
1 1 0 |
|
0 0 1 1 |
1 0 1 |
|
0 1 0 0 |
1 1 1 |
|
0 1 0 1 |
1 0 0 |
|
0 1 1 0 |
0 0 1 |
|
0 1 1 1 |
0 1 0 |
|
1 0 0 0 |
1 0 1 |
|
1 0 0 1 |
1 0 0 |
|
1 0 1 0 |
0 1 1 |
|
1 0 1 1 |
0 0 0 |
|
1 1 0 0 |
0 1 0 |
|
1 1 0 1 |
0 0 1 |
|
1 1 1 0 |
1 0 0 |
|
1 1 1 1 |
1 1 1 |
На рис.1 приведена блок-схема кодера – устройства автоматически кодирующего
информационные разряды в кодовые комбинации в соответствии с табл.1

Рис. 1 Кодер для (7,4)-кода Хемминга
На рис. 1.4 приведена схема декодера для (7,4) – кода Хемминга, на вход которого
поступает кодовое слово
. Апостроф означает, что любой символ слова может
быть искажен помехой в телекоммуникационном канале.
В декодере в режиме исправления ошибок строится последовательность:
Трехсимвольная последовательность (s1, s2, s3) называется синдромом. Термин «синдром»
используется и в медицине, где он обозначает сочетание признаков, характерных для
определенного заболевания. В данном случае синдром S = (s1, s2, s3) представляет собой
сочетание результатов проверки на четность соответствующих символов кодовой группы и
характеризует определенную конфигурацию ошибок (шумовой вектор).
Число возможных синдромов определяется выражением:
При числе проверочных символов m =3 имеется восемь возможных синдромов (23 = 
Нулевой синдром (000) указывает на то, что ошибки при приеме отсутствуют или не обнаружены.
Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и
исправляется. Классические коды Хемминга имеют число синдромов, точно равное их
необходимому числу (что позволяет исправить все однократные ошибки в любом информативном
и проверочном символах) и включают один нулевой синдром. Такие коды называются
плотноупакованными.
Усеченные коды являются неплотноупакованными, так как число синдромов у них
превышает необходимое. Так, в коде (9,5) при четырех проверочных символах число синдромов
будет равно 24 =16, в то время как необходимо всего 10. Лишние 6 синдромов свидетельствуют о
неполной упаковке кода (9,5).

Рис. 2 Декодер для (7, 4)-кода Хемминга
Для рассматриваемого кода (7,4) в табл. 2 представлены ненулевые синдромы и
соответствующие конфигурации ошибок.
Таблица 2 Синдромы (7, 4)-кода Хемминга
|
Синдром |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
Конфигурация ошибок |
0000001 |
0000010 |
0000100 |
0001000 |
0010000 |
0100000 |
1000000 |
|
Ошибка в символе |
m1 |
m2 |
i4 |
m1 |
i1 |
i3 |
i2 |
Таким образом, (7,4)-код позволяет исправить все одиночные ошибки. Простая проверка
показывает, что каждая из ошибок имеет свой единственный синдром. При этом возможно
создание такого цифрового корректора ошибок (дешифратора синдрома), который по
соответствующему синдрому исправляет соответствующий символ в принятой кодовой группе.
После внесения исправления проверочные символы ri можно на выход декодера (рис. 2) не
выводить. Две или более ошибок превышают возможности корректирующего кода Хемминга, и
декодер будет ошибаться. Это означает, что он будет вносить неправильные исправления и
выдавать искаженные информационные символы.
Идея построения подобного корректирующего кода, естественно, не меняется при
перестановке позиций символов в кодовых словах. Все такие варианты также называются (7,4)-
кодами Хемминга.
Циклические коды
Своим названием эти коды обязаны такому факту, что для них часть комбинаций, либо все
комбинации могут быть получены путем циклическою сдвига одной или нескольких базовых
комбинаций кода.
Построение такого кода основывается на использовании неприводимых многочленов в поле
двоичных чисел. Такие многочлены не могут быть представлены в виде произведения
многочленов низших степеней подобно тому, как простые числа не могут быть представлены
произведением других чисел. Они делятся без остатка только на себя или на единицу.
Для определения неприводимых многочленов раскладывают на простые множители бином
хn -1. Так, для n = 7 это разложение имеет вид:
(x7)=(x-1)(x3+x2)(x3+x-1)
Каждый из полученных множителей разложения может применяться для построения
корректирующего кода.
Неприводимый полином g(x) называют задающим, образующим или порождающим
для корректирующего кода. Длина n (число разрядов) создаваемого кода произвольна.
Кодовая последовательность (комбинация) корректирующего кода состоит из к информационных
разрядов и n — к контрольных (проверочных) разрядов. Степень порождающего полинома
r = n — к равна количеству неинформационных контрольных разрядов.
Если из сделанного выше разложения (при n = 7) взять полипом (х — 1), для которого
r=1, то k=n-r=7-1=6. Соответствующий этому полиному код используется для контроля
на чет/нечет (обнаружение ошибок). Для него минимальное кодовое расстояние D0 = 2
(одна единица от D0 — для исходного двоичного кода, вторая единица — за счет контрольного разряда).
Если же взять полином (x3+x2+1) из указанного разложения, то степень полинома
r=3, а k=n-r=7-3=4.
Контрольным разрядам в комбинации для некоторого кода могут быть четко определено место (номера разрядов).
Тогда код называют систематическим или разделимым. В противном случае код является неразделимым.
Способы построения циклических кодов по заданному полиному.
1) На основе порождающей (задающей) матрицы G, которая имеет n столбцов, k строк, то есть параметры которой
связаны с параметрами комбинаций кода. Порождающую матрицу строят, взяв в качестве ее строк порождающий
полином g(x) и (k — 1) его циклических сдвигов:

Пример; Определить порождающую матрицу, если известно, что n=7, k=4, задающий полином g(x)=x3+х+1.
Решение: Кодовая комбинация, соответствующая задающему полиному g(x)=x3+х+1, имеет вид 1011.
Тогда порождающая матрица G7,4 для кода при n=7, к=4 с учетом того, что k-1=3, имеет вид:

Порождающая матрица содержит k разрешенных кодовых комбинаций. Остальные комбинации кода,
количество которых (2k — k) можно определить суммированием по модулю 2 всевозможных сочетаний
строк матрицы Gn,k. Для матрицы, полученной в приведенном выше примере, суммирование по модулю 2
четырех строк 1-2, 1-3, 1-4, 2-3, 2-4, 3-4 дает следующие кодовые комбинации циклического кода:
001110101001111010011011101010011101110100
Другие комбинации искомого корректирующего кода могут быть получены сложением трех комбинаций, например,
из сочетания строк 1-3-4, что дает комбинацию 1111111, а также сложением четырех строк 1-2-3-4, что
дает комбинацию 1101001 и т.д.
Ряд комбинаций искомого кода может быть получено путем дальнейшего циклического сдвига комбинаций
порождающей матрицы, например, 0110001, 1100010, 1000101. Всего для образования искомого циклического
кода требуется 2k=24=16 комбинаций.
2) Умножение исходных двоичных кодовых комбинаций на задающий полином.
Исходными комбинациями являются все k-разрядные двоичные комбинации. Так, например, для исходной
комбинации 1111 (при k = 4) умножение ее на задающий полином g(x)=x3+х+1=1011 дает 1101001.
Полученные на основе двух рассмотренных способов циклические коды не являются разделимыми.
3) Деление на задающий полином.
Для получения разделимого (систематического) циклического кода необходимо разделить многочлен
xn-k*h(x), где h(x) — исходная двоичная комбинация, на задающий полином g(x) и прибавить полученный
остаток от деления к многочлену xn-k*h(x).
Заметим, что умножение исходной комбинации h(x) на xn-k эквивалентно сдвигу h(x) на (n-к) разрядов влево.
Пример: Требуется определить комбинации циклического разделимого кода, заданного полиномом g(x)=x3+х+1=1011 и
имеющего общее число разрядов 7, число информационных разрядов 4, число контрольных разрядов (n-k)=3.
Решение: Пусть исходная комбинация h(x)=1100. Умножение ее на xn-k=x3=1000 дает
x3*(x3+x2)=1100000, то есть эквивалентно
сдвигу исходной комбинации на 3 разряда влево. Деление комбинации 1100000 на комбинацию 1011, эквивалентно задающему полиному, дает:

Полученный остаток от деления, содержащий xn-k=3 разряда, прибавляем к полиному, в результате чего получаем искомую комбинацию
разделимого циклического кода: 1100010. В ней 4 старших разряда (слева) соответствуют исходной двоичной комбинации, а три младших
разряда являются контрольными.
Следует сделать ряд указаний относительно процедуры деления:
1) При делении задающий полином совмещается старшим разрядом со старшим «единичными разрядом делимого.
2) Вместо вычитания по модулю 2 выполняется эквивалентная ему процедура сложения по модулю 2.
3) Деление продолжается до тех пор, пока степень очередного остатка не будет меньше степени делителя (задающего полинома). При достижении
этого полученный остаток соответствует искомому содержанию контрольных разрядов для данной искомой двоичной комбинации.
Для проверки правильности выполнения процедуры определения комбинации циклического кода необходимо разделить полученную комб1шацию на задающий полином с
учетом сделанных выше замечаний. Получение нулевого остатка от такого деления свидетельствует о правильности определения комбинации.
Логический код 4В/5В
Логический код 4В/5В заменяет исходные символы длиной в 4 бита на символы длиной в 5 бит. Так как результирующие символы содержат избыточные биты, то
общее количество битовых комбинаций в них больше, чем в исходных. Таким образом, пяти-битовая схема дает 32 (25) двухразрядных буквенно-цифровых символа,
имеющих значение в десятичном коде от 00 до 31. В то время как исходные данные могут содержать только четыре бита или 16 (24) символов.
Поэтому в результирующем коде можно подобрать 16 таких комбинаций, которые не содержат большого количества нулей, а остальные считать запрещенными кодами
(code violation). В этом случае длинные последовательности нулей прерываются, и код становится самосинхронизирующимся для любых передаваемых данных.
Исчезает также постоянная составляющая, а значит, еще более сужается спектр сигнала. Но этот метод снижает полезную пропускную способность линии,
так как избыточные единицы пользовательской информации не несут, и только «занимают эфирное время». Избыточные коды позволяют приемнику распознавать
искаженные биты. Если приемник принимает запрещенный код, значит, на линии произошло искажение сигнала.
Итак, рассмотрим работу логического кода 4В/5В. Преобразованный сигнал имеет 16 значений для передачи информации и 16 избыточных значений. В декодере
приемника пять битов расшифровываются как информационные и служебные сигналы.
Для служебных сигналов отведены девять символов, семь символов — исключены.
Исключены комбинации, имеющие более трех нулей (01 — 00001, 02 — 00010, 03 — 00011, 08 — 01000, 16 — 10000). Такие сигналы интерпретируются символом
V и командой приемника VIOLATION — сбой. Команда означает наличие ошибки из-за высокого уровня помех или сбоя передатчика. Единственная
комбинация из пяти нулей (00 — 00000) относится к служебным сигналам, означает символ Q и имеет статус QUIET — отсутствие сигнала в линии.
Такое кодирование данных решает две задачи — синхронизации и улучшения помехоустойчивости. Синхронизация происходит за счет исключения
последовательности более трех нулей, а высокая помехоустойчивость достигается приемником данных на пяти-битовом интервале.
Цена за эти достоинства при таком способе кодирования данных — снижение скорости передачи полезной информации.
К примеру, В результате добавления одного избыточного бита на четыре информационных, эффективность использования полосы
частот в протоколах с кодом MLT-3 и кодированием данных 4B/5B уменьшается соответственно на 25%.
Схема кодирования 4В/5В представлена в таблице.
|
Двоичный код 4В |
Результирующий код 5В |
|
0 0 0 0 |
1 1 1 1 0 |
|
0 0 0 1 |
0 1 0 0 1 |
|
0 0 1 0 |
1 0 1 0 0 |
|
0 0 1 1 |
1 0 1 0 1 |
|
0 1 0 0 |
0 1 0 1 0 |
|
0 1 0 1 |
0 1 0 1 1 |
|
0 1 1 0 |
0 1 1 1 0 |
|
0 1 1 1 |
0 1 1 1 1 |
|
1 0 0 0 |
1 0 0 1 0 |
|
1 0 0 1 |
1 0 0 1 1 |
|
1 0 1 0 |
1 0 1 1 0 |
|
1 0 1 1 |
1 0 1 1 1 |
|
1 1 0 0 |
1 1 0 1 0 |
|
1 1 0 1 |
1 1 0 1 1 |
|
1 1 1 0 |
1 1 1 0 0 |
|
1 1 1 1 |
1 1 1 0 1 |
Итак, соответственно этой таблице формируется код 4В/5В, затем передается по линии с помощью физического кодирования по
одному из методов потенциального кодирования, чувствительному только к длинным последовательностям нулей — например, в помощью
цифрового кода NRZI.
Символы кода 4В/5В длиной 5 бит гарантируют, что при любом их сочетании на линии не могут встретиться более трех нулей подряд.
Буква ^ В в названии кода означает, что элементарный сигнал имеет 2 состояния — от английского binary — двоичный. Имеются
также коды и с тремя состояниями сигнала, например, в коде 8В/6Т для кодирования 8 бит исходной информации используется
код из 6 сигналов, каждый из которых имеет три состояния. Избыточность кода 8В/6Т выше, чем кода 4В/5В, так как на 256
исходных кодов приходится 36=729 результирующих символов.
Как мы говорили, логическое кодирование происходит до физического, следовательно, его осуществляют оборудование канального
уровня сети: сетевые адаптеры и интерфейсные блоки коммутаторов и маршрутизаторов. Поскольку, как вы сами убедились,
использование таблицы перекодировки является очень простой операцией, поэтому метод логического кодирования избыточными
кодами не усложняет функциональные требования к этому оборудованию.
Единственное требование — для обеспечения заданной пропускной способности линии передатчик, использующий избыточный код,
должен работать с повышенной тактовой частотой. Так, для передачи кодов 4В/5В со скоростью 100 Мб/с передатчик должен
работать с тактовой частотой 125 МГц. При этом спектр сигнала на линии расширяется по сравнению со случаем, когда по
линии передается чистый, не избыточный код. Тем не менее, спектр избыточного потенциального кода оказывается уже
спектра манчестерского кода, что оправдывает дополнительный этап логического кодирования, а также работу приемника
и передатчика на повышенной тактовой частоте.
В основном для локальных сетей проще, надежней, качественней, быстрей — использовать логическое кодирование данных
с помощью избыточных кодов, которое устранит длительные последовательности нулей и обеспечит синхронизацию
сигнала, потом на физическом уровне использовать для передачи быстрый цифровой код NRZI, нежели без предварительного
логического кодирования использовать для передачи данных медленный, но самосинхронизирующийся манчестерский код.
Например, для передачи данных по линии с пропускной способностью 100М бит/с и полосой пропускания 100 МГц,
кодом NRZI необходимы частоты 25 — 50 МГц, это без кодирования 4В/5В. А если применить для NRZI еще и
кодирование 4В/5В, то теперь полоса частот расширится от 31,25 до 62,5 МГц. Но тем не менее, этот диапазон
еще «влазит» в полосу пропускания линии. А для манчестерского кода без применения всякого дополнительного
кодирования необходимы частоты от 50 до 100 МГц, и это частоты основного сигнала, но они уже не будут пропускаться
линией на 100 МГц.
Скрэмблирование
Другой метод логического кодирования основан на предварительном «перемешивании» исходной информации таким
образом, чтобы вероятность появления единиц и нулей на линии становилась близкой.
Устройства, или блоки, выполняющие такую операцию, называются скрэмблерами (scramble — свалка, беспорядочная сборка) .
При скремблировании данные перемешиваються по определенному алгоритму и приемник, получив двоичные данные, передает
их на дескрэмблер, который восстанавливает исходную последовательность бит.
Избыточные биты при этом по линии не передаются.
Суть скремблирования заключается просто в побитном изменении проходящего через систему потока данных. Практически
единственной операцией, используемой в скремблерах является XOR — «побитное исключающее ИЛИ», или еще говорят —
сложение по модулю 2. При сложении двух единиц исключающим ИЛИ отбрасывается старшая единица и результат записывается — 0.
Метод скрэмблирования очень прост. Сначала придумывают скрэмблер. Другими словами придумывают по какому соотношению
перемешивать биты в исходной последовательности с помощью «исключающего ИЛИ». Затем согласно этому соотношению из текущей
последовательности бит выбираются значения определенных разрядов и складываются по XOR между собой. При этом все разряды
сдвигаются на 1 бит, а только что полученное значение («0» или «1») помещается в освободившийся самый младший разряд.
Значение, находившееся в самом старшем разряде до сдвига, добавляется в кодирующую последовательность, становясь очередным
ее битом. Затем эта последовательность выдается в линию, где с помощью методов физического кодирования передается к
узлу-получателю, на входе которого эта последовательность дескрэмблируется на основе обратного отношения.
Например, скрэмблер может реализовывать следующее соотношение:
где Bi — двоичная цифра результирующего кода, полученная на i-м такте работы скрэмблера, Ai — двоичная цифра исходного
кода, поступающая на i-м такте на вход скрэмблера, Bi-3 и Bi-5 — двоичные цифры результирующего кода, полученные на
предыдущих тактах работы скрэмблера, соответственно на 3 и на 5 тактов ранее текущего такта, ⊕ — операция исключающего
ИЛИ (сложение по модулю 2).
Теперь давайте, определим закодированную последовательность, например, для такой исходной последовательности 110110000001.
Скрэмблер, определенный выше даст следующий результирующий код:
B1=А1=1 (первые три цифры результирующего кода будут совпадать с исходным, так как еще нет нужных предыдущих цифр)

Таким образом, на выходе скрэмблера появится последовательность 110001101111. В которой нет последовательности из шести нулей, п
рисутствовавшей в исходном коде.
После получения результирующей последовательности приемник передает ее дескрэмблеру, который восстанавливает исходную
последовательность на основании обратного соотношения.
Существуют другие различные алгоритмы скрэмблирования, они отличаются количеством слагаемых, дающих цифру
результирующего кода, и сдвигом между слагаемыми.
Главная проблема кодирования на основе скремблеров — синхронизация передающего (кодирующего) и принимающего
(декодирующего) устройств. При пропуске или ошибочном вставлении хотя бы одного бита вся передаваемая информация
необратимо теряется. Поэтому, в системах кодирования на основе скремблеров очень большое внимание уделяется методам синхронизации.
На практике для этих целей обычно применяется комбинация двух методов:
а) добавление в поток информации синхронизирующих битов, заранее известных приемной стороне, что позволяет ей при ненахождении
такого бита активно начать поиск синхронизации с отправителем,
б) использование высокоточных генераторов временных импульсов, что позволяет в моменты потери синхронизации производить
декодирование принимаемых битов информации «по памяти» без синхронизации.
Существуют и более простые методы борьбы с последовательностями единиц, также относимые к классу скрэмблирования.
Для улучшения кода ^ Bipolar AMI используются два метода, основанные на искусственном искажении последовательности нулей запрещенными символами.

Рис. 3 Коды B8ZS и HDB3
На этом рисунке показано использование метода ^ B8ZS (Bipolar with 8-Zeros Substitution) и метода HDB3 (High-Density Bipolar 3-Zeros) для корректировки
кода AMI. Исходный код состоит из двух длинных последовательностей нулей (8- в первом случае и 5 во втором).
Код B8ZS исправляет только последовательности, состоящие из 8 нулей. Для этого он после первых трех нулей вместо оставшихся пяти нулей вставляет пять
цифр: V-1*-0-V-1*. V здесь обозначает сигнал единицы, запрещенной для данного такта полярности, то есть сигнал, не изменяющий полярность предыдущей
единицы, 1* — сигнал единицы корректной полярности, а знак звездочки отмечает тот факт, что в исходном коде в этом такте была не единица, а ноль. В
результате на 8 тактах приемник наблюдает 2 искажения — очень маловероятно, что это случилось из-за шума на линии или других сбоев передачи. Поэтому
приемник считает такие нарушения кодировкой 8 последовательных нулей и после приема заменяет их на исходные 8 нулей.
Код B8ZS построен так, что его постоянная составляющая равна нулю при любых последовательностях двоичных цифр.
Код HDB3 исправляет любые 4 подряд идущих нуля в исходной последовательности. Правила формирования кода HDB3 более сложные, чем кода B8ZS.
Каждые четыре нуля заменяются четырьмя сигналами, в которых имеется один сигнал V. Для подавления постоянной составляющей полярность сигнала
V чередуется при последовательных заменах.
Кроме того, для замены используются два образца четырехтактовых кодов. Если перед заменой исходный код содержал нечетное число единиц, то
используется последовательность 000V, а если число единиц было четным — последовательность 1*00V.
Таким образом, применение логическое кодирование совместно с потенциальным кодированием дает следующие преимущества:
Улучшенные потенциальные коды обладают достаточно узкой полосой пропускания для любых последовательностей единиц и нулей,
которые встречаются в передаваемых данных. В результате коды, полученные из потенциального путем логического кодирования,
обладают более узким спектром, чем манчестерский, даже при повышенной тактовой частоте.
Линейные блочные коды
При передаче информации по каналам связи возможны ошибки вследствие помех и искажений сигналов. Для обнаружения и
исправления возникающих ошибок используются помехоустойчивые коды. Упрощенная схема системы передачи информации
при помехоустойчивом кодировании показана на рис. 4
Кодер служит для преобразования поступающей от источника сообщений последовательности из k информационных
символов в последовательность из n cимволов кодовых комбинаций (или кодовых слов). Совокупность кодовых слов образует код.
Множество символов, из которых составляется кодовое слово, называется алфавитом кода, а число различных символов в
алфавите – основанием кода. В дальнейшем вследствие их простоты и наибольшего распространения рассматриваются главным
образом двоичные коды, алфавит которых содержит два символа: 0 и 1.

Рис. 4 Система передачи дискретных сообщений
Правило, по которому информационной последовательности сопоставляется кодовое слово, называется правилом кодирования.
Если при кодировании каждый раз формируется блок А из k информационных символов, превращаемый затем в n-символьную
кодовую комбинацию S, то код называется блочным. При другом способе кодирования информационная последовательность на
блоки не разбивается, и код называется непрерывным.
С математической точки зрения кодер осуществляет отображение множества из 2k элементов (двоичных информационных
последовательностей) в множество, состоящее из 2n элементов (двоичных последовательностей длины n). Для практики
интересны такие отображения, в результате которых получаются коды, обладающие способностью исправлять часть ошибок
и допускающие простую техническую реализацию кодирующих и декодирующих устройств.
Дискретный канал связи – это совокупность технических средств вместе со средой распространения радиосигналов, включенных
между кодером и декодером для передачи сигналов, принимающих конечное число разных видов. Для описания реальных каналов
предложено много математических моделей, с разной степенью детализации отражающих реальные процессы. Ограничимся рассмотрением
простейшей модели двоичного канала, входные и выходные сигналы которого могут принимать значения 0 и 1.
Наиболее распространено предположение о действии в канале аддитивной помехи. Пусть S=(s1,s2,…,sn)
и Y=(y1,y2,…,yn) соответственно входная и выходная последовательности двоичных символов.
Помехой или вектором ошибки называется последовательность из n символов E=(e1,e2,…,en), которую
надо поразрядно сложить с переданной последовательностью, чтобы получить принятую:
Y=S+E
Таким образом, компонента вектора ошибки ei=0 указывает на то, что 2-й символ принят правильно (yi=si),
а компонента ei=1 указывает на ошибку при приеме (yi≠si).Поэтому важной характеристикой вектора ошибки
является число q ненулевых компонентов, которое называется весом или кратностью ошибки. Кратность ошибки – дискретная случайная величина,
принимающая целочисленные значения от 0 до n.
Классификация двоичных каналов ведется по виду распределения случайного вектора E. Основные результаты теории кодирования получены в
предположении, что вероятность ошибки в одном символе не зависит ни от его номера в последовательности, ни от его значения. Такой
канал называется стационарным и симметричным. В этом канале передаваемые символы искажаются с одинаковой вероятностью
P, т.е. P(ei=1)=P, i=1,2,…,n.
Для симметричного стационарного канала распределение вероятностей векторов ошибки кратности q является биноминальным:
P(Ei)=Pq(1-P)n-q
которая показывает, что при P<0,5 вероятность β2=αj является убывающей функцией q,
т.е. в симметричном стационарном канале более вероятны ошибки меньшей кратности. Этот важный факт используется при построении
помехоустойчивых кодов, т.к. позволяет обосновать тактику обнаружения и исправления в первую очередь ошибок малой кратности.
Конечно, для других моделей канала такая тактика может и не быть оптимальной.
Декодирующее устройство (декодер) предназначено оценить по принятой последовательности Y=(y1,y2,…,yn)
значения информационных символов A‘=(a‘1,a‘2,…,a‘k,).
Из-за действия помех возможны неправильные решения. Процедура декодирования включает решение двух задач: оценивание переданного кодового
слова и формирование оценок информационных символов.
Вторая задача решается относительно просто. При наиболее часто используемых систематических кодах, кодовые слова которых содержат информационные
символы на известных позициях, все сводится к простому их стробированию. Очевидно также, что расположение информационных символов внутри кодового
слова не имеет существенного значения. Удобно считать, что они занимают первые k позиций кодового слова.
Наибольшую трудность представляет первая задача декодирования. При равновероятных информационных последовательностях ее оптимальное решение
дает метод максимального правдоподобия. Функция правдоподобия как вероятность получения данного вектора Y при передаче кодовых слов
Si, i=1,2,…,2k на основании Y=S+E определяется вероятностями появления векторов ошибок:
P(Y/Si)=P(Ei)=Pqi(1-P)n-qi
где qi – вес вектора Ei=Y+Si
Очевидно, вероятность P(Y/Si) максимальна при минимальном qi. На основании принципа максимального правдоподобия оценкой S‘ является кодовое слово,
искажение которого для превращения его в принятое слово Y имеет минимальный вес, т. е. в симметричном канале является наиболее вероятным (НВ):
S‘=Y+EHB
Если несколько векторов ошибок Ei имеют равные минимальные веса, то наивероятнейшая ошибка EHB определяется случайным выбором среди них.
В качестве расстояния между двумя кодовыми комбинациями принимают так называемое расстояние Хэмминга, которое численно равно количеству символов, в которых одна
комбинация отлична от другой, т.е. весу (числу ненулевых компонентов) разностного вектора. Расстояние Хэмминга между принятой последовательностью Y и всеми
возможными кодовыми словами 5, есть функция весов векторов ошибок Ei:

Поэтому декодирование по минимуму расстояния, когда в качестве оценки берется слово, ближайшее к принятой
последовательности, является декодированием по максимуму правдоподобия.
Таким образом, оптимальная процедура декодирования для симметричного канала может быть описана следующей последовательностью операций. По принятому
вектору Y определяется вектор ошибки с минимальным весом EHB, который затем вычитается (в двоичном канале — складывается по модулю 2) из Y:
Y→EHB→S‘=Y+EHB
Наиболее трудоемкой операцией в этой схеме является определение наи-вероятнейшего вектора ошибки, сложность которой
существенно возрастает при увеличении длины кодовых комбинаций. Правила кодирования, которые нацелены на упрощение
процедур декодирования, предполагают придание всем кодовым словам технически легко проверяемых признаков.
Широко распространены линейные коды, называемые так потому, что их кодовые слова образуют линейное
подпространство над конечным полем. Для двоичных кодов естественно использовать поле характеристики p=2.
Принадлежность принятой комбинации Y известному подпространству является тем признаком, по которому
выносится решение об отсутствии ошибок (EHB=0).
Так как по данному коду все пространство последовательностей длины n разбивается на смежные классы,
то для каждого смежного класса можно заранее определить вектор ошибки минимального веса,
называемый лидером смежного класса. Тогда задача декодера состоит в определении номера смежного класса,
которому принадлежит Y, и формировании лидера этого класса.
Понятие о минимальном кодовом расстоянии
Одним из основных понятий, на котором базируется любая теория помехоустойчивого
кодирования, является понятие о кодовом расстоянии вообще и о минимальном
кодовом расстоянии в частности.
Пример. Допустим, m = 8, и сообщения
закодированы простым неизбыточным двоичным кодом. Тогда из выражения M
= 2n = 2m следует m
= n = 3. Список рабочих комбинаций имеет следующий вид:
Изобразим так называемую геометрическую модель кода, вводя систему координат
из трех осей, каждая из которых отображает один из разрядов. Модель кода
– куб (рис.25). Каждая кодовая комбинация отображается одной из вершин
куба. Будем называть ребро кубы, определяющее две соседние кодовые комбинации,
одним кодовым переходом и рассматривать как единичное расстояние
между двумя соседними кодовыми комбинациями. Кодовым расстоянием
между парой любых кодовых комбинаций будем называть минимальное число ребер
(кодовых переходов), разделяющих эти комбинации:
кодовых переходов .
Например,
Рис. 25 Геометрическая модель двоичного трехразрядного кода
Понятие минимального кодового расстояния характеризует код в целом.
Минимальным кодовым расстоянием dmin
является минимум среди всех кодовых расстояний данного кода, то есть определяется
по всем возможным парам кодовых комбинаций данного кода
Для рассматриваемого кода dmin= 1. Учитывая, что рассматриваемый код по построению является неизбыточным,
можно утверждать, что любой неизбыточный код имеет dmin= 1 и наоборот, если dmin= 1, код является неизбыточным.
Из геометрической модели кода видно, что любая, даже одиночная, ошибка
не может быть обнаружена кодом с dmin= 1, так как любая кодовая комбинация, в которой произошла ошибка,
переместившись на один кодовый переход, совпадет с соседней кодовой комбинацией
и будет разрешенной.
Для построения простейшего избыточного кода, который может обнаруживать
одну ошибку (r = 1) нужно отобрать рабочие
комбинации на расстоянии
В рассматриваемом коде можно выбрать следующие комбинации:
где MРАБ
– число рабочих комбинаций.
Избыточность полученного кода
.
Если требуется обнаруживать две ошибки (r =
2), то рабочих комбинаций будет только две (например, 000 и 111), минимальное
кодовое расстояние в этом случае dmin
= 3, избыточность
.
Если r = 3, dmin≥ 4, что невозможно обеспечить в рассматриваемом
коде, так как кодовое расстояние
.
Если бы сообщения кодировались неизбыточным кодом, то для получения
четырех кодовых комбинаций потребовалось бы m =
2 информационных элементов.
В двоичных кодах кодовое расстояние между любыми двумя комбинациями
можно определить как число отличающихся разрядов.
В общем случае в кодах, используемых в режиме обнаружения ошибок кратности
r должно обеспечиваться минимальное кодовое
расстояние
dmin ≥ r + 1. (4)
Определим минимальное кодовое расстояние в кодах, работающих в режиме
исправления s ошибок.
Для исправления s ошибок нужно, очевидно,
искаженную кодовую комбинацию bi
отождествить с комбинацией ai, которая
является рабочей и из которой bi
получилась в результате s искажений. Такое
отождествление производится на базе критерия правдоподобия, под которым
понимается
где P(bi / ai) – вероятность образования bi из
ai;
P(ai / bi) – вероятность образования ai из
bi.
λ сравнивается с некоторым
пороговым значением, чаще всего с единицей. Если λ > 1,
то выносится решение о том, что bi
получилось из ai. Если λ < 1,
то выносится решение о том, что bi
нельзя отождествлять с ai.
Значения условных вероятностей, необходимых для вычисления λ,
нельзя установить непосредственно, но можно воспользоваться связью между
ними и соответствующими кодовыми расстояниями. Из факта уменьшения вероятности
появления ошибки при увеличении ее кратности следует:
Кодовое расстояние между bi и
ai равно
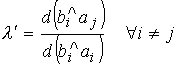
Если , то bi
получилось из aj, так как ai
ближе к bi, чем ai.
Если , то bi
получилось из ai.
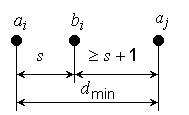
Геометрически этот результат можно интерпретировать следующим образом:
Минимальное расстояние кода, работающего в режиме исправления s
ошибок,
dmin ≥ 2s + 1. (5)
По аналогии можно утверждать, что код, способный обнаруживать r
ошибок и исправлять s из них, должен иметь
минимальное кодовое расстояние
dmin ≥ r + s + 1 (r ≥
s). (6)
Выражения (5) и (6) не противоречат друг другу, так как прежде чем исправлять
ошибку, ее надо сначала обнаружить
Можно показать, что для исправления e ошибок
стирания нужно обеспечить минимальное кодовое расстояние
dmin ≥ e + 1. (7)
В общем случае для обнаружения r ошибок
трансформации, исправления s из них и для исправления
e ошибок стирания нужно обеспечить минимальное
кодовое расстояние
dmin ≥ r + s + e + 1 (r ≥
s). (8)
Выражения (4) — (7) вытекают из (8).