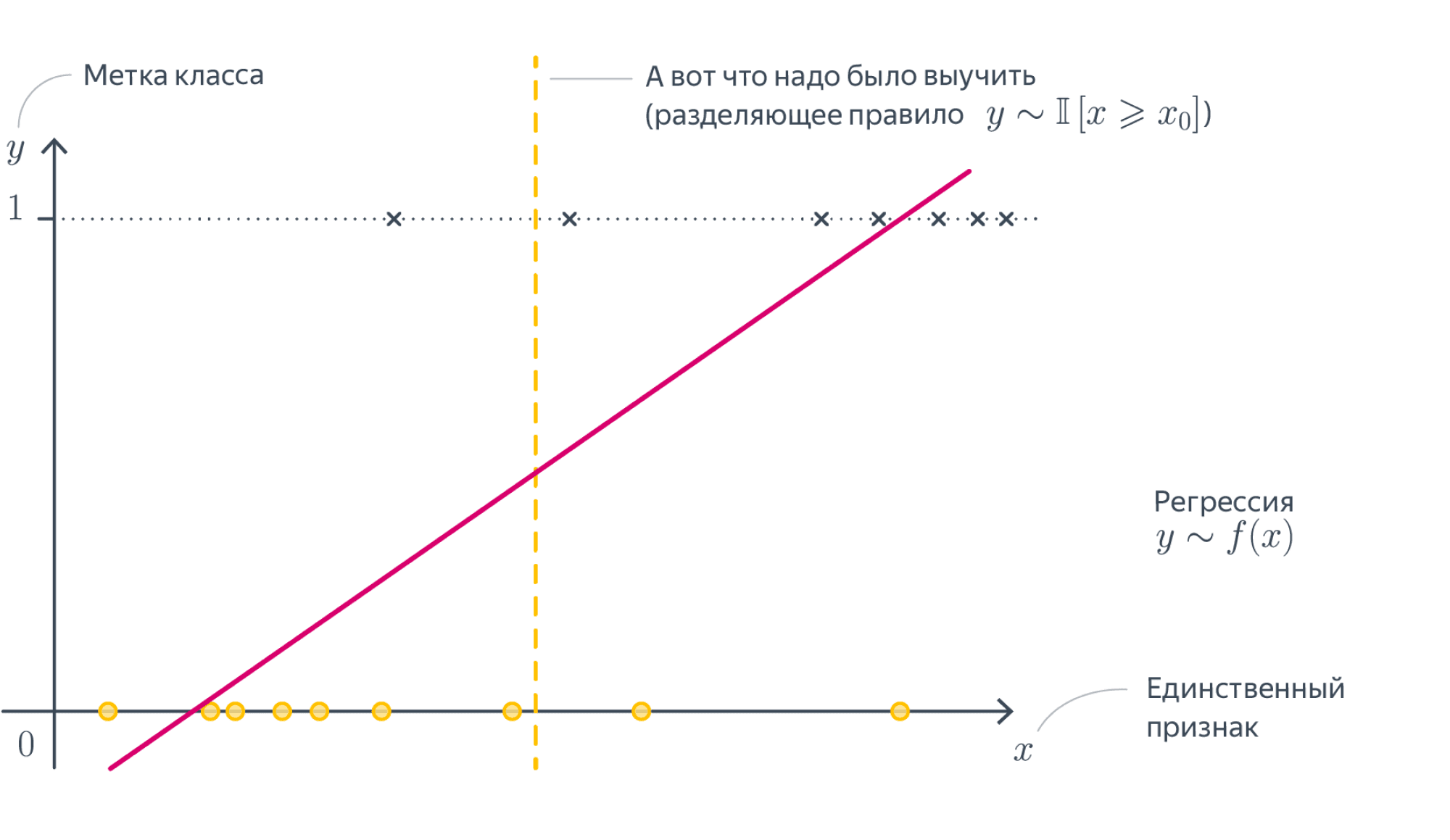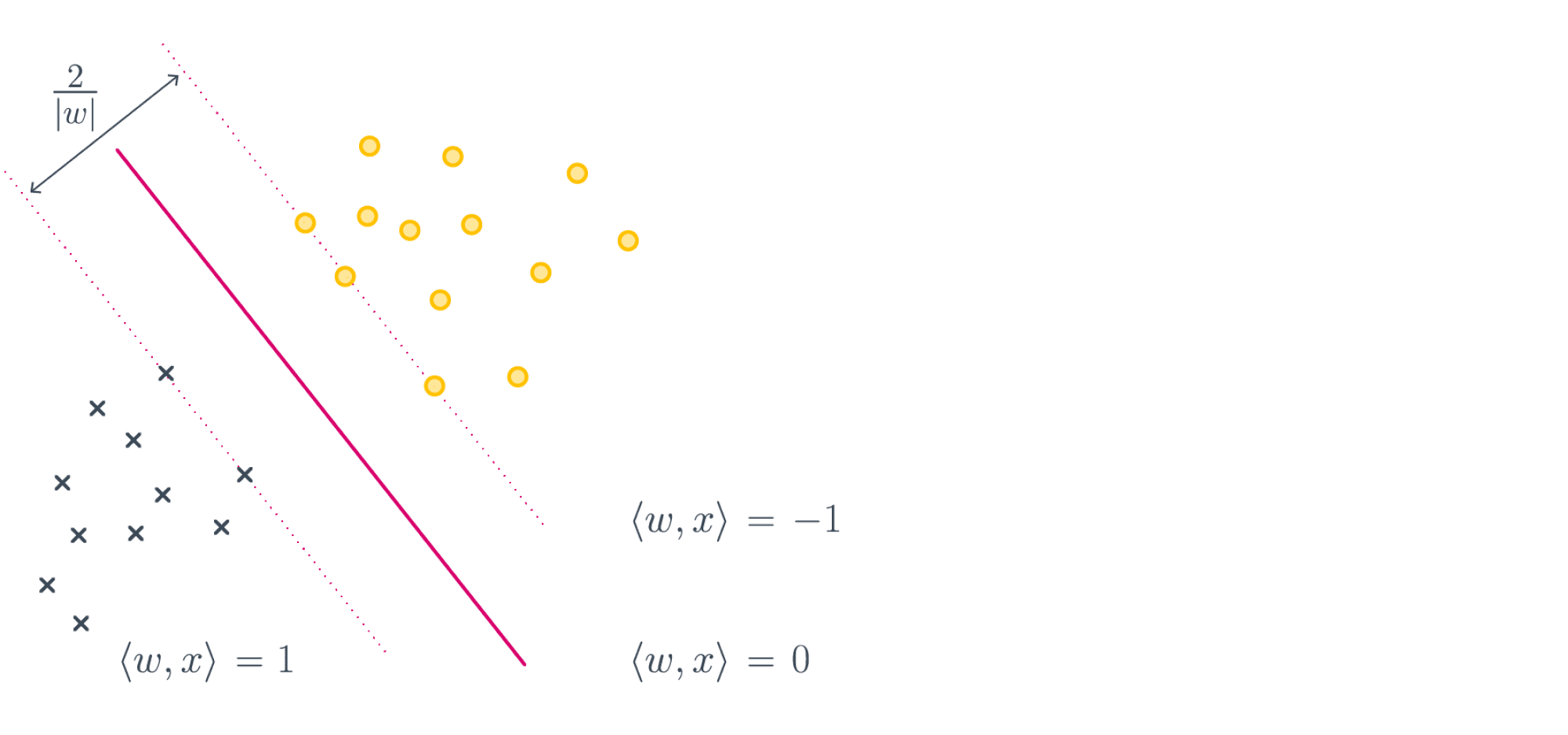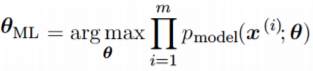1. Что такое объект, целевая переменная, признак, модель, функционал ошибки и обучение?
Объект – некая абстрактная сущность, с которой мы хотим работать и для которой хотим делать предсказания.
Пространство объектов – множество всех возможных объектов в данной задаче.
Целевая переменная – некая характеристика объекта, которую мы хотим научиться предсказывать с помощью методов машинного обучения. Обычно объект обозначается \(x\), пространство объектов — \(\mathbb{X}\). Целевая переменная обозначается — \(y\), пространство ответов — \(\mathbb{Y}\).
Объекты описываются с помощью своих характеристик, называемых признаками (т.е. признак – некая характеристика объекта), вектор признаков является признаковым описанием объекта. Мы будем отождествлять объект и его признаковое описание.
Модель – некоторый алгоритм, позволяющий предсказывать целевую переменную по признаковому описанию объекта. По сути, это функция \(a: \mathbb{X} \to \mathbb{Y}\).
Функционал качества позволяет оценить качество работы такого алгоритма, при этом, если функционал устроен так, что его нужно минимизировать, будем называть его функционалом ошибки. Функционал обозначается \(Q(a, X)\) и чаще всего представляет собой сумму ошибок на отдельных объектах, а функция, измеряющая ошибку на одном объекте, называется функцией потерь.
Пусть нам дано множество объектов \(\mathbb{X}\) — матрица объекты-признаки — с известными ответами \(\mathbb{Y}\). Назовем совокупность (\(\mathbb{X}\), \(\mathbb{Y}\)) обучающей выборкой. Обучением будем называть процесс построения оптимального с точки зрения функционала ошибки на обучающей выборке алгоритма \(a\).
2. Запишите формулы для линейной модели регрессии и для среднеквадратичной ошибки. Запишите среднеквадратичную ошибку в матричном виде.
Линейная модель:
\[
\mathbb{A}
=
\{
a(x) = w_0 + w_1 x_1 + \dots + w_d x_d|w_0, w_1, \dots, w_d \in \mathbb{R}
\}
\], где через \(x_i\) обозначается значение \(i\) -го признака у объекта \(x\), a \(d\) – количество объектов, \(w_{i}\) – вес для $i$-го признака.
MSE:
В общем виде
\[
Q(a,X)=\frac{1}{\ell}\sum_{i=1}^{\ell}(a(x_{i})-y_{i})^{2}
\], где \(a(x)\) – модель, \(l\) – количество объектов.
Для некой модели \(a(x)\) описанной выше
\[
\frac{1}{\ell}\sum_{i = 1}^{\ell} \left(w_0+\sum_{j = 1}^{d}w_j x_{ij}-y_i\right)^2\to\min_{w_0, w_1,\dots, w_d}.
\]
В матричном виде
\[
\frac{1}{\ell}||Xw-y||^{2}_{2}\to \min_{w}
\]
\[
Q(w)=(y-Xw)^{T}(y-Xw)
\]
где \(X\) — матрица объекты-признаки, \(w\) — вектор весов, \(y\) — вектор целевых значений,\(||x||^{2}_{2}\) — L2 норма (квадратный корень из суммы квадратов значений вектора)
3. Что такое коэффициент детерминации? Как интерпретировать его значения?
\[
R^{2}(a,X)=1-\frac{\sum_{i=1}^{l}(a(x_{i}-y_{i})^{2})}{\sum_{i=1}^{l}(y_{i}-\hat{y})^{2}}
\]
Коэффициент детерминации измеряет долю дисперсии, объяснённую моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
4. Чем отличаются функционалы MSE и MAE?
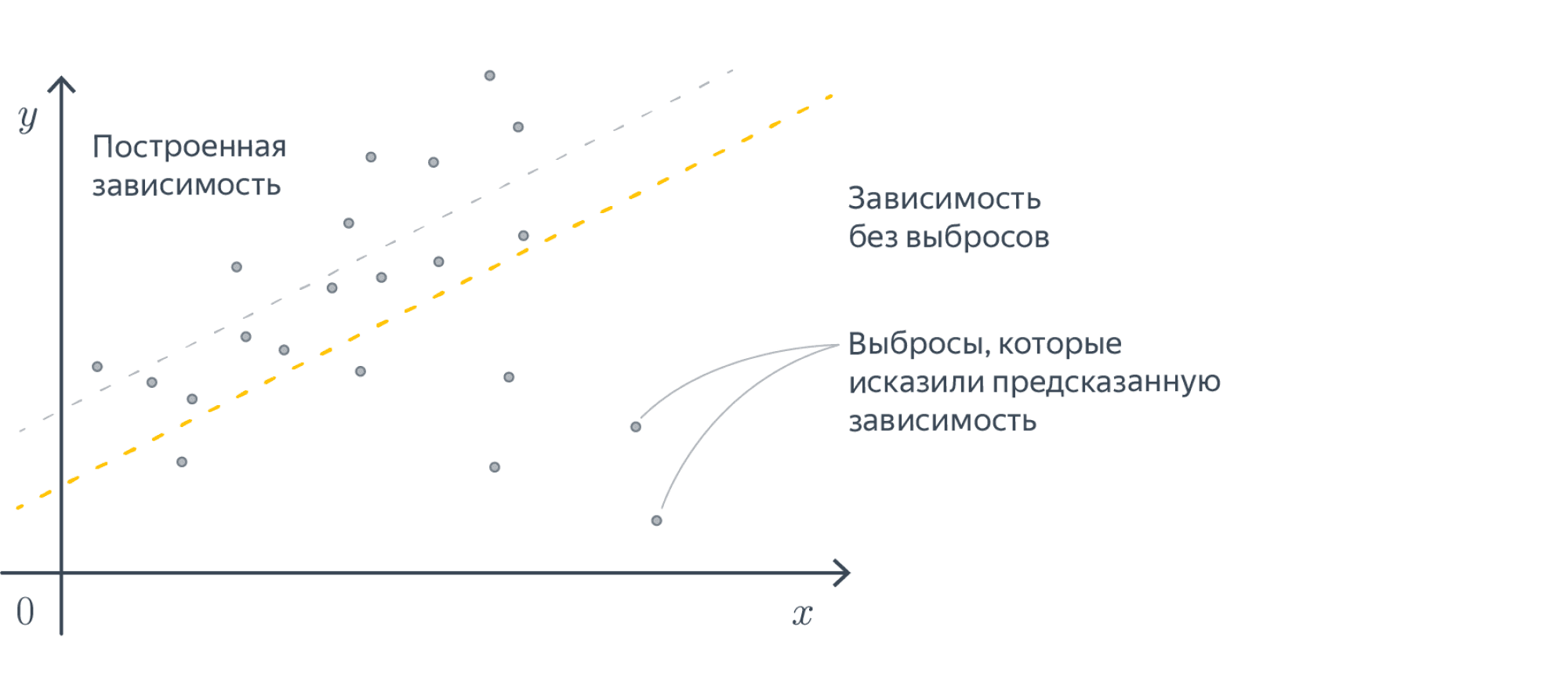
- MAE более устойчива к выбросам (но гораздо менее точна при приближении к минимуму (произв не содержит инф о близости к экстремуму (в 0 вообще ее нет)) и большим значениям
- MSE увеличит ошибку из-за возведения в квадрат из-за чего появится некоторое искажение реальной ошибки. Если выбросов больше чем нормальных объектов, то устойчивость MAE пропадает.
5. Как устроены робастные функции потерь (Huber loss, log-cosh)? Чем log-cosh лучше функции потерь Хубера?
Huber loss
Huber Loss объединяет в себе MSE и MAE с параметром дельта, этот параметр определяет, что мы считаем за выброс. При \(\delta\rightarrow0\) функция потерь Хубера вырождается в абсолютную функцию (MAE) потерь, а при \(\delta\rightarrow\infty\) — в квадратичную (MSE). Не имеет вторую производную
\[
L_\delta(y, a)=
\left\{\begin{aligned}
&\frac12 (y — a)^2, \quad |y — a| < \delta \\
&\delta \left(|y — a| — \frac12 \delta
\right), \quad |y — a| \geq \delta
\end{aligned}
\right.
\]
Log Cosh
Log Cosh (логарифм от гиперболического косинуса) имеет вторую производную. Как и в случае с функцией потерь Хубера, для маленьких отклонений здесь имеет место квадратичное поведение, а для больших — линейное.
\[
L(y,a)=\log(\cosh(a-y))
\]
Сравнение
Log Cosh > Huber Loss т.к. Вторая производная в Хубере имеет разрывы, Log Cosh же без разрывов, не нужно подбирать параметр дельта.
6. Что такое градиент? Какое его свойство используется при минимизации функций?
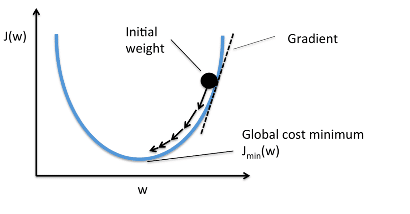
Градиент — направление наискорейшего роста функции, а антиградиент (т.е. \(−\nabla f\) ) направлением наискорейшего убывания функции. Это ключевое свойство градиента, обосновывающее его использование в методах оптимизации.
7. Как устроен градиентный спуск?
Пусть \(w^0\) начальный набор параметров (например, нулевой или сгенерированный из некоторого случайного распределения). Тогда градиентный спуск состоит в повторении следующих шагов до сходимости:
\[
w^{(k)}=w^{(k — 1)}-\eta_k\nabla Q(w^{(k — 1)})
\]
Здесь под \(Q(w)\) понимается значение функционала ошибки для набора параметров \(w\).
Через \(\eta_k\) обозначается длина шага, которая нужна для контроля скорости движения.
Можно делать её константной: \(\eta_k = c\). При этом если длина шага слишком большая, то есть риск постоянно <перепрыгивать> через точку минимума, а если шаг слишком маленький, то движение к минимуму может занять слишком много итераций. Иногда длину шага монотонно уменьшают по мере движения — например, по простой формуле (\(\frac{1}{k}\)).
8. Почему не всегда можно использовать полный градиентный спуск? Какие способы оценивания градиента вы знаете? Почему в стохастическом градиентном спуске важно менять длину шага по мере итераций? Какие стратегии изменения шага вы знаете?
Использование полного градиентного спуска может быть очень трудоёмко при больших размерах выборки. В то же время точное вычисление градиента может быть не так уж необходимо — как правило, мы делаем не очень большие шаги в сторону антиградиента, и наличие в нём неточностей не должно сильно сказаться на общей траектории. Опишем несколько способов оценивания полного градиента.
SGD
\[
w^{(k)}=w^{(k — 1)}-\eta_k\nabla q_{ik}(w^{(k — 1)})
\] где \(i_k\) – случайно выбранный номер слагаемого из функционала.
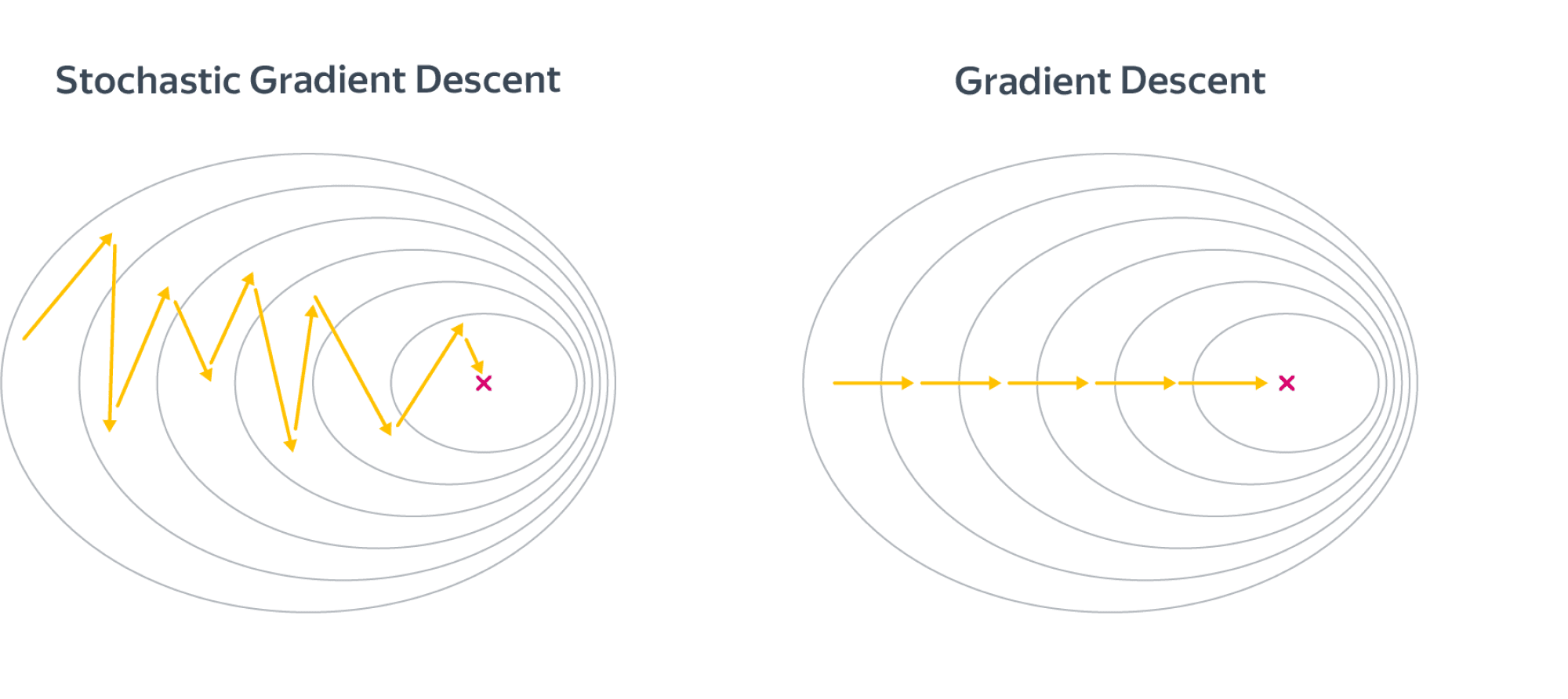
Параметры, оптимальные для средней ошибки на всей выборке, не обязаны являться оптимальными для ошибки на одном из объектов. Поэтому SGD метод запросто может отдаляться от минимума, даже оказавшись рядом с ним. Чтобы исправить эту проблему, важно в SGD делать длину шага убывающей – тогда в окрестности оптимума мы уже не сможем делать длинные шаги и, как следствие, не сможем из этой окрестности выйти. Разумеется, потребуется выбирать формулу для длины шага аккуратно, чтобы не остановиться слишком рано и не уйти от минимума. В частности, сходимость для выпуклых дифференцируемых функций гарантируется (с вероятностью 1), если функционал удовлетворяет ряду условий (как правило, это выпуклость, дифференцируемость и липшицевость градиента) и длина шага удовлетворяет условиям Роббинса-Монро:
\[
\sum_{k = 1}^{\infty} \eta_k = \infty; \quad
\sum_{k = 1}^{\infty} \eta_k^2 < \infty.
\]
Этим условиям, например, удовлетворяет шаг \(\eta_k = \frac{1}{k}\).
Примеры использования
\(\eta_{k}=\frac{1}{k}\)
\(\eta_{k}=\lambda(\frac{s_{0}}{s_{0}+k})^{p}\)
SAG
На \(k\) -й итерации выбирается случайное слагаемое \(i_{k}\) и обновляются вспомогательные переменные:
\[
z_i^{(k)}
=
\begin{cases}
\nabla q_i(w^{(k — 1)}),
\quad
&\text{если}\ i = i_k;\\
z_i^{(k — 1)}
\quad
&\text{иначе}.
\end{cases}\]
\[
w^{(k)}=w^{(k — 1)}-\eta_k\frac{1}{\ell}\sum_{i = 1}^{\ell}z_i^{(k)}
\]
9. В чём заключаются метод инерции и AdaGrad/RMSProp?
Adagrad
В методе AdaGrad предлагается сделать свою длину шага для каждой компоненты вектора параметров. При этом шаг будет тем меньше, чем более длинные шаги мы делали на предыдущих итерациях
\[
G_{kj} = G_{k-1,j} + (\nabla_w Q(w^{(k-1)}))_j^2
\]
\[
w_j^{(k)} = w_j^{(k-1)} — \frac{\eta_t}{\sqrt{G_{kj} + \varepsilon}} (\nabla_w Q(w^{(k-1)}))_j
\]
недостаток: переменная \(G_{kj}\) монотонно растёт, из-за чего шаги становятся всё медленнее и могут остановиться ещё до того, как достигнут минимум функционала
RMSprop
Улучшение над AdaGrad. В этом случае размер шага по координате зависит в основном от того, насколько быстро мы двигались по ней на последних итерациях
\[G_{kj} = \alpha G_{k-1,j} + (1 — \alpha) (\nabla_w Q(w^{(k-1)}))_j^2.\]
10. Что такое кросс-валидация? На что влияет количество блоков в кросс-валидации? Как построить итоговую модель после того, как по кросс-валидации подобраны оптимальные гиперпараметры?
- CV – размеченные данные разбиваются на \(k\) блоков примерно одинакового размера. Затем обучается \(k\) моделей \(a_1(x), \dots, a_k(x)\) причём \(i\) -я модель обучается на объектах из всех блоков, кроме блока \(i\).
После этого качество каждой модели оценивается по тому блоку, который не участвовал в её обучении, и результаты усредняются:
\[\text{CV}
=
\frac{1}{k}
\sum_{i = 1}^{k}
Q\left( a_i(x), X_i \right).\] - можно построить композицию из моделей \(a_1(x), \dots, a_k(x)\), полученных в процессе кросс-валидации. Под композицией может пониматься, например, усреднение прогнозов этих моделей, если мы решаем задачу регрессии.
11. Чем гиперпараметры отличаются от параметров? Что является параметрами и гиперпараметрами в линейных моделях и в решающих деревьях?
- Параметры — величины, которые настраиваются по обучающей выборке
- Гиперпараметры — относят величины, которые контролируют сам процесс обучения и не могут быть подобраны по обучающей выборке
- Параметры для линейных моделей:
- Веса
- Гиперпараметр для линейных моделей:
- Коэффициент регуляризации
- Размер шага градиента
- Параметр для деревьев:
- Разбиение
- Гиперпараметр для деревьев:
- Глубина дерева
- Минимальное количество элементов в листьях
- Минимальное количество элементов для разбиения
12. Что такое регуляризация? Запишите L1- и L2-регуляризаторы.
Регуляризация – способ штрафовать модель за высокую норму весов с помощью коэффициента регуляризации для предотвращения переобучения.
Наиболее распространенными являются \(L_2\) и \(L_1\) -регуляризаторы:
\[
R(w) = \|w\|_2 = \sum_{i = 1}^d w_i^2,
\]
\[
R(w) = \|w\|_1 = \sum_{i = 1}^d |w_i|.
\]
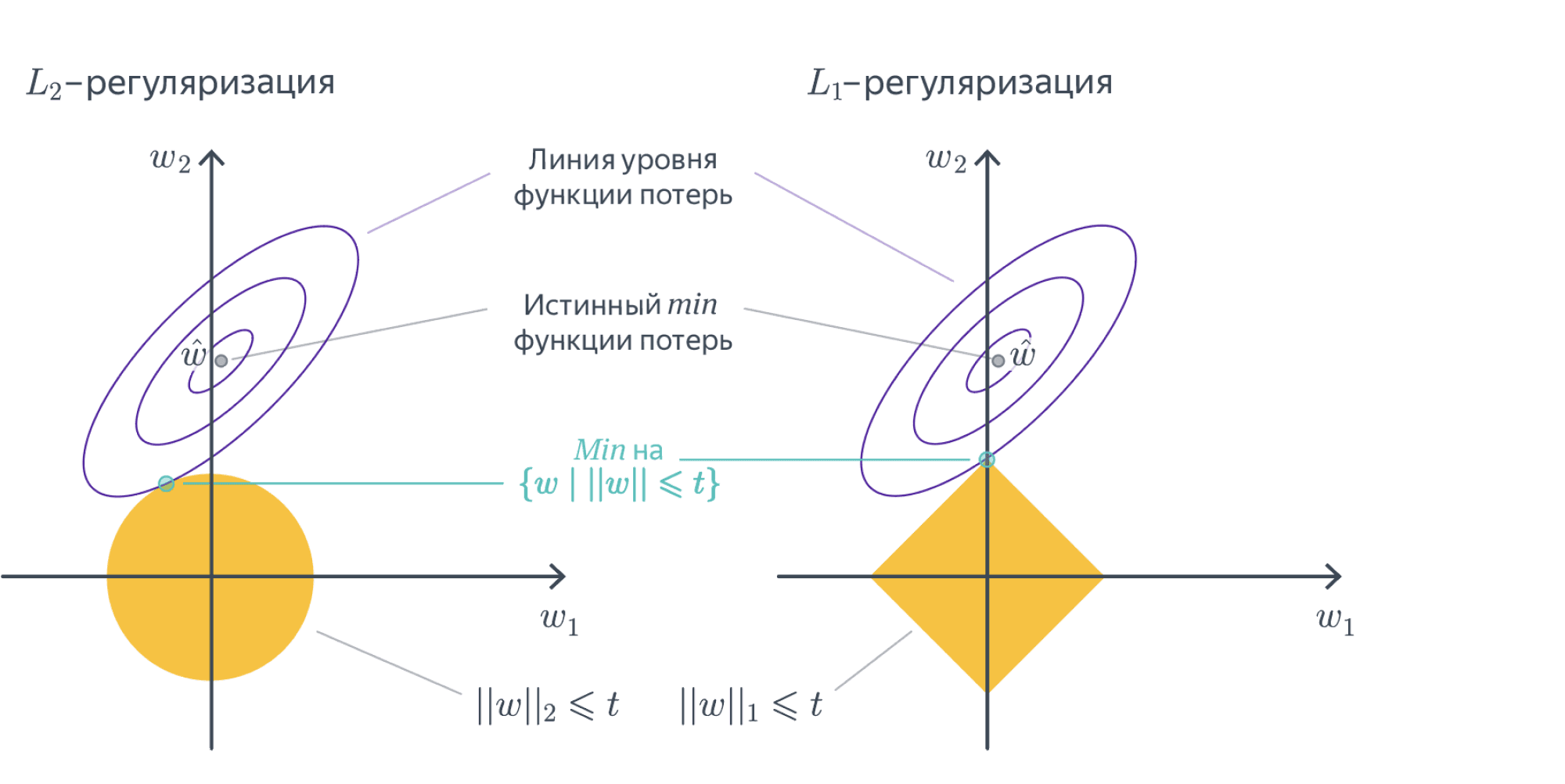
13. Почему L1-регуляризация отбирает признаки?
Зануление весов
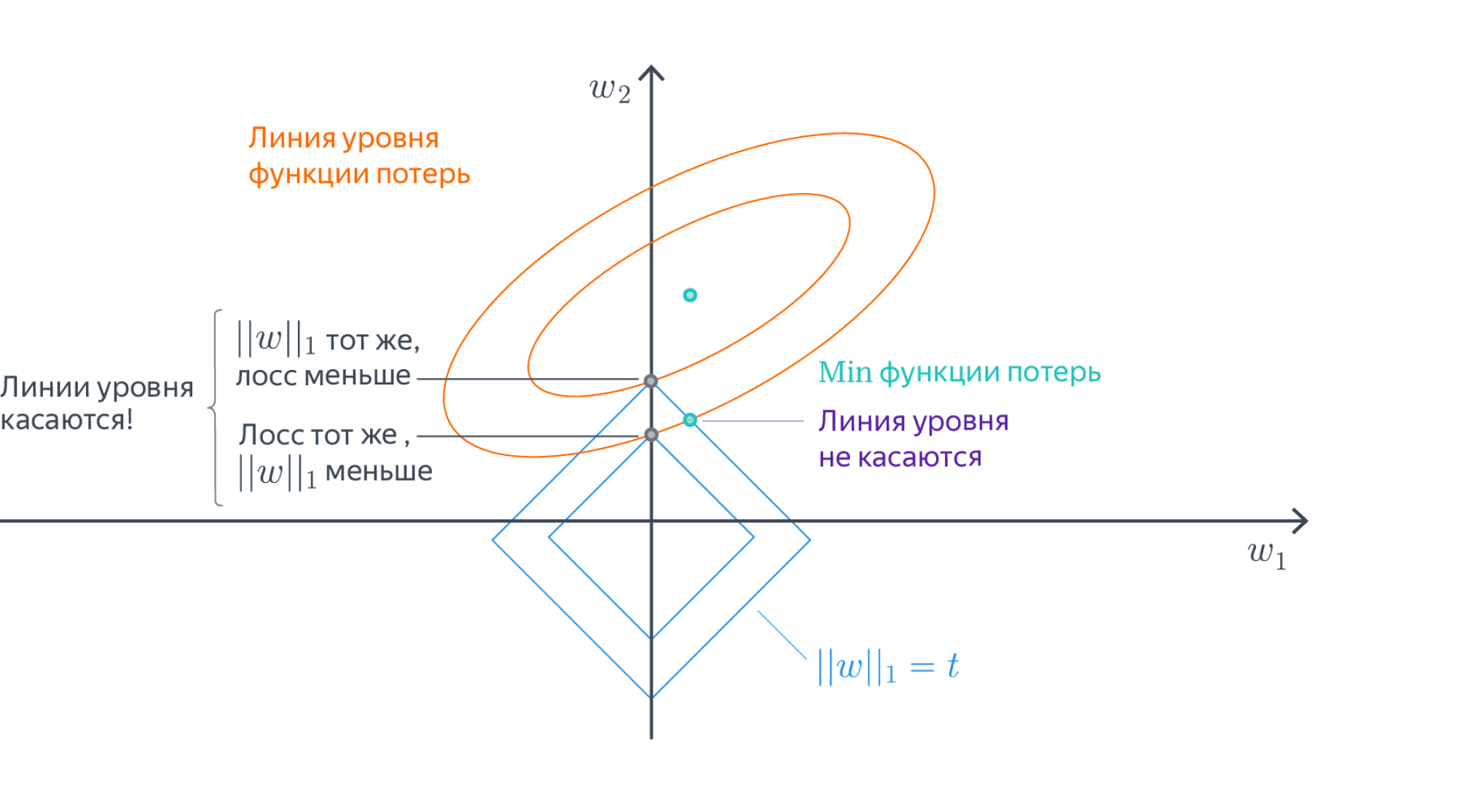
Можно показать, что если функционал \(Q(w)\) является выпуклым, то задача безусловной минимизации функции \(Q(w) + \alpha \|w\|_1\) эквивалентна задаче условной оптимизации \[Q(w) \to \min_{w}\] \[\|w\|_1 \leq C\] для некоторого \(C\). Изображены линии уровня функционала \(Q(w)\), а также множество, определяемое ограничением \(\|w\|_1 \leq C\). Решение определяется точкой пересечения допустимого множества с линией уровня, ближайшей к безусловному минимуму. Из изображения можно предположить, что в большинстве случаев эта точка будет лежать на одной из вершин ромба, что соответствует решению с одной зануленной компонентой.
Штрафы при малых весах
Предположим, что текущий вектор весов состоит из двух элементов \(w = (1, \varepsilon)\), где \(\varepsilon\) близко к нулю, и мы хотим немного изменить данный вектор по одной из координат. Найдём изменение \(L_2\) — и \(L_1\) -норм вектора при уменьшении первой компоненты на некоторое положительное число \(\delta < \varepsilon\):
\[\|w — (\delta, 0)\|_2^2=1 — 2 \delta + \delta^2 + \varepsilon^2\]
\[\|w — (\delta, 0)\|_1=1 — \delta + \varepsilon\]
Вычислим то же самое для изменения второй компоненты:
\[\|w — (0, \delta)\|_2^2=1 — 2 \varepsilon \delta + \delta^2 + \varepsilon^2\]
\[\|w — (0, \delta)\|_1 =1 — \delta + \varepsilon\]
Видно, что с точки зрения \(L_2\) -нормы выгоднее уменьшать первую компоненту, а для \(L_1\) -нормы оба изменения равноценны. Таким образом, при выборе \(L_2\) -регуляризации гораздо меньше шансов, что маленькие веса будут окончательно обнулены.
Проксимальный шаг
Проксимальные методы – это класс методов оптимизации, которые хорошо подходят для функционалов с негладкими слагаемыми. Формула для шага проксимального метода в применении к линейной регрессии с квадратичным функционалом ошибки и \(L_1\) -регуляризатором:
\[w^{(k)}=S_{\eta \alpha} \left(w^{(k — 1)}-\eta\nabla_w F(w^{(k — 1)})\right),\]
где \(F(w) = \|Xw — y\|^2\) – функционал ошибки без регуляризатора, \(\eta\) – длина шага, \(\alpha\) – коэффициент регуляризации, а функция \(S_{\eta \alpha}(w)\) применяется к вектору весов покомпонентно, и для одного элемента выглядит как
\[S_{\eta \alpha} (w_i)=
\begin{cases}
w_i — \eta \alpha, \quad &w_i > \eta \alpha\\
0, \qquad &|w_i| < \eta \alpha\\
w_i + \eta \alpha, \quad &w_i < -\eta \alpha
\end{cases}\]
Из формулы видно, что если на данном шаге значение некоторого веса не очень большое, то на следующем шаге этот вес будет обнулён, причём чем больше коэффициент регуляризации, тем больше весов будут обнуляться.
14. Почему плохо накладывать регуляризацию на свободный коэффициент? Почему регуляризация может странно работать на немасштабированных данных?
-
Отметим, что свободный коэффициент \(w_0\) нет смысла регуляризовывать — если мы будем штрафовать за его величину, то получится, что мы учитываем некие априорные представления о близости целевой переменной к нулю и отсутствии необходимости в учёте её смещения. Такое предположение является достаточно странным. Особенно об этом следует помнить, если в выборке есть константный признак и коэффициент \(w_0\) обучается наряду с остальными весами; в этом случае следует исключить слагаемое, соответствующее константному признаку, из регуляризатора.
-
Может быть большой разброс порядков весов.
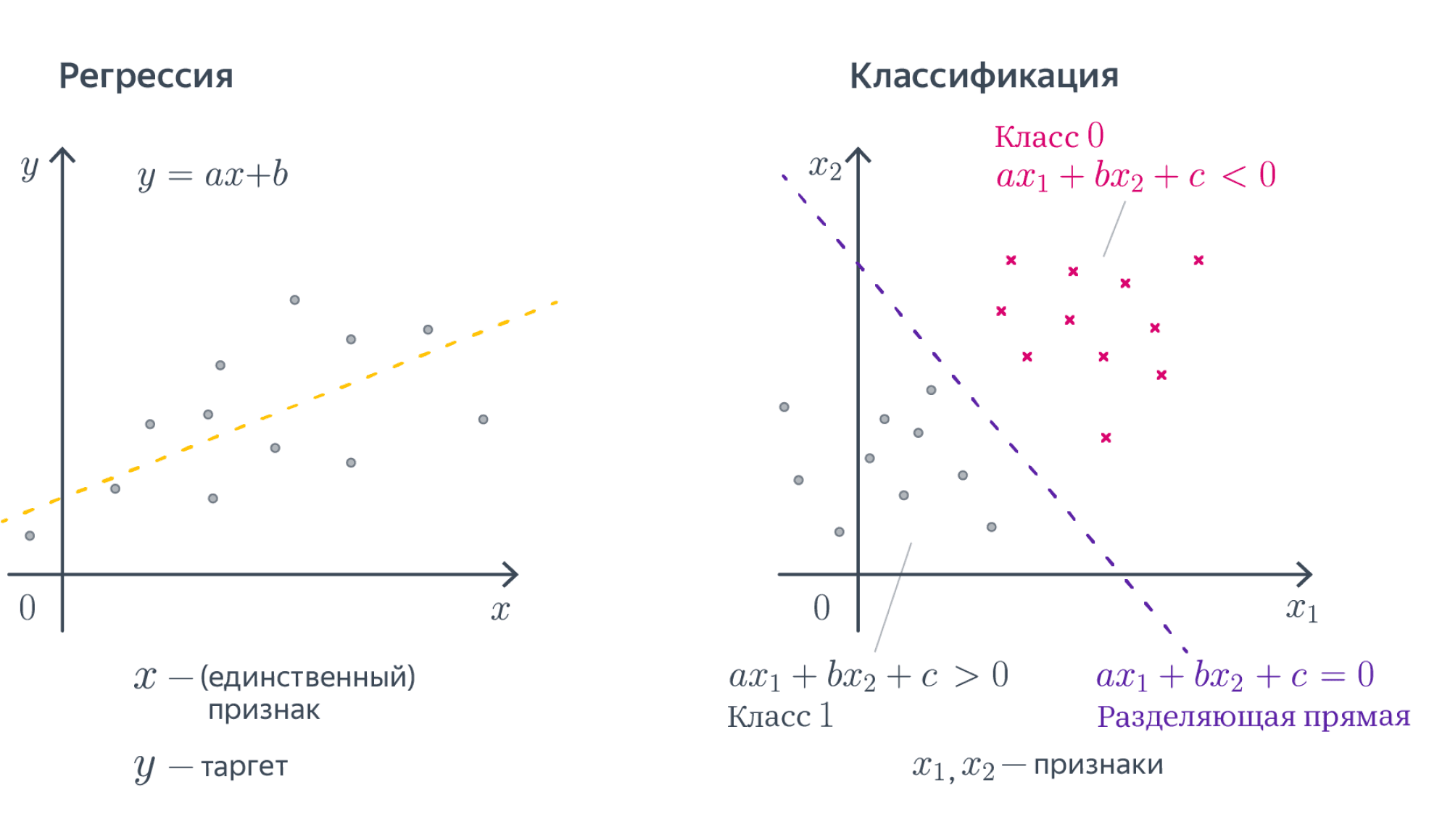
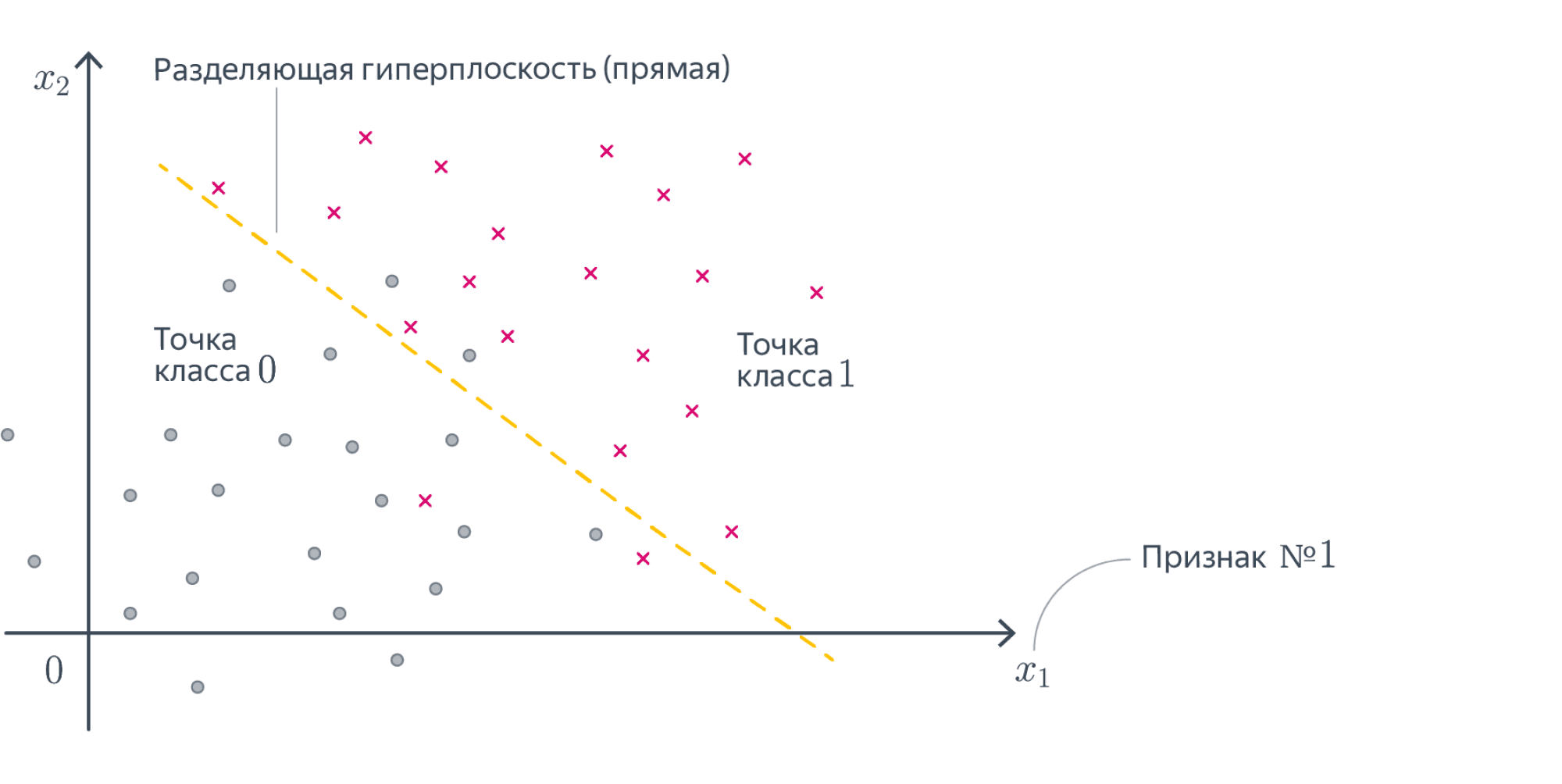
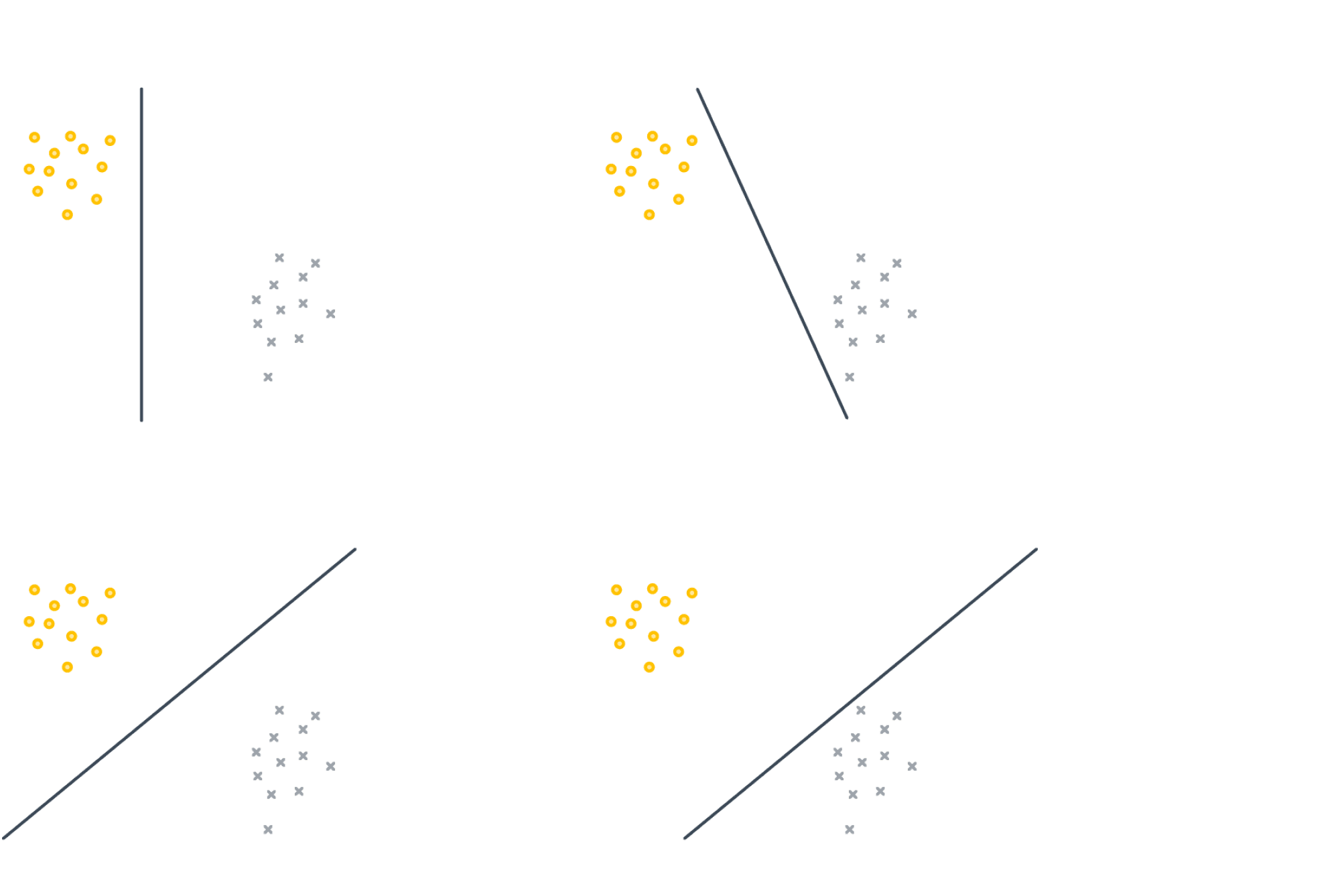
15. Запишите формулу для линейной модели классификации. Что такое отступ? Как обучаются линейные классификаторы и для чего нужны верхние оценки пороговой функции потерь?
Формула
\[
a(x) = \text{sign}\left(
\langle w, x \rangle + w_0
\right)
=
\text{sign} \left(
\sum_{j = 1}^{d} w_j x_j + w_0
\right)
\]
Отступ
\[
M_i = y<w,x_i>
\]
Знак отступа говорит о корректности ответа классификатора (положительный отступ соответствует правильному ответу, отрицательный неправильному), а его абсолютная величина характеризует степень уверенности классификатора в своём ответе. Напомним, что скалярное произведение \(<w,x_i>\) пропорционально расстоянию от разделяющей гиперплоскости до объекта; соответственно, чем ближе отступ к нулю, тем ближе объект к границе классов, тем ниже уверенность в его принадлежности.
Обучение линейных классификаторов
Нам будет удобнее решать задачу минимизации, поэтому будем вместо этого использовать долю неправильных ответов
\[
Q(a, X)=
\frac{1}{\ell}
\sum_{i = 1}^{\ell}
[a(x_i) \neq y_i]
=
\frac{1}{\ell}
\sum_{i = 1}^{\ell}
[\mathop{\rm sign}\limits \langle w, x_i \rangle \neq y_i]
\to
\min_w
\]
Этот функционал является дискретным относительно весов, и поэтому искать его минимум с помощью градиентных методов мы не сможем. Более того, у данного функционала может быть много глобальных минимумов вполне может оказаться, что существует много способов добиться оптимального количества ошибок. Чтобы не пытаться решать все эти проблемы, попытаемся свести задачу к минимизации гладкого функционала (верхней оценки).
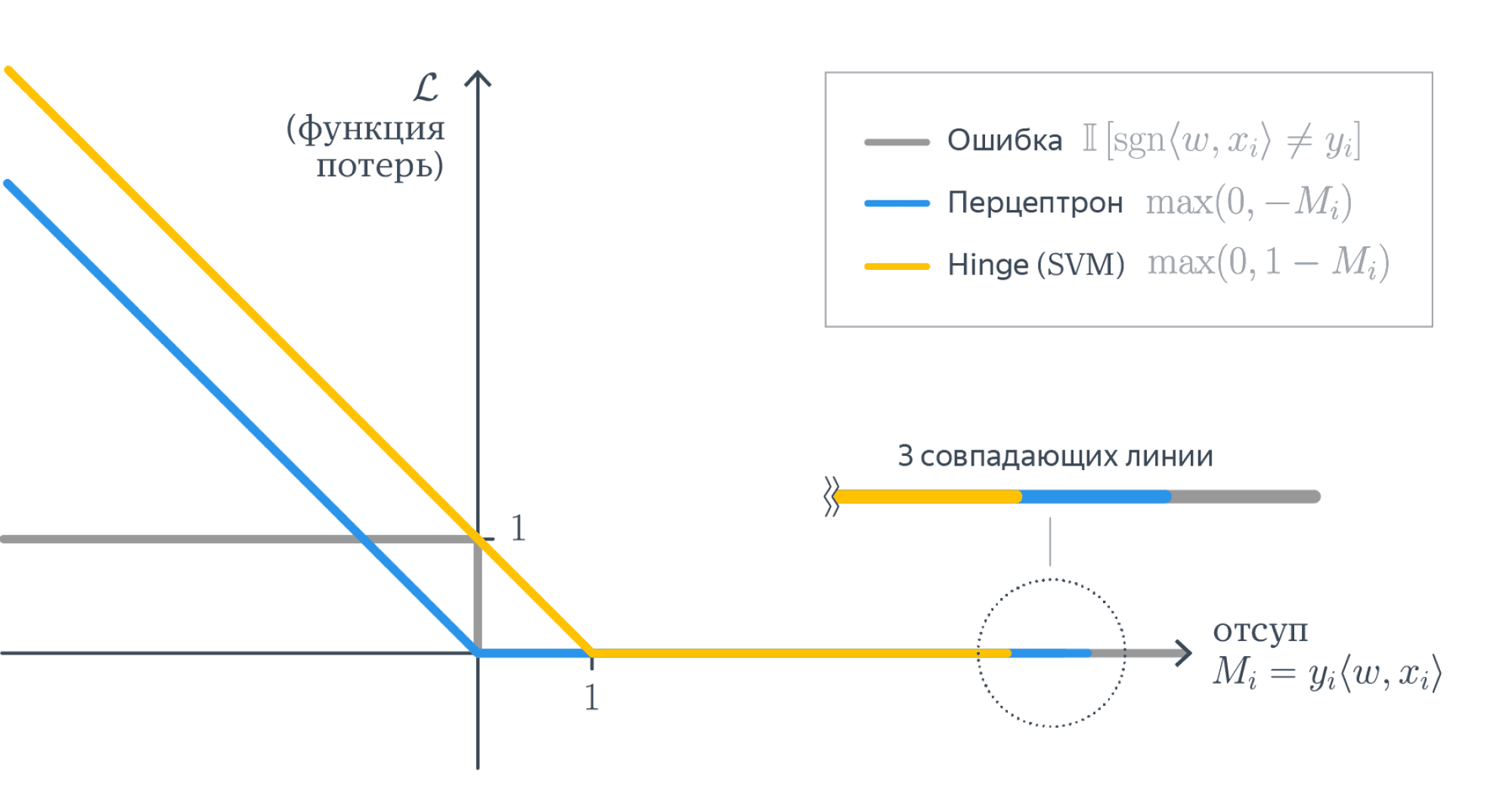
Верхние оценки
Функционал оценивает ошибку алгоритма на объекте \(x\) с помощью пороговой функции потерь \(L(M) = [M < 0]\),
где аргументом функции является отступ \(M = y \langle w, x \rangle\). Оценим эту функцию сверху во всех точках \(M\) кроме, может быть, небольшой полуокрестности левее нуля:\[
L(M) \leq \tilde L(M).
\]
После этого можно получить верхнюю оценку на функционал:
\[
Q(a, X)
\leq
\frac{1}{\ell}
\sum_{i = 1}^{\ell}
\tilde L(y_i \langle w, x_i \rangle)
\to
\min_w
\]
Если верхняя оценка \(\tilde L(M)\) является гладкой, то и данная верхняя оценка будет гладкой. В этом случае её можно будет минимизировать с помощью, например, градиентного спуска. Если верхнюю оценку удастся приблизить к нулю, то и доля неправильных ответов тоже будет близка к нулю.
Приведём несколько примеров верхних оценок:
- \(\tilde L(M) = \log \left(1 + e^{-M} \right)\) – логистическая функция потерь
- \(\tilde L(M) = (1 — M)_+ = \max(0, 1 — M)\) – кусочно-линейная функция потерь (используется в методе опорных векторов)
- \(\tilde L(M) = (-M)_+ = \max(0, -M)\) – кусочно-линейная функция потерь (соответствует персептрону Розенблатта)
- \(\tilde L(M) = e^{-M}\) – экспоненциальная функция потерь
- \(\tilde L(M) = 2/(1 + e^M)\) – сигмоидная функция потерь
Любая из них подойдёт для обучения линейного классификатора.
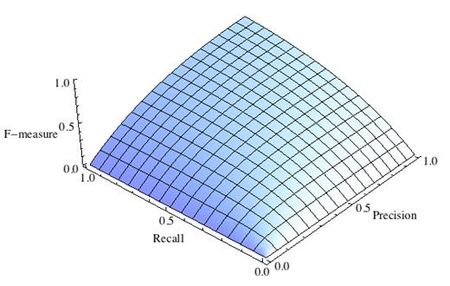
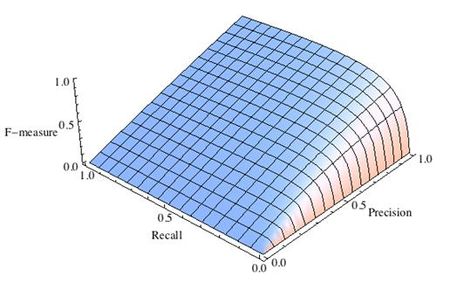
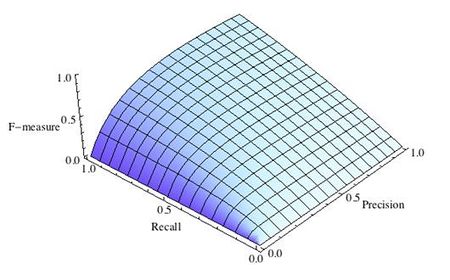
16. Что такое точность, полнота и F-мера? Почему F-мера лучше арифметического среднего и минимума?
| y=1 | y=-1 | |
|---|---|---|
| a(x)=1 | True Positive (TP) | False Positive (FP) |
| a(x)=-1 | False Negative (FN) | True Negative (TN) |
Точность
Точность (которая не accuracy (которой точный перевод — доля верных ответов), а precision) — метрика того, насколько можно доверять модели если она сказала что объект относится к положительному классу.
\[
\text{precision}=\frac{\text{TP}}{\text{TP} + \text{FP}}
\]
Полнота
Полнота (recall) — метрика того, насколько хорошо модель покрыла положительный класс
\[
\text{recall}=\frac{\text{TP}}{\text{TP} + \text{FN}}
\]
F-мера
F — мера — гармоническое среднее точности и полноты, (сохраняет хорошее от ариф. минимума, но более гладкая. Близко к 0 если хотя бы 1 из аргументов близок к нулю). В отличие от геометрического среднего — гармоническое среднее гораздо устойчивее к выбросам.
\[
F=\frac{2 * \text{precision} * \text{recall}}{\text{precision} + \text{recall}}
\]
17. Для чего нужен порог в линейном классификаторе? Из каких соображений он может выбираться?
- Для определения класса объекта
- Может выбираться:
- из цен ошибок
- из требуемого количества
- из требований к recall и precision
18. Что такое AUC-ROC? Опишите алгоритм построения ROC-кривой.
AUC ROC-area under ROC (receiving operating characteristic) curve, — площадь под ROC-кривой.
Сортируем объекты \(b(x)\), по размеру порога; размер шага для объектов с \([y = 0] =\frac{1}{L_{-}}\) отрицательных (шаги по FPR (горизонт ось)), шаги для \([y = 1] =\frac{1}{L_+}\) положительных (шаги по TPR (верт ось) )
19. Что такое AUC-PRC? Опишите алгоритм построения PR-кривой.
Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (AUC-PR).
Описание алгоритма
Стартуем из точки (0, 1). Будем идти по ранжированной выборке, начиная с первого объекта; пусть текущий объект находится на позиции \(k\). Если он относится к классу −1, то полнота не меняется, точность падает соответственно, кривая опускается строго вниз на \(\frac{1}{l_{-}}\). Если же объект относится к классу 1, то полнота увеличивается на \(\frac{1}{l_+}\), точность растет, и кривая поднимается вправо и вверх. Площадь под этим участком можно аппроксимировать площадью прямоугольника с высотой, равной precision@k и шириной \(\frac{1}{l_{+}}\).
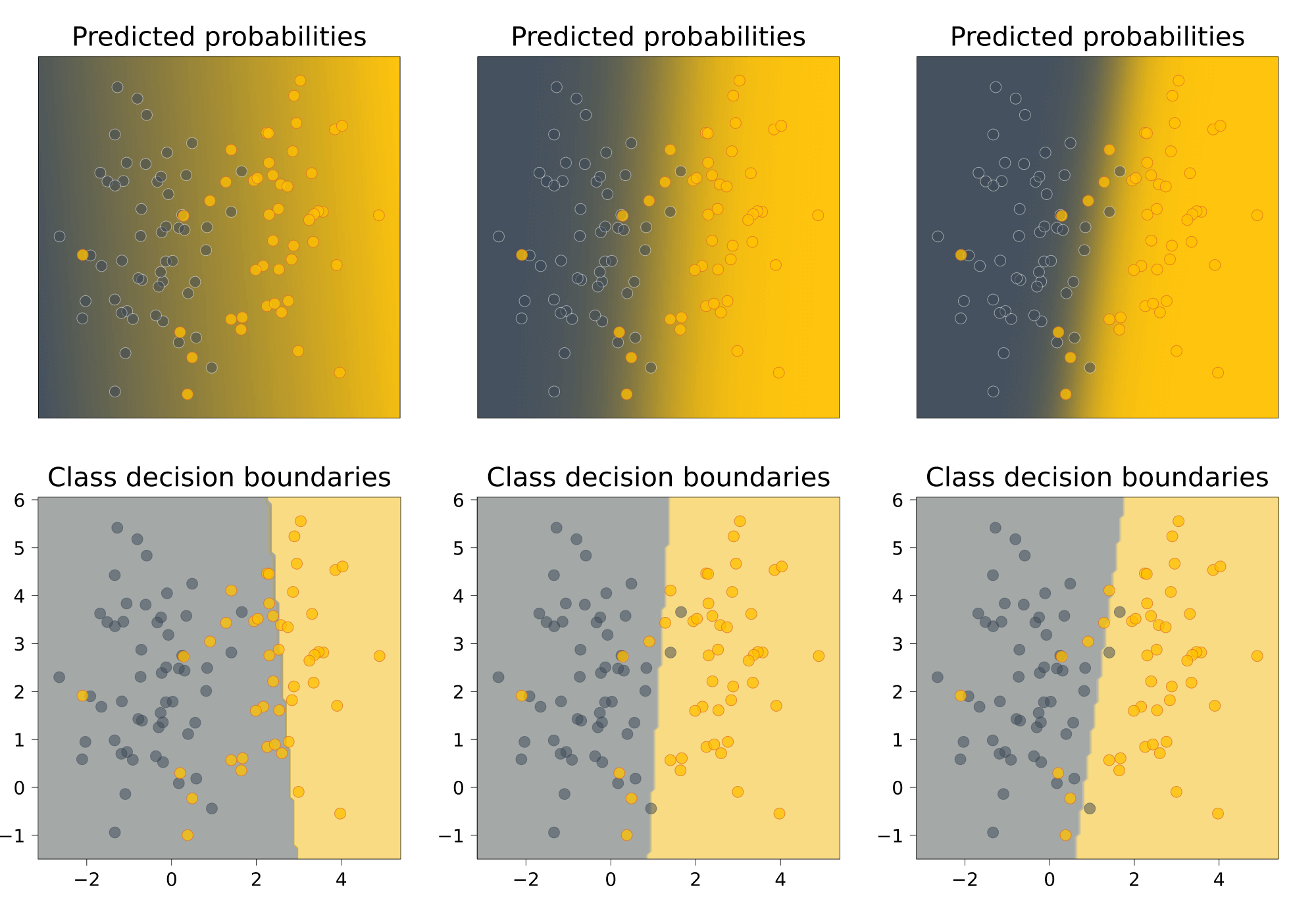
20. Что означает “модель оценивает вероятность положительного класса”? Как можно внедрить это требование в процедуру обучения модели?
Рассмотрим точку \(x\) пространства объектов. Как мы договорились, в ней имеется распределение на ответах \(p(y = +1 | x)\). Допустим, алгоритм \(b(x)\) возвращает числа из отрезка \([0, 1]\). Наша задача – выбрать для него такую процедуру обучения, что в точке \(x\) ему будет оптимально выдавать число \(p(y = +1 | x)\).
Если в выборке объект \(x\) встречается \(n\) раз с ответами \(\{y_1, \dots, y_n\}\), то получаем следующее требование:
\[
\mathop{\rm arg\,min}\limits_{b \in \mathbb{R}}
\frac{1}{n}
\sum_{i = 1}^{n}
L(y_i, b)
\approx
p(y = +1 | x)
\]
При стремлении \(n\) к бесконечности получим, что функционал стремится к матожиданию ошибки:
\[
\mathop{\rm arg\,min}\limits_{b \in \mathbb{R}}\mathbb{E} \left[L(y, b)|x\right]
=
p(y = +1 | x)
\]
На семинаре будет показано, что этим свойством обладает, например, квадратичная функция потерь \(L(y, z) = (y — z)^2\), если в ней для положительных объектов использовать истинную метку \(y = 1\), а для отрицательных брать \(y = 0\). Если функция потерь \(L\) удовлетворяет второй формуле, то \(b(x)\approx p(y=+1|x)\)
21. Что такое калибровочная кривая? Какие методы калибровки вероятности вы знаете? Почему важно проводить калибровку не на обучающей выборке?
Калибровка вероятностей нужна для того, чтобы заставить модель выдавать корректные вероятности принадлежности к классам. В задаче бинарной классификации откалиброванным алгоритмом называют такой алгоритм, для которого доля положительных примеров (на основе реальных меток классов) для предсказаний в окрестности произвольной вероятности \(p\) совпадает с этим значением \(p\).
На этой кривой абсцисса точки соответствуют значению \(p\) (предсказаний алгоритма), а ордината соответствует доле положительных примеров, для которых алгоритм предсказал вероятность, близкую к \(p\). В идеальном случае эта кривая совпадает с прямой \(y = x\).
Есть два подхода к калибровке.
- Масштабирование Платта. Он заключается к подгонке всех предсказаний к логистической кривой (по сути, логистическая регрессия на ответах классификатора) \[P(y = 1 | x) = \frac{1}{1+\exp (af(x) + b)},\] где \(a, b\) – скалярные параметры. Эти параметры настраиваются методом максимума правдоподобия (минимизируя логистическую функцию потерь) на отложенной выборке или с помощью кросс валидации. Также Платт предложил настраивать параметры на обучающей выборке базовой модели, а для избежания переобучения изменить метки объектов на следующие значения:
- \[t_{+} = \frac{N_{+} + 1}{N_{-} + 2}\] для положительных примеров
- \[t_{-} = \frac{1}{N_{-} + 2}\] для отрицательных.
- Изотоническая регрессия. В этом методе также строится отображение из предсказаний модели в откалиброванные вероятности. Для этого используем изотоническую функцию (неубывающая кусочно-постоянная функция), в которой \(x\) – выходы нашего алгоритма, а \(y\) – целевая переменная. Мы хотим найти такую функцию \(m(t)\): \(P(y = 1 | x) = m(f(x))\). Она настраивается под квадратичную ошибку:
\[m = \mathop{\rm arg\,min}\limits_{z} \sum (y_i — z(f(x_i))^2,\] с помощью специального алгоритма (Pool-Adjacent-Violators Algorithm). В результате калибровки получаем надстройку над нашей моделью, которая применяется поверх предсказаний базовой модели.
22. Запишите функционал логистической регрессии. Как он связан с методом максимума правдоподобия?
Модель: \[
p(y = 1| x)
=
\frac{1}{1 + \exp(-\langle w, x \rangle)}.
\]
Подставим трансформированный ответ линейной модели в логарифмическую функцию потерь:
\[
-\sum_{i = 1}^{\ell}\left([y_i = +1]
\log \frac{1}{1 + \exp(-\langle w, x_i \rangle)}
+[y_i = -1]\log \frac{\exp(-\langle w, x_i \rangle)}{1 + \exp(-\langle w, x_i \rangle)}
\right)
=
-\sum_{i = 1}^{\ell} \left(
[y_i = +1]\log \frac{1}{1 + \exp(-\langle w, x_i \rangle)}
+[y_i = -1]\log \frac{1}{1 + \exp(\langle w, x_i \rangle)}
\right)
=
\sum_{i = 1}^{\ell}
\log \left(
1 + \exp(-y_i \langle w, x_i \rangle)
\right).
\]
Попробуем сконструировать функцию потерь из других соображений. Если алгоритм \(b(x) \in [0, 1]\) действительно выдает вероятности, то они должны согласовываться с выборкой. С точки зрения алгоритма вероятность того, что в выборке встретится объект \(x_i\) с классом \(y_i\), равна \(b(x_i)^{[y_i = +1]} (1 — b(x_i))^{[y_i = -1]}\).
Исходя из этого, можно записать правдоподобие выборки (т.е. вероятность получить такую выборку с точки зрения алгоритма):
\[
Q(a, X)=
\prod_{i = 1}^{\ell}
b(x_i)^{[y_i = +1]} (1 — b(x_i))^{[y_i = -1]}.
\]
Данное правдоподобие можно использовать как функционал для обучения алгоритма – с той лишь оговоркой, что удобнее оптимизировать его логарифм:\[-\sum_{i = 1}^{\ell} \left([y_i = +1] \log b(x_i) + [y_i = -1] \log (1 — b(x_i))\right)
\to\min
\]
23. Запишите задачу метода опорных векторов для линейно неразделимого случая. Как функционал этой задачи связан с отступом классификатора? Как выглядит задача безусловной оптимизации в SVM?
Условный
\[
\left\{\begin{aligned}
& \frac{1}{2} \|w\|^2 + C \sum_{i = 1}^{\ell} \xi_i \to \min_{w, b, \xi} \\
& y_i \left(
\langle w, x_i \rangle + b
\right) \geq 1 — \xi_i, \quad i = 1, \dots, \ell, \\
& \xi_i \geq 0, \quad i = 1, \dots, \ell.
\end{aligned}
\right.
\]
Безусловный
\[
\frac12 \|w\|^2+
C
\sum_{i = 1}^{\ell}
\max(0,
1 — y_i (\langle w, x_i \rangle + b))
\to
\min_{w, b}
\]
Величина \(\frac{1}{\|w\|}\) в данном случае называется мягким отступом (soft margin). С одной стороны, мы хотим максимизировать отступ, с другой – минимизировать штраф за неидеальное разделение выборки \(\sum_{i = 1}^{\ell} \xi_i\).
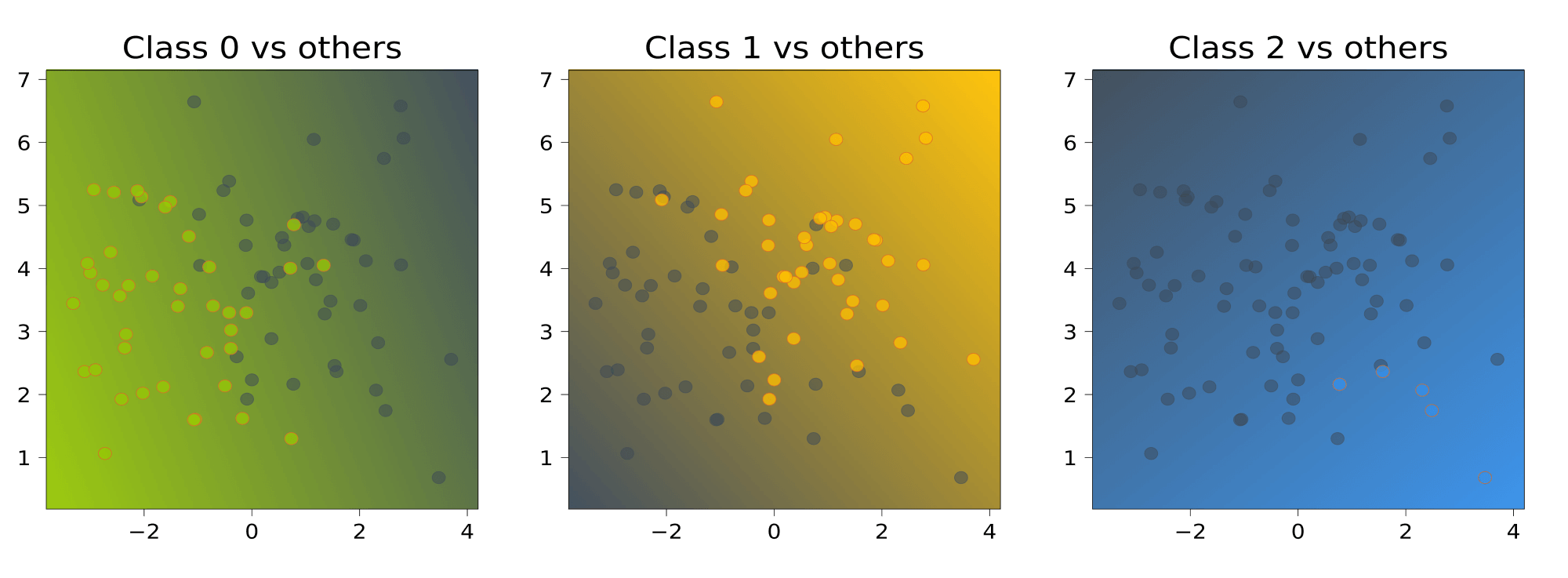
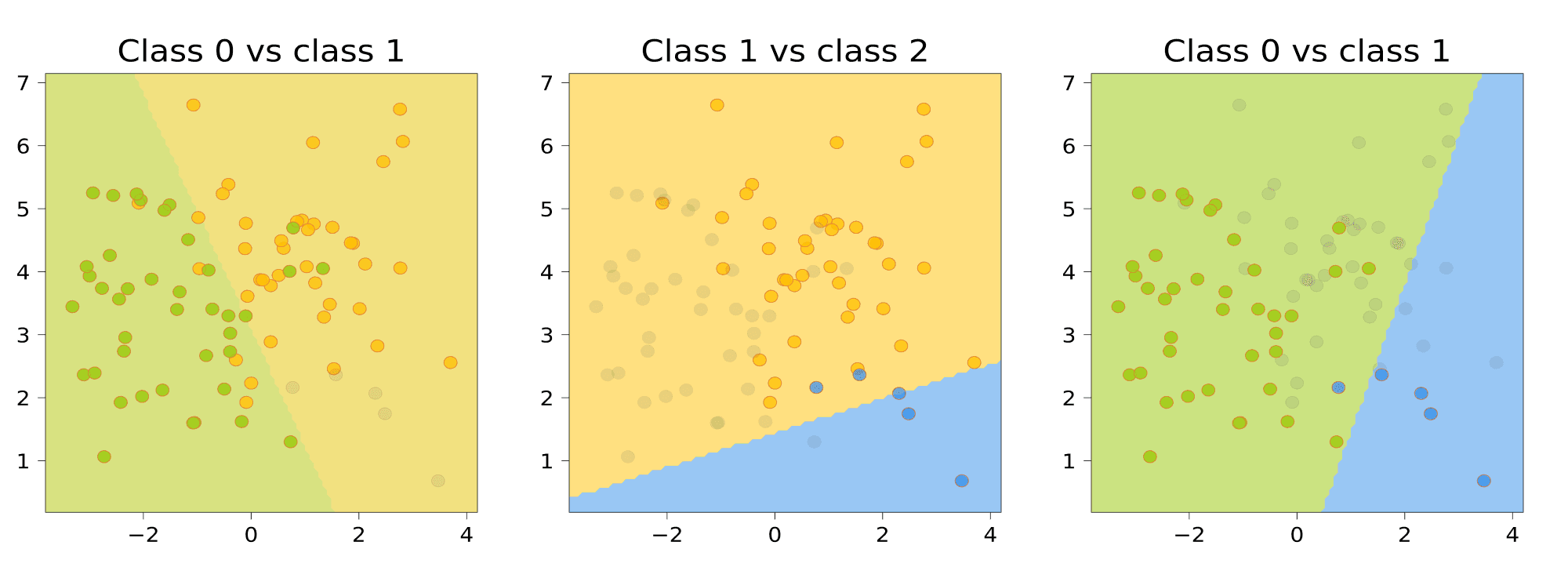
24. В чём заключаются one-vs-all и all-vs-all подходы в многоклассовой классификации?
One-vs-all
Обучим \(K\) линейных классификаторов \(b_1(x), \dots, b_K(x)\), выдающих оценки принадлежности классам \(1, \dots, K\) соответственно. Например, в случае с линейными моделями эти модели будут иметь вид \(b_k(x) = \langle w_k, x \rangle + w_{0k}\). Классификатор с номером \(k\) будем обучать по выборке \(\left(x_i, 2 [y_i = k] — 1\right)_{i = 1}^{\ell}\); иными словами, мы учим классификатор отличать \(k\) -й класс от всех остальных.
Итоговый классификатор будет выдавать класс, соответствующий самому уверенному из бинарных алгоритмов:
\[
a(x)
=
\mathop{\rm arg\,max}\limits_{k \in \{1, \dots, K\}}
b_k(x).
\]
Проблема данного подхода заключается в том, что каждый из классификаторов \(b_1(x), \dots, b_K(x)\) обучается на своей выборке, и выходы этих классификаторов могут иметь разные масштабы, из-за чего сравнивать их будет неправильно. Нормировать вектора весов, чтобы они выдавали ответы в одной и той же шкале, не всегда может быть разумным решением – так, в случае с SVM веса перестанут являться решением задачи, поскольку нормировка изменит норму весов.
All-vs-all
Обучим \(C_K^2\) классификаторов \(a_{ij}(x)\), \(i, j = 1, \dots, K\), \(i \neq j\).
Например, в случае с линейными моделями эти модели будут иметь вид
\[
b_k(x) = \mathop{\rm sign}\limits(\langle w_k, x \rangle + w_{0k} ).
\]
Классификатор \(a_{ij}(x)\) будем настраивать по подвыборк \(X_{ij} \subset X\), содержащей только объекты классов \(i\) и \(j\):
\[
X_{ij} = \{(x_n, y_n) \in X | [y_n = i] = 1 \ \text{или}\ [y_n = j] = 1 \}.
\]
Соответственно, классификатор \(a_{ij}(x)\) будет выдавать для любого объекта либо класс \(i\), либо класс \(j\).
Чтобы классифицировать новый объект, подадим его на вход каждого из построенных бинарных классификаторов. Каждый из них проголосует за своей класс; в качестве ответа выберем тот класс, за который наберется больше всего голосов:
\[
a(x) = \mathop{\rm arg\,max}\limits_{k \in \{1, \dots, K\}}
\sum_{i = 1}^{K} \sum_{j \neq i}
[a_{ij}(x) = k].
\]
25. Как измеряется качество в задаче многоклассовой классификации? Что такое микро- и макро-усреднение?
В многоклассовых задачах, как правило, стараются свести подсчет качества к вычислению одной из двухклассовых метрик. Выделяют два подхода к такому сведению: микро- и макро-усреднение.
Пусть выборка состоит из \(K\) классов. Рассмотрим \(K\) двухклассовых задач, каждая из которых заключается в отделении своего класса от остальных, то есть целевые значения для \(k\) -й задаче вычисляются как \(y_i^k = [y_i = k]\). Для каждой из них можно вычислить различные характеристики (TP, FP, и т.д.) алгоритма \(a^k(x) = [a(x) = k]\); будем обозначать эти величины как \(\text{TP}_k, \text{FP}_k, \text{FN}_k, \text{TN}_k\). Заметим, что в двухклассовом случае все метрики качества, которые мы изучали, выражались через эти элементы матрицы ошибок.
Микро-усренднение
При микро-усреднении сначала эти характеристики усредняются по всем классам, а затем вычисляется итоговая двухклассовая метрика – например, точность, полнота или F-мера. Например, точность будет вычисляться по формуле
\[
\text{precision}(a, X)
=
\frac{\overline{\text{TP}}}{\overline{\text{TP}}+\overline{\text{FP}}},
\] где, например, \(\overline{\text{TP}}\) вычисляется по формуле \[
\overline{\text{TP}}
=
\frac{1}{K}
\sum_{k = 1}^{K}
\text{TP}_k.
\]
Макро-усреднение
При макро-усреднении сначала вычисляется итоговая метрика для каждого класса, а затем результаты усредняются по всем классам. Например, точность будет вычислена как \[\text{precision}(a, X)=\frac{1}{K}\sum_{k = 1}^{K}\text{precision}_k(a, X);\qquad\]
\[
\text{precision}_k(a, X)=\frac{\text{TP}_k}{\text{TP}_k+\text{FP}_k}.
\]
Сравнение
Если какой-то класс имеет очень маленькую мощность, то при микро-усреднении он практически никак не будет влиять на результат, поскольку его вклад в средние TP, FP, FN и TN будет незначителен. В случае же с макро-вариантом усреднение проводится для величин, которые уже не чувствительны к соотношению размеров классов (если мы используем, например, точность или полноту), и поэтому каждый класс внесет равный вклад в итоговую метрику.
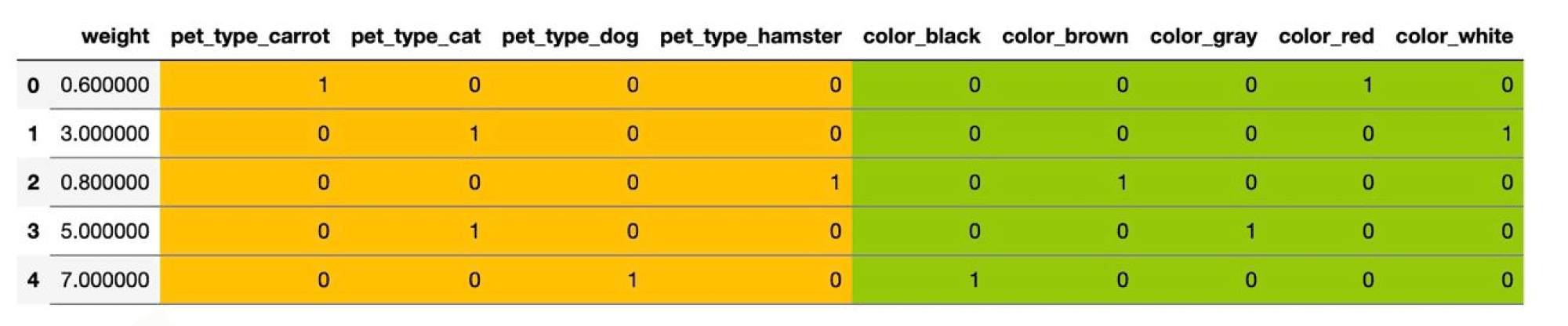
26. В чём заключается преобразование категориальных признаков в вещественные с помощью mean-target encoding? Почему использование этого способа кодирования может привести к переобучению? Какие методы борьбы с этой проблемой вам известны?
Mean target encoding
Более сложный метод кодирования категориальных признаков – через целевую переменную. Идея в том, что алгоритму для предсказания цены необходимо знать не конкретный цвет автомобиля, а то, как этот цвет сказывается на цене. Разберём сначала базовый подход – mean target encoding (иногда его называют ).
Заменим каждую категорию на среднее значение целевой переменной по всем объектам этой категории. Пусть \(j\) -й признак является категориальным. Для бинарной классификации новый признак будет выглядеть следующим образом:
\[
g_j(x, X)
=
\frac{
\sum_{i=1}^{\ell}
[f_j(x) = f_j(x_i)][y_i = +1]
}{
\sum_{i=1}^{\ell}
[f_j(x) = f_j(x_i)]
},
\]
где \(f_j(x_i)\) – \(j\) -й признак \(i\) -го объекта, \(y_i\) – класс \(i\) -го объекта.
Отметим, что эту формулу легко перенести как на случай многоклассовой классификации (в этом случае будем считать \(K\) признаков, по одному для каждого класса, и в числителе будет подсчитывать долю объектов с заданной категорией и с заданным классом), так и на случай регрессии (будем вычислять среднее значение целевой переменной среди объектов данной категории).
Вернёмся к бинарной классификации. Можно заметить, что для редких категорий мы получим некорректные средние значения целевой переменной. Например, в выборке было только три золотистых автомобиля, которые оказались старыми и дешёвыми. Из-за этого наш алгоритм начнёт считать золотистый цвет дешёвым. Для исправления этой проблемы можно регуляризировать признак средним значением целевой переменной по всем категориям так, чтобы у редких категорий значение было близко к среднему по всей выборке, а для популярных к среднему значению по категории.
Формально для задачи бинарной классификации это выражается так:
\[
g_j(x, X)
=
\frac{
\sum_{i=1}^{\ell}[f_j(x) = f_j(x_i)][y_i = +1]+
\frac{C}{\ell}\sum_{i=1}^{\ell}[y_i = +1]
}{
\sum_{i=1}^{\ell}
[f_j(x) = f_j(x_i)] + C
},
\]
где \(C\) – коэффициент, отвечающий за баланс между средним значением по категории и глобальным средним значением.
Однако если мы вычислим значения \(g_j(x, X)\) по всей выборке, то столкнёмся с переобучением, так как мы внесли информацию о целевой переменной в признаки (новый признак слабая, но модель, предсказывающая целевое значение). Поэтому вычисление таких признаков следует производить по блокам, то есть вычислять средние значения на основе одних фолдов для заполнения на другом блоке (аналогично процессу кросс-валидации). Если же ещё планируется оценка качества модели с помощью кросс-валидации по блокам, то придётся применить для подсчёта признаков. Этот подход заключается в кодировании категориальных признаков по блокам внутри блоков, по которым оценивается качество модели.
Разберём этот процесс. Представим, что хотим посчитать качество модели на 3-м блоке. Для этого:
- Разбиваем все внешние блоки, кроме 3-го, на внутренние блоки. Количество внутренних блоков может не совпадать с количеством внешних.
- Рассмотрим конкретный внешний
Для каждого из его внутренних блоков считаем значение \(g(x, X)\) на основе средних значений целевой переменной по блокам, исключая текущий. Для 3-го внешнего блока (который сейчас играет роль тестовой выборки) вычисляем \(g(x, X)\) как среднее вычисленных признаков по каждому из внутренних фолдов. - Обучаем модель на всех блоках, кроме 3-го, делаем предсказание на 3-м и считаем на нём качество.
Существуют альтернативы кодированию категориальных признаков по блокам.
Зашумление
Можно посчитать новые признаки по базовой формуле, а затем просто добавить к каждому значению случайный шум (например, нормальный). Это действительно снизит уровень корреляции счётчиков с целевой переменной. Проблема в том, что это делается за счёт снижения силы такого признака, а значит, мы ухудшаем итоговое качество модели. Поэтому важно подбирать дисперсию шума, чтобы соблюсти баланс между борьбой с переобучением и предсказательной силой счётчиков.
Сглаживание
Можно немного модифицировать формулу, чтобы сила регуляризации зависела от объёма данных по конкретной категории:
\[
g_j(x, X)
=
\lambda \left( n(f_j(x)) \right)
\frac{
\sum_{i=1}^{\ell}[f_j(x) = f_j(x_i)][y_i = +1]
}{
\sum_{i=1}^{\ell}[f_j(x) = f_j(x_i)]
}
+\left( 1 — \lambda \left( n(f_j(x)) \right) \right)
\frac{1}{\ell}
\sum_{i = 1}^{\ell}
[y_i = +1]
,
\]
где \(n(z) = \sum_{i = 1}^{\ell} [f_j(x_i) = z]\) – число объектов категории \(z\), \(\lambda(n)\) – некоторая монотонно возрастающая функция, дающая значения из отрезка \([0, 1]\).
Примером может служить \(\lambda(n) = \frac{1}{1 + \exp(-n)}\). Если грамотно подобрать эту функцию, то она будет вычищать значение целевой переменной из редких категорий и мешать переобучению.
Кодирование по времени.
Можно отсортировать выборку некоторым образом и для \(i\) -го объекта вычислять статистики только по предыдущим объектам:
\[
g_j(x_k, X)
=
\frac{
\sum_{i=1}^{k — 1}
[f_j(x) = f_j(x_i)][y_i = +1]
}{
\sum_{i=1}^{k — 1}
[f_j(x) = f_j(x_i)]
}.
\]
Для хорошего качества имеет смысл отсортировать выборку случайным образом несколько раз, и для каждого такого порядка посчитать свои счётчики.
Это даёт улучшение качества, например, потому что для объектов, находящихся в начале выборки, признаки будут считаться по очень небольшой подвыборке, и поэтому вряд ли будут хорошо предсказывать целевую переменную. При наличии нескольких перестановок хотя бы один из новых признаков будет вычислен по подвыборке достаточного размера. Такой подход, например, используется в библиотеке CatBoost.
Weight of Evidence
Существует альтернативный способ кодирования категориальных признаков, основанный на подсчёте соотношения положительных и отрицательных объектов среди объектов данной категории. Этот подход, в отличие от других, сложнее обобщить на многоклассовый случай или для регрессии.
Введём обозначение для доли объектов класса \(b\) внутри заданной категории \(c\) среди всех объектов данного класса в выборке:
\[
P(c | y = b)=
\frac{
\sum_{i = 1}^{\ell}[y_i = b] [f_j(x_i) = c]+\alpha
}{
\sum_{i = 1}^{\ell}[y_i = b]+2 \alpha
},
\]
где \(\alpha\) – параметр сглаживания.
Вычислим новое значение признака как
\[
g_j(x, X)
=
\log\left(
\frac{
P(f_j(x) | y = +1)
}{
P(f_j(x) | y = -1)
}
\right).
\]
Если \(g_j(x, X)\) близко к нулю, то данная категория примерно с одинаковой вероятностью встречается в обоих классах, и поэтому вряд ли будет хорошо предсказывать значение целевой переменной. Чем сильнее отличие от нуля, тем сильнее категория характеризует один из классов.
Разумеется, в конкретной задаче лучше всего может себя проявлять любой из этих подходов, поэтому имеет смысл сравнивать их и выбирать лучший – или использовать все сразу.
27. Как определить для линейной модели, какие признаки являются самыми важными?
- наибольшим модулем соответствующего параметра линейной модели
- \(t\) -статистика
\[
t(j) = \frac{|\mu_+ — \mu_-|}{\sqrt{\frac{n_+ \sigma^2_+ + n_- \sigma^2_-}{n_+ + n_-}}}
\] - исключаем по очереди один из признаков и смотрим, как это влияет на качество. Удаляем признаки таким жадным способом, пока не окажется выполненным некоторое условие (количество признаков или ухудшение качества).
- Можно использовать L1-регуляризацию, которая занулит веса на самых бесполезных признаках.
- Можно, в конце концов, посчитать корреляцию таргета и признака.
28. Опишите жадный алгоритм обучения решающего дерева.
Опишем базовый жадный алгоритм построения бинарного решающего дерева. Начнем со всей обучающей выборки \(X\) и найдем наилучшее ее разбиение на две части \(R_1(j, t) = \{x | x_j < t\}\) и \(R_2(j, t) = \{x | x_j \geq t\}\)
с точки зрения заранее заданного функционала качества \(Q(X, j, t)\). Найдя наилучшие значения \(j\) и \(t\), создадим корневую вершину дерева, поставив ей в соответствие предикат \([x_j < t]\).
Объекты разобьются на две части – одни попадут в левое поддерево, другие в правое. Для каждой из этих подвыборок рекурсивно повторим процедуру, построив дочерние вершины для корневой, и так далее. В каждой вершине мы проверяем, не выполнилось ли некоторое условие останова – и если выполнилось, то прекращаем рекурсию и объявляем эту вершину листом. Когда дерево построено, каждому листу ставится в соответствие ответ. В случае с классификацией это может быть класс, к которому относится больше всего объектов в листе, или вектор вероятностей (скажем, вероятность класса может быть равна доле его объектов в листе). Для регрессии это может быть среднее значение, медиана или другая функция от целевых переменных объектов в листе. Выбор конкретной функции зависит от функционала качества в исходной задаче.
29. Почему с помощью бинарного решающего дерева можно достичь нулевой ошибки на обучающей выборке без повторяющихся объектов?
Для выборки без повторяющихся объектов мы можем построить такое дерево, что количество листов в нем будет равно количеству объектов в выборке, и в каждом листе будет стоять отдельный объект. У каждого объекта будет уникальное признаковое описание, а значит, мы можем построить дерево предикатов так, чтобы оно делило выборку идеально. Само собой, обобщающая способность такого дерева будет не очень хорошей.
30. Как в общем случае выглядит критерий хаотичности? Как он используется для выбора предиката во внутренней вершине решающего дерева? Как вывести критерий Джини и энтропийный критерий?
Общий случай
\[
H( R)
=
\min_{c \in \mathbb{Y}}
\frac{1}{|R|}
\sum_{(x_i, y_i) \in R}
L(y_i, c),
\]
Т.е. критерий показывает, насколько хорошо целевая переменная в данном множестве приближается константой.
Чем менее разнообразно значение целевой переменной среди объектов, тем меньше значение критерия — поэтому мы пытаемся его минимизировать. При этом в процессе разбиения мы пытаемся максимизировать такой функционал:
\[
Q(R_m, j, s)=H(R_m)-\frac{|R_\ell|}{|R_m|}H(R_\ell)-\frac{|R_r|}{|R_m|}H(R_r)
\]
Джини
Рассмотрим ситуацию, в которой мы выдаём в вершине не один класс, а распределение на всех классах \(c = (c_1, \dots, c_K)\), \(\sum_{k = 1}^{K} c_k = 1\). Качество такого распределения можно измерять, например, с помощью критерия Бриера (Brier score):
\[
H( R)
=
\min_{\sum_k c_k = 1}
\frac{1}{|R|}
\sum_{(x_i, y_i) \in R}
\sum_{k = 1}^{K}
(c_k — [y_i = k])^2.
\]
Легко заметить, что здесь мы, по сути, ищем каждый \(c_k\) как оптимальную с точки зрения MSE константу, приближающую индикаторы попадания объектов выборки в класс \(k\). Это означает, что оптимальный вектор вероятностей состоит из долей классов \(p_k\): \[c_* = (p_1, \dots, p_K)\]
Если подставить эти вероятности в исходный критерий информативности и провести ряд преобразований, то мы получим критерий Джини: \[H( R)=\sum_{k = 1}^{K}p_k (1 — p_k).\]
Энтропийный
Мы уже знакомы с более популярным способом оценивания качества вероятностей – логарифмическими потерями, или логарифмом правдоподобия:
\[
H( R)=\min_{\sum_k c_k = 1} \left(-\frac{1}{|R|}\sum_{(x_i, y_i) \in R}\sum_{k = 1}^{K}[y_i = k]\log c_k\right)
\]
Для вывода оптимальных значений \(c_k\) вспомним, что все значения \(c_k\) должны суммироваться в единицу.
Как известного из методов оптимизации, для учёта этого ограничения необходимо искать минимум лагранжиана:
\[
L(c, \lambda)=-\frac{1}{|R|}\sum_{(x_i, y_i) \in R}\sum_{k = 1}^{K}[y_i = k]\log c_k+\lambda\sum_{k = 1}^{K}c_k\to\min_{c_k}
\]
Дифференцируя, получаем:
\[
\frac{\partial}{\partial c_k}L(c, \lambda)=-\frac{1}{|R|}\sum_{(x_i, y_i) \in R}[y_i = k]\frac{1}{c_k}+\lambda=-\frac{p_k}{c_k}+\lambda=0
\]
откуда выражаем \(c_k = p_k / \lambda\).
Суммируя эти равенства по \(k\), получим
\[
1 = \sum_{k = 1}^{K} c_k = \frac{1}{\lambda} \sum_{k = 1}^{K} p_k = \frac{1}{\lambda},
\] откуда \(\lambda = 1\).
Значит, минимум достигается при \(c_k = p_k\), как и в предыдущем случае. Подставляя эти выражения в критерий, получим, что он будет представлять собой энтропию распределения классов:
\[H( R)=-\sum_{k = 1}^{K}p_k\log p_k.\]
Из теории вероятностей известно, что энтропия ограничена снизу нулем, причем минимум достигается на вырожденных распределениях (\(p_i = 1\), \(p_j = 0\) для \(i \neq j\)). Максимальное же значение энтропия принимает для равномерного распределения. Отсюда видно, что энтропийный критерий отдает предпочтение более распределениям классов в вершине.
31. Для какой ошибки строится разложение на шум, смещение и разброс? Запишите формулу этой ошибки.
Разложение ошибки на три компоненты, которое мы только что вывели, верно только для квадратичной функции потерь. Существуют более общие формы этого разложения, которые состоят из трёх компонент с аналогичным смыслом, поэтому можно утверждать, что для большинства распространённых функций потерь ошибка метода обучения складывается из шума, смещения и разброса; значит, и дальнейшие рассуждения про изменение этих компонент в композициях также можно обобщить на другие функции потерь (например, на индикатор ошибки классификации).
BVD для среднеквадратичного риска метода \(\mu\) (обученного на выборке \(X\)), усредненного по всем возможным выборкам.
\[
L(\mu)=
\mathbb{E}_{X} \Bigl[
\mathbb{E}_{x, y} \Bigl[
\bigl(
y — \mu(X)(x)
\bigr)^2
\Bigr]
\Bigr]
\]
\[
L(\mu)=
\underbrace{\mathbb{E}_{x, y}\Bigl[\bigl(y — \mathbb{E}[y | x]\bigr)^2\Bigr]}_{\text{шум}}+
\underbrace{\mathbb{E}_{x} \Bigl[\bigl(\mathbb{E}_{X} \bigl[ \mu(X) \bigr]-\mathbb{E}[y | x]\bigr)^2\Bigr]}_{\text{смещение}}
+\underbrace{\mathbb{E}_{x} \Bigl[\mathbb{E}_{X} \Bigl[\bigl(\mu(X)-\mathbb{E}_{X} \bigl[ \mu(X) \bigr]\bigr)^2\Bigr]\Bigr]}_{\text{разброс}}.
\]
32. Запишите формулы для шума, смещения и разброса метода обучения для случая квадратичной функции потерь.
\[
L(\mu)=
\underbrace{\mathbb{E}_{x, y}\Bigl[\bigl(y — \mathbb{E}[y | x]\bigr)^2\Bigr]}_{\text{шум}}+
\underbrace{\mathbb{E}_{x} \Bigl[\bigl(\mathbb{E}_{X} \bigl[ \mu(X) \bigr]-\mathbb{E}[y | x]\bigr)^2\Bigr]}_{\text{смещение}}
+\underbrace{\mathbb{E}_{x} \Bigl[\mathbb{E}_{X} \Bigl[\bigl(\mu(X)-\mathbb{E}_{X} \bigl[ \mu(X) \bigr]\bigr)^2\Bigr]\Bigr]}_{\text{разброс}}.
\]
33. Приведите пример семейства алгоритмов с низким смещением и большим разбросом; семейства алгоритмов с большим смещением и низким разбросом. Поясните примеры.
Смещение показывает, насколько хорошо с помощью данных метода обучения и семейства алгоритмов можно приблизить оптимальный алгоритм. Как правило, смещение маленькое у сложных (precision) семейств (например, у деревьев) и большое у простых семейств (например, линейных классификаторов). Дисперсия показывает, насколько сильно может изменяться ответ обученного алгоритма в зависимости от выборки иными словами, она характеризует чувствительность метода обучения к изменениям в выборке. Как правило, простые семейства имеют маленькую дисперсию (variance), а сложные семейства большую дисперсию.
34. Что такое бэггинг? Как его смещение и разброс связаны со смещением и разбросом базовых моделей?
Для начала, бутстрап – способ ресэмплинга. По имеющейся выборке \(X\) создадим \(N\) новых выборок путем взятия элементов из \(X\) с повторениями.
Пусть имеется некоторый метод обучения \(\mu(X)\). Построим на его основе метод \(\tilde \mu(X)\), который генерирует случайную подвыборку \(\tilde X\) с помощью бутстрапа и подает ее на вход метода \(\mu\): \(\tilde \mu(X) = \mu(\tilde X)\). Напомним, что бутстрап представляет собой сэмплирование \(\ell\) объектов из выборки с возвращением, в результате чего некоторые объекты выбираются несколько раз, а некоторые – ни разу.
Помещение нескольких копий одного объекта в бутстрапированную выборку соответствует выставлению веса при данном объекте – соответствующее ему слагаемое несколько раз войдет в функционал, и поэтому штраф за ошибку на нем будет больше.
В бэггинге (bagging, bootstrap aggregation) предлагается обучить некоторое число алгоритмов \(b_n(x)\) с помощью метода \(\tilde \mu\), и построить итоговую композицию как среднее данных базовых алгоритмов:
\[
a_N(x)
=
\frac{1}{N}
\sum_{n = 1}^{N}
b_n(x)
=
\frac{1}{N}
\sum_{n = 1}^{N}
\tilde \mu(X)(x).
\]
Такая композиция и называется бэггингом. Он позволяет объединить базовые алгоритмы с низким смещением, но высоким разбросом, в композицию с низким смещением и разбросом, причем, в идеальном случае (модели совсем не коррелируют) разброс падает в N раз. Если же корреляция имеет место, то уменьшение дисперсии может быть гораздо менее существенным.
Помещение нескольких копий одного объекта в бутстрапированную выборку соответствует выставлению веса при данном объекте соответствующее ему слагаемое несколько раз войдет в функционал, и поэтому штраф за ошибку на нем будет больше.
35. Что такое случайный лес? Чем он отличается от бэггинга над решающими деревьями?
Случайный лес — метод построения композиции, основанный на бэггинге над деревьями. Т.к. Бэггинг сильнее понижает разброс при слабой корреляции моделей, в RF предлагается специально ее понижать с помощью
- рандомизации по признакам (для каждого базового алгоритма используется некое подмножество признаков вместо всех) (это отличие от бэггинга над деревьями)
- рандомизации по объектам (для каждого базового алгоритма в бутстрапе используется не вся выборка X, а какая-то подвыборка)
36. Что такое out-of-bag оценка в бэггинге?
Мы можем для каждого объекта \(x_{i}\) найти деревья, которые были обучены без него, и вычислить по их ответам out-of-bag-ошибку
Каждое дерево в случайном лесе обучается по подмножеству объектов. Это значит, что те объекты, которые не вошли в бутстрапированную выборку \(X_n\) дерева \(b_n\), по сути являются контрольными для данного дерева.
Значит, мы можем для каждого объекта \(x_i\) найти деревья, которые были обучены без него, и вычислить по их ответам out-of-bag-ошибку:
\[
\text{OOB}
=
\sum_{i = 1}^{\ell}
L \left(
y_i,
\frac{1}{\sum_{n = 1}^{N} [x_i \notin X_n]}
\sum_{n = 1}^{N}
[x_i \notin X_n] b_n(x_i)
\right),
\] где \(L(y, z)\) – функция потерь.
Можно показать, что по мере увеличения числа деревьев \(N\) данная оценка стремится к leave-one-out-оценке, но при этом существенно проще для вычисления.
37. Запишите вид композиции, которая обучается в градиентном бустинге. Как выбирают количество базовых алгоритмов в ней?
\(a_{N}(x)=\sum\limits_{n=0}^{N}\gamma_{n}b_{n}(x)\)
В такой композиции каждый следующий базовый алгоритм исправляет ошибки предыдущего.
При большом их числе мы начинаем переобучаться — можем использовать валидационную выборку для подбора (это просто гиперпараметр).
38. Что такое сдвиги в градиентном бустинге? Как они вычисляются и для чего используются?
Сдвиг (остаток) — расстояния от ответа нашего алгоритма до истинного ответа.
\[
s_i^{(N)}=y_i — \sum_{n = 1}^{N — 1} b_n(x_i)=y_i- a_{N — 1}(x_i),\qquad i = 1, \dots, \ell
\]
Или
\[
s_i=-\left.\frac{\partial L}{\partial z}\right|_{z = a_{N — 1}(x_i)}
\]
С помощью сдвига мы настраиваем очередной базовой алгоритм:
\[
b_N(x)
:=
\mathop{\rm arg\,min}\limits_{b \in \mathbb{A}}
\frac12
\sum_{i = 1}^{\ell}
(b(x_i) — s_i^{(N)})^2
\]
39. Как обучается очередной базовый алгоритм в градиентном бустинге? Что такое сокращение шага?
Пусть мы построили композицию \(a_{N-1}(x)\) из \(N-1\) базовых алгоритмов. Хотим выбрать такой алгоритм следующим, чтобы как можно сильнее уменьшить ошибку
Допустим, мы построили композицию \(a_{N — 1}(x)\) из \(N — 1\) алгоритма, и хотим выбрать следующий базовый алгоритм \(b_N(x)\) так, чтобы как можно сильнее уменьшить ошибку:
\[
\sum_{i = 1}^{\ell}L(y_i, a_{N — 1}(x_i) + \gamma_N b_N(x_i))\to\min_{b_N, \gamma_N}
\]
Ответим в первую очередь на следующий вопрос: если бы в качестве алгоритма \(b_{N}(x)\) мы могли выбрать совершенно любую функцию, то какие значения ей следовало бы принимать на объектах обучающей выборки? Иными словами, нам нужно понять, какие числа \(s_1, \dots, s_\ell\) надо выбрать для решения следующей задачи:
\[
\sum_{i = 1}^{\ell}L(y_i, a_{N — 1}(x_i) + s_i)\to\min_{s_1, \dots, s_\ell}
\]
Понятно, что можно требовать \(s_i = y_i — a_{N — 1}(x_i)\), но такой подход никак не учитывает особенностей функции потерь \(L(y, z)\) и требует лишь точного совпадения предсказаний и истинных ответов. Более разумно потребовать, чтобы сдвиг \(s_i\) был противоположен производной функции потерь в точке \(z = a_{N — 1}(x_i)\):
\[
s_i=-\left.\frac{\partial L}{\partial z}\right|_{z = a_{N — 1}(x_i)}
\]
В этом случае мы сдвинемся в сторону скорейшего убывания функции потерь. Заметим, что вектор сдвигов \(s = (s_1, \dots, s_\ell)\) совпадает с антиградиентом:
\[
\left(-\left.\frac{\partial L}{\partial z}\right|_{z = a_{N — 1}(x_i)}\right)_{i = 1}^{\ell}=-\nabla_z\sum_{i = 1}^{\ell}L(y_i, z_i)\big|_{z_i = a_{N — 1}(x_i)}
\]
При таком выборе сдвигов \(s_i\) мы, по сути, сделаем один шаг градиентного спуска, двигаясь в сторону наискорейшего убывания ошибки на обучающей выборке. Отметим, что речь идет о градиентном спуске в \(\ell\) -мерном пространстве предсказаний алгоритма на объектах обучающей выборки. Поскольку вектор сдвига будет свой на каждой итерации, правильнее обозначать его как \(s_i^{(N)}\), но для простоты будем иногда опускать верхний индекс. Итак, мы поняли, какие значения новый алгоритм должен принимать на объектах обучающей выборки. По данным значениям в конечном числе точек необходимо построить функцию, заданную на всем пространстве объектов. Это классическая задача обучения с учителем, которую мы уже хорошо умеем решать. Один из самых простых функционалов – среднеквадратичная ошибка. Воспользуемся им для поиска базового алгоритма, приближающего градиент функции потерь на обучающей выборке:
\[
b_N(x)=\mathop{\rm arg\,min}\limits_{b \in \mathbb{A}}\sum_{i = 1}^{\ell}\left(b(x_i) — s_i\right)^2
\]
Отметим, что здесь мы оптимизируем квадратичную функцию потерь независимо от функционала исходной задачи – вся информация о функции потерь \(L\) находится в антиградиенте \(s_i\), а на данном шаге лишь решается задача аппроксимации функции по \(\ell\) точкам. Разумеется, можно использовать и другие функционалы, но среднеквадратичной ошибки, как правило, оказывается достаточно.
Ещё одна причина для использования среднеквадратичной ошибки состоит в том, что от алгоритма требуется как можно точнее приблизить направление наискорейшего убывания функционала (то есть направление \((s_i)_i\)); совпадение направлений вполне логично оценивать через косинус угла между ними, который напрямую связан со среднеквадратичной ошибкой.
После того, как новый базовый алгоритм найден, можно подобрать коэффициент при нем по аналогии с наискорейшим градиентным спуском:
\[
\gamma_N=\mathop{\rm arg\,min}\limits_{\gamma \in \mathbb{R}}\sum_{i = 1}^{\ell}L(y_i, a_{N — 1}(x_i) + \gamma b_N(x_i))
\]
Описанный подход с аппроксимацией антиградиента базовыми алгоритмами и называется градиентным бустингом. Данный метод представляет собой поиск лучшей функции, восстанавливающей истинную зависимость ответов от объектов, в пространстве всех возможных функций. Ищем мы данную функцию с помощью спуска – каждый шаг делается вдоль направления, задаваемого некоторым базовым алгоритмом. При этом сам базовый алгоритм выбирается так, чтобы как можно лучше приближать антиградиент ошибки на обучающей выборке.
Сокращение шага — вместо перехода в оптимальную точку делаем укороченный шаг. По сути, мы снижаем доверие к каждому базовому алгоритму. \(\eta \in (0, 1]\) \(a_{N}(x)=a_{N-1}(x)+\eta\gamma_{N}b_{N}(x)\)
40. В чём заключается переподбор прогнозов в листьях решающих деревьев в градиентном бустинге?
Вспомним, что решающее дерево разбивает все пространство на непересекающиеся области,в каждой из которых его ответ равен константе:
\[
b_n(x)=\sum_{j = 1}^{J_n}b_{nj}[x \in R_j],
\]
где \(j = 1, \dots, J_n\) – индексы листьев, \(R_j\) – соответствующие области разбиения, \(b_{nj}\) – значения в листьях.
Значит, на \(N\) -й итерации бустинга композиция обновляется как
\[
a_N(x)=a_{N — 1}(x)+\gamma_N\sum_{j = 1}^{J_N}b_{Nj}[x \in R_j]=a_{N — 1}(x)+\sum_{j = 1}^{J_N}\gamma_Nb_{Nj}[x \in R_j].
\]
Видно, что добавление в композицию одного дерева с \(J_N\) листьями равносильно добавлению \(J_N\) базовых алгоритмов, представляющих собой предикаты вида \([x \in R_j]\). Если бы вместо общего коэффициента \(\gamma_N\) был свой коэффициент \(\gamma_{Nj}\) при каждом предикате, то мы могли бы его подобрать так, чтобы повысить качество композиции. Если подбирать свой коэффициент \(\gamma_{Nj}\) при каждом слагаемом, то потребность в \(b_{Nj}\) отпадает, его можно просто убрать:
\[
\sum_{i = 1}^{\ell}L\left(y_i,a_{N — 1}(x_i)+\sum_{j = 1}^{J_N}\gamma_{Nj}[x \in R_j]\right)\to\min_{\{\gamma_{Nj}\}_{j = 1}^{J_N}}.
\]
Поскольку области разбиения \(R_j\) не пересекаются, данная задача распадается на \(J_N\) независимых подзадач:
\[
\gamma_{Nj}=\mathop{\rm arg\,min}\limits_\gamma\sum_{x_i \in R_j}L(y_i, a_{N — 1}(x_i) + \gamma),\qquad j = 1, \dots, J_N.
\]
41. Как в xgboost выводится функционал ошибки с помощью разложения в ряд Тейлора?
Мы хотим найти алгоритм \(b(x)\), решающий следующую задачу:
\[
\sum_{i = 1}^{\ell}
L(y_i, a_{N — 1}(x_i) + b(x_i))
\to
\min_{b}
\]
Разложим функцию \(L\) в каждом слагаемом в ряд Тейлора до второго члена с центром в ответе композиции \(a_{N — 1}(x_i)\):
\[
\sum_{i = 1}^{\ell}L(y_i, a_{N — 1}(x_i) + b(x_i))\approx
\sum_{i = 1}^{\ell} \left(L(y_i, a_{N — 1}(x_i))-s_i b(x_i)+\frac12h_i b^2(x_i)\right),
\]
где через \(h_i\) обозначены вторые производные по сдвигам:
\[
h_i
=
\left.
\frac{\partial^2}{\partial z^2}
L(y_i, z)
\right|_{a_{N — 1}(x_i)}
\]
Первое слагаемое не зависит от нового базового алгоритма, и поэтому его можно выкинуть. Получаем функционал:
\[
\sum_{i = 1}^{\ell} \left(-s_i b(x_i)+\frac{1}{2}h_i b^2(x_i)\right)\to\min_{b}
\]
Покажем, что он очень похож на среднеквадратичный из формулы. Преобразуем его:
\[
\sum_{i = 1}^{\ell}\left(b(x_i) — s_i\right)^2\\
=
\sum_{i = 1}^{\ell} \left(b^2(x_i)-2 s_i b(x_i)+s_i^2\right) = \{\text{последнее слагаемое не зависит от $b$}\} \\
=
\sum_{i = 1}^{\ell} \left(b^2(x_i)-2 s_i b(x_i)\right)\\
=
2\sum_{i = 1}^{\ell}\left(-s_ib(x_i)+\frac{1}{2}b^2(x_i)\right)
\to\min_{b}
\]
Видно, что последняя формула совпадает с точностью до константы, если положить \(h_i = 1\). Таким образом, в обычном градиентном бустинге мы используем аппроксимацию второго порядка при обучении очередного базового алгоритма, и при этом отбрасываем информацию о вторых производных (то есть считаем, что функция имеет одинаковую кривизну по всем направлениям).
42. Какие регуляризации используются в xgboost?
Будем далее работать с функционалом. Он измеряет лишь ошибку композиции после добавления нового алгоритма, никак при этом не штрафуя за излишнюю сложность этого алгоритма. Ранее мы решали проблему переобучения путем ограничения глубины деревьев, но можно подойти к вопросу и более гибко. Мы выясняли, что дерево \(b(x)\) можно описать формулой
\[
b(x)
=
\sum_{j = 1}^{J}
b_{j}
[x \in R_{j}]
\]
Его сложность зависит от двух показателей:
- Число листьев \(J\). Чем больше листьев имеет дерево, тем сложнее его разделяющая поверхность, тем больше у него параметров и тем выше риск переобучения.
- Норма коэффициентов в листьях \(\|b\|_2^2 = \sum_{j = 1}^{J} b_j^2\). Чем сильнее коэффициенты отличаются от нуля, тем сильнее данный базовый алгоритм будет влиять на итоговый ответ композиции.
Добавляя регуляризаторы, штрафующие за оба этих вида сложности, получаем следующую задачу:
\[
\sum_{i = 1}^{\ell} \left(-s_i b(x_i)+\frac{1}{2}h_i b^2(x_i)\right)
+\gamma J
+\frac{\lambda}{2}\sum_{j = 1}^{J}b_j^2
\to\min_{b}
\]
Если вспомнить, что дерево \(b(x)\) дает одинаковые ответы на объектах, попадающих в один лист, то можно упростить функционал:
\[
\sum_{j = 1}^{J} \Biggl\{
\underbrace{
\Biggl(-\sum_{i \in R_j} s_i\Biggr)
}_{=-S_j}
b_j+\frac12
\Biggl(\lambda+
\underbrace{\sum_{i \in R_j} h_i}_{=H_j}
\Biggr)
b_j^2+\gamma
\Biggr\}
\to
\min_{b}
\]
Каждое слагаемое здесь можно минимизировать по \(b_j\) независимо. Заметим, что отдельное слагаемое представляет собой параболу относительно \(b_j\), благодаря чему можно аналитически найти оптимальные коэффициенты в листьях:
\[
b_j
=
\frac{S_j}{H_j + \lambda}
\]
Подставляя данное выражение обратно в функционал, получаем, что ошибка дерева с оптимальными коэффициентами в листьях вычисляется по формуле
\[
H(b)=
-\frac12\sum_{j = 1}^{J}
\frac{S_j^2}{H_j + \lambda}+\gamma J
\]
43. Задача кластеризации. Метрики качества.
Приведём несколько примеров внутренних метрик качества. Будем считать, что каждый кластер характеризуется своим центром \(c_k\).
Внутрикластерное расстояние
\[
\sum_{k = 1}^{K}\sum_{i = 1}^{\ell}[a(x_i) = k]\rho(x_i, c_k),
\]
где \(\rho(x, z)\) – некоторая функция расстояния. Данный функционал требуется минимизировать, поскольку в идеале все объекты кластера должны быть одинаковыми.
Межкластерное расстояние
\[
\sum_{i, j = 1}^{\ell}[a(x_i) \neq a(x_j)]\rho(x_i, x_j).
\]
Данный функционал нужно максимизировать, поскольку объекты из разных кластеров должны быть как можно менее похожими друг на друга.
Индекс Данна (Dunn Index)
\[
\frac{
\min_{1 \leq k < k^\prime \leq K}d(k, k^\prime)
}{
\max_{1 \leq k \leq K}d(k)
},
\]
где \(d(k, k^\prime)\) – расстояние между кластерами \(k\) и \(k^\prime\) (например, евклидово расстояние между их центрами), а \(d(k)\) – внутрикластерное расстояние для \(k\) -го кластера (например, сумма расстояний от всех объектов этого кластера до его центра). Данный индекс необходимо максимизировать.
44. Метод K-Means, вывод его шагов.
Одним из наиболее популярных методов кластеризации является, который оптимизирует внутрикластерное расстояние, в котором используется квадрат евклидовой метрики.
Заметим, что в данном функционале имеется две степени свободы: центры кластеров \(c_k\) и распределение объектов по кластерам \(a(x_i)\). Выберем для этих величин произвольные начальные приближения, а затем будем оптимизировать их по очереди:
- Зафиксируем центры кластеров.
В этом случае внутрикластерное расстояние будет минимальным, если каждый объект будет относиться к тому кластеру, чей центр является ближайшим:
\[
a(x_i)=\mathop{\rm arg\,min}\limits_{1 \leq k \leq K}\rho(x_i, c_k).
\] - Зафиксируем распределение объектов по кластерам. В этом случае внутрикластерное расстояние с квадратом евклидовой метрики можно продифференцировать по центрам кластеров и вывести аналитические формулы для них:
\[
c_k=\frac{1}{\sum_{i = 1}^{\ell} [a(x_i) = k]}\sum_{i = 1}^{\ell}[a(x_i) = k] x_i.
\]
Повторяя эти шаги до сходимости, мы получим некоторое распределение объектов по кластерам. Новый объект относится к тому кластеру, чей центр является ближайшим.
Результат работы метода K-Means существенно зависит от начального приблжения. Существует большое количество подходов к инициализации; одним из наиболее успешных считается k-means++.
| Error function | |
|---|---|

Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
Some authors define 

This nonelementary integral is a sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit.
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[3] The error function complement was also discussed by Glaisher in a separate publication in the same year.[4]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
Integrand exp(−z2)
erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[5]
The defining integral cannot be evaluated in closed form in terms of elementary functions (see Liouville’s theorem), but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[6]
Bürmann series[edit]
An expansion,[7] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[8]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series[9]
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[10]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder is
which follows easily by induction, writing
and integrating by parts.
The asymptotic behavior of the remainder term, in Landau notation, is
as x → ∞. This can be found by
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[11]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[12] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[13][14]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[15]
- The above have been generalized to sums of N exponentials[16] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[17] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[18] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[19]
- A single-term lower bound is[20]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[21][22]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[23]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[24]
with
and
- An approximation of
with a maximum relative error less than
in absolute value is:[25]
for
,
and for
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[26] (which can be used instead of erfc to avoid arithmetic underflow[26][27]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[28]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[29]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[26]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[30]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In POSIX-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[31]
- The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[32]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
- Standard score
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Whittaker, E. T.; Watson, G. N. (1927). A Course of Modern Analysis. Cambridge University Press. p. 341. ISBN 978-0-521-58807-2.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Dominici, Diego (2006). «Asymptotic analysis of the derivatives of the inverse error function». arXiv:math/0607230.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse» (Document).
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ Dia, Yaya D. (2023). Approximate Incomplete Integrals, Application to Complementary Error Function. Available at SSRN: https://ssrn.com/abstract=4487559 or http://dx.doi.org/10.2139/ssrn.4487559, 2023
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ «math.h — mathematical declarations». opengroup.org. 2018. Retrieved 21 April 2023.
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
External links[edit]
- A Table of Integrals of the Error Functions
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
- 1 Оценки качества классификации
- 1.1 Матрица ошибок (англ. Сonfusion matrix)
- 1.2 Аккуратность (англ. Accuracy)
- 1.3 Точность (англ. Precision)
- 1.4 Полнота (англ. Recall)
- 1.5 F-мера (англ. F-score)
- 1.6 ROC-кривая
- 1.7 Precison-recall кривая
- 2 Оценки качества регрессии
- 2.1 Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
- 2.2 Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
- 2.3 Коэффициент детерминации
- 2.4 Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
- 2.5 Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
- 2.6 Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
- 2.7 Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
- 3 Кросс-валидация
- 4 Примечания
- 5 См. также
- 6 Источники информации
Оценки качества классификации
Матрица ошибок (англ. Сonfusion matrix)
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов.
Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика () можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- Кредитоспособный заёмщик распознается моделью как некредитоспособный и ему отказывается в кредите. Данный случай можно трактовать как «ложную тревогу».
- Некредитоспособный заёмщик распознаётся как кредитоспособный и ему ошибочно выдаётся кредит. Данный случай можно рассматривать как «пропуск цели».
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой , чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный — отрицательным (заемщик кредитоспособен ). Тогда возможны следующие исходы классификации:
- Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются истинно-положительными (True Positive — TP).
- Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются истинно отрицательными (True Negative — TN).
- Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются ложно-положительными (False Positive — FP), а ошибка классификации называется ошибкой I рода.
- Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются ложно-отрицательными (False Negative — FN), а ошибка классификации называется ошибкой II рода.
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
-
Истинно-положительный (True Positive — TP) Ложно-положительный (False Positive — FP) Ложно-отрицательный (False Negative — FN) Истинно-отрицательный (True Negative — TN)
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
# код для матрицы ошибок # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import confusion_matrix from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (англ. Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе # Для расчета матрицы ошибок сначала понадобится иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687], # [ 1891, 3530]])
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.metrics import confusion_matrix
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
y_train_perfect_predictions = y_train_5 # притворись, что мы достигли совершенства
print(confusion_matrix(y_train_5, y_train_perfect_predictions))
# array([[54579, 0],
# [ 0, 5421]])
Аккуратность (англ. Accuracy)
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
# код для для подсчета аккуратности: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import accuracy_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(accuracy_score(y_train_5, y_train_pred)) # == (53892 + 3530) / (53892 + 3530 + 1891 +687) # 0.9570333333333333
Точность (англ. Precision)
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall)
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
# код для для подсчета точности и полноты: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import precision_score, recall_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(precision_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 687) print(recall_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 1891) # 0.8370879772350012 # 0.6511713705958311
F-мера (англ. F-score)
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где принимает значения в диапазоне если вы хотите отдать приоритет точности, а при приоритет отдается полноте. При формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют ).
-
Рис.1 Сбалансированная F-мера,
-
Рис.2 F-мера c приоритетом точности,
-
Рис.3 F-мера c приоритетом полноты,
F-мера достигает максимума при максимальной полноте и точности, и близка к нулю, если один из аргументов близок к нулю.
F-мера является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея «F-меру» гораздо проще ответить на вопрос: «поменялся алгоритм в лучшую сторону или нет?»
# код для подсчета метрики F-mera: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier from sklearn.metrics import f1_score mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распознавать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(f1_score(y_train_5, y_train_pred)) # 0.7325171197343846
ROC-кривая
Кривая рабочих характеристик (англ. Receiver Operating Characteristics curve).
Используется для анализа поведения классификаторов при различных пороговых значениях.
Позволяет рассмотреть все пороговые значения для данного классификатора.
Показывает долю ложно положительных примеров (англ. false positive rate, FPR) в сравнении с долей истинно положительных примеров (англ. true positive rate, TPR).
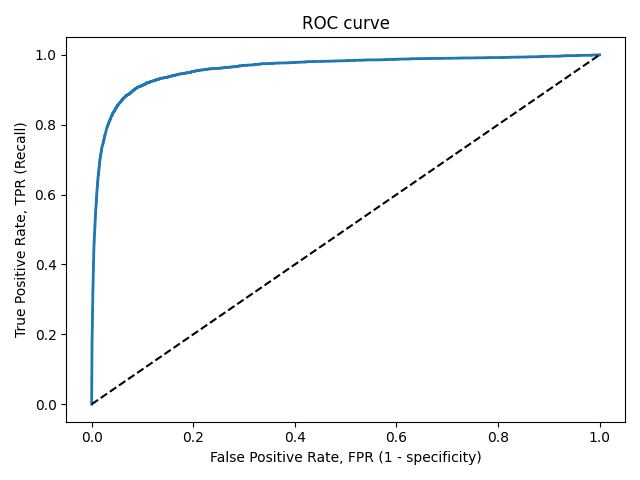
Доля FPR — это пропорция отрицательных образцов, которые были некорректно классифицированы как положительные.
- ,
где TNR — доля истинно отрицательных классификаций (англ. Тrие Negative Rate), представляющая собой пропорцию отрицательных образцов, которые были корректно классифицированы как отрицательные.
Доля TNR также называется специфичностью (англ. specificity). Следовательно, ROC-кривая изображает чувствительность (англ. seпsitivity), т.е. полноту, в сравнении с разностью 1 — specificity.
Прямая линия по диагонали представляет ROC-кривую чисто случайного классификатора. Хороший классификатор держится от указанной линии настолько далеко, насколько это
возможно (стремясь к левому верхнему углу).
Один из способов сравнения классификаторов предусматривает измерение площади под кривой (англ. Area Under the Curve — AUC). Безупречный классификатор будет иметь площадь под ROC-кривой (ROC-AUC), равную 1, тогда как чисто случайный классификатор — площадь 0.5.
# Код отрисовки ROC-кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import roc_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") fpr, tpr, thresholds = roc_curve(y_train_5, y_scores) def plot_roc_curve(fpr, tpr, label=None): plt.plot(fpr, tpr, linewidth=2, label=label) plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal plt.xlabel('False Positive Rate, FPR (1 - specificity)') plt.ylabel('True Positive Rate, TPR (Recall)') plt.title('ROC curve') plt.savefig("ROC.png") plot_roc_curve(fpr, tpr) plt.show()
Precison-recall кривая
Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма.
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
Precison-recall (PR) кривая. Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
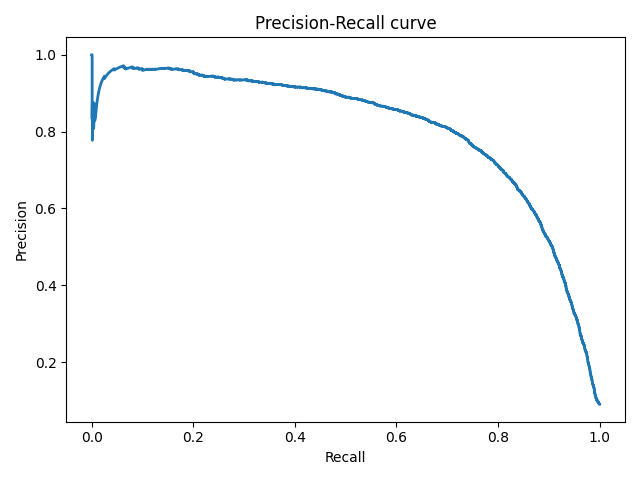
# Код отрисовки Precison-recall кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import precision_recall_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores) def plot_precision_recall_vs_threshold(precisions, recalls, thresholds): plt.plot(recalls, precisions, linewidth=2) plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall curve') plt.savefig("Precision_Recall_curve.png") plot_precision_recall_vs_threshold(precisions, recalls, thresholds) plt.show()
Оценки качества регрессии
Наиболее типичными мерами качества в задачах регрессии являются
Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
MSE применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза. Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок.
- и
Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
Среднеквадратичный функционал сильнее штрафует за большие отклонения по сравнению со среднеабсолютным, и поэтому более чувствителен к выбросам. При использовании любого из этих двух функционалов может быть полезно проанализировать, какие объекты вносят наибольший вклад в общую ошибку — не исключено, что на этих объектах была допущена ошибка при вычислении признаков или целевой величины.
Среднеквадратичная ошибка подходит для сравнения двух моделей или для контроля качества во время обучения, но не позволяет сделать выводов о том, на сколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации —
Коэффициент детерминации
Коэффициент детерминации измеряет долю дисперсии, объясненную моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что MAPE=11.4%, то это говорит о том, что ошибка составила 11,4% от фактических значений.
Основная проблема данной ошибки — нестабильность.
Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
Примерно такая же проблема, как и в MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня.
Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
MASE является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Обратите внимание, что в MASE мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тенденцию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Недостаток MASE в том, что её тяжело интерпретировать. Например, MASE=1.21 ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более.
Кросс-валидация
Хороший способ оценки модели предусматривает применение кросс-валидации (cкользящего контроля или перекрестной проверки).
В этом случае фиксируется некоторое множество разбиений исходной выборки на две подвыборки: обучающую и контрольную. Для каждого разбиения выполняется настройка алгоритма по обучающей подвыборке, затем оценивается его средняя ошибка на объектах контрольной подвыборки. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках.
Примечания
- [1] Лекция «Оценивание качества» на www.coursera.org
- [2] Лекция на www.stepik.org о кросвалидации
- [3] Лекция на www.stepik.org о метриках качества, Precison и Recall
- [4] Лекция на www.stepik.org о метриках качества, F-мера
- [5] Лекция на www.stepik.org о метриках качества, примеры
См. также
- Оценка качества в задаче кластеризации
- Кросс-валидация
Источники информации
- [6] Соколов Е.А. Лекция линейная регрессия
- [7] — Дьяконов А. Функции ошибки / функционалы качества
- [8] — Оценка качества прогнозных моделей
- [9] — HeinzBr Ошибка прогнозирования: виды, формулы, примеры
- [10] — egor_labintcev Метрики в задачах машинного обучения
- [11] — grossu Методы оценки качества прогноза
- [12] — К.В.Воронцов, Классификация
- [13] — К.В.Воронцов, Скользящий контроль
Мы начнем с самых простых и понятных моделей машинного обучения: линейных. В этом параграфе мы разберёмся, что это такое, почему они работают и в каких случаях их стоит использовать. Так как это первый класс моделей, с которым вы столкнётесь, мы постараемся подробно проговорить все важные моменты. Заодно объясним, как работает машинное обучение, на сравнительно простых примерах.
Почему модели линейные?
Представьте, что у вас есть множество объектов $\mathbb{X}$, а вы хотели бы каждому объекту сопоставить какое-то значение. К примеру, у вас есть набор операций по банковской карте, а вы бы хотели, понять, какие из этих операций сделали мошенники. Если вы разделите все операции на два класса и нулём обозначите законные действия, а единицей мошеннические, то у вас получится простейшая задача классификации. Представьте другую ситуацию: у вас есть данные геологоразведки, по которым вы хотели бы оценить перспективы разных месторождений. В данном случае по набору геологических данных ваша модель будет, к примеру, оценивать потенциальную годовую доходность шахты. Это пример задачи регрессии. Числа, которым мы хотим сопоставить объекты из нашего множества иногда называют таргетами (от английского target).
Таким образом, задачи классификации и регрессии можно сформулировать как поиск отображения из множества объектов $\mathbb{X}$ в множество возможных таргетов.
Математически задачи можно описать так:
- классификация: $\mathbb{X} \to {0,1,\ldots,K}$, где $0, \ldots, K$ – номера классов,
- регрессия: $\mathbb{X} \to \mathbb{R}$.
Очевидно, что просто сопоставить какие-то объекты каким-то числам — дело довольно бессмысленное. Мы же хотим быстро обнаруживать мошенников или принимать решение, где строить шахту. Значит нам нужен какой-то критерий качества. Мы бы хотели найти такое отображение, которое лучше всего приближает истинное соответствие между объектами и таргетами. Что значит «лучше всего» – вопрос сложный. Мы к нему будем много раз возвращаться. Однако, есть более простой вопрос: среди каких отображений мы будем искать самое лучшее? Возможных отображений может быть много, но мы можем упростить себе задачу и договориться, что хотим искать решение только в каком-то заранее заданном параметризированном семействе функций. Весь этот параграф будет посвящена самому простому такому семейству — линейным функциям вида
$$
y = w_1 x_1 + \ldots + w_D x_D + w_0,
$$
где $y$ – целевая переменная (таргет), $(x_1, \ldots, x_D)$ – вектор, соответствующий объекту выборки (вектор признаков), а $w_1, \ldots, w_D, w_0$ – параметры модели. Признаки ещё называют фичами (от английского features). Вектор $w = (w_1,\ldots,w_D)$ часто называют вектором весов, так как на предсказание модели можно смотреть как на взвешенную сумму признаков объекта, а число $w_0$ – свободным коэффициентом, или сдвигом (bias). Более компактно линейную модель можно записать в виде
$$y = \langle x, w\rangle + w_0$$
Теперь, когда мы выбрали семейство функций, в котором будем искать решение, задача стала существенно проще. Мы теперь ищем не какое-то абстрактное отображение, а конкретный вектор $(w_0,w_1,\ldots,w_D)\in\mathbb{R}^{D+1}$.
Замечание. Чтобы применять линейную модель, нужно, чтобы каждый объект уже был представлен вектором численных признаков $x_1,\ldots,x_D$. Конечно, просто текст или граф в линейную модель не положить, придётся сначала придумать для него численные фичи. Модель называют линейной, если она является линейной по этим численным признакам.
Разберёмся, как будет работать такая модель в случае, если $D = 1$. То есть у наших объектов есть ровно один численный признак, по которому они отличаются. Теперь наша линейная модель будет выглядеть совсем просто: $y = w_1 x_1 + w_0$. Для задачи регрессии мы теперь пытаемся приблизить значение игрек какой-то линейной функцией от переменной икс. А что будет значить линейность для задачи классификации? Давайте вспомним про пример с поиском мошеннических транзакций по картам. Допустим, нам известна ровно одна численная переменная — объём транзакции. Для бинарной классификации транзакций на законные и потенциально мошеннические мы будем искать так называемое разделяющее правило: там, где значение функции положительно, мы будем предсказывать один класс, где отрицательно – другой. В нашем примере простейшим правилом будет какое-то пороговое значение объёма транзакций, после которого есть смысл пометить транзакцию как подозрительную.
В случае более высоких размерностей вместо прямой будет гиперплоскость с аналогичным смыслом.
Вопрос на подумать. Если вы посмотрите содержание учебника, то не найдёте в нём ни «полиномиальных» моделей, ни каких-нибудь «логарифмических», хотя, казалось бы, зависимости бывают довольно сложными. Почему так?
Ответ (не открывайте сразу; сначала подумайте сами!)Линейные зависимости не так просты, как кажется. Пусть мы решаем задачу регрессии. Если мы подозреваем, что целевая переменная $y$ не выражается через $x_1, x_2$ как линейная функция, а зависит ещё от логарифма $x_1$ и ещё как-нибудь от того, разные ли знаки у признаков, то мы можем ввести дополнительные слагаемые в нашу линейную зависимость, просто объявим эти слагаемые новыми переменными и добавив перед ними соответствующие регрессионные коэффициенты
$$y \approx w_1 x_1 + w_2 x_2 + w_3\log{x_1} + w_4\text{sgn}(x_1x_2) + w_0,$$
и в итоге из двумерной нелинейной задачи мы получили четырёхмерную линейную регрессию.
Вопрос на подумать. А как быть, если одна из фичей является категориальной, то есть принимает значения из (обычно конечного числа) значений, не являющихся числами? Например, это может быть время года, уровень образования, марка машины и так далее. Как правило, с такими значениями невозможно производить арифметические операции или же результаты их применения не имеют смысла.
Ответ (не открывайте сразу; сначала подумайте сами!)В линейную модель можно подать только численные признаки, так что категориальную фичу придётся как-то закодировать. Рассмотрим для примера вот такой датасет
Здесь два категориальных признака – pet_type и color. Первый принимает четыре различных значения, второй – пять.
Самый простой способ – использовать one-hot кодирование (one-hot encoding). Пусть исходный признак мог принимать $M$ значений $c_1,\ldots, c_M$. Давайте заменим категориальный признак на $M$ признаков, которые принимают значения $0$ и $1$: $i$-й будет отвечать на вопрос «принимает ли признак значение $c_i$?». Иными словами, вместо ячейки со значением $c_i$ у объекта появляется строка нулей и единиц, в которой единица стоит только на $i$-м месте.
В нашем примере получится вот такая табличка:
Можно было бы на этом остановиться, но добавленные признаки обладают одним неприятным свойством: в каждом из них ровно одна единица, так что сумма соответствующих столбцов равна столбцу из единиц. А это уже плохо. Представьте, что у нас есть линейная модель
$$y \sim w_1x_1 + \ldots + w_{D-1}x_{d-1} + w_{c_1}x_{c_1} + \ldots + w_{c_M}x_{c_M} + w_0$$
Преобразуем немного правую часть:
$$y\sim w_1x_1 + \ldots + w_{D-1}x_{d-1} + \underbrace{(w_{c_1} — w_{c_M})}_{=:w’_{c_1}}x_{c_1} + \ldots + \underbrace{(w_{c_{M-1}} — w_{c_M})}_{=:w’_{C_{M-1}}}x_{c_{M-1}} + w_{c_M}\underbrace{(x_{c_1} + \ldots + x_{c_M})}_{=1} + w_0 = $$
$$ = w_1x_1 + \ldots + w_{D-1}x_{d-1} + w’_{c_1}x_{c_1} + \ldots + w’_{c_{M-1}}x_{c_{M-1}} + \underbrace{(w_{c_M} + w_0)}_{=w’_{0}}$$
Как видим, от одного из новых признаков можно избавиться, не меняя модель. Больше того, это стоит сделать, потому что наличие «лишних» признаков ведёт к переобучению или вовсе ломает модель – подробнее об этом мы поговорим в разделе про регуляризацию. Поэтому при использовании one-hot-encoding обычно выкидывают признак, соответствующий одному из значений. Например, в нашем примере итоговая матрица объекты-признаки будет иметь вид:
Конечно, one-hot кодирование – это самый наивный способ работы с категориальными признаками, и для более сложных фичей или фичей с большим количеством значений оно плохо подходит. С рядом более продвинутых техник вы познакомитесь в разделе про обучение представлений.
Помимо простоты, у линейных моделей есть несколько других достоинств. К примеру, мы можем достаточно легко судить, как влияют на результат те или иные признаки. Скажем, если вес $w_i$ положителен, то с ростом $i$-го признака таргет в случае регрессии будет увеличиваться, а в случае классификации наш выбор будет сдвигаться в пользу одного из классов. Значение весов тоже имеет прозрачную интерпретацию: чем вес $w_i$ больше, тем «важнее» $i$-й признак для итогового предсказания. То есть, если вы построили линейную модель, вы неплохо можете объяснить заказчику те или иные её результаты. Это качество моделей называют интерпретируемостью. Оно особенно ценится в индустриальных задачах, цена ошибки в которых высока. Если от работы вашей модели может зависеть жизнь человека, то очень важно понимать, как модель принимает те или иные решения и какими принципами руководствуется. При этом не все методы машинного обучения хорошо интерпретируемы, к примеру, поведение искусственных нейронных сетей или градиентного бустинга интерпретировать довольно сложно.
В то же время слепо доверять весам линейных моделей тоже не стоит по целому ряду причин:
- Линейные модели всё-таки довольно узкий класс функций, они неплохо работают для небольших датасетов и простых задач. Однако, если вы решаете линейной моделью более сложную задачу, то вам, скорее всего, придётся выдумывать дополнительные признаки, являющиеся сложными функциями от исходных. Поиск таких дополнительных признаков называется feature engineering, технически он устроен примерно так, как мы описали в вопросе про «полиномиальные модели». Вот только поиском таких искусственных фичей можно сильно увлечься, так что осмысленность интерпретации будет сильно зависеть от здравого смысла эксперта, строившего модель.
- Если между признаками есть приближённая линейная зависимость, коэффициенты в линейной модели могут совершенно потерять физический смысл (об этой проблеме и о том, как с ней бороться, мы поговорим дальше, когда будем обсуждать регуляризацию).
- Особенно осторожно стоит верить в утверждения вида «этот коэффициент маленький, значит, этот признак не важен». Во-первых, всё зависит от масштаба признака: вдруг коэффициент мал, чтобы скомпенсировать его. Во-вторых, зависимость действительно может быть слабой, но кто знает, в какой ситуации она окажется важна. Такие решения принимаются на основе данных, например, путём проверки статистического критерия (об этом мы коротко упомянем в разделе про вероятностные модели).
- Конкретные значения весов могут меняться в зависимости от обучающей выборки, хотя с ростом её размера они будут потихоньку сходиться к весам «наилучшей» линейной модели, которую можно было бы построить по всем-всем-всем данным на свете.
Обсудив немного общие свойства линейных моделей, перейдём к тому, как их всё-таки обучать. Сначала разберёмся с регрессией, а затем настанет черёд классификации.
Линейная регрессия и метод наименьших квадратов (МНК)
Мы начнём с использования линейных моделей для решения задачи регрессии. Простейшим примером постановки задачи линейной регрессии является метод наименьших квадратов (Ordinary least squares).
Пусть у нас задан датасет $(X, y)$, где $y=(y_i)_{i=1}^N \in \mathbb{R}^N$ – вектор значений целевой переменной, а $X=(x_i)_{i = 1}^N \in \mathbb{R}^{N \times D}, x_i \in \mathbb{R}^D$ – матрица объекты-признаки, в которой $i$-я строка – это вектор признаков $i$-го объекта выборки. Мы хотим моделировать зависимость $y_i$ от $x_i$ как линейную функцию со свободным членом. Общий вид такой функции из $\mathbb{R}^D$ в $\mathbb{R}$ выглядит следующим образом:
$$\color{#348FEA}{f_w(x_i) = \langle w, x_i \rangle + w_0}$$
Свободный член $w_0$ часто опускают, потому что такого же результата можно добиться, добавив ко всем $x_i$ признак, тождественно равный единице; тогда роль свободного члена будет играть соответствующий ему вес:
$$\begin{pmatrix}x_{i1} & \ldots & x_{iD} \end{pmatrix}\cdot\begin{pmatrix}w_1\\ \vdots \\ w_D\end{pmatrix} + w_0 =
\begin{pmatrix}1 & x_{i1} & \ldots & x_{iD} \end{pmatrix}\cdot\begin{pmatrix}w_0 \\ w_1\\ \vdots \\ w_D \end{pmatrix}$$
Поскольку это сильно упрощает запись, в дальнейшем мы будем считать, что это уже сделано и зависимость имеет вид просто $f_w(x_i) = \langle w, x_i \rangle$.
Сведение к задаче оптимизации
Мы хотим, чтобы на нашем датасете (то есть на парах $(x_i, y_i)$ из обучающей выборки) функция $f_w$ как можно лучше приближала нашу зависимость.
Для того, чтобы чётко сформулировать задачу, нам осталось только одно: на математическом языке выразить желание «приблизить $f_w(x)$ к $y$». Говоря простым языком, мы должны научиться измерять качество модели и минимизировать её ошибку, как-то меняя обучаемые параметры. В нашем примере обучаемые параметры — это веса $w$. Функция, оценивающая то, как часто модель ошибается, традиционно называется функцией потерь, функционалом качества или просто лоссом (loss function). Важно, чтобы её было легко оптимизировать: скажем, гладкая функция потерь – это хорошо, а кусочно постоянная – просто ужасно.
Функции потерь бывают разными. От их выбора зависит то, насколько задачу в дальнейшем легко решать, и то, в каком смысле у нас получится приблизить предсказание модели к целевым значениям. Интуитивно понятно, что для нашей текущей задачи нам нужно взять вектор $y$ и вектор предсказаний модели и как-то сравнить, насколько они похожи. Так как эти вектора «живут» в одном векторном пространстве, расстояние между ними вполне может быть функцией потерь. Более того, положительная непрерывная функция от этого расстояния тоже подойдёт в качестве функции потерь. При этом способов задать расстояние между векторами тоже довольно много. От всего этого разнообразия глаза разбегаются, но мы обязательно поговорим про это позже. Сейчас давайте в качестве лосса возьмём квадрат $L^2$-нормы вектора разницы предсказаний модели и $y$. Во-первых, как мы увидим дальше, так задачу будет нетрудно решить, а во-вторых, у этого лосса есть ещё несколько дополнительных свойств:
-
$L^2$-норма разницы – это евклидово расстояние $|y — f_w(x)|_2$ между вектором таргетов и вектором ответов модели, то есть мы их приближаем в смысле самого простого и понятного «расстояния».
-
Как мы увидим в разделе про вероятностные модели, с точки зрения статистики это соответствует гипотезе о том, что наши данные состоят из линейного «сигнала» и нормально распределенного «шума».
Так вот, наша функция потерь выглядит так:
$$L(f, X, y) = |y — f(X)|_2^2 = $$
$$= \|y — Xw\|_2^2 = \sum_{i=1}^N(y_i — \langle x_i, w \rangle)^2$$
Такой функционал ошибки не очень хорош для сравнения поведения моделей на выборках разного размера. Представьте, что вы хотите понять, насколько качество модели на тестовой выборке из $2500$ объектов хуже, чем на обучающей из $5000$ объектов. Вы измерили $L^2$-норму ошибки и получили в одном случае $300$, а в другом $500$. Эти числа не очень интерпретируемы. Гораздо лучше посмотреть на среднеквадратичное отклонение
$$L(f, X, y) = \frac1N\sum_{i=1}^N(y_i — \langle x_i, w \rangle)^2$$
По этой метрике на тестовой выборке получаем $0,12$, а на обучающей $0,1$.
Функция потерь $\frac1N\sum_{i=1}^N(y_i — \langle x_i, w \rangle)^2$ называется Mean Squared Error, MSE или среднеквадратическим отклонением. Разница с $L^2$-нормой чисто косметическая, на алгоритм решения задачи она не влияет:
$$\color{#348FEA}{\text{MSE}(f, X, y) = \frac{1}{N}|y — X w|_2^2}$$
В самом широком смысле, функции работают с объектами множеств: берут какой-то входящий объект из одного множества и выдают на выходе соответствующий ему объект из другого. Если мы имеем дело с отображением, которое на вход принимает функции, а на выходе выдаёт число, то такое отображение называют функционалом. Если вы посмотрите на нашу функцию потерь, то увидите, что это именно функционал. Для каждой конкретной линейной функции, которую задают веса $w_i$, мы получаем число, которое оценивает, насколько точно эта функция приближает наши значения $y$. Чем меньше это число, тем точнее наше решение, значит для того, чтобы найти лучшую модель, этот функционал нам надо минимизировать по $w$:
$$\color{#348FEA}{|y — Xw|_2^2 \longrightarrow \min_w}$$
Эту задачу можно решать разными способами. В этом параграфе мы сначала решим эту задачу аналитически, а потом приближенно. Сравнение двух этих решений позволит нам проиллюстрировать преимущества того подхода, которому посвящена эта книга. На наш взгляд, это самый простой способ «на пальцах» показать суть машинного обучения.
МНК: точный аналитический метод
Точку минимума можно найти разными способами. Если вам интересно аналитическое решение, вы можете найти его в параграфе про матричные дифференцирования (раздел «Примеры вычисления производных сложных функций»). Здесь же мы воспользуемся геометрическим подходом.
Пусть $x^{(1)},\ldots,x^{(D)}$ – столбцы матрицы $X$, то есть столбцы признаков. Тогда
$$Xw = w_1x^{(1)}+\ldots+w_Dx^{(D)},$$
и задачу регрессии можно сформулировать следующим образом: найти линейную комбинацию столбцов $x^{(1)},\ldots,x^{(D)}$, которая наилучшим способом приближает столбец $y$ по евклидовой норме – то есть найти проекцию вектора $y$ на подпространство, образованное векторами $x^{(1)},\ldots,x^{(D)}$.
Разложим $y = y_{\parallel} + y_{\perp}$, где $y_{\parallel} = Xw$ – та самая проекция, а $y_{\perp}$ – ортогональная составляющая, то есть $y_{\perp} = y — Xw\perp x^{(1)},\ldots,x^{(D)}$. Как это можно выразить в матричном виде? Оказывается, очень просто:
$$X^T(y — Xw) = 0$$
В самом деле, каждый элемент столбца $X^T(y — Xw)$ – это скалярное произведение строки $X^T$ (=столбца $X$ = одного из $x^{(i)}$) на $y — Xw$. Из уравнения $X^T(y — Xw) = 0$ уже очень легко выразить $w$:
$$w = (X^TX)^{-1}X^Ty$$
Вопрос на подумать Для вычисления $w_{\ast}$ нам приходится обращать (квадратную) матрицу $X^TX$, что возможно, только если она невырожденна. Что это значит с точки зрения анализа данных? Почему мы верим, что это выполняется во всех разумных ситуациях?
Ответ (не открывайте сразу; сначала подумайте сами!)Как известно из линейной алгебры, для вещественной матрицы $X$ ранги матриц $X$ и $X^TX$ совпадают. Матрица $X^TX$ невырожденна тогда и только тогда, когда её ранг равен числу её столбцов, что равно числу столбцов матрицы $X$. Иными словами, формула регрессии поломается, только если столбцы матрицы $X$ линейно зависимы. Столбцы матрицы $X$ – это признаки. А если наши признаки линейно зависимы, то, наверное, что-то идёт не так и мы должны выкинуть часть из них, чтобы остались только линейно независимые.
Другое дело, что зачастую признаки могут быть приближённо линейно зависимы, особенно если их много. Тогда матрица $X^TX$ будет близка к вырожденной, и это, как мы дальше увидим, будет вести к разным, в том числе вычислительным проблемам.
Вычислительная сложность аналитического решения — $O(D^2N + D^3)$, где $N$ — длина выборки, $D$ — число признаков у одного объекта. Слагаемое $N^2D$ отвечает за сложность перемножения матриц $X^T$ и $X$, а слагаемое $D^3$ — за сложность обращения их произведения. Перемножать матрицы $(X^TX)^{-1}$ и $X^T$ не стоит. Гораздо лучше сначала умножить $y$ на $X^T$, а затем полученный вектор на $(X^TX)^{-1}$: так будет быстрее и, кроме того, не нужно будет хранить матрицу $(X^TX)^{-1}X^T$.
Вычисление можно ускорить, используя продвинутые алгоритмы перемножения матриц или итерационные методы поиска обратной матрицы.
Проблемы «точного» решения
Заметим, что для получения ответа нам нужно обратить матрицу $X^TX$. Это создает множество проблем:
- Основная проблема в обращении матрицы — это то, что вычислительно обращать большие матрицы дело сложное, а мы бы хотели работать с датасетами, в которых у нас могут быть миллионы точек,
- Матрица $X^TX$, хотя почти всегда обратима в разумных задачах машинного обучения, зачастую плохо обусловлена. Особенно если признаков много, между ними может появляться приближённая линейная зависимость, которую мы можем упустить на этапе формулировки задачи. В подобных случаях погрешность нахождения $w$ будет зависеть от квадрата числа обусловленности матрицы $X$, что очень плохо. Это делает полученное таким образом решение численно неустойчивым: малые возмущения $y$ могут приводить к катастрофическим изменениям $w$.
Пара слов про число обусловленности.Пожертвовав математической строгостью, мы можем считать, что число обусловленности матрицы $X$ – это корень из отношения наибольшего и наименьшего из собственных чисел матрицы $X^TX$. Грубо говоря, оно показывает, насколько разного масштаба бывают собственные значения $X^TX$. Если рассмотреть $L^2$-норму ошибки предсказания, как функцию от $w$, то её линии уровня будут эллипсоидами, форма которых определяется квадратичной формой с матрицей $X^TX$ (проверьте это!). Таким образом, число обусловленности говорит о том, насколько вытянутыми являются эти эллипсоиды.ПодробнееДанные проблемы не являются поводом выбросить решение на помойку. Существует как минимум два способа улучшить его численные свойства, однако если вы не знаете про сингулярное разложение, то лучше вернитесь сюда, когда узнаете.
-
Построим $QR$-разложение матрицы $X$. Напомним, что это разложение, в котором матрица $Q$ ортогональна по столбцам (то есть её столбцы ортогональны и имеют длину 1; в частности, $Q^TQ=E$), а $R$ квадратная и верхнетреугольная. Подставив его в формулу, получим
$$w = ((QR)^TQR)^{-1}(QR)^T y = (R^T\underbrace{Q^TQ}_{=E}R)^{-1}R^TQ^Ty = R^{-1}R^{-T}R^TQ^Ty = R^{-1}Q^Ty$$
Отметим, что написать $(R^TR)^{-1} = R^{-1}R^{-T}$ мы имеем право благодаря тому, что $R$ квадратная. Полученная формула намного проще, обращение верхнетреугольной матрицы (=решение системы с верхнетреугольной левой частью) производится быстро и хорошо, погрешность вычисления $w$ будет зависеть просто от числа обусловленности матрицы $X$, а поскольку нахождение $QR$-разложения является достаточно стабильной операцией, мы получаем решение с более хорошими, чем у исходной формулы, численными свойствами.
-
Также можно использовать псевдообратную матрицу, построенную с помощью сингулярного разложения, о котором подробно написано в разделе про матричные разложения. А именно, пусть
$$A = U\underbrace{\mathrm{diag}(\sigma_1,\ldots,\sigma_r)}_{=\Sigma}V^T$$
– это усечённое сингулярное разложение, где $r$ – это ранг $A$. В таком случае диагональная матрица посередине является квадратной, $U$ и $V$ ортогональны по столбцам: $U^TU = E$, $V^TV = E$. Тогда
$$w = (V\Sigma \underbrace{U^TU}_{=E}\Sigma V^T)^{-1}V\Sigma U^Ty$$
Заметим, что $V\Sigma^{-2}V^T\cdot V\Sigma^2V^T = E = V\Sigma^2V^T\cdot V\Sigma^{-2}V^T$, так что $(V\Sigma^2 V^T)^{-1} = V\Sigma^{-2}V^T$, откуда
$$w = V\Sigma^{-2}\underbrace{V^TV}_{=E}\Sigma U^Ty = V\Sigma^{-1}Uy$$
Хорошие численные свойства сингулярного разложения позволяют утверждать, что и это решение ведёт себя довольно неплохо.
Тем не менее, вычисление всё равно остаётся довольно долгим и будет по-прежнему страдать (хоть и не так сильно) в случае плохой обусловленности матрицы $X$.
Полностью вылечить проблемы мы не сможем, но никто и не обязывает нас останавливаться на «точном» решении (которое всё равно никогда не будет вполне точным). Поэтому ниже мы познакомим вас с совершенно другим методом.
МНК: приближенный численный метод
Минимизируемый функционал является гладким и выпуклым, а это значит, что можно эффективно искать точку его минимума с помощью итеративных градиентных методов. Более подробно вы можете прочитать о них в разделе про методы оптимизации, а здесь мы лишь коротко расскажем об одном самом базовом подходе.
Как известно, градиент функции в точке направлен в сторону её наискорейшего роста, а антиградиент (противоположный градиенту вектор) в сторону наискорейшего убывания. То есть имея какое-то приближение оптимального значения параметра $w$, мы можем его улучшить, посчитав градиент функции потерь в точке и немного сдвинув вектор весов в направлении антиградиента:
$$w_j \mapsto w_j — \alpha \frac{d}{d{w_j}} L(f_w, X, y) $$
где $\alpha$ – это параметр алгоритма («темп обучения»), который контролирует величину шага в направлении антиградиента. Описанный алгоритм называется градиентным спуском.
Посмотрим, как будет выглядеть градиентный спуск для функции потерь $L(f_w, X, y) = \frac1N\vert\vert Xw — y\vert\vert^2$. Градиент квадрата евклидовой нормы мы уже считали; соответственно,
$$
\nabla_wL = \frac2{N} X^T (Xw — y)
$$
Следовательно, стартовав из какого-то начального приближения, мы можем итеративно уменьшать значение функции, пока не сойдёмся (по крайней мере в теории) к минимуму (вообще говоря, локальному, но в данном случае глобальному).
Алгоритм градиентного спуска
w = random_normal() # можно пробовать и другие виды инициализации
repeat S times: # другой вариант: while abs(err) > tolerance
f = X.dot(w) # посчитать предсказание
err = f - y # посчитать ошибку
grad = 2 * X.T.dot(err) / N # посчитать градиент
w -= alpha * grad # обновить веса
С теоретическими результатами о скорости и гарантиях сходимости градиентного спуска вы можете познакомиться в главе про методы оптимизации. Мы позволим себе лишь несколько общих замечаний:
- Поскольку задача выпуклая, выбор начальной точки влияет на скорость сходимости, но не настолько сильно, чтобы на практике нельзя было стартовать всегда из нуля или из любой другой приятной вам точки;
- Число обусловленности матрицы $X$ существенно влияет на скорость сходимости градиентного спуска: чем более вытянуты эллипсоиды уровня функции потерь, тем хуже;
- Темп обучения $\alpha$ тоже сильно влияет на поведение градиентного спуска; вообще говоря, он является гиперпараметром алгоритма, и его, возможно, придётся подбирать отдельно. Другими гиперпараметрами являются максимальное число итераций $S$ и/или порог tolerance.
Иллюстрация.Рассмотрим три задачи регрессии, для которых матрица $X$ имеет соответственно маленькое, среднее и большое числа обусловленности. Будем строить для них модели вида $y=w_1x_1 + w_2x_2$. Раскрасим плоскость $(w_1, w_2)$ в соответствии со значениями $\|X_{\text{train}}w — y_{\text{train}}\|^2$. Тёмная область содержит минимум этой функции – оптимальное значение $w_{\ast}$. Также запустим из двух точек градиентный спуск с разными значениями темпа обучения $\alpha$ и посмотрим, что получится:
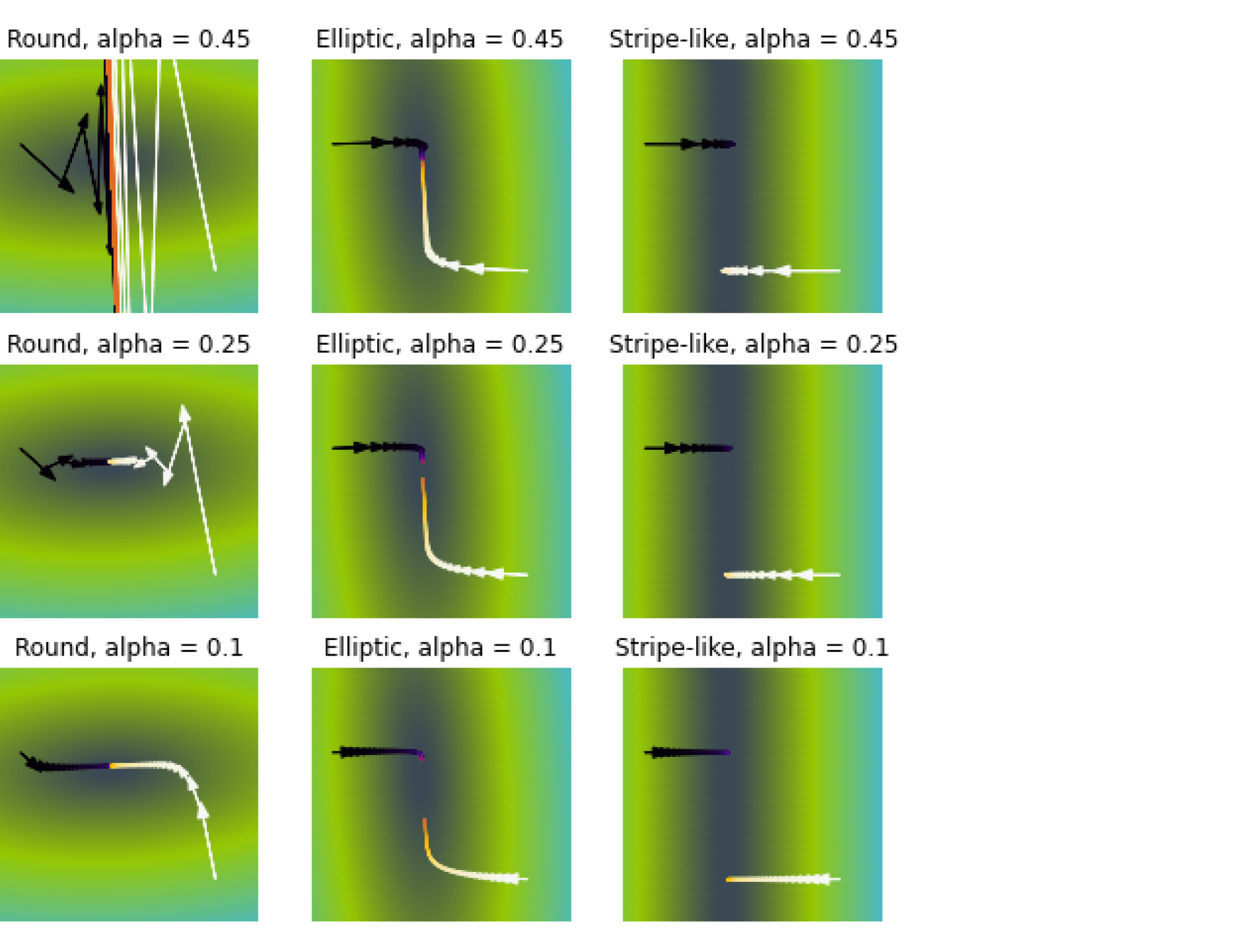
Итог: при неудачном выборе $\alpha$ алгоритм не сходится или идёт вразнос, а для плохо обусловленной задачи он сходится абы куда.
Вычислительная сложность градиентного спуска – $O(NDS)$, где, как и выше, $N$ – длина выборки, $D$ – число признаков у одного объекта. Сравните с оценкой $O(N^2D + D^3)$ для «наивного» вычисления аналитического решения.
Сложность по памяти – $O(ND)$ на хранение выборки. В памяти мы держим и выборку, и градиент, но в большинстве реалистичных сценариев доминирует выборка.
Стохастический градиентный спуск
На каждом шаге градиентного спуска нам требуется выполнить потенциально дорогую операцию вычисления градиента по всей выборке (сложность $O(ND)$). Возникает идея заменить градиент его оценкой на подвыборке (в английской литературе такую подвыборку обычно именуют batch или mini-batch; в русской разговорной терминологии тоже часто встречается слово батч или мини-батч).
А именно, если функция потерь имеет вид суммы по отдельным парам объект-таргет
$$L(w, X, y) = \frac1N\sum_{i=1}^NL(w, x_i, y_i),$$
а градиент, соответственно, записывается в виде
$$\nabla_wL(w, X, y) = \frac1N\sum_{i=1}^N\nabla_wL(w, x_i, y_i),$$
то предлагается брать оценку
$$\nabla_wL(w, X, y) \approx \frac1B\sum_{t=1}^B\nabla_wL(w, x_{i_t}, y_{i_t})$$
для некоторого подмножества этих пар $(x_{i_t}, y_{i_t})_{t=1}^B$. Обратите внимание на множители $\frac1N$ и $\frac1B$ перед суммами. Почему они нужны? Полный градиент $\nabla_wL(w, X, y)$ можно воспринимать как среднее градиентов по всем объектам, то есть как оценку матожидания $\mathbb{E}\nabla_wL(w, x, y)$; тогда, конечно, оценка матожидания по меньшей подвыборке тоже будет иметь вид среднего градиентов по объектам этой подвыборки.
Как делить выборку на батчи? Ясно, что можно было бы случайным образом сэмплировать их из полного датасета, но даже если использовать быстрый алгоритм вроде резервуарного сэмплирования, сложность этой операции не самая оптимальная. Поэтому используют линейный проход по выборке (которую перед этим лучше всё-таки случайным образом перемешать). Давайте введём ещё один параметр нашего алгоритма: размер батча, который мы обозначим $B$. Теперь на $B$ очередных примерах вычислим градиент и обновим веса модели. При этом вместо количества шагов алгоритма обычно задают количество эпох $E$. Это ещё один гиперпараметр. Одна эпоха – это один полный проход нашего сэмплера по выборке. Заметим, что если выборка очень большая, а модель компактная, то даже первый проход бывает можно не заканчивать.
Алгоритм:
w = normal(0, 1)
repeat E times:
for i = B, i <= n, i += B
X_batch = X[i-B : i]
y_batch = y[i-B : i]
f = X_batch.dot(w) # посчитать предсказание
err = f - y_batch # посчитать ошибку
grad = 2 * X_batch.T.dot(err) / B # посчитать градиент
w -= alpha * grad
Сложность по времени – $O(NDE)$. На первый взгляд, она такая же, как и у обычного градиентного спуска, но заметим, что мы сделали в $N / B$ раз больше шагов, то есть веса модели претерпели намного больше обновлений.
Сложность по памяти можно довести до $O(BD)$: ведь теперь всю выборку не надо держать в памяти, а достаточно загружать лишь текущий батч (а остальная выборка может лежать на диске, что удобно, так как в реальности задачи, в которых выборка целиком не влезает в оперативную память, встречаются сплошь и рядом). Заметим, впрочем, что при этом лучше бы $B$ взять побольше: ведь чтение с диска – намного более затратная по времени операция, чем чтение из оперативной памяти.
В целом, разницу между алгоритмами можно представлять как-то так:
Шаги стохастического градиентного спуска заметно более шумные, но считать их получается значительно быстрее. В итоге они тоже сходятся к оптимальному значению из-за того, что матожидание оценки градиента на батче равно самому градиенту. По крайней мере, сходимость можно получить при хорошо подобранных коэффициентах темпа обучения в случае выпуклого функционала качества. Подробнее мы об этом поговорим в главе про оптимизацию. Для сложных моделей и лоссов стохастический градиентный спуск может сходиться плохо или застревать в локальных минимумах, поэтому придумано множество его улучшений. О некоторых из них также рассказано в главе про оптимизацию.
Существует определённая терминологическая путаница, иногда стохастическим градиентным спуском называют версию алгоритма, в которой размер батча равен единице (то есть максимально шумная и быстрая версия алгоритма), а версии с бОльшим размером батча называют batch gradient descent. В книгах, которые, возможно, старше вас, такая процедура иногда ещё называется incremental gradient descent. Это не очень принципиально, но вы будьте готовы, если что.
Вопрос на подумать. Вообще говоря, если объём данных не слишком велик и позволяет это сделать, объекты лучше случайным образом перемешивать перед тем, как подавать их в алгоритм стохастического градиентного спуска. Как вам кажется, почему?
Также можно использовать различные стратегии отбора объектов. Например, чаще брать объекты, на которых ошибка больше. Какие ещё стратегии вы могли бы придумать?
Ответ (не открывайте сразу; сначала подумайте сами!)Легко представить себе ситуацию, в которой объекты как-нибудь неудачно упорядочены, скажем, по возрастанию таргета. Тогда модель будет попеременно то запоминать, что все таргеты маленькие, то – что все таргеты большие. Это может и не повлиять на качество итоговой модели, но может привести и к довольно печальным последствиям. И вообще, чем более разнообразные батчи модель увидит в процессе обучения, тем лучше.
Стратегий можно придумать много. Например, не брать объекты, на которых ошибка слишком большая (возможно, это выбросы – зачем на них учиться), или вообще не брать те, на которых ошибка достаточно мала (они «ничему не учат»). Рекомендуем, впрочем, прибегать к этим эвристикам, только если вы понимаете, зачем они вам нужны и почему есть надежда, что они помогут.
Неградиентные методы
После прочтения этой главы у вас может сложиться ощущение, что приближённые способы решения ML задач и градиентные методы – это одно и тоже, но вы будете правы в этом только на 98%. В принципе, существуют и другие способы численно решать эти задачи, но в общем случае они работают гораздо хуже, чем градиентный спуск, и не обладают таким хорошим теоретическим обоснованием. Мы не будем рассказывать про них подробно, но можете на досуге почитать, скажем, про Stepwise regression, Orthogonal matching pursuit или LARS. У LARS, кстати, есть довольно интересное свойство: он может эффективно работать на выборках, в которых число признаков больше числа примеров. С алгоритмом LARS вы можете познакомиться в главе про оптимизацию.
Регуляризация
Всегда ли решение задачи регрессии единственно? Вообще говоря, нет. Так, если в выборке два признака будут линейно зависимы (и следовательно, ранг матрицы будет меньше $D$), то гарантировано найдётся такой вектор весов $\nu$ что $\langle\nu, x_i\rangle = 0\ \ \forall x_i$. В этом случае, если какой-то $w$ является решением оптимизационной задачи, то и $w + \alpha \nu $ тоже является решением для любого $\alpha$. То есть решение не только не обязано быть уникальным, так ещё может быть сколь угодно большим по модулю. Это создаёт вычислительные трудности. Малые погрешности признаков сильно возрастают при предсказании ответа, а в градиентном спуске накапливается погрешность из-за операций со слишком большими числами.
Конечно, в жизни редко бывает так, что признаки строго линейно зависимы, а вот быть приближённо линейно зависимыми они вполне могут быть. Такая ситуация называется мультиколлинеарностью. В этом случае у нас, всё равно, возникают проблемы, близкие к описанным выше. Дело в том, что $X\nu\sim 0$ для вектора $\nu$, состоящего из коэффициентов приближённой линейной зависимости, и, соответственно, $X^TX\nu\approx 0$, то есть матрица $X^TX$ снова будет близка к вырожденной. Как и любая симметричная матрица, она диагонализуется в некотором ортонормированном базисе, и некоторые из собственных значений $\lambda_i$ близки к нулю. Если вектор $X^Ty$ в выражении $(X^TX)^{-1}X^Ty$ будет близким к соответствующему собственному вектору, то он будет умножаться на $1 /{\lambda_i}$, что опять же приведёт к появлению у $w$ очень больших по модулю компонент (при этом $w$ ещё и будет вычислен с большой погрешностью из-за деления на маленькое число). И, конечно же, все ошибки и весь шум, которые имелись в матрице $X$, при вычислении $y\sim Xw$ будут умножаться на эти большие и неточные числа и возрастать во много-много раз, что приведёт к проблемам, от которых нас не спасёт никакое сингулярное разложение.
Важно ещё отметить, что в случае, когда несколько признаков линейно зависимы, веса $w_i$ при них теряют физический смысл. Может даже оказаться, что вес признака, с ростом которого таргет, казалось бы, должен увеличиваться, станет отрицательным. Это делает модель не только неточной, но и принципиально не интерпретируемой. Вообще, неадекватность знаков или величины весов – хорошее указание на мультиколлинеарность.
Для того, чтобы справиться с этой проблемой, задачу обычно регуляризуют, то есть добавляют к ней дополнительное ограничение на вектор весов. Это ограничение можно, как и исходный лосс, задавать по-разному, но, как правило, ничего сложнее, чем $L^1$- и $L^2$-нормы, не требуется.
Вместо исходной задачи теперь предлагается решить такую:
$$\color{#348FEA}{\min_w L(f, X, y) = \min_w(|X w — y|_2^2 + \lambda |w|^k_k )}$$
$\lambda$ – это очередной параметр, а $|w|^k_k $ – это один из двух вариантов:
$$\color{#348FEA}{|w|^2_2 = w^2_1 + \ldots + w^2_D}$$
или
$$\color{#348FEA}{|w|_1^1 = \vert w_1 \vert + \ldots + \vert w_D \vert}$$
Добавка $\lambda|w|^k_k$ называется регуляризационным членом или регуляризатором, а число $\lambda$ – коэффициентом регуляризации.
Коэффициент $\lambda$ является гиперпараметром модели и достаточно сильно влияет на качество итогового решения. Его подбирают по логарифмической шкале (скажем, от 1e-2 до 1e+2), используя для сравнения моделей с разными значениями $\lambda$ дополнительную валидационную выборку. При этом качество модели с подобранным коэффициентом регуляризации уже проверяют на тестовой выборке, чтобы исключить переобучение. Более подробно о том, как нужно подбирать гиперпараметры, вы можете почитать в соответствующем параграфе.
Отдельно надо договориться о том, что вес $w_0$, соответствующий отступу от начала координат (то есть признаку из всех единичек), мы регуляризовать не будем, потому что это не имеет смысла: если даже все значения $y$ равномерно велики, это не должно портить качество обучения. Обычно это не отображают в формулах, но если придираться к деталям, то стоило бы написать сумму по всем весам, кроме $w_0$:
$$|w|^2_2 = \sum_{\color{red}{j=1}}^{D}w_j^2,$$
$$\|w\|_1 = \sum_{\color{red}{j=1}}^{D} \vert w_j \vert$$
В случае $L^2$-регуляризации решение задачи изменяется не очень сильно. Например, продифференцировав новый лосс по $w$, легко получить, что «точное» решение имеет вид:
$$w = (X^TX + \lambda I)^{-1}X^Ty$$
Отметим, что за этой формулой стоит и понятная численная интуиция: раз матрица $X^TX$ близка к вырожденной, то обращать её сродни самоубийству. Мы лучше слегка исказим её добавкой $\lambda I$, которая увеличит все собственные значения на $\lambda$, отодвинув их от нуля. Да, аналитическое решение перестаёт быть «точным», но за счёт снижения численных проблем мы получим более качественное решение, чем при использовании «точной» формулы.
В свою очередь, градиент функции потерь
$$L(f_w, X, y) = |Xw — y|^2 + \lambda|w|^2$$
по весам теперь выглядит так:
$$
\nabla_wL(f_w, X, y) = 2X^T(Xw — y) + 2\lambda w
$$
Подставив этот градиент в алгоритм стохастического градиентного спуска, мы получаем обновлённую версию приближенного алгоритма, отличающуюся от старой только наличием дополнительного слагаемого.
Вопрос на подумать. Рассмотрим стохастический градиентный спуск для $L^2$-регуляризованной линейной регрессии с батчами размера $1$. Выберите правильный вариант шага SGD:
(а) $w_i\mapsto w_i — 2\alpha(\langle w, x_j\rangle — y_j)x_{ji} — \frac{2\alpha\lambda}N w_i,\quad i=1,\ldots,D$;
(б) $w_i\mapsto w_i — 2\alpha(\langle w, x_j\rangle — y_j)x_{ji} — 2\alpha\lambda w_i,\quad i=1,\ldots,D$;
(в) $w_i\mapsto w_i — 2\alpha(\langle w, x_j\rangle — y_j)x_{ji} — 2\lambda N w_i,\quad i=1,\ldots D$.
Ответ (не открывайте сразу; сначала подумайте сами!)Не регуляризованная функция потерь имеет вид $\mathcal{L}(X, y, w) = \frac1N\sum_{i=1}^N\mathcal{L}(x_i, y_i, w)$, и её можно воспринимать, как оценку по выборке $(x_i, y_i)_{i=1}^N$ идеальной функции потерь
$$\mathcal{L}(w) = \mathbb{E}_{x, y}\mathcal{L}(x, y, w)$$
Регуляризационный член не зависит от выборки и добавляется отдельно:
$$\mathcal{L}_{\text{reg}}(w) = \mathbb{E}_{x, y}\mathcal{L}(x, y, w) + \lambda\|w\|^2$$
Соответственно, идеальный градиент регуляризованной функции потерь имеет вид
$$\nabla_w\mathcal{L}_{\text{reg}}(w) = \mathbb{E}_{x, y}\nabla_w\mathcal{L}(x, y, w) + 2\lambda w,$$
Градиент по батчу – это тоже оценка градиента идеальной функции потерь, только не на выборке $(X, y)$, а на батче $(x_{t_i}, y_{t_i})_{i=1}^B$ размера $B$. Он будет выглядеть так:
$$\nabla_w\mathcal{L}_{\text{reg}}(w) = \frac1B\sum_{i=1}^B\nabla_w\mathcal{L}(x_{t_i}, y_{t_i}, w) + 2\lambda w.$$
Как видите, коэффициентов, связанных с числом объектов в батче или в исходной выборке, во втором слагаемом нет. Так что верным является второй вариант. Кстати, обратите внимание, что в третьем ещё и нет коэффициента $\alpha$ перед производной регуляризационного слагаемого, это тоже ошибка.
Вопрос на подумать. Распишите процедуру стохастического градиентного спуска для $L^1$-регуляризованной линейной регрессии. Как вам кажется, почему никого не волнует, что функция потерь, строго говоря, не дифференцируема?
Ответ (не открывайте сразу; сначала подумайте сами!)Распишем для случая батча размера 1:
$$w_i\mapsto w_i — \alpha(\langle w, x_j\rangle — y_j)x_{ji} — \frac{\lambda}\alpha \text{sign}(w_i),\quad i=1,\ldots,D$$
Функция потерь не дифференцируема лишь в одной точке. Так как в машинном обучении чаще всего мы имеем дело с данными вероятностного характера, это не влечёт каких-то особых проблем. Дело в том, что попадание прямо в ноль очень маловероятно из-за численных погрешностей в данных, так что мы можем просто доопределить производную в одной точке, а если даже пару раз попадём в неё за время обучения, это не приведёт к каким-то значительным изменениям результатов.
Отметим, что $L^1$- и $L^2$-регуляризацию можно определять для любой функции потерь $L(w, X, y)$ (и не только в задаче регрессии, а и, например, в задаче классификации тоже). Новая функция потерь будет соответственно равна
$$\widetilde{L}(w, X, y) = L(w, X, y) + \lambda|w|_1$$
или
$$\widetilde{L}(w, X, y) = L(w, X, y) + \lambda|w|_2^2$$
Разреживание весов в $L^1$-регуляризации
$L^2$-регуляризация работает прекрасно и используется в большинстве случаев, но есть одна полезная особенность $L^1$-регуляризации: её применение приводит к тому, что у признаков, которые не оказывают большого влияния на ответ, вес в результате оптимизации получается равным $0$. Это позволяет удобным образом удалять признаки, слабо влияющие на таргет. Кроме того, это даёт возможность автоматически избавляться от признаков, которые участвуют в соотношениях приближённой линейной зависимости, соответственно, спасает от проблем, связанных с мультиколлинеарностью, о которых мы писали выше.
Не очень строгим, но довольно интуитивным образом это можно объяснить так:
- В точке оптимума линии уровня регуляризационного члена касаются линий уровня основного лосса, потому что, во-первых, и те, и другие выпуклые, а во-вторых, если они пересекаются трансверсально, то существует более оптимальная точка:
- Линии уровня $L^1$-нормы – это $N$-мерные октаэдры. Точки их касания с линиями уровня лосса, скорее всего, лежат на грани размерности, меньшей $N-1$, то есть как раз в области, где часть координат равна нулю:
Заметим, что данное построение говорит о том, как выглядит оптимальное решение задачи, но ничего не говорит о способе, которым это решение можно найти. На самом деле, найти такой оптимум непросто: у $L^1$ меры довольно плохая производная. Однако, способы есть. Можете на досуге прочитать, например, вот эту статью о том, как работало предсказание CTR в google в 2012 году. Там этой теме посвящается довольно много места. Кроме того, рекомендуем посмотреть про проксимальные методы в разделе этой книги про оптимизацию в ML.
Заметим также, что вообще-то оптимизация любой нормы $L_x, \ 0 < x \leq 1$, приведёт к появлению разреженных векторов весов, просто если c $L^1$ ещё хоть как-то можно работать, то с остальными всё будет ещё сложнее.
Другие лоссы
Стохастический градиентный спуск можно очевидным образом обобщить для решения задачи линейной регрессии с любой другой функцией потерь, не только квадратичной: ведь всё, что нам нужно от неё, – это чтобы у функции потерь был градиент. На практике это делают редко, но тем не менее рассмотрим ещё пару вариантов.
MAE
Mean absolute error, абсолютная ошибка, появляется при замене $L^2$ нормы в MSE на $L^1$:
$$\color{#348FEA}{MAE(y, \widehat{y}) = \frac1N\sum_{i=1}^N \vert y_i — \widehat{y}_i\vert}$$
Можно заметить, что в MAE по сравнению с MSE существенно меньший вклад в ошибку будут вносить примеры, сильно удалённые от ответов модели. Дело тут в том, что в MAE мы считаем модуль расстояния, а не квадрат, соответственно, вклад больших ошибок в MSE получается существенно больше. Такая функция потерь уместна в случаях, когда вы пытаетесь обучить регрессию на данных с большим количеством выбросов в таргете.
Иначе на эту разницу можно посмотреть так: MSE приближает матожидание условного распределения $y \mid x$, а MAE – медиану.
MAPE
Mean absolute percentage error, относительная ошибка.
$$MAPE(y, \widehat{y}) = \frac1N\sum_{i=1}^N \left|\frac{\widehat{y}_i-y_i}{y_i}\right|$$
Часто используется в задачах прогнозирования (например, погоды, загруженности дорог, кассовых сборов фильмов, цен), когда ответы могут быть различными по порядку величины, и при этом мы бы хотели верно угадать порядок, то есть мы не хотим штрафовать модель за предсказание 2000 вместо 1000 в разы сильней, чем за предсказание 2 вместо 1.
Вопрос на подумать. Кроме описанных выше в задаче линейной регрессии можно использовать и другие функции потерь, например, Huber loss:
$$\mathcal{L}(f, X, y) = \sum_{i=1}^Nh_{\delta}(y_i — \langle w_i, x\rangle),\mbox{ где }h_{\delta}(z) = \begin{cases}
\frac12z^2,\ |z|\leqslant\delta,\\
\delta(|z| — \frac12\delta),\ |z| > \delta
\end{cases}$$
Число $\delta$ является гиперпараметром. Сложная формула при $\vert z\vert > \delta$ нужна, чтобы функция $h_{\delta}(z)$ была непрерывной. Попробуйте объяснить, зачем может быть нужна такая функция потерь.
Ответ (не открывайте сразу; сначала подумайте сами!)Часто требования формулируют в духе «функция потерь должна слабее штрафовать то-то и сильней штрафовать вот это». Например, $L^2$-регуляризованный лосс штрафует за большие по модулю веса. В данном случае можно заметить, что при небольших значениях ошибки берётся просто MSE, а при больших мы начинаем штрафовать нашу модель менее сурово. Например, это может быть полезно для того, чтобы выбросы не так сильно влияли на результат обучения.
Линейная классификация
Теперь давайте поговорим про задачу классификации. Для начала будем говорить про бинарную классификацию на два класса. Обобщить эту задачу до задачи классификации на $K$ классов не составит большого труда. Пусть теперь наши таргеты $y$ кодируют принадлежность к положительному или отрицательному классу, то есть принадлежность множеству ${-1,1}$ (в этом параграфе договоримся именно так обозначать классы, хотя в жизни вам будут нередко встречаться и метки ${0,1}$), а $x$ – по-прежнему векторы из $\mathbb{R}^D$. Мы хотим обучить линейную модель так, чтобы плоскость, которую она задаёт, как можно лучше отделяла объекты одного класса от другого.
В идеальной ситуации найдётся плоскость, которая разделит классы: положительный окажется с одной стороны от неё, а отрицательный с другой. Выборка, для которой это возможно, называется линейно разделимой. Увы, в реальной жизни такое встречается крайне редко.
Как обучить линейную модель классификации, нам ещё предстоит понять, но уже ясно, что итоговое предсказание можно будет вычислить по формуле
$$y = \text{sign} \langle w, x_i\rangle$$
Почему бы не решать, как задачу регрессии?Мы можем попробовать предсказывать числа $-1$ и $1$, минимизируя для этого, например, MSE с последующим взятием знака, но ничего хорошего не получится. Во-первых, регрессия почти не штрафует за ошибки на объектах, которые лежат близко к *разделяющей плоскости*, но не с той стороны. Во вторых, ошибкой будет считаться предсказание, например, $5$ вместо $1$, хотя нам-то на самом деле не важно, какой у числа модуль, лишь бы знак был правильным. Если визуализировать такое решение, то проблемы тоже вполне заметны:
Нам нужна прямая, которая разделяет эти точки, а не проходит через них!
Сконструируем теперь функционал ошибки так, чтобы он вышеперечисленными проблемами не обладал. Мы хотим минимизировать число ошибок классификатора, то есть
$$\sum_i \mathbb{I}[y_i \neq sign \langle w, x_i\rangle]\longrightarrow \min_w$$
Домножим обе части на $$y_i$$ и немного упростим
$$\sum_i \mathbb{I}[y_i \langle w, x_i\rangle < 0]\longrightarrow \min_w$$
Величина $M = y_i \langle w, x_i\rangle$ называется отступом (margin) классификатора. Такая фунция потерь называется misclassification loss. Легко видеть, что
-
отступ положителен, когда $sign(y_i) = sign(\langle w, x_i\rangle)$, то есть класс угадан верно; при этом чем больше отступ, тем больше расстояние от $x_i$ до разделяющей гиперплоскости, то есть «уверенность классификатора»;
-
отступ отрицателен, когда $sign(y_i) \ne sign(\langle w, x_i\rangle)$, то есть класс угадан неверно; при этом чем больше по модулю отступ, тем более сокрушительно ошибается классификатор.
От каждого из отступов мы вычисляем функцию
$$F(M) = \mathbb{I}[M < 0] = \begin{cases}1,\ M < 0,\\ 0,\ M\geqslant 0\end{cases}$$
Она кусочно-постоянная, и из-за этого всю сумму невозможно оптимизировать градиентными методами: ведь её производная равна нулю во всех точках, где она существует. Но мы можем мажорировать её какой-нибудь более гладкой функцией, и тогда задачу можно будет решить. Функции можно использовать разные, у них свои достоинства и недостатки, давайте рассмотрим несколько примеров:
Вопрос на подумать. Допустим, мы как-то обучили классификатор, и подавляющее большинство отступов оказались отрицательными. Правда ли нас постигла катастрофа?
Ответ (не открывайте сразу; сначала подумайте сами!)Наверное, мы что-то сделали не так, но ситуацию можно локально выправить, если предсказывать классы, противоположные тем, которые выдаёт наша модель.
Вопрос на подумать. Предположим, что у нас есть два классификатора с примерно одинаковыми и достаточно приемлемыми значениями интересующей нас метрики. При этом одна почти всегда выдаёт предсказания с большими по модулю отступами, а вторая – с относительно маленькими. Верно ли, что первая модель лучше, чем вторая?
Ответ (не открывайте сразу; сначала подумайте сами!)На первый взгляд кажется, что первая модель действительно лучше: ведь она предсказывает «увереннее», но на самом деле всё не так однозначно: во многих случаях модель, которая умеет «честно признать, что не очень уверена в ответе», может быть предпочтительней модели, которая врёт с той же непотопляемой уверенностью, что и говорит правду. В некоторых случаях лучше может оказаться модель, которая, по сути, просто отказывается от классификации на каких-то объектах.
Ошибка перцептрона
Реализуем простейшую идею: давайте считать отступы только на неправильно классифицированных объектах и учитывать их не бинарно, а линейно, пропорционально их размеру. Получается такая функция:
$$F(M) = \max(0, -M)$$
Давайте запишем такой лосс с $L^2$-регуляризацией:
$$L(w, x, y) = \lambda\vert\vert w\vert\vert^2_2 + \sum_i \max(0, -y_i \langle w, x_i\rangle)$$
Найдём градиент:
$$
\nabla_w L(w, x, y) = 2 \lambda w + \sum_i
\begin{cases}
0, & y_i \langle w, x_i \rangle > 0 \\
— y_i x_i, & y_i \langle w, x_i \rangle \leq 0
\end{cases}
$$
Имея аналитическую формулу для градиента, мы теперь можем так же, как и раньше, применить стохастический градиентный спуск, и задача будет решена.
Данная функция потерь впервые была предложена для перцептрона Розенблатта, первой вычислительной модели нейросети, которая в итоге привела к появлению глубокого обучения.
Она решает задачу линейной классификации, но у неё есть одна особенность: её решение не единственно и сильно зависит от начальных параметров. Например, все изображённые ниже классификаторы имеют одинаковый нулевой лосс:
Hinge loss, SVM
Для таких случаев, как на картинке выше, возникает логичное желание не только найти разделяющую прямую, но и постараться провести её на одинаковом удалении от обоих классов, то есть максимизировать минимальный отступ:
Это можно сделать, слегка поменяв функцию ошибки, а именно положив её равной:
$$F(M) = \max(0, 1-M)$$
$$L(w, x, y) = \lambda||w||^2_2 + \sum_i \max(0, 1-y_i \langle w, x_i\rangle)$$
$$
\nabla_w L(w, x, y) = 2 \lambda w + \sum_i
\begin{cases}
0, & 1 — y_i \langle w, x_i \rangle \leq 0 \\
— y_i x_i, & 1 — y_i \langle w, x_i \rangle > 0
\end{cases}
$$
Почему же добавленная единичка приводит к желаемому результату?
Интуитивно это можно объяснить так: объекты, которые проклассифицированы правильно, но не очень «уверенно» (то есть $0 \leq y_i \langle w, x_i\rangle < 1$), продолжают вносить свой вклад в градиент и пытаются «отодвинуть» от себя разделяющую плоскость как можно дальше.
К данному выводу можно прийти и чуть более строго; для этого надо совершенно по-другому взглянуть на выражение, которое мы минимизируем. Поможет вот эта картинка:
Если мы максимизируем минимальный отступ, то надо максимизировать $\frac{2}{|w|_2}$, то есть ширину полосы при условии того, что большинство объектов лежат с правильной стороны, что эквивалентно решению нашей исходной задачи:
$$\lambda|w|^2_2 + \sum_i \max(0, 1-y_i \langle w, x_i\rangle) \longrightarrow\min\limits_{w}$$
Отметим, что первое слагаемое у нас обратно пропорционально ширине полосы, но мы и максимизацию заменили на минимизацию, так что тут всё в порядке. Второе слагаемое – это штраф за то, что некоторые объекты неправильно расположены относительно разделительной полосы. В конце концов, никто нам не обещал, что классы наши линейно разделимы и можно провести оптимальную плоскость вообще без ошибок.
Итоговое положение плоскости задаётся всего несколькими обучающими примерами. Это ближайшие к плоскости правильно классифицированные объекты, которые называют опорными векторами или support vectors. Весь метод, соответственно, зовётся методом опорных векторов, или support vector machine, или сокращённо SVM. Начиная с шестидесятых годов это был сильнейший из известных методов машинного обучения. В девяностые его сменили методы, основанные на деревьях решений, которые, в свою очередь, недавно передали «пальму первенства» нейросетям.
Почему же SVM был столь популярен? Из-за небольшого количества параметров и доказуемой оптимальности. Сейчас для нас нормально выбирать специальный алгоритм под задачу и подбирать оптимальные гиперпараметры для этого алгоритма перебором, а когда-то трава была зеленее, а компьютеры медленнее, и такой роскоши у людей не было. Поэтому им нужны были модели, которые гарантированно неплохо работали бы в любой ситуации. Такой моделью и был SVM.
Другие замечательные свойства SVM: существование уникального решения и доказуемо минимальная склонность к переобучению среди всех популярных классов линейных классификаторов. Кроме того, несложная модификация алгоритма, ядровый SVM, позволяет проводить нелинейные разделяющие поверхности.
Строгий вывод постановки задачи SVM можно прочитать тут или в лекции К.В. Воронцова.
Логистическая регрессия
В этом параграфе мы будем обозначать классы нулём и единицей.
Ещё один интересный метод появляется из желания посмотреть на классификацию как на задачу предсказания вероятностей. Хороший пример – предсказание кликов в интернете (например, в рекламе и поиске). Наличие клика в обучающем логе не означает, что, если повторить полностью условия эксперимента, пользователь обязательно кликнет по объекту опять. Скорее у объектов есть какая-то «кликабельность», то есть истинная вероятность клика по данному объекту. Клик на каждом обучающем примере является реализацией этой случайной величины, и мы считаем, что в пределе в каждой точке отношение положительных и отрицательных примеров должно сходиться к этой вероятности.
Проблема состоит в том, что вероятность, по определению, величина от 0 до 1, а простого способа обучить линейную модель так, чтобы это ограничение соблюдалось, нет. Из этой ситуации можно выйти так: научить линейную модель правильно предсказывать какой-то объект, связанный с вероятностью, но с диапазоном значений $(-\infty,\infty)$, и преобразовать ответы модели в вероятность. Таким объектом является logit или log odds – логарифм отношения вероятности положительного события к отрицательному $\log\left(\frac{p}{1-p}\right)$.
Если ответом нашей модели является $\log\left(\frac{p}{1-p}\right)$, то искомую вероятность посчитать не трудно:
$$\langle w, x_i\rangle = \log\left(\frac{p}{1-p}\right)$$
$$e^{\langle w, x_i\rangle} = \frac{p}{1-p}$$
$$p=\frac{1}{1 + e^{-\langle w, x_i\rangle}}$$
Функция в правой части называется сигмоидой и обозначается
$$\color{#348FEA}{\sigma(z) = \frac1{1 + e^{-z}}}$$
Таким образом, $p = \sigma(\langle w, x_i\rangle)$
Как теперь научиться оптимизировать $w$ так, чтобы модель как можно лучше предсказывала логиты? Нужно применить метод максимума правдоподобия для распределения Бернулли. Это самое простое распределение, которое возникает, к примеру, при бросках монетки, которая орлом выпадает с вероятностью $p$. У нас только событием будет не орёл, а то, что пользователь кликнул на объект с такой вероятностью. Если хотите больше подробностей, почитайте про распределение Бернулли в теоретическом минимуме.
Правдоподобие позволяет понять, насколько вероятно получить данные значения таргета $y$ при данных $X$ и весах $w$. Оно имеет вид
$$ p(y\mid X, w) =\prod_i p(y_i\mid x_i, w) $$
и для распределения Бернулли его можно выписать следующим образом:
$$ p(y\mid X, w) =\prod_i p_i^{y_i} (1-p_i)^{1-y_i} $$
где $p_i$ – это вероятность, посчитанная из ответов модели. Оптимизировать произведение неудобно, хочется иметь дело с суммой, так что мы перейдём к логарифмическому правдоподобию и подставим формулу для вероятности, которую мы получили выше:
$$ \ell(w, X, y) = \sum_i \big( y_i \log(p_i) + (1-y_i)\log(1-p_i) \big) =$$
$$ =\sum_i \big( y_i \log(\sigma(\langle w, x_i \rangle)) + (1-y_i)\log(1 — \sigma(\langle w, x_i \rangle)) \big) $$
Если заметить, что
$$
\sigma(-z) = \frac{1}{1 + e^z} = \frac{e^{-z}}{e^{-z} + 1} = 1 — \sigma(z),
$$
то выражение можно переписать проще:
$$
\ell(w, X, y)=\sum_i \big( y_i \log(\sigma(\langle w, x_i \rangle)) + (1 — y_i) \log(\sigma(-\langle w, x_i \rangle)) \big)
$$
Нас интересует $w$, для которого правдоподобие максимально. Чтобы получить функцию потерь, которую мы будем минимизировать, умножим его на минус один:
$$\color{#348FEA}{L(w, X, y) = -\sum_i \big( y_i \log(\sigma(\langle w, x_i \rangle)) + (1 — y_i) \log(\sigma(-\langle w, x_i \rangle)) \big)}$$
В отличие от линейной регрессии, для логистической нет явной формулы решения. Деваться некуда, будем использовать градиентный спуск. К счастью, градиент устроен очень просто:
$$
\nabla_w L(y, X, w) = -\sum_i x_i \big( y_i — \sigma(\langle w, x_i \rangle)) \big)
$$
Вывод формулы градиентаНам окажется полезным ещё одно свойство сигмоиды:
$$
\frac{d \log \sigma(z)}{d z} = \left( \log \left( \frac{1}{1 + e^{-z}} \right) \right)’ = \frac{e^{-z}}{1 + e^{-z}} = \sigma(-z) \
$$ $$
\frac{d \log \sigma(-z)}{d z} = -\sigma(z)
$$
Отсюда:
$$
\nabla_w \log \sigma(\langle w, x_i \rangle) = \sigma(-\langle w, x_i \rangle) x_i \
$$ $$
\nabla_w \log \sigma(-\langle w, x_i \rangle) = -\sigma(\langle w, x_i \rangle) x_i
$$
и градиент оказывается равным
$$
\nabla_w L(y, X, w) = -\sum_i \big( y_i x_i \sigma(-\langle w, x_i \rangle) — (1 — y_i) x_i \sigma(\langle w, x_i \rangle)) \big) = \
$$ $$
= -\sum_i \big( y_i x_i (1 — \sigma(\langle w, x_i \rangle)) — (1 — y_i) x_i \sigma(\langle w, x_i \rangle)) \big) = \
$$ $$
= -\sum_i \big( y_i x_i — y_i x_i \sigma(\langle w, x_i \rangle) — x_i \sigma(\langle w, x_i \rangle) + y_i x_i \sigma(\langle w, x_i \rangle)) \big) = \
$$ $$
= -\sum_i \big( y_i x_i — x_i \sigma(\langle w, x_i \rangle)) \big)
$$
Предсказание модели будет вычисляться, как мы договаривались, следующим образом:
$$p=\sigma(\langle w, x_i\rangle)$$
Это вероятность положительного класса, а как от неё перейти к предсказанию самого класса? В других методах нам достаточно было посчитать знак предсказания, но теперь все наши предсказания положительные и находятся в диапазоне от 0 до 1. Что же делать? Интуитивным и не совсем (и даже совсем не) правильным является ответ «взять порог 0.5». Более корректным будет подобрать этот порог отдельно, для уже построенной регрессии минимизируя нужную вам метрику на отложенной тестовой выборке. Например, сделать так, чтобы доля положительных и отрицательных классов примерно совпадала с реальной.
Отдельно заметим, что метод называется логистической регрессией, а не логистической классификацией именно потому, что предсказываем мы не классы, а вещественные числа – логиты.
Вопрос на подумать. Проверьте, что, если метки классов – это $\pm1$, а не $0$ и $1$, то функцию потерь для логистической регрессии можно записать в более компактном виде:
$$\mathcal{L}(w, X, y) = \sum_{i=1}^N\log(1 + e^{-y_i\langle w, x_i\rangle})$$
Вопрос на подумать. Правда ли разделяющая поверхность модели логистической регрессии является гиперплоскостью?
Ответ (не открывайте сразу; сначала подумайте сами!)Разделяющая поверхность отделяет множество точек, которым мы присваиваем класс $0$ (или $-1$), и множество точек, которым мы присваиваем класс $1$. Представляется логичным провести отсечку по какому-либо значению предсказанной вероятности. Однако, выбор этого значения — дело не очевидное. Как мы увидим в главе про калибровку классификаторов, это может быть не настоящая вероятность. Допустим, мы решили провести границу по значению $\frac12$. Тогда разделяющая поверхность как раз задаётся равенством $p = \frac12$, что равносильно $\langle w, x\rangle = 0$. А это гиперплоскость.
Вопрос на подумать. Допустим, что матрица объекты-признаки $X$ имеет полный ранг по столбцам (то есть все её столбцы линейно независимы). Верно ли, что решение задачи восстановления логистической регрессии единственно?
Ответ (не открывайте сразу; сначала подумайте сами!)В этот раз хорошего геометрического доказательства, как было для линейной регрессии, пожалуй, нет; нам придётся честно посчитать вторую производную и доказать, что она является положительно определённой. Сделаем это для случая, когда метки классов – это $\pm1$. Формулы так получатся немного попроще. Напомним, что в этом случае
$$L(w, X, y) = -\sum_{i=1}^N\log(1 + e^{-y_i\langle w, x_i\rangle})$$
Следовательно,
$$\frac{\partial}{\partial w_{j}}L(w, X, y) = \sum_{i=1}^N\frac{y_ix_{ij}e^{-y_i\langle w, x_i\rangle}}{1 + e^{-y_i\langle w, x_i\rangle}} = \sum_{i=1}^Ny_ix_{ij}\left(1 — \frac1{1 + e^{-y_i\langle w, x_i\rangle}}\right)$$
$$\frac{\partial^2L}{\partial w_j\partial w_k}(w, X, y) = \sum_{i=1}^Ny^2_ix_{ij}x_{ik}\frac{e^{-y_i\langle w, x_i\rangle}}{(1 + e^{-y_i\langle w, x_i\rangle})^2} =$$
$$ = \sum_{i=1}^Ny^2_ix_{ij}x_{ik}\sigma(y_i\langle w, x_i\rangle)(1 — \sigma(y_i\langle w, x_i\rangle))$$
Теперь заметим, что $y_i^2 = 1$ и что, если обозначить через $D$ диагональную матрицу с элементами $\sigma(y_i\langle w, x_i\rangle)(1 — \sigma(y_i\langle w, x_i\rangle))$ на диагонали, матрицу вторых производных можно представить в виде:
$$\nabla^2L = \left(\frac{\partial^2\mathcal{L}}{\partial w_j\partial w_k}\right) = X^TDX$$
Так как $0 < \sigma(y_i\langle w, x_i\rangle) < 1$, у матрицы $D$ на диагонали стоят положительные числа, из которых можно извлечь квадратные корни, представив $D$ в виде $D = D^{1/2}D^{1/2}$. В свою очередь, матрица $X$ имеет полный ранг по столбцам. Стало быть, для любого вектора приращения $u\ne 0$ имеем
$$u^TX^TDXu = u^TX^T(D^{1/2})^TD^{1/2}Xu = \vert D^{1/2}Xu \vert^2 > 0$$
Таким образом, функция $L$ выпукла вниз как функция от $w$, и, соответственно, точка её экстремума непременно будет точкой минимума.
А теперь – почему это не совсем правда. Дело в том, что, говоря «точка её экстремума непременно будет точкой минимума», мы уже подразумеваем существование этой самой точки экстремума. Только вот существует этот экстремум не всегда. Можно показать, что для линейно разделимой выборки функция потерь логистической регрессии не ограничена снизу, и, соответственно, никакого экстремума нет. Доказательство мы оставляем читателю.
Вопрос на подумать. На картинке ниже представлены результаты работы на одном и том же датасете трёх моделей логистической регрессии с разными коэффициентами $L^2$-регуляризации:
Наверху показаны предсказанные вероятности положительного класса, внизу – вид разделяющей поверхности.
Как вам кажется, какие картинки соответствуют самому большому коэффициенту регуляризации, а какие – самому маленькому? Почему?
Ответ (не открывайте сразу; сначала подумайте сами!)Коэффициент регуляризации максимален у левой модели. На это нас могут натолкнуть два соображения. Во-первых, разделяющая прямая проведена достаточно странно, то есть можно заподозрить, что регуляризационный член в лосс-функции перевесил функцию потерь исходной задачи. Во-вторых, модель предсказывает довольно близкие к $\frac12$ вероятности – это значит, что значения $\langle w, x\rangle$ близки к нулю, то есть сам вектор $w$ близок к нулевому. Это также свидетельствует о том, что регуляризационный член играет слишком важную роль при оптимизации.
Наименьший коэффициент регуляризации у правой модели. Её предсказания достаточно «уверенные» (цвета на верхнем графике сочные, то есть вероятности быстро приближаются к $0$ или $1$). Это может свидетельствовать о том, что числа $\langle w, x\rangle$ достаточно велики по модулю, то есть $\vert\vert w \vert\vert$ достаточно велик.
Многоклассовая классификация
В этом разделе мы будем следовать изложению из лекций Евгения Соколова.
Пусть каждый объект нашей выборки относится к одному из $K$ классов: $\mathbb{Y} = {1, \ldots, K}$. Чтобы предсказывать эти классы с помощью линейных моделей, нам придётся свести задачу многоклассовой классификации к набору бинарных, которые мы уже хорошо умеем решать. Мы разберём два самых популярных способа это сделать – one-vs-all и all-vs-all, а проиллюстрировать их нам поможет вот такой игрушечный датасет
Один против всех (one-versus-all)
Обучим $K$ линейных классификаторов $b_1(x), \ldots, b_K(x)$, выдающих оценки принадлежности классам $1, \ldots, K$ соответственно. В случае с линейными моделями эти классификаторы будут иметь вид
$$b_k(x) = \text{sgn}\left(\langle w_k, x \rangle + w_{0k}\right)$$
Классификатор с номером $k$ будем обучать по выборке $\left(x_i, 2\mathbb{I}[y_i = k] — 1\right)_{i = 1}^{N}$; иными словами, мы учим классификатор отличать $k$-й класс от всех остальных.
Логично, чтобы итоговый классификатор выдавал класс, соответствующий самому уверенному из бинарных алгоритмов. Уверенность можно в каком-то смысле измерить с помощью значений линейных функций:
$$a(x) = \text{argmax}_k \left(\langle w_k, x \rangle + w_{0k}\right) $$
Давайте посмотрим, что даст этот подход применительно к нашему датасету. Обучим три линейных модели, отличающих один класс от остальных:
Теперь сравним значения линейных функций
и для каждой точки выберем тот класс, которому соответствует большее значение, то есть самый «уверенный» классификатор:
Хочется сказать, что самый маленький класс «обидели».
Проблема данного подхода заключается в том, что каждый из классификаторов $b_1(x), \dots, b_K(x)$ обучается на своей выборке, и значения линейных функций $\langle w_k, x \rangle + w_{0k}$ или, проще говоря, «выходы» классификаторов могут иметь разные масштабы. Из-за этого сравнивать их будет неправильно. Нормировать вектора весов, чтобы они выдавали ответы в одной и той же шкале, не всегда может быть разумным решением: так, в случае с SVM веса перестанут являться решением задачи, поскольку нормировка изменит норму весов.
Все против всех (all-versus-all)
Обучим $C_K^2$ классификаторов $a_{ij}(x)$, $i, j = 1, \dots, K$, $i \neq j$. Например, в случае с линейными моделями эти модели будут иметь вид
$$b_{ij}(x) = \text{sgn}\left( \langle w_{ij}, x \rangle + w_{0,ij} \right)$$
Классификатор $a_{ij}(x)$ будем настраивать по подвыборке $X_{ij} \subset X$, содержащей только объекты классов $i$ и $j$. Соответственно, классификатор $a_{ij}(x)$ будет выдавать для любого объекта либо класс $i$, либо класс $j$. Проиллюстрируем это для нашей выборки:
Чтобы классифицировать новый объект, подадим его на вход каждого из построенных бинарных классификаторов. Каждый из них проголосует за свой класс; в качестве ответа выберем тот класс, за который наберется больше всего голосов:
$$a(x) = \text{argmax}_k\sum_{i = 1}^{K} \sum_{j \neq i}\mathbb{I}[a_{ij}(x) = k]$$
Для нашего датасета получается следующая картинка:
Обратите внимание на серый треугольник на стыке областей. Это точки, для которых голоса разделились (в данном случае каждый классификатор выдал какой-то свой класс, то есть у каждого класса было по одному голосу). Для этих точек нет явного способа выдать обоснованное предсказание.
Многоклассовая логистическая регрессия
Некоторые методы бинарной классификации можно напрямую обобщить на случай многих классов. Выясним, как это можно проделать с логистической регрессией.
В логистической регрессии для двух классов мы строили линейную модель
$$b(x) = \langle w, x \rangle + w_0,$$
а затем переводили её прогноз в вероятность с помощью сигмоидной функции $\sigma(z) = \frac{1}{1 + \exp(-z)}$. Допустим, что мы теперь решаем многоклассовую задачу и построили $K$ линейных моделей
$$b_k(x) = \langle w_k, x \rangle + w_{0k},$$
каждая из которых даёт оценку принадлежности объекта одному из классов. Как преобразовать вектор оценок $(b_1(x), \ldots, b_K(x))$ в вероятности? Для этого можно воспользоваться оператором $\text{softmax}(z_1, \ldots, z_K)$, который производит «нормировку» вектора:
$$\text{softmax}(z_1, \ldots, z_K) = \left(\frac{\exp(z_1)}{\sum_{k = 1}^{K} \exp(z_k)},
\dots, \frac{\exp(z_K)}{\sum_{k = 1}^{K} \exp(z_k)}\right).$$
В этом случае вероятность $k$-го класса будет выражаться как
$$P(y = k \vert x, w) = \frac{
\exp{(\langle w_k, x \rangle + w_{0k})}}{ \sum_{j = 1}^{K} \exp{(\langle w_j, x \rangle + w_{0j})}}.$$
Обучать эти веса предлагается с помощью метода максимального правдоподобия: так же, как и в случае с двухклассовой логистической регрессией:
$$\sum_{i = 1}^{N} \log P(y = y_i \vert x_i, w) \to \max_{w_1, \dots, w_K}$$
Масштабируемость линейных моделей
Мы уже обсуждали, что SGD позволяет обучению хорошо масштабироваться по числу объектов, так как мы можем не загружать их целиком в оперативную память. А что делать, если признаков очень много, или мы не знаем заранее, сколько их будет? Такое может быть актуально, например, в следующих ситуациях:
- Классификация текстов: мы можем представить текст в формате «мешка слов», то есть неупорядоченного набора слов, встретившихся в данном тексте, и обучить на нём, например, определение тональности отзыва в интернете. Наличие каждого слова из языка в тексте у нас будет кодироваться отдельной фичой. Тогда размерность каждого элемента обучающей выборки будет порядка нескольких сотен тысяч.
- В задаче предсказания кликов по рекламе можно получить выборку любой размерности, например, так: в качестве фичи закодируем индикатор того, что пользователь X побывал на веб-странице Y. Суммарная размерность тогда будет порядка $10^9 \cdot 10^7 = 10^{16}$. Кроме того, всё время появляются новые пользователи и веб-страницы, так что на этапе применения нас ждут сюрпризы.
Есть несколько хаков, которые позволяют бороться с такими проблемами:
- Несмотря на то, что полная размерность объекта в выборке огромна, количество ненулевых элементов в нём невелико. Значит, можно использовать разреженное кодирование, то есть вместо плотного вектора хранить словарь, в котором будут перечислены индексы и значения ненулевых элементов вектора.
- Даже хранить все веса не обязательно! Можно хранить их в хэш-таблице и вычислять индекс по формуле
hash(feature) % tablesize. Хэш может вычисляться прямо от слова или id пользователя. Таким образом, несколько фичей будут иметь общий вес, который тем не менее обучится оптимальным образом. Такой подход называется hashing trick. Ясно, что сжатие вектора весов приводит к потерям в качестве, но, как правило, ценой совсем небольших потерь можно сжать этот вектор на много порядков.
Примером открытой библиотеки, в которой реализованы эти возможности, является vowpal wabbit.
Parameter server
Если при решении задачи ставки столь высоки, что мы не можем разменивать качество на сжатие вектора весов, а признаков всё-таки очень много, то задачу можно решать распределённо, храня все признаки в шардированной хеш-таблице
Кружки здесь означают отдельные сервера. Жёлтые загружают данные, а серые хранят части модели. Для обучения жёлтый кружок запрашивает у серого нужные ему для предсказания веса, считает градиент и отправляет его обратно, где тот потом применяется. Схема обладает бесконечной масштабируемостью, но задач, где это оправдано, не очень много.
Подытожим
На линейную модель можно смотреть как на однослойную нейросеть, поэтому многие методы, которые были изначально разработаны для них, сейчас переиспользуются в задачах глубокого обучения, а базовые подходы к регрессии, классификации и оптимизации вообще выглядят абсолютно так же. Так что несмотря на то, что в целом линейные модели на сегодня применяются редко, то, из чего они состоят и как строятся, знать очень и очень полезно.
Надеемся также, что главным итогом прочтения этой главы для вас будет осознание того, что решение любой ML-задачи состоит из выбора функции потерь, параметризованного класса моделей и способа оптимизации. В следующих главах мы познакомимся с другими моделями и оптимизаторами, но эти базовые принципы не изменятся.
Адаптированный перевод прекрасной статьи энтузиаста технологий машинного обучения Javaid Nabi.
Чтобы понимать как алгоритм машинного обучения учится предсказывать результаты на основе данных, важно разобраться в основных концепциях и понятиях, используемых при обучении алгоритма.
Функции оценки
В контексте технологии машинного обучения, оценка – это
статистический термин для нахождения некоторого приближения неизвестного
параметра на основе некоторых данных. Точечная
оценка – это попытка найти единственное лучшее приближение некоторого
количества интересующих нас параметров. Или на более формальном языке математической статистики — точечная оценка это число, оцениваемое на основе наблюдений,
предположительно близкое к оцениваемому параметру.
Под количеством
интересующих параметров обычно подразумевается:
• Один параметр
• Вектор параметров – например, веса в линейной
регрессии
• Целая функция
Точечная оценка
Чтобы отличать оценки параметров от их истинного значения, представим точечную оценку параметра θ как θˆ. Пусть {x(1), x(2), .. x(m)} будут m независимыми и одинаково распределенными величинами. Тогда точечная оценка может быть записана как некоторая функция этих величин:
Такое определение точечной оценки является очень общим и предоставляет разработчику большую свободу действий. Почти любая функция, таким образом, может рассматриваться как оценщик, но хороший оценщик – это функция, значения которой близки к истинному базовому значению θ, которое сгенерированно обучающими данными.
Точечная оценка также может относиться к оценке взаимосвязи между
входными и целевыми переменными, в этом случае чаще называемой функцией оценки.
Функция оценки
Задача, решаемая машинным обучением, заключается в попытке
предсказать переменную y по
заданному входному вектору x. Мы
предполагаем, что существует функция f(x), которая описывает приблизительную
связь между y и x. Например, можно предположить, что y = f(x) + ε, где ε обозначает
часть y, которая явно не
предсказывается входным вектором x.
При оценке функций нас интересует приближение f с помощью модели или оценки fˆ.
Функция оценки в действительности это тоже самое, что оценка параметра θ; функция оценки f это просто точечная
оценка в функциональном пространстве. Пример: в полиномиальной регрессии мы
либо оцениваем параметр w, либо оцениваем функцию отображения из x в y.
Смещение и дисперсия
Смещение и дисперсия измеряют два разных источника ошибки функции оценки.
Смещение измеряет ожидаемое отклонение от истинного значения функции или
параметра. Дисперсия, с другой стороны, показывает меру отклонения от
ожидаемого значения оценки, которую может вызвать любая конкретная выборка
данных.
Смещение
Смещение определяется следующим
образом:
где ожидаемое значение E(θˆm) для данных (рассматриваемых как выборки из случайной величины) и
θ является истинным базовым значением, используемым для определения
распределения, генерирующего данные.
Оценщик θˆm называется несмещенным, если bias(θˆm)=0, что подразумевает что E(θˆm) = θ.
Дисперсия и Стандартная ошибка
Дисперсия оценки обозначается как Var(θˆ), где случайная величина
является обучающим множеством. Альтернативно, квадратный корень дисперсии
называется стандартной ошибкой, обозначаемой как SE(θˆ). Дисперсия или стандартная ошибка
оценщика показывает меру ожидания того, как оценка, которую мы вычисляем, будет
изменяться по мере того, как мы меняем выборки из базового набора данных,
генерирующих процесс.
Точно так же, как мы хотели бы, чтобы функция оценки имела малое
смещение, мы также стремимся, чтобы у нее была относительно низкая дисперсия.
Давайте теперь рассмотрим некоторые обычно используемые функции оценки.
Оценка Максимального Правдоподобия (MLE)
Оценка максимального правдоподобия может быть определена как метод
оценки параметров (таких как среднее значение или дисперсия) из выборки данных,
так что вероятность получения наблюдаемых данных максимальна.
Рассмотрим набор из m примеров X={x(1),… , x(m)} взятых независимо из неизвестного набора данных,
генерирующих распределение Pdata(x). Пусть Pmodel(x;θ) –
параметрическое семейство распределений вероятностей над тем же пространством,
индексированное параметром θ.
Другими словами, Pmodel(x;θ) отображает любую конфигурацию x в значение, оценивающее истинную
вероятность Pdata(x).
Оценка максимального правдоподобия для θ определяется как:
Поскольку мы предположили, что примеры являются независимыми выборками, приведенное выше
уравнение можно записать в виде:
Эта произведение многих вероятностей может быть неудобным по ряду
причин. В частности, оно склонно к числовой недооценке. Кроме того, чтобы найти
максимумы/минимумы этой функции, мы должны взять производную этой функции от θ и приравнять ее к 0. Поскольку это
произведение членов, нам нужно применить правило цепочки, которое довольно
громоздко. Чтобы получить более удобную, но эквивалентную задачу оптимизации,
можно использовать логарифм вероятности, который не меняет его argmax, но
удобно превращает произведение в сумму, и поскольку логарифм – строго
возрастающая функция (функция натурального логарифма – монотонное
преобразование), это не повлияет на итоговое значение θ.
В итоге, получаем:
Два важных свойства: сходимость и
эффективность
Сходимость. По мере того, как число обучающих выборок приближается к
бесконечности, оценка максимального правдоподобия сходится к истинному значению
параметра.
Эффективность. Способ измерения того, насколько мы близки к истинному
параметру, – это ожидаемая средняя квадратичная ошибка, вычисление квадратичной
разницы между оценочными и истинными значениями параметров, где математическое
ожидание вычисляется над m обучающими выборками из данных, генерирующих
распределение. Эта параметрическая среднеквадратичная ошибка уменьшается с
увеличением m, и для
больших m нижняя
граница неравенства Крамера-Рао показывает, что ни у одной сходящейся функции оценки нет
среднеквадратичной ошибки меньше, чем у оценки максимального правдоподобия.
Именно по причине
сходимости и эффективности, оценка максимального правдоподобия часто считается
предпочтительным оценщиком для машинного обучения.
Когда количество примеров достаточно мало, чтобы привести к
переобучению, стратегии регуляризации, такие как понижающие веса, могут
использоваться для получения смещенной версии оценки максимального
правдоподобия, которая имеет меньшую дисперсию, когда данные обучения
ограничены.
Максимальная апостериорная (MAP) оценка
Согласно байесовскому подходу, можно учесть влияние предварительных
данных на выбор точечной оценки. MAP может использоваться для получения
точечной оценки ненаблюдаемой величины на основе эмпирических данных. Оценка
MAP выбирает точку максимальной апостериорной вероятности (или максимальной
плотности вероятности в более распространенном случае непрерывного θ):
где с правой стороны, log(p(x|θ)) – стандартный член
логарифмической вероятности и log(p(θ)) соответствует изначальному
распределению.
Как и при полном байесовском методе, байесовский MAP имеет преимущество
использования изначальной информации, которой нет
в обучающих данных. Эта дополнительная информация помогает уменьшить дисперсию
для точечной оценки MAP (по сравнению с оценкой MLE). Однако, это происходит ценой повышенного смещения.
Функции потерь
В большинстве обучающих сетей ошибка рассчитывается как разница
между фактическим выходным значением y и прогнозируемым выходным значением ŷ.
Функция, используемая для вычисления этой ошибки, известна как функция потерь,
также часто называемая функцией ошибки или затрат.
До сих пор наше основное внимание уделялось оценке параметров с
помощью MLE или MAP. Причина, по которой мы обсуждали это раньше, заключается в
том, что и MLE, и MAP предоставляют механизм для получения функции потерь.
Давайте рассмотрим некоторые часто используемые функции потерь.
Средняя
квадратичная ошибка (MSE): средняя
квадратичная ошибка является наиболее распространенной функцией потерь. Функция
потерь MSE широко используется в линейной регрессии в качестве показателя
эффективности. Чтобы рассчитать MSE, надо взять разницу между предсказанными
значениями и истинными, возвести ее в квадрат и усреднить по всему набору
данных.
где y(i) – фактический ожидаемый результат, а ŷ(i) – прогноз модели.
Многие функции потерь (затрат), используемые в машинном обучении,
включая MSE, могут быть получены из метода максимального правдоподобия.
Чтобы увидеть, как мы можем вывести функции потерь из MLE или MAP,
требуется некоторая математика. Вы можете пропустить ее и перейти к следующему
разделу.
Получение MSE из MLE
Алгоритм линейной регрессии учится принимать входные данные x и получать выходные значения ŷ. Отображение x в ŷ делается так,
чтобы минимизировать среднеквадратичную ошибку. Но как мы выбрали MSE в
качестве критерия для линейной регрессии? Придем к этому решению с точки зрения
оценки максимального правдоподобия. Вместо того, чтобы производить одно
предсказание ŷ , давайте рассмотрим
модель условного распределения p(y|x).
Можно смоделировать модель
линейной регрессии следующим образом:
мы предполагаем, что у имеет
нормальное распределение с ŷ в качестве
среднего значения распределения и некоторой постоянной σ² в качестве дисперсии, выбранной пользователем. Нормальное
распределения являются разумным выбором во многих случаях. В отсутствие
предварительных данных о том, какое распределение в действительности
соответствует рассматриваемым данным, нормальное распределение является хорошим
выбором по умолчанию.
Вернемся к логарифмической вероятности, определенной ранее:
где ŷ(i) – результат
линейной регрессии на i-м входе, а m – количество обучающих примеров. Мы видим,
что две первые величины являются постоянными, поэтому максимизация
логарифмической вероятности сводится к минимизации MSE:
Таким образом, максимизация логарифмического правдоподобия
относительно θ дает такую же оценку параметров θ, что и минимизация
среднеквадратичной ошибки. Два критерия имеют разные значения, но одинаковое
расположение оптимума. Это оправдывает использование MSE в качестве функции
оценки максимального правдоподобия.
Кросс-энтропия
(или логарифмическая функция потерь – log loss): Кросс-энтропия измеряет расхождение между двумя вероятностными
распределениями. Если кросс-энтропия велика, это означает, что разница между
двумя распределениями велика, а если кросс-энтропия мала, то распределения
похожи друг на друга.
Кросс-энтропия определяется как:
где P – распределение истинных ответов, а Q – распределение
вероятностей прогнозов модели. Можно
показать, что функция кросс-энтропии также получается из MLE, но я не буду
утомлять вас большим количеством математики.
Давайте еще
упростим это для нашей модели с:
• N – количество наблюдений
• M – количество возможных меток класса (собака,
кошка, рыба)
• y – двоичный индикатор (0 или 1) того, является
ли метка класса C правильной классификацией для наблюдения O
• p – прогнозируемая вероятность модели
Бинарная классификация
В случае бинарной классификации (M=2),
формула имеет вид:
При двоичной классификации каждая предсказанная вероятность
сравнивается с фактическим значением класса (0 или 1), и вычисляется оценка,
которая штрафует вероятность на основе расстояния от ожидаемого значения.
Визуализация
На приведенном ниже графике показан диапазон возможных значений
логистической функции потерь с учетом истинного наблюдения (y = 1). Когда
прогнозируемая вероятность приближается к 1, логистическая функция потерь
медленно уменьшается. Однако при уменьшении прогнозируемой вероятности она быстро возрастает.
Логистическая функция потерь наказывает оба типа ошибок, но
особенно те прогнозы, которые являются достоверными и ошибочными!
Мульти-классовая классификация
В случае мульти-классовой классификации (M>2) мы берем сумму значений логарифмических функций потерь для
каждого прогноза наблюдаемых классов.
Кросс-энтропия для бинарной или двух-классовой задачи
прогнозирования фактически рассчитывается как средняя кросс-энтропия среди всех
примеров. Log loss использует отрицательные
значения логарифма, чтобы обеспечить удобную метрику для сравнения. Этот подход
основан на том, что логарифм чисел <1 возвращает отрицательные значения, что
затрудняет работу при сравнении производительности двух моделей. Вы можете
почитать эту статью, где детально обсуждается функция кросс-энтропии потерь.
Задачи ML и соответствующие функции потерь
Давайте посмотрим, какие обычно используются выходные слои и
функции потерь в задачах машинного обучения:
Задача регрессии
Задача, когда
вы прогнозируете вещественное число.
• Конфигурация выходного уровня: один
узел с линейной единицей активации.
• Функция
потерь: средняя квадратическая ошибка (MSE).
Задача бинарной классификации
Задача состоит в том, чтобы классифицировать пример как
принадлежащий одному из двух классов. Или более точно, задача сформулирована
как предсказание вероятности того, что пример принадлежит первому классу,
например, классу, которому вы присваиваете целочисленное значение 1, тогда как
другому классу присваивается значение 0.
• Конфигурация выходного
уровня: один узел с сигмовидной активационной функцией.
• Функция
потерь: кросс-энтропия, также называемая логарифмической функцией потерь.
Задача мульти-классовой классификации
Эта задача состоит в том, чтобы классифицировать пример как
принадлежащий одному из нескольких классов. Задача сформулирована как
предсказание вероятности того, что пример принадлежит каждому классу.
• Конфигурация выходного уровня: один
узел для каждого класса, использующий функцию активации softmax.
• Функция потерь: кросс-энтропия, также называемая логарифмической функцией потерь.
Рассмотрев оценку и различные функции потерь, давайте перейдем к
роли оптимизаторов в алгоритмах ML.
Оптимизаторы
Чтобы свести к минимуму ошибку или потерю в прогнозировании,
модель, используя примеры из обучающей выборки, обновляет параметры модели W. Расчеты
ошибок строятся в зависимости от W и также описываются графиком функции затрат
J(w), поскольку она определяет затраты/наказание модели. Таким образом, минимизация
ошибки также часто называется минимизацией функции затрат.
Но как именно это делается? Используя оптимизаторы.
Оптимизаторы используются для обновления весов и смещений, то есть
внутренних параметров модели, чтобы уменьшить ошибку.
Самым важным методом и основой того, как мы обучаем и оптимизируем
нашу модель, является метод Градиентного Спуска.
Градиентный Спуск
Когда мы строим функцию затрат J(w), это можно представить следующим
образом:
Как видно из кривой, существует значение параметров W, которое
имеет минимальное значение Jmin. Нам нужно найти способ достичь
этого минимального значения.
В алгоритме градиентного спуска мы начинаем со случайных
параметров модели и вычисляем ошибку для каждой итерации обучения, продолжая
обновлять параметры, чтобы приблизиться к минимальным значениям.
Повторяем до достижения минимума:
{
}
В приведенном выше уравнении мы обновляем параметры модели после
каждой итерации. Второй член уравнения вычисляет наклон или градиент кривой на
каждой итерации.
Градиент функции затрат вычисляется как частная производная
функции затрат J по каждому параметру модели Wj, где j принимает
значение числа признаков [1, n]. α – альфа, это скорость обучения, определяющий
как быстро мы хотим двигаться к минимуму. Если α слишком велико, мы можем
проскочить минимум. Если α слишком мало, это приведет к небольшим этапам обучения,
поэтому общее время, затрачиваемое моделью для достижения минимума, будет
больше.
Есть три способа сделать градиентный спуск:
Пакетный
градиентный спуск: использует
все обучающие данные для обновления параметров модели в каждой итерации.
Мини-пакетный градиентный спуск: вместо использования всех данных, мини-пакетный градиентный спуск делит тренировочный набор на меньший размер, называемый партией, и обозначаемый буквой «b». Таким образом, мини-пакет «b» используется для обновления параметров модели на каждой итерации.
Вот некоторые другие часто
используемые Оптимизаторы:
Стохастический
Градиентный Спуск (SGD): обновляет
параметры, используя только один обучающий параметр на каждой итерации. Такой
параметр обычно выбирается случайным образом. Стохастический градиентный спуск
часто предпочтителен для оптимизации функций затрат, когда есть сотни тысяч
обучающих или более параметров, поскольку он будет сходиться быстрее, чем
пакетный градиентный спуск.
Адаград
Адаград адаптирует скорость обучения конкретно к индивидуальным
особенностям: это означает, что некоторые веса в вашем наборе данных будут
отличаться от других. Это работает очень хорошо для разреженных наборов данных,
где пропущено много входных значений. Однако, у Адаграда есть одна серьезная
проблема: адаптивная скорость обучения со временем становится очень маленькой.
Некоторые другие оптимизаторы, описанные ниже, пытаются справиться
с этой проблемой.
RMSprop
RMSprop – это специальная версия Adagrad,
разработанная профессором Джеффри Хинтоном в его
классе нейронных сетей. Вместо того,
чтобы вычислять все градиенты, он вычисляет градиенты только в фиксированном
окне. RMSprop похож на Adaprop, это еще один оптимизатор, который пытается
решить некоторые проблемы, которые Адаград оставляет открытыми.
Адам
Адам означает адаптивную оценку момента и является еще одним способом использования
предыдущих градиентов для вычисления текущих градиентов. Адам также использует
концепцию импульса,
добавляя доли предыдущих градиентов к текущему. Этот оптимизатор получил
довольно широкое распространение и практически принят для использования в
обучающих нейронных сетях.
Вы только что ознакомились с кратким обзором
оптимизаторов. Более подробно об этом можно прочитать здесь.
Я надеюсь,
что после прочтения этой статьи, вы будете лучше понимать что происходит, когда
Вы пишите следующий код:
# loss function: Binary Cross-entropy and optimizer: Adam
model.compile(loss='binary_crossentropy', optimizer='adam')или
# loss function: MSE and optimizer: stochastic gradient descent
model.compile(loss='mean_squared_error', optimizer='sgd')Спасибо за проявленный интерес!
Ссылки:
[1] https://www.deeplearningbook.org/contents/ml.html
[2] https://machinelearningmastery.com/loss-and-loss-functions-for-training-deep-learning-neural-networks/
[3] https://blog.algorithmia.com/introduction-to-optimizers/
[4] https://jhui.github.io/2017/01/05/Deep-learning-Information-theory/
[5] https://blog.algorithmia.com/introduction-to-loss-functions/
[6] https://gombru.github.io/2018/05/23/cross_entropy_loss/
[7] https://www.kdnuggets.com/2018/04/right-metric-evaluating-machine-learning-models-1.html
[8] https://rohanvarma.me/Loss-Functions/
[9] http://blog.christianperone.com/2019/01/mle/

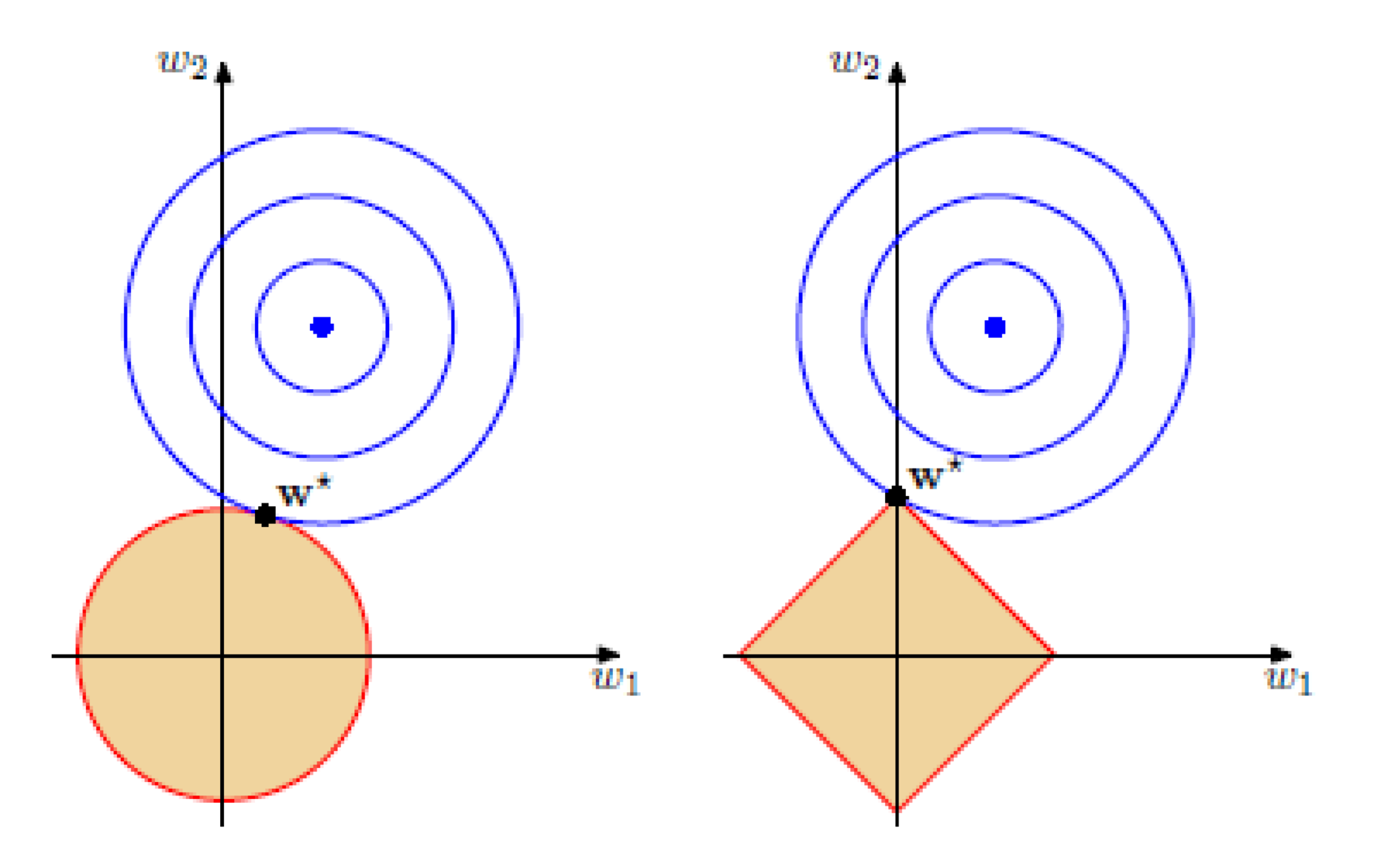
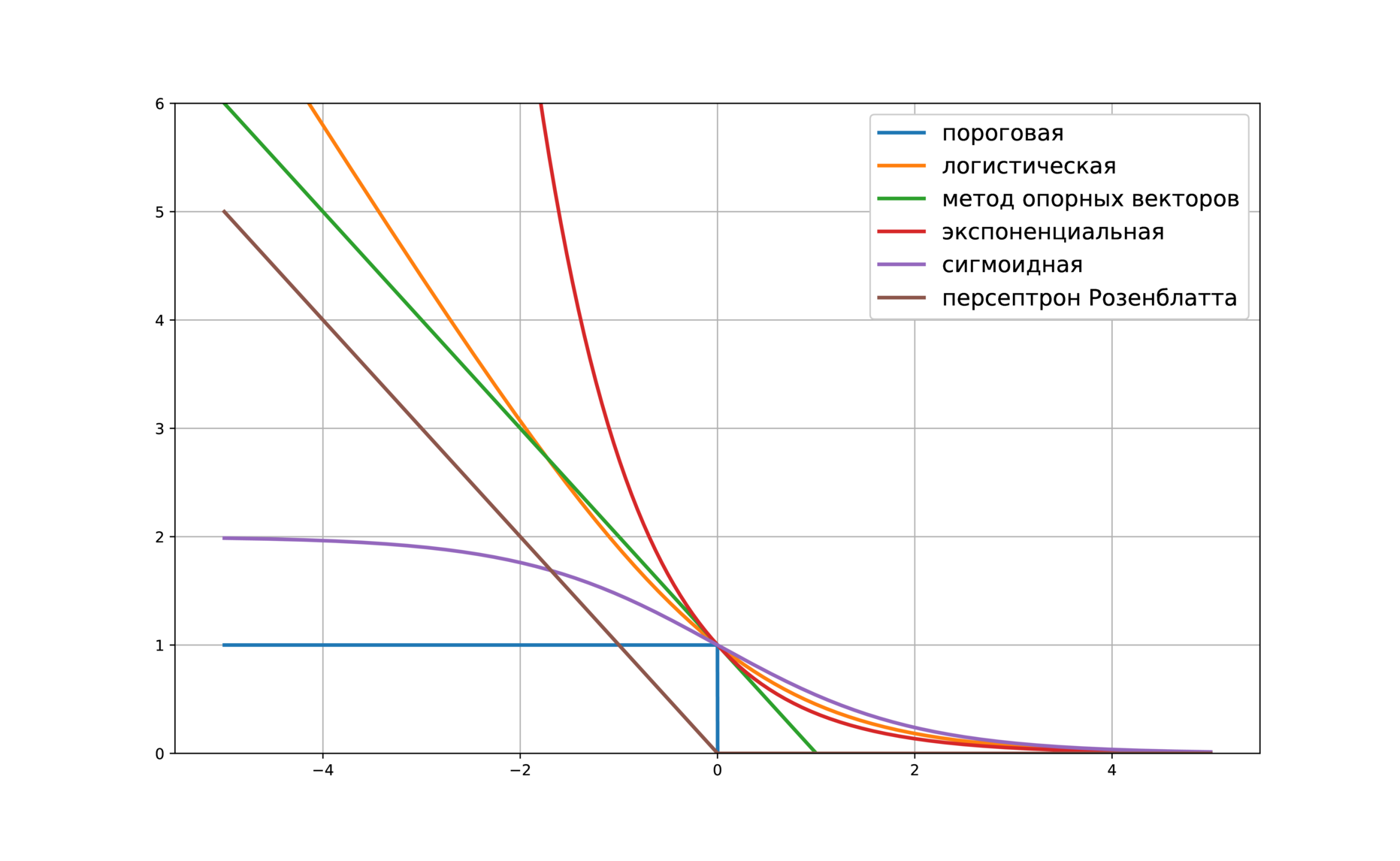
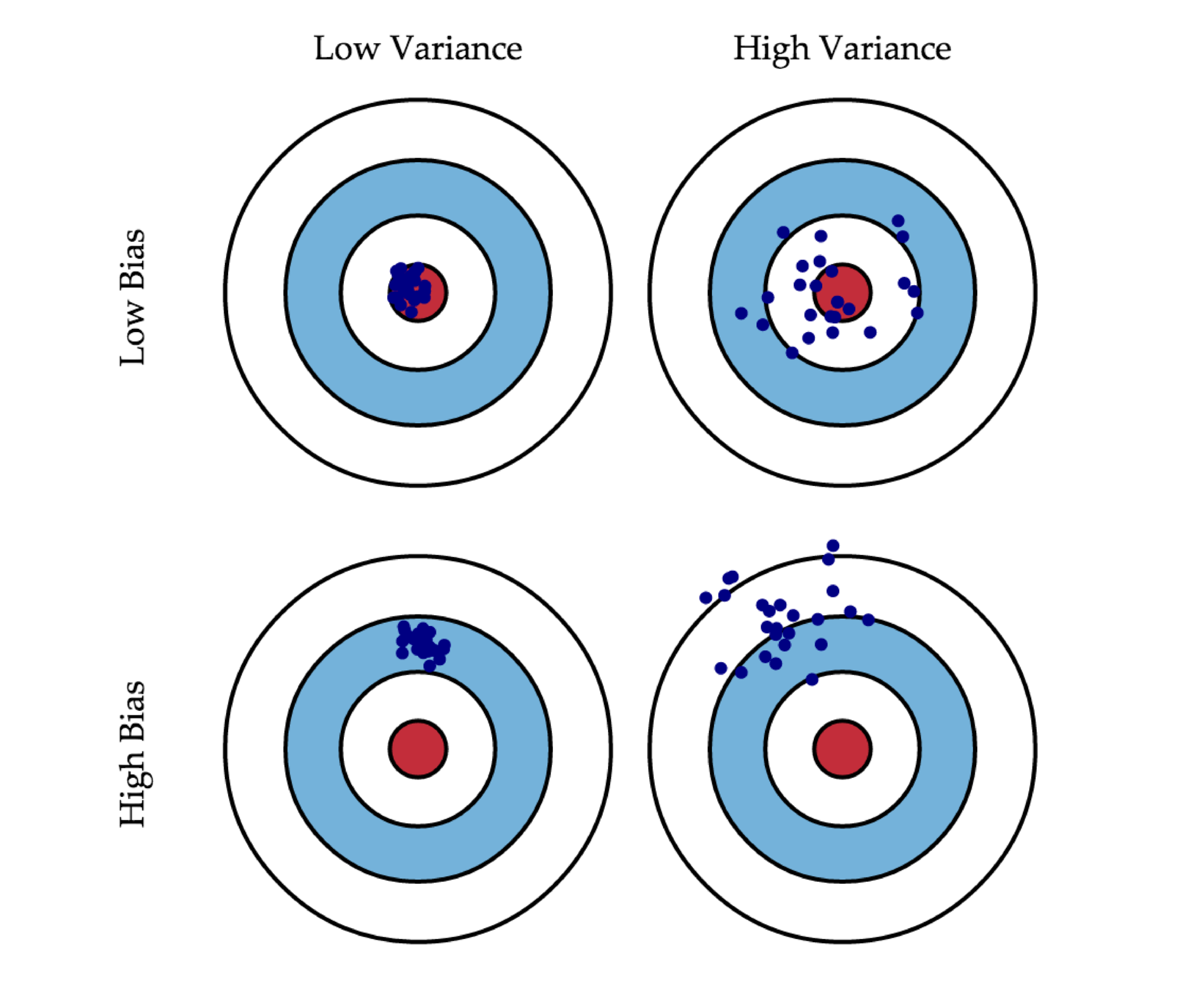





![{\displaystyle {\begin{aligned}\Pr[X\leq L]&={\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} {\frac {L-\mu }{{\sqrt {2}}\sigma }}\\&\approx A\exp \left(-B\left({\frac {L-\mu }{\sigma }}\right)^{2}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3cb760eaf336393db9fd0bb12c4465655a27de8)
![{\displaystyle \Pr[X\leq L]\leq A\exp(-B\ln {k})={\frac {A}{k^{B}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2baadea015e20a45d1034fd88eed861e7fcce178)
![{\displaystyle {\begin{aligned}\Pr[L_{a}\leq X\leq L_{b}]&=\int _{L_{a}}^{L_{b}}{\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\,\mathrm {d} x\\&={\frac {1}{2}}\left(\operatorname {erf} {\frac {L_{b}-\mu }{{\sqrt {2}}\sigma }}-\operatorname {erf} {\frac {L_{a}-\mu }{{\sqrt {2}}\sigma }}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd2214f0db2c1d36075815825b616501175c6283)


![{\displaystyle {\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}-{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}-\cdots \right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c80541f305af070bb0510625c584fe1559a0cd2c)
![{\displaystyle {\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }\left(z\prod _{k=1}^{n}{\frac {-(2k-1)z^{2}}{k(2k+1)}}\right)\\[6pt]&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dca22e8e7dee0297e87a455249c282c6b92fedcb)
![{\displaystyle {\begin{aligned}\operatorname {erfi} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z+{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}+{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}+\cdots \right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff91095cd6825137cc951ec0a786db0b7f68fac)





![{\displaystyle {\begin{aligned}\operatorname {erf} x&={\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left(1-{\frac {1}{12}}\left(1-e^{-x^{2}}\right)-{\frac {7}{480}}\left(1-e^{-x^{2}}\right)^{2}-{\frac {5}{896}}\left(1-e^{-x^{2}}\right)^{3}-{\frac {787}{276480}}\left(1-e^{-x^{2}}\right)^{4}-\cdots \right)\\[10pt]&={\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left({\frac {\sqrt {\pi }}{2}}+\sum _{k=1}^{\infty }c_{k}e^{-kx^{2}}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/164e7f029977edb47c83845b04abfe5b2d28b837)








![{\displaystyle {\begin{aligned}\operatorname {erfc} x&={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\left(1+\sum _{n=1}^{\infty }(-1)^{n}{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{\left(2x^{2}\right)^{n}}}\right)\\[6pt]&={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n-1)!!}{\left(2x^{2}\right)^{n}}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35a11e2e5b22ca898c74f2e913d276c9ac11124a)































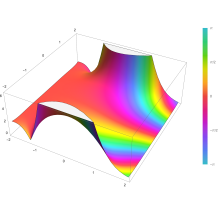
![{\displaystyle {\begin{aligned}\operatorname {erfc} x&=1-\operatorname {erf} x\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t\\[5pt]&=e^{-x^{2}}\operatorname {erfcx} x,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4acd0062271e2a19c209a02c8cc33d44a28af7cc)



![{\displaystyle {\begin{aligned}\operatorname {erfi} x&=-i\operatorname {erf} ix\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{t^{2}}\,\mathrm {d} t\\[5pt]&={\frac {2}{\sqrt {\pi }}}e^{x^{2}}D(x),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd2dd94cd6d0325224d412f6b5e5ed63ca81d4a)

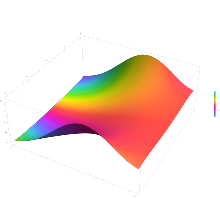
![{\displaystyle {\begin{aligned}\Phi (x)&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{\tfrac {-t^{2}}{2}}\,\mathrm {d} t\\[6pt]&={\frac {1}{2}}\left(1+\operatorname {erf} {\frac {x}{\sqrt {2}}}\right)\\[6pt]&={\frac {1}{2}}\operatorname {erfc} \left(-{\frac {x}{\sqrt {2}}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89a9e9eaaddcd7a91ade15a41b8d1e272d437559)
![{\displaystyle {\begin{aligned}\operatorname {erf} (x)&=2\Phi \left(x{\sqrt {2}}\right)-1\\[6pt]\operatorname {erfc} (x)&=2\Phi \left(-x{\sqrt {2}}\right)\\&=2\left(1-\Phi \left(x{\sqrt {2}}\right)\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c84a4d2d79631fe9996e30f1d6c0da3089bfe2)








![{\displaystyle {\begin{aligned}\operatorname {i} ^{n}\!\operatorname {erfc} z&=\int _{z}^{\infty }\operatorname {i} ^{n-1}\!\operatorname {erfc} \zeta \,\mathrm {d} \zeta \\[6pt]\operatorname {i} ^{0}\!\operatorname {erfc} z&=\operatorname {erfc} z\\\operatorname {i} ^{1}\!\operatorname {erfc} z&=\operatorname {ierfc} z={\frac {1}{\sqrt {\pi }}}e^{-z^{2}}-z\operatorname {erfc} z\\\operatorname {i} ^{2}\!\operatorname {erfc} z&={\tfrac {1}{4}}\left(\operatorname {erfc} z-2z\operatorname {ierfc} z\right)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e7b953efaa4d730a5479bd61a2c378c8f761dc)