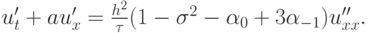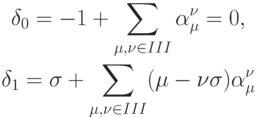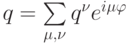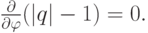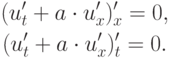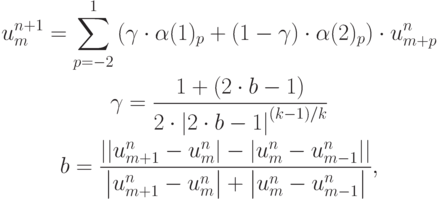Диссипативная и дисперсионная ошибка - Решение и исправление самых разных ошибок на TopOshibok.ru

и единственную на данном шаблоне схему третьего порядка аппроксимации с
порядком 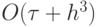$O(\tau + h^{3})$ :

${\alpha_{- 2} = \frac{{{\sigma}\cdot \left({{\sigma}- 1}\right)}}{6}.}$

(
3.16)

Остальные коэффициенты находятся с использованием (3.15) и (3.16).

Введем пространство коэффициентов 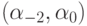$(\alpha_{- 2},{\alpha}_0)$ . Тогда
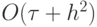
любая точка в этом пространстве есть разностная схема с порядком аппроксимации $O(\tau + h)$ . Прямая (3.15) отделяет в пространстве множество схем с порядком $O(\tau + h^{2})$ (рис.
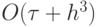
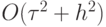
3.2), на ней лежит единственная точка — аппроксимация $O(\tau + h^{3})$ . Должна быть также и точка с порядком аппроксимации $O(\tau ^{2} + h^{2})$ .

Зафиксируем какое — либо число Куранта, например, $\sigma = 0, 5$ .
Применим к разностной схеме (3.14) с неопределенными коэффициентами
спектральный признак устойчивости (фон Неймана). Получится кривая, которая определяет границу устойчивости разностных схем в пространстве неопределенных коэффициентов.

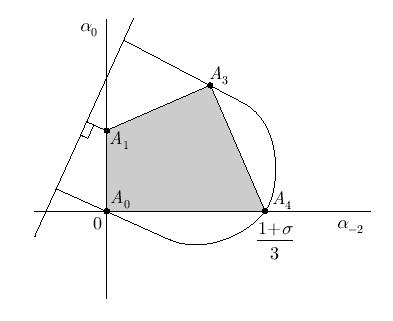
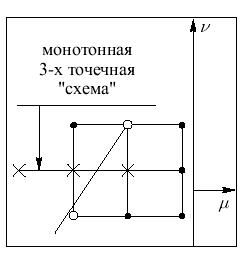
Рис.
3.2.

Для схем первого порядка выпишем первое дифференциальное приближение:

$u^{\prime}_t + au^{\prime}_x = \frac{{h^2}}{\tau}(1 - {\sigma}^2 -{\alpha}_0 + 3{\alpha}_{- 1})u^{\prime\prime}_{xx} .$

Можно также выделить множество таких схем, что ${\alpha}_{\mu}\ge 0$ .
Это — монотонные схемы (заштрихованный многоугольник на рис. 3.2). Среди монотонных схем можно найти схему с наименьшей ошибкой аппроксимации. Это точка многоугольника, которая при данном $\sigma$ лежит ближе всего к прямой со схемами второго порядка аппроксимации.

Закончим рассмотрение примера с модельным линейным уравнением переноса:

На выбранном шаблоне любая разностная схема, как указывалось ранее,
представляется в виде

$u_m^{n + 1} = \sum\limits_{\mu \in III}{\alpha}_{\mu} u_{m + \mu}^{n}.$

В случае монотонной схемы можно оценить норму погрешности. Заметим, что
погрешность v определяется тем же разностным уравнением (3.14),
тогда с использованием первой нормы (максимум абсолютной величины)

$\| v^{n + 1}\| = \| v^{n}\| \sum\limits_{\mu \in III}{\alpha}_{\mu}$

в силу аппроксимации

$\sum\limits_{\mu \in III}{\alpha}_{\mu}\le 1.$

Отсюда следует, что монотонные разностные схемы всегда устойчивы. В общем
случае можно рассматривать многослойные шаблоны для уравнения переноса (рис. 3.3)

$u_m^{n + 1} = \sum\limits_{\mu,{\nu} \in III}{\alpha}_{\mu}^{\nu} u_{m + \mu}^{n +{\nu}}$

и записывать условия порядка для аппроксимации соответствующего порядка:

$\begin{gather*} \delta_0 = - 1 + \sum\limits_{\mu,{\nu} \in III}{\alpha}_{\mu}^{\nu} = 0, \\ \delta_1 = {\sigma}+ \sum\limits_{\mu,{\nu} \in III} (\mu - {\nu}\sigma){\alpha}_{\mu}^{\nu} \end{gather*}$

Рис.
3.3.

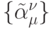
Исключая два коэффициента из условий порядка, можно от пространства неопределенных коэффициентов $\{{\alpha}_{\mu}^{\nu} \}$ перейти к пространству $\{\tilde{\alpha}_{\mu}^{\nu} \}$ , размерность
которого на 2 меньше, например:

$\begin{gather*} {\alpha}_{- 1}^0 = \frac{1}{2} \left({1 + \sigma- \sum (\mu - \nu \sigma) {\alpha}_{\mu}^{\nu}}\right), \\ {\alpha}_1^0 = \frac{1}{2} \left({1 - \sigma- \sum (\mu - \nu \sigma ){\alpha}_{\mu}^{\nu} }\right), \end{gather*} $$

где, конечно, точки (0; — 1) и (0; 1) не включаются в
суммирование. Условие устойчивости в пространстве неопределенных коэффициентов имеет вид

$|q({\alpha}_{\mu}^{\nu} , {\varphi})| \le 1,$

где q есть спектр оператора послойного перехода. Эта величина
определяется из условия

$q = \sum\limits_{\mu ,{\nu} }{q^{\nu} e^{i \mu {\varphi}}}$

и дополнительного требования

$\frac{{\partial}}{{\partial}{\varphi}}(|q| - 1) = 0.$

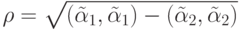
Основная гипотеза: Разностным схемам, которым в пространстве $\{\tilde{\alpha}_{\mu}^{\nu} \},$ соответствуют близкие друг к другу точки (в смысле ${\rho} = \sqrt{(\tilde{\alpha}_1, \tilde{\alpha}_1 ) - (\tilde{\alpha}_2, \tilde{\alpha}_2 )}$ ) по своим свойствам также близки.

Расширяя шаблон, как и в случае пятиточечного шаблона, можно строить области схем высокого порядка аппроксимации, монотонные схемы ( ${\alpha}_{\mu}^{\nu} \ge 0$ ) и т.д.

Монотонные разностные схемы в пространстве неопределенных коэффициентов
занимают некий выпуклый многоугольник, вершины которого определяются довольно просто: это все возможные при данном числе Куранта $\sigma$ трехточечные разностные схемы, причем для характеристики, проходящей через $u_m^{n + 1}$ , одна точка схемы лежит выше (левее) характеристики, а другая ниже (правее), см. рис. 3.3.

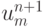
Метод построения разностных схем в пространстве неопределенных коэффициентов для квазилинейных систем уравнений гиперболического типа (к ним относятся системы уравнений механики сплошных сред, в частности, газовой динамики, механики деформируемого твердого тела (МДТТ) и т.п.) допускает обобщение и на многомерные случаи. Подробное описание можно найти в монографии [13.9]. Здесь же многомерные обобщения рассматриваться не будут. Они приводят к эффективным численным методам для нестационарных многомерных задач.

Исследовав схемы (3.14) на устойчивость по спектральному признаку, получаем множество устойчивых схем, а потребовав выполнения условия ${\alpha}_k \ge 0$ для всех точек шаблона, получаем множество схем с положительной аппроксимацией (монотонных по Фридрихсу схем). На рассматриваемом
шаблоне устойчивые схемы существуют при 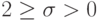$2 \ge {\sigma} > 0$ (для a > 0 ).

Множество схем с положительной аппроксимацией не пересекается с множеством
схем с порядком аппроксимации выше первого, как это следует из теоремы С.К. Годунова.

Первое дифференциальное приближение. Дисперсионная и диссипативная
ошибки

Поскольку решения дифференциальной задачи и разностного уравнения
принадлежат разным функциональным пространствам, что порождает определенные трудности при теоретическом анализе свойств разностных схем, для такого исследования возможно рассматривать разностные операторы в том же пространстве. Будем считать, что разностные схемы удовлетворяются функциями непрерывного аргумента в каждой точке рассматриваемой области.

Обычно ограничиваются рассмотрением уравнений, в которых оставлены члены в
разложении в ряд Тейлора проекции точного решения на сетку по 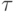$\tau$ и h, порядок которых совпадает с порядком погрешности аппроксимации схемы. Получающиеся при этом уравнения называют первым дифференциальным
приближением (ПДП).

Для схемы первого порядка (5) при выполнении условия (6) первым дифференциальным приближением будет

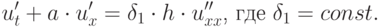$u^{\prime}_t + a \cdot u^{\prime}_x = \delta_1 \cdot h \cdot u^{\prime\prime}_{{x}{x}} \mbox{, где } \delta_1 = {const}.$

(
3.17)

Из уравнения (3.17) исключены члены со второй производной u’_tt, с использованием так называемой продолженной системы:

$\begin{gather*} (u^{\prime}_t + a \cdot u^{\prime}_x )^{\prime}_x = 0, \\ (u^{\prime}_t + a \cdot u^{\prime}_x )^{\prime}_t = 0. \end{gather*}$

Иногда уравнение (3.17) называют $\Pi$ — формой (параболической формой) первого дифференциального приближения. Если производные по времени не исключаются из ПДП, то имеем Г — форму (гиперболическую
форму) ПДП, которая, как правило, не применяется в исследованиях как малоинформативная.

При $\delta_1 > 0$ уравнение (3.17) можно трактовать как
присутствие в схеме некоторой диссипации ( схемной вязкости ). Ее наличие проявляется в расчетах в виде размазывания точного решения, причем его интенсивность увеличивается при ухудшении аппроксимации (увеличении шага h ). В этом случае говорят, что ошибка схемы носит диссипативный характер. Если схемная вязкость получается отрицательной, то приходим к обратной задаче теплопроводности. Как известно из курсов математической физики, такая задача поставлена некорректно. А соответствующая разностная схема при исследовании по спектральному признаку оказывается неустойчивой — по ПДП можно сделать вывод об устойчивости схемы.

Для более высокого (второго) порядка ПДП имеет вид

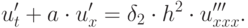${u^{\prime}_t + a \cdot u^{\prime}_x = \delta_2 \cdot h^2 \cdot u^{\prime\prime\prime}_{xxx}.}$

(
3.18)

Уравнение (3.18) обладает дисперсией, т.е. разные пространственные гармоники разложения начального возмущения в ряд Фурье распространяются по сетке с разными скоростями. Говорят, что ошибка носит дисперсионный характер. Сеточная дисперсия легко получается, если искать частное решение последнего уравнения в виде комплексной экспоненты: $u = \lambda (t) exp(ikx\} )$ . Подробнее о ПДП в [13.4].

Интересна связь ПДП и исследования свойств схем в пространствах неопределенных коэффициентов. Так, для схем первого порядка расстояние от точки в пространстве неопределенных коэффициентов до прямой схем высокого порядка (3.15) по абсолютной
величине равен коэффициенту 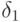$\delta_1$ в уравнении (3.17), а знак определяется положением внутри области устойчивости.

Понятие о гибридных схемах

Численные расчеты по разностным схемам высокого порядка показывают, что
осцилляции нефизического характера появляются в окрестности разрывов
решения или его первой производной. В связи с этим возникает идея
построения численного метода, имеющего высокий порядок аппроксимации на
участках гладкого решения, в то время как в окрестности разрывов функций
или их производных применяется монотонная схема (с положительной
аппроксимацией) первого порядка.

Можно формализовать этот подход:

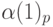
$\begin{gather*} u_m^{n + 1} = \sum\limits_{p = - 2}^1 {\left({\gamma \cdot {\alpha} (1)_p + (1 - \gamma ) \cdot{\alpha} (2)_p }\right) \cdot u_{{m} + {p}}^{n}} \\ \gamma = \frac{{1 + \left({2 \cdot b - 1}\right)}}{{2 \cdot \left| {2 \cdot b - 1}\right|^{({k} - 1)/{k}}}} \\ b = \frac{{\left|{\left| {u_{{m} + 1}^{n} - u_m^{n}}\right| - \left|{u_m^{n} - u_{m - 1}^{n}}\right|}\right|}}{{\left| {u_{m + 1}^{n} - u_m^{n}}\right| + \left|{u_m^{n} - u_{m - 1}^{n}}\right|}}, \end{gather*}$

где ${\alpha} (1)_p$ — коэффициенты первой схемы (высокого
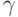
порядка аппроксимации), применяемой в области гладкого решения, ${\alpha} (2)_p$ — коэффициенты второй (монотонной) схемы, $\gamma$ — весовой коэффициент, вспомогательный параметр b характеризует гладкость решения (очевидно, что b = 0, при $u \equiv {const}$ ), k — коэффициент гибридности — целое число из диапазона $2 \le {k} \le 10$ .

При этом реализовано достаточно гладкое переключение со схем высокого порядка аппроксимации на монотонные схемы.

Источник

Old
June 21, 2013, 04:29

Default
dissipative and dispersive error of finite difference methods

New Member

Join Date: Apr 2013

Posts: 15

Rep Power: 12

Hi all,

We know that for the spatial derivative using a finite difference method, if the leading error term is odd, then the results contain dispersive error, while if the leading error term is even, then it has dissipative error.

I want to compare the degree of such errors. Say, the leading error term is 7th order (FD7), compared with the leading error term is 5th order (FD5), which one has more severe dispersive error? For sure, FD7 is more accurate, what’s its performance with regard to dispersive error?

Thanks.

Shu

Old
June 21, 2013, 06:29

Default

Senior Member

Filippo Maria Denaro

Join Date: Jul 2010

Posts: 6,595

Rep Power: 70

Quote:

Originally Posted by shubiaohewan

Hi all,

Thanks.

Shu

This is a classical numerical analysis task, you can analyze the local truncation error of the discretization formula, it gives much information about the character of the error.
Furthermore, I suggest using the spectral analysis too, that is the modified wavenumber that each formula produces.
It is important to remark that not necessarily a higher order accurate formula performs better than a lower one on a given grid. Accuracy order is only an asymptotic estimation that does not tell you how the formula behaves for the chosen grid. Thus, the modified wavenumber analysis can help to understand the error distribution for the grid you want to use.

Old
June 21, 2013, 06:31

Default

Senior Member

cfdnewbie

Join Date: Mar 2010

Posts: 557

Rep Power: 19

There is a standard procedure of analysing dispersive and dissipative behavior of FD schemes. Discretize a linear advection equation, plug in a wave with frequency k and amplitude a and check the resulting frequency and amplitude response — that gives you the dissipation and dispersion error of your scheme.

Old
June 21, 2013, 06:46

Default

Senior Member

Filippo Maria Denaro

Join Date: Jul 2010

Posts: 6,595

Rep Power: 70

Quote:

Originally Posted by cfdnewbie

Such analysis can be extended, in a suitable way, also for the non linear equation (e.g., Burgers)

Old
June 21, 2013, 07:01

Default

Senior Member

cfdnewbie

Join Date: Mar 2010

Posts: 557

Rep Power: 19

Hello Prof. Denaro,
I have only seen this done for linear equations. I assume that Burger’s would lead to a non-linear system to solve for? Do you have any good reference on the details of this? that would be a very interesting read!
thanks in advance!

Old
June 21, 2013, 07:15

Default

Senior Member

Paolo Lampitella

Join Date: Mar 2009

Location: Italy

Posts: 2,120

Blog Entries: 29

Rep Power: 38

I don’t know if Prof. Denaro is referencing what i have in mind; however, a possible practical (i.e., non analytical) approach is this:

http://www.sciencedirect.com/science…21999111001148

Old
June 21, 2013, 07:20

Default

Senior Member

cfdnewbie

Join Date: Mar 2010

Posts: 557

Rep Power: 19

Thank you Paolo,
that looks very interesting!

Источник

← Назад Далее →

Все построенные на равномерной сетке разностные операторы являются однородными — их коэффициенты в вычислительных шаблонах инвариантны относительно сдвигов шаблона по сетке. Для однородных дискретных операторов можно построить частные решения в виде бегущих волн:

$$u_{j}^{n} =D\cdot \exp \left\{i\left[{\rm\omega }\cdot n{\rm\tau }-kjh\right]\right\}=A\cdot q^{n} \cdot \exp \left\{-i\left(kjh\right)\right\};{\rm\; \; \; } (2.38)$$

здесь ${\rm\; \; \; }q=\exp \left\{i\left({\rm\omega \tau }\right)\right\}$ — множитель переходана следующий временной слой.

Подставим (2.38) в разностный оператор схемы «уголок» (2.26). Получаем:

$$\begin{array}{l} {q=r\cdot e^{ikh} +\left(1-r\right)\cdot ,\; \Rightarrow \; } \\{\Rightarrow \left|q\left(r,kh\right)\right|{\rm =}\sqrt{\left[\left(1- r\right)+r\cdot \cos \left(kh\right)\right]^{2} {\rm +}\left[{\rm sin}\left(kh\right)\right]^{2} } {\rm\; \; }} \end{array} (2.39)$$

Соотношение, выражающее множитель перехода через параметры дискретного оператора, будем называть характеристическим уравнениемразностной схемы.

Модуль множителя перехода $\left|q\right|$ является функцией от числа Куранта — Фридрихса-Леви $r$ и приведенного волнового числа $kh$, изменяющегося в пределах от $-{\rm\pi }$: $\left(-{\rm\pi }\le kh\le {\rm\pi }\right)$. Он показывает, как изменяется амплитуда бегущей волны при переходе на следующий слой. Если модуль перехода меньше или равен единице, то амплитуда волны не возрастает. Если для заданного $r$ амплитуды всех волн при $\left(-{\rm\pi }\le kh\le {\rm\pi }\right)$ не возрастают, то говорят, что данное число $r$ принадлежит области устойчивости дискретного оператора. Опираясь на (2.39) можно показать, что область устойчивости разностной схемы «уголок» представляет собой единичный отрезок $r\in \left[0,1\right]$. Если в области устойчивости модуль перехода любой волны равен единице, то дискретный оператор называется бездиссипативным, в противном случае имеет место численная диссипация.

Диссипативные свойства дискретного оператора для всех приведенных волновых чисел наиболее наглядно можно представить в виде двумерной поверхности $\left|q\right|=f\left(r,kh\right)$. Для схемы «уголок» диссипативная поверхность изображена на рис. 6а, где по оси $z$ отложены значения модуля перехода, по оси $x$ — значения числа $r\in \left[0,1\right]$, по оси $y$ — значения приведенного волнового числа $kh\in \left[-{\rm\pi },{\rm\pi }\right]$. Видно, что модуль перехода стремится к единице для длинноволновых гармоник, для которых $kh\approx 0$, и равен единице на границе области устойчивости, при $r=1,{\rm\; }\left(-{\rm\pi }\le kh\le {\rm\pi }\right)$.

Из (2.39) также следует дисперсионное соотношение:

$$q=e^{i{\rm\omega \tau }} =r\cdot e^{ikh} +\left(1-r\right)\cdot ,\; \Rightarrow \; {\rm\omega }=-\frac{i}{{\rm\tau }} \arg \left[r\cdot e^{ikh} +\left(1-r\right)\right]$$

откуда получается выражение для приведенной фазовой скорости бегущих волн:

$$\begin{array}{l} {\gamma \left(r,kh\right){\rm =}\frac{{\rm\omega }}{kc} {\rm\; }=-\frac{i}{{\rm\tau }kc} \arg \left[r\cdot e^{ikh} +\left(1-r\right)\right]{\rm =}} \\{{\rm =}-\frac{i}{r\cdot kh} \arg \left[r\cdot e^{ikh} +\left(1-r\right)\right]{\rm\; \; }} \end{array}$$

Приведенная фазовая скорость бегущих волн, описываемых исходным дифференциальным оператором, не зависит от номера гармоники и равна единице. Как ранее уже отмечалось, зависимость фазовой скорости от длины волны называется дисперсией. В разностном случае приведенная фазовая скорость может принимать значения как меньшие, так и большие единицы. В первом случае дисперсия называется «нормальной», во втором — «аномальной». В случае нормальной дисперсии гармоника отстает от «эталонной» гармоники, двигающейся с фазовой скоростью $c$, в случае аномальной дисперсии — опережает ее.

Дисперсионные свойства дискретного оператора представляются его «дисперсионной поверхностью». На рис. 6в приведена дисперсионная поверхность разностного оператора «уголок». Здесь по оси $z$ отложены значения приведенной фазовой скорости ${\rm\gamma }$, по оси $x$- значения числа $r\in \left[0,1\right]$, по оси $y$ — значения приведенного волнового числа $kh\in \left[-{\rm\pi },{\rm\pi }\right]$. Дисперсия стремится к нулю, что соответствует стремлению ${\rm\gamma }$ к единице, для длинноволновых гармоник, для которых $kh\approx 0$ и на границе области устойчивости, при $r=1,{\rm\; }\left(-{\rm\pi }\le kh\le {\rm\pi }\right)$.

Стремление к нулю дисперсии и диссипации длинноволновых гармоник является общим свойством всех дискретных операторов, аппроксимирующих исходный дифференциальный оператор. Характер касания дисперсионных и диссипативных поверхностей единичной плоскости определяется порядком аппроксимации разностного оператора. Тот факт, что при $r = 1$все гармоники не диссипируют и не диспергируют, говорит о том, что разностный оператор при данном числе Куранта переносит начальный профиль без каких либо искажений.

Из непрерывности дисперсионной и диссипативной поверхностей следует, что в некоторой окрестности этого числа точность численного решения также будет аномально высокой и эту область можно назвать «каналом высокой точности» дискретного оператора.

Из рис. 6в видно, что дисперсия схемы «уголок» при $r < 0.5$ является нормальной, а при $r > 0.5$ — аномальной. При $r = 0.5$дисперсия отсутствует.

Диссипативная и дисперсионная поверхности дают полное представление о свойствах разностной схемы, позволяют предсказывать поведение дискретного решения на разных начальных условиях. Рассмотрим модельную задачу (2.1) с периодическими начальными условиями на отрезке $x\in \left[0,2{\rm\pi }\right]$:

$$\begin{array}{l} {\frac{\partial u}{\partial t} +c\cdot \frac{\partial u}{\partial x} =0,{\rm\; \; }c=1;{\rm\; \; }t\in \left[0,\infty \right);} \\{u\left(x,0\right)=f\left(x\right);{\rm\; \; \; }u\left(0,t\right)=u\left(1,t\right);x\in \left[0,2{\rm\pi }\right];} \end{array} (2.40)$$

и двумя видами начальных условий — достаточно гладкими и разрывными.

В качестве гладкого начального условия возьмем «двойной гауссиан» с параметрами:

$$\begin{array}{l} {f\left(x\right)=\exp \left[-\left(x-x_{1} \right)^{2} /\Delta ^{2} \right]+\exp \left[-\left(x-x_{2} \right)^{2} /\Delta ^{2} \right];} \\{x_{1} =0.5\cdot {\rm\pi },{\rm\; \; \; }x_{2} =0.7\cdot {\rm\pi },{\rm\; \; \; }\Delta =0.1\cdot {\rm\pi }} \end{array} (2.41)$$

в качестве разрывного — «ступеньку»:

$$f\left(x\right)=\left\{\begin{array}{l} {1,{\rm\; \; \; \; if\; \; \; \; \; \; }0.2\cdot {\rm\pi }\le x\le 0.4\cdot {\rm\pi }} \\{0,{\rm\; \; \; \; if\; \; \; \; \; \; }\left(0\le x \le 0.2\cdot {\rm\pi }\right)\& \left(0.4\cdot {\rm\pi } \le x \le 2{\rm\pi }\right)} \end{array}\right. (2.42)$$

Аппроксимируем дифференциальную задачу (2.40) — (2.42) разностной схемой «уголок». Разобьём отрезок $x\in \left[0,2{\rm\pi }\right]$ на N=100 равных интервалов с шагом $h=0.2{\rm\pi }$ и спроектируем на нее начальные данные (2.41) — (2.42):

$$\begin{array}{l} {f_{i}^{\left(1\right)} =\exp \left\{-\left[\left(i-1\right)h-x_{1} \right]^{2} /\left(0.1\cdot {\rm\pi }\right)^{2} \right\}+} \\{+\exp \left\{-\left[\left(i-1\right)h-x_{2} \right]^{2} /\left(0.1\cdot {\rm\pi }\right)^{2} \right\};} \\{f_{i}^{\left(2\right)} =\left\{\begin{array}{l} {1,{\rm\; \; \; \; if\; \; \; \; \; \; }11\le i\le 21} \\{0,{\rm\; \; \; \; if\; \; \; \; \; \; }\left(1\le i \le 11\right)\& \left(21 \le i\le 101\right)} \end{array}\right. ;{\rm\; }\quad i=1,…,101} \end{array} (2.43)$$

Разложим эти сеточные функции в ряд Фурье:

$$f_{n}^{\left(m\right)} =\sum _{k=0}^{N}a_{k}^{\left(m\right)} \cdot \exp \left[-i\left(kh\right)\cdot n\right];{\rm\; \; }m=1,2;{\rm\; \; }n=1,…,N+1 (2.44)$$

где коэффициенты разложения определяются по формуле:

$$a_{k}^{\left(m\right)} =\frac{1}{N+1} \cdot \sum _{n=1}^{N+1}f_{n}^{\left(m\right)} \cdot \exp \left[i\left(kh\right)\cdot n\right] (2.45)$$

На рис. 7 представлены графики начальных данных (2.43), на рис. 8 — модули их коэффициентов разложения $a_{k}^{\left(m\right)}$.

В начальный момент времени все гармоники разложения (2.44) подогнаны друг к другу так, что в сумме составляют начальные данные. В последующие моменты времени каждая гармоника будет уменьшаться в амплитуде в соответствии с ее местом на диссипативной поверхности, и распространяться со своей фазовой скоростью, определяемой дисперсионной поверхностью, так что «пакет» гармоник начнет разъезжаться. Полная картина будет еще зависеть от числа Куранта-Фридрихса-Леви $r$.

Из рис. 6 видно, что наибольшая диссипация высоких гармоник имеет место при $r = 0.5$. На рис. 9 приведен результаты расчета переноса начальных профилей (2.43), рассчитанные по схеме «уголок» при разных числах Куранта, до одного и того же момента времени. Сплошной линией показано аналитическое решение дифференциальной задачи, линией с маркерами — решение, рассчитанное по разностной схеме.

← Назад Далее →

Источник