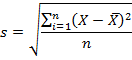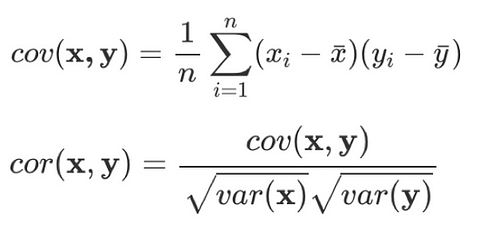Дисперсия среднеквадратическая ошибка - Решение и исправление самых разных ошибок на TopOshibok.ru

From Wikipedia, the free encyclopedia

In statistics, the mean squared error (MSE)^[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.^[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.^[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).

The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.

The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).^{[citation needed]} For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.

Definition and basic properties[edit]

The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.

Predictor[edit]

If a vector of predictions is generated from a sample of data points on all variables, and is the vector of observed values of the variable being predicted, with $\hat{Y}$ being the predicted values (e.g. as from a least-squares fit), then the within-sample MSE of the predictor is computed as

$\operatorname {MSE} ={\frac {1}{n}}\sum _{i=1}^{n}\left(Y_{i}-{\hat {Y_{i}}}\right)^{2}.$

In other words, the MSE is the mean ${\textstyle \left({\frac {1}{n}}\sum _{i=1}^{n}\right)}$ of the squares of the errors ${\textstyle \left(Y_{i}-{\hat {Y_{i}}}\right)^{2}}$ . This is an easily computable quantity for a particular sample (and hence is sample-dependent).

In matrix notation,

$\operatorname {MSE} ={\frac {1}{n}}\sum _{i=1}^{n}(e_{i})^{2}={\frac {1}{n}}\mathbf {e} ^{\mathsf {T}}\mathbf {e}$

where $e_{i}$ is $(Y_{i}-{\hat {Y_{i}}})$ and $\mathbf {e}$ is a $n\times 1$ column vector.

The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as cross-validation, the MSE is often called the test MSE,^[4] and is computed as

$\operatorname {MSE} ={\frac {1}{q}}\sum _{i=n+1}^{n+q}\left(Y_{i}-{\hat {Y_{i}}}\right)^{2}.$

Estimator[edit]

The MSE of an estimator $\hat{\theta}$ with respect to an unknown parameter $\theta$ is defined as^[1]

$\operatorname {MSE} ({\hat {\theta }})=\operatorname {E} _{\theta }\left[({\hat {\theta }}-\theta )^{2}\right].$

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator $\hat{\theta}$ is derived as a sample statistic and is used to estimate some population parameter, then the expectation is with respect to the sampling distribution of the sample statistic.

The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.^[5]

$\operatorname {MSE} ({\hat {\theta }})=\operatorname {Var} _{\theta }({\hat {\theta }})+\operatorname {Bias} ({\hat {\theta }},\theta )^{2}.$

Proof of variance and bias relationship[edit]

${\begin{aligned}\operatorname {MSE} ({\hat {\theta }})&=\operatorname {E} _{\theta }\left[({\hat {\theta }}-\theta )^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]+\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}+2\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+\operatorname {E} _{\theta }\left[2\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)\right]+\operatorname {E} _{\theta }\left[\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+2\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)\operatorname {E} _{\theta }\left[{\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right]+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}&&\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta ={\text{const.}}\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+2\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}&&\operatorname {E} _{\theta }[{\hat {\theta }}]={\text{const.}}\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\\&=\operatorname {Var} _{\theta }({\hat {\theta }})+\operatorname {Bias} _{\theta }({\hat {\theta }},\theta )^{2}\end{aligned}}$

An even shorter proof can be achieved using the well-known formula that for a random variable ${\textstyle X}$ , ${\textstyle \mathbb {E} (X^{2})=\operatorname {Var} (X)+(\mathbb {E} (X))^{2}}$ . By substituting ${\textstyle X}$ with, ${\textstyle {\hat {\theta }}-\theta }$ , we have

${\begin{aligned}\operatorname {MSE} ({\hat {\theta }})&=\mathbb {E} [({\hat {\theta }}-\theta )^{2}]\\&=\operatorname {Var} ({\hat {\theta }}-\theta )+(\mathbb {E} [{\hat {\theta }}-\theta ])^{2}\\&=\operatorname {Var} ({\hat {\theta }})+\operatorname {Bias} ^{2}({\hat {\theta }},\theta )\end{aligned}}$

But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.

In regression[edit]

In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,^[6] but whose limitation is related to known distribution of the data.

The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).^[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.

In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.

In the context of gradient descent algorithms, it is common to introduce a factor of 1/2 to the MSE for ease of computation after taking the derivative. So a value which is technically half the mean of squared errors may be called the MSE.

Examples[edit]

Mean[edit]

Suppose we have a random sample of size from a population, $X_{1},\dots ,X_{n}$ . Suppose the sample units were chosen with replacement. That is, the units are selected one at a time, and previously selected units are still eligible for selection for all draws. The usual estimator for the $\mu$ is the sample average

$\overline{X}=\frac{1}{n}\sum_{i=1}^n X_i$

which has an expected value equal to the true mean $\mu$ (so it is unbiased) and a mean squared error of

$\operatorname {MSE} \left({\overline {X}}\right)=\operatorname {E} \left[\left({\overline {X}}-\mu \right)^{2}\right]=\left({\frac {\sigma }{\sqrt {n}}}\right)^{2}={\frac {\sigma ^{2}}{n}}$

where $\sigma ^{2}$ is the population variance.

For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.

Variance[edit]

The usual estimator for the variance is the corrected sample variance:

$S_{n-1}^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}\left(X_{i}-{\overline {X}}\right)^{2}={\frac {1}{n-1}}\left(\sum _{i=1}^{n}X_{i}^{2}-n{\overline {X}}^{2}\right).$

This is unbiased (its expected value is $\sigma ^{2}$ ), hence also called the unbiased sample variance, and its MSE is^[8]

$\operatorname {MSE} (S_{n-1}^{2})={\frac {1}{n}}\left(\mu _{4}-{\frac {n-3}{n-1}}\sigma ^{4}\right)={\frac {1}{n}}\left(\gamma _{2}+{\frac {2n}{n-1}}\right)\sigma ^{4},$

where $\mu _{4}$ is the fourth central moment of the distribution or population, and $\gamma_2=\mu_4/\sigma^4-3$ is the excess kurtosis.

However, one can use other estimators for $\sigma ^{2}$ which are proportional to $S^2_{n-1}$ , and an appropriate choice can always give a lower mean squared error. If we define

$S_{a}^{2}={\frac {n-1}{a}}S_{n-1}^{2}={\frac {1}{a}}\sum _{i=1}^{n}\left(X_{i}-{\overline {X}}\,\right)^{2}$

then we calculate:

${\begin{aligned}\operatorname {MSE} (S_{a}^{2})&=\operatorname {E} \left[\left({\frac {n-1}{a}}S_{n-1}^{2}-\sigma ^{2}\right)^{2}\right]\\&=\operatorname {E} \left[{\frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2\left({\frac {n-1}{a}}S_{n-1}^{2}\right)\sigma ^{2}+\sigma ^{4}\right]\\&={\frac {(n-1)^{2}}{a^{2}}}\operatorname {E} \left[S_{n-1}^{4}\right]-2\left({\frac {n-1}{a}}\right)\operatorname {E} \left[S_{n-1}^{2}\right]\sigma ^{2}+\sigma ^{4}\\&={\frac {(n-1)^{2}}{a^{2}}}\operatorname {E} \left[S_{n-1}^{4}\right]-2\left({\frac {n-1}{a}}\right)\sigma ^{4}+\sigma ^{4}&&\operatorname {E} \left[S_{n-1}^{2}\right]=\sigma ^{2}\\&={\frac {(n-1)^{2}}{a^{2}}}\left({\frac {\gamma _{2}}{n}}+{\frac {n+1}{n-1}}\right)\sigma ^{4}-2\left({\frac {n-1}{a}}\right)\sigma ^{4}+\sigma ^{4}&&\operatorname {E} \left[S_{n-1}^{4}\right]=\operatorname {MSE} (S_{n-1}^{2})+\sigma ^{4}\\&={\frac {n-1}{na^{2}}}\left((n-1)\gamma _{2}+n^{2}+n\right)\sigma ^{4}-2\left({\frac {n-1}{a}}\right)\sigma ^{4}+\sigma ^{4}\end{aligned}}$

This is minimized when

$a=\frac{(n-1)\gamma_2+n^2+n}{n} = n+1+\frac{n-1}{n}\gamma_2.$

For a Gaussian distribution, where $\gamma_2=0$ , this means that the MSE is minimized when dividing the sum by a=n+1 . The minimum excess kurtosis is $\gamma_2=-2$ ,^[a] which is achieved by a Bernoulli distribution with p = 1/2 (a coin flip), and the MSE is minimized for $a=n-1+{\tfrac {2}{n}}.$ Hence regardless of the kurtosis, we get a «better» estimate (in the sense of having a lower MSE) by scaling down the unbiased estimator a little bit; this is a simple example of a shrinkage estimator: one «shrinks» the estimator towards zero (scales down the unbiased estimator).

Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be $S^2_{n-1}.$

Gaussian distribution[edit]

The following table gives several estimators of the true parameters of the population, μ and σ², for the Gaussian case.^[9]

True value	Estimator	Mean squared error
$\theta =\mu$	$\hat{\theta}$ = the unbiased estimator of the population mean, $\overline{X}=\frac{1}{n}\sum_{i=1}^n(X_i)$	$\operatorname{MSE}(\overline{X})=\operatorname{E}((\overline{X}-\mu)^2)=\left(\frac{\sigma}{\sqrt{n}}\right)^2$
$\theta =\sigma ^{2}$	$\hat{\theta}$ = the unbiased estimator of the population variance, $S^2_{n-1} = \frac{1}{n-1}\sum_{i=1}^n\left(X_i-\overline{X}\,\right)^2$	$\operatorname{MSE}(S^2_{n-1})=\operatorname{E}((S^2_{n-1}-\sigma^2)^2)=\frac{2}{n - 1}\sigma^4$
$\theta =\sigma ^{2}$	$\hat{\theta}$ = the biased estimator of the population variance, $S^2_{n} = \frac{1}{n}\sum_{i=1}^n\left(X_i-\overline{X}\,\right)^2$	$\operatorname{MSE}(S^2_{n})=\operatorname{E}((S^2_{n}-\sigma^2)^2)=\frac{2n - 1}{n^2}\sigma^4$
$\theta =\sigma ^{2}$	$\hat{\theta}$ = the biased estimator of the population variance, $S^2_{n+1} = \frac{1}{n+1}\sum_{i=1}^n\left(X_i-\overline{X}\,\right)^2$	$\operatorname{MSE}(S^2_{n+1})=\operatorname{E}((S^2_{n+1}-\sigma^2)^2)=\frac{2}{n + 1}\sigma^4$

Interpretation[edit]

An MSE of zero, meaning that the estimator $\hat{\theta}$ predicts observations of the parameter $\theta$ with perfect accuracy, is ideal (but typically not possible).

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).

Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.

In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.

MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.

Applications[edit]

Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.

Loss function[edit]

Squared error loss is one of the most widely used loss functions in statistics^{[citation needed]}, though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.^[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.

Criticism[edit]

The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.^[10]

Like variance, mean squared error has the disadvantage of heavily weighting outliers.^[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.

Notes[edit]

^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.

References[edit]

^ ^a ^b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20. If we use quadratic loss, our risk function is called the mean squared error (MSE) …
^ ^a ^b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.{{cite book}}: CS1 maint: others (link)
^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.

Источник

Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

где

s² – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

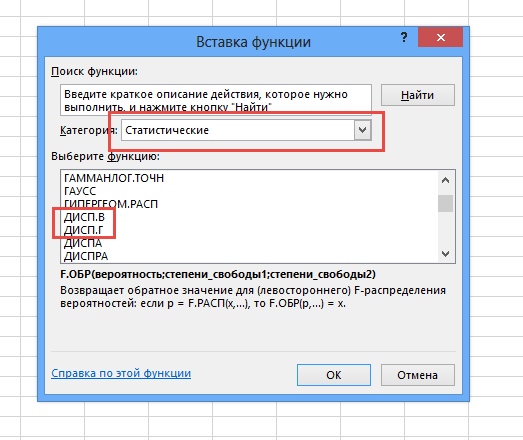
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).

D(A) = 0

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А² раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

D(AX) = А² D(X)

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

D(A + X) = D(X)

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

D(X+Y) = D(X) + D(Y)

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

D(X-Y) = D(X) + D(Y)

Среднеквадратичное (стандартное) отклонение

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:

На практике формула стандартного отклонения следующая:

Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

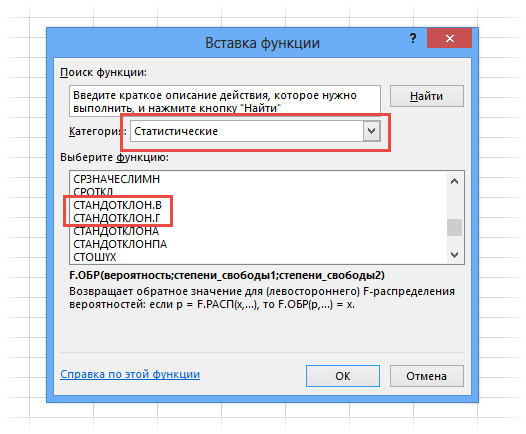
Расчет cреднеквадратичного (стандартного) отклонения в Excel

Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Расчет коэффициента вариации в Excel

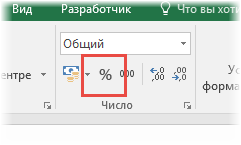
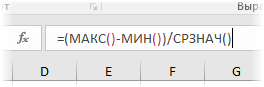
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:

=СТАНДОТКЛОН.В()/СРЗНАЧ()

Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Поделиться в социальных сетях:

Источник

Ошибка оценки

Ошибка
оценки – это отклонение полученной
оценки от неизвестного значения
оцениваемой вероятностной характеристики
случайной величины.

Ошибка
оценки сама по себе является случайной
величиной. Она имеет нулевое математическое
ожидание (предполагается, что смещение
оценки отсутствует) и некоторую ненулевую
дисперсию _n²,
величина которой зависит от объёма
выборки n.
Чем больше объём выборки n,
тем меньше дисперсия _n²
и тем точнее оценка.

Обычно
для характеристики ошибки оценки
используется корень квадратный из
дисперсии оценки _n²,
и эта величина _n
носит название среднеквадратической
ошибки.

Поскольку
среднеквадратическая ошибка оценки _n
заранее не известна, она также подлежит
оцениванию. Её оценка обозначается
добавлением «крышечки»:
.

Выборочное среднее

Выборочное среднее
– это оценка неизвестного значения
математического ожидания случайной
величины по выборочным данным.

Вычисляется по
формуле среднего арифметического:

=
(x₁
+ x₂
+ … + x_n) / n = ,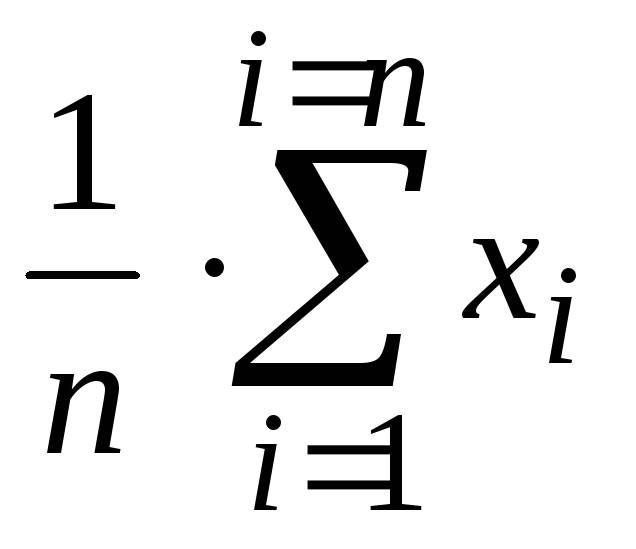
гдеn
– объём выборки.

С ростом объёма
выборки возможное отклонение выборочного
среднего

от оцениваемого неизвестного
математического ожидания случайной
величины M(X)
уменьшается.

Выборочная дисперсия

Выборочная дисперсия
– это оценка неизвестного значения
дисперсии наблюдаемой в опыте случайной
величины.

Вычисляется по
формуле среднего арифметического, в
которой выборочные значения заменены
квадратами отклонений выборочных
значений от математического ожидания.
Как правило, математическое ожидание
генеральной совокупности неизвестно,
поэтому оно без большой ошибки заменяется
его оценкой, т.е. выборочным средним.

Таким образом,
выборочная дисперсия – это средний
квадрат отклонения выборочных значений
от выборочного среднего.

Формула для
вычисления выборочной дисперсии такова:

s²
= ( (x₁
–
)²
+ (x₂
–
)²
+ … + (x_n
–
)²
) / n = .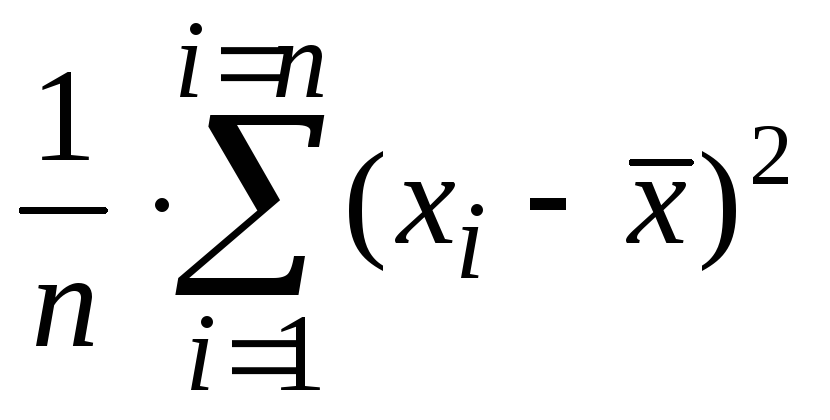

С ростом объёма
выборки n
возможное отклонение выборочной
дисперсии s²
от оцениваемой неизвестной дисперсии
случайной величины D(X)
уменьшается.

Выборочное среднеквадратическое отклонение

Выборочное
среднеквадратическое отклонение – это
оценка неизвестного значения
среднеквадратического отклонения
(стандартного отклонения) наблюдаемой
в опыте случайной величины.

Вычисляется как
квадратный корень из выборочной дисперсии
s².

Буквенное
обозначение: s
.

С ростом объёма
выборки n
возможное отклонение выборочного
среднеквадратического отклонения s
от оцениваемого среднеквадратического
отклонения 
случайной величины уменьшается.

Выборочная среднеквадратическая ошибка

Выборочная
среднеквадратическая ошибка – это
вычисленное по выборке отклонение
полученной оценки от неизвестного
значения оцениваемой вероятностной
характеристики случайной величины.

Вычисляется как
квадратный корень из выборочной дисперсии
оценки _n².

Буквенное
обозначение:
.

С ростом объёма
выборки n
возможное значение выборочной
среднеквадратической ошибки
уменьшается, изменяясь обратно
пропорционально.

Выборочный коэффициент корреляции

Выборочный
коэффициент корреляции – это оценка
неизвестного значения коэффициента
корреляции наблюдаемых случайных
величин X
и Y
по парам выборочных данных (x₁, y₁),
(x₂, y₂),
…, (x_n, y_n).
Буквенное обозначение: r .

Выборочный
коэффициент корреляции показывает
степень тесноты статистической связи
между отклонениями выборочных значений
двух наблюдаемых в опыте случайных
величин X
и Y
от своих математических ожиданий M(X)
и M(Y),
или, если они не известны, от выборочных
средних

и
.

Формула
для выборочного коэффициента корреляции
такова:

r
=
=.

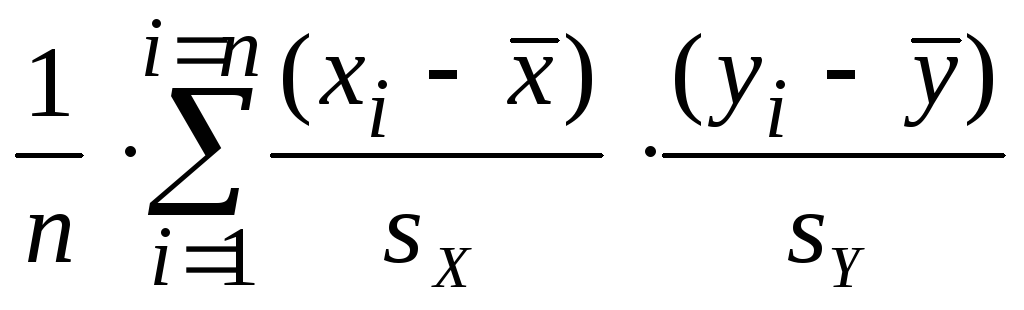
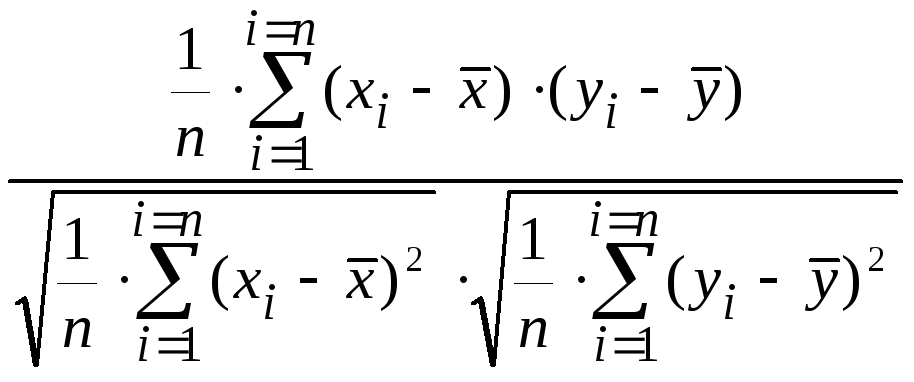
С ростом объёма
выборки n
возможное отклонение выборочного
коэффициента корреляции r
от оцениваемого неизвестного коэффициента
корреляции 
пары случайных величин уменьшается.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Статистика — это разновидность математического анализа, использующая количественные модели и репрезентации для анализа экспериментальных или реальных данных. Главное преимущество статистики — простота представления информации. Недавно я пересматривала материалы по статистике и выделила 8 основных понятий, которые должен знать каждый специалист по обработке данных:

дескриптивная аналитика;
вероятность;
среднее значение;
изменчивость;
взаимозависимость переменных;
вероятностное распределение;
проверка гипотезы и статистическая значимость;
регрессия.

Дескриптивная аналитика

Дескриптивная аналитика описывает события в прошлом и помогает бизнесу оценить эффективность деятельности, предоставляя всем участникам процесса контекст, необходимый для интерпретации информации.

Вероятность

Вероятность — это мера возможности наступления события при случайном эксперименте.

Дополнение: P(A)+P(A’) =1

Пересечение: P(A∩B)=P(A)P(B)

Объединение: P(A∪B)=P(A)+P(B)−P(A∩B)

Пересечение и объединение

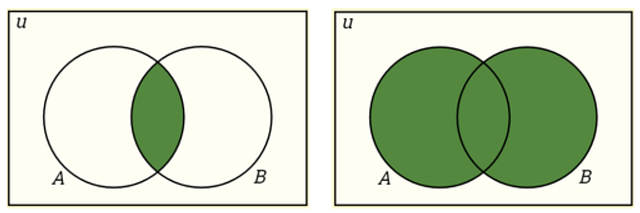
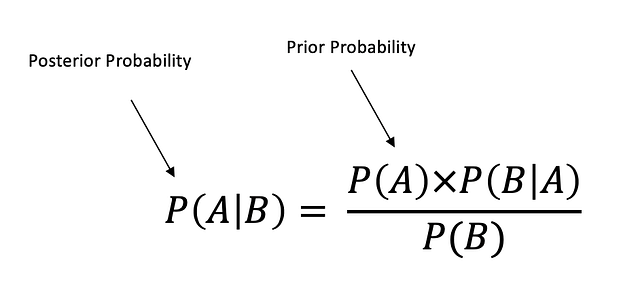
Условная вероятность: P(A|B) — это мера возможности наступления одного события по отношению к другому/-им событию/-ям. P(A|B)=P(A∩B)/P(B), когда P(B)>0.

Независимые события: два события считаются независимыми, если наступление одного из них не влияет на возможность наступления другого. P(A∩B)=P(A)P(B), где P(A) != 0 и P(B) != 0 , P(A|B)=P(A), P(B|A)=P(B).

Взаимоисключающие события: два события считаются взаимоисключающими, если оба они не могут произойти в одно и то же время. P(A∩B)=0 и P(A∪B)=P(A)+P(B).

Теорема Байеса описывает вероятность наступления события, исходя из ранее известной информации об условиях, которые могут иметь отношение к этому событию.

Теорема Байеса (слева — апостериорная вероятность, справа — априорная вероятность)

Среднее значение

Среднее арифметическое: среднее значение набора данных.

Медиана: срединное значение упорядоченного набора данных.

Мода: наиболее часто встречающееся значение в наборе данных. Если таких значений несколько, это называется мультимодальным распределением.

Асимметрия: мера симметричности.

Эксцесс: мера, показывающая медленное или быстрое убывание “хвоста” данных относительно нормального распределения.

Асимметрия

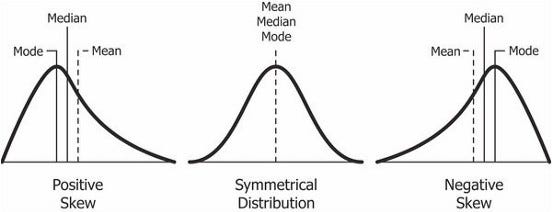
Positive Skew — Положительная асимметрия
Symmetrical Distribution — Симметричное распределение
Negative Skew — Отрицательная асимметрия
Mode — Мода
Median — Медиана
Mean — Среднее арифметическое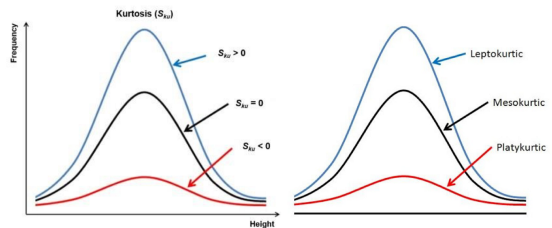

Эксцесс

Kurtosis - Эксцесс
Frequency - Частота
Height - Высота
Leptokurtic - Положительный эксцесс
Mesokurtic - Нормальный эксцесс
Platykurtic - Отрицательный эксцесс

Изменчивость

Амплитуда: разница между минимальным и максимальным значениями в наборе данных.

Межквартильный размах (IQR): IQR = Q3−Q1

Межквартильный размах

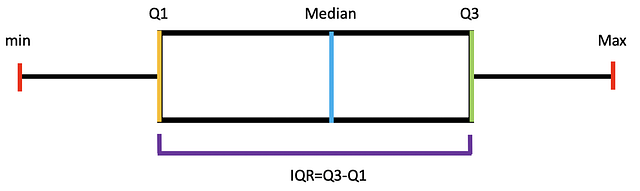
Min - Минимум
Max - Максимум
Median - Медиана

Дисперсия: среднеквадратичное отклонение значений от среднего арифметического, показывающее разброс данных относительно него.

Стандартное отклонение: стандартный разброс между каждым отдельным значением и средним арифметическим, квадратный корень из дисперсии.

Выборочная и генеральная дисперсии и стандартное отклонение

Sample Variance - Выборочная дисперсия
Population Variance - Генеральная дисперсия
Sample Standard Deviation - Выборочное стандартное отклонение
Population Standard Deviation - Генеральное стандартное отклонение

Среднеквадратическая ошибка (SE): приблизительная величина стандартного отклонения выборочного распределения.

Взаимозависимость переменных

Причинность: такая зависимость между двумя событиями, когда одно из них влияет на другое.

Ковариантность: количественная мера совокупной изменчивости двух или более переменных.

Корреляция: мера взаимозависимости между двумя переменными с коэффициентом от -1 до 1, нормализованная версия ковариантности.

Ковариантность и корреляция

Positive Relationship - Прямая зависимость
Negative Relationship - Обратная зависимость
No Relationship - Отсутствие зависимости

Вероятностное распределение

Функции вероятностного распределения

Функция распределения масс (PMF): функция, которая указывает, что дискретная случайная переменная в точности равна какому-либо значению.

Функция плотности вероятности (PDF): функция для непрерывных данных, согласно которой значение в любой выборке может расцениваться как добавляющее относительной вероятности тому, что значение случайной переменной равно значению этой выборки.

Функция кумулятивной плотности (CDF): функция, которая указывает, что случайная переменная меньше определённого значения или равна ему.

Сравнение PMF, PDF и CDF

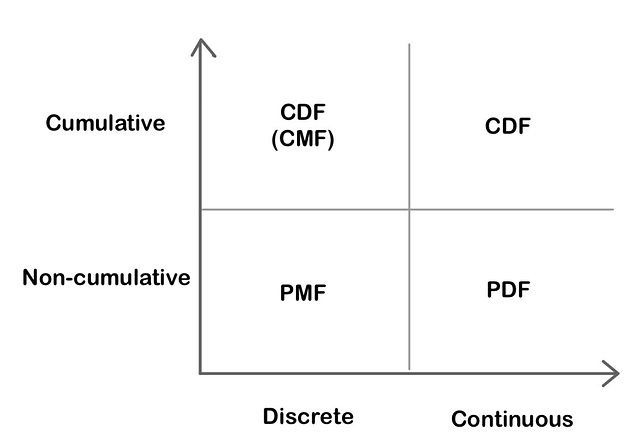
Cumulative - Кумулятивный
Non-cumulative - Некумулятивный
Discrete - Дискретный
Continuous - Непрерывный

Непрерывное распределение вероятностей

Равномерное распределение: распределение, при котором все исходы имеют одинаковую вероятность (также известно как прямоугольное распределение).

Нормальное/гауссово распределение: кривая распределения имеет форму колокола и симметрична. Согласно центральной предельной теореме, выборочное распределение средних арифметических приближается к нормальному при увеличении объёма выборки.

Uniform Distribution - Равномерное распределение
Normal Distribution - Нормальное распределение

Экспоненциальное распределение: вероятностное распределение времени между событиями в пуассоновском точечном процессе.

Распределение хи-квадрат: распределение суммы квадратов стандартных нормальных отклонений.

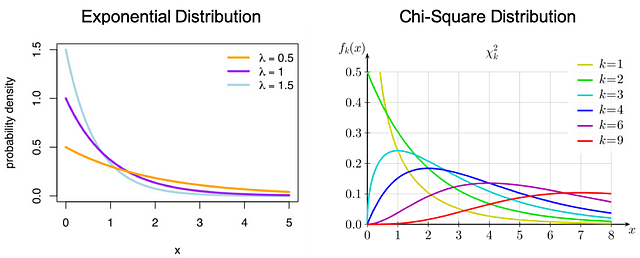
Exponential Distribution - Экспоненциальное распределение
Chi-Square Distribution - Распределение хи-квадрат
Probability Density - Плотность вероятностей

Дискретное распределение вероятностей

Распределение Бернулли: распределение случайной переменной, при котором для наступления события есть одна попытка и 2 возможных исхода: 1 — успех с вероятностью p и 0 — неудача с вероятностью 1-p.

Биномиальное распределение: распределение некоторого количества успешных исходов события в количестве n независимых экспериментов. У каждого события есть только 2 возможных исхода: 1 — успех с вероятностью p и 0 — неудача с вероятностью 1-p.

Распределение Пуассона: распределение, которое отражает вероятность заданного числа событий k, происходящих в течение фиксированного промежутка времени, если эти события наступают с известной постоянной усреднённой вероятностью λ и независимо от времени.

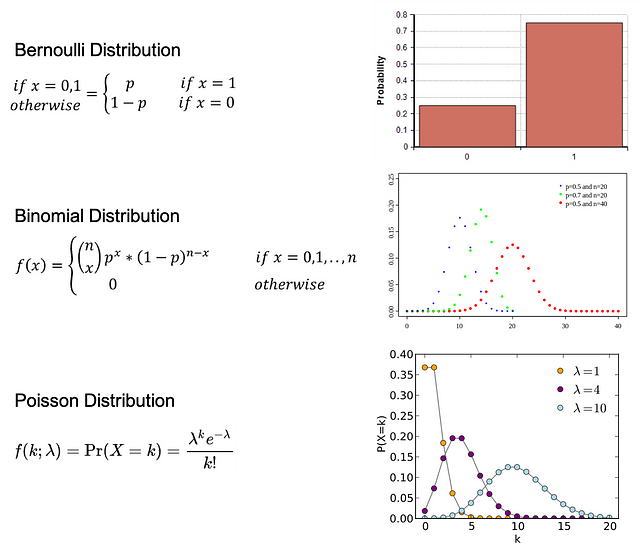
Bernoulli Distribution - Распределение Бернулли
Binomial Distribution - Биномиальное распределение
Poisson Distribution - Распределение Пуассона
Probability - Вероятность
If - Если
Otherwise - Иначе

Проверка гипотезы и статистическая значимость

Нулевая и альтернативная гипотезы

Нулевая гипотеза: общее утверждение, согласно которому между измеряемыми явлениями или их группами нет взаимозависимости.

Альтернативная гипотеза: гипотеза, обратная нулевой.

При проверке статистической гипотезы ошибка типа I — это непринятие истинной нулевой гипотезы, а ошибка типа II — принятие ложной нулевой гипотезы.

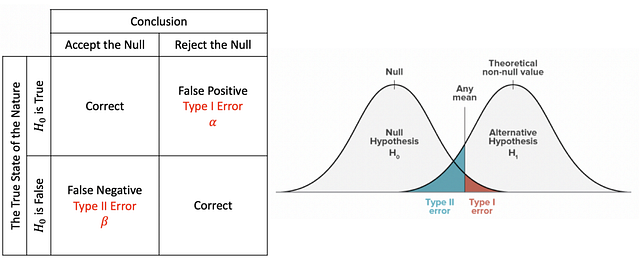
The True State of the Nature - Истинное положение вещей
False - Ложь
True - Истина
Conclusion - Вывод
Accept the Null - Принятие нуля
Reject the Null - Непринятие нуля
Correct - Верно
False Negative - Ложный отрицательный
False Positive - Ложный положительный
Type I Error - Ошибка типа I
Type II Error - Ошибка типа II
Any mean - Любое среднее арифметическое
Theoretical non-null value - Теоретическое ненулевое значение
Null Hypothesis - Нулевая гипотеза
Alternative Hypothesis - Альтернативная гипотеза

Интерпретация

P-значение: вероятность того, что данная статистика будет иметь как минимум такие же экстремальные значения, как и ранее наблюдаемая, при условии, что нулевая гипотеза верна. Когда p-значение > α, нулевую гипотезу невозможно не принять, в том время как если p-значение ≤ α, нулевая гипотеза не принимается, следовательно, мы имеем статистически значимый результат.

Критическое значение: точка на шкале статистики, выше которой нулевая гипотеза не принимается (зависит от уровня значимости проверки, α). Значение зависит от статистики (отдельная для каждого типа проверки) и уровня значимости проверки α (определяет точность проверки).

Уровень значимости и область непринятия: область непринятия зависит от уровня значимости. Уровень значимости (α) — это вероятность непринятия нулевой гипотезы при условии, что она верна.

Z-тест

Z-тест — это статистическая проверка, при которой распределение статистики при нулевой гипотезе может приближаться к нормальному, а также проверяет среднее арифметическое распределения при известной генеральной дисперсии. Следовательно, при больших объёмах выборки или известной генеральной дисперсии многие статистические проверки удобно проводить в форме Z-тестов.

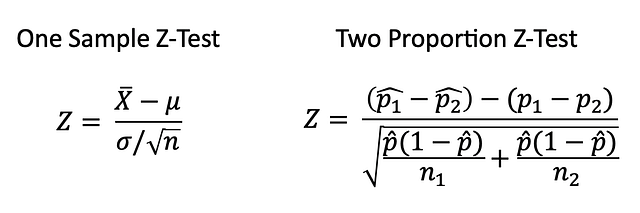
One Sample Z-Test - Z-тест одной выборки
Two Proportion Z-Test - Z-тест двух долей

T-тест

T-тест — это статистическая проверка, используемая, когда генеральная дисперсия неизвестна, а объём выборки небольшой (n < 30).

Парная выборка означает, что сбор данных производится дважды с одной и той же группы, человека, образца, предмета. Независимая выборка подразумевает, что две выборки должны быть получены с двух абсолютно разных совокупностей.

One Sample T-Test - T-тест одной выборки
Two Sample T-Test - T-тест двух выборок
Paired Sample - Парная выборка
Independent Sample - Независимая выборка
Equal/Unequal Sample Size - Одинаковый/неодинаковый объём выборки
Not Variance - Без дисперсии
Similar Variance - Одинаковая дисперсия
Unequal Variance - Неодинаковая дисперсия
Where - Где

ANOVA(дисперсионный анализ)

Аназиз ANOVA позволяет выяснить, являются ли результаты эксперимента статистически значимыми. При однофакторном дисперсионном анализе сравниваются два средних арифметических двух независимых групп с помощью одной независимой переменной. Двухфакторный дисперсионный анализ — продолжение однофакторного, здесь для вычисления главного эффекта и эффекта взаимодействия используются две независимые переменные.

Таблица ANOVA

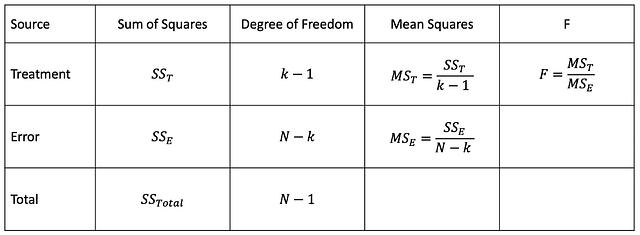
Source - Источник
Sum of Squares - Сумма квадратов
Degree of Freedom - Степень свободы
Mean Squares - Квадраты средних арифметических
Treatment - Комбинация условий
Error - Ошибка
Total - Итог

Тест хи-квадрат

Формула теста хи-квадрат

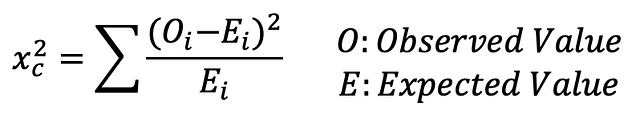
Observed Value - Наблюдаемая величина
Expected Value - Ожидаемая величина

Тест хи-квадрат определяет, соответствует ли модель нормальному распределению при введении набора дискретных данных. Критерий согласия определяет, соответствует ли распределению выборка совокупности одной категориальной переменной. Критерий независимости хи-квадрат позволяет проверить два набора данных на предмет наличия взаимосвязи.

Регрессия

Линейная регрессия

Постулаты линейной регрессии:

линейная зависимость;
многомерная нормальность;
небольшая мультиколлинеарность или её отсутствие;
небольшая автокорреляция или её отсутствие;
гомоскедастичность.

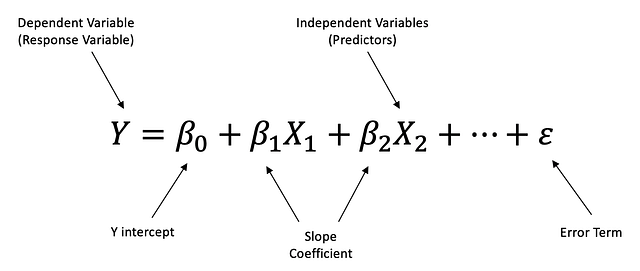
Линейная регрессия — это линейный подход к моделированию взаимозависимости между зависимой и независимой переменными. Независимая переменная — это контролируемая в ходе научного эксперимента переменная, используемая для измерения влияния на зависимую переменную. Зависимая переменная — это переменная, измеряемая в ходе научного эксперимента.

Формула линейной регрессии

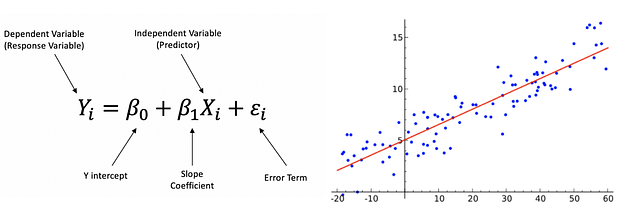
Dependent (Response) Variable - Зависимая переменная
Predictor - Регрессор
Y Intercept - Отрезок по оси Y
Slope Coefficient - Коэффициент наклона
Error Term - Величина погрешности

Множественная линейная регрессия — это линейный подход к моделированию взаимозависимости между одной зависимой и двумя или более независимыми переменными.

Формула множественной линейной регрессии (перевод понятий — под предыдущей формулой)

Этапы построения линейной регрессии

Этап 1: Проанализируйте описание модели, причинные зависимости и направленность.

Этап 2: Проверьте данные, в том числе категориальные, недостающие и выбросы.

Выброс — это образец данных, значительно отличающийся от других наблюдений. Можно использовать метод стандартного отклонения и межквартильного размаха (IQR).
Вспомогательная переменная принимает только 0 и 1 в качестве значения и отражает влияние на категориальные переменные.

Этап 3: Простой анализ — проверьте результат сравнения независимой и зависимой переменных, а также двух независимых переменных.

Используйте диаграмму рассеивания для проверки взаимозависимости.
Когда более двух независимых переменных имеют сильную взаимосвязь, это называется мультиколлинеарностью. Для количественной оценки можно использовать фактор, увеличивающий дисперсию (VIF): если VIF > 5, между переменными существует сильная взаимосвязь, если VIF > 10, между переменными возникает мультиколлинеарность.
Величина взаимодействия отражает изменения в наклоне кривой между значениями.

Этап 4: Множественная линейная регрессия — проверьте модель и истинные переменные.

Этап 5: Остаточный анализ.

Проверьте нормальное распределение, а также соответствуют ли ему остатки.
Гомоскедастичность описывает ситуацию, когда величина погрешности одинакова для всех значений независимых переменных, следовательно, значения остатков также одинаковы на протяжении всей кривой регрессии.

Этап 6: Интерпретация результатов регрессии.

R-квадрат — это статистический показатель точности подбора, который указывает, насколько отклонение зависимой переменной было отражено независимыми переменными. Более высокие значения R-квадрата указывают, что разница между данными наблюдений и подобранными значениями небольшая.
P-значение.
Уравнение регрессии.