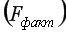Очевидно, что
точность прогноза тем выше, чем меньше
величина ошибки, которая представляет
собой разность между прогнозируемым и
фактическим значениями исследуемой
величины.
Вся проблема
состоит в том, чтобы вычислить ошибку
прогноза, так как фактическое значение
прогнозируемой величины станет известно
только в будущем. Следовательно, методы
оценки точности по уже свершившимся
событиям (апостериорные) не имеют
практической ценности, так как являются
лишь констатацией факта. При разработке
прогноза оценку его точности требуется
производить заранее (априорно), когда
истинное значение прогнозируемой
величины еще не известно. Как же поступать
в этих случаях ? Дискуссии в специальной
литературе отмечают эти трудности, в
итоге все предложения так или иначе
связаны с определением доверительного
интервала на основе статистического
выборочного метода. При этом точность
прогноза оценивается величиной
доверительного интервала для заданной
вероятности его осуществления, а под
достоверностью понимают оценку
вероятности осуществления прогноза в
заданном доверительном интервале. Таким
образом, точность прогноза выражается
с помощью вероятностных пределов
фактической величины от прогнозируемого
значения.
Следует отметить,
что точное совпадение фактических
данных и прогностических точечных
оценок, полученных путем экстраполяции
кривых, характеризующих тенденцию, –
явление маловероятное, этому виной
следующие источники погрешности:
-
выбор
формы кривой (порядка полинома и так
далее), характеризующей тренд, содержит
элемент субъективизма. Во всяком случае,
часто нет твердой основы для того, чтобы
утверждать, что выбранная форма кривой
является единственно возможной или
тем более наилучшей для экстраполяции
в данных конкретных условиях; -
оценивание
параметров кривых (иначе говоря,
оценивание тренда) производится на
основе ограниченной совокупности
наблюдений, каждое из которых содержит
случайную компоненту. В силу этого
параметрам кривой, а следовательно, и
ее положению в пространстве свойственна
некоторая неопределенность; -
тренд
характеризует некоторый средний уровень
ряда на каждый момент времени. Отдельные
наблюдения, как правило, отклоняются
от него в прошлом. Естественно ожидать,
что подобного рода отклонения будут
происходить и в будущем.
Погрешность,
связанная со вторым и третьим ее
источниками, может быть отражена в виде
доверительного интервала прогноза при
принятии допущений о свойстве ряда.
По теории
математической статистики при условии,
что случайные ошибки имеют нормальное
распределение, величины разброса событий
(доверительный интервал) при вероятности
,
для
,
для
(рис. 2.1), где
– среднеквадратическая ошибка прогноза.
Однако полученные
в ходе статистического оценивания
параметры не свободны от погрешности,
связанной с тем, что объем информации,
на основе которой производилось
оценивание, ограничен и в некотором
смысле эту информацию можно рассматривать
как выборку. Строго говоря, так как
величина
является среднеквадратичной ошибкой
(СКО) «генеральной совокупности» величин
yi,
достигаемой лишь при i,
то необходимо вводить поправку на
недостаточный объем выборки. С этой
целью в формулу вычисления доверительных
границ интервала необходимо ввести
коэффициент – значение t-статистики
Стьюдента и оперировать выборочной
СКО:
,
где
– выборочная среднеквадратическая
ошибка тренда;
– значение
t-статистики
Стьюдента.
Рис.
2.1. Доверительный интервал прогноза
Величину
выбирают из таблиц в зависимости от
(
,
где Р
– заданная
вероятность осуществления прогноза) и
v(
,
где n
– число уровней динамического ряда, m
– число параметров уравнения тренда,
для линейного тренда
).
Доверительный
интервал для прогноза, очевидно, должен
учитывать не только неопределенность,
связанную с положением тренда
,
но и возможность отклонения от этого
тренда. Если
(где z
– количество единиц времени, на которые
продлен тренд), то доверительный интервал
прогноза, учитывающий эту ошибку
(среднеквадратическую ошибку прогноза),
составит
.
При определении
средней квадратической ошибки (дисперсии)
прогноза, основанного на линейной
модели, исходя из вышеизложенных
соображений, необходимо учитывать, по
крайней мере, два источника неопределенностей.
Во-первых, естественно полагать, что
действительные значения зависимой
переменной не будут совпадать с расчетными
(прогнозными), так как сама линия регрессии
описывает взаимосвязь лишь в среднем,
в общем. Отдельные наблюдения рассеяны
вокруг нее. Таким образом, наиболее
очевидным фактором, во многом определяющим
надежность получаемых по уравнению
регрессии прогностических оценок,
является рассеяние наблюдений вокруг
линии регрессии. Во-вторых, в силу того,
что оценивание параметров модели
осуществляется по выборочным данным,
оценки a
и b
сами содержат некоторую погрешность.
Причем погрешность в значении а
приводит к вертикальному сдвигу линии
регрессии. В свою очередь, колебание
оценки b,
связанное
с ее выборочным происхождением, приводит
к «покачиванию» линии регрессии.
В качестве меры
рассеяния наблюдений вокруг линии
регрессии примем такую общераспространенную
характеристику, как дисперсия. Оценка
ее, как известно, равна сумме квадратов
отклонений, деленной на число степеней
свободы. В данном случае она составит
.
(2.5)
Учитывая то, что
две степени свободы теряются при
определении двух
параметров уравнения
прямой, последнее выражение можно
переписать в виде
.
Данную
дисперсию часто называют остаточной
(дисперсией остатков).
Погрешность в
оценке параметров модели также учитывается
дисперсиями – дисперсией параметра а
и дисперсией параметра b.
Для их определения удобно воспользоваться
формулами для вычисления коэффициентов
линейной регрессии при центрированной
независимой переменной, а именно
и
,
где
.
В этом случае
параметр а
есть выборочное среднее. Оценка дисперсии
выборочного среднего при его распределении
по нормальному закону представляет
собой отношение остаточной дисперсии
к общему числу наблюдений, то есть
.
Дисперсия параметра
b
представляет собой отношение остаточной
дисперсии к сумме квадратов отклонений
(от средней) значений независимой
переменной
с учетом квадрата значения независимой
переменной
(переменной, для которой определяется
прогноз):
.
Из данного выражения
видно, что
в точке
.
Таким образом,
оценка дисперсии прогноза, осуществленного
на основании линейного тренда,

или,
переходя к независимой переменной t:
.
При статистической
постановке прогнозной задачи
,
где
– заданное;
а
– среднее значение независимой переменной
x.
Если нанести
доверительные границы на график, то они
расположатся выше и ниже линии регрессии
в виде ветвей гиперболы, ограничивая
доверительную область (рис. 2.2).
Доверительный
интервал уменьшается при увеличении
продолжительности наблюдения (периода
основания прогноза) и растет с увеличением
периода упреждения прогноза.
Определим
доверительный интервал в рамках примера
(см табл. 2.1). Так как линейное уравнение
регрессии содержит два оцениваемых
параметра, а число наблюдений
,
то число степеней свободы при расчете
составит 14–2=12. Необходимые для расчета
квадратического отклонения показатели
разности между фактическими и расчетными
значениями уровней представлены в табл.
2.2.
Таблица 2.2.
Расчет отклонений от линейного тренда
|
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
yt |
227 |
219 |
209 |
197 |
193 |
2100 |
199 |
197 |
191 |
177 |
175 |
167 |
193 |
144 |
|
|
221 |
216 |
212 |
207 |
203 |
199 |
194 |
190 |
185 |
181 |
177 |
172 |
168 |
163 |
|
|
6 |
3 |
-3 |
-10 |
-10 |
1 |
5 |
7 |
6 |
-4 |
-2 |
-5 |
25 |
-19 |
Сумма квадратов
отклонений равна 1396.
Р
ис.
2.2. Динамика доверительного интервала
Таким образом,
.
Учитывая, что
прогноз осуществляется для
(на 2005 г.),
и
.
.
При доверительной
вероятности 0,9,
и
значение t—статистики
Стьюдента равно 1,78 и
.
Таким образом, интервальный прогноз
объектов.
Уравнения трендов
иногда определяют на основе относительно
коротких динамических рядов. Естественно,
что в этом случае возникает опасность
того, что доверительные интервалы для
линии тренда, а следовательно, и для
прогностических оценок окажутся весьма
широкими. Поэтому, задавшись некоторыми
ограничениями на размер ошибки прогноза
или ошибки уравнения тренда, можно найти
минимальное число наблюдений, при
котором поставленное условие будет
соблюдено. Так, например, уравнение,
определяющее средние квадратические
ошибки линии тренда (
),
в общем виде можно представить как
,
где k
– некоторая функция числа наблюдений
и периода упреждения. Для линейного
тренда выражение для k
можно определить из следующих соображений
[6].
Величина k
характеризует
собой отношение средних квадратических
ошибок
.
Так как
последовательность значений ti
составляет натуральный ряд
чисел,
то
и
(величины,
характеризующие разности
,
являются членами ряда с равноотстоящими
элементами). Далее, величина
характеризует расстояние z
от середины динамического ряда до точки
на оси времени, для которой делается
прогностическая оценка. следовательно,
.
Таким образом,

и
представляет собой среднюю квадратическую
ошибку уравнения, измеренную в единицах
среднего квадратического отклонения
от тренда. Этой величиной можно
воспользоваться в качестве некоторого
критерия погрешности и, исходя из ее
значения, определить минимально
необходимое число наблюдений при
заданном периоде упреждения. Допустим,
что средняя квадратическая ошибка
уравнения не должна превышать 1 при z
=1. Тогда
,
откуда
.
Определение
доверительных интервалов полиномов
невысоких степеней связано с более
объемными по содержанию выводами
зависимостей. Эти выводы широко
представлены в специальной литературе,
поэтому в целях более компактного
изложения материала далее приводятся
лишь конечные выражения.
Дисперсия прогноза,
основанного на квадратичной модели
(знак
означает
суммирование
):

Дисперсия прогноза,
основанного на кубичной параболе:

Простое сопоставление
подкоренных выражений приведенных
формул говорит о том, что при одной и
той же величине доверительный интервал
тем шире, чем выше степень полинома,
характеризующего тренд. Это и понятно,
поскольку дисперсия уравнения тренда
определяется как взвешенная сумма
дисперсий соответствующих параметров
уравнений. И все-таки, если тренд лучше
описывается кривой более высокого
порядка, то соответственно
среднеквадратическая ошибка будет
ниже и, следовательно, доверительный
интервал уже, чем, скажем, при линейном
тренде.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Research
- Open Access
- Published:
Genetics Selection Evolution
volume 41, Article number: 23 (2009)
Cite this article
-
8327 Accesses
-
18 Citations
-
Metrics details
Abstract
Calculation of the exact prediction error variance covariance matrix is often computationally too demanding, which limits its application in REML algorithms, the calculation of accuracies of estimated breeding values and the control of variance of response to selection. Alternatively Monte Carlo sampling can be used to calculate approximations of the prediction error variance, which converge to the true values if enough samples are used. However, in practical situations the number of samples, which are computationally feasible, is limited. The objective of this study was to compare the convergence rate of different formulations of the prediction error variance calculated using Monte Carlo sampling. Four of these formulations were published, four were corresponding alternative versions, and two were derived as part of this study. The different formulations had different convergence rates and these were shown to depend on the number of samples and on the level of prediction error variance. Four formulations were competitive and these made use of information on either the variance of the estimated breeding value and on the variance of the true breeding value minus the estimated breeding value or on the covariance between the true and estimated breeding values.
Introduction
In quantitative genetics the prediction error variance-covariance matrix is central to the calculation of accuracies of estimated breeding values (
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafCyDauNbaKaaaaa@2D5C@
) [e.g. [1]], to REML algorithms for the estimation of variance components [2], to methods which restrict the variance of response to selection [3], and can be used to explore trends in Mendelian sampling deviations over time [4]. The mixed model equations (MME) for most national genetic evaluations range from 100,000 to 20,000,000 equations and inversion of systems of equations of this size is generally not possible because of their magnitude or because of loss of numerical precision [5]. Methods that approximate the prediction error variances (PEV) and calculate the accuracy of
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
provide biased estimates in some circumstances by ignoring certain information [e.g. [6]]. Variance components upon which genetic evaluations of large populations are based are generally estimated using reduced data sets. The use of reduced data sets may create bias in the estimates as REML only provides unbiased estimates of variance components when all the data on which selection has taken place is included in the analysis [7]. Variance of response to selection is generally not controlled in breeding programs although it might be a risk to them [3].
Approximations of the PEV without needing to invert the coefficient matrix or to delete data, can be obtained by comparing Monte Carlo samples of the data and successive solutions of the mixed model equations of this data.
However different formulations have been presented to approximate the PEV in this way [8–11]. Approximations of the PEV using these formulations converge to the exact PEV (PEV
exact
) as the number of Monte Carlo samples increases, but the number of samples is generally limited by computational requirements in practice [e.g. [12]]. Also, differences in the rates of convergence have been shown to depend on the level of PEVexact for a given genetic variance (
σ
g
2
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGaeq4Wdm3aa0baaSqaaiabdEgaNbqaaiabikdaYaaaaaa@300E@
) [10]. Consequently, when finding the optimal number of iterations required, both the different formulations, and the level of PEVexact need to be taken into account. Some of the formulations are weighted averages of other formulations, with the weighting depending on the sampling variances of these. Garcia-Cortes et al. [10] use asymptotic approximations of these sampling variances. Alternative weighting strategies could use empirically approximated sampling variances based on independent replicates of samples or using leave-one-out Jackknife procedures [13, 14].
The objective of this study was to compare the convergence to PEVexact of ten different formulations of the PEV, using simulations based on data and pedigree from a commercial population containing animals with different levels of PEV and using different numbers of samples (n = 50, 100, …, 950, 1000). Four of the formulations were previously published, four were alternative versions of these, and two were derived as part of this study.
Methods
Monte Carlo sampling procedure for calculating PEV
The Monte Carlo sampling procedure for calculating the sampled PEV has been described extensively elsewhere for single breed [8–10] and multiple breed scenarios [12]. Assuming a simple additive genetic animal model without genetic groups y = Xb + Zu + e, where the distribution of random variables is y ~ N(Xb, ZGZ‘ + R), u ~ N(0, G), and e ~ N(0, R), the three steps involved in calculating the sampled PEV are as follows: 1. Simulate n samples of y and u using the pedigree and the distributions of the original data, modified to account for the fact that the expectation of Xb does not affect the distribution of random variables [15, 16] thus the samples of y can be simulated using random normal deviates from N(0, ZGZ‘ + R) instead of N(Xb, ZGZ‘ + R). 2. Set up and solve the mixed model equations for the data set using the n simulated samples of y instead of the true y. This accounts for the fixed effects structure of the real data. 3. Calculate the sampled PEV for some formulation.
Formulations of PEV
Ten formulations of the sampled PEV are shown in Table 1. The first three formulations (PEVGC1, PEVGC2, and PEVGC3) were outlined by Garcia-Cortes et al. [10] and the fourth formulation (PEVFL) was outlined by Fouilloux and Laloë [8]. PEVAF1, PEVAF2, PEVAF3, and PEVAF4 are alternative versions of these formulations, which rescale the formulations from the Var (u) and to the
σ
g
2
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGaeq4Wdm3aa0baaSqaaiabdEgaNbqaaiabikdaYaaaaaa@300E@
in order to account for the effects of sampling on the Var(u). Two new formulations of the sampled PEV (PEVNF1, and PEVNF2) are also given in Table 1. The ten formulations differ from each other in the way in which they compare information relating to the Var(u), the Var(
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
), the Var (u —
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
), or the Cov(u,
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
).
σ
g
2
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGaeq4Wdm3aa0baaSqaaiabdEgaNbqaaiabikdaYaaaaaa@300E@
, the assumptions pertinent to each formulation, the information used in each formulation, and the asymptotic sampling variances of each formulation
Full size table
Approximation of sampling variance of PEV
Formulae, based on Taylor series approximations, to predict the asymptotic sampling variances for each of the ten formulations of sampled PEV at different levels of PEVexact are given in Table 1. The sampling variance can also be approximated stochastically using a number (e.g. 100) of independent replicates of the n samples or by applying a leave-one-out Jackknife [13, 14] to the n samples.
Application to test data set
Data and model
A data set containing 32,128 purebred Limousin animals with records for a trait (height) and a corresponding pedigree of 50,435 animals was extracted from the Irish Cattle Breeding Federation database. In the simulations the trait was assumed to have a
σ
g
2
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGaeq4Wdm3aa0baaSqaaiabdEgaNbqaaiabikdaYaaaaaa@300E@
of 1.0 and residual variance
σ
r
2
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGaeq4Wdm3aa0baaSqaaiabhkhaYbqaaiabhkdaYaaaaaa@3027@
of 3.0. Fixed effects were contemporary group, technician who scored the animal, parity of dam, age of animal at scoring and sex.
Calculation of exact PEV
The PEVexact were calculated for the extracted data set by setting up and solving the MME, with fixed effects of contemporary group, technician who scored the animal, parity of dam, and a second order polynomial of age of animal at scoring nested within sex, and random animal and residual effects, using the BLUP option in ASReml [17] which fully inverts the left hand side of the MME.
Sampled PEV
Following the Monte Carlo sampling procedure described above, 100,000 samples of the extracted data set were simulated assuming a
σ
g
2
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGaeq4Wdm3aa0baaSqaaiabdEgaNbqaaiabikdaYaaaaaa@300E@
of 1.0 and
σ
r
2
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGaeq4Wdm3aa0baaSqaaiabdkhaYbqaaiabikdaYaaaaaa@3024@
of 3.0. For each of the simulated data sets MME, using the same design matrix (X) as used when estimating the PEVexact, were set up and solved using MiX99 [18]. The sampled PEV of the
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
for each animal in the pedigree was approximated using the formulations of the sampled PEV described in Table 1 using n samples (n = 50, 100, …, 950, 1000).
Stochastic approximations of the sampling variance of the sampled PEV were calculated using 100 independent replicates of the n samples, and using the leave-one-out Jackknife on n samples, for the different formulations, with the exception of PEVGC3 and PEVAF3. To calculate the sampling variance for PEVGC3 and PEVAF3 using n independent replicates would have required more than 100,000 samples (due to the need to generate sampling variances of component formulations) generated for this study so therefore these were not considered. Asymptotic sampling variances for all ten formulations were calculated using the formulae in Table 1.
Alternative weighting strategies
Of the formulations presented in Table 1, PEVGC3 and PEVAF3 are weighted averages of PEVGC1 and PEVGC2 and of PEVAF1 and PEVAF2 respectively with the weighting dependent on the sampling variances of the component formulations. Garcia-Cortes et al. [10] suggest weighting by asymptotic approximations of the sampling variances. The sampling variances could also be approximated empirically using independent replicates of n samples or by leave-one-out Jackknife procedures [13, 14]. These alternative weighting strategies were compared by calculating sampling variances using 100 independent replicates of the n samples, using the n samples and a leave-one-out Jackknife procedure [14], and using the asymptotic sampling variances outlined in Table 1 as part of an iterative procedure, which involved two iterations. In the first iterations the asymptotic sampling variances were calculated using the PEVGC1 and PEVGC2 of the component formulations, in the second they used the PEVGC3 approximated in the first iteration.
Calculation of required variances and covariances
It was not possible to store each of the 100,000 simulated values for each of the 50,435 animals in the main memory of the computer simultaneously meaning that textbook formulae to calculate the different variances and covariances required for the different formulations was not possible. Textbook updating algorithms to calculate the variance can be numerically unreliable [19]. Instead the required variances were calculated using a one pass updating algorithm based on Chan et al. [19] which updates the estimated sum of squares with a new record as it reads through the data and takes the form:
S
n
=
S
n
−
1
+
(
(
n
−
1
)
(
[
(
T
n
−
1
n
−
1
)
−
x
i
]
2
n
)
)
,
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGaem4uam1aaSbaaSqaaiabd6gaUbqabaGccqGH9aqpcqWGtbWudaWgaaWcbaGaemOBa4MaeyOeI0IaeGymaedabeaakiabgUcaRmaabmaabaWaaeWaaeaacqWGUbGBcqGHsislcqaIXaqmaiaawIcacaGLPaaadaqadaqcfayaamaalaaabaWaamWaaeaadaqadaqaamaaliaabaGaemivaq1aaSbaaeaacqWGUbGBcqGHsislcqaIXaqmaeqaaaqaaiabd6gaUjabgkHiTiabigdaXaaaaiaawIcacaGLPaaacqGHsislcqWG4baEdaWgaaqaaiabdMgaPbqabaaacaGLBbGaayzxaaWaaWbaaeqabaGaeGOmaidaaaqaaiabd6gaUbaaaOGaayjkaiaawMcaaaGaayjkaiaawMcaaiabcYcaSaaa@509F@
where n are the number samples at any stage in the updating procedure and T and S are the sum and sum of squares of the data points 1 through n. It was modified to calculate the covariances between X and Y by changing
[
(
T
n
−
1
n
−
1
)
−
x
i
]
2
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaWaamWaaeaadaqadaqcfayaamaaliaabaGaemivaq1aaSbaaeaacqWGUbGBcqGHsislcqaIXaqmaeqaaaqaaiabd6gaUjabgkHiTiabigdaXaaaaOGaayjkaiaawMcaaiabgkHiTiabdIha4naaBaaaleaacqWGPbqAaeqaaaGccaGLBbGaayzxaaWaaWbaaSqabeaacqaIYaGmaaaaaa@3CE6@
to
[
(
T
x
n
−
1
n
−
1
)
−
x
i
]
×
[
(
T
y
n
−
1
n
−
1
)
−
y
i
]
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaWaamWaaeaadaqadaqcfayaamaaliaabaGaemivaq1aaSbaaeaacqWG4baEdaWgaaqaaiabd6gaUjabgkHiTiabigdaXaqabaaabeaaaeaacqWGUbGBcqGHsislcqaIXaqmaaaakiaawIcacaGLPaaacqGHsislcqWG4baEdaWgaaWcbaGaemyAaKgabeaaaOGaay5waiaaw2faaiabgEna0oaadmaabaWaaeWaaKqbagaadaWccaqaaiabdsfaunaaBaaabaGaemyEaK3aaSbaaeaacqWGUbGBcqGHsislcqaIXaqmaeqaaaqabaaabaGaemOBa4MaeyOeI0IaeGymaedaaaGccaGLOaGaayzkaaGaeyOeI0IaemyEaK3aaSbaaSqaaiabdMgaPbqabaaakiaawUfacaGLDbaaaaa@5108@
. Both of these algorithms were tested using one replication of 100,000 samples and found to be stable.
Results
As the
σ
g
2
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGaeq4Wdm3aa0baaSqaaiabdEgaNbqaaiabikdaYaaaaaa@300E@
was taken to be 1.0, the PEV ranged between 0.00 and 1.0. For the purpose of categorizing the results PEV with values between 0.00 and 0.33 were regarded as low, values between 0.34 and 0.66 were regarded as medium, and values between 0.67 and 1.00 were regarded as high.
Henderson [20] showed that it is much easier to form A-1 than A, where A is the numerator relationship matrix among animals. This follows from the fact that, if the individuals are listed with ancestors above descendants, A can be written as TMT‘ where M is a diagonal matrix and T is a lower triangular matrix with non-zero diagonal elements and i, j th elements that are non-zero if the j th individual is an ancestor of the i th [21]. The matrix T has a simple inverse with both the diagonal elements and i, j th elements being non-zero if the j th individual is a parent of the i th individual. Hence A has a simple inverse. It is interesting to note that an animal effect can be written as an accumulation of independent terms from its ancestors
u
i
=
(
u
s
i
+
u
d
i
)
2
+
m
i
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGaemyDau3aaSbaaSqaaiabdMgaPbqabaGccqGH9aqpjuaGdaWcaaqaamaabmaabaGaemyDau3aaSbaaeaacqWGZbWCcqWGPbqAaeqaaiabgUcaRiabdwha1naaBaaabaGaemizaqMaemyAaKgabeaaaiaawIcacaGLPaaaaeaacqaIYaGmaaGccqGHRaWkcqWGTbqBdaWgaaWcbaGaemyAaKgabeaaaaa@404E@
, where u
si
and u
di
are the additive genetic effects of the sire and dam of animal i and m
i
is the Mendelian sampling effect with variance
A
m
i
=
(
1
−
F
i
)
2
σ
g
2
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGaemyqae0aaSbaaSqaaiabd2gaTnaaBaaameaacqWGPbqAaeqaaaWcbeaakiabg2da9KqbaoaalaaabaWaaeWaaeaacqaIXaqmcqGHsislcqWGgbGrdaWgaaqaaiabdMgaPbqabaaacaGLOaGaayzkaaaabaGaeGOmaidaaiabeo8aZPWaa0baaSqaaiabdEgaNbqaaiabikdaYaaaaaa@3CDC@
, where F
i
is the average inbreeding of the parents of animal i. Hence there is a simple recursive procedure for generation of the additive effects u
i
by generating independent Mendelian sampling terms m
i
with diagonal variance matrix
A
m
i
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGaeCyqae0aaSbaaSqaaiabd2gaTnaaBaaameaacqWGPbqAaeqaaaWcbeaaaaa@3006@
.
General trends of sampled PEV
While all different formulations of the sampled PEV converged to the PEVexact and the sampling variance of the PEV reduced as the number of samples (n) increased, convergence rates differed between the formulations. For example, PEVGC2 converged at a slower rate than all other formulations when the convergence rate was measured by the correlation between PEVexact and sampled PEV (Fig. 1). PEVGC1, PEVAF3, PEVAF4, and PEVNF2, all converged at a very similar rates and had the best convergence across all formulations.
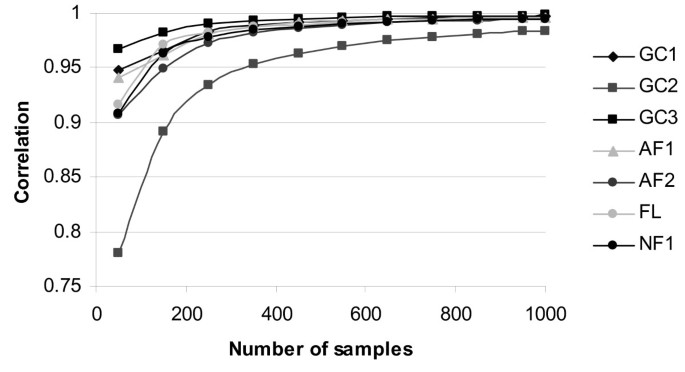
Correlations between exact prediction error variance and different formulations of sampled prediction error variance1 using n samples ( n = 50, 100, …, 950, 1000), for 18,855 non-inbred animals. 1PEVNF2, PEVAF3, PEVAF4 are not shown as they have trends, which match PEVGC3
Full size image
As well as depending on the numbers of samples, the convergence rate also depended on the level of the PEVexact. The sampled PEV calculated using different formulations had different sampling variances and within each formulation the sampling variances differed depending on the level of the PEVexact (Fig. 2). Of the previously published formulations PEVGC1 and PEVFL had low sampling variance at high PEVexact, with PEVGC1 being better than PEVFL. PEVGC2 had low sampling variance at low PEVexact. Accounting for the effects of sampling on the Var(u) reduced the sampling variance in regions where the previously published formulations had high sampling variances but had little (or even slightly negative) effect where these formulations had low sampling variances. PEVAF4, which is the alternative version of PEVFL gave major improvements in terms of sampling variance low and intermediate PEVexact. Its performance was almost identical to PEVNF2, PEVAF3, and PEVGC3, which had low sampling variance at both high and low PEV. No formulation had relatively low sampling variance for intermediate PEV.
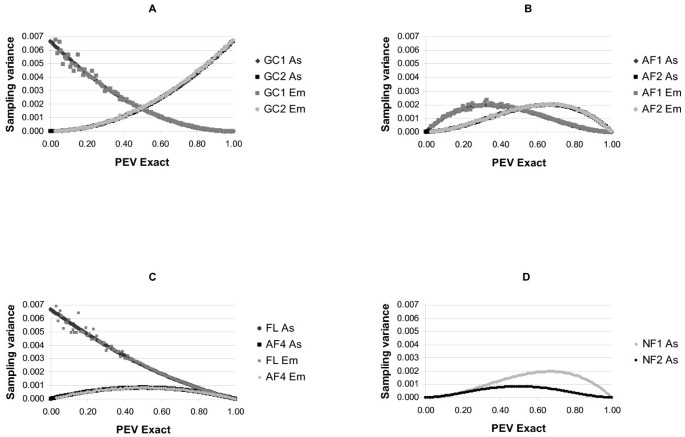
Sampling variances of sampled prediction error variance approximated asymptotically (As) and empirically1 (Em) using different formulations of the prediction error variance using 300 samples for different levels of exact prediction error variance. (A) Sampling variances for PEVGC1 and PEVGC2. (B) Sampling variances for PEVAF1 and PEVAF2. (C) Sampling variances for PEVFL and PEVAF4. (D) Sampling variances for PEVNF1 and PEVNF22. 1Empirical sampling variances were approximated using 100 independent replicates and presented as averages within windows of 0.001 of the exact prediction error variance. 2PEVGC3, and PEVAF3 were similar to PEVNF2.
Full size image
Comparison of formulations
Different formulations were compared in greater detail using n = 300 samples (Table 2), which is a practical number of samples. PEVGC3, PEVAF3, PEVAF4, and PEVNF2 were the best formulations across all of the ten formulations. The slopes and R2 of their regressions were always among the best where PEVexact was low, intermediate, or high (Table 2). These formulations gave good approximations at both high and low PEVexact their performance was less good at intermediate PEV, measured by each of the summary statistics (Table 2).
Full size table
PEVGC1 and PEVFL gave good approximations for high PEVexact and poor approximations for low PEVexact. PEVGC2 gave good approximations for low PEVexact and poor approximations for high PEVexact. Improving the published formulations by correcting for the effects of sampling resulted in better approximations in areas where the published formulations were weak. Slight (dis)improvements were observed where the previously published formulations were strong. Of the new formulations PEVNF1 gave poor approximations and PEVNF2 gave good approximations.
Using the three alternative weighting strategies to combine the component formulations for PEVGC3 and PEVAF3 gave almost identical results (Table 3).
Full size table
Required number of samples
The formulations PEVGC3, PEVAF3, PEVAF4, and PEVNF2 gave similar approximations and had the lowest sampling variance. Even when a few samples (n = 50) were used, low and high PEV were well approximated and intermediate PEVexact were poorly approximated. Correlations between PEVNF2 and PEVexact were 0.88 for low, 0.96 for high PEVexact and 0.51 for intermediate PEVexact. To increase the correlation for intermediate PEVexact to at least 0.90 at least 550 samples was needed. At this number of samples the correlations for low and high PEVexact were ≥ 0.99. To obtain a satisfactory level of convergence 300 samples were sufficient.
Discussion
Differences between formulations
Ten different formulations of the PEV approximated using sampling were compared and these were each shown to converge to the PEVexact at different rates. Within each of these formulations differences in convergence were observed at different levels of PEVexact. PEVGC1 and its corresponding alternative formulation PEVAF1 make use of information on the Var(
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
). PEVGC2 and its corresponding alternative formulation PEVAF2 makes use of information on the Var(u —
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
). The sampling variance of the Var(
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
) is lower at high PEVexact than it is at low PEVexact (Fig. 3), therefore the formulations using information on the Var(
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
) are more suited to approximating high PEVexact than to low PEVexact. The opposite is the case for formulations which use information on the Var(u —
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
), they perform better at low PEVexact. Formulations PEVGC3, PEVAF3, and PEVNF2 use information on both the Var(
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
)and the Var (u —
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
) and result in curves for their sampling variance which are symmetric about the mean PEVexact. They either explicitly or implicitly weight this information by the inverse of its sampling variance. PEVFL and PEVAF4 make use of information on the Cov(u,
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
).
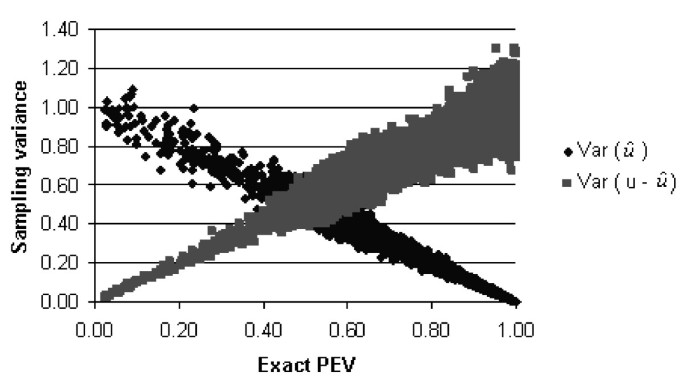
X-Y plot of the exact prediction error variance and the Var(
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
) and Var(u —
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
).
Full size image
With infinite samples the Var(u) is equal to the
σ
g
2
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGaeq4Wdm3aa0baaSqaaiabdEgaNbqaaiabikdaYaaaaaa@300E@
, but due to sampling error resulting from using a limited number of samples this not likely to be true in practice. Therefore each of the alternative formulations makes use of information on the Var(u) in addition to making use of information on either/or/both of the Var(
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
) and the Var(u —
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
) or the Cov(u,
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
). The Var(
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
) = Cov(u,
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
) when the Cov((u —
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
),
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
) = 0. The Var(
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
) ≠ Cov(u,
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
) when the Cov((u —
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
),
u
^
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGafeyDauNbaKaaaaa@2D56@
) ≠ 0.
Competitive formulations
Of the ten different approaches four competitive formulations, PEVGC3, PEVAF3, PEVAF4, and PEVNF2, were identified. These gave similar approximations. Of the four, two, PEVGC3 and PEVAF3, were weighted averages of component formulations. The weighting was based on the sampling variances of their component formulations. These sampling variances can be calculated using a number of independent replicates, using Jackknife procedures, or asymptotically. Each of these approaches gave almost identical results but the Jackknife and asymptotic approaches were far less computationally demanding.
Computational time
A single BLUP evaluation for the routine Irish multiple breed beef genetic cattle evaluation (January 2007) which included a pedigree of 1,500,000 and 493,092 animals with performance records on at least one of the 15 traits could be run using MiX99 [18] in 366 min on a 64 bit PC, with a 2.40 GHz AMD Opteron dual-core processor and 8 gigabytes of RAM [12]. Using n = 300 samples and PEVNF2 the accuracy of the estimated breeding values could be estimated in 1,830 hours on a single processor. Several samples can be solved simultaneously on multiple processors thereby reducing computer time. Nowadays PC’s are available that contain two quad core 64 bit processors (i.e. 8 CPU’s) and cost approximately 5,000 euro. Using six of these PC’s the accuracy of estimated breeding values for the Irish data set could be estimated in less than 38.1 h.
Application
The Monte Carlo sampling approach using one of these four competitive formulations can be used to improve many tasks in animal breeding. Stochastic REML algorithms [e.g. [9]] can be improved in terms of speed of calculation using these formulations, therefore allowing variance components to be estimated using REML in large data sets. These REML formulations are usually written in terms of additive genetic effects u‘A-1u and trace [A-1PEV], where PEV is the prediction error covariance matrix for the estimated breeding values. The results of Henderson [22] show how the REML formulations can be equivalently written as in terms of Mendelian sampling effects m m‘A-1m and trace [A
m
-1PEV
m
], where PEV
m
is the prediction error covariance matrix for the Mendelian sampling effects. As A
m
is diagonal we see that we only need to compute the sampling variances of the Mendelian sampling terms. When the sampling was carried out in this study we, in error, did not correct the Mendelian sampling terms for inbreeding. We therefore have only reported results for non-inbred animals and think that the incorrect generation will have a minimal effect on the sampling variances, which are presented as an empirical check on the formulae. There may be circumstances where a Stochastic REML approach may be faster than Gibbs sampling and have less bias than Method R [23]. Calculating variance components using more complete data sets would facilitate a reduction in the bias of estimated variance components caused by the ignoring of data on which selection has taken place in the population [12], due to computational limitations. Calculation of unbiased accuracy of within breed [8] and across breed [12] estimated breeding values can be improved by reducing the computational time required of calculation or reducing the sampling error for a given computational time. Application of an algorithm controlling the variance of response to selection [24] to large data sets can be speeded up. The variance of response to selection is a risk to breeding programs [3], which is generally not explicitly controlled using the approach outlined by Meuwissen [24] due to the inability to generate a prediction error (co)variance matrix for large data sets.
Computational power is a major limitation of stochastic methods, particularly when large data sets are involved, however this is dissipating rapidly with the improvement in processor speed, parallelization, and the adoption of 64-bit technology, however in the meantime deterministic methods will continue to be used for large scale BLUP analysis.
Conclusion
PEV approximations using Monte Carlo estimation were affected by the formulation used to calculate the PEV. The difference between the formulations was small when the number of samples increased, but differed depending on the level of the exact PEV and the number of samples. Rescaling from the scale of Var(u) to the scale of
σ
g
2
MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi=xH8viVGI8Gi=hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI+fsY=rqGqVepae9pg0db9vqaiVgFr0xfr=xfr=xc9adbaqaaeGaciGaaiaabeqaaeqabiWaaaGcbaGaeq4Wdm3aa0baaSqaaiabdEgaNbqaaiabikdaYaaaaaa@300E@
improved the approximation of the PEV and four of the 10 formulations gave the best approximations of PEVexact thereby improving the efficiency of the Monte Carlo sampling procedure for calculating the PEV. The fewer samples that are required the less the computational time will be.
References
-
Henderson CR: Best linear unbiased estimation and prediction under a selection model. Biometrics. 1975, 31: 423-447. 10.2307/2529430.
Article
CAS
PubMedGoogle Scholar
-
Patterson HD, Thompson R: Recovery of inter-block information when block sizes are unequal. Biometrika. 1971, 58: 545-554. 10.1093/biomet/58.3.545.
Article
Google Scholar
-
Meuwissen THE, Woolliams JA: Maximizing genetic response in breeding schemes of dairy cattle with constraints on variance of response. J Dairy Sci. 1994, 77: 1905-1916.
Article
CAS
PubMedGoogle Scholar
-
Lidauer M, Vuori K, Stranden I, Mantysaari E: Experiences with Interbull Test IV: Estimation of genetic variance. Proceedings of the Interbull Annual Meeting: Dublin, Ireland. 2007, 37: 69-72.
Google Scholar
-
Harris B, Johnson D: Approximate reliability of genetic evaluations under an animal model. J Dairy Sci. 1998, 81: 2723-2728.9.
Article
CAS
PubMedGoogle Scholar
-
Tier B, Meyer K: Approximating prediction error covariances among additive genetic effects within animals in multiple-trait and random regression models. J Anim Breed Genet. 2004, 121: 77-89. 10.1111/j.1439-0388.2003.00444.x.
Article
Google Scholar
-
Jensen J, Mao IL: Transformation algorithms in analysis of single trait and of multitrait models with equal design matrices and one random factor per trait: a review. J Anim Sci. 1988, 66: 2750-2761.
Google Scholar
-
Fouilloux MN, Laloë D: A sampling method for estimating the accuracy of predicted breeding values in genetic evaluation. Genet Sel Evol. 2001, 33: 473-486. 10.1051/gse:2001128.
Article
PubMed Central
CAS
PubMedGoogle Scholar
-
Garcia-Cortes LA, Moreno C, Varona L, Altarriba J: Variance component estimation by resampling. J Anim Breed Genet. 1992, 109: 358-363.
Article
Google Scholar
-
Garcia-Cortes LA, Moreno C, Varona L, Altarriba J: Estimation of prediction error variances by resampling. J Anim Breed Genet. 1995, 112: 176-182.
Article
Google Scholar
-
Thompson R: Integrating best linear unbiased prediction and maximum likelihood estimation. Proceedings of the 5th World Congress on Genetics Applied to Livestock Production: Guelph, Canada. 1994, 18: 337-340.
Google Scholar
-
Hickey JM, Keane MG, Kenny DA, Cromie AR, Mulder HA, Veerkamp RF: Estimation of accuracy and bias in genetic evaluations with genetic groups using sampling. J Anim Sci. 2008, 86: 1047-1056. 10.2527/jas.2007-0653.
Article
CAS
PubMedGoogle Scholar
-
Efron B: Bootstrap methods: another look at the jackknife. Ann Stat. 1979, 7: 1-26. 10.1214/aos/1176344552.
Article
Google Scholar
-
Tukey J: Bias and confidence in not quite large samples. Ann Math Statist. 1958, 29: 614-10.1214/aoms/1177706647.
Article
Google Scholar
-
Klassen DJ, Smith SP: Animal model estimation using simulated REML. Proceedings of the 4th World Congress on Genetics Applied to Livestock Production: Edinburgh. 1990, 12: 472-475.
Google Scholar
-
Thallman RM, Taylor JF: An indirect method of computing REML estimates of variance components from large data sets using an animal model. J Dairy Sci. 1991, 74 (Suppl 1): 160-
Google Scholar
-
Gilmour AR, Cullis BR, Welham SJ, Thompson R: ASReml User Guide (Release 2). 2006, VSN International, Hemel Hempstead, HP1 1ES, UK
Google Scholar
-
Lidauer M, Stranden I, Vuori K, Mantysaari E: MiX99 User Manual. 2006, MTT, Jokioinen, Finland
Google Scholar
-
Chan TF, Golub GH, LeVeque RJ: Algorithms for computing the sample variance: analysis and recommendations. Am Stat. 1983, 37: 242-247. 10.2307/2683386.
Google Scholar
-
Henderson CR: A simple method for computing the inverse of a numerator relationship matrix used in prediction of breeding values. Biometrics. 1976, 32: 69-10.2307/2529339.
Article
Google Scholar
-
Thompson R: Sire evaluation. Biometrics. 1979, 35: 339-353. 10.2307/2529955.
Article
Google Scholar
-
Henderson CR: Applications of Linear Models in Animal Breeding. 1984, Guelph, Ontario, Canada, University of Guelph
Google Scholar
-
Reverter A, Golden BL, Bourdon RM, Brinks JS: Method R variance components procedure: application on the simple breeding value model. J Anim Sci. 1994, 72: 2247-2253.
CAS
PubMedGoogle Scholar
-
Meuwissen TH: Maximizing the response of selection with a predefined rate of inbreeding. J Anim Sci. 1997, 75: 934-940.
CAS
PubMedGoogle Scholar
Download references
Acknowledgements
The authors acknowledge the Irish Cattle Breeding Federation for providing funding and data. Robin Thompson acknowledges the support of the Lawes Agricultural Trust.
Author information
Authors and Affiliations
-
Animal Breeding and Genomics Centre, Animal Sciences Group, PO Box 65, 8200 AB, Lelystad, The Netherlands
John M Hickey, Roel F Veerkamp, Mario PL Calus & Han A Mulder
-
Grange Beef Research Centre, Teagasc, Dunsany, Co. Meath, Ireland
John M Hickey
-
School of Agriculture, Food and Veterinary Medicine, College of Life Sciences, University College Dublin, Belfield, Dublin 4, Ireland
John M Hickey
-
School of Mathematical Sciences, Queen Mary, University of London, Mile End Road, London, E1 4NS, UK
Robin Thompson
-
Centre for Mathematical and Computational Biology, Rothamsted Research, Harpenden, AL5 2JQ, UK
Robin Thompson
-
Department of Biomathematics and Bioinformatics, Rothamsted Research, Harpenden, AL5 2JQ, UK
Robin Thompson
Authors
- John M Hickey
You can also search for this author in
PubMed Google Scholar - Roel F Veerkamp
You can also search for this author in
PubMed Google Scholar - Mario PL Calus
You can also search for this author in
PubMed Google Scholar - Han A Mulder
You can also search for this author in
PubMed Google Scholar - Robin Thompson
You can also search for this author in
PubMed Google Scholar
Corresponding author
Correspondence to
John M Hickey.
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
RT derived most of the mathematical equations. JH derived the remaining equations, carried out the simulations and wrote the first draft of the paper. RV supervised the research and mentored JH. MC and HM took part in useful discussions and advised on the simulations. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Rights and permissions
This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Reprints and Permissions
About this article
Cite this article
Hickey, J.M., Veerkamp, R.F., Calus, M.P. et al. Estimation of prediction error variances via Monte Carlo sampling methods using different formulations of the prediction error variance.
Genet Sel Evol 41, 23 (2009). https://doi.org/10.1186/1297-9686-41-23
Download citation
-
Received:
-
Accepted:
-
Published:
-
DOI: https://doi.org/10.1186/1297-9686-41-23
Keywords
- Sampling Variance
- Monte Carlo Sampling
- Prediction Error Variance
- Jackknife Procedure
- Mixed Model Equation
15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
где n – это объём выборочной совокупности;
еi– остатки регрессионной модели:
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
где k – число оцениваемых параметров модели регрессии.
Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:
где In – единичная матрица.
Оценка дисперсии случайной ошибки модели регрессии распределена по ?2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
Доказательство. Примем без доказательства справедливость следующих равенств:
где G2(?) – генеральная дисперсия случайной ошибки;
S2(?) – выборочная дисперсия случайной ошибки;
– выборочная оценка дисперсии случайной ошибки.
Тогда:
т. е.
что и требовалось доказать.
Следовательно, выборочная оценка дисперсии случайной ошибки
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты ?. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
от величины случайной ошибки ?.
МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:
В связи с тем, что переменная у зависит от случайной компоненты ? (yi=?0+?1xi+?i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
Для дальнейших преобразования используются свойства ковариации:
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,?0)=0 (?0=const);
Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= ?1G2(x)+Cov(x,?).
В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:
Таким образом, МНК-оценка
может быть представлена как сумма двух компонент:
1) константы ?1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ?.
Данный текст является ознакомительным фрагментом.
Читайте также
11. Критерии оценки неизвестных коэффициентов модели регрессии
11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
18. Характеристика качества модели регрессии
18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.Необходимость проверки
25. Точечный и интервальный прогнозы для модели парной регрессии
25. Точечный и интервальный прогнозы для модели парной регрессии
Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
39. Модели регрессии, нелинейные по факторным переменным
39. Модели регрессии, нелинейные по факторным переменным
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по
41. Модели регрессии с точками разрыва
41. Модели регрессии с точками разрыва
Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)
44. Методы нелинейного оценивания коэффициентов модели регрессии
44. Методы нелинейного оценивания коэффициентов модели регрессии
Функцией потерь или ошибок называется функционал вида
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
57. Гетероскедастичность остатков модели регрессии
57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается
60. Устранение гетероскедастичности остатков модели регрессии
60. Устранение гетероскедастичности остатков модели регрессии
Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.Наиболее простым методом устранения гетероскедастичности остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков
67. Модели регрессии с переменной структурой. Фиктивные переменные
67. Модели регрессии с переменной структурой. Фиктивные переменные
При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую
Пример 9.1. По 15 сельскохозяйственным предприятиям (табл. 9.1) известны: 

1) определить зависимость 
2) построить корреляционные поля и график уравнения линейной регрессии
3) сделать вывод о качестве модели и рассчитать прогнозное значение 
Таблица 9.1
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
x |
2,97 |
1,65 |
9,02 |
4,95 |
3,63 |
6,38 |
3,3 |
7,81 |
1,32 |
11,44 |
5,39 |
5,72 |
12,65 |
10,34 |
7,15 |
|
y |
121 |
77 |
341 |
132 |
82,5 |
187 |
110 |
198 |
33 |
484 |
209 |
165 |
429 |
341 |
253 |
Решение:
1) В Excel составим вспомогательную таблицу 9.2.
Таблица 9.2
Рис. 9.1. Таблица для расчета промежуточных значений
Вычислим количество измерений 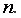
С помощью функции ∑ (Автосумма) на панели инструментов Стандартная найдем сумму всех 
Рис. 9.2. Расчет суммы значений и средних
Для вычисления средних значений используем встроенную функцию MS Excel СРЗНАЧ(), в скобках указывается диапазон значений для определения средней. Таким образом, средний объем выращенной продукции по 15 хозяйствамсоставляет 210,833 тыс.ден. ед., а средние количество техники – 6,248ед/га.
Для заполнения столбцов D, E, Fвведем формулувычисления произведения: в ячейку D2 поместим =B2*C2, затем на клавиатуре нажмем ENTER. Щелкнем левой кнопкой мыши по ячейке D2и, ухватив за правый нижний угол этой ячейки (черный плюсик), потянем вниз до ячейки D16. Произойдет автоматическое заполнение диапазона D3 – D16.
Для вычисления выборочной ковариациимежду 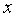
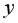
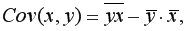
Рис. 9.3. Вычисление
Выборочную дисперсиюдля 
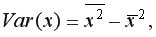
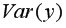
Рис. 9.4. Вычисление Var(x) и Var (y)
Далее используя стандартную функцию MS Excel «КОРРЕЛ» вычисляем значение линейного коэффициента корреляции для нашей задачи функция будет иметь вид «=КОРРЕЛ(B2:B16;C2:C16)», а значение rxy=0,96. Полученное значение коэффициента корреляции указывает на прямую и сильную связь наличия техники и объемов выращенной продукции.
Находим выборочный коэффициент линейной регрессии 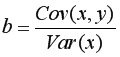
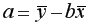
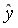
Коэффициент 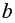
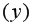
Рис. 9.5. Расчет параметров уравнения регрессии.
Таким образом, уравнение регрессии будет иметь вид: 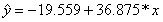
Подставляем в полученное уравнение фактические значения x (количество техники) находим теоретические значения объемов выращенной продукции (рис. 9.6).
Рис. 9.6. Расчет теоретических значений объемов выращенной продукции
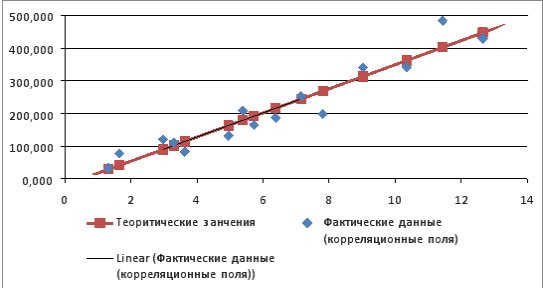
Используя Мастер диаграмм строим корреляционные поля (выделяя столбцы со значениями 


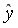
Рис. 9.7. График зависимости объема выращенной продукции от количества техники
Для оценки качества построенной модели регрессии вычислим:
• коэффициент детерминации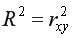
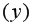
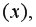
• среднюю ошибку аппроксимации. Для этого в столбце H вычислим разность фактического и теоретического значений 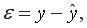
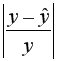
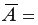
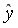
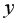
С помощью 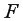
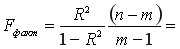
На уровне значимости 0,05 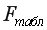
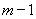
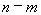
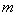
Так как 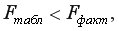
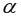
Рис. 9.8. Определение коэффициента детерминации и средней ошибки апроксимации
Рис. 9.9. Диалоговое окно функции FРАСПОБР
Далее определяем средний коэффициент эластичности по формуле. 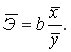
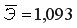
Рассчитаем прогнозное значение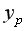
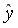
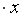
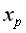
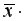
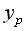
Найдем остаточную дисперсию, для этого вычислим сумму квадратов разности фактического и теоретического значений. 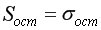
Рис. 9.10. Определение остаточной дисперсии
Средняя стандартная ошибка прогноза:
На уровне значимости 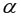
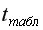
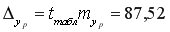
Доверительный интервал прогноза:
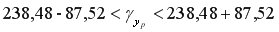
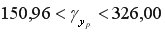
Выполненный прогноз затрат на выпуск продукции оказался надежным (1-0,05=0,95), но неточным, так как диапазон верхней и нижней границ доверительного интервала составляет 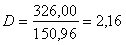
Необходимо отменить, что в MS Excel встроены статистические функции позволяющие значительно снизить количество промежуточных вычислений, например (рис. 9.11.):
Для вычисления выборочных средних используем функцию СРЗНАЧ(число1:числоN) из категории Статистические.
Выборочная ковариация между 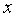
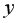
Выборочные дисперсииопределяются статистической функцией ДИСПР(число1:числоN).
Рис.9.11. Вычисление показателей встроенными функциями MSExcel
Параметры линейной регрессии 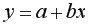
1 способ) С помощью встроенной функции ЛИНЕЙН. Порядок действий следующий:
1. Выделить область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1×2 – для получения только коэффициентов регрессии.
2. С помощью Мастера функций 
Рис. 9.12. Диалоговое окно ввода аргументов функции ЛИНЕЙН
Известные_значения_y – диапазон, содержащий данные результативного признака Y;
Известные_значения_x – диапазон, содержащий данные объясняющего признака X;
Конст – логическое значение (1 или 0), которое указывает на наличие или отсутствие свободного члена в уравнении; ставим 1;
Статистика – логическое значение (1 или 0), которое указывает, выводить дополнительную информацию по регрессионному анализу или нет; ставим 1.
3. В левой верхней ячейке выделенной области появится первое число таблицы. Для раскрытия всей таблицы нужно нажать на клавишу <F2>, а затем – на комбинацию клавиш <CTRL>+ <SHIFT>+ <ENTER>.
Дополнительная регрессионная статистика будет выведена в виде (табл. 9.3):
Таблица 9.3
|
Значение коэффициента |
Значение коэффициента |
|
Среднеквадратическое |
Среднеквадратическое |
|
Коэффициент |
Среднеквадратическое |
|
|
Число степеней свободы |
|
Регрессионная сумма квадратов |
Остаточная сумма квадратов |
В результате применения функции ЛИНЕЙН получим:
|
36,87457 |
-19,55899932 |
|
3,003392 |
21,316623 |
|
0,920606 |
39,16615351 |
|
150,7405 |
13 |
|
231234 |
19941,83855 |
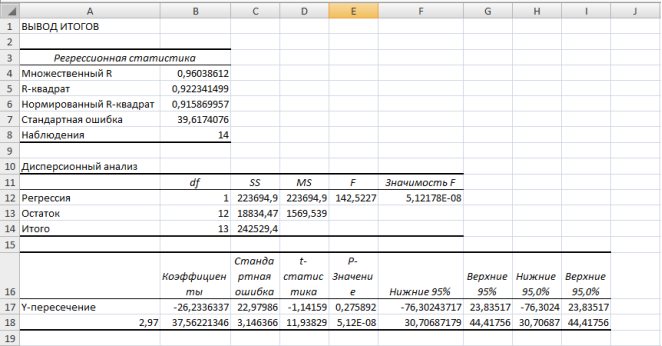
(2 способ) С помощью инструмента анализа данных Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа, доверительные интервалы, остатки, графики подбора линий регрессии, графики остатков и нормальной вероятности. Порядок действий следующий:
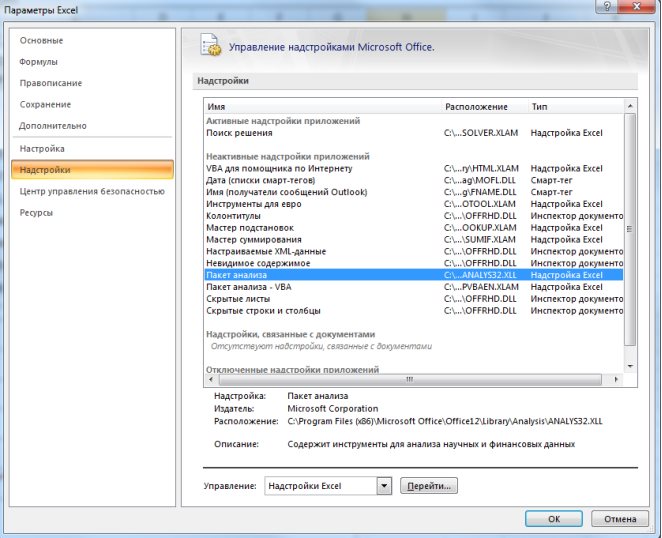
1. Необходимо проверить доступ к Пакету анализа. Для этого в главном меню (через кнопку Microsoft Office получить доступ к параметрам MS Excel) в диалоговом окне «Параметры MSExcel» выбрать команду «Надстройки» и справа выбрать надстройку Пакета анализа далее нажать кнопку «Перейти» (рис. 9.13). В открывшемся диалоговом окне поставить галочку напротив «Пакет анализа» и нажать «ОК» (рис. 9.14).
На вкладке «Данные» в группе «Анализ» появится доступ к установленной надстройке. (рис. 9.15).
Рис. 9.13. Включение надстроек в MSExcel
Рис. 9.14. Диалоговое окно «Надстройки»
Рис. 9.15. Надстройка «Анализ данных» на ленте MSExcel 2007.
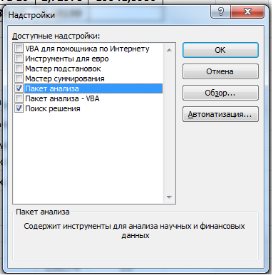
2. Выбрать на «Данные» в группе «Анализ» выбираем команду Анализ данных в открывшемся диалоговом окне выбрать инструмент анализа «Регрессия» и нажать «ОК» (рис. 9.16):
Рис. 9.16. Диалоговое окно «Анализ данных»
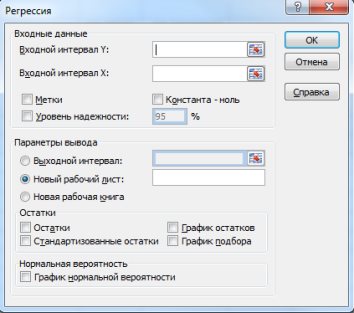
В появившемся диалоговом окне (рис. 9.17) заполнить поля:
Входной интервалY – диапазон, содержащий данные результативного признака Y;
Входной интервалX– диапазон, содержащий данные объясняющего признака X;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист – можно задать произвольное имя нового листа, на который будут выведены результаты.
Рис. 9.17. Диалоговое окно «Регрессия»
Для получения информации об остатках, графиков остатков, подбора и нормальной вероятности нужно установить соответствующие флажки в диалоговом окне.
Рис. 9.18. Результаты применения инструмента Регрессия
В MSExcel линия тренда может быть добавлена в диаграмму с областями гистограммы или в график. Для этого:
1. Необходимо выделить область построения диаграммы и в ленте выбрать «Макет» и в группе анализ выбрать команду «Линия тренда» (рис. 9.19.). В выпадающем пункте меню выбрать «Дополнительные параметры линии тренда».
Рис. 1.19. Лента
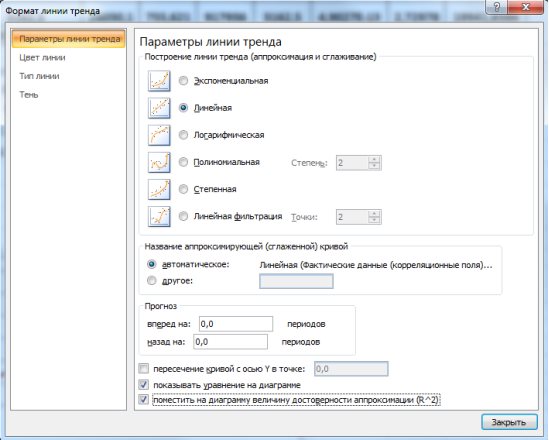
2. В появившемся диалоговом окне выбрать фактические значения, затем откроется диалоговое окно «Формат линии тренда» (рис. 9.20.) в котором выбирается вид линии тренда и устанавливаются соответствующие параметры.
Рис. 9.20. Диалоговое окно «Формат линии тренда»
Для полиноминального тренда необходимо задать степень аппроксимирующего полинома, для линейной фильтрации – количество точек усреднения.
Выбираем Линейная для построения уравнения линейной регрессии.
В качестве дополнительной информации можно показать уравнение на диаграмме и поместить на диаграмму величину (рис.9.21).
Рис. 9.21. Линейный тренд
Нелинейные модели регрессии иллюстрируются при вычислении параметров уравнения 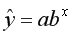
В предыдущем параграфе мы научились описывать облако точек некоторой прямой, не делая никаких предположений по поводу природы анализируемых данных. Иными словами, мы не предполагали никакой конкретной модели, описывающей процесс порождения наших данных. Для дальнейшего продвижения, однако, это будет нам необходимо.
Вернемся к нашему примеру с квартирами. Естественно ожидать, что на цену квартиры (y) влияет её площадь (x), а также прочие факторы, например, удаленность квартиры от метро, этаж, наличие балкона и так далее. Обозначим эти прочие факторы переменной (varepsilon ). С учетом этих соображений естественно предположить следующую модель цены квартиры:
( {y}_i = {β}_1 + {β}_2 {x}_i + {ε}_i , i = 1,2 , … , n ).
Здесь — площадь i-ой квартиры в квадратных метрах, — цена i-ой квартиры в миллионах рублей, — прочие факторы, которые оказывают влияние на цену квартиры (y_i). Переменную (varepsilon ) принято называть случайной ошибкой модели. Буквой n будем обозначать число наблюдений в доступной нам выборке.
В целом такая модель выглядит достаточно разумно. Если бы мы знали точные значения коэффициентов (beta _1) и (beta _2), мы могли бы использовать её в практических целях. Например, зная, что (beta _2=0,3), строительная компания могла бы учитывать при планировании продаж, что один дополнительный квадратный метр площади квартиры оценивается рынком в 0,3 млн рублей. К сожалению, на практике значения параметров (beta _1) и (beta _2) нам не известны, зато мы можем собрать статистические данные и получить их (приблизительные) оценки.
Здесь уместно подчеркнуть важное различие между
- параметрами (beta _k) (без «крышек») в выражении (y_i=beta _1+beta _2x_i+varepsilon _i),
- и их оценками (widehat {beta _k})(c «крышками») в выражении .
Это различие состоит в том, что и — это некоторые истинные значения параметров модели, которые на практике никогда не известны исследователю. Все, что исследователь в силах сделать — собрать данные и эти значения оценить приближенно. — это оценки истинных значений, которые мы получаем, используя наши выборочные данные. Так как (widehat {beta _1}text{и}widehat {beta _2}) рассчитываются на основе случайной выборки, то они являются случайными величинами.
Естественно, мы хотим, чтобы оценки были близки к истинным значениям оцениваемых параметров. Поэтому нам важно знать: при каких условиях мы можем доверять этим оценкам, то есть рассчитывать на то, что результат использования МНК будет близок к истине? Эти условия называют предпосылками классической линейной модели парной регрессии.
Предпосылки классической линейной модели парной регрессии (КЛМПР):
- Модель линейна по параметрам и корректно специфицирована
(y_i=beta _1+beta _2x_i+varepsilon _i,i=1,2,{dots},n.) - (x_1,x_2,{dots},x_n) — детерминированные (неслучайные) величины, не все одинаковые.
- Математическое ожидание случайных ошибок равно нулю
(Evarepsilon _i=0). - Дисперсия случайной ошибки одинакова для всех наблюдений (mathit{var}left(varepsilon _iright)=sigma ^2).
- Случайные ошибки, относящиеся к разным наблюдениям, взаимно независимы.
- Случайные ошибки имеют нормальное распределение (varepsilon _iNleft(0,sigma ^2right)).
Мы обсудили выше соображения, исходя из которых может быть сформулирована предпосылка №1. Как мы увидим в дальнейшем, правильная спецификация подразумевает в первую очередь отсутствие среди прочих факторов других переменных, которые одновременно влияют на y и коррелируют с x. Нарушение этого требования приводит к серьезным проблемам, которые мы осветим в конце данной главы.
Предпосылка №2 касается двух важных аспектов. Во-первых, мы предполагаем, что регрессоры (x_i) являются неслучайными величинами. Это техническое предположение, которое упростит некоторые выкладки в этом разделе. Обратите внимание, что (varepsilon _i) в отличие от регрессоров являются случайными величинами, а следовательно, и (y_i) тоже случайны, так как представляют собой сумму неслучайной компоненты (beta _1+beta _2x_i) и случайной величины (varepsilon _i). В терминах нашего примера с квартирами про эту предпосылку можно думать так: представим, что вы собрали случайную выборку из 100 квартир площадью 30 м2, 100 квартир площадью 35 м2 и 100 квартир площадью 40 м2. Если вы соберете другую выборку из трехсот квартир с такими же площадями, то значения регрессоров (x_i) останутся теми же самыми, а вот значения объясняемой переменной (y_i) поменяются, поэтому в данном примере разумно думать про регрессоры как про неслучайные величины, а про величины (y_i) — как про случайные.
Во-вторых, в рамках предпосылки №2 мы предполагаем, что не все значения регрессоров одинаковы. Нетрудно понять, зачем нужно это предположение, если взглянуть на формулу оценки коэффициента
(widehat {beta _2}=frac{widehat {mathit{Cov}}left(x,yright)}{widehat {mathit{Var}}left(xright)}). Обратите внимание, что в знаменателе этой формулы стоит выборочная дисперсия переменной x, но если все значения этой переменной в выборке будут одинаковы, то эта дисперсия окажется равной нулю, и из-за этого мы не сможем рассчитать МНК-оценку (widehat {beta _2}).
Предпосылка №3 говорит о том, что прочие факторы могут приводить к отклонению (y_i) от величины (beta _1+beta _2x_i) как вверх, так и вниз, но в среднем эти отклонения компенсируют друг друга.
Предпосылка №4 требует, чтобы разброс случайных ошибок в среднем был постоянен для всех наблюдений. Её смысл удобно пояснить, используя картинку. Посмотрите на рисунки 2.3а и 2.3б. В первом случае предпосылка о постоянстве дисперсии случайной ошибки выполнена, а во втором — нет, так как разброс точек вокруг линии регрессии растет по мере увеличения объясняющей переменной, следовательно, мы можем заключить, что дисперсия случайной ошибки не является одинаковой для всех наблюдений. Ситуация, когда предпосылка №4 выполнена (то есть ситуация, соответствующая рисунку 2.3а) называется гомоскедастичностью случайных ошибок. Альтернативная ситуация называется гетероскедастичностью случайных ошибок.
Рисунок 2.3а. Гомоскедастичность случайных ошибок
Рисунок 2.3б. Гетероскедастичность случайных ошибок
Из предпосылки №5 следует, что случайные ошибки, относящиеся к разным наблюдениям, не коррелированы друг с другом: (mathit{cov}left(varepsilon _i,varepsilon _jright)=0) при (i{neq}j).
Предпосылка №6 не требуется для обеспечения хороших свойств оценок коэффициентов (обратите внимание, что ниже, в формулировке теоремы Гаусса — Маркова, она не фигурирует), однако будет полезна для тестирования гипотез и построения доверительных интервалов.
Теорема Гаусса — Маркова. Если выполнены предпосылки 1-5 классической линейной модели парной регрессии, то МНК-оценки коэффициентов (widehat {beta _1}text{и}widehat {beta _2}) будут:
(а) несмещенными,
(б) эффективными в классе всех несмещенных и линейных по y оценок1.
Напомним, что оценка называется несмещенной, если её математическое ожидание совпадает с истинным значением оцениваемого параметра: (Ewidehat {beta _2}=beta _2). Свойство эффективности означает, что оценка характеризуется минимальной дисперсией среди всех альтернативных оценок в данном классе, то есть является «наиболее точной» оценкой интересующего нас параметра. Линейность по y означает, что мы рассматриваем все оценки, которые могут быть представлены в виде линейной комбинации значений объясняемой переменной, то есть записаны в виде (sum _{i=1}^nc_i{ast}y_i).
Если переформулировать свойства несмещенности и эффективности нестрого, то можно сказать, что при выполнении предпосылок 1-5 МНК-оценки параметров окажутся хорошими: они будут «в среднем правильными» и наиболее точными. Теорема Гаусса — Маркова дает нам важную мотивацию для того, чтобы оценивать параметры нашей модели именно методом наименьших квадратов, а не каким-то альтернативным способом.
Лирическое отступление о предпосылках
Каждый раз, когда я рассказываю студентам об этой теореме, в моей голове разыгрывается примерно такой диалог между двумя эконометристами (назовем их Филипп и Дима).
Дима: Реалистичны ли предпосылки КЛМПР?
Филипп: Не очень. Например, в реальных исследованиях на пространственных данных ты почти всегда будешь сталкиваться с нарушением требования постоянства дисперсии случайной ошибки (нарушением предпосылки №4). Во многих прикладных исследованиях также окажется более целесообразным думать про регрессоры как про случайные, а не детерминированные случайные величины (это отклонение от предпосылки №2). На нормальность случайных ошибок (предпосылка №6) я бы тоже не рассчитывал…
Дима: Зачем же тогда мы её изучаем? Давайте сразу перейдем к более реалистичной модели.
Филипп: Мы начинаем с КЛМПР, так как это самая простая модель, на примере которой мы можем обсудить ряд важных эконометрических идей и при этом не погрязнуть в технических трудностях. В последующих главах мы будем постепенно отказываться от предпосылок КЛМПР и в результате получим набор моделей и методов, которые хорошо подходят для реальных исследований на живых данных. Кроме того, мы научимся проверять выполнение тех или иных предположений КЛМПР, чтобы понять, когда стоит их использовать, а когда — нет.
В частности, последствия нарушения предпосылки №3 читателю предлагается проанализировать уже в этом параграфе, в одном из заданий для самостоятельного решения.
- Несмещенность и эффективность — это свойства оценок при фиксированном объеме выборки (при фиксированном n). Во многих случаях удобно также использовать асимптотические свойства оценок, то есть свойства, которые имеют место при (nrightarrow {infty}) (например, состоятельность). Об асимптотических свойствах МНК-оценок мы подробно поговорим в одной из последующих глав. ↵
В зависимости от контекста термин «прогнозирование» в эконометрике может трактоваться по-разному. Применительно к данным временных рядов речь обычно идет о прогнозировании будущего значения зависимой переменной, например, курса рубля или ВВП. Когда же речь идет о пространственных выборках, под прогнозированием понимают предсказание значения зависимой переменной для заданных значений объясняющих переменных. Например, предсказание цены квартиры с заданной жилой площадью.
Формально задачу построения прогноза можно представить следующим образом. Имеется модель, для которой выполнены все предпосылки КЛМПР:
\begin{equation*} y_i=\beta _1+\beta _2x_i+\varepsilon _i \end{equation*}
Представим, что мы уже воспользовались МНК и получили оцененную на основе n наблюдений линию регрессии:
\begin{equation*} \widehat y_i=\widehat {\beta }_1+\widehat {\beta }_2x_i \end{equation*}
Теперь пусть у нас есть известное (n+1)-ое наблюдение регрессора \(x_{n+1}\), но неизвестно соответствующее значение зависимой переменной \(y_{n+1}\) и нужно построить его прогноз. Естественной идеей будет подставить известное значение в оцененную регрессию: \
\begin{equation*} \widehat y_{n+1}=\widehat {\beta }_1+\widehat {\beta }_2x_{n+1} \end{equation*}
Оказывается, что это хорошая мысль: такой прогноз будет несмещенным и эффективным (то есть будет характеризоваться минимальной ожидаемой квадратичной ошибкой прогноза).
Докажем несмещенность этого прогноза.
Вычислим математическое ожидание фактического значения \(y_{n+1}\) и нашего прогноза \(\widehat y_{n+1}\). Если прогноз несмещенный, то эти математические ожидания будут совпадать.
Воспользуемся тем, что, как мы доказали выше, \(\widehat {\beta }_1\) и \(\widehat {\beta }_2\) — несмещенные оценки коэффициентов \(\beta _1\) и \(\beta _2\):
\begin{equation*} E\left(\widehat y_{n+1}\right)=E\left(\widehat {\beta }_1+\widehat {\beta }_2x_{n+1}\right)=E\left(\widehat {\beta }_1\right)+E\left(\widehat {\beta }_2\right)x_{n+1}=\beta _1+\beta _2x_{n+1} \end{equation*}
Кроме того:
\begin{equation*} E\left(y_{n+1}\right)=E\left(\beta _1+\beta _2x_{n+1}+\varepsilon _{n+1}\right)=\end{equation*}
\begin{equation*} =\beta _1+\beta _2x_{n+1}+E\left(\varepsilon _{n+1}\right)=\beta _1+\beta _2x_{n+1} \end{equation*}
Следовательно, \(E\left(y_{n+1}\right)=E\left(\widehat y_{n+1}\right)\).
Кроме самого прогноза нас интересует его точность. Чтобы её оценить, целесообразно вычислить математические ожидания квадрата ошибки прогноза:
\begin{equation*} E\left(\widehat y_{n+1}-y_{n+1}\right)^2=E\left(\widehat {\beta }_1+\widehat {\beta }_2x_{n+1}-\beta _1-\beta _2x_{n+1}-\varepsilon _{n+1}\right)^2= \end{equation*}
\begin{equation*} =E\left(\left(\widehat {\beta }_1-\beta _1\right)+\left(\widehat {\beta }_2-\beta _2\right)x_{n+1}-\varepsilon _{n+1}\right)^2= \end{equation*}
\begin{equation*} =E\left(\widehat {\beta }_1-\beta _1\right)^2+x_{n+1}^2E\left(\widehat {\beta }_2-\beta _2\right)^2+E\left(\varepsilon _{n+1}\right)^2+ \end{equation*}
\begin{equation*} +2x_{n+1}E\left(\left(\widehat {\beta }_1-\beta _1\right)\left(\widehat {\beta }_2-\beta _2\right)\right)-2E\left(\left(\widehat {\beta }_1-\beta _1\right)\varepsilon _{n+1}\right)-\end{equation*}
\begin{equation*}-2x_{n+1}E\left(\left(\widehat {\beta }_2-\beta _2\right)\varepsilon _{n+1}\right)= \end{equation*}
\begin{equation*} \mathit{var}\left(\widehat {\beta }_1\right)+x_{n+1}^2\mathit{var}\left(\widehat {\beta }_2\right)+\sigma ^2+2x_{n+1}\mathit{cov}\left(\widehat {\beta }_1,\widehat {\beta }_2\right)-0-0= \end{equation*}
\begin{equation*} \frac{\frac{\sigma ^2} n{\ast}\sum x_i^2}{\sum \left(x_i-\overline x\right)^2}+x_{n+1}^2\frac{\sigma ^2}{\Sigma \left(x_i-\overline x\right)^2}+\sigma ^2-2x_{n+1}\frac{\overline x{\ast}\sigma ^2}{\Sigma \left(x_i-\overline x\right)^2}= \end{equation*}
\begin{equation*} =\sigma ^2{\ast}\left(1+\frac 1 n+\frac{\left(x_{n+1}-\overline x\right)^2}{\sum \left(x_i-\overline x\right)^2}\right)\end{equation*}
Здесь в предпоследнем равенстве мы воспользовались формулами для \(\mathit{var}\left(\widehat {\beta }_1\right)\), \(\mathit{var}\left(\widehat {\beta }_2\right)\) и \(\mathit{cov}\left(\widehat {\beta }_1,\widehat {\beta }_2\right)\), представленными выше.
Дисперсия ошибки прогноза \(\sigma ^2\), неизвестная нам в реальности, может быть заменена несмещенной оценкой \(S^2.\) Если проделать эту замену, а затем извлечь из полученного результата корень, то получим стандартную ошибку прогноза:
\begin{equation*} \delta =\sqrt{s^2{\ast}\left(1+\frac 1 n+\frac{\left(x_{n+1}-\overline x\right)^2}{\sum \left(x_i-\overline x\right)^2}\right)}\end{equation*}
Эту стандартную ошибку прогноза можно использовать для построения доверительного интервала прогноза.
95-процентный доверительный интервал для прогноза — это такой интервал, который накрывает истинное прогнозное значение зависимой переменной с вероятностью 95%. Он имеет вид:
\begin{equation*} \left(\widehat y_{n+1}-\delta {\ast}t_{n-2}^{\alpha },\widehat y_{n+1}+\delta {\ast}t_{n-2}^{\alpha }\right.) \end{equation*}
Обратите внимание, что величина стандартной ошибки прогноза зависит от соотношения \(x_{n+1}\) и \(\overline x\). Если \(x_{n+1}=\overline x\), то последняя дробь в этой большой формуле окажется равной нулю, и стандартная ошибка прогноза будет минимальной. Чем сильнее \(x_{n+1}\) отличается от \(\overline x\), тем больше будет эта дробь. Таким образом, чем меньше наблюдение, для которого вы строите прогноз, похоже на вашу исходную выборку, тем менее точным этот прогноз окажется.
Пример 2.6. Построение прогноза
Рассматривается классическая линейная модель парной регрессии \(y_i=\beta _1+\beta _2{\ast}x_i+\varepsilon _i.\) Имеется следующая информация о 10 наблюдениях анализируемых переменных:
\begin{equation*} \sum _{i=1}^{10}x_i=20,\sum _{i=1}^{10}x_i^2=50,\sum _{i=1}^{10}y_i=8,\sum _{i=1}^{10}y_i^2=26, \end{equation*}
\begin{equation*} \sum _{i=1}^{10}x_i{\ast}y_i=10 \end{equation*}
Для одиннадцатого наблюдения дано \(x_{11}=5\). Предполагая, что это наблюдение удовлетворяет исходной модели, вычислите наилучший линейный несмещенный прогноз \(y_{11}\) и оцените его точность, построив для него 95-процентный доверительный интервал.
Решение:
\begin{equation*} \widehat {\beta _2}=\frac{\overline{\mathit{xy}}-\overline x{\ast}\overline y}{\overline{x^2}-\overline x^2}=-0,6 \end{equation*}
\begin{equation*} \widehat {\beta _1}=\overline y-\widehat {\beta _2}{\ast}\overline x=2 \end{equation*}
Прогноз \(\widehat y_{11}=\widehat {\beta _1}+\widehat {\beta _2}{\ast}x_{11}=2-0,6{\ast}5=-1\).
Сумма квадратов остатков равна:
\begin{equation*} \sum _{i=1}^{10}e_i^2=\sum _{i=1}^{10}e_i{\ast}\left(y_i-\widehat {\beta _1}-\widehat {\beta _2}{\ast}x_i\right)= \end{equation*}
\begin{equation*} \sum _{i=1}^{10}e_iy_i-\widehat {\beta _1}\sum _{i=1}^{10}e_i-\widehat {\beta _2}\sum _{i=1}^{10}e_ix_i=\sum _{i=1}^{10}e_iy_i-\widehat {\beta _1}{\ast}0-\widehat {\beta _2}{\ast}0 \end{equation*}
Последнее равенство верно в силу свойств остатков регрессии. Таким образом:
\begin{equation*} \sum _{i=1}^{10}e_i^2=\sum _{i=1}^{10}e_iy_i=\sum _{i=1}^{10}\left(y_i-\widehat {\beta _1}-\widehat {\beta _2}{\ast}x_i\right)y_i= \end{equation*}
\begin{equation*} \sum _{i=1}^{10}y_i^2-\widehat {\beta _1}\sum _{i=1}^{10}y_i-\widehat {\beta _2}{\ast}\sum _{i=1}^{10}x_iy_i=26-2{\ast}8+0,6{\ast}10=16 \end{equation*}
\begin{equation*} \delta =\sqrt{s^2{\ast}\left(1+\frac 1 n+\frac{\left(x_{11}-\overline x\right)^2}{\sum \left(x_i-\overline x\right)^2}\right)}=\end{equation*}
\begin{equation*}=\sqrt{\frac{\sum e_i^2}{n-2}{\ast}\left(1+\frac 1 n+\frac{\left(x_{11}-\overline x\right)^2}{\sum \left(x_i-\overline x\right)^2}\right)}= \end{equation*}
\begin{equation*} =\sqrt{\frac{16}{10-2}{\ast}\left(1+\frac 1{10}+\frac{\left(5-2\right)^2}{10}\right)}=2 \end{equation*}
Теперь можно посчитать доверительный интервал прогноза:
\begin{equation*} \left(\widehat y_{11}-\delta {\ast}t_8,\widehat y_{11}+\delta {\ast}t_8\right) \end{equation*}
\begin{equation*} \left(-1-2{\ast}2,306,-1+2{\ast}2,306\right) \end{equation*}
\begin{equation*} \left(-5,612,3,612\right) \end{equation*}
Заметим, что в этом примере точность прогноза не слишком высока, что объясняется маленьким количеством наблюдений и тем, что \(x_{11}\) довольно далек от среднего по выборке значения переменной \(x\).
Для получения более точного прогноза лучше, конечно, использовать больше данных.
Ответ: \(\widehat y_{11}=-1,\) доверительный интервал: \(\left(-5,612,3,612\right)\)
Пусть мы имеем модель наблюдений в виде модели простой линейной регрессии
И хотим дать прогноз, каким будет значение объясняемой переменной при некотором выбранном (фиксированном) значении
объясняющей переменной
, если мы будем продолжать наблюдения.
Мы умеем оценивать коэффициенты и
методом наименьших квадратов, и естественно использовать для целей прогнозирования получаемую в результате такого оценивания (подобранную) модель линейной связи
Что приводит к Прогнозируемому значению Объясняемой переменной, равному
Вопрос только в том, Сколь надежным является выбор такого значения в качестве прогнозного. И здесь надо иметь в виду следующее.
Поскольку мы используем для прогноза оценки, полученные, исходя из модели наблюдений то для того, чтобы этот прогноз был осмысленным, нам по необходимости приходится предполагать, что структура модели наблюдений и ее параметры Не изменятся при переходе к новому наблюдению, так что соответствующее
значение
должно описываться Тем же линейным соотношением
. В таком случае, мы по-существу имеем дело с расширенной линейной моделью с
наблюдениями, в которой дополнительное наблюдение удовлетворяет соотношению
При этом, случайная величина должна иметь То же распределение, что и случайные величины
и должна образовывать вместе с ними множество случайных величин, независимых в совокупности.
Итак, мы договорились, что в расширенной модели
Выбирая в качестве прогноза для значение
Мы тем самым допускаем Ошибку прогноза, равную
Поскольку вычисленные оценки являются (как мы уже выяснили выше) реализациями случайных величин, наблюдаемая ошибка прогноза также является реализацией случайной величины
и включает два источника неопределенности:
· неопределенность, связанную с отклонением вычисленных значений случайных величин От истинных значений параметров
;
· неопределенность, связанную со случайной ошибкой в
— м наблюдении.
При наших Стандартных предположениях о линейной модели наблюдений ошибка прогноза является Случайной величиной , имеющей математическое ожидание
(Мы использовали здесь справедливые при выполнении стандартных предположений соотношения )
Точность прогноза характеризуется Дисперсией ошибки прогноза
Здесь использован тот факт, что сумма Неслучайна (хотя ее точное значение и не известно). Далее, из предположенной независимости случайных ошибок
и
вытекает независимость случайных величин
(эта величина зависит от случайных ошибок
) и
(последняя Не зависит от случайных ошибок
). В силу же независимости
и
,
(использовано правило сложения дисперсий). Остается заметить, что
Где, как обычно, (Мы не будем выводить эту формулу.) Таким образом,
Если случайные ошибки имеют Нормальное распределение, то тогда случайные величины
и
Также имеют нормальные распределения. При этом, ошибка прогноза имеет нормальное распределение с нулевым математическим ожиданием и дисперсией, вычисляемой по последней формуле.
Разделив разность на квадратный корень из ее дисперсии, получаем случайную величину
Имеющую Стандартное нормальное распределение . Заменяя в правой части выражения для
Неизвестное значение
его несмещенной оценкой
, получаем оценку дисперсии
в виде
Заменяя, наконец, в знаменателе отношения, имеющего стандартное нормальное распределение, неизвестное значение его оценкой
, приходим к
-статистике (
-отношению)
Имеющей При выполнении сделанных предположений о модели наблюдений -распределение Стьюдента
с
Степенями свободы.
Последний факт дает возможность построения -процентного доверительного интервала для значения
А именно,
На основании которого получаем -процентный доверительный интервал для
:
— здесь мы использовали то, что в силу симметрии распределения Стьюдента, .
Заметим, что при заданных значениях (по которым строится прогноз) доверительный интервал для
будет Тем длинее, чем больше значение
. Последнее же равно
при
и возрастает с ростом
. Это означает, что длина доверительного интервала Возрастает при удалении значения
, при котором строится прогноз, от среднего арифметического значений
.
Таким образом, прогнозы для значений , далеко отстоящих от
, становятся менее определенными, поскольку длина соответствующих доверительных интервалов для значений объясняемой переменной возрастает.
Пример. Для данных о размерах совокупного располагаемого дохода и совокупных расходах на личное потребление в США в период с 1970 по 1979 год (в млрд. долларов, в ценах 1972 года), оцененная модель линейной связи имеет вид .
Представим себе, что мы находимся в 1979 году и ожидаем увеличения в 1980 году совокупного располагаемого дохода (в тех же ценах) до млрд. долларов. Тогда прогнозируемый по подобранной модели объем совокупных расходов на личное потребление в 1980 году равен
Так что если выбрать уровень доверия , то
И доверительный интервал для соответствующего значения
имеет вид
Т. е.
Или
Заметим, что интервал достаточно широк и его нижняя граница допускает даже возможность некоторого снижения уровня потребления по сравнению с предыдущим годом.
В действительности, в 1980 г. совокупный располагаемый доход достиг 1021 млрд. долларов, а совокупное потребление — 931.8 млрд. долларов. Тем самым, ошибка прогноза составила
Если бы мы исходили при прогнозе из Действительного значения , а не из
, то прогнозируемое значение для
равнялось бы 931.94 и ошибка прогноза составила всего лишь
Проиллюстрируем, наконец, как изменяется в этом примере длина 95%-доверительных интервалов в интервале наблюдавшихся значений объясняющей переменной . На графике приведены отклонения нижней и верхней границ таких интервалов от центра интервала:
В случае модели Множественной линейной регрессии
Точечный прогноз значения соответствующего Фиксированному набору
значений объясняющих переменных, дается формулой
Где — оценки наименьших квадратов параметров
. Интервальный прогноз Имеет вид
Где
— оценка дисперсии ошибки прогноза, а — несмещенная оценка дисперсии
Случайных ошибок.
| < Предыдущая | Следующая > |
|---|


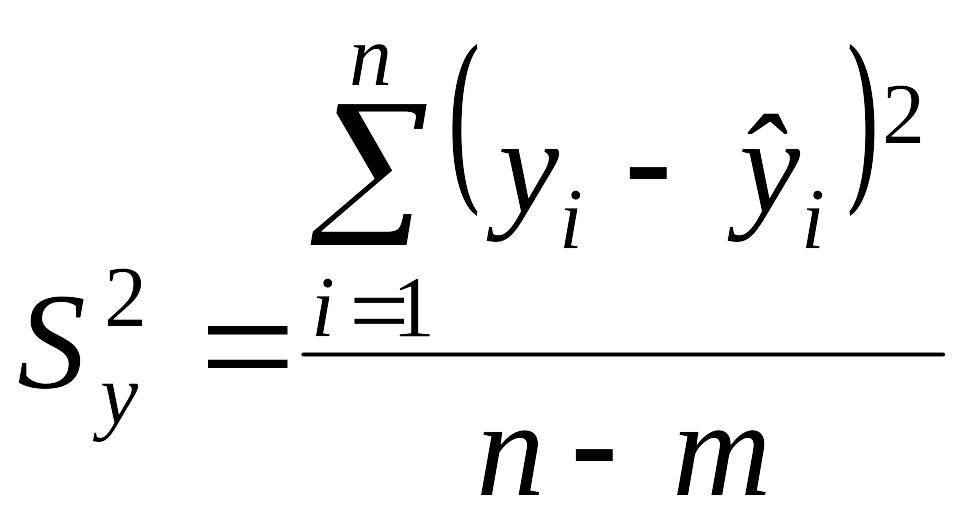


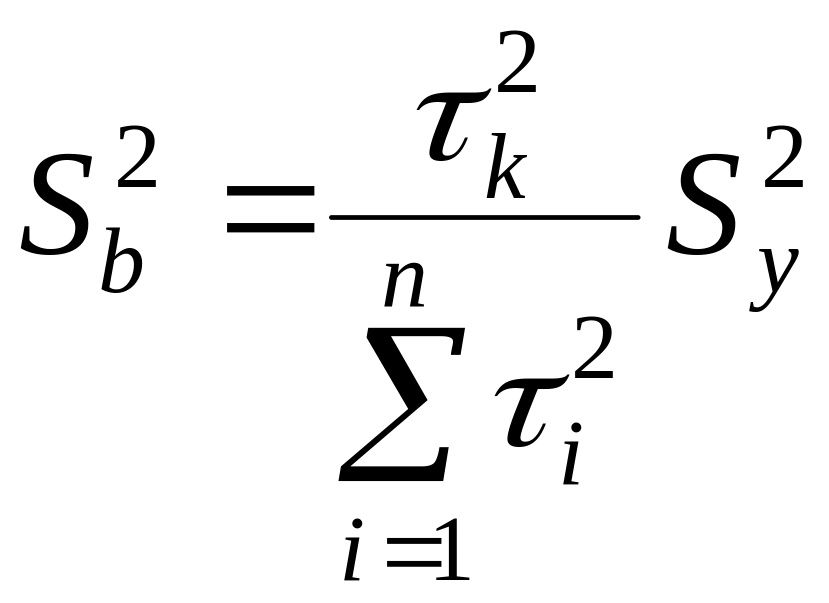







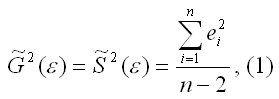
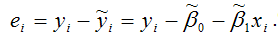
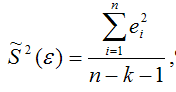
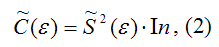
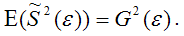
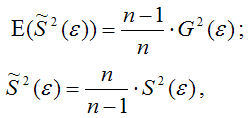
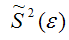
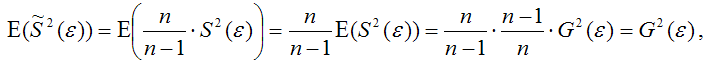
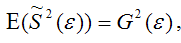
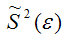
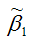
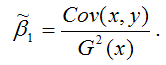
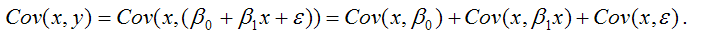
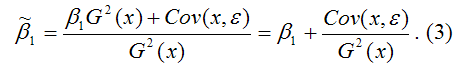
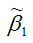
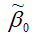
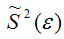
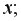
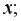
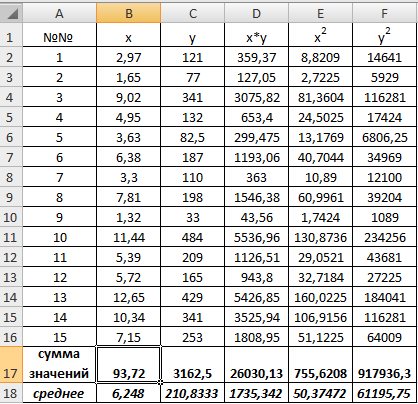
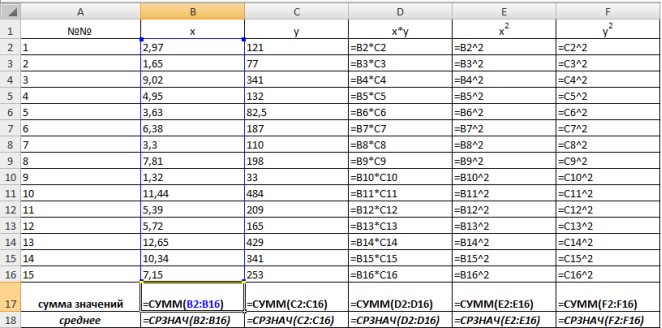
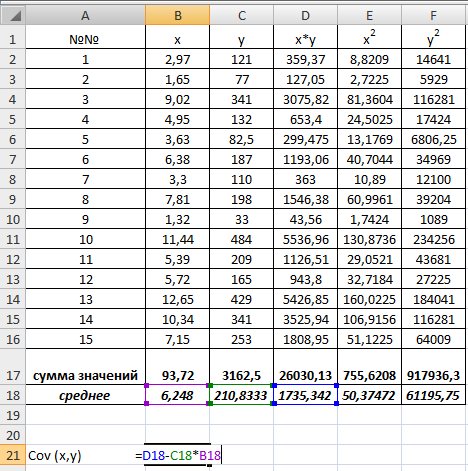
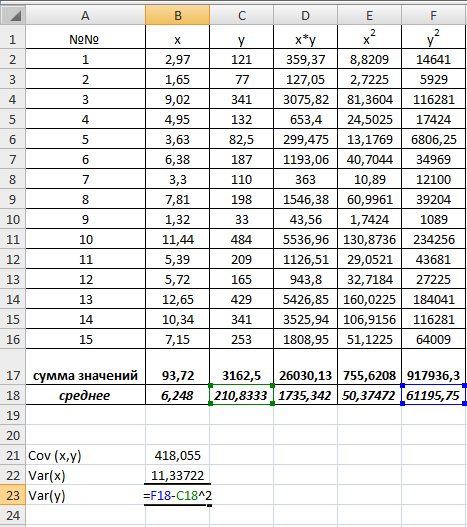
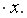
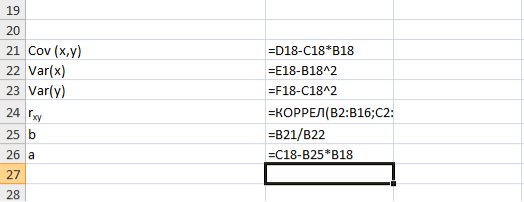
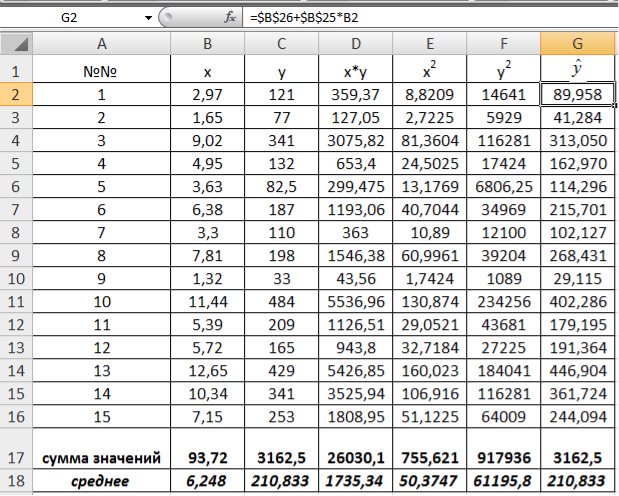
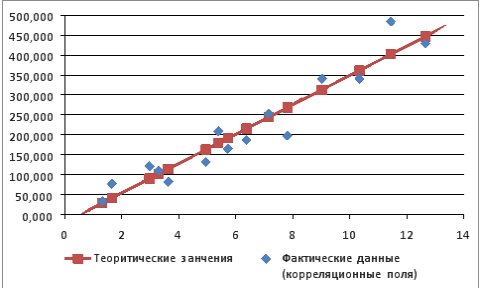
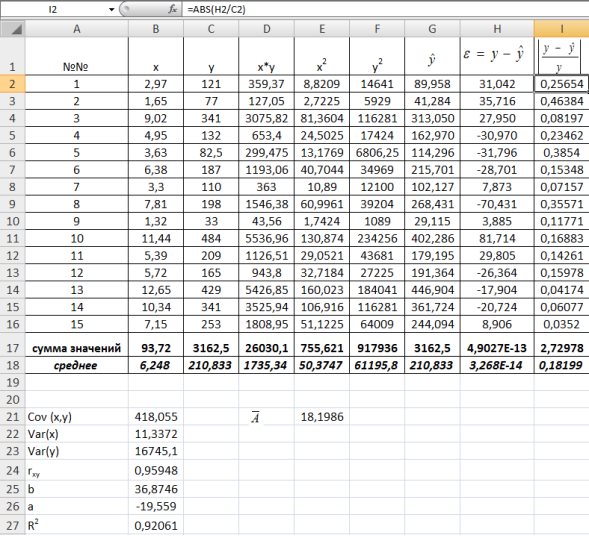
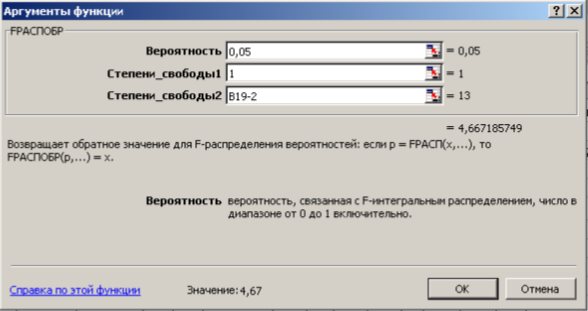
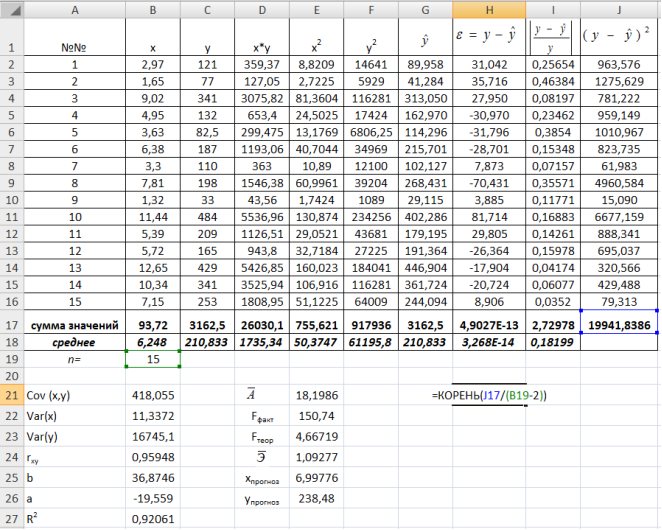
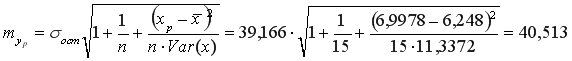
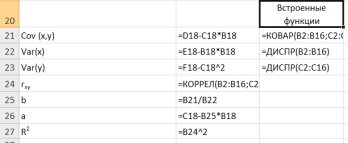
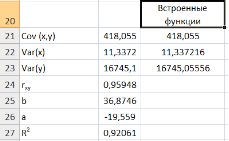
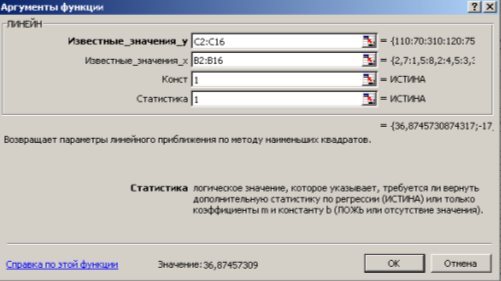
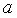
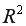
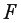 -статистика
-статистика