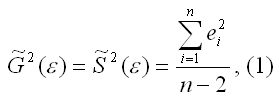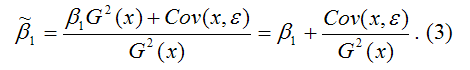Дисперсия ошибки модели

При проведении регрессионного анализа
основная трудность заключается в том,
что генеральная дисперсия случайной
ошибки является неизвестной величиной,
что вызывает необходимость в расчёте
её несмещённой выборочной оценки.

Несмещённой оценкой дисперсии(или
исправленной дисперсией) случайной
ошибки линейной модели парной регрессии
называется величина, рассчитываемая
по формуле:

где n
– это объём выборочной совокупности;

еi– остатки регрессионной модели:

Для линейной модели множественной
регрессии несмещённая оценка дисперсии
случайной ошибки рассчитывается по
формуле:

где k
– число оцениваемых параметров модели
регрессии.

Оценка матрицы ковариаций случайных
ошибок Cov(ε) будет являться оценочная
матрица ковариаций:

где In
– единичная матрица.

Оценка дисперсии случайной
ошибки модели регрессии распределена
по ε2(хи-квадрат)
закону распределения с (n-k-1)
степенями свободы.

Для доказательства несмещённости оценки
дисперсии случайной ошибки модели
регрессии необходимо доказать
справедливость равенства

Доказательство. Примем без
доказательства справедливость следующих
равенств:

где G2(ε)
– генеральная дисперсия случайной
ошибки;

S2(ε)– выборочная дисперсия случайной
ошибки;

– выборочная оценка дисперсии
случайной ошибки.

Тогда:

т. е.

что и требовалось доказать.

Следовательно, выборочная оценка
дисперсии случайной ошибки

является несмещённой оценкой
генеральной дисперсии случайной ошибки
модели регрессии G2(ε).

При условии извлечения из
генеральной совокупности нескольких
выборок одинакового объёма n
и при одинаковых значениях объясняющих
переменных х,
наблюдаемые значения зависимой переменной
у будут случайным образом колебаться
за счёт случайного характера случайной
компоненты β.
Отсюда можно сделать вывод, что будут
варьироваться и зависеть от значений
переменной у значения оценок коэффициентов
регрессии и оценка дисперсии случайной
ошибки модели регрессии.

Для иллюстрации данного утверждения
докажем зависимость значения МНК-оценки

от величины случайной ошибки
ε.

МНК-оценка коэффициента β1 модели
регрессии определяется по формуле:

В связи с тем, что переменная
у зависит от случайной компоненты ε
(yi=β0+β1xi+εi), то ковариация
между зависимой переменной у
и независимой переменной х
может быть представлена следующим
образом:

Для дальнейших преобразования используются
свойства ковариации:

1) ковариация между переменной
х и
константой С
равна нулю: Cov(x,C)=0,
C=const;

2) ковариация
переменной х
с самой собой равна дисперсии этой
переменной: Cov(x,x)=G2(x).

Исходя из указанных свойств ковариации,
справедливы следующие равенства:

Cov(x,β0)=0
(β0=const);

Cov(x, β1x)=
β1*Cov(x,x)=
β1*G2(x).

Следовательно, ковариация
между зависимой и независимой переменными
Cov(x,y)
может быть записана как:

Cov(x,y)=
β1G2(x)+Cov(x,ε).

В результате МНК-оценка коэффициента
β1 модели регрессии примет вид:

Таким образом, МНК-оценка

может быть представлена как сумма двух
компонент:

1) константы β1,
т. е. истинного значения коэффициента;

2) случайной ошибки Cov(x,ε),
вызывающей вариацию коэффициента модели
регрессии.

Однако на практике подобное разложение
МНК-оценки невозможно, потому что
истинные значения коэффициентов модели
регрессии и значения случайной ошибки
являются неизвестными. Теоретически
данное разложение можно использовать
при изучении статистических свойств
МНК-оценок.

Аналогично доказывается, что МНК-оценка

коэффициента модели регрессии и
несмещённая оценка дисперсии случайной
ошибки

могут быть представлены как сумма
постоянной составляющей (константы) и
случайной компоненты, зависящей от
ошибки модели регрессии ε.

Декомпозиция алгоритмов машинного обучения по дисперсии смещения на практическом примере в Python

Смещение и дисперсия — два ключевых понятия в оценке модели для машинного обучения, поскольку они тесно связаны с производительностью модели на невидимых данных. И смещение, и дисперсия являются типами ошибок ошибки прогнозирования. Третий тип ошибки — это неустранимая ошибка, которая является неотъемлемой ошибкой в ​​данных, которую нельзя уменьшить независимо от того, какой алгоритм используется.

Одной из основных трудностей, с которой сталкиваются специалисты по данным при внедрении новой модели, является так называемая дилемма смещения-дисперсии или проблема смещения-дисперсии. Это связано с противоречием минимизации обоих источников ошибок в алгоритмах обучения с учителем, которые можно оценить с помощью метода декомпозиции смещения и дисперсии.

В этой статье мы рассмотрим эти концепции, чтобы закончить основной вклад этой статьи, который представляет собой объяснение декомпозиции смещения-дисперсии вместе с практическим примером на Python для всех, кто заинтересован в реализации декомпозиции для своих моделей.

Предвзятость и дисперсия

Предвзятость определяется как разница между предсказанием модели и истинной реальностью. Высокое смещение может привести к тому, что алгоритм упустит соответствующие отношения между функциями и целевыми выходными данными (недообучение).

Дисперсия определяется как чувствительность к колебаниям обучающей выборки. Другими словами, это относится к тому, насколько сильно меняются результаты при изменении обучающих данных. Высокая дисперсия предполагает большие изменения в оценке целевой функции при изменении обучающего набора данных (переобучение).

Оба термина, выраженные в математике, соответствуют следующим формулам:

Оба члена могут быть легко получены из формулы среднеквадратичной ошибки (MSE):

Пример того, как интерпретировать эти формулы, показан в конце статьи.

Вот график с четырьмя различными сценариями для высокого-низкого смещения и высокого-низкого отклонения. Каждое попадание представляет собой индивидуальную реализацию нашей модели с учетом случайной изменчивости обучающих данных, которые мы собираем [1]. Центр цели означает, что модель точно предсказывает значения.

Компромисс смещения и дисперсии

Несмотря на то, что оптимальной задачей было бы иметь минимально возможное смещение и дисперсию, на практике существует явный компромисс между обеими ошибками. Нахождение компромисса между обоими терминами называется компромисс между смещением и дисперсией.

Для моделей машинного обучения смещение и дисперсия тесно связаны со сложностью модели, которая затем связана с тем, когда модель переобучает или недообучает данные обучения. Как показано на рис. 2, когда сложность модели превышает допустимое значение, наша модель переоснащает обучающие данные, тогда как если сложность модели ниже, модель не соответствует данным.

В реальных сценариях не существует аналитического способа найти золотую середину, поэтому необходимо протестировать несколько моделей разной сложности и выбрать ту, которая минимизирует общую ошибку.

Разложение смещения-дисперсии

Разложение смещения-дисперсии является полезным методом для понимания производительности алгоритма.

Основная идея этого метода заключается в измерении систематической ошибки и дисперсии при обучении одной и той же модели с разными обучающими наборами и тестировании ее на одном и том же тестовом наборе.

Чтобы реализовать это, для подвыборки данных используется метод начальная загрузка (название бэггинг происходит от загрузка + агрегация ). Этот метод состоит в выполнении случайной выборки с заменой данных, что означает, что подмножества обучающих данных будут перекрываться, поскольку мы не разделяем данные, а передискретизируем их.

Таким образом, многократно запуская метод самозагрузки и получая точность модели для тестового набора, мы можем получить среднее смещение и дисперсию для всех раундов, для которых мы выполнили итерацию.

Вот часть кода задачи регрессии, которая обобщает основную логику метода. Весь код получен из библиотеки MLxtend.

Input:
- X_train
- y_train
- X_test
- y_test
- num_rounds: Number of iterations
Output:
- avg_expected_loss: Average MSE loss for all the rounds
- avg_bias: Average bias for all the rounds
- avg_var: Average variance for all the rounds
(avg_expected_loss = avg_bias^2 + avg_var)
(1) Iterate for num_rounds, in each implementing bootstrapping, training the model and getting the predictions
for i in range(num_rounds):
- X_boot, y_boot = _draw_bootstrap_sample(rng, X_train, y_train)
- pred = estimator.fit(X_boot, y_boot).predict(X_test)
- all_pred[i] = pred
(2) Obtain the average MSE error
avg_expected_loss = np.apply_along_axis(lambda x: ((x — y_test)**2).mean(), axis=1, arr=all_pred).mean()
(3) Obtain the average bias and variance
main_predictions = np.mean(all_pred, axis=0)
avg_bias = np.sum((main_predictions — y_test)**2) / y_test.size
avg_var = np.sum((main_predictions — all_pred)**2) / all_pred.size

Наконец, вот практический пример на Python, который показывает, как реализовать декомпозицию смещения-дисперсии.

В качестве примера мы использовали свободно доступный набор данных о жилье в Бостоне [2], задачей которого является прогнозирование цен на жилье с помощью регрессора. Сначала мы разделили данные на обучающий набор и тестовый набор.

Пример 1. Дерево решений

Чтобы проанализировать декомпозицию смещения-дисперсии, мы сначала реализовали регрессор дерева решений и прогнали его через функцию bias_variance_decomp, псевдокод которой показан выше.

Average expected loss: 32.419
Average bias: 14.197
Average variance: 18.222

Чтобы сравнить этот вывод с другой моделью, мы также запустили метод ансамбля пакетов с использованием регрессора дерева решений.

Average expected loss: 18.693
Average bias: 15.292
Average variance: 3.402

По сравнению с предыдущим результатом мы можем наблюдать, как увеличилось смещение, что означает, что модель регрессора с бэггингом работает хуже, чем модель дерева решений. Однако дисперсия сильно уменьшилась, что указывает на то, что модель более соответствует своим предсказаниям.

Пример 2. Нейронная сеть

Мы также оценили производительность модели на основе нейронной сети, реализованной в Keras, поскольку, насколько нам известно, эта функция не может быть реализована в PyTorch.

Average expected loss: 25.470
Average bias: 19.927
Average variance: 5.543

По сравнению с первой моделью мы увеличили сложность модели за счет увеличения количества нейронов для каждого слоя.

Average expected loss: 23.458
Average bias: 17.608
Average variance: 5.850

Как и ожидалось, систематическая ошибка уменьшилась за счет увеличения дисперсии модели.

Способы управления предвзятостью и дисперсией

Есть несколько советов, как управлять ошибками смещения и дисперсии.

Прежде всего, не зацикливайтесь только на минимизации смещения или, другими словами, не забывайте о дисперсии. Оба они одинаково важны для создания надежной модели.

Затем смещение модели может быть уменьшено за счет увеличения сложности путем (1) реализации ансамблевого метода ускорения или (2) добавления дополнительных функций или разработки функций.

Вместо этого дисперсию можно уменьшить, (1) внедрив ансамблевый метод бэггинга или (2) ограничив или уменьшив оценочные коэффициенты путем регуляризации.

Для получения более подробной информации о том, как управлять смещением и дисперсией с помощью ансамблевых методов, я предлагаю прочитать статью Введение в ансамблевые методы в машинном обучении.

Подробное объяснение того, как интерпретировать смещение и дисперсию

Если бы у нас было следующее распределение,

ожидаемое значение и дисперсия рассчитываются следующим образом:

• Ожидаемые значения

• Дисперсия

Если вам понравился этот пост, рассмотрите возможность подписаться. Вы получите доступ ко всему моему контенту и ко всем остальным статьям на Medium от замечательных авторов!

Рекомендации

[1] Скотт Фортманн-Роу, Понимание компромисса смещения и дисперсии

[2] Харрисон, Д. и Рубинфельд, Д.Л. «Гедонистические цены и спрос на чистый воздух», J. Environ. Экономика и менеджмент, том 5, 81–102, 1978 г.

[3] The Machine Learners, Entiende de una vez qué es el Tradeoff Bias-Variance

[4] GitHub, Функцияbias_variance_decomp.py

[5] Stack Exchange, Что означает 𝐸(𝑋) в буквальном смысле?

[6] Medium, Объяснение компромисса смещения и дисперсии

[7] Мастерство машинного обучения, Нежное введение в компромисс между смещением и дисперсией в машинном обучении.

[8] GitHub, Смещение ошибки машинного обучения и неустранимая ошибка с python

[9] GitHub, Разложение смещения-дисперсии для классификации и регрессионных потерь

[10] Блог Genius, Что такое компромисс смещения и дисперсии?

You are quite right. In the context of linear regression, or of any other model that can yield predictions on one variable (response) from values of other variables (predictors), we usually have a set of observations, that is, points where we observed the actual response and the predictors. Given a model, for each observation we can compute the predicted value (from model and predictors) and the actual value. The error is the difference between predicted and observed value.

Since we have a set of observations, we have a set of errors and therefore we can compute its variance. Furthermore, if observations are seen as a random variable, we can estimate its variance.

That is error variance.

Colman’s definition is equivalent to this one, but from another point of view.

In our set of observations, we can compute variance of the response. If we have a model, we can explain part of the variance of the response from the variance of predictors. The part we can’t explain is error variance — the same error variance explained above.

And to summarize: Please have a look at the page of Corman’s book and notice that just before «error variance» there is the definition of «error variable». A short definition of error variance is that it is the variance of the error variable.

---

Когда мы подгоняем регрессионную модель к набору данных, нас часто интересует, насколько хорошо регрессионная модель «подходит» к набору данных. Две метрики, обычно используемые для измерения согласия, включают R -квадрат (R2) и стандартную ошибку регрессии , часто обозначаемую как S.

В этом руководстве объясняется, как интерпретировать стандартную ошибку регрессии (S), а также почему она может предоставить более полезную информацию, чем R 2 .

Стандартная ошибка по сравнению с R-квадратом в регрессии

Предположим, у нас есть простой набор данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их баллы за экзамен:

Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:

R-квадрат — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной. При этом 65,76% дисперсии экзаменационных баллов можно объяснить количеством часов, потраченных на учебу.

Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом случае наблюдаемые значения отклоняются от линии регрессии в среднем на 4,89 единицы.

Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:

Обратите внимание, что некоторые наблюдения попадают очень близко к линии регрессии, в то время как другие не так близки. Но в среднем наблюдаемые значения отклоняются от линии регрессии на 4,19 единицы .

Стандартная ошибка регрессии особенно полезна, поскольку ее можно использовать для оценки точности прогнозов. Примерно 95% наблюдений должны находиться в пределах +/- двух стандартных ошибок регрессии, что является быстрым приближением к 95% интервалу прогнозирования.

Если мы заинтересованы в прогнозировании с использованием модели регрессии, стандартная ошибка регрессии может быть более полезной метрикой, чем R-квадрат, потому что она дает нам представление о том, насколько точными будут наши прогнозы в единицах измерения.

Чтобы проиллюстрировать, почему стандартная ошибка регрессии может быть более полезной метрикой для оценки «соответствия» модели, рассмотрим другой пример набора данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их экзаменационная оценка:

Обратите внимание, что это точно такой же набор данных, как и раньше, за исключением того, что все значения s сокращены вдвое.Таким образом, студенты из этого набора данных учились ровно в два раза дольше, чем студенты из предыдущего набора данных, и получили ровно половину экзаменационного балла.

Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:

Обратите внимание, что R-квадрат 65,76% точно такой же, как и в предыдущем примере.

Однако стандартная ошибка регрессии составляет 2,095 , что ровно вдвое меньше стандартной ошибки регрессии в предыдущем примере.

Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:

Обратите внимание на то, что наблюдения располагаются гораздо плотнее вокруг линии регрессии. В среднем наблюдаемые значения отклоняются от линии регрессии на 2,095 единицы .

Таким образом, несмотря на то, что обе модели регрессии имеют R-квадрат 65,76% , мы знаем, что вторая модель будет давать более точные прогнозы, поскольку она имеет более низкую стандартную ошибку регрессии.

Преимущества использования стандартной ошибки

Стандартную ошибку регрессии (S) часто бывает полезнее знать, чем R-квадрат модели, потому что она дает нам фактические единицы измерения. Если мы заинтересованы в использовании регрессионной модели для получения прогнозов, S может очень легко сказать нам, достаточно ли точна модель для прогнозирования.

Например, предположим, что мы хотим создать 95-процентный интервал прогнозирования, в котором мы можем прогнозировать результаты экзаменов с точностью до 6 баллов от фактической оценки.

Наша первая модель имеет R-квадрат 65,76%, но это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. К счастью, мы также знаем, что у первой модели показатель S равен 4,19. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*4,19 = +/- 8,38 единиц, что слишком велико для нашего интервала прогнозирования.

Наша вторая модель также имеет R-квадрат 65,76%, но опять же это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. Однако мы знаем, что вторая модель имеет S 2,095. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*2,095= +/- 4,19 единиц, что меньше 6 и, следовательно, будет достаточно точным для использования для создания интервалов прогнозирования.

Дальнейшее чтение

Введение в простую линейную регрессию
Что такое хорошее значение R-квадрата?

1.2.1. Стандартная ошибка оценки по регрессии

Обозначается как
S_y,xи вычисляется по формуле

S_y,x=.

Стандартная ошибка
оценки по регрессии показывает, на
сколько в среднем мы ошибаемся, оценивая
значение зависимой переменной по
найденному уравнению регрессии при
фиксированном значении независимой
переменной.

Квадрат стандартной
ошибки по регрессии является несмещенной
оценкой дисперсии ²,
т.е.

=

=.

Дисперсия ошибок
характеризует воздействие в модели
(1.1) неучтенных факторов и ошибок.

1.2.2. Оценка
значимости уравнения регрессии
(дисперсионный анализ регрессии)

Для оценки
значимости уравнения регрессии
устанавливают, соответствует ли выбранная
модель анализируемым данным. Для этого
используется дисперсионный анализ
регрессии. Основная его посылка – это
разложение общей суммы квадратов
отклонений
на
составляющие. Известно, что такое
разложение имеет вид

=+.

Второе слагаемое
в правой части разложения – это часть
общей суммы квадратов отклонений,
объясняемая действием случайных и
неучтенных факторов. Первое слагаемое
этого разложения – это часть общей
суммы квадратов отклонений, объясняемая
регрессионной зависимостью. Следовательно,
если регрессионная зависимость между
уихотсутствует, то
общая сумма квадратов отклонений
объясняется действием только случайных
факторов или ошибок, т.е.=.
В случае функциональной зависимости
между уихдействие
случайных факторов и ошибок отсутствует
и тогда=.
Будучи отнесенными к соответствующему
числу степеней свободы, эти суммы
называются средними квадратами отклонений
и служат оценками дисперсиив
разных предположениях.

MSE= ()/(n–2)
– остаточная дисперсия, которая является
оценкойв
предположении отсутствия регрессионной
зависимости, аMSR= ()/1
– аналогичная оценка без этого
предположения. Следовательно, если
регрессионная зависимость отсутствует,
то эти оценки должны быть близкими.
Сравниваются они на основе критерия
Фишера:F=MSR/MSE.

Расчетное значение
этого критерия сравнивается с критическим
значением F_(с числом степеней свободы числителя,
равным 1, числом степеней свободы
знаменателя, равнымn–2,
и фиксированным уровнем значимости).
ЕслиF<F, то гипотеза о не значимости
уравнения регрессии не отклоняется, т.
е. признается, что уравнение регрессии
незначимо. В этом случае надо либо
изменить вид зависимости, либо пересмотреть
набор исходных данных.

При компьютерных
расчетах оценка значимости уравнения
регрессии осуществляется на основе
дисперсионного анализа регрессии в
таблицах вида:

Таблица
1.1

Дисперсионный
анализ регрессии

Источник вариации	Суммы квадратов	Степени свободы	Средние квадраты	F-отношение	p-value
Модель	SSR	1	MSR	MSR/MSE	Уровень
Ошибки	SSE	n–2	MSE		значимости
общая	SST	n–1

Здесь p-value– это вероятность выполнения неравенстваF<F,
т. е. того, что расчетное значениеF-статистики попало в
область принятия гипотезы. Если эта
вероятность мала (меньше),
то нулевая гипотеза отклоняется.

Для множественной регрессии формула несмещенной оценки дисперсии случайной ошибки имеет вид

begin{equation*} widehat {sigma ^2}=S^2=frac 1{n-k}{ast}sum _{i=1}^ne_i^2 end{equation*}

Она почти такая же, как для парной регрессии за тем исключением, что в знаменателе вместо выражения (left(n-2right)) стоит (left(n-kright)). Если извлечь корень из этой величины, то можно получить стандартную ошибку регрессии

begin{equation*} mathit{SEE}=sqrt{S^2}=sqrt{frac 1{n-k}{ast}sum _{i=1}^ne_i^2} end{equation*}

Расчет стандартной ошибки регрессии — это один из способов оценить точность вашей модели в целом. То есть оценить, насколько хорошо она соответствует данным. Чем меньше стандартная ошибка регрессии, тем лучше ваша модель соответствует доступным вам наблюдениям.

Следующая характеристика качества подгонки — это коэффициент детерминации (R^2).

Для множественной регрессии с константой так же, как и для парной, верно, что общая сумма квадратов может быть представлена как сумма квадратов остатков и объясненная сумма квадратов:

begin{equation*} sum _{i=1}^nleft(y_i-overline yright)^2=sum _{i=1}^ne_i^2+sum _{i=1}^nleft(widehat y_i-overline yright)^2 end{equation*}

Поэтому и (R^2) может быть рассчитан в точности таким же образом, как и для модели парной регрессии:

begin{equation*} R^2=1-frac{sum _{i=1}^ne_i^2}{sum _{i=1}^nleft(y_i-overline yright)^2}=frac{sum _{i=1}^nleft(widehat y_i-overline yright)^2}{sum _{i=1}^nleft(y_i-overline yright)^2}=frac{widehat {mathit{Var}}left(widehat yright)}{widehat {mathit{Var}}left(yright)} end{equation*}

И точно так же, как и в случае парной регрессии, он будет лежать между нулем и единицей. Если ваша модель хорошо соответствует данным, то (R^2) будет близок к единице, если нет, то к нулю. Ещё раз подчеркнем, что условие (sum _{i=1}^nleft(y_i-overline yright)^2=sum _{i=1}^ne_i^2+sum _{i=1}^nleft(widehat y_i-overline yright)^2) выполняется только тогда, когда в модели есть константа. Если же ее нет, то указанное равенство, вообще говоря, неверно, и (R^2) не обязан лежать между нулем и единицей, и интерпретировать стандартным образом его нельзя.

Некоторые эконометристы старой школы придают важное значение величине коэффициента (R^2). Действительно, если он близок к единице, то это, как правило, приятная новость. Однако не стоит переоценивать эту характеристику качества модели потому, что у коэффициента (R^2) есть существенные ограничения:

1. Высокий (R^2) характеризует наличие множественной корреляции между регрессорами и зависимой переменной, но ничего не говорит о наличии или отсутствии причинно-следственной связи между анализируемыми переменными. Вспомните примеры из первой главы, где мы обсуждали, что высокая корреляция не гарантирует причинно-следственной связи.
2. (R^2) не может быть использован для принятия решения о том, стоит ли добавлять в модель новые переменные или нет. Дело в том, что, когда вы добавляете новые переменные в ваше уравнение, качество подгонки данных не может стать хуже, следовательно, и сумма квадратов остатков не может увеличиться. В теории она может остаться неизменной, но на практике она всегда будет уменьшаться. А в этом случае, как видно из расчетной формулы, (R^2) будет увеличиваться. Получается, что какие бы дурацкие новые переменные вы ни добавляли в модель, коэффициент (R^2) будет увеличиваться (или, в крайнем случае, оставаться неизменным).

Последний из указанных недостатков легко можно преодолеть. Для этого есть усовершенствованная версия (R^2), которую называют скорректированным (или нормированным) коэффициентом (R^2) ( (R^2) adjusted):

begin{equation*} R_{mathit{adj}}^2=R^2-frac{k-1}{n-k}{ast}left(1-R^2right) end{equation*}

(R_{mathit{adj}}^2) меньше, чем обычный (R^2), на величину (frac{k-1}{n-k}{ast}left(1-R^2right)), которая представляет собой штраф за добавление избыточных переменных. Обратите внимание, что при прочих равных этот штраф растет по мере увеличения параметра (k), характеризующего число коэффициентов в вашей модели. Если вы будете добавлять в модель много регрессоров, которые не вносят существенного вклада в объяснение зависимой переменной, то (R^2_{mathit{adj}}) будет снижаться.

Поэтому, если вы хотите сравнить межу собой модели с разным числом объясняющих переменных, то лучше использовать (R^2_{mathit{adj}}), чем обычный (R^2). А ещё лучше обращать внимание не только на этот коэффициент, но и на прочие характеристики адекватности вашей модели, которые мы обсудим в этой книге.

Чтобы понять, откуда берется формула для скорректированного R-квадрата, запишем обычный R-квадрат следующим образом:

begin{equation*} R^2=1-frac{sum _{i=1}^ne_i^2}{sum _{i=1}^nleft(y_i-overline yright)^2}=1-frac{frac{sum _{i=1}^ne_i^2} n}{frac{sum _{i=1}^nleft(y_i-overline yright)^2} n}. end{equation*}

В числителе дроби стоит выборочная дисперсия остатков, а в знаменателе — выборочная дисперсия зависимой переменной. Если и ту, и другую дисперсии заменить их несмещенными аналогами, то получим следующее выражение:

begin{equation*} 1-frac{S^2}{frac{sum _{i=1}^nleft(y_i-overline yright)^2}{n-1}}=1-frac{frac{sum _{i=1}^ne_i^2}{n-k}}{frac{sum _{i=1}^nleft(y_i-overline yright)^2}{n-1}}. end{equation*}

Легко проверить, что это и есть скорректированный R-квадрат:

begin{equation*} 1-frac{frac{sum _{i=1}^ne_i^2}{n-k}}{frac{sum _{i=1}^nleft(y_i-overline yright)^2}{n-1}}=1-frac{n-1}{n-k}frac{sum _{i=1}^ne_i^2}{sum _{i=1}^nleft(y_i-overline yright)^2}=1-frac{n-1}{n-k}left(1-R^2right)= end{equation*}

begin{equation*} R^2-frac{k-1}{n-k}{ast}left(1-R^2right)=R_{mathit{adj}}^2. end{equation*}