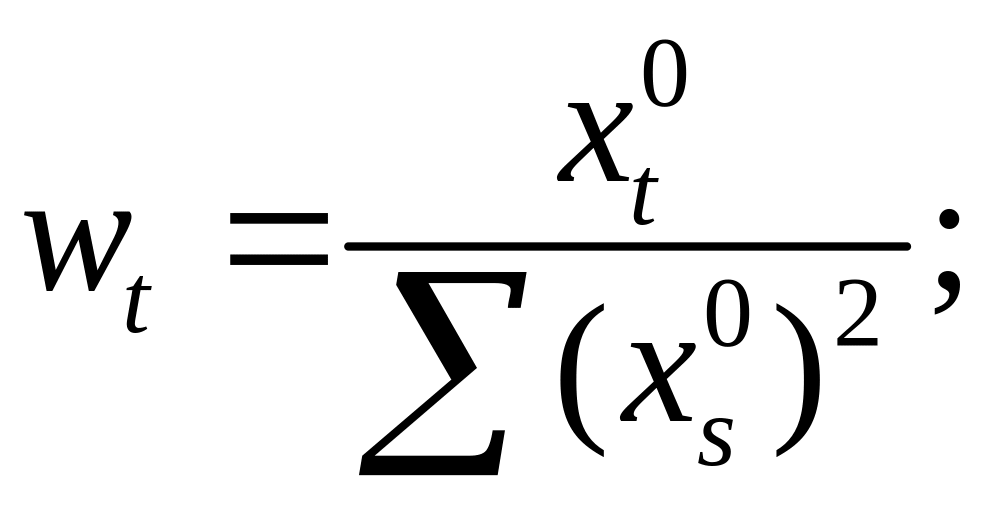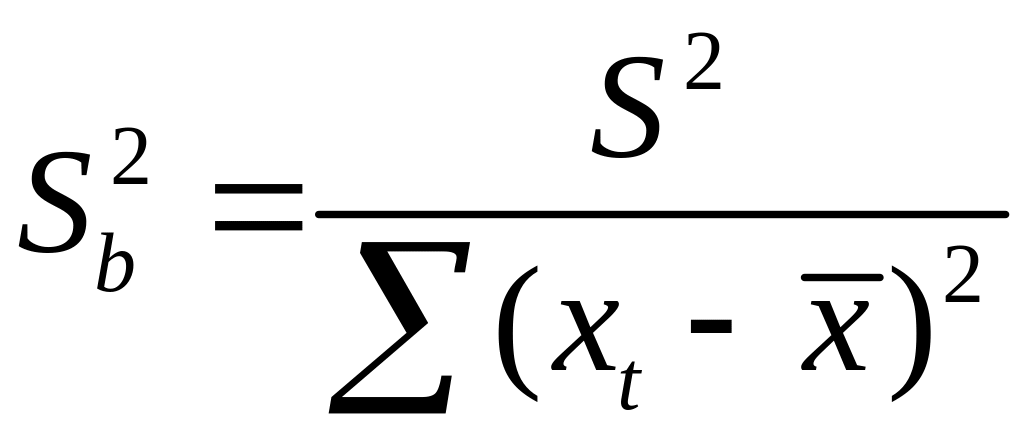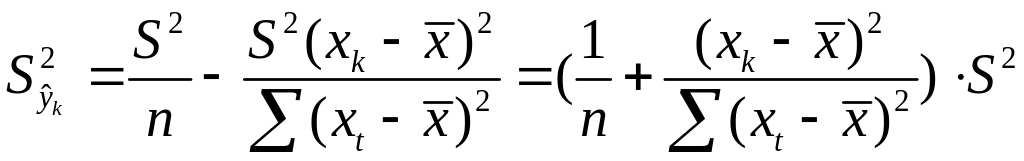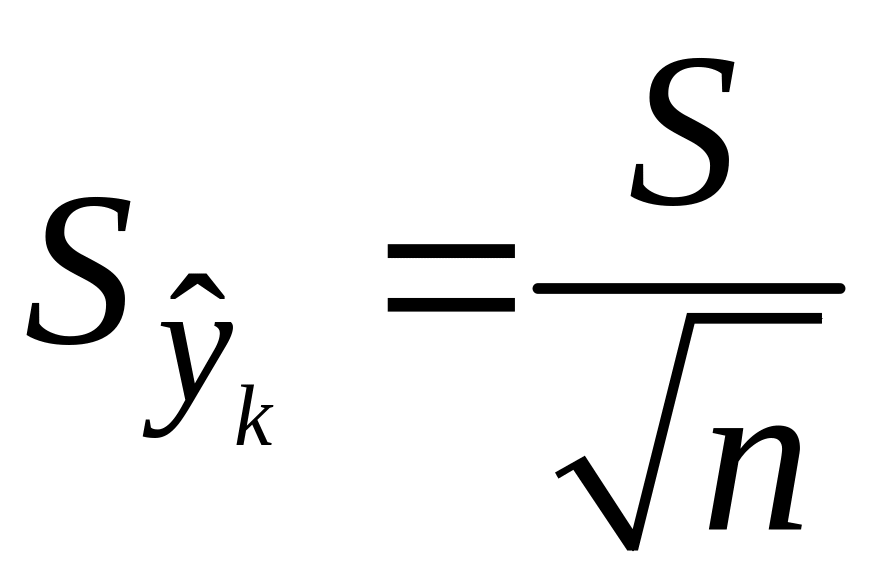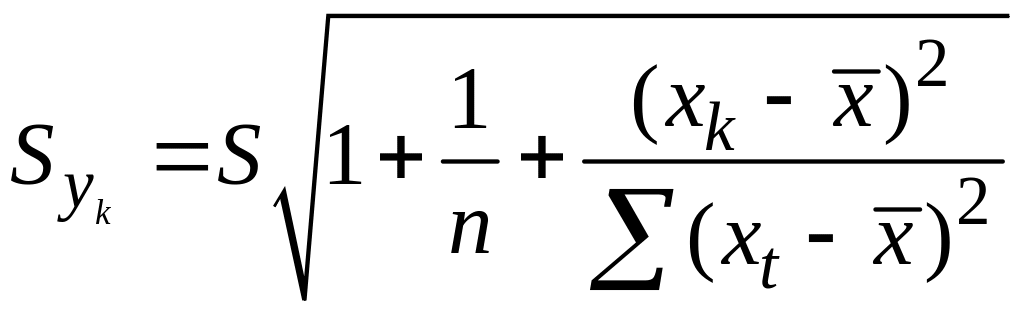Дисперсия ошибки что показывает - Решение и исправление самых разных ошибок на TopOshibok.ru

,

—
уравнение регрессии,

—
случайная ошибка (с ограничениями).

;

;

—
остатки регрессии. Надо различать
остатки и
ошибки регрессии.
Остатки в отличии от ошибок наблюдаемы.

Предположим,
что оценка σ²
связана с
суммой квадратов остатков регрессии

Вычислим:

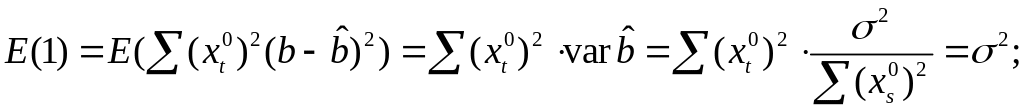
Используя,

получим

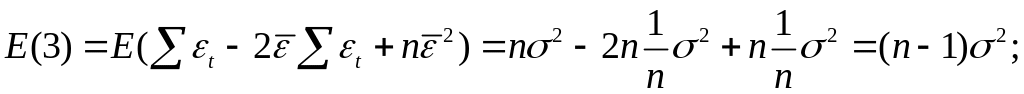
где

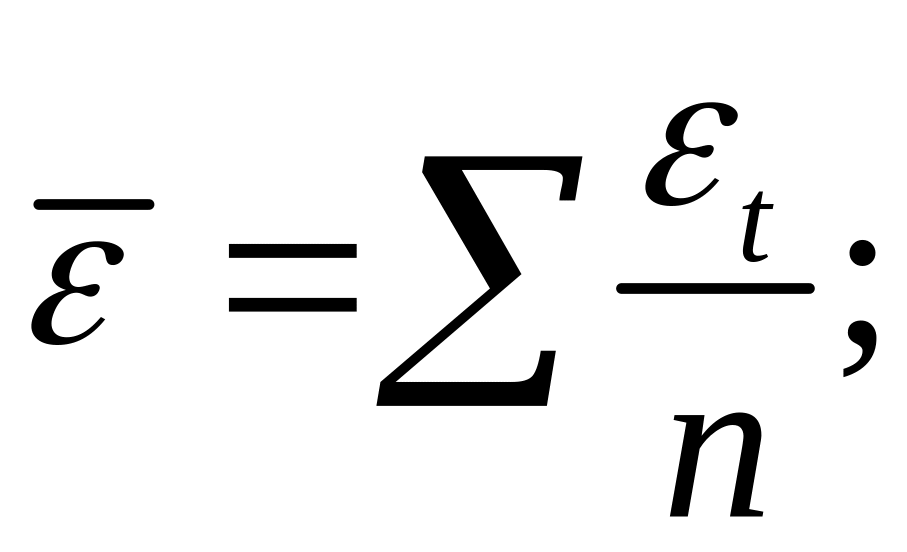
Таким образом

откуда следует,
что

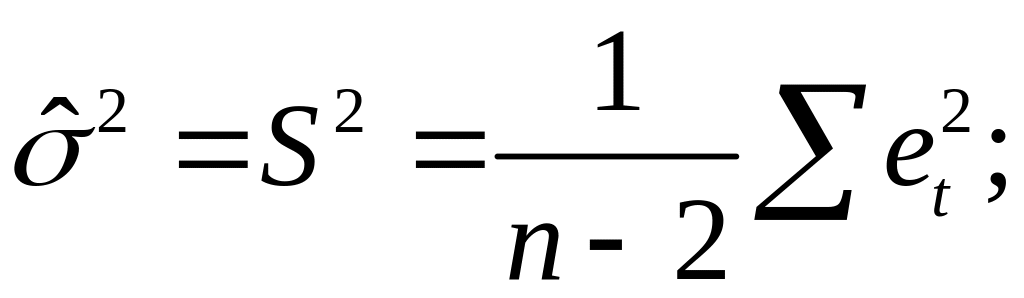
является
несмещенной оценкой дисперсии ошибок
σ².

12. Оценка существенности параметров линейной регрессии и корреляции

Существенность
коэф-ов регрессии определяет можно ли
его заменить нулем. Если данный коэф-т
несуществ., то его можно заменить нулем.

При выполнении
дополнительного условия о совместном
нормальном распределении ошибок,
стандартная ошибка коэффициента
регрессии параметра S_b
рассчитывается
по формуле

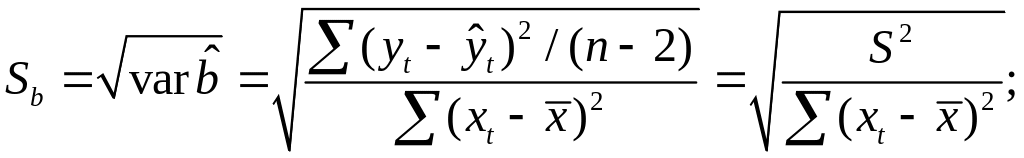
где S²
— остаточная
дисперсия на одну степень свободы.

Отношение коэф-та
регрессии к его стандартной ошибке дает
t-статистику,
кот. подчиняется статистике Стьюдента
при (n-2)
степенях свободы.
Эта статистика применяется для проверки
стат. значимости коэф-та
регрессии.

Для оценки значимости
коэф-та регрессии опр-ют фактическое
знач. t-критерия
Стьюдента: t_b=b/S_b
, которое
затем сравнивают с табличным значением
при определенном уровне значимости
и числе степеней
свободы (n-2).
Если t_b>t_кр,
коэф-т b значим и
его нельзя заменить 0.

Доверительный
интервал для коэф-та регрессии опр-ся
как

.

Замечание: Т.к.
коэф-т регрессии b для эк. Исследований
имеет четкую интерпритацию доверит.
Интервалы не должны содержать
противоречивыхрезультатов, напр., от
«-10» до 20 , т.е. положит. и отрицат.

Значимость линейного
коэффициента корреляции r
проверяется на основе величины ошибки
коэффициента корреляции S_r=m_r(заменить):

О
тсюда
фактическое значение

Данная формула
свидетельствует, что в парной лин.
регрессииt_r²=F
=>t_r²=
t_b²
.

Таким образом,
проверка гипотез о значимости коэффициентов
регрессии и корреляции равносильна
проверке гипотезы о значимости линейного
уравнения регрессии.

13. Интервалы прогноза по линейному уравнению регрессии

Основное назначение
ур-ия регрессии — прогноз возможных
знач. результата при заданном значении
фактора.

Этот прогноз
осущ-ся путем подстановки знач. фактора
х=х_k
в ур-ние
регрессии

.
Но данный
точечный прогноз не всегда реален. Он
должен дополняться интервальной
оценкой прогноза значения результата
y*.
Т.е.

,
где

—
стандартная ошибка оценки

.

Получим данную
оценку для лин. регрессии

.
Подставим это
выражение в ур-ие

.
Отсюда следует,
что стандартная ошибка

зависит от
ошибки

и ошибки
коэффициента b,
т.е.

.

В курсе мат. стат.
получено:

=S²/n,где
S²
– оценка дисперсии рез-ого признака.

;Получим

Откуд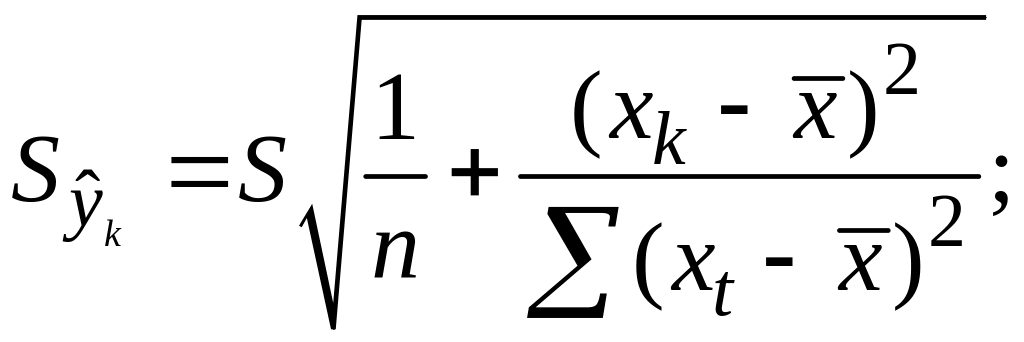

Где t=1,…n
– номера измерений, x_k
не обязано совпадать с одним из x_t_.

Видно, что величина
стандартной ошибки x_k
зависит от

.
Она достигает
мин. при x_к=

и возрастает
по мере того, как «удаляется» от

в любом
направлении.

Т.е.

.

Можно строить
интервальные оценки рез-ого признака
при заданном x_к

,которые
определяются как

,
где

—
критическое значение распределения
Стьюдента, при (n-2) степенями свободы.

На графике
доверительные границы для

представляют собой гиперболы,
расположенные по обе стороны от линии
регрессии.

Фактические знач.
y_k
варьируют
около ср. знач.

на величину случ. ошибки ε, дисперсия
кот. оценивается как S², поэтому
ошибка предсказываемого индивид-ого
значения y
должно включать как станд.ошибку

так и случ.ошибку S.

Средняя ошибка
прогнозного индив.значения составит

.
На основе этой оценки м.также строить
интервальные оценки, кот. б. содержать
заданные доверительной вероятностью,
измеряемые значения рез-ого признака.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

You are quite right. In the context of linear regression, or of any other model that can yield predictions on one variable (response) from values of other variables (predictors), we usually have a set of observations, that is, points where we observed the actual response and the predictors. Given a model, for each observation we can compute the predicted value (from model and predictors) and the actual value. The error is the difference between predicted and observed value.

Since we have a set of observations, we have a set of errors and therefore we can compute its variance. Furthermore, if observations are seen as a random variable, we can estimate its variance.

That is error variance.

Colman’s definition is equivalent to this one, but from another point of view.

In our set of observations, we can compute variance of the response. If we have a model, we can explain part of the variance of the response from the variance of predictors. The part we can’t explain is error variance — the same error variance explained above.

And to summarize: Please have a look at the page of Corman’s book and notice that just before «error variance» there is the definition of «error variable». A short definition of error variance is that it is the variance of the error variable.

Источник

Декомпозиция алгоритмов машинного обучения по дисперсии смещения на практическом примере в Python

Смещение и дисперсия — два ключевых понятия в оценке модели для машинного обучения, поскольку они тесно связаны с производительностью модели на невидимых данных. И смещение, и дисперсия являются типами ошибок ошибки прогнозирования. Третий тип ошибки — это неустранимая ошибка, которая является неотъемлемой ошибкой в данных, которую нельзя уменьшить независимо от того, какой алгоритм используется.

Одной из основных трудностей, с которой сталкиваются специалисты по данным при внедрении новой модели, является так называемая дилемма смещения-дисперсии или проблема смещения-дисперсии. Это связано с противоречием минимизации обоих источников ошибок в алгоритмах обучения с учителем, которые можно оценить с помощью метода декомпозиции смещения и дисперсии.

В этой статье мы рассмотрим эти концепции, чтобы закончить основной вклад этой статьи, который представляет собой объяснение декомпозиции смещения-дисперсии вместе с практическим примером на Python для всех, кто заинтересован в реализации декомпозиции для своих моделей.

Предвзятость и дисперсия

Предвзятость определяется как разница между предсказанием модели и истинной реальностью. Высокое смещение может привести к тому, что алгоритм упустит соответствующие отношения между функциями и целевыми выходными данными (недообучение).

Дисперсия определяется как чувствительность к колебаниям обучающей выборки. Другими словами, это относится к тому, насколько сильно меняются результаты при изменении обучающих данных. Высокая дисперсия предполагает большие изменения в оценке целевой функции при изменении обучающего набора данных (переобучение).

Оба термина, выраженные в математике, соответствуют следующим формулам:

Оба члена могут быть легко получены из формулы среднеквадратичной ошибки (MSE):

Пример того, как интерпретировать эти формулы, показан в конце статьи.

Вот график с четырьмя различными сценариями для высокого-низкого смещения и высокого-низкого отклонения. Каждое попадание представляет собой индивидуальную реализацию нашей модели с учетом случайной изменчивости обучающих данных, которые мы собираем [1]. Центр цели означает, что модель точно предсказывает значения.

Компромисс смещения и дисперсии

Несмотря на то, что оптимальной задачей было бы иметь минимально возможное смещение и дисперсию, на практике существует явный компромисс между обеими ошибками. Нахождение компромисса между обоими терминами называется компромисс между смещением и дисперсией.

Для моделей машинного обучения смещение и дисперсия тесно связаны со сложностью модели, которая затем связана с тем, когда модель переобучает или недообучает данные обучения. Как показано на рис. 2, когда сложность модели превышает допустимое значение, наша модель переоснащает обучающие данные, тогда как если сложность модели ниже, модель не соответствует данным.

В реальных сценариях не существует аналитического способа найти золотую середину, поэтому необходимо протестировать несколько моделей разной сложности и выбрать ту, которая минимизирует общую ошибку.

Разложение смещения-дисперсии

Разложение смещения-дисперсии является полезным методом для понимания производительности алгоритма.

Основная идея этого метода заключается в измерении систематической ошибки и дисперсии при обучении одной и той же модели с разными обучающими наборами и тестировании ее на одном и том же тестовом наборе.

Чтобы реализовать это, для подвыборки данных используется метод начальная загрузка (название бэггинг происходит от загрузка + агрегация ). Этот метод состоит в выполнении случайной выборки с заменой данных, что означает, что подмножества обучающих данных будут перекрываться, поскольку мы не разделяем данные, а передискретизируем их.

Таким образом, многократно запуская метод самозагрузки и получая точность модели для тестового набора, мы можем получить среднее смещение и дисперсию для всех раундов, для которых мы выполнили итерацию.

Вот часть кода задачи регрессии, которая обобщает основную логику метода. Весь код получен из библиотеки MLxtend.

Input:
- X_train
- y_train
- X_test
- y_test
- num_rounds: Number of iterations
Output:
- avg_expected_loss: Average MSE loss for all the rounds
- avg_bias: Average bias for all the rounds
- avg_var: Average variance for all the rounds
(avg_expected_loss = avg_bias^2 + avg_var)
(1) Iterate for num_rounds, in each implementing bootstrapping, training the model and getting the predictions
for i in range(num_rounds):
- X_boot, y_boot = _draw_bootstrap_sample(rng, X_train, y_train)
- pred = estimator.fit(X_boot, y_boot).predict(X_test)
- all_pred[i] = pred
(2) Obtain the average MSE error
avg_expected_loss = np.apply_along_axis(lambda x: ((x — y_test)**2).mean(), axis=1, arr=all_pred).mean()
(3) Obtain the average bias and variance
main_predictions = np.mean(all_pred, axis=0)
avg_bias = np.sum((main_predictions — y_test)**2) / y_test.size
avg_var = np.sum((main_predictions — all_pred)**2) / all_pred.size

Наконец, вот практический пример на Python, который показывает, как реализовать декомпозицию смещения-дисперсии.

В качестве примера мы использовали свободно доступный набор данных о жилье в Бостоне [2], задачей которого является прогнозирование цен на жилье с помощью регрессора. Сначала мы разделили данные на обучающий набор и тестовый набор.

Пример 1. Дерево решений

Чтобы проанализировать декомпозицию смещения-дисперсии, мы сначала реализовали регрессор дерева решений и прогнали его через функцию bias_variance_decomp, псевдокод которой показан выше.

Average expected loss: 32.419
Average bias: 14.197
Average variance: 18.222

Чтобы сравнить этот вывод с другой моделью, мы также запустили метод ансамбля пакетов с использованием регрессора дерева решений.

Average expected loss: 18.693
Average bias: 15.292
Average variance: 3.402

По сравнению с предыдущим результатом мы можем наблюдать, как увеличилось смещение, что означает, что модель регрессора с бэггингом работает хуже, чем модель дерева решений. Однако дисперсия сильно уменьшилась, что указывает на то, что модель более соответствует своим предсказаниям.

Пример 2. Нейронная сеть

Мы также оценили производительность модели на основе нейронной сети, реализованной в Keras, поскольку, насколько нам известно, эта функция не может быть реализована в PyTorch.

Average expected loss: 25.470
Average bias: 19.927
Average variance: 5.543

По сравнению с первой моделью мы увеличили сложность модели за счет увеличения количества нейронов для каждого слоя.

Average expected loss: 23.458
Average bias: 17.608
Average variance: 5.850

Как и ожидалось, систематическая ошибка уменьшилась за счет увеличения дисперсии модели.

Способы управления предвзятостью и дисперсией

Есть несколько советов, как управлять ошибками смещения и дисперсии.

Прежде всего, не зацикливайтесь только на минимизации смещения или, другими словами, не забывайте о дисперсии. Оба они одинаково важны для создания надежной модели.

Затем смещение модели может быть уменьшено за счет увеличения сложности путем (1) реализации ансамблевого метода ускорения или (2) добавления дополнительных функций или разработки функций.

Вместо этого дисперсию можно уменьшить, (1) внедрив ансамблевый метод бэггинга или (2) ограничив или уменьшив оценочные коэффициенты путем регуляризации.

Для получения более подробной информации о том, как управлять смещением и дисперсией с помощью ансамблевых методов, я предлагаю прочитать статью Введение в ансамблевые методы в машинном обучении.

Подробное объяснение того, как интерпретировать смещение и дисперсию

Если бы у нас было следующее распределение,

ожидаемое значение и дисперсия рассчитываются следующим образом:

Ожидаемые значения

Дисперсия

Если вам понравился этот пост, рассмотрите возможность подписаться. Вы получите доступ ко всему моему контенту и ко всем остальным статьям на Medium от замечательных авторов!

Рекомендации

[1] Скотт Фортманн-Роу, Понимание компромисса смещения и дисперсии

[2] Харрисон, Д. и Рубинфельд, Д.Л. «Гедонистические цены и спрос на чистый воздух», J. Environ. Экономика и менеджмент, том 5, 81–102, 1978 г.

[3] The Machine Learners, Entiende de una vez qué es el Tradeoff Bias-Variance

[4] GitHub, Функцияbias_variance_decomp.py

[5] Stack Exchange, Что означает 𝐸(𝑋) в буквальном смысле?

[6] Medium, Объяснение компромисса смещения и дисперсии

[7] Мастерство машинного обучения, Нежное введение в компромисс между смещением и дисперсией в машинном обучении.

[8] GitHub, Смещение ошибки машинного обучения и неустранимая ошибка с python

[9] GitHub, Разложение смещения-дисперсии для классификации и регрессионных потерь

[10] Блог Genius, Что такое компромисс смещения и дисперсии?

Источник

Особенности модели. Коэффициенты модели и их нахождение. Граница эффективности. Дисперсия ошибок. Измерение весов. Использование модели в реальной действительности [c.85]

Основные положения теории Шарпа. Коэффициенты регрессии. Измерение ожидаемой доходности и риска портфеля. Дисперсия ошибок. Определение весов ценных бумаг в модели Шарпа. Нахождение оптимального портфеля. Сравнительный анализ методов Г. Марковица и В. Шарпа. [c.335]

Наиболее хорошо изучены линейные регрессионные модели, удовлетворяющие условиям (1.6), (1.7) и свойству постоянства дисперсии ошибок регрессии, — они называются классическими моделями. [c.19]

Очевидно, для продвижения к этой цели необходимы некоторые дополнительные предположения относительно характера гетероскедастичности. В самом деле, без подобных предположений, очевидно, невозможно было бы оценить п параметров (п дисперсий ошибок регрессии а ) с помощью п наблюдений. [c.161]

Решение. Предположим, что дисперсии ошибок о, связаны уравнением регрессии [c.163]

Вспомним, что наиболее часто употребляемые процедуры устранения гетероскедастичности так или иначе были основаны на предположении, что дисперсия ошибок регрессии ст2 является функцией от каких-то регрессоров. Если а2 существенно зависит от регрессора Z, а при спецификации модели регрессор Z не был включен в модель, стандартные процедуры могут не привести к устранению гетероскедастичности. [c.250]

В случае постоянства дисперсии ошибок МНК необъясненная дисперсия для меньших значений X должна быть приблизительно равна необъясненной дисперсии для больших значений X, то есть должно быть справедливым следующее равенство [c.125]

Чем ближе к единице отношение / S2, тем больше оснований рассчитывать на то, что дисперсия ошибок МНК постоянна. Случайная величина F = Sl / S2 подчиняется F -распределению [c.125]

Непостоянство дисперсии ошибок МНК возникает как правило в том случае, если неправильно выбран вид математической модели зависимости фактора X и отклика 7. Например, если нелинейную зависимость пытаются аппроксимировать линейной функцией. [c.126]

Пятая часть полностью посвящена приложению матричного дифференциального исчисления к линейной регрессионной модели. Она содержит исчерпывающее изложение проблемы оценивания, связанной с неслучайной частью модели при различных предположениях о рангах и других ограничениях. Кроме того, она содержит ряд параграфов, связанных со стохастической частью модели, например оценивание дисперсии ошибок и прогноз ошибок. Включен также небольшой параграф, посвященный анализу чувствительности. Вводная глава содержит необходимые предварительные сведения из теории вероятностей и математической статистики. [c.16]

Дисперсия ошибок прогноза в задаче (3.6) — (3.7) достигает минимума в точке , являющейся основанием перпендикуляра, опущенного из точки т] на подпространство Q, определяемое равенством (3.7). Соотношение (3.10) эквивалентно равенству [c.309]

Ограничение (а) не вызывает претензий. Условие (б) также естественно. Ясно, что механизм сглаживания и прогноза, при котором математическое ожидание или дисперсия ошибок фильтрации или интенсивность искусственного рассеивания достаточно велики, вряд ли рационален и тем более не может быть признан оптимальным. [c.320]

Задача прогнозирования по минимуму дисперсии ошибок при различных статистических характеристиках входных случайных процессов и ошибок измерений подробно обсуждалась в литературе. Имеются и стандартные аналоговые устройства и программы для ЦВМ, реализующие соответствующие схемы. Экстремальная задача, к которой сводится вычисление характеристик генераторов случайных шумов, несомненно, проще исходной вариационной задачи. [c.334]

Матрица корреляции k j R регулируемых ошибок прогноза, оптимального в смысле показателя качества R( k ), может быть получена из корреляционной матрицы kff a ошибок прогноза, оптимальных в смысле минимума дисперсии ошибок в каждой координате в каждый момент времени, по следующей формуле [c.339]

Из (1.14), в частности, следует, что коэффициент корреляции признаков, на которые наложены ошибки измерения, всегда меньше по абсолютной величине, чем коэффициент корреляции исходных признаков. Другими словами, ошибки измерения всегда ослабляют исследуемую корреляционную связь между исходными переменными, и это искажение тем меньше, чем меньше отношения дисперсий ошибок к дисперсиям самих исходных переменных. Формула (1.14) позволяет скорректировать искаженное значение коэффициента корреляции для этого нужно либо знать разрешающие характеристики измерительных приборов (и, следовательно, величины дисперсий ошибок а и а ), либо провести дополнительное исследование по их выявлению. [c.73]

Пример 7.4 ]. Известно, что дисперсия о2, вызванная ошибками измерения, при некоторых видах количественного анализа составляет 0,5. Если заменить измерительный прибор и произвести 10-кратное измерение одного и того же стандартного образца, а затем подсчитать дисперсию, то она составит s2 = 0,25. Может показаться, что дисперсия ошибок измерения изменилась, превысив 5%-ный уровень значимости. Так ли это [c.128]

Теорема Гаусса-Маркова. Оценка дисперсии ошибок сг2 [c.41]

Оценка дисперсии ошибок а2 [c.43]

Формулы (2.11), (2.13) дают дисперсии оценок о, Ь коэффициентов регрессии в том случае, если а2 известно. На практике, как правило, дисперсия ошибок а2 неизвестна и оценивается по наблюдениям одновременно с коэффициентами регрессии а, Ь. В этом случае вместо дисперсий оценок о, b мы можем получить лишь оценки дисперсий о, 6, заменив а2 на s2 из (2.15) в (2.11), (2.13), (2.14) [c.45]

Распределение оценки дисперсии ошибок s2 [c.47]

Так как оценка дисперсии ошибок s2 является функцией от остатков регрессии et, то для того чтобы доказать независимость s2 и (2,6), достаточно доказать независимость et и (2,6). Оценки 2, 6 так же, как и остатки регрессии et, являются линейными функциями ошибок t (см. (2.4а), (2.46), (2.20)) и поэтому имеют совместное нормальное распределение. Известно (приложение МС, п. 4, N4), что два случайных вектора, имеющие совместное нормальное распределение, независимы тогда и только тогда, когда они некоррелированы. Таким образом, чтобы доказать независимость s2 и (а, 6), нам достаточно доказать некоррелированность et и (2,6). [c.48]

Значение Д2 увеличилось по сравнению с первой регрессией. Переход к удельным данным приводит к уменьшению дисперсии ошибок модели. [c.58]

Пусть SML = Y et/ n и OLS — ] et/ (n — 1 — оценки методов максимального правдоподобия и наименьших квадратов для дисперсии ошибок <т2 в классической модели парной регрессии Yt = [c.62]

Оценка дисперсии ошибок а1. Распределение s2 [c.72]

Сумма квадратов остатков е2 = е е является естественным кандидатом на оценку дисперсии ошибок а1 (конечно, с некоторым поправочным коэффициентом, зависящим от числа степеней свободы) [c.73]

Тест ранговой корреляции Спирмена использует наиболее общие предположения о зависимости дисперсий ошибок регрессии от значений регрессоров [c.158]

Тест Уайта. Тест ранговой корреляции Спирмена и тест Голдфелда—Квандта позволяют обнаружить лишь само наличие гетероскедастичности, но они не дают возможности проследить количественный характер зависимости дисперсий ошибок регрессии от значений регрессоров и, следовательно, не представляют каких-либо способов устранения гетероскедастичности. [c.161]

Наиболее простой и часто употребляемый тест на гетероске-дастичность — тест Уайта. При использовании этого теста предполагается, что дисперсии ошибок регрессии представляют собой одну и ту же функцию от наблюдаемых значений регрессоров, т.е. [c.161]

Другим недостатком тестов Уайта и Глейзера является то, что факт невыявления ими гетероскедастичности, вообще говоря, не означает ее отсутствия. В самом деле, принимая гипотезу Щ, мы принимаем лишь тот факт, что отсутствует определенного вида зависимость дисперсий ошибок регрессии от значений регрессоров. [c.166]

Построенные экологометрические модели требуют оценки их достоверности. При выполнении статистических исследований полученные данные тщательно анализируются на предмет удовлетворения их предположения о независимости случайных наблюдений, симметричности распределения, из которого получена выборка, равенства дисперсии ошибок, одинаковости распределения нескольких случайных величин и т.д. Все эти предположения могут рассматриваться как гипотезы, которые необходимо проверить. [c.57]

Доказано (см., например, [37]), что приведенную задачу оптимального стохастического управления можно разделить на две задачу сглаживания и лрогноза по минимуму дисперсии ошибок и задачу оптимального детерминированного управления. При более сложном критерии качества управления и при дополнительных ограничениях на переменные состояния и управляющие параметры такое разделение не всегда удается я, его, по-видимому, не всегда целесообразно производить. [c.44]

Здесь Paaa(tt, » ) — система функций веса, минимизирующих дисперсию ошибок За(/г-) прогноза W (ti, т) — тождественно не равные нулю функ-22 339 [c.339]

В ходе анализа финансовых данных любой ряд динамики, будь то процентные ставки или цены на финансовые активы, можно разбить на две компоненты, одна из которых изменяется случайным образом, а другая подчиняется определенному закону. Колебания финансовых переменных значительно изменяются во времени бурные периоды с высокой волатильностью переменных сменяют спокойные периоды и наоборот. В некоторых случаях вола-тильность играет ключевую роль в ценообразовании на финансовые активы. В частности, курсы акций напрямую зависят от ожидаемой волатильности доходов корпораций. Все финансовые учреждения без исключения стремятся адекватно оценить волатильность в целях успешного управления рисками. В свое время Трюгве Хаавельмо, нобелевский лауреат по экономике 1989 г., предложил рассматривать изменение экономических переменных как однородный стохастический (случайный) процесс. Вплоть до 1980-х гг. экономисты для анализа финансовых рынков применяли статистические методы, предполагавшие постоянную волатильность во времени. В 1982 г. Роберт Ингл развил новую эконометрическую концепцию, позволяющую анализировать периоды с разной волатильностью. Он ввел кластеризацию данных и условную дисперсию ошибок, которая завесит от времени. Свою разработку Ингл назвал авторегрессионной гетероскедастической моделью , с ее помощью можно точно описать множество временных рядов, встречающихся в экономике. Метод Ингла сегодня применяется финансовыми аналитиками в целях оценки финансовых активов и портфельных рисков. [c.197]

Отметим, что оценки максимального правдоподобия параметров а, 6 совпадают с оценками метода наименьших квадратов OML = SOLS, ML OLS- Это легко видеть из того, что уравнения (2.37а) и (2.376) совпадают с соответствующими уравнениями метода наименьших квадратов (2.2). Оценка максимального правдоподобия для <т2 не совпадает с

несмещенной оценкой дисперсии ошибок. Таким образом, с = ((п — 2)/n)<7OLS является смещенной, но тем не менее состоятельной оценкой <т2. [c.57]

В этом разделе мы рассмотрим частный случай обобщенной регрессионной модели, а именно, модель с гетероскедастичностъю, Это означает, что ошибки некоррелированы, но имеют непостоянные дисперсии. (Классическая модель с постоянными дисперсиями ошибок называется гомоскедастичной.) Как уже отмечалось, Гетероскедастичность довольно часто возникает, если анализируемые объекты, говоря нестрого, неоднородны. Например, если исследуется зависимость прибыли предприятия от каких-либо факторов, скажем, от размера основного фонда, то естественно ожидать, что для больших предприятий колебание прибыли будет выше, чем для малых. [c.168]

Источник

Результат любого измерения не определён однозначно и имеет случайную составляющую.
Поэтому адекватным языком для описания погрешностей является язык вероятностей.
Тот факт, что значение некоторой величины «случайно», не означает, что
она может принимать совершенно произвольные значения. Ясно, что частоты, с которыми
возникает те или иные значения, различны. Вероятностные законы, которым
подчиняются случайные величины, называют распределениями.

2.1 Случайная величина

Случайной будем называть величину, значение которой не может быть достоверно определено экспериментатором. Чаще всего подразумевается, что случайная величина будет изменяться при многократном повторении одного и того же эксперимента. При интерпретации результатов измерений в физических экспериментах, обычно случайными также считаются величины, значение которых является фиксированным, но не известно экспериментатору. Например смещение нуля шкалы прибора. Для формализации работы со случайными величинами используют понятие вероятности. Численное значение вероятности того, что какая-то величина примет то или иное значение определяется либо как относительная частота наблюдения того или иного значения при повторении опыта большое количество раз, либо как оценка на основе данных других экспериментов.

Замечание.
Хотя понятия вероятности и случайной величины являются основополагающими, в литературе нет единства в их определении. Обсуждение формальных тонкостей или построение строгой теории лежит за пределами данного пособия. Поэтому на начальном этапе лучше использовать «интуитивное» понимание этих сущностей. Заинтересованным читателям рекомендуем обратиться к специальной литературе: [5].

Рассмотрим случайную физическую величину x, которая при измерениях может
принимать непрерывный набор значений. Пусть
P[x0,x0+δ⁢x] — вероятность того, что результат окажется вблизи
некоторой точки x0 в пределах интервала δ⁢x: x∈[x0,x0+δ⁢x].
Устремим интервал
δ⁢x к нулю. Нетрудно понять, что вероятность попасть в этот интервал
также будет стремиться к нулю. Однако отношение
w⁢(x0)=P[x0,x0+δ⁢x]δ⁢x будет оставаться конечным.
Функцию w⁢(x) называют плотностью распределения вероятности или кратко
распределением непрерывной случайной величины x.

Замечание. В математической литературе распределением часто называют не функцию
w⁢(x), а её интеграл W⁢(x)=∫w⁢(x)⁢𝑑x. Такую функцию в физике принято
называть интегральным или кумулятивным распределением. В англоязычной литературе
для этих функций принято использовать сокращения:
pdf (probability distribution function) и
cdf (cumulative distribution function)
соответственно.

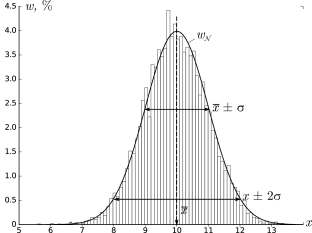
Гистограммы.

Проиллюстрируем наглядно понятие плотности распределения. Результат
большого числа измерений случайной величины удобно представить с помощью
специального типа графика — гистограммы.
Для этого область значений x, размещённую на оси абсцисс, разобьём на
равные малые интервалы — «корзины» или «бины» (англ. bins)
некоторого размера h. По оси ординат будем откладывать долю измерений w,
результаты которых попадают в соответствующую корзину. А именно,
пусть k — номер корзины; nk — число измерений, попавших
в диапазон x∈[k⁢h,(k+1)⁢h]. Тогда на графике изобразим «столбик»
шириной h и высотой wk=nk/n.
В результате получим картину, подобную изображённой на рис. 2.1.

Рис. 2.1: Пример гистограммы для нормального распределения (x¯=10,
σ=1,0, h=0,1, n=104)

Высоты построенных столбиков будут приближённо соответствовать значению
плотности распределения w⁢(x) вблизи соответствующей точки x.
Если устремить число измерений к бесконечности (n→∞), а ширину корзин
к нулю (h→0), то огибающая гистограммы будет стремиться к некоторой
непрерывной функции w⁢(x).

Самые высокие столбики гистограммы будут группироваться вблизи максимума
функции w⁢(x) — это наиболее вероятное значение случайной величины.
Если отклонения в положительную и отрицательную стороны равновероятны,
то гистограмма будет симметрична — в таком случае среднее значение ⟨x⟩
также будет лежать вблизи этого максимума. Ширина гистограммы будет характеризовать разброс
значений случайной величины — по порядку величины
она, как правило, близка к среднеквадратичному отклонению sx.

Свойства распределений.

Из определения функции w⁢(x) следует, что вероятность получить в результате
эксперимента величину x в диапазоне от a до b
можно найти, вычислив интеграл:

Px∈[a,b]=∫abw⁢(x)⁢𝑑x.

(2.1)

Согласно определению вероятности, сумма вероятностей для всех возможных случаев
всегда равна единице. Поэтому интеграл распределения w⁢(x) по всей области
значений x (то есть суммарная площадь под графиком w⁢(x)) равен единице:

Это соотношение называют условием нормировки.

Среднее и дисперсия.

Вычислим среднее по построенной гистограмме. Если размер корзин
h достаточно мал, все измерения в пределах одной корзины можно считать примерно
одинаковыми. Тогда среднее арифметическое всех результатов можно вычислить как

Переходя к пределу, получим следующее определение среднего значения
случайной величины:

где интегрирование ведётся по всей области значений x.
В теории вероятностей x¯ также называют математическим ожиданием
распределения.
Величину

σ2=(x-x¯)2¯=∫(x-x¯)2⁢w⁢𝑑x

(2.3)

называют дисперсией распределения. Значение σ есть
срекднеквадратичное отклонение в пределе n→∞. Оно имеет ту
же размерность, что и сама величина x и характеризует разброс распределения.
Именно эту величину, как правило, приводят как характеристику погрешности
измерения x.

Доверительный интервал.

Обозначим как P|Δ⁢x|<δ вероятность
того, что отклонение от среднего Δ⁢x=x-x¯ составит величину,
не превосходящую по модулю значение δ:

P|Δ⁢x|<δ=∫x¯-δx¯+δw⁢(x)⁢𝑑x.

(2.4)

Эту величину называют доверительной вероятностью для
доверительного интервала |x-x¯|≤δ.

2.2 Нормальное распределение

Одним из наиболее примечательных результатов теории вероятностей является
так называемая центральная предельная теорема. Она утверждает,
что сумма большого количества независимых случайных слагаемых, каждое
из которых вносит в эту сумму относительно малый вклад, подчиняется
универсальному закону, не зависимо от того, каким вероятностным законам
подчиняются её составляющие, — так называемому нормальному
распределению (или распределению Гаусса).

Доказательство теоремы довольно громоздко и мы его не приводим (его можно найти
в любом учебнике по теории вероятностей). Остановимся
кратко на том, что такое нормальное распределение и его основных свойствах.

Плотность нормального распределения выражается следующей формулой:

w𝒩⁢(x)=12⁢π⁢σ⁢e-(x-x¯)22⁢σ2.

(2.5)

Здесь x¯ и σ
— параметры нормального распределения: x¯ равно
среднему значению x, a σ —
среднеквадратичному отклонению, вычисленным в пределе n→∞.

Как видно из рис. 2.1, распределение представляет собой
симметричный
«колокол», положение вершины которого
соответствует x¯ (ввиду симметрии оно же
совпадает с наиболее вероятным значением — максимумом
функции w𝒩⁢(x)).

При значительном отклонении x от среднего величина
w𝒩⁢(x)
очень быстро убывает. Это означает, что вероятность встретить отклонения,
существенно большие, чем σ, оказывается пренебрежимо
мала. Ширина «колокола» по порядку величины
равна σ — она характеризует «разброс»
экспериментальных данных относительно среднего значения.

Замечание. Точки x=x¯±σ являются точками
перегиба графика w⁢(x) (в них вторая производная по x
обращается в нуль, w′′=0), а их положение по высоте составляет
w⁢(x¯±σ)/w⁢(x¯)=e-1/2≈0,61
от высоты вершины.

Универсальный характер центральной предельной теоремы позволяет широко
применять на практике нормальное (гауссово) распределение для обработки
результатов измерений, поскольку часто случайные погрешности складываются из
множества случайных независимых факторов. Заметим, что на практике
для приближённой оценки параметров нормального распределения
случайной величины используются выборочные значения среднего
и дисперсии: x¯≈⟨x⟩, sx≈σx.

x-x0σ2=2w⁢(x)σ1=1

Рис. 2.2: Плотность нормального распределения

Доверительные вероятности.

Вычислим некоторые доверительные вероятности (2.4) для нормально
распределённых случайных величин.

Замечание. Значение интеграла вида ∫e-x2/2⁢𝑑x
(его называют интегралом ошибок) в элементарных функциях не выражается,
но легко находится численно.

Вероятность того, что результат отдельного измерения x окажется
в пределах x¯±σ оказывается равна

P|Δ⁢x|<σ=∫x¯-σx¯+σw𝒩⁢𝑑x≈0,68.

Вероятность отклонения в пределах x¯±2⁢σ:

а в пределах x¯±3⁢σ:

Иными словами, при большом числе измерений нормально распределённой
величины можно ожидать, что лишь треть измерений выпадут за пределы интервала
[x¯-σ,x¯+σ]. При этом около 5%
измерений выпадут за пределы [x¯-2⁢σ;x¯+2⁢σ],
и лишь 0,27% окажутся за пределами
[x¯-3⁢σ;x¯+3⁢σ].

Пример. В сообщениях об открытии бозона Хиггса на Большом адронном коллайдере
говорилось о том, что исследователи ждали подтверждение результатов
с точностью «5 сигма». Используя нормальное распределение (2.5)
нетрудно посчитать, что они использовали доверительную вероятность
P≈1-5,7⋅10-7=0,99999943. Такую точность можно назвать фантастической.

Полученные значения доверительных вероятностей используются при
стандартной записи результатов измерений. В физических измерениях
(в частности, в учебной лаборатории), как правило, используется P=0,68,
то есть, запись

означает, что измеренное значение лежит в диапазоне (доверительном
интервале) x∈[x¯-δ⁢x;x¯+δ⁢x] с
вероятностью 68%. Таким образом погрешность ±δ⁢x считается
равной одному среднеквадратичному отклонению: δ⁢x=σ.
В технических измерениях чаще используется P=0,95, то есть под
абсолютной погрешностью имеется в виду удвоенное среднеквадратичное
отклонение, δ⁢x=2⁢σ. Во избежание разночтений доверительную
вероятность следует указывать отдельно.

Замечание. Хотя нормальный закон распределения встречается на практике довольно
часто, стоит помнить, что он реализуется далеко не всегда.
Полученные выше соотношения для вероятностей попадания значений в
доверительные интервалы можно использовать в качестве простейшего
признака нормальности распределения: в частности, если количество попадающих
в интервал ±σ результатов существенно отличается от 2/3 — это повод
для более детального исследования закона распределения ошибок.

Сравнение результатов измерений.

Теперь мы можем дать количественный критерий для сравнения двух измеренных
величин или двух результатов измерения одной и той же величины.

Пусть x1 и x2 (x1≠x2) измерены с
погрешностями σ1 и σ2 соответственно.
Ясно, что если различие результатов |x2-x1| невелико,
его можно объяснить просто случайными отклонениями.
Если же теория предсказывает, что вероятность обнаружить такое отклонение
слишком мала, различие результатов следует признать значимым.
Предварительно необходимо договориться о соответствующем граничном значении
вероятности. Универсального значения здесь быть не может,
поэтому приходится полагаться на субъективный выбор исследователя. Часто
в качестве «разумной» границы выбирают вероятность 5%,
что, как видно из изложенного выше, для нормального распределения
соответствует отклонению более, чем на 2⁢σ.

Допустим, одна из величин известна с существенно большей точностью:
σ2≪σ1 (например, x1 — результат, полученный
студентом в лаборатории, x2 — справочное значение).
Поскольку σ2 мало, x2 можно принять за «истинное»:
x2≈x¯. Предполагая, что погрешность измерения
x1 подчиняется нормальному закону с и дисперсией σ12,
можно утверждать, что
различие считают будет значимы, если

Пусть погрешности измерений сравнимы по порядку величины:
σ1∼σ2. В теории вероятностей показывается, что
линейная комбинация нормально распределённых величин также имеет нормальное
распределение с дисперсией σ2=σ12+σ22
(см. также правила сложения погрешностей (2.7)). Тогда
для проверки гипотезы о том, что x1 и x2 являются измерениями
одной и той же величины, нужно вычислить, является ли значимым отклонение
|x1-x2| от нуля при σ=σ12+σ22.

Пример. Два студента получили следующие значения для теплоты испарения
некоторой жидкости: x1=40,3±0,2 кДж/моль и
x2=41,0±0,3 кДж/моль, где погрешность соответствует
одному стандартному отклонению. Можно ли утверждать, что они исследовали
одну и ту же жидкость?
Имеем наблюдаемую разность |x1-x2|=0,7 кДж/моль,
среднеквадратичное отклонение для разности
σ=0,22+0,32=0,36 кДж/моль.
Их отношение |x2-x1|σ≈2. Из
свойств нормального распределения находим вероятность того, что измерялась
одна и та же величина, а различия в ответах возникли из-за случайных
ошибок: P≈5%. Ответ на вопрос, «достаточно»
ли мала или велика эта вероятность, остаётся на усмотрение исследователя.

Замечание. Изложенные здесь соображения применимы, только если x¯ и
его стандартное отклонение σ получены на основании достаточно
большой выборки n≫1 (или заданы точно). При небольшом числе измерений
(n≲10) выборочные средние ⟨x⟩ и среднеквадратичное отклонение
sx сами имеют довольно большую ошибку, а
их распределение будет описываться не нормальным законом, а так
называемым t-распределением Стъюдента. В частности, в зависимости от
значения n интервал ⟨x⟩±sx будет соответствовать несколько
меньшей доверительной вероятности, чем P=0,68. Особенно резко различия
проявляются при высоких уровнях доверительных вероятностей P→1.

2.3 Независимые величины

Величины x и y называют независимыми если результат измерения одной
из них никак не влияет на результат измерения другой. Для таких величин вероятность того, что x окажется в некоторой области X, и одновременно y — в области Y,
равна произведению соответствующих вероятностей:

Обозначим отклонения величин от их средних как Δ⁢x=x-x¯ и
Δ⁢y=y-y¯.
Средние значения этих отклонений равны, очевидно, нулю: Δ⁢x¯=x¯-x¯=0,
Δ⁢y¯=0. Из независимости величин x и y следует,
что среднее значение от произведения Δ⁢x⋅Δ⁢y¯
равно произведению средних Δ⁢x¯⋅Δ⁢y¯
и, следовательно, равно нулю:

Δ⁢x⋅Δ⁢y¯=Δ⁢x¯⋅Δ⁢y¯=0.

(2.6)

Пусть измеряемая величина z=x+y складывается из двух независимых
случайных слагаемых x и y, для которых известны средние
x¯ и y¯, и их среднеквадратичные погрешности
σx и σy. Непосредственно из определения (1.1)
следует, что среднее суммы равно сумме средних:

Найдём дисперсию σz2. В силу независимости имеем

Δ⁢z2¯=Δ⁢x2¯+Δ⁢y2¯+2⁢Δ⁢x⋅Δ⁢y¯≈Δ⁢x2¯+Δ⁢y2¯,

то есть:

Таким образом, при сложении независимых величин их погрешности
складываются среднеквадратичным образом.

Подчеркнём, что для справедливости соотношения (2.7)
величины x и y не обязаны быть нормально распределёнными —
достаточно существования конечных значений их дисперсий. Однако можно
показать, что если x и y распределены нормально, нормальным
будет и распределение их суммы.

Замечание. Требование независимости
слагаемых является принципиальным. Например, положим y=x. Тогда
z=2⁢x. Здесь y и x, очевидно, зависят друг от друга. Используя
(2.7), находим σ2⁢x=2⁢σx,
что, конечно, неверно — непосредственно из определения
следует, что σ2⁢x=2⁢σx.

Отдельно стоит обсудить математическую структуру формулы (2.7).
Если одна из погрешностей много больше другой, например,
σx≫σy,
то меньшей погрешностью можно пренебречь, σx+y≈σx.
С другой стороны, если два источника погрешностей имеют один порядок
σx∼σy, то и σx+y∼σx∼σy.

Эти обстоятельства важны при планирования эксперимента: как правило,
величина, измеренная наименее точно, вносит наибольший вклад в погрешность
конечного результата. При этом, пока не устранены наиболее существенные
ошибки, бессмысленно гнаться за повышением точности измерения остальных
величин.

Пример. Пусть σy=σx/3,
тогда σz=σx⁢1+19≈1,05⁢σx,
то есть при различии двух погрешностей более, чем в 3 раза, поправка
к погрешности составляет менее 5%, и уже нет особого смысла в учёте
меньшей погрешности: σz≈σx. Это утверждение
касается сложения любых независимых источников погрешностей в эксперименте.

2.4 Погрешность среднего

Выборочное среднее арифметическое значение ⟨x⟩, найденное
по результатам n измерений, само является случайной величиной.
Действительно, если поставить серию одинаковых опытов по n измерений,
то в каждом опыте получится своё среднее значение, отличающееся от
предельного среднего x¯.

Вычислим среднеквадратичную погрешность среднего арифметического
σ⟨x⟩.
Рассмотрим вспомогательную сумму n слагаемых

Если {xi} есть набор независимых измерений
одной и той же физической величины, то мы можем, применяя результат
(2.7) предыдущего параграфа, записать

σZ=σx12+σx22+…+σxn2=n⁢σx,

поскольку под корнем находится n одинаковых слагаемых. Отсюда с
учётом ⟨x⟩=Z/n получаем

Таким образом, погрешность среднего значения x по результатам
n независимых измерений оказывается в n раз меньше погрешности
отдельного измерения. Это один из важнейших результатов, позволяющий
уменьшать случайные погрешности эксперимента за счёт многократного
повторения измерений.

Подчеркнём отличия между σx и σ⟨x⟩:

величина σx — погрешность отдельного
измерения — является характеристикой разброса значений
в совокупности измерений {xi}, i=1..n. При
нормальном законе распределения примерно 68% измерений попадают в
интервал ⟨x⟩±σx;

величина σ⟨x⟩ — погрешность
среднего — характеризует точность, с которой определено
среднее значение измеряемой физической величины ⟨x⟩ относительно
предельного («истинного») среднего x¯;
при этом с доверительной вероятностью P=68% искомая величина x¯
лежит в интервале
⟨x⟩-σ⟨x⟩<x¯<⟨x⟩+σ⟨x⟩.

2.5 Результирующая погрешность опыта

Пусть для некоторого результата измерения известна оценка его максимальной
систематической погрешности Δсист и случайная
среднеквадратичная
погрешность σслуч. Какова «полная»
погрешность измерения?

Предположим для простоты, что измеряемая величина в принципе
может быть определена сколь угодно точно, так что можно говорить о
некотором её «истинном» значении xист
(иными словами, погрешность результата связана в основном именно с
процессом измерения). Назовём полной погрешностью измерения
среднеквадратичное значения отклонения от результата измерения от
«истинного»:

Отклонение x-xист можно представить как сумму случайного
отклонения от среднего δ⁢xслуч=x-x¯
и постоянной (но, вообще говоря, неизвестной) систематической составляющей
δ⁢xсист=x¯-xист=const:

Причём случайную составляющую можно считать независимой от систематической.
В таком случае из (2.7) находим:

σполн2=⟨δ⁢xсист2⟩+⟨δ⁢xслуч2⟩≤Δсист2+σслуч2.

(2.9)

Таким образом, для получения максимального значения полной
погрешности некоторого измерения нужно квадратично сложить максимальную
систематическую и случайную погрешности.

Если измерения проводятся многократно, то согласно (2.8)
случайная составляющая погрешности может быть уменьшена, а систематическая
составляющая при этом остаётся неизменной:

Отсюда следует важное практическое правило
(см. также обсуждение в п. 2.3): если случайная погрешность измерений
в 2–3 раза меньше предполагаемой систематической, то
нет смысла проводить многократные измерения в попытке уменьшить погрешность
всего эксперимента. В такой ситуации измерения достаточно повторить
2–3 раза — чтобы убедиться в повторяемости результата, исключить промахи
и проверить, что случайная ошибка действительно мала.
В противном случае повторение измерений может иметь смысл до
тех пор, пока погрешность среднего
σ⟨x⟩=σxn
не станет меньше систематической.

Замечание. Поскольку конкретная
величина систематической погрешности, как правило, не известна, её
можно в некотором смысле рассматривать наравне со случайной —
предположить, что её величина была определена по некоторому случайному
закону перед началом измерений (например, при изготовлении линейки
на заводе произошло некоторое случайное искажение шкалы). При такой
трактовке формулу (2.9) можно рассматривать просто
как частный случай формулы сложения погрешностей независимых величин
(2.7).
Подчеркнем, что вероятностный закон, которому подчиняется
систематическая ошибка, зачастую неизвестен. Поэтому неизвестно и
распределение итогового результата. Из этого, в частности, следует,
что мы не можем приписать интервалу x±Δсист какую-либо
определённую доверительную вероятность — она равна 0,68
только если систематическая ошибка имеет нормальное распределение.
Можно, конечно, предположить,
— и так часто делают — что, к примеру, ошибки
при изготовлении линеек на заводе имеют гауссов характер. Также часто
предполагают, что систематическая ошибка имеет равномерное
распределение (то есть «истинное» значение может с равной вероятностью
принять любое значение в пределах интервала ±Δсист).
Строго говоря, для этих предположений нет достаточных оснований.

Пример. В результате измерения диаметра проволоки микрометрическим винтом,
имеющим цену деления h=0,01 мм, получен следующий набор из n=8 значений:

Вычисляем среднее значение: ⟨d⟩≈386,3 мкм.
Среднеквадратичное отклонение:
σd≈9,2 мкм. Случайная погрешность среднего согласно
(2.8):
σ⟨d⟩=σd8≈3,2
мкм. Все результаты лежат в пределах ±2⁢σd, поэтому нет
причин сомневаться в нормальности распределения. Максимальную погрешность
микрометра оценим как половину цены деления, Δ=h2=5 мкм.
Результирующая полная погрешность
σ≤Δ2+σd28≈6,0 мкм.
Видно, что σслуч≈Δсист и проводить дополнительные измерения
особого смысла нет. Окончательно результат измерений может быть представлен
в виде (см. также правила округления
результатов измерений в п. 4.3.2)

d=386±6⁢мкм,εd=1,5%.

Заметим, что поскольку случайная погрешность и погрешность
прибора здесь имеют один порядок величины, наблюдаемый случайный разброс
данных может быть связан как с неоднородностью сечения проволоки,
так и с дефектами микрометра (например, с неровностями зажимов, люфтом
винта, сухим трением, деформацией проволоки под действием микрометра
и т. п.). Для ответа на вопрос, что именно вызвало разброс, требуются
дополнительные исследования, желательно с использованием более точных
приборов.

Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δ⁢v=±1 м/c.
Результаты измерений для n=6 выстрелов представлены в таблице:

Усреднённый результат ⟨v⟩=162,0⁢м/с,
среднеквадратичное отклонение σv=13,8⁢м/c, случайная
ошибка для средней скорости
σv¯=σv/6=5,6⁢м/с.
Поскольку разброс экспериментальных данных существенно превышает погрешность
каждого измерения, σv≫δ⁢v, он почти наверняка связан
с реальным различием скоростей пули в разных выстрелах, а не с ошибками
измерений. В качестве результата эксперимента представляют интерес
как среднее значение скоростей ⟨v⟩=162±6⁢м/с
(ε≈4%), так и значение σv≈14⁢м/с,
характеризующее разброс значений скоростей от выстрела к выстрелу.
Малая инструментальная погрешность в принципе позволяет более точно
измерить среднее и дисперсию, и исследовать закон распределения выстрелов
по скоростям более детально — для этого требуется набрать
бо́льшую статистику по выстрелам.

Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δ⁢v=10 м/c. Результаты
измерений для n=6 выстрелов представлены в таблице:

Усреднённый результат ⟨v⟩=163,3⁢м/с,
σv=12,1⁢м/c, σ⟨v⟩=5⁢м/с,
σполн≈11,2⁢м/с. Инструментальная
погрешность каждого измерения превышает разброс данных, поэтому в
этом опыте затруднительно сделать вывод о различии скоростей от выстрела
к выстрелу. Результат измерений скорости пули:
⟨v⟩=163±11⁢м/с,
ε≈7%. Проводить дополнительные выстрелы при такой
большой инструментальной погрешности особого смысла нет —
лучше поработать над точностью приборов и методикой измерений.

2.6 Обработка косвенных измерений

Косвенными называют измерения, полученные в результате расчётов,
использующих результаты прямых (то есть «непосредственных»)
измерений физических величин. Сформулируем основные правила пересчёта
погрешностей при косвенных измерениях.

2.6.1 Случай одной переменной

Пусть в эксперименте измеряется величина x, а её «наилучшее»
(в некотором смысле) значение равно x⋆ и оно известно с
погрешностью σx. После чего с помощью известной функции
вычисляется величина y=f⁢(x).

В качестве «наилучшего» приближения для y используем значение функции
при «наилучшем» x:

Найдём величину погрешности σy. Обозначая отклонение измеряемой
величины как Δ⁢x=x-x⋆, и пользуясь определением производной,
при условии, что функция y⁢(x) — гладкая
вблизи x≈x⋆, запишем

где f′≡d⁢yd⁢x — производная фукнции f⁢(x), взятая в точке
x⋆. Возведём полученное в квадрат, проведём усреднение
(σy2=⟨Δ⁢y2⟩,
σx2=⟨Δ⁢x2⟩), и затем снова извлечём
корень. В результате получим

Пример. Для степенной функции
y=A⁢xn имеем σy=n⁢A⁢xn-1⁢σx, откуда

σyy=n⁢σxx,или εy=n⁢εx,

то есть относительная погрешность степенной функции возрастает пропорционально
показателю степени n.

Пример. Для y=1/x имеем ε1/x=εx
— при обращении величины сохраняется её относительная
погрешность.

Упражнение. Найдите погрешность логарифма y=ln⁡x, если известны x
и σx.

Упражнение. Найдите погрешность показательной функции y=ax,
если известны x и σx. Коэффициент a задан точно.

2.6.2 Случай многих переменных

Пусть величина u вычисляется по измеренным значениям нескольких
различных независимых физических величин x, y, …
на основе известного закона u=f⁢(x,y,…). В качестве
наилучшего значения можно по-прежнему взять значение функции f
при наилучших значениях измеряемых параметров:

Для нахождения погрешности σu воспользуемся свойством,
известным из математического анализа, — малые приращения гладких
функции многих переменных складываются линейно, то есть справедлив
принцип суперпозиции малых приращений:

где символом fx′≡∂⁡f∂⁡x обозначена
частная производная функции f по переменной x —
то есть обычная производная f по x, взятая при условии, что
все остальные аргументы (кроме x) считаются постоянными параметрами.
Тогда пользуясь формулой для нахождения дисперсии суммы независимых
величин (2.7), получим соотношение, позволяющее вычислять
погрешности косвенных измерений для произвольной функции
u=f⁢(x,y,…):

σu2=fx′⁣2⁢σx2+fy′⁣2⁢σy2+…

(2.11)

Это и есть искомая общая формула пересчёта погрешностей при косвенных
измерениях.

Отметим, что формулы (2.10) и (2.11) применимы
только если относительные отклонения всех величин малы
(εx,εy,…≪1),
а измерения проводятся вдали от особых точек функции f (производные
fx′, fy′ … не должны обращаться в бесконечность).
Также подчеркнём, что все полученные здесь формулы справедливы только
для независимых переменных x, y, …

Остановимся на некоторых важных частных случаях формулы
(2.11).

Пример. Для суммы (или разности) u=∑i=1nai⁢xi имеем

σu2=∑i=1nai2⁢σxi2.

(2.12)

Пример. Найдём погрешность степенной функции:
u=xα⋅yβ⋅…. Тогда нетрудно получить,
что

σu2u2=α2⁢σx2x2+β2⁢σy2y2+…

или через относительные погрешности

εu2=α2⁢εx2+β2⁢εy2+…

(2.13)

Пример. Вычислим погрешность произведения и частного: u=x⁢y или u=x/y.
Тогда в обоих случаях имеем

εu2=εx2+εy2,

(2.14)

то есть при умножении или делении относительные погрешности складываются
квадратично.

Пример. Рассмотрим несколько более сложный случай: нахождение угла по его тангенсу

u=arctgyx.

В таком случае, пользуясь тем, что (arctgz)′=11+z2,
где z=y/x, и используя производную сложной функции, находим
ux′=uz′⁢zx′=-yx2+y2,
uy′=uz′⁢zy′=xx2+y2, и наконец

σu2=y2⁢σx2+x2⁢σy2(x2+y2)2.

Упражнение. Найти погрешность вычисления гипотенузы z=x2+y2
прямоугольного треугольника по измеренным катетам x и y.

По итогам данного раздела можно дать следующие практические рекомендации.

•

Как правило, нет смысла увеличивать точность измерения какой-то одной
величины, если другие величины, используемые в расчётах, остаются
измеренными относительно грубо — всё равно итоговая погрешность
скорее всего будет определяться самым неточным измерением. Поэтому
все измерения имеет смысл проводить примерно с одной и той же
относительной погрешностью.
•

При этом, как следует из (2.13), особое внимание
следует уделять измерению величин, возводимых при расчётах в степени
с большими показателями. А при сложных функциональных зависимостях
имеет смысл детально проанализировать структуру формулы
(2.11):
если вклад от некоторой величины в общую погрешность мал, нет смысла
гнаться за высокой точностью её измерения, и наоборот, точность некоторых
измерений может оказаться критически важной.
•

Следует избегать измерения малых величин как разности двух близких
значений (например, толщины стенки цилиндра как разности внутреннего
и внешнего радиусов): если u=x-y, то абсолютная погрешность
σu=σx2+σy2
меняется мало, однако относительная погрешность
εu=σux-y
может оказаться неприемлемо большой, если x≈y.

Источник