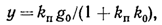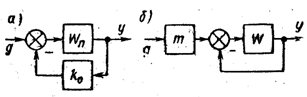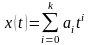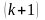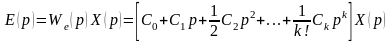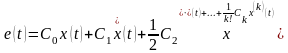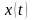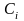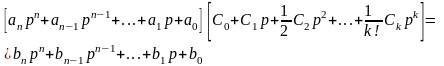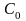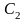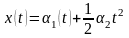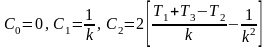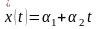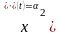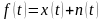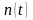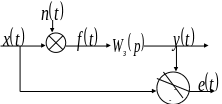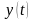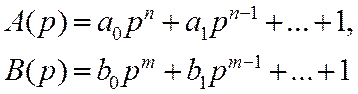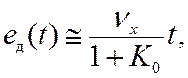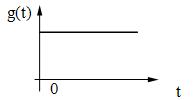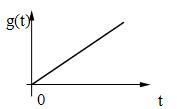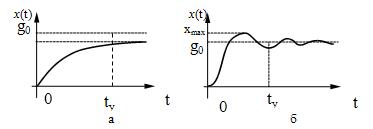В
любой реальной CАУ
невозможно точное равенство задающего
воздействия g
и управляемой величины y.
Ошибку САУ при этом вычислим согласно
уравнению ошибки как разность этих
воздействий, т.е.:

Учитывая
историю переходных процессов, ошибку
можно представить в виде двух составляющих:
установившейся (статической) и переходной
(динамической):
В
линейных САУ установившаяся (статическая)
ошибка определяется частным решением
её дифференциального уравнения, а
переходная (динамическая) ошибка –
решением однородного дифференциального
уравнения.
Таким
образом, установившуюся ошибку САУ в
неподвижном состоянии называют
статической, а ошибку при переходных
режимах – динамической.
Текущая
ошибка отработки переменного сигнала
называется динамической ошибкой САУ.
Динамическая ошибка системы изменяется
с течением времени. Она зависит от
структуры, параметров и характера
изменения воздействий САУ.
38 Повышение качества и синтез линейных сау
В
системе регулирования по отклонению
установившаяся [ошибка имеет три
составляющие:
(5—24)
|
где
—
ошибка воспроизведения задающего
воздействия
—
ошибка, вызываемая действием возмущений;
—
ошибка чувствительного элемента,
измеряющего рассогласование
Как
было показано в гл. 4, установившаяся
ошибка может [быть представлена в виде
ряда (4.3). При этом коэффициенты [ошибок
воспроизведения
вычисляют
по передаточной функции
замкнутой
системы для ошибки воспроизведения
Нужно,
заметить, что в статической системе
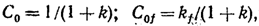
где
k
—
передаточный коэффициент разомкнутой
системна;
—
передаточный коэффициент прямой, цепи
от возмущения
до
выходной координаты у.
Следовательно,
уменьшение установившейся ошибки
постоянных значениях задающего
воздействия и возмущения достигается
увеличением передаточного коэффициента
разомкнутой системы. Однако с
увеличением статической точности в
большинстве случаев уменьшаются запасы
устойчивости I
и при значительном увеличении k
система
становится неустойчивой.
Противоречие
между статической точностью и
устойчивостью проиллюстрировано на
рис. 5.9, где сплошными линиями показаны
логарифмические частотные характеристики
разомкнутой системы с передаточной
функцией
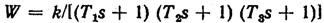
при
Если
передаточный коэффициент увеличить
до k
— 60,
то ЛАЧХ принимает положение, показанное
пунктиром. Частота среза увеличилась
и запас устойчивости по фазе уменьшился
с
до
Столь
малый запас по фазе совершенно недопустим.
При
повышении статической точности путем
увеличения передаточного коэффициента
k
разомкнутой
системы необходимы мероприятия для
обеспечения достаточного запаса
устойчивости. Они будут рассмотрены
в следующем параграфе. Возможно,
вообще говоря, создание такой структуры
системы, которая допускает неограниченное
увеличение передаточного коэффициента
k
разомкнутой
цепи 121.
Другой
путь повышения статической точности
— обеспечение астатизма. В астатической
системе младшие коэффициенты ошибки
имеют следующие значения:

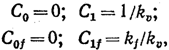
где
k0
—
передаточный коэффициент разомкнутой
системы называемый в данном случае
добротностью системы по скорости
(или коэффициентом добротности
по скорости). Таким образом, в астатической
системе отсутствует установившаяся
ошибка от постоянного задающего
воздействия и постоянных возмущений.
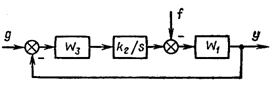
Для
астатизма относительно возмущения
интегрирующее звено должно быть введено
до точки, в которой приложено возмущение
(рис. 5.10).
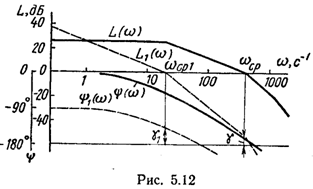
Влияние
интегрирующего звена на динамические
свойства системы
где
сплошными линиями показаны
логарифмические частотные характеристики
системы с передаточной функцией
(5.26). При введении в разомкнутую цепь
этой системы интегрирующего звена
характеристики принимают положение,
показанное пунктиром. Фазочастотная
характеристика переместилась вниз
на —90°, а амплитудно-частотная
характеристика повернулась вокруг
точки а
по
направлению часовой стрелки . В
результате запас устойчивости по фазе
уменьшился с
до
недопустимо малого значения
Система
остается устойчивой, но переходный
процесс будет сильно колебательным.
Кроме того, уменьшилась частота среза
и переходные процессы будут более
продолжительными.
Однако
в других ситуациях введение интегрирующего
звена может не только не ухудшить, а
даже улучшить динамические свойства
системы. Пусть, например, постоянные
времени системы с передаточной функцией
(5.26) имеют следующие значения: Т1
=
= 0,05 с, Т2
=
0,0025 с и T3
= 0,001 с. Логарифмические частотные
характеристики разомкнутой системы
показаны
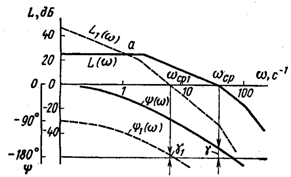
При
введении интегрирующего звена
характеристики принимают положение,
показанное пунктирными линиями. В
данном случае интегрирующее звено
уменьшило частоту среза, но запас
устойчивости по фазе увеличился с
|до
.
Хотя быстродействие системы
уменьшилось, но уменьшилась и
колебательность.
Таким
образом, при повышении статической
точности путем введения интегрирующего
звена могут оказаться необходимыми
мероприятия по сохранению запасов
устойчивости САУ.
Значительно
лучшие результаты получают при получении
астатизма с помощью изодромного звена,
т. е- звена с передаточной функцией
постоянная
времени изодрома.
Если
постоянная времени
достаточно
велика, то запас устойчивости может
быть сохранен неизменным. Уменьшение
передаточного коэффициента разомкнутой
системы должно быть скомпенсировано
увеличением коэффициента усиления
усилителя. Следует учитывать, что при
большом значении
могут
увеличиться старшие коэффициенты
ошибки.
Астатизм
САУ относительно задающего воздействия
можно обеспечить более простыми
способами: неединичной обратной
связью и масштабированием [3).
Структурная
схема системы с неединичной обратной
связью показана на рис. 5.13, а.
В
установившемся режиме регулируемая
координата связана с постоянным задающим
воздействием соотношением
(5.27)
где
kn
—
передаточный коэффициент прямой цепи
системы.
Если
выполнить основную обратную связь
системы с коэффициентом
и
система относительно задающего
воздействия будет астатической.Структурная
схема системы масштабированием входной
(величины показана на рис. 5.13, б.
Ее
особенность — наличие
усилительного
звена с передаточным коэффициентом
m
на входе. В установившемся режиме
где
k
—
передаточный коэффициент разомкнутой
системы.
При
/л = 1 -f-
УЬ
получаем
у
= g0
и
система является астатической
относительно задающего воздействия.
Недостаток
этих способов в том, что астатизм
обеспечивается только при сохранении
указанных соотношений между передаточными
коэффициентами. Неточное определение
передаточного коэффициента какого-либо
элемента системы и его изменение в
процессе эксплуатации ведут к появлению
статической ошибки. Астатизм,
достигнутый введением интегрирующего
или изодромного звена, сохраняется и
при изменении параметров системы.
Однако нужно иметь в виду, что введение
двух интегрирующих звеньев в систему,
состоящую из усилительных, апериодических
и колебательных звеньев, сделает ее
структурно-неустойчивой. Возможно
обеспечение астатизма и более высокого
порядка. При этом из-за введения большого
числа интегрирующих или изодромных
звеньев и мероприятий, обеспечивающих
требуемые динамические свойства,
структура САУ значительно усложняется.
Компенсация
внешнего воздействия (обеспечение
инвариантности). Рассмотренные выше
способы улучшения статических и
динамических свойств системы связаны
лишь с изменениями параметров
элементов САУ и структуры ее отдельных
участков, но при этом не затрагивают
принципа действия системы.
Помимо
принципа регулирования по отклонению
существует принцип регулирования
по внешнему воздействию. Значительный
эффект дает их одновременное использование.
В этом случае системы называются
комбинированными. Кроме замкнутого
контура они имеют дополнительную
цепь влияния внешнего воздействия —
возмущения или задающего.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Глава 8. Типовые законы регулирования. Одноконтурные САР
8.1. Основные типы автоматических регуляторов
Регулятор на основе усилительного звена называется П-регулятором (пропорциональный). Его положительной характеристикой является высокое быстродействие: при отклонении регулируемой величины от заданного значения регулятор выдает регулирующее воздействие, пропорциональное величине отклонения x, что обеспечивает быструю компенсацию возмущения. Существенным недостатком П-регулятора является наличие статической ошибки в переходном процессе АСР с П-регулятором (рис. 37). Статическая ошибка возникает потому, что у П-регулятора между регулируемой величиной x и регулирующим воздействием xр существует зависимость, однозначно определяемая коэффициентом K. Поэтому генерировать регулирующее воздействие xр для компенсации возмущения xв П-регулятор может только путем изменения регулируемой величины x, что и создает статическую ошибку.
Регулятор на основе интегрирующего звена (48) называется И‑регулятором:
Если xвых усилительного звена (П-регулятор) однозначно определяется величиной правой части уравнения, что является причиной возникновения статической погрешности в АСР с П-регулятором, то правая часть уравнения (48) интегрирующего звена (И-регулятор) определяет не величину, а скорость изменения xвых. Величина xвых будет изменяться до тех пор, пока правая часть уравнения (48) не станет равна нулю, т. е. пока регулируемая величина x при наличии возмущения xв не вернется к заданному значению. Следовательно, в АСР с И-регулятором не возникает статическая погрешность.
Однако у И-регулятора имеется свой недостаток сравнительно с П-регулятором: в случае возникновения возмущения регулирующее воздействие П-регулятора меняется быстрее, чем у И-регулятора с его конечной скоростью, что замедляет процесс компенсации возмущения и ухудшает критерии качества регулирования (рис. 40).
Рис. 40. Переходные процессы в АСР с П- и И-регуляторами
Таким образом, П-регулятор обеспечивает высокое быстродействие (что уменьшает динамическую ошибку), но не может обеспечить при наличии возмущения заданное значение регулируемой величины (статическая ошибка). И-регулятор, наоборот, не создает статическую ошибку, но вследствие относительно медленного изменения xр имеет большую динамическую ошибку.
Сравнивая характеристики П- и И-регуляторов можно сделать вывод: если включить усилительное и интегрирующие звенья параллельно, то автоматический регулятор будет лишен указанных недостатков. Такой регулятор называется ПИ-регулятором (рис. 41).
Рис. 41. Принципиальная схема АСР с ПИ-регулятором
Действительно, быстродействие ПИ-регулятора обеспечивает усилительное звено, а статическую ошибку снимает интегрирующее звено. Для управления производственными процессами чаще всего используются ПИ-регуляторы.
Кривая разгона идеального ПИ-регулятора показана на рис. 42 .
Уравнение ПИ-регулятора при нулевых начальных условиях имеет вид:

Отношение коэффициентов Kp1/Kp определяет степень влияния интегрирующей части, и его обратная величина называется временем изодрома Tи.

Время изодрома – это время, в течение которого интегрирующее звено изменяет регулирующее воздействие xр ПИ-регулятора на величину Dxр, равную предварительному изменению Dxр усилительного звена (рис. 42). Поэтому иногда время изодрома называют временем удвоения.
Рис. 42. График кривой разгона идеального ПИ-регулятора:
а – скачкообразное изменение входного воздействия x;
б – реакция (кривая разгона) ПИ-регулятора xр
Уравнение ПИ-регулятора можно записать как
откуда передаточная функция
Амплитудно-фазовая характеристика:

В том случае, если рассмотренные регуляторы не обеспечивают требуемое качество регулирования, необходимо увеличить интенсивность процесса компенсации возмущения. Этого можно достигнуть увеличением регулирующего воздействия, которое в свою очередь определяется коэффициентом усиления автоматического регулятора Kp
. Однако ниже будет показано, что увеличение коэффициента усиления регулятора в АСР приводит к тому, что в системе начинают генерироваться незатухающие колебания.
В связи с этим представляет интерес рассмотреть алгоритм, который реализует дифференцирующее звено.
Входной величиной любого регулятора является кривая разгона регулируемой величины (рис. 27), которая определяется величиной возмущения и передаточной функцией объекта регулирования (9). В свою очередь, регулирующее воздействие xp (рис. 27) определяется кривой разгона x и передаточной функцией регулятора.
На рис. 43 показана реакция дифференцирующего звена (Д‑регулятора) на входное воздействие в виде кривой разгона в соответствии с уравнением (51).
Рис. 43. Реакция дифференцирующего звена на кривую разгона
а –изменение входного воздействия x в виде кривой разгона;
б – реакция xр дифференцирующего звена
Из рис. 43,а следует, что дифференцирующее звено обеспечивает большее регулирующее воздействие в начале переходного процесса. Это означает, что дифференцирующий регулятор активно компенсирует возмущение и исключает возникновение незатухающих колебаний.
Если включить дифференцирующее звено параллельно ПИ‑регулятору (рис. 44), то получим ПИД-регулятор, обеспечивающий интенсивную компенсацию возмущений. При этом недостаток дифференцирующего звена (при Хвх = const, Хвых = 0 ) компенсируется усилительным и интегрирующим звеньями.
Рис. 44. Принципиальная схема АСР с ПИД-регулятором
На рис. 45 показана кривая разгона ПИД-регулятора.
Рис. 45. Кривая разгона ПИД-регулятора
На рис. 46 показаны переходные процессы на с различными регуляторами. ПИД-регулятор уменьшает динамическую ошибку сравнительно с ПИ-регулятором на 25–30%. Также можно объединить дифференцирующее звено с усилительным звеном и улучшить показатели П-регулятора, получив ПД-регулятор.

Все пять типов рассмотренных автоматических регуляторов имеют общую особенность своего функционирования – обеспечивают стабилизацию регулируемой величины после окончания переходного процесса.
8.2. Критерии качества регулирования
Качество процесса регулирования в АСР характеризуют следующие показатели (критерии) (рис. 16):
Рис. 16. Показатели качества регулирования:
1 – переходной процесс без статической ошибки;
2 – переходной процесс со статической ошибкой
1. Максимальное отклонение в процессе регулирования от заданного значения (динамическая ошибка) ΔХдин.
2. Статическая ошибка ΔХст — возможные отклонения от заданного значения по окончании переходного процесса при использовании некоторых типов регуляторов (подробнее такие АСР рассмотрены ниже).
3. Длительность переходного процесса Тр – период времени с момента начала отклонения регулируемого параметра от задания до возвращения его к заданному значению с определенной степенью точности регулирования ±Δ.
Например, если ±Δ=±25%, это означает, что для заданного значения температуры в 100 °С процесс регулирования будет завершен при достижении диапазона (100 ± 2,5) °С.
4. Степень затухания показывает характер затухания переходного процесса регулирования:
Для того, чтобы переходный процесс затухал за 2 ¸ 3 периода колебаний, степень затухания должна быть равна

5. Степень колебательности процесса m определяет характер колебательности процесса и равна отношению действительной части корня характеристического уравнения к коэффициенту при его мнимой части. Степень колебательности связана со степенью затухания следующим соотношением:
6. Интегральный квадратичный критерий – критерий, определяющий площадь под кривой переходного процесса, возведенной в квадрат (рис. 17):
Уменьшение интегрального критерия соответствует ускорению процесса регулирования.
Рис. 17. Интегральный квадратичный критерий качества регулирования
Однако все приведенные шесть критериев качества не определяют величину потерь производства при отклонениях регулируемой величины от оптимального значения в переходных процессах регулирования. Для определения таких потерь можно использовать экономический критерий.
7. Экономический критерий рассмотрим на примере, регулирования температуры химического реактора θ, когда степень превращения Q в реакторе определяется температурой (рис. 18а).
Разделим переходной процесс на равные интервалы времени Δt и запишем значения θ
в этих точках по графику (18, б). На графике (18, а) для этих температур определим уменьшение степени превращения вследствие отклонения от оптимального режима, а затем сделаем расчет потерь исходных продуктов для каждого интервала Δθ, суммируем эти потери для всего переходного процесса и представим потери в денежном выражении.
Рис. 18. Экономический критерий качества регулирования:
а – зависимость степени превращения Q от температуры θ;
б – переходный процесс регулирования температуры
Совместно со специалистом по технологии или по его заданию необходимо определить, какой из указанных критериев для рассматриваемой АСР является превалирующим, и задать максимально допустимую величину этого критерия, т. е. определить, какое качество регулирования должна обеспечить проектируемая АСР.
8.3. Выбор закона регулирования
При выборе регулятора следует определиться с группой регулирующих устройств – непрерывного, релейного или импульсного действия. Такой выбор ориентировочно может быть сделан по величине отношения запаздывания к постоянной времени объекта τ/Tоб:
· при отношении τ/Tоб меньше 0.2 целесообразно использовать регулятор релейного действия;
· если отношение τ/Tоб от 0.2 до 1.0, то нужно использовать регулятор непрерывного действия;
· при отношении τ/Tоб больше единицы можно использовать регулятор импульсного действия, или специальные регуляторы, например, регулятор («предиктор») Смита.
Затем необходимо определиться с типом регулятора, т.е. выбрать определенный закон регулирования: П-, И-, ПИ-, ПД- или ПИД-закон
8.4. Методы расчета одноконтурных САР
Как указывалось выше, качество автоматического регулирования определяется свойствами системы в целом, т. е. суммарными свойствами объекта и регулятора. Поскольку объект обычно является неизменяемой частью системы, то обеспечить определенные свойства системы, а следовательно и заданное качество регулирования, можно соответствующим подбором свойств автоматического регулятора, что зависит от параметров его настройки. В свою очередь, параметры настройки являются коэффициентами передачи в уравнении автоматического регулятора.
Таким образом, параметры настройки автоматического регулятора определяются свойствами объекта регулирования, т. е. величинами τоб, Тоб, Коб.
8.4.1. Расчет по «приближенным» формулам
Приближенные формулы для расчета параметров настройки автоматических регуляторов (Kр – коэффициент усиления; Tи – время изодрома; Тд – время дифференцирования) сведены в следующую таблицу:
Таблица 8.1. Формулы для приближенного расчета
параметров настройки регуляторов

Формулы сгруппированы в столбцы в зависимости от характера переходного процесса, который желательно получить, используя рассчитанный таким образом регулятор: апериодический или с перерегулированием в 20 %. В формулы входят следующие свойства объекта регулирования: Коб – коэффициент усиления; Тоб – постоянная времени; τоб – время запаздывания (полного).
Рис. 53. Кривые разгона:
1 – фактическая кривая разгона промышленного объекта;
2 – аппроксимированная (приближенная) кривая разгона
Необходимо отметить, что для пневматических регуляторов требуется определять не Kp, а диапазон дросселирования:
Рассмотрим методику более точного определения параметров настройки на примере расчета наиболее «популярного» регулятора – ПИ-регулятора.
8.4.2. Метод незатухающих колебаний
(метод Циглера-Никольса)
При использовании метода незатухающих колебаний [6], который иногда также называется по именам авторов методом Циглера-Никольса, поиск оптимальных параметров настройки осуществляется по величине критического коэффициента усиления П-регулятора и величине периода автоколебательного процесса.
Рис. 54. К поиску параметров настройки методом Циглера-Никольса
Расчет параметров настройки регуляторов проводится в два этапа.
1. На исследуемом объекте устанавливается П-регулятор и, последовательно увеличивая коэффициент усиления (уменьшая диапазон дросселирования), АСР выводится в режим незатухающих колебаний (автоколебаний на границе устойчивости). При этом фиксируется величина коэффициента усиления П-регулятора Ккрр и период незатухающих автоколебаний Т (рис. 54).
2. На втором этапе по величинам Кркр и Т определяются параметры настройки П-, ПИ- и ПИД-регуляторов:
Метод незатухающих колебаний не требует сложных вычислений, но имеет свои характерные недостатки:
· получить Кркр и Т можно только на действующем объекте, оснащенном АСР с П-регулятором;
· не все объекты химической технологии допускают режим автоколебаний;
· практически трудно уловить момент начала автоколебаний.
Данные недостатки имеют место лишь при настройке регулятора методом Циглера-Никольса непосредственно на действующем объекте. Если заменить реальный объект его математической моделью, данный метод лишается указанных недостатков, кроме того, моделирование позволяет на порядок ускорить процесс поиска параметров настройки. Но для выполнения моделирования требуется достаточно точное математическое описание объекта регулирования, а получить его удается не всегда.
8.4.3. Метод расширенных частотных характеристик
Уравнение ПИ-регулятора (65) или (66):
Передаточная функция ПИ-регулятора:

Знак «минус» указывает, что действие регулятора направлено против возмущения.
Из передаточной функции получаем амплитудно-фазовую характеристику ПИ-регулятора путем замены p на iw:

Так как по формуле Эйлера


с затуханием за три периода
Заменив iw на комплексную переменную (-mw+iw), получаем расширенную амплитудно-фазовую характеристику (РАФХ)Ю

Расширенными такие характеристики называются потому, что они как бы «расширены» по отношению к обычной АФХ (рис. 56).
Предположим, что объект регулирования имеет передаточную функцию второго порядка следующего вида:

Для дальнейшего математического моделирования АСР передаточную функцию необходимо преобразовать:

Рис. 56. АФХ объекта регулирования с самовыравниванием:
1 – обычная; 2 – расширенная
Расширенная амплитудно-фазовая характеристика объекта регулирования при замене p на (-mw+iw) будет иметь вид:



Где Rоб(m,w) -расширенная амплитудно-частотная характеристика объекта; Fоб(m,w) -расширенная фазочастотная харктеристика объекта. Величина 40w в выражении для Fоб (m,w) опеделяет угол в радианах и для пересчета в градусы неоходимо 40w умножить на 57,3
Условием нахождения замкнутой АСР на границе устойчивости является уравнение:

Аналогично, исходным уравнением для получения заданной степени колебательности m, а следовательно, определенной степени затухания y, является соотношение:
Это соотношение двух комплексных чисел возможно в том случае, если произведение модулей РАФХ равно единице, а аргументы (фазы) равны между собой, т. е.

Решая эти уравнения относительно S0 и Kp, получаем:


Обычно принимают степень колебательности m = 0,221, что соответствует степени затухания ψ=0,75 и обеспечивает затухание процесса регулирования примерно за три периода. Тогда

Уравнения для определения параметров настройки ПИ-регулятора можно преобразовать:


Подставляя в приведенные уравнения численные значения частоты w от 0 до значения, когда S0 становится отрицательной величиной, строим на плоскости параметров настройки кривую равной степени колебательности


Пример кривых равной степени колебательности в плоскости параметров настройки ПИ-регулятора показан на рис. 57. Графики процессов регулирования с различными параметрами настройки ПИ-регулятора при m = 0,221 показаны на рис. 58. Все процессы регулирования, показанные на рис. 58, реализованы ПИ-регулятором с параметрами настройки, полученными по кривой равной степени колебательности в точках 1, 2, 3, 4 (рис. 57), и все имеют m = 0,221, т. е. затухают примерно за три периода, но обладают существенно различным характером.
В связи с этим возникает задача определения оптимальных параметров настройки на кривой равной степени колебательности.
Рис. 57. Кривые равной степени колебательности
В качестве критерия оптимальности выбираем продолжительность переходного процесса – время регулирования (т. е. быстродействие АСР) и отсутствие постоянной или врéменной статической ошибки. Это исключает из рассмотрения параметры настройки в точке 4 (параметры настройки П-регулятора) и в точке 3 (врéменная статическая ошибка) (рис. 58).
Рис. 58. Графики процессов регулирования для ПИ-регулятора
с различными параметрами настройки в точках 1, 2, 3 и 4
при степени колебательности m =0,221
Быстродействие автоматического регулятора прежде всего зависит от величины регулирующего воздействия, которое для ПИ-регулятора, как следует из уравнения (65), прямо пропорционально величине коэффициента усиления Kp и обратно пропорционально времени изодрома Tи. Расчеты показывают, что если двигаться по кривой равной степени колебательности вправо, то величина регулирующего воздействия при прочих равных условиях сначала возрастает и достигает максимального значения на кривой равной степени колебательности вблизи ее вершины, когда
а затем начинает уменьшаться в связи с резким увеличением Tи (рис. 57).
Рис. 59. Выбор оптимальных параметров настройки
Таким образом, оптимальные параметры настройки ПИ-регулятора находятся в точке 2 на кривой равной степени колебательности (рис. 59).
Источник
Плютто В. П., Дубровский И. И. Элементы теории управления химико-технологическими процессами и системами. Конспект лекций: Учеб. пособие – М.: РХТУ им. Д. И. Менделеева, 2003. – 127 с.
Помимо статистических ошибок точность работы систем радиоавтоматики характеризуется динамическими и переходными ошибками.
Динамическая ошибка – ошибка в установившемся режиме работы системы при действии на неё нестационарного сигнала.
Переходная ошибка – ошибка при работе системы в переходном процессе, который возникает при отработке начального рассогласования.
Динамическая точность работы систем радиоавтоматики определяется при медленно изменяющихся входных сигналах (воздействия, число производных от которых ограничено).
Cигнал 



Переходные процессы в системах радиоавтоматики затухают значительно быстрее по сравнению с изменением медленно изменяющегося сигнала, поэтому и достигается установившейся динамический режим работы системы.
По определению передаточной функции рассогласования преобразование Лапласа для ошибки системы:

или в области действительного переменного

Число слагаемых в последнем выражении ограничено, так как сигнал 

1)
2) Вторым способом коэффициенты ошибок находятся путём деления числителя передаточной функции ошибки на её знаменатель.
3) Для реализации третьего способа представим передаточную функцию ошибки в виде:

Перемножив полином знаменателя на (6.1), получим:

Приравняв коэффициенты при одинаковых степенях 

2 Влияние на ошибку системы коэффициента усиления системы и введение форсирующего звена
В инженерных расчётах коэффициенты ошибок удобнее рассчитывать через коэффициенты передаточной функции разомкнутой системы:

где 
Первое слагаемое в выражении (6.2) называют ошибкой по положению, а коэффициент 


В астатических системах первых коэффициентов ошибок равны нулю, где — порядок астатизма системы радиоавтоматики.
При анализе качества работы систем радиоавтоматики помимо вычисления ошибок при медленно изменяющихся сигналах приходится оценивать точность и при гармонических воздействиях. В этом случае нельзя применять метод коэффициентов ошибок, так как число производных от гармонического сигнала не ограничено. При этом для расчёта ошибок необходимо использовать частотные характеристики. По амплитудно-частотной характеристике ошибки вычисляется амплитуда колебаний ошибки, по фазочастотной характеристике – сдвиг колебаний ошибки относительно входного сигнала.
Пример 6.1. Найти динамическую ошибку при входном сигнале 

Преобразуем 
Коэффициент астатизма 



Подставим данные в выражение (2), получим:
Вывод. При увеличении коэффициента усиления системы и введении форсирующего звена ошибка уменьшается, увеличение же постоянных времени инерционных звеньев ухудшает динамическую ошибку системы.
3 Средняя квадратическая ошибка системы.
В большинстве случаев закон распределения ошибки системы можно считать гауссовским, поэтому для расчёта составляющих суммарной средней квадратической ошибки достаточно учесть математическое ожидание и корреляционную функцию ошибки или её спектральную плотность.
На вход системы подаётся воздействие вида:

где
— случайный сигнал; 



Рис. 7.1. К определению суммарной ошибки
На приведённом рисунке круг означает сумматор, а сектор круга со знаком минус означает операцию вычитания.
Преобразование Лапласа для суммарной ошибки:

Вывод. Суммарная ошибка состоит из двух составляющих, одна из которых, определяющая точность воспроизведения сигнала, зависит от передаточной функции ошибки, вторая, обусловленная действием помехи, — от передаточной функции замкнутой системы.
Предположим, что сигнал и помеха являются стационарными случайными функциями. Тогда математическое ожидание помехи 

где


Математическое ожидание суммарной ошибки рассчитывают по теореме о конечном значении функции:

-
Динамическая ошибка сау. Нахождение коэффициентов ошибок.
Помимо статистических
ошибок точность работы систем
радиоавтоматики характеризуется
динамическими и переходными ошибками.
Динамическая
ошибка – ошибка в установившемся режиме
работы системы при действии на неё
нестационарного сигнала.
Переходная ошибка
– ошибка при работе системы в переходном
процессе, который возникает при отработке
начального рассогласования.
Динамическая
точность работы систем радиоавтоматики
определяется при медленно изменяющихся
входных сигналах (воздействия, число
производных от которых ограничено).
Cигнал
относится
к медленно изменяющемуся воздействию,
так как число производных от этого
сигнала неравных нулю, равно
,
а
-я
производная равна нулю. Гармонический
сигнал не является медленно изменяющимся,
так как число производных от него равно
.
Переходные процессы
в системах радиоавтоматики затухают
значительно быстрее по сравнению с
изменением медленно изменяющегося
сигнала, поэтому и достигается
установившейся динамический режим
работы системы.
По определению
передаточной функции рассогласования
преобразование Лапласа для ошибки
системы:
(6.1)
или
в области действительного переменного
(6.2)
Число слагаемых
в последнем выражении ограничено, так
как сигнал
является медленно изменяющимся
воздействием. Для нахождения неизвестных
коэффициентов
,
которые называются коэффициентами
ошибки, известны три способа.
1)
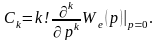
2) Вторым способом
коэффициенты ошибок находятся путём
деления числителя передаточной функции
ошибки на её знаменатель.
3) Для реализации
третьего способа представим передаточную
функцию ошибки в виде:
.
Перемножив полином
знаменателя на (6.1), получим:
(6.3)
Приравняв
коэффициенты при одинаковых степенях
слева и справа в выражении (6.3), определим
формулы для последовательного вычисления
коэффициентов ошибок:

2 Влияние на ошибку системы коэффициента усиления системы и введение форсирующего звена
В
инженерных расчётах коэффициенты ошибок
удобнее рассчитывать через коэффициенты
передаточной функции разомкнутой
системы:
,
(6.4)
где
—
порядок астатизма системы.
Первое
слагаемое в выражении (6.2) называют
ошибкой по положению, а коэффициент
-коэффициентом
ошибки по положению, второе слагаемое
– ошибкой по скорости, а коэффициент
—
коэффициентом ошибки по скорости.
Аналогично, третье слагаемое в (6.2)
называют ошибкой по ускорению, а
коэффициент
— коэффициентом ошибки по ускорению.
В
астатических системах
первых коэффициентов ошибок равны нулю,
где
—
порядок астатизма системы радиоавтоматики.
При
анализе качества работы систем
радиоавтоматики помимо вычисления
ошибок при медленно изменяющихся
сигналах приходится оценивать точность
и при гармонических воздействиях. В
этом случае нельзя применять метод
коэффициентов ошибок, так как число
производных от гармонического сигнала
не ограничено. При этом для расчёта
ошибок необходимо использовать частотные
характеристики. По амплитудно-частотной
характеристике ошибки вычисляется
амплитуда колебаний ошибки, по
фазочастотной характеристике – сдвиг
колебаний ошибки относительно входного
сигнала.
Пример
6.1. Найти динамическую ошибку при входном
сигнале
следящей системы, передаточная функция
которой в разомкнутом состоянии
.
Преобразуем
.
Коэффициент
астатизма
.Тогда
,
,
.
Подставим
данные в выражение (2), получим:
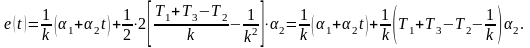
Вывод.
При увеличении коэффициента усиления
системы и введении форсирующего звена
ошибка уменьшается, увеличение же
постоянных времени инерционных звеньев
ухудшает динамическую ошибку системы.
3
Средняя
квадратическая ошибка системы.
В
большинстве случаев закон распределения
ошибки системы можно считать гауссовским,
поэтому для расчёта составляющих
суммарной средней квадратической ошибки
достаточно учесть математическое
ожидание и корреляционную функцию
ошибки или её спектральную плотность.
На
вход системы подаётся воздействие вида:
,
где
—
случайный сигнал;
— случайная помеха.
—
cуммарная
ошибка системы, где
— выходной сигнал системы.
Рис.
7.1. К определению суммарной ошибки
На
приведённом рисунке круг означает
сумматор, а сектор круга со знаком минус
означает операцию вычитания.
Преобразование
Лапласа для суммарной ошибки:
(7.1)
Вывод.
Суммарная ошибка состоит из двух
составляющих, одна из которых, определяющая
точность воспроизведения сигнала,
зависит от передаточной функции ошибки,
вторая, обусловленная действием помехи,
— от передаточной функции замкнутой
системы.
Предположим,
что сигнал и помеха являются стационарными
случайными функциями. Тогда математическое
ожидание помехи
,
а случайный сигнал представим в виде:
,
где
—
математическое ожидание сигнала;
— случайная составляющая сигнала.
Математическое
ожидание суммарной ошибки рассчитывают
по теореме о конечном значении функции:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение динамических ошибок (по
скорости, по ускорению) для статической и астатических систем.
Точность АС
характеризуется величиной ошибки в установившемся режиме и зависит от характера
воздействия, а также структуры и параметров системы.
Реальные воздействия
в радиотехнических следящих системах описывается сложными (случайными)
функциями времени. Однако при анализе точности управления часто используют
простые детерминированные воздействия: постоянное ступенчатое, линейное,
квадратичное и другие. Это позволяет упростить анализ и в то же время сохранить
в модели задающего воздействия наиболее существенные признаки (начальное
значение, скорость изменения, ускорение). Большинство систем радиоавтоматики
описываются передаточными функциями вида
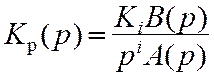
где Ki — общее усиление
разомкнутой системы, i – число интегрирующих
звеньев, определяющее порядок астатизма системы;
– полиномы, порядок которых определяется числом типовых
звеньев (n и m соответственно инерционных и форсирующих), а
коэффициенты полиномов – постоянными времени типовых звеньев.
11.1. Статические ошибки
Ошибка системы при постоянном
(ступенчатом) воздействии x(t)=x0=const при t³0
называется статическойeст.
Для установившейся
ошибки, учитывая, что изображение X(p)=x0/p,
запишем:
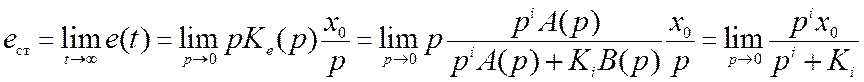
Для статической
системы (не содержащей интегрирующих звеньев) статическая ошибка равна
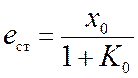
Таким образом, в
статических системах установившееся значение управляемой переменной не равно
заданному: меньше на величину ошибки, значение которой обратно пропорционально
усилению К0 по постоянному току (обычно К0>>1).
Для астатических
систем (i ³ 1) ошибка при постоянном воздействии
,
так как числитель в (11.2) равен нулю, а знаменатель равен
Кi.
Отсутствие
статической ошибки обусловило название таких систем – астатические.
11.2. Динамические ошибки
Ошибка,
характеризующая точность замкнутой системы при меняющемся воздействии,
называется динамической eд(t).
Любое детерминированное
воздействие (при условии существования его производных d(k)/dt(k),
k=1, 2, …) можно представить в виде ряда
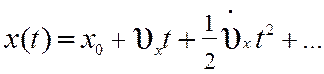
где x0 — начальное значение, — скорость изменения,
— ускорение и т. д.
Для вычисления
динамических ошибок при типовых воздействиях (линейном и квадратическом)
представим выражение для ошибки в операторной форме:
(11.5)
Используя разложение
передаточной функции Ke(p) в ряд Маклорена по степеням
переменной р, перепишем (11.5) в виде
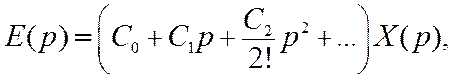
где C0, C1, C2,
… — коэффициенты ошибок, определяемые
как
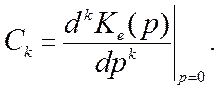
Установившееся
значение ошибки при произвольном воздействии x(t)
на основании (11.6) определяется временным рядом
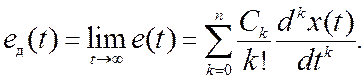
Чем меньше
коэффициенты ошибок, тем выше точность системы при произвольном
детерминированном воздействии. При вычислении коэффициентов Ck
обычно ограничиваются только первыми тремя (для систем с астатизмом не выше
второго порядка).
Коэффициент C0
в соответствии с (11.7) равен
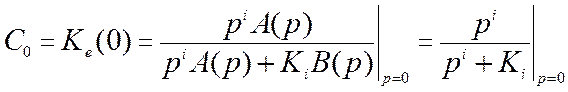
Для статических
систем (i=0) C0=1/(1+K0), а для
астатических систем C0=0.
Определим динамические
ошибки типовых систем при линейном воздействии (изменение с постоянной
скоростью) x(t)=nxt.
В соответствии с
формулой (11.8) динамическая ошибка (ошибка по скорости) определяется как
.
Для статической
системы она равна
так как вклад составляющей C1nx
значительно меньше, чем C0 x(t), которая растет
линейно со временем. Таким образом, скоростная ошибка в статических системах
накапливается со временем со скоростью nx/(1+K0), что делает неприемлемым использование
таких систем при меняющемся воздействии. Для астатических систем C0=0 и скоростная ошибка
.
Нахождение
коэффициента ошибки C1 с использованием формулы (11.7)
затруднительно. Более простой способ его вычисления основан на сравнении
точного выражения для передаточной функции Ke(p) и
аппроксимирующего ее ряда:

Уравнение (11.9)
можно представить в виде
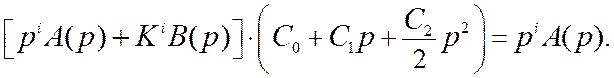
Полагая i= 1 (астатическая система первого порядка) и приравнивая
коэффициенты при переменной p в левой и правой частях уравнения, находим
или C1=1/K1, так как C0=0.
Таким образом,
скоростная ошибка системы первого порядка астатизма eд=nx/K1
определяется усилением разомкнутой системы K1 и не зависит от
времени. Параметр K1, имеющий размерность c –1,
называется добротностью системы по скорости (чем выше добротность, тем
точнее система).
Для астатической
системы второго порядка скоростная ошибка равна нулю, так как оба коэффициента C0=C1=0.
Равенство C1=0 вытекает из уравнения (11.10), так как в
правой части уравнения не содержится слагаемого, в которое входит переменная p
(есть только с p2 и выше).
Оценим динамические
ошибки типовых систем при квадратичном воздействии (изменение с постоянным
ускорением).
В соответствии с (11.8)
для динамической ошибки (ошибки по ускорению) запишем
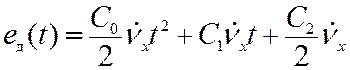
Для статической
системы ошибка по ускорению равна
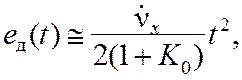
так как составляющие ошибки с коэффициентами C1 и C2
вносят пренебрежимо малый вклад в результирующую ошибку. Накопление ошибки по
квадратичному закону исключает применение статических систем при наличии
ускорения.
Для системы первого
порядка астатизма ошибка по ускорению равна
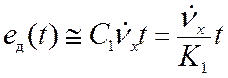
(вкладом составляющей можно
пренебречь). Накопление ошибки со временем (со скоростью ) не позволяет применять такие
системы при наличии ускорения. Для астатической системы второго порядка ошибка
по ускорению равна
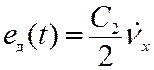
Определение
коэффициента ошибки C2 с использованием уравнения (11.7)
сводится к приравниванию коэффициентов при p2 в обеих частях
уравнения:
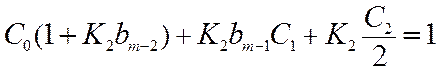
Откуда
C2/2=1/K2, так как C0=C1=0.
Динамическая ошибка
- Динамическая ошибка
-
динамическая погрешность, динамическое отклонение, разность между требуемым и действительным значениями регулируемой величины, возникающая и измеряющаяся в процессе регулирования; см. Регулирование автоматическое.
Большая советская энциклопедия. — М.: Советская энциклопедия.
1969—1978.
Смотреть что такое «Динамическая ошибка» в других словарях:
-
динамическая ошибка — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN dynamic errordynamic lag … Справочник технического переводчика
-
динамическая ошибка — dinaminis nuokrypis statusas T sritis automatika atitikmenys: angl. dynamic error; transient deviation vok. dynamischer Fehler, m; vorübergehende Abweichung, f rus. динамическая ошибка, f; динамическая погрешность, f; динамическое отклонение, n… … Automatikos terminų žodynas
-
Динамическая ошибка распознавания опасного состояния оборудования (динамическая ошибка первого рода) — 2.22. Динамическая ошибка распознавания опасного состояния оборудования (динамическая ошибка первого рода): пропуск своевременного распознавания опасного состояния оборудования, вызванный тем, что период мониторинга (диагностирования) превышает… … Словарь-справочник терминов нормативно-технической документации
-
динамическая погрешность — динамическая ошибка — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы динамическая ошибка EN dynamic error … Справочник технического переводчика
-
динамическая погрешность — dinaminis nuokrypis statusas T sritis automatika atitikmenys: angl. dynamic error; transient deviation vok. dynamischer Fehler, m; vorübergehende Abweichung, f rus. динамическая ошибка, f; динамическая погрешность, f; динамическое отклонение, n… … Automatikos terminų žodynas
-
СА 03-001-05: Стандарт ассоциации. Центробежные насосные и компрессорные агрегаты опасных производств. Эксплуатационные нормы вибрации — Терминология СА 03 001 05: Стандарт ассоциации. Центробежные насосные и компрессорные агрегаты опасных производств. Эксплуатационные нормы вибрации: 2.1. Агрегат: совокупность механически соединенных механизмов, узлов, машин и конструкций,… … Словарь-справочник терминов нормативно-технической документации
-
СА 03-002-05: Стандарт ассоциации. Системы мониторинга агрегатов опасных производственных объектов. Общие технические требования — Терминология СА 03 002 05: Стандарт ассоциации. Системы мониторинга агрегатов опасных производственных объектов. Общие технические требования: 2.1. Агрегат : совокупность механически соединенных механизмов, узлов, машин и конструкций, работающих… … Словарь-справочник терминов нормативно-технической документации
-
Регулирование автоматическое — (от нем. regulieren регулировать, от лат. regula норма, правило) поддержание постоянства (стабилизация) некоторой регулируемой величины, характеризующей технический процесс, либо её изменение по заданному закону (программное… … Большая советская энциклопедия
-
динамическое отклонение — динамическая ошибка — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы динамическая ошибка EN dynamic… … Справочник технического переводчика
-
dinaminis nuokrypis — statusas T sritis automatika atitikmenys: angl. dynamic error; transient deviation vok. dynamischer Fehler, m; vorübergehende Abweichung, f rus. динамическая ошибка, f; динамическая погрешность, f; динамическое отклонение, n pranc. écart… … Automatikos terminų žodynas
Динамическая ошибка
Cтраница 1
Динамическая ошибка в этом случае носит колебательно-затухающий характер.
[1]
Динамическая ошибка представляет собой дополнительное рассогласование между входной и выходной величинами, появляющееся при движении следящей системы. Эта ошибка определяется, с одной стороны, формой входного сигнала, с другой — инерционностью элементов, составляющих следящую систему.
[2]
Динамическая ошибка в процессе регулирования определяется в основном величиной коэффициента колебательности т а / для доминирующих комплексных полюсов и степенью близости к началу плоскости р остальных полюсов и нулей замкнутой системы. При этом близкие к началу плоскости р нули увеличивают перерегулирование, а близкие, но не доминирующие полюсы — его уменьшают.
[4]
Динамическая ошибка в этом случае носит колебательно-затухающий характер.
[5]
Динамические ошибки в неустановившихся режимах движения могут дополнительно увеличиваться за счет переходных составляющих. Так как при уменьшении ап, ас и ат колебательность системы увеличивается, переходные составляющие ошибки могут возрастать, в то время как установившаяся динамическая ошибка ( 11 — 27) при этом уменьшается.
[6]
Динамические ошибки возникают в установившемся режиме и обусловлены параметрами следящей системы и характером изменения измеряемого параметра. Флук-туационные ошибки вызваны влиянием помех и возмущений, которые воздействуют на следящую систему.
[7]
Динамическая ошибка интегрирующих скоростных счетчиков, датчик которых реагирует на мгновенный расход, будет значительно больше, чем объемных счетчиков, отмеряющих определенные объемные порции потока.
[9]
Динамическая ошибка не накапливается в процессе работы ШД и, как правило, остается в пределах я эл.
[10]
Динамическая ошибка, ее величина, характер изменения во времени может быть различной в зависимости от параметров системы автоматического регулирования.
[11]
Динамические ошибки в равной степени присущи как астатическим, так и статическим САУ.
[12]
Динамические ошибки равны: стационарные — до 2 мкм, переходные — до 3 мкм. Прочие ошибки не превышают 4 мкм. Сложение этих ошибок как случайных величин с нормальным законом распределения в сумме дает ошибку в 13 мкм.
[13]
Динамическая ошибка, ее величина, характер изменения во времени может быть различной в зависимости от параметров системы автоматического регулирования.
[14]
Динамические ошибки в равной степени присущи как астатическим, так и статическим САУ.
[15]
Страницы:
1
2
3
4
Точность систем управления является
важнейшим показателем их качества. Чем выше точность, тем выше качество
системы. Однако предъявление повышенных требований к точности вызывает
неоправданное удорожание системы, усложняет ее конструкцию. Недостаточная
точность может привести к несоответствию характеристик системы условиям
функционирования и необходимости ее повторной разработки. Поэтому на этапе
проектирования системы должно быть проведено тщательное обоснование требуемых
показателей точности.
В этом разделе рассматриваются методы
определения ошибок, возникающих при работе систем управления с детерминированными
входными воздействиями. Вначале анализируются ошибки систем в переходном
режиме. Затем особое внимание уделено простым способам расчета ошибок систем в
установившемся режиме. Будет показано, что все системы управления можно разделить
по величине установившихся ошибок на системы без памяти, так называемые статические
системы, и системы, обладающие памятью, – астатические
системы управления.
Типовые
входные воздействия
Для оценки качества работы систем
управления рассматривают их поведение при некоторых типовых воздействиях.
Обычно такими воздействиями служат следующие три основные вида функций:
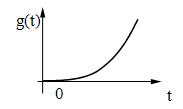
а) ступенчатое воздействие: g(t) = 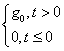
;
б) линейное воздействие: g(t) = t , t > 0
; ;
в) квадратичное воздействие:
/2 , t > 0 ;
g(p) = .
В
некоторых случаях рассматривают обобщенное полиномиальное воздействие:
, t > 0.
Ступенчатое воздействие является одним
из простейших, но именно с его помощью определяется ряд важных свойств систем
управления, связанных с видом переходного процесса. Линейное и квадратичное
воздействия часто бывают связаны с задачами слежения за координатами
движущегося объекта. Тогда линейное воздействие соответствует движению объекта
с постоянной скоростью; квадратичное — движению объекта с постоянным ускорением.
Переходные процессы при типовых
воздействиях можно построить следующим образом. Пусть задана передаточная
функция замкнутой системы управления W(p). Тогда
x(p)
= W(p) g(p),
где g(p) – изображение соответствующего воздействия.
Например, если , то
и для g(t) = g0
получим .
С помощью вычетов или по таблицам
находим обратное преобразование Лапласа и получаем вид переходного процесса x(t)
для заданного входного воздействия:
,
где Res
x(p)
– вычет функции x(p)
в точке a.
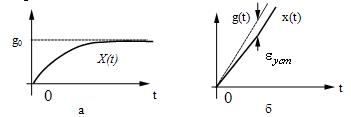
Обычно реакция системы на ступенчатое
воздействие имеет вид, показанный на рис. 21,а или рис. 21,б.
Рис.
21.
Переходный процесс,
как правило, характеризуют двумя параметрами – длительностью переходного
процесса (временем установления) и величиной перерегулирования.
Под временем установления tу
понимают временной интервал, по истечении которого отклонение |x(t) — xуст
| выходного процесса от установившегося значения xуст не
превышает определенную величину, например, 0,1gо. Время
установления является важным параметром САУ, позволяющим оценить ее быстродействие.
Величину tу можно оценить приближенно по амплитудно-частотной
характеристике системы. При заданной частоте среза . Для оценки качества системы
используется также величина перерегулирования, определяемая соотношением .
В зависимости от
характера собственных колебаний системы переходный процесс в ней может быть
колебательным, как это показано на рис. 21, б, или плавным гладким, называемым
апериодическим (рис. 21,а). Если корни характеристического уравнения системы
действительны, то переходный процесс в ней апериодический. В случае
комплексных корней характеристического уравнения собственные колебания
устойчивой системы управления являются затухающими гармоническими и переходный
процесс в системе имеет колебательный характер.
При малом запасе устойчивости САУ ее
собственные колебания затухают медленно, и перерегулирование в переходном режиме
получается значительным. Как следствие, величина перерегулирования может
служить мерой запаса устойчивости системы. Для многих систем запас
устойчивости считается достаточным, если величина перерегулирования .
Установившийся
режим
При проектировании систем управления
часто требуется оценить ошибку слежения в установившемся режиме . В зависимости от
вида воздействия и свойств системы эта ошибка может быть нулевой, постоянной
или бесконечно большой величиной.
Очень важно, что величина
установившейся ошибки может быть легко найдена с помощью теоремы о предельном
значении оригинала: .
При использовании этой теоремы нужно
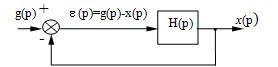
выразить величину ошибки e (p) через g(p). Для этого рассмотрим
структурную схему замкнутой системы управления (рис. 22).
Рис.
22
Очевидно, e (p) = g(p) — x(p)
= g(p) — H(p)e(p). Отсюда или e (p) = He(p)g(p)
, где He(p) = называется передаточной функцией
системы управления от входного воздействия g(p) к ошибке слежения e(p).
Таким образом, величину установившейся ошибки можно найти с помощью следующего
соотношения:
,
где He(p) = 1/(1+H(p));
g(p) — изображение типового входного воздействия.
Пример 1. Рассмотрим
систему управления, в составе которой нет интеграторов, например,
.
Найдем величину установившейся
ошибки при ступенчатом входном воздействии g(t) = g0, t ³ 0.
В этом случае
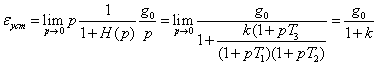
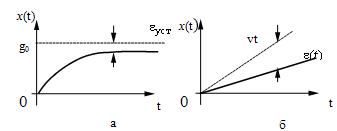
Предположим теперь, что входное
воздействие изменяется линейно t или
.
Тогда . Соответствующие входные воздействия и
переходные процессы можно представить графиками на рис. 23,а и б.
Рис.
23
Пример 2. Рассмотрим
теперь систему, содержащую один интегратор. Типичным примером может быть
система сервопривода (рис. 6) с .
Для ступенчатого воздействия g(t) = g0
или g(p) = получим
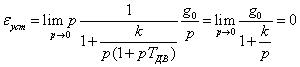
При линейном входном воздействии
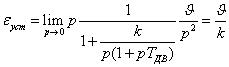
Такие процессы можно проиллюстрировать
соответствующими кривыми на рис.24, а и б.
Рис.
24
Пример 3.
Рассмотрим систему с двумя интеграторами. Пусть, например, . При ступенчатом
воздействии 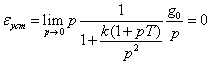
При линейном 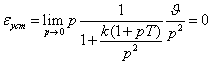
Наконец, если входное воздействие
квадратичное g(t) = at2/2 (g(p) = a/p3),
то
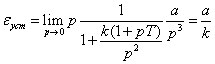
Таким образом, в системе с двумя
интеграторами может осуществляться слежение за квадратичным входным
воздействием при конечной величине установившейся ошибки. Например, можно
следить за координатами объекта, движущегося с постоянным ускорением.
Статические
и астатические системы управления
Анализ рассмотренных примеров
показывает, что системы управления, содержащие интегрирующие звенья, выгодно
отличаются от систем без интеграторов. По этому признаку все системы делятся на
статические системы, не содержащие интегрирующих звеньев, и астатические
системы, которые содержат интеграторы. Системы с одним интегратором называются
системами с астатизмом первого порядка. Системы с двумя интеграторами –
системами с астатизмом второго порядка и т.д.
Для статических систем даже при
неизменяющемся воздействии g(t) = g0 установившаяся ошибка имеет
конечную величину g(t) = g0 . В системах с астатизмом первого
порядка при ступенчатом воздействии установившаяся ошибка равна нулю, но при линейно
изменяющемся воздействии . Наконец, в системах с астатизмом
второго порядка ненулевая установившаяся ошибка появляется только при
квадратичных входных воздействиях g(t) = at2 /2 и
составляет величину eуст =
a/k.
Какие же физические причины лежат в
основе таких свойств астатических систем управления?
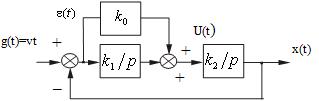
Рассмотрим систему управления с
астатизмом второго порядка (рис. 25)
Рис.
25
Пусть входной сигнал системы управления
изменяется линейно:
t. Как было
установлено, в такой системе установившаяся ошибка равна нулю, т.е. e
(t) =0. Каким же образом система работает при нулевом сигнале ошибки? Если x(t)
= t , то на
входе второго интегратора должен быть сигнал . Действительно, при нулевом
рассогласовании e (t) =0 в системе с интеграторами
возможно существование ненулевого выходного сигнала первого интегратора . Первый интегратор
после окончания переходного процесса «запоминает» скорость изменения входного
воздействия и в дальнейшем работа системы управления осуществляется по
«памяти». Таким образом, физическим объяснением такого значительного различия
статических и астатических систем является наличие памяти у астатических систем
управления.
*
* *
Итак, существуют простые возможности
определения важнейшего показателя систем управления – величины их динамических
ошибок. Детальный анализ переходных процессов в системах управления обычно
выполняют с помощью моделирования на ПЭВМ. Вместе с тем величины
установившихся ошибок легко находятся аналитически. При этом астатические
системы управления, т.е. системы с интеграторами, имеют существенно лучшие
показатели качества по сравнению со статическими системами.
В
любой реальной CАУ
невозможно точное равенство задающего
воздействия g
и управляемой величины y.
Ошибку САУ при этом вычислим согласно
уравнению ошибки как разность этих
воздействий, т.е.:

Учитывая
историю переходных процессов, ошибку
можно представить в виде двух составляющих:
установившейся (статической) и переходной
(динамической):
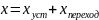
В
линейных САУ установившаяся (статическая)
ошибка определяется частным решением
её дифференциального уравнения, а
переходная (динамическая) ошибка –
решением однородного дифференциального
уравнения.
Таким
образом, установившуюся ошибку САУ в
неподвижном состоянии называют
статической, а ошибку при переходных
режимах – динамической.
Текущая
ошибка отработки переменного сигнала
называется динамической ошибкой САУ.
Динамическая ошибка системы изменяется
с течением времени. Она зависит от
структуры, параметров и характера
изменения воздействий САУ.
38 Повышение качества и синтез линейных сау
В
системе регулирования по отклонению
установившаяся [ошибка имеет три
составляющие:
(5—24)
|
где
—
ошибка воспроизведения задающего
воздействия
—
ошибка, вызываемая действием возмущений;
—
ошибка чувствительного элемента,
измеряющего рассогласование
Как
было показано в гл. 4, установившаяся
ошибка может [быть представлена в виде
ряда (4.3). При этом коэффициенты [ошибок
воспроизведения
вычисляют
по передаточной функции
замкнутой
системы для ошибки воспроизведения
Нужно,
заметить, что в статической системе
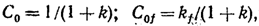
где
k
—
передаточный коэффициент разомкнутой
системна;
—
передаточный коэффициент прямой, цепи
от возмущения
до
выходной координаты у.
Следовательно,
уменьшение установившейся ошибки
постоянных значениях задающего
воздействия и возмущения достигается
увеличением передаточного коэффициента
разомкнутой системы. Однако с
увеличением статической точности в
большинстве случаев уменьшаются запасы
устойчивости I
и при значительном увеличении k
система
становится неустойчивой.
Противоречие
между статической точностью и
устойчивостью проиллюстрировано на
рис. 5.9, где сплошными линиями показаны
логарифмические частотные характеристики
разомкнутой системы с передаточной
функцией
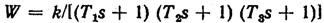
при
Если
передаточный коэффициент увеличить
до k
— 60,
то ЛАЧХ принимает положение, показанное
пунктиром. Частота среза увеличилась
и запас устойчивости по фазе уменьшился
с
до
Столь
малый запас по фазе совершенно недопустим.
При
повышении статической точности путем
увеличения передаточного коэффициента
k
разомкнутой
системы необходимы мероприятия для
обеспечения достаточного запаса
устойчивости. Они будут рассмотрены
в следующем параграфе. Возможно,
вообще говоря, создание такой структуры
системы, которая допускает неограниченное
увеличение передаточного коэффициента
k
разомкнутой
цепи 121.
Другой
путь повышения статической точности
— обеспечение астатизма. В астатической
системе младшие коэффициенты ошибки
имеют следующие значения:

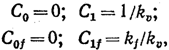
где
k0
—
передаточный коэффициент разомкнутой
системы называемый в данном случае
добротностью системы по скорости
(или коэффициентом добротности
по скорости). Таким образом, в астатической
системе отсутствует установившаяся
ошибка от постоянного задающего
воздействия и постоянных возмущений.
Для
астатизма относительно возмущения
интегрирующее звено должно быть введено
до точки, в которой приложено возмущение
(рис. 5.10).
Влияние
интегрирующего звена на динамические
свойства системы
где
сплошными линиями показаны
логарифмические частотные характеристики
системы с передаточной функцией
(5.26). При введении в разомкнутую цепь
этой системы интегрирующего звена
характеристики принимают положение,
показанное пунктиром. Фазочастотная
характеристика переместилась вниз
на —90°, а амплитудно-частотная
характеристика повернулась вокруг
точки а
по
направлению часовой стрелки . В
результате запас устойчивости по фазе
уменьшился с
до
недопустимо малого значения
Система
остается устойчивой, но переходный
процесс будет сильно колебательным.
Кроме того, уменьшилась частота среза
и переходные процессы будут более
продолжительными.
Однако
в других ситуациях введение интегрирующего
звена может не только не ухудшить, а
даже улучшить динамические свойства
системы. Пусть, например, постоянные
времени системы с передаточной функцией
(5.26) имеют следующие значения: Т1
=
= 0,05 с, Т2
=
0,0025 с и T3
= 0,001 с. Логарифмические частотные
характеристики разомкнутой системы
показаны

При
введении интегрирующего звена
характеристики принимают положение,
показанное пунктирными линиями. В
данном случае интегрирующее звено
уменьшило частоту среза, но запас
устойчивости по фазе увеличился с
|до
.
Хотя быстродействие системы
уменьшилось, но уменьшилась и
колебательность.

Таким
образом, при повышении статической
точности путем введения интегрирующего
звена могут оказаться необходимыми
мероприятия по сохранению запасов
устойчивости САУ.
Значительно
лучшие результаты получают при получении
астатизма с помощью изодромного звена,
т. е- звена с передаточной функцией
постоянная
времени изодрома.
Если
постоянная времени
достаточно
велика, то запас устойчивости может
быть сохранен неизменным. Уменьшение
передаточного коэффициента разомкнутой
системы должно быть скомпенсировано
увеличением коэффициента усиления
усилителя. Следует учитывать, что при
большом значении
могут
увеличиться старшие коэффициенты
ошибки.
Астатизм
САУ относительно задающего воздействия
можно обеспечить более простыми
способами: неединичной обратной
связью и масштабированием [3).
Структурная
схема системы с неединичной обратной
связью показана на рис. 5.13, а.
В
установившемся режиме регулируемая
координата связана с постоянным задающим
воздействием соотношением
(5.27)
где
kn
—
передаточный коэффициент прямой цепи
системы.
Если
выполнить основную обратную связь
системы с коэффициентом
и
система относительно задающего
воздействия будет астатической.Структурная
схема системы масштабированием входной
(величины показана на рис. 5.13, б.
Ее
особенность — наличие
усилительного
звена с передаточным коэффициентом
m
на входе. В установившемся режиме
где
k
—
передаточный коэффициент разомкнутой
системы.
При
/л = 1 -f-
УЬ
получаем
у
= g0
и
система является астатической
относительно задающего воздействия.
Недостаток
этих способов в том, что астатизм
обеспечивается только при сохранении
указанных соотношений между передаточными
коэффициентами. Неточное определение
передаточного коэффициента какого-либо
элемента системы и его изменение в
процессе эксплуатации ведут к появлению
статической ошибки. Астатизм,
достигнутый введением интегрирующего
или изодромного звена, сохраняется и
при изменении параметров системы.
Однако нужно иметь в виду, что введение
двух интегрирующих звеньев в систему,
состоящую из усилительных, апериодических
и колебательных звеньев, сделает ее
структурно-неустойчивой. Возможно
обеспечение астатизма и более высокого
порядка. При этом из-за введения большого
числа интегрирующих или изодромных
звеньев и мероприятий, обеспечивающих
требуемые динамические свойства,
структура САУ значительно усложняется.
Компенсация
внешнего воздействия (обеспечение
инвариантности). Рассмотренные выше
способы улучшения статических и
динамических свойств системы связаны
лишь с изменениями параметров
элементов САУ и структуры ее отдельных
участков, но при этом не затрагивают
принципа действия системы.
Помимо
принципа регулирования по отклонению
существует принцип регулирования
по внешнему воздействию. Значительный
эффект дает их одновременное использование.
В этом случае системы называются
комбинированными. Кроме замкнутого
контура они имеют дополнительную
цепь влияния внешнего воздействия —
возмущения или задающего.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение динамических ошибок (по
скорости, по ускорению) для статической и астатических систем.
Точность АС
характеризуется величиной ошибки в установившемся режиме и зависит от характера
воздействия, а также структуры и параметров системы.
Реальные воздействия
в радиотехнических следящих системах описывается сложными (случайными)
функциями времени. Однако при анализе точности управления часто используют
простые детерминированные воздействия: постоянное ступенчатое, линейное,
квадратичное и другие. Это позволяет упростить анализ и в то же время сохранить
в модели задающего воздействия наиболее существенные признаки (начальное
значение, скорость изменения, ускорение). Большинство систем радиоавтоматики
описываются передаточными функциями вида
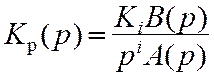
где Ki — общее усиление
разомкнутой системы, i – число интегрирующих
звеньев, определяющее порядок астатизма системы;
– полиномы, порядок которых определяется числом типовых
звеньев (n и m соответственно инерционных и форсирующих), а
коэффициенты полиномов – постоянными времени типовых звеньев.
11.1. Статические ошибки
Ошибка системы при постоянном
(ступенчатом) воздействии x(t)=x0=const при t³0
называется статическойeст.
Для установившейся
ошибки, учитывая, что изображение X(p)=x0/p,
запишем:
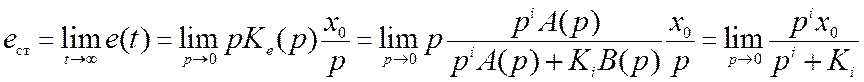
Для статической
системы (не содержащей интегрирующих звеньев) статическая ошибка равна
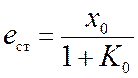
Таким образом, в
статических системах установившееся значение управляемой переменной не равно
заданному: меньше на величину ошибки, значение которой обратно пропорционально
усилению К0 по постоянному току (обычно К0>>1).
Для астатических
систем (i ³ 1) ошибка при постоянном воздействии
,
так как числитель в (11.2) равен нулю, а знаменатель равен
Кi.
Отсутствие
статической ошибки обусловило название таких систем – астатические.
11.2. Динамические ошибки
Ошибка,
характеризующая точность замкнутой системы при меняющемся воздействии,
называется динамической eд(t).
Любое детерминированное
воздействие (при условии существования его производных d(k)/dt(k),
k=1, 2, …) можно представить в виде ряда
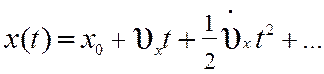
где x0 — начальное значение, — скорость изменения,
— ускорение и т. д.
Для вычисления
динамических ошибок при типовых воздействиях (линейном и квадратическом)
представим выражение для ошибки в операторной форме:
(11.5)
Используя разложение
передаточной функции Ke(p) в ряд Маклорена по степеням
переменной р, перепишем (11.5) в виде
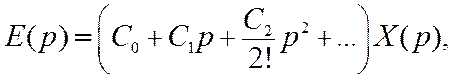
где C0, C1, C2,
… — коэффициенты ошибок, определяемые
как
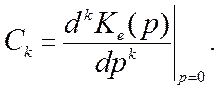
Установившееся
значение ошибки при произвольном воздействии x(t)
на основании (11.6) определяется временным рядом
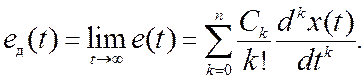
Чем меньше
коэффициенты ошибок, тем выше точность системы при произвольном
детерминированном воздействии. При вычислении коэффициентов Ck
обычно ограничиваются только первыми тремя (для систем с астатизмом не выше
второго порядка).
Коэффициент C0
в соответствии с (11.7) равен
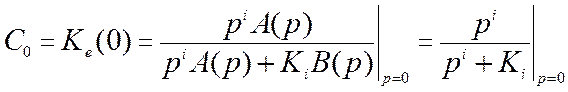
Для статических
систем (i=0) C0=1/(1+K0), а для
астатических систем C0=0.
Определим динамические
ошибки типовых систем при линейном воздействии (изменение с постоянной
скоростью) x(t)=nxt.
В соответствии с
формулой (11.8) динамическая ошибка (ошибка по скорости) определяется как
.
Для статической
системы она равна
так как вклад составляющей C1nx
значительно меньше, чем C0 x(t), которая растет
линейно со временем. Таким образом, скоростная ошибка в статических системах
накапливается со временем со скоростью nx/(1+K0), что делает неприемлемым использование
таких систем при меняющемся воздействии. Для астатических систем C0=0 и скоростная ошибка
.
Нахождение
коэффициента ошибки C1 с использованием формулы (11.7)
затруднительно. Более простой способ его вычисления основан на сравнении
точного выражения для передаточной функции Ke(p) и
аппроксимирующего ее ряда:

Уравнение (11.9)
можно представить в виде
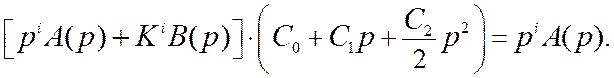
Полагая i= 1 (астатическая система первого порядка) и приравнивая
коэффициенты при переменной p в левой и правой частях уравнения, находим
или C1=1/K1, так как C0=0.
Таким образом,
скоростная ошибка системы первого порядка астатизма eд=nx/K1
определяется усилением разомкнутой системы K1 и не зависит от
времени. Параметр K1, имеющий размерность c –1,
называется добротностью системы по скорости (чем выше добротность, тем
точнее система).
Для астатической
системы второго порядка скоростная ошибка равна нулю, так как оба коэффициента C0=C1=0.
Равенство C1=0 вытекает из уравнения (11.10), так как в
правой части уравнения не содержится слагаемого, в которое входит переменная p
(есть только с p2 и выше).
Оценим динамические
ошибки типовых систем при квадратичном воздействии (изменение с постоянным
ускорением).
В соответствии с (11.8)
для динамической ошибки (ошибки по ускорению) запишем
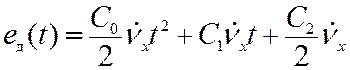
Для статической
системы ошибка по ускорению равна
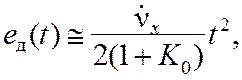
так как составляющие ошибки с коэффициентами C1 и C2
вносят пренебрежимо малый вклад в результирующую ошибку. Накопление ошибки по
квадратичному закону исключает применение статических систем при наличии
ускорения.
Для системы первого
порядка астатизма ошибка по ускорению равна
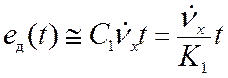
(вкладом составляющей можно
пренебречь). Накопление ошибки со временем (со скоростью ) не позволяет применять такие
системы при наличии ускорения. Для астатической системы второго порядка ошибка
по ускорению равна
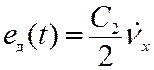
Определение
коэффициента ошибки C2 с использованием уравнения (11.7)
сводится к приравниванию коэффициентов при p2 в обеих частях
уравнения:
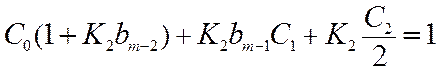
Откуда
C2/2=1/K2, так как C0=C1=0.
Измерительные каналы являются наиболее сложной частью систем автоматизации и требуют глубоких знаний для получения достоверных результатов измерений. Качество полученных данных зависит не только от погрешности средств измерений, вовремя выполненной поверки или калибровки, но в большей степени от корректности методики измерений, правильности выполнения системы заземления, экранирования и кабельной разводки [1]. Измерительные каналы систем автоматизации, в отличие от измерительных приборов, создаются в полевых условиях, что является причиной появления ошибок, которые не всегда удаётся обнаружить. Множество проблем возникает при выполнении статистической обработки результатов измерений, при стремлении достичь предела разрешающей способности системы, при выполнении косвенных, совместных и многократных измерений.
Для получения достоверных результатов требуются знания в области метрологии, математической статистики, теории случайных процессов, теории информации и электроники. Это самостоятельные объёмные области знаний, которые являются темой множества учебников и монографий. Поэтому далее в статье рассматриваются только наиболее важные вопросы измерений в промышленной автоматизации, которые часто понимаются неправильно или неоднозначно.
Измеряемые физические параметры обычно изменяются с течением времени, поэтому для оценки точности измерений необходимо знать, как зависит погрешность измерений от динамических характеристик измеряемой величины, то есть какова динамическая компонента погрешности измерений. Несмотря на то что динамическая погрешность очень часто в несколько раз превышает статическую, её редко принимают во внимание, поскольку измерить величину этой погрешности технически достаточно сложно и необходимые для этого приборы часто отсутствуют. Так, в пользовательской документации на устройства аналогового ввода, как правило, отсутствует информация, необходимая для оценки динамической погрешности (импульсная, переходная, амплитудно-частотная и фазочастотная характеристики, амплитудно-фазовая или передаточная функция).
Другой проблемой, которая имеет место при вводе аналоговой информации в компьютер или контроллер, является появление алиасных (ложных) частот, которые снижают точность измерений. Опасность этого явления заключается в том, что помехи, лежащие гораздо выше частоты дискретизации, могут трансформироваться в низкочастотную область, если в измерительном канале неправильно выбран или отсутствует антиалиасный фильтр. Антиалиасный фильтр необходим для уменьшения помех на входе средства измерений, однако его наличие приводит к возникновению динамической погрешности.
Далее описываются причины возникновения динамической погрешности и пути её оценки.
Теорема Котельникова
В системах автоматизации самой распространённой операцией является дискретизация сигнала по времени. Выбор частоты дискретизации опирается на теорему Котельникова, которая распространяется на любые сигналы с ограниченным спектром. Если спектр сигнала ограничен частотой fmax, то частота отсчётов должна быть в 2 раза выше, чтобы сигнал можно было восстановить без потери информации. Иначе говоря, если самая высокочастотная гармоника в спектре сигнала имеет период T, то на один период гармоники должно приходиться 2 отсчёта при дискретизации сигнала – при этом непрерывный сигнал преобразуется в импульсный без потери информации.
Отметим несколько особенностей применения теоремы.
Во-первых, в теореме Котельникова предполагается, что сигнал s(t) будет восстановлен с помощью замены каждого отсчёта функцией sin(x)/x, то есть

где τ – интервал между отсчётами, k – номер отсчёта, t – время. Однако на практике такую функцию реализовать невозможно, поскольку её спектральная характеристика является идеально прямоугольной и для её получения требуется фильтр с идеально прямоугольной АЧХ. Поэтому восстановление сигнала после дискретизации выполняют с помощью фильтров невысоких порядков.
Во-вторых, сигналы с ограниченным спектром имеют бесконечную протяжённость во времени, а реальные сигналы, ограниченные во времени, имеют неограниченный частотный спектр, поэтому разложение их в ряд Котельникова требует пренебрежения частью спектра, лежащего выше частоты fmax.
В-третьих, теорема Котельникова предполагает, что при дискретизации сигнала использованы импульсы бесконечно малой длительности.
Указанные факторы являются причиной того, что на практике частоту дискретизации выбирают в несколько раз выше, чем требуется в соответствии с теоремой Котельникова.
Теорема Котельникова позволяет оценить предельную пропускную способность измерительного канала с известной полосой пропускания fс. Если средство измерений имеет погрешность Δ, то количество различимых уровней при измерении величины x будет равно x/Δ, а количество информации, полученное при однократном измерении, будет равно log2 [(x+Δ)/Δ]. Если систематическая составляющая погрешности исключена и преобладает случайная составляющая с дисперсией Δ2, то количество различимых уровней следует искать как отношение мощностей, то есть количество информации будет равно
.jpg)
где Pс – мощность сигнала, Pш – мощность погрешности. Поскольку в соответствии с теоремой Котельникова сигнал со спектром шириной fс должен быть дискретизирован с частотой 2fс, чтобы сохранить всю содержащуюся в нём информацию, то для сигнала длительностью T потребуется 2Tfс отсчётов. Следовательно, измерительный канал с полосой fс позволяет передать 2Tfс отсчётов, каждый из которых содержит 1/2 log2 [(Pc + Pш)/Pш] бит информации, то есть пропускная способность канала (количество передаваемой информации в единицу времени) составит
.jpg)
Величина 2Tfс называется базой сигнала, Tfсlog2[(Pс+Pш)/Pш] – объёмом сигнала, log2 [(Pс+Pш)/Pш] – динамическим диапазоном.
Фильтр и динамическая погрешность
Измеряемая величина в системах автоматизации обычно не является постоянной во времени. Поэтому возникает вопрос: насколько медленно она должна изменяться, чтобы погрешность измерения не превышала заданного значения? Для ответа на этот вопрос используется понятие динамической погрешности.
Нормированию динамических погрешностей уделено недостаточно внимания как в нормативной литературе, так и в эксплуатационной документации средств измерений. Так, динамические характеристики, необходимые для оценки динамической погрешности, как правило, отсутствуют в пользовательской документации на модули аналогового ввода, за редким исключением (например, модули аналогового ввода RealLab! серии NL содержат необходимую информацию).
Оценка величины динамической погрешности является сравнительно сложным процессом. Проблема возникает потому, что динамическая погрешность зависит не только от динамической модели измерительного канала, но и от формы измеряемого сигнала.
Основными источниками динамической погрешности являются естественная инерционность физических процессов, протекающих в датчиках, процессы заряда входной ёмкости измерительного устройства, инерционность фильтров, использованных для устранения алиасного эффекта и подавления помех в измерительном канале.
Для количественного описания динамических свойств измерительного канала используют линейные динамические модели в виде дифференциальных уравнений, операторных передаточных функций, импульсных переходных характеристик или реакций на единичный скачок, амплитудно-частотные и амплитудно-фазовые характеристики (ГОСТ 8.256-77 [2]). Описание этих моделей может быть указано в эксплуатационной документации на средство измерений. Идентификацию динамической модели средства измерений выполняет его разработчик, используя те же методы, что и при идентификации объекта управления.
В некоторых случаях, например, когда уравнения динамической модели пользователю известны, могут быть заданы только коэффициенты уравнений, постоянные времени, время реакции (время установления), коэффициент демпфирования, полоса пропускания по уровню 0,707 и др. Для модулей аналогового ввода может быть также задана погрешность положения отсчёта измеряемого сигнала на оси времени.
Рассмотрим типовую динамическую модель измерительного канала (рис. 1), которая включает в себя модели датчика Wд(s) и модуля ввода аналоговых сигналов W(s). Передаточная функция W(s) обычно представляет собой произведение передаточных функций антиалиасного фильтра, стоящего до АЦП, и цифрового режекторного фильтра, стоящего после АЦП. Измерительный преобразователь часто входит в состав модуля ввода.
При проектировании системы автоматизации динамические характеристики её звеньев можно выбрать так, что инерционность всего измерительного канала будет определяться инерционностью самого медленного звена. Это существенно упрощает процесс оценки величины динамической погрешности. Например, при измерении температуры самым инерционным звеном должен быть датчик; инерционность термопар характеризуется постоянной времени в десятки секунд и намного превышает инерционность модуля ввода (доли секунды).
Многоканальные средства измерений бывают двух типов: с коммутацией источников сигнала и с параллельно работающими каналами. В первом случае на входе модуля ввода используется аналоговый коммутатор (рис. 1), во втором случае коммутатор не используется, а многоканальность достигается применением нескольких одинаковых каналов с одновременно работающими АЦП.
В системе с параллельно работающими каналами можно считать, что сигнал на входе средства измерений действует неограниченно долго. При коммутации каналов сигнал объекта измерений x(t) действует, пока ключ коммутатора замкнут. Описание динамической погрешности этих двух типов систем имеет свои особенности.
Измерение при синусоидальном сигнале
Сначала рассмотрим случай, когда входной (измеряемый) сигнал изменяется по синусоидальному закону x(t) = A sin(ωt) (рис. 2), а измерительный канал не содержит коммутатора. Считая, что канал линеен, получим на его выходе сигнал y(t) = A|W(ω)| sin(ωt+φ(ω)), где |W(ω)| – амплитудно-частотная характеристика (АЧХ) измерительного канала,
.jpg)
– фазочастотная характеристика (ФЧХ), фактически сдвиг фазы выходного сигнала относительно входного. Таким образом, погрешность измерительного канала в данном случае состоит из двух компонентов (рис. 2): погрешности амплитуды
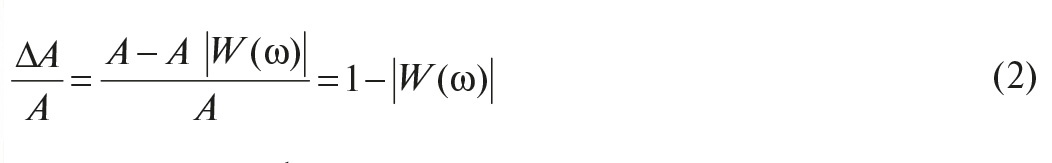
и погрешности фазы

Наиболее простые соотношения для оценки указанных погрешностей получаются для случая, когда динамику измерительного канала можно представить моделью первого порядка (фильтром первого порядка):

где ω0,7 – граничная частота по уровню 1/√2=0,707. Для неё АЧХ и ФЧХ имеют вид:
.jpg)
Поскольку погрешность средств измерений в системах автоматизации, как правило, не превышает 1%, в приведённых соотношениях можно считать ω/ω0,7 << 1, что позволяет разложить нелинейные функции в ряд Тейлора и ограничиться первыми двумя членами разложения. При этих условиях получим:
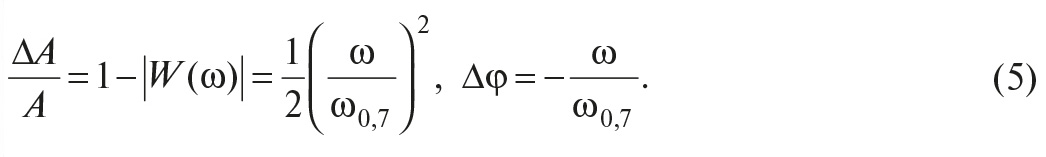
Например, если модуль ввода имеет граничную частоту ω0,7 = 5 Гц, то для того чтобы динамическая погрешность не превышала 0,05%, частота входного сигнала должна составлять не более √0,05%•2 = 0,032, или 3,2% от граничной частоты ω0,7, то есть не более 0,16 Гц.
Отметим, что оценки (5) относятся только к погрешности амплитуды и фазы синусоидального сигнала, но не к погрешности отдельных его отсчётов. Наибольшая погрешность измерения входного сигнала как функции времени будет при ωt = 0, π, 2π, … Её величину можно оценить следующим образом:
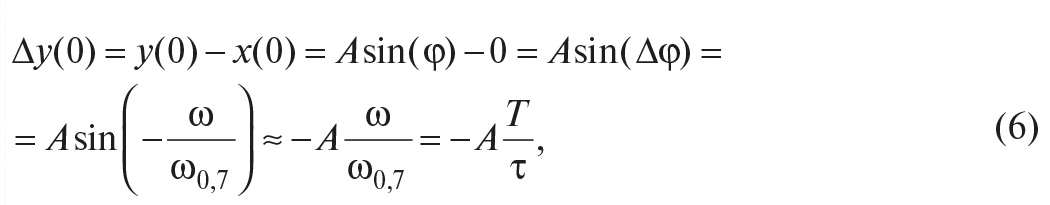
где T = 2π/ω0,7 – постоянная времени фильтра, τ = 2π/ω – период измеряемого сигнала. Относительная погрешность будет равна:
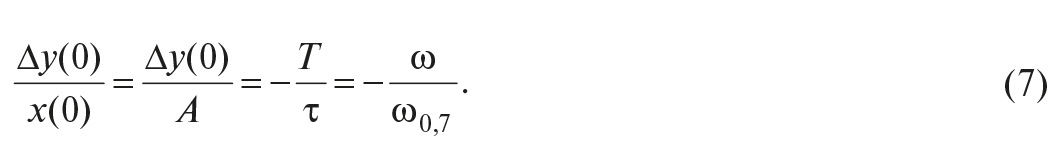
Таким образом, для получения динамической погрешности величиной 0,1% при измерении отсчётов синусоидального сигнала в моменты времени ωt = 0, π, 2π, … частота входного сигнала должна быть в 1000 раз ниже граничной частоты фильтра. Отметим, что погрешность амплитуды, измеренная в моменты времени ωt = π/2, 3π/2, …, уменьшается в зависимости от частоты по квадратичному закону (5), в то время как погрешность в моменты времени ωt = 0, π, 2π, … – только линейно (7).
Измерение при входном сигнале «единичный скачок»
Если входной сигнал изменяется скачком, то для измерительного канала, который описывается моделью первого порядка (4) и не содержит коммутатора, реакцию на скачок можно получить с помощью преобразования Лапласа. Для этого в выражении (4) можно вместо jω использовать комплексную частоту p [3] и умножить (4) на изображение единичного скачка 1/p (по Лапласу). Переходя от изображения к оригиналу с помощью обратного преобразования Лапласа, получим сигнал на выходе измерительного канала как функцию времени:
y(t) = y0(1 – e–t/τ), (8)
где τ = 1/ω0,7, y0 – значение y(t) при t = ∞.
Поскольку точное значение единичного скачка y(∞) = y0 = 1, погрешность измерений Δy(t) = y0 – y(t) с течением времени будет уменьшаться по экспоненциальному закону:
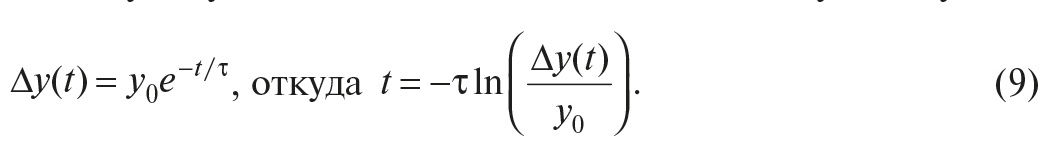
Например, для получения относительной динамической погрешности 1% измерение нужно делать не раньше чем через t = 4,6π после подачи измеряемого сигнала. Для получения погрешности 0,05% задержка перед измерением должна быть не менее 7,6τ.
Измерение сигнала произвольной формы
Когда измеряемый сигнал имеет произвольную форму x(t), выражение для y(t) в общем случае имеет вид свёртки входного сигнала и импульсной характеристики измерительного канала hδ(t) [4]:

где ξ – переменная интегрирования.
Импульсная характеристика hδ(t) является реакцией измерительного канала на входной сигнал в форме дельта-функции Дирака δ(t). Вместо импульсной характеристики можно использовать реакцию на единичный скачок h1(t), при этом выражение для y(t) запишется в виде интеграла Дюамеля [4]:
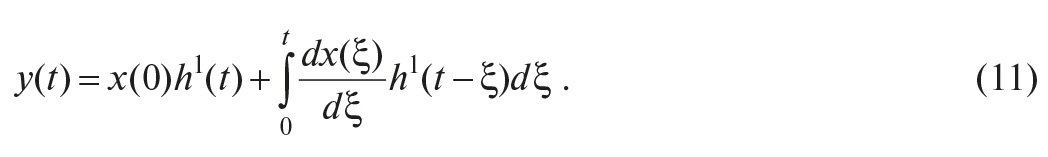
К сожалению, более простого выражения не существует, и интегралы (10) и (11) нужно брать для каждой конкретной формы входного сигнала x(t). Сделать это аналитически, как правило, невозможно. Наиболее удобным способом является численное интегрирование или моделирование, например, с помощью программ Matlab, MathCAD.
Однако для многоканальной системы сбора данных с одним АЦП и коммутацией входных каналов (рис. 1) получить приближённое выражение для динамической погрешности в общем случае, независимо от формы сигнала на входе системы, возможно. Для этого воспользуемся тем, что отсчёты входного сигнала в системах сбора данных обычно берутся так часто, что при разложении функции x(t) в ряд Тейлора на интервале между отсчётами можно ограничиться линейным членом разложения. Иначе говоря, при произвольной форме входного сигнала и достаточно высокой частоте дискретизации функцию x(t) можно аппроксимировать прямой линией на участке t∈[t0, t1] (рис. 3), где t0 – момент замыкания ключа входного коммутатора; t1 – момент появления сигнала на выходе модуля ввода:
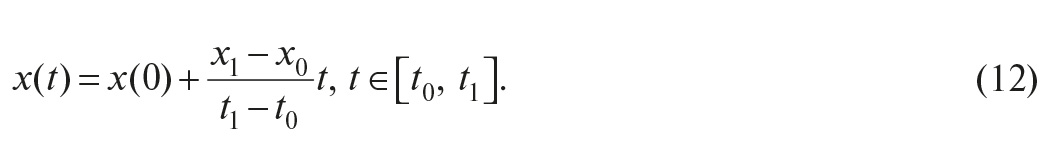
Максимальную погрешность такой аппроксимации можно оценить по величине третьего члена ряда Тейлора:

где точка ξ выбирается на интервале t∈[t0, t1] таким образом, чтобы величина второй производной в ней была наибольшей. В частности, если входной сигнал описывается линейной зависимостью, то для него
.jpg)
для всех точек интервала t∈[t0, t1].
Итак, сигнал после коммутатора, перед антиалиасным фильтром, имеет форму трапеции на интервалe t∈[t0, t1] (рис. 3). Начальные условия для фильтра после каждого переключения входного коммутатора являются приближённо нулевыми, поскольку постоянная времени фильтра T=2π/ω0,7 много меньше интервала между отсчётами t1 – t0.
Рассмотрим сначала случай с фильтром первого порядка, когда передаточная функция W(s) описывается выражением (4). Импульсную характеристику фильтра можно получить с помощью обратного преобразования Лапласа от выражения (4), в котором переменная jω заменена на комплексную частоту p:

Подставляя (14) и (12) в (10), получим выражение для функции y(t) на интервале t∈[t0, t1]:
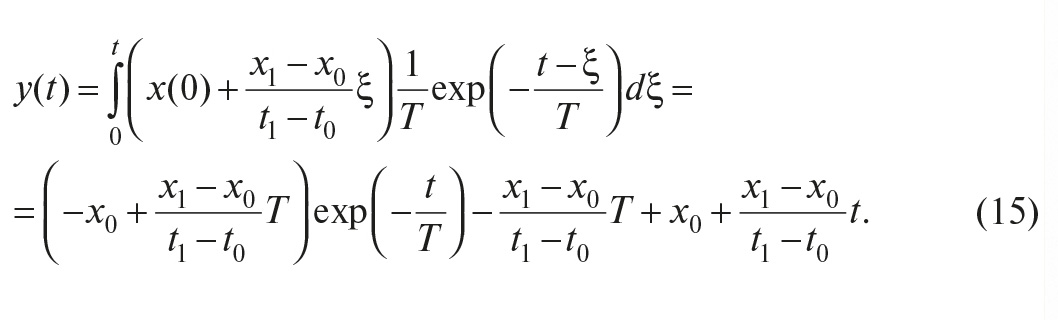
Вычитая из полученного выражения сигнал на входе x(t) (12), получим величину абсолютной погрешности Δy(t) в виде:
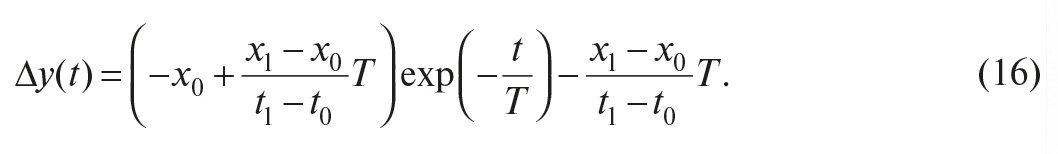
Таким образом, при достаточно большом t (точнее, при t → ∞) абсолютная динамическая погрешность не приближается к нулю, а остаётся постоянной, равной Δy(∞) = (x1–x0) T / (t1–t0). При малых t, на начальном участке переходного процесса, погрешность экспоненциально уменьшается с течением времени.
Пользуясь (16), можно записать выражение для приведённой погрешности:
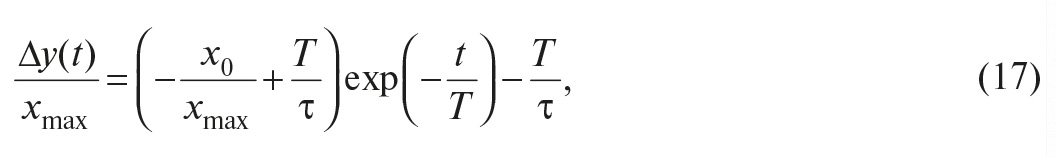
где xmax – верхняя граница диапазона измерений;
.jpg)
Используя это обозначение t в выражении (12), получим:

Из этой формулы виден физический смысл параметра τ – это время, за которое входной сигнал проходит интервал от x(t) = 0 до x(t) = xmax при условии, что он сохранит линейность на этом интервале.
Отметим, что при t → ∞ выражение (17) совпадает с (7), а при τ → ∞ – с (9).
Графики зависимости модуля динамической погрешности от времени, построенные по выражению (17) при x0/xmax = 0,5, показаны на рис. 4. Например, если постоянная времени фильтра первого порядка T равна 1 с, то для того чтобы динамическая погрешность не превышала 0,1%, отношение T/τ должно быть не более 0,001 (рис. 4), откуда τ > 1000T, то есть скорость нарастания входного сигнала должна быть такой, чтобы интервал от x(t) = 0 до xmax был пройден за время не менее 1000T = 1000 с. Если уравнение (18) нормировать по xmax, чтобы перейти к относительным величинам x=x/xmax

то можно сказать, что скорость нарастания входного сигнала 1/τ должна быть не более 0,001 с–1, или 0,1%/с.
Аналогичное соотношение можно получить для фильтра второго порядка с передаточной функцией
.jpg)
Выражение для приведённой погрешности будет иметь вид:
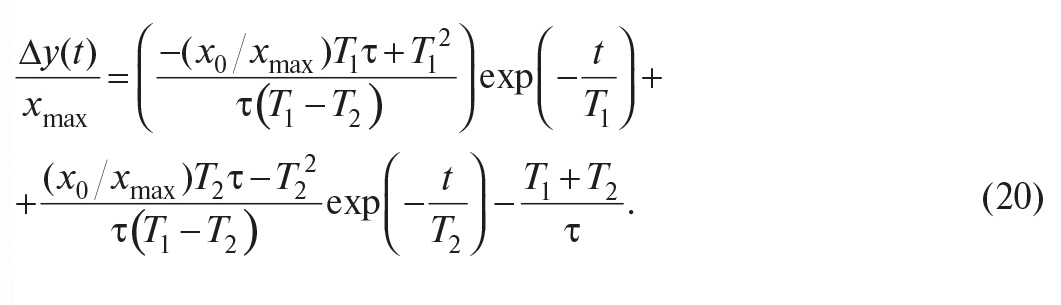
При t → ∞ , как и в системе первого порядка, погрешность стремится к постоянной величине.
Можно показать, что для фильтра N-го порядка, описываемого полиномом вида
.jpg)
погрешность стремится к величине
.jpg)
Таким образом, для многоканальной системы сбора данных с одним АЦП и коммутацией входных каналов (рис. 1) динамическая погрешность измерений не зависит от формы измеряемого сигнала и её величину можно оценить по графику на рис. 4 или по формуле (17).
Sinc-фильтр в измерительных модулях ввода
В системах автоматизации обычно используют режекторные фильтры для ослабления помехи с частотой 50 Гц, проникающей из сети питания. Такой фильтр, как правило, входит в состав микросхемы АЦП, из чего следует требование к простоте его реализации. Наиболее популярным для этих целей оказался sinc-фильтр (sinc, sinc2, sinc3, sinc4) [5, 6].
Структура цифрового sinc-фильтра представлена на рис. 5. Он состоит из двух каскадов: первый каскад – до ключа R, второй – после. На вход фильтра поступают отсчёты сигнала x(k) с частотой дискретизации fд. Блок z–1 выполняет задержку на один такт отсчётов, поступающих на его вход. Блок z–M выполняет задержку на M = 1 или M = 2 (тактов). Ключ R пропускает только каждый R-й отсчёт, поэтому частота следования отсчётов после него и на выходе фильтра составляет fд /R, то есть такой фильтр выполняет также функцию прореживания (децимации) отсчётов.
Первый каскад фильтра выполняет суммирование входных отсчётов, второй каскад выполняет функцию вычитания из поступившей на его вход суммы предыдущей суммы отсчётов (суммы, полученной на предыдущем такте fд /R), то есть выбирает суммы из R слагаемых. Таким образом, фильтр в целом выполняет операцию нахождения среднего арифметического в окне шириной R отсчётов, точнее, как будет показано далее, в окне шириной RM.
Непосредственно по рис. 5 можно записать передаточную функцию одного звена с блоком задержки z–1:

Аналогично для одного звена с блоком z–M передаточная функция будет иметь вид:

Здесь в показателе степени стоит произведение RM, поскольку вследствие прореживания отсчётов ключом R задержка отсчётов относительно k выполняется на RM тактов.
Поскольку в фильтре использовано N блоков до ключа и N блоков после, выражение для передаточной функции всего фильтра можно записать в виде произведения HI(z) HC(z) в степени N:
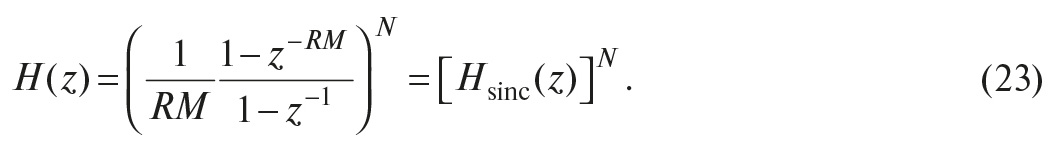
Здесь в знаменателе использован нормирующий множитель RM, чтобы коэффициент передачи фильтра на нулевой частоте был равен единице;
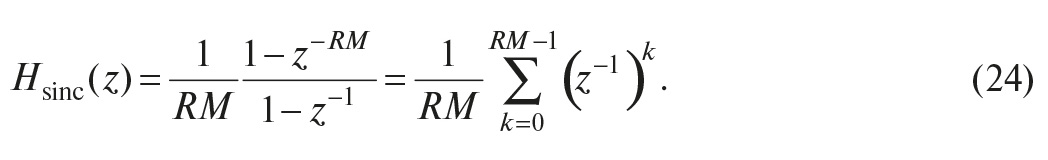
Для перехода к сумме в (24) использована формула суммы членов геометрической прогрессии:
.jpg)
По правилам преобразования Фурье задержке оригинала на один такт 1/fд соответствует оператор сдвига z–1 = e–jω/fд. Подставляя это значение в (24), получим Фурье-изображение передаточной функции sinc-фильтра в виде:

Выполнив ряд преобразований (подробнее см. в [1]), получим выражение для передаточной функции sinc-фильтра в виде:
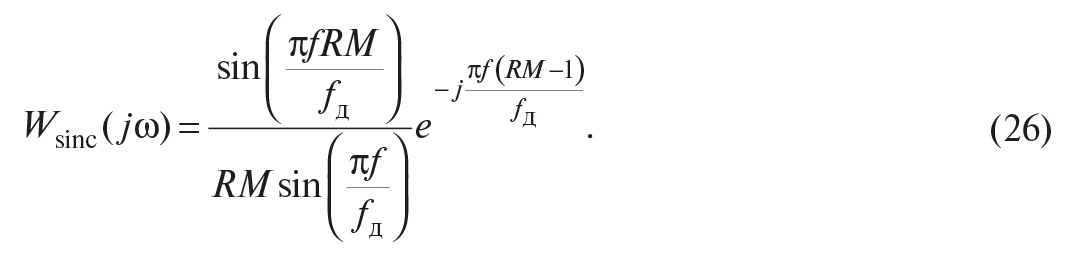
Для упрощения аналитических выкладок передаточную функцию sinc-фильтра упрощают путём разложения знаменателя в (26) в ряд Тейлора с отбрасыванием всех членов, кроме первого:
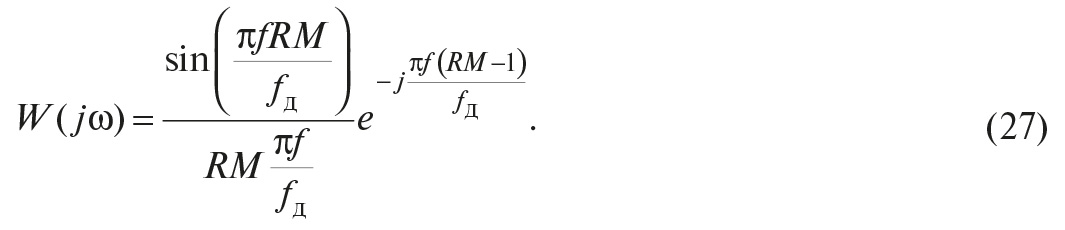
Это приближение выполняется достаточно точно, поскольку обычно частота дискретизации гораздо выше частот, на которых используется sinc-фильтр ( f<< fд). Вероятно, такая аппроксимация объясняет название «sinc-фильтр» (по определению sinc-функции sinc(x) = sin(x)/x), хотя на самом деле функция sin(nx) / nsix(x) называется функцией Дирихле [7], или периодической sinc-функцией.
Поскольку при x = π функция sin(x)/x = 0, то частота режекции фильтра находится из условия fRM /fд = 1. Поэтому при типовой частоте дискретизации в АЦП fд = 32 768 Гц для ослабления помехи c частотой f = 50 Гц (T = 20 мс) выбирают RM = 656.
Рассмотрим принцип действия фильтра во временной области. Для упрощения будем считать N = 1 (фильтр первого порядка), то есть с одним звеном до ключа и одним после (рис. 5). Звено с элементом задержки z–1 выполняет функцию интегрирования, то есть суммирования в дискретной области. Сигнал на его выходе равен k∑n=0x(n). Ключ R замыкается через R тактов и пропускает на свой выход сумму Rm∑n=0n(x), где m – номер прореженного отсчёта (после ключа R).
Звено фильтра с элементом задержки z–M при M = 1 выполняет вычитание из текущей суммы отсчётов предыдущей суммы, то есть пропускает на свой выход сумму отсчётов в окне шириной R. Таким образом, sinc-фильтр первого порядка выполняет усреднение (вычисляет среднее арифметическое) входных отсчётов во временном окне шириной R, то есть формирует сумму
.jpg)
Поэтому sinc-фильтр можно представить как окно, движущееся вдоль оси времени и усредняющее попадающие в него R отсчётов.
При ширине окна, равной периоду помехи синусоидальной формы (например, помехи с частотой сети 50 Гц), среднее значение за период равно нулю. Этим объясняется подавление (режекция) sinc-фильтром помехи с частотой 50 Гц. Практически коэффициент ослабления определяется частотой отсчётов, разрядностью АЦП, погрешностью и стабильностью частоты тактового генератора фильтра. Например, ослабление sinc-фильтром помехи с частотой 50 Гц в модулях RealLab! серии NL составляет –120 дБ.
При постоянной частоте отсчётов fд sinc-фильтр позволяет изменять частоту режекции с помощью коэффициента прореживания R. На рис. 6 представлена АЧХ sinc-фильтров первого, второго и третьего порядка. Зависимость динамической погрешности измерения амплитуды синусоидального сигнала ΔA/A от частоты для трёх sinc-фильтров с параметрами T = 0,02 с и RM = 656 показана на рис. 7.
На рис. 8 показана реакция sinc-фильтров на линейно нарастающий сигнал (рис. 3). Как видим, линейно нарастающий сигнал проходит через фильтр с задержкой; возникающая при этом погрешность при t > 60 мс остаётся постоянной во времени, равной для sinc-фильтра первого порядка 0,5 T/τ, для фильтра второго порядка – T/τ, для фильтра третьего порядка – 1,5 T/τ, где T = 1/(50 Гц) = 20 мс – ширина временного окна фильтра, настроенного на частоту режекции 50 Гц.
Например, для получения динамической погрешности, равной 0,05%, для sinc3-фильтра входной сигнал должен изменяться со скоростью не более чем 100% за 60 с, или 1,67% за 1 с. Здесь проценты берутся от верхней границы динамического диапазона xmax (см. (17)).
Алиасные частоты, антиалиасные фильтры
Первой неожиданностью, с которой обычно сталкиваются те, кто первый раз начал собирать данные в компьютер, является появление низкочастотной помехи, которой нет в реальном процессе и которой, казалось бы, не должно быть в собранных данных. Помеха может иметь форму периодического сигнала (сплошная кривая на рис. 9 а) или напоминать сигнал с амплитудной модуляцией (рис. 9 б, в). В реальности такой помехи нет, она появляется только после дискретизации сигнала, поэтому её называют ложной, или алиасной (от английского alias – вымышленный). Алиасные помехи увеличивают погрешность измерительных каналов.
Аналогичные эффекты проявляются и в других областях человеческой деятельности как биения колебаний, интерференция, стробоскопический эффект, муар и т.п.
Принцип образования помехи с алиасной частотой иллюстрирует рис. 9 а. Здесь пунктирной линией показан дискретизируемый периодический сигнал с периодом T, точки на линии показывают моменты выборки текущих значений. При дискретизации с высокой частотой, когда шаг дискретизации много меньше периода колебаний (таким образом дискретизирован первый период синусоидального сигнала на рис. 9 а), дискретизированный сигнал качественно не отличается от исходного, если пренебречь погрешностью дискретизации. Если же шаг дискретизации приближается к периоду исходного сигнала, то, как показано сплошной линией на рис. 9 а, после дискретизации получается сигнал, по форме похожий на исходный, но с гораздо большим периодом. Период стремится к бесконечности при τ > T.
Аналогичный эффект, состоящий в появлении новых компонент спектра в низкочастотной области, возникает и при дискретизации функций произвольной формы. Рассмотрим этот эффект подробнее.
Пусть имеется непрерывный сигнал x(t) (рис. 10), заданный на интервале времени [0, T]. Выберем отсчёты сигнала с шагом τ в точках kτ и полученную последовательность отсчётов назовём дискретным сигналом xд(k). Последовательность отсчётов можно записать в виде функции от непрерывной переменной t, если использовать понятие дискретной импульсной функции:
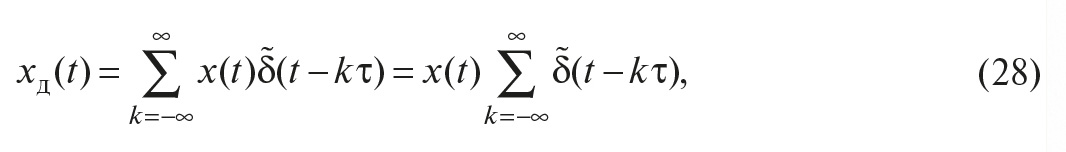
где δ(•) – дискретная импульсная (игольчатая) функция, определяемая как

В отличие от дельта-функции Дирака, она не стремится к бесконечности при t = 0. В выражении (28) функция x(t) вынесена за знак суммирования потому, что она не зависит от k.
Найдём спектр сигнала xд(t) (28). Для этого сначала разложим функцию
.jpg)
в ряд Фурье [3], воспользовавшись её периодичностью:
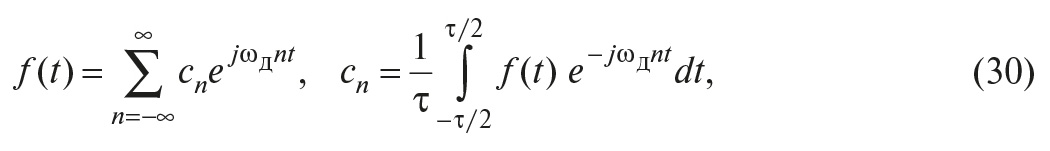
где ωд = 2π/τ, n – номер коэффициента ряда, τ – период функции.
Найдём коэффициенты cn:
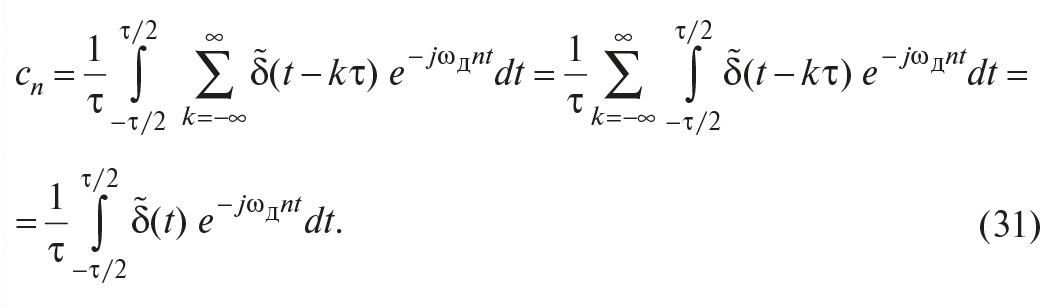
Знак суммирования в выражении (31) отсутствует потому, что за пределами интервала интегрирования –τ/2 < t < τ/2 все члены суммы для k ≠ 0 равны нулю.
Для того чтобы найти интеграл (31), представим игольчатую функцию как предел, к которому стремится прямоугольный импульс шириной tи << τ при tи → 0:
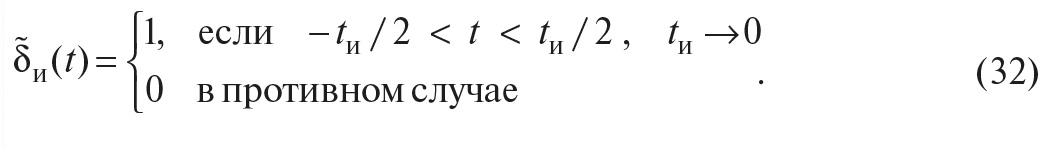
Тогда из (31) получим:
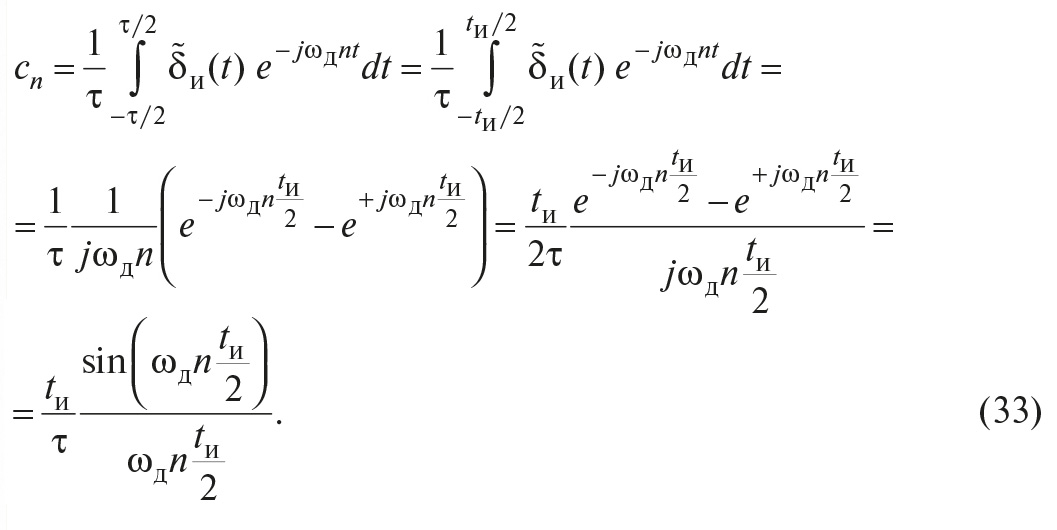
Если ширина импульса стремится к нулю, то limx→0(sin(x) / x) = 1, следовательно,
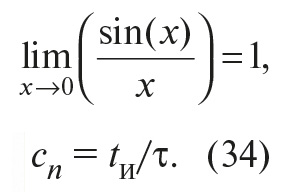
Используя это выражение, ряд Фурье для f(t) = ∞∑k=–∞δ(t–kτ) можно записать в виде (см. (30)):
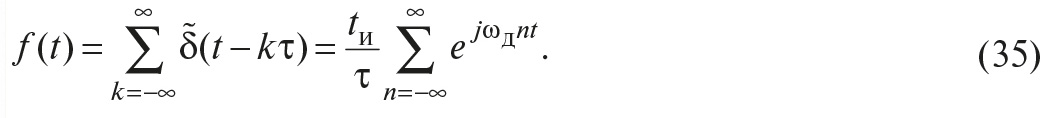
Подставляя полученное выражение в (28), получим:
Здесь функция x(t) внесена под знак суммирования, поскольку она не зависит от n.
Найдём теперь спектральную плотность Xд(jω) дискретного сигнала xд(t) с помощью преобразования Фурье:
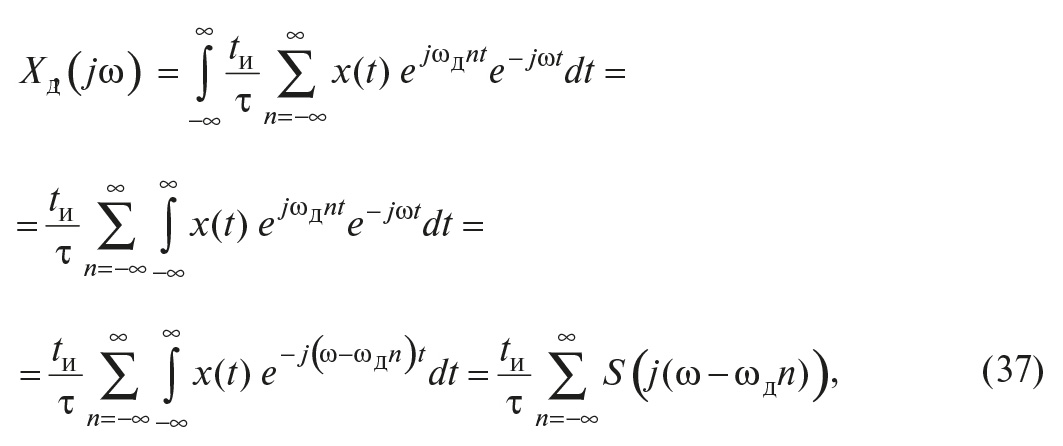
где S(j(ω – ωдn)) – спектральная плотность исходного не-прерывного сигнала x(t), сдвинутая по оси частот на ωдn = = 2πn/τ.
Таким образом, спектр дискретного сигнала Xд(jω) представляет собой серию копий спектров непрерывного сигнала X(jω), сдвинутых друг относительно друга на частоту дискретизации ωд= 2π/τ = 2fд:
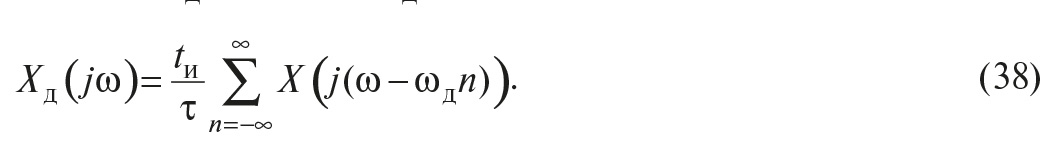
На рис. 11 а показан график непрерывного сигнала x(t) (на рисунке слева) и модуля его спектральной плотности |X(f)|, f = ω/2π (на рисунке справа). Поскольку функция |X(f)| симметрична относительно оси ординат, на рис. 11 показан только график в правой полуплоскости. Исходный непрерывный сигнал x(t) можно рассматривать как дискретный с нулевым периодом дискретизации (τ → 0, ωд → ∞). Поэтому модуль его спектральной плотности является непериодической функцией (рис. 11 а, справа).
После дискретизации функции x(t) с частотой fд на графике модуля спектральной плотности появляется бесконечное количество копий |X(f)| (рис. 11 б, в, справа), сдвинутых друг относительно друга на величину fд. Степень отличия спектра дискретного сигнала от спектра непрерывного характеризует величину погрешности дискретизации. С уменьшением частоты дискретизации, как следует из (38) и как видно на рис. 11, копии спектров сближаются, увеличивая погрешность дискретизации.
Предположим, что вся полезная информация, содержащаяся в непрерывном сигнале, заключена в области от 0 до частоты fc, которую поэтому можно считать границей спектра непрерывного сигнала (на рис. 11 эта область спектра заштрихована). Если для восстановления сигнала используется фильтр с граничной частотой 2fc (рис. 11 в), который убирает все составляющие спектра, лежащие выше 2fc, то наличие копий в спектре дискретного сигнала не искажает форму сигнала после его восстановления.
Если же ближайшая копия спектра приблизится к оригиналу настолько, что внесёт искажения в его форму (рис. 11 г), то восстановить исходный сигнал становится невозможно. Поэтому для исключения наложения спектров частота дискретизации fд должна быть, по крайней мере, в 2 раза выше граничной частоты спектра fc, то есть

как и требуется по теореме Котельникова.
Спектр произвольного непрерывного сигнала, показанный на рис. 11 а, в общем случае является неограниченным. Поэтому копии спектров, появляющиеся после дискретизации, всегда частично перекрываются. Это является причиной потери информации при восстановлении сигнала. И только для сигнала с ограниченным спектром эффект наложения отсутствует, что позволяет восстановить сигнал без потери информации.
Описанный алиасный эффект не может быть устранён с помощью цифровой фильтрации, если частота дискретизации равна удвоенной частоте верхней границы спектра полезного сигнала, так как при этом в спектре дискретизированного сигнала будет потеряна информация о помехах. Для решения этой проблемы можно использовать аналоговый (антиалиасный) фильтр с граничной частотой fc ≤ 0,5 fд на входе блока дискретизации или выбрать частоту дискретизации выше верхней граничной частоты спектра помех, чтобы в последующем выполнить цифровую фильтрацию.
В модулях аналогового ввода антиалиасный фильтр обычно настроен на максимальную частоту дискретизации, обеспечиваемую модулем, и не может быть перестроен. Поэтому если при измерении медленно протекающих процессов частота дискретизации программно выбрана низкой, а антиалиасный фильтр не перестроен, то помеха не ослабляется антиалиасным фильтром и в измеренном сигнале появляются алиасные помехи. ●
Литература
-
Денисенко В.В. Компьютерное управление технологическим процессом, экспериментом, оборудованием. – М. : Горячая линия – Телеком, 2008. – 608 с.
-
ГОСТ 8.256-77. Государственная система обеспечения единства измерений. Нормирование и определение динамических характеристик аналоговых средств измерений. Основные положения.
-
Баскаков С.И. Радиотехнические цепи и сигналы. – М. : Высшая школа, 1983. – 536 с.
-
Попов В.П. Основы теории цепей. – М. : Высшая школа, 1985. – 496 с.
-
Laddomada M., Lo Presti L., Mondin M., Ricchiuto C. An efficient decimation sinc-filter design for software radio applications // 2001 IEEE Third Workshop on Signal Processing, Advances in Wireless Communications, March 2001. – Р. 337–339.
-
Hogenauer E. An economical class of digital filters for decimation and interpolation // IEEE Transactions on Signal Processing. – 1981. – Vol. 29. – No. 2. – P. 155–162.
-
Сергиенко А.Б. Цифровая обработка сигналов. – СПб. : Питер, 2002. – 608 с.