Простой расчет контрольной суммы
Время на прочтение
12 мин
Количество просмотров 204K
При передачи данных по линиям связи, используется контрольная сумма, рассчитанная по некоторому алгоритму. Алгоритм часто сложный, конечно, он обоснован математически, но очень уж неудобен при дефиците ресурсов, например при программировании микроконтроллеров.
Чтобы упростить алгоритм, без потери качества, нужно немного «битовой магии», что интересная тема сама по себе.
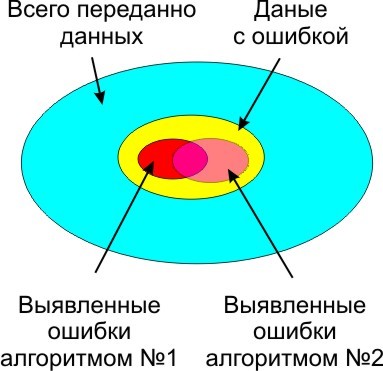
Без контрольной суммы, передавать данные опасно, так как помехи присутствуют везде и всегда, весь вопрос только в их вероятности возникновения и вызываемых ими побочных эффектах. В зависимости от условий и выбирается алгоритм выявления ошибок и количество данных в контрольной сумме. Сложнее алгоритм, и больше контрольная сумма, меньше не распознанных ошибок.
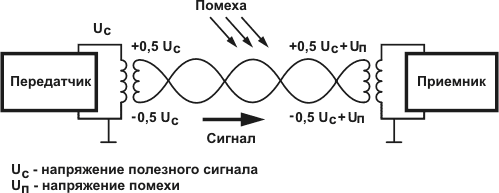
Причина помех на физическом уровне, при передаче данных.
Вот пример самого типичного алгоритма для микроконтроллера, ставшего, фактически, промышленным стандартом с 1979 года.
Расчет контрольной суммы для протокола Modbus
void crc_calculating(unsigned char puchMsg, unsigned short usDataLen) /*##Расчёт контрольной суммы##*/
{
{
unsigned char uchCRCHi = 0xFF ; /* Инициализация последнего байта CRC */
unsigned char uchCRCLo = 0xFF ; /* Инициализация первого байта CRC */
unsigned uIndex ; /* will index into CRC lookup table */
while (usDataLen--) /* pass through message buffer */
{
uIndex = uchCRCHi ^ *puchMsg++ ; /* Расчёт CRC */
uchCRCLo = uchCRCLo ^ auchCRCHi[uIndex] ;
uchCRCHi = auchCRCLo[uIndex] ;
}
return (uchCRCHi << 8 | uchCRCLo) ;
/* Table of CRC values for high–order byte */
static unsigned char auchCRCHi[] = {
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01,
0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81,
0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01,
0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01,
0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01,
0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40
};
/* Table of CRC values for low–order byte */
static char auchCRCLo[] = {
0x00, 0xC0, 0xC1, 0x01, 0xC3, 0x03, 0x02, 0xC2, 0xC6, 0x06, 0x07, 0xC7, 0x05, 0xC5, 0xC4,
0x04, 0xCC, 0x0C, 0x0D, 0xCD, 0x0F, 0xCF, 0xCE, 0x0E, 0x0A, 0xCA, 0xCB, 0x0B, 0xC9, 0x09,
0x08, 0xC8, 0xD8, 0x18, 0x19, 0xD9, 0x1B, 0xDB, 0xDA, 0x1A, 0x1E, 0xDE, 0xDF, 0x1F, 0xDD,
0x1D, 0x1C, 0xDC, 0x14, 0xD4, 0xD5, 0x15, 0xD7, 0x17, 0x16, 0xD6, 0xD2, 0x12, 0x13, 0xD3,
0x11, 0xD1, 0xD0, 0x10, 0xF0, 0x30, 0x31, 0xF1, 0x33, 0xF3, 0xF2, 0x32, 0x36, 0xF6, 0xF7,
0x37, 0xF5, 0x35, 0x34, 0xF4, 0x3C, 0xFC, 0xFD, 0x3D, 0xFF, 0x3F, 0x3E, 0xFE, 0xFA, 0x3A,
0x3B, 0xFB, 0x39, 0xF9, 0xF8, 0x38, 0x28, 0xE8, 0xE9, 0x29, 0xEB, 0x2B, 0x2A, 0xEA, 0xEE,
0x2E, 0x2F, 0xEF, 0x2D, 0xED, 0xEC, 0x2C, 0xE4, 0x24, 0x25, 0xE5, 0x27, 0xE7, 0xE6, 0x26,
0x22, 0xE2, 0xE3, 0x23, 0xE1, 0x21, 0x20, 0xE0, 0xA0, 0x60, 0x61, 0xA1, 0x63, 0xA3, 0xA2,
0x62, 0x66, 0xA6, 0xA7, 0x67, 0xA5, 0x65, 0x64, 0xA4, 0x6C, 0xAC, 0xAD, 0x6D, 0xAF, 0x6F,
0x6E, 0xAE, 0xAA, 0x6A, 0x6B, 0xAB, 0x69, 0xA9, 0xA8, 0x68, 0x78, 0xB8, 0xB9, 0x79, 0xBB,
0x7B, 0x7A, 0xBA, 0xBE, 0x7E, 0x7F, 0xBF, 0x7D, 0xBD, 0xBC, 0x7C, 0xB4, 0x74, 0x75, 0xB5,
0x77, 0xB7, 0xB6, 0x76, 0x72, 0xB2, 0xB3, 0x73, 0xB1, 0x71, 0x70, 0xB0, 0x50, 0x90, 0x91,
0x51, 0x93, 0x53, 0x52, 0x92, 0x96, 0x56, 0x57, 0x97, 0x55, 0x95, 0x94, 0x54, 0x9C, 0x5C,
0x5D, 0x9D, 0x5F, 0x9F, 0x9E, 0x5E, 0x5A, 0x9A, 0x9B, 0x5B, 0x99, 0x59, 0x58, 0x98, 0x88,
0x48, 0x49, 0x89, 0x4B, 0x8B, 0x8A, 0x4A, 0x4E, 0x8E, 0x8F, 0x4F, 0x8D, 0x4D, 0x4C, 0x8C,
0x44, 0x84, 0x85, 0x45, 0x87, 0x47, 0x46, 0x86, 0x82, 0x42, 0x43, 0x83, 0x41, 0x81, 0x80,
0x40
};
}
}
Не слабый такой код, есть вариант без таблицы, но более медленный (необходима побитовая обработка данных), в любом случае способный вынести мозг как программисту, так и микроконтроллеру. Не во всякий микроконтроллер алгоритм с таблицей влезет вообще.
Давайте разберем алгоритмы, которые вообще могут подтвердить целостность данных невысокой ценой.
Бит четности (1-битная контрольная сумма)
На первом месте простой бит четности. При необходимости формируется аппаратно, принцип простейший, и подробно расписан в википедии. Недостаток только один, пропускает двойные ошибки (и вообще четное число ошибок), когда четность всех бит не меняется. Можно использовать для сбора статистики о наличии ошибок в потоке передаваемых данных, но целостность данных не гарантирует, хотя и снижает вероятность пропущенной ошибки на 50% (зависит, конечно, от типа помех на линии, в данном случае подразумевается что число четных и нечетных сбоев равновероятно).
Для включения бита четности, часто и код никакой не нужен, просто указываем что UART должен задействовать бит четности. Типично, просто указываем:
включение бита четности на микроконтроллере
void setup(){
Serial.begin(9600,SERIAL_8N1); // по умолчанию, бит четности выключен;
Serial1.begin(38400,SERIAL_8E1); // бит четности включен
Serial.println("Hello Computer");
Serial1.println("Hello Serial 1");
}
Часто разработчики забывают даже, что UART имеет на борту возможность проверки бита четности. Кроме целостности передаваемых данных, это позволяет избежать устойчивого срыва синхронизации (например при передаче данных по радиоканалу), когда полезные данные могу случайно имитировать старт и стоп биты, а вместо данных на выходе буфера старт и стоп биты в случайном порядке.
8-битная контрольная сумма
Если контроля четности мало (а этого обычно мало), добавляется дополнительная контрольная сумма. Рассчитать контрольную сумму, можно как сумму ранее переданных байт, просто и логично
Естественно биты переполнения не учитываем, результат укладываем в выделенные под контрольную сумму 8 бит. Можно пропустить ошибку, если при случайном сбое один байт увеличится на некоторое значение, а другой байт уменьшится на то же значение. Контрольная сумма не изменится. Проведем эксперимент по передаче данных. Исходные данные такие:
- Блок данных 8 байт.
- Заполненность псевдослучайными данными Random($FF+1)
- Случайным образом меняем 1 бит в блоке данных операцией XOR со специально подготовленным байтом, у которого один единичный бит на случайной позиции.
- Повторяем предыдущий пункт 10 раз, при этом может получится от 0 до 10 сбойных бит (2 ошибки могут накладываться друг на друга восстанавливая данные), вариант с 0 сбойных бит игнорируем в дальнейшем как бесполезный для нас.
Передаем виртуальную телеграмму N раз. Идеальная контрольная сумма выявит ошибку по количеству доступной ей информации о сообщении, больше информации, выше вероятность выявления сбойной телеграммы. Вероятность пропустить ошибку, для 1 бита контрольной суммы:
.
Для 8 бит:
,
на 256 отправленных телеграмм с ошибкой, одна пройдет проверку контрольной суммы. Смотрим статистику от виртуальной передачи данных, с помощью простой тестовой программы:
Статистика
1: 144 (тут и далее — вероятность прохождения ошибки)
1: 143
1: 144
1: 145
1: 144
1: 142
1: 143
1: 143
1: 142
1: 140
Общее число ошибок 69892 из 10 млн. итераций, или 1: 143.078
Или условный КПД=55%, от возможностей «идеальной» контрольной суммы. Такова плата за простоту алгоритма и скорость обработки данных. В целом, для многих применений, алгоритм работоспособен. Используется одна операция сложения и одна переменная 8-битовая. Нет возможности не корректной реализации. Поэтому алгоритм и применяется в контроллерах ADAMS, ICP, в составе протокола DCON (там дополнительно может быть включен бит четности, символы только ASCI, что так же способствует повышению надежности передачи данных и итоговая надежность несколько выше, так как часть ошибок выявляется по другим, дополнительным признакам, не связанных с контрольной суммой).
Не смотря на вероятность прохождения ошибки 1:143, вероятность обнаружения ошибки лучше, чем 1:256 невозможна теоретически. Потери в качестве работы есть, но не всегда это существенно. Если нужна надежность выше, нужно использовать контрольную сумму с большим числом бит. Или, иначе говоря, простая контрольная сумма, недостаточно эффективно использует примерно 0.75 бита из 8 имеющихся бит информации в контрольной сумме.
Для сравнения применим, вместо суммы, побитовое сложение XOR. Стало существенно хуже, вероятность обнаружения ошибки 1:67 или 26% от теоретического предела. Упрощенно, это можно объяснить тем, что XOR меняет при возникновении ошибке еще меньше бит в контрольной сумме, ниже отклик на единичный битовый сбой, и повторной ошибке более вероятно вернуть контрольную сумму в исходное состояние.
Так же можно утверждать, что контрольная сумма по XOR представляет из себя 8 независимых контрольных сумм из 1 бита. Вероятность того, что ошибка придется на один из 8 бит равна 1:8, вероятность двойного сбоя 1:64, что мы и наблюдаем, теоретическая величина совпала с экспериментальными данными.
Нам же нужен такой алгоритм, чтобы заменял при единичной ошибке максимальное количество бит в контрольной сумме. Но мы, в общей сложности, ограниченны сложностью алгоритма, и ресурсами в нашем распоряжении. Не во всех микроконтроллерах есть аппаратный блок расчета CRC. Но, практически везде, есть блок умножения. Рассчитаем контрольную сумму как произведение последовательности байт, на некоторую «магическую» константу:
CRC=CRC + byte*211
Константа должна быть простой, и быть достаточно большой, для изменения большего числа бит после каждой операции, 211 вполне подходит, проверяем:
Статистика
1: 185
1: 186
1: 185
1: 185
1: 193
1: 188
1: 187
1: 194
1: 190
1: 200
Всего 72% от теоретического предела, небольшое улучшение перед простой суммой. Алгоритм в таком виде не имеет смысла. В данном случае теряется важная информация из отбрасываемых старших 8..16 бит, а их необходимо учитывать. Проще всего, смешать функцией XOR с младшими битами 1..8. Приходим к еще более интенсивной модификации контрольной суммы, желательно с минимальным затратами ресурсов. Добавляем фокус из криптографических алгоритмов
CRC=CRC + byte*211
CRC= CRC XOR (CRC SHR 8); // "миксер" битовый, далее его применяем везде
CRC=CRC AND $FF; //или просто возвращаем результат как 8, а не 16 бит
- Промежуточная CRC для первого действия 16-битная (после вычислений обрезается до 8 бит) и в дальнейшем работаем как с 8-битной, если у нас 8-битный микроконтроллер это ускорит обработку данных.
- Возвращаем старшие биты и перемешиваем с младшими.
Проверяем:
Статистика
1: 237
1: 234
1: 241
1: 234
1: 227
1: 238
1: 235
1: 233
1: 231
1: 236
Результат 91% от теоретического предела. Вполне годится для применения.
Если в микроконтроллере нет блока умножения, можно имитировать умножение операций сложения, смещения и XOR. Суть процесса такая же, модифицированный ошибкой бит, равномерно «распределяется» по остальным битам контрольной суммы.
CRC := (CRC shl 3) + byte;
CRC := (CRC shl 3) + byte;
CRC:=(CRC XOR (CRC SHR 8)) ; // как и в предыдущем алгоритме
Результат:
Статистика
1: 255
1: 257
1: 255
1: 255
1: 254
1: 255
1: 250
1: 254
1: 256
1: 254
На удивление хороший результат. Среднее значение 254,5 или 99% от теоретического предела, операций немного больше, но все они простые и не используется умножение.
Если для внутреннего хранения промежуточных значений контрольной суммы отдать 16 бит переменную (но передавать по линии связи будем только младшие 8 бит), что не проблема даже для самого слабого микроконтроллера, получим некоторое улучшение работы алгоритма. В целом экономить 8 бит нет особого смысла, и 8-битовая промежуточная переменная использовалась ранее просто для упрощения понимания работы алгоритма.
Статистика
1: 260
1: 250
1: 252
1: 258
1: 261
1: 255
1: 254
1: 261
1: 264
1: 262
Что соответствует 100.6% от теоретического предела, вполне хороший результат для такого простого алгоритма из одной строчки:
CRC:=CRC + byte*44111; // все переменные 16-битные
Используется полноценное 16-битное умножение. Опять же не обошлось без магического числа 44111 (выбрано из общих соображений без перебора всего подмножества чисел). Более точно, константу имеет смысл подбирать, только определившись с предполагаемым типом ошибок в линии передачи данных.
Столь высокий результат объясняется тем, что 2 цикла умножения подряд, полностью перемешивают биты, что нам и требовалось. Исключением, похоже, является последний байт телеграммы, особенно его старшие биты, они не полностью замешиваются в контрольную сумму, но и вероятность того, что ошибка придется на них невелика, примерно 4%. Эта особенность практически ни как не проявляется статистически, по крайней мере на моем наборе тестовых данных и ошибке ограниченной 10 сбойными битами. Для исключения этой особенности можно делать N+1 итераций, добавив виртуальный байт в дополнение к имеющимся в тестовом блоке данных (но это усложнение алгоритма).
Вариант без умножения с аналогичным результатом. Переменная CRC 16-битная, данные 8-битные, результат работы алгоритма — младшие 8 бит найденной контрольной суммы:
CRC := (CRC shl 2) + CRC + byte;
CRC := (CRC shl 2) + CRC + byte;
CRC:=(CRC XOR (CRC SHR 8));
Результат 100.6% от теоретического предела.
Вариант без умножения более простой, оставлен самый минимум функций, всего 3 математических операции:
CRC:=byte + CRC;
CRC:=CRC xor (CRC shr 2);
Результат 86% от теоретического предела.
В этом случае потери старших бит нет, они возвращаются в младшую часть переменной через функцию XOR (битовый миксер).
Небольшое улучшение в некоторых случаях дает так же:
- Двойной проход по обрабатываемым данным. Но ценой усложнения алгоритма (внешний цикл нужно указать), ценой удвоения времени обработки данных.
- Обработка дополнительного, виртуального байта в конце обрабатываемых данных, усложнения алгоритма и времени работы алгоритма практически нет.
- Использование переменной для хранения контрольной суммы большей по разрядности, чем итоговая контрольная сумма и перемешивание младших бит со старшими.
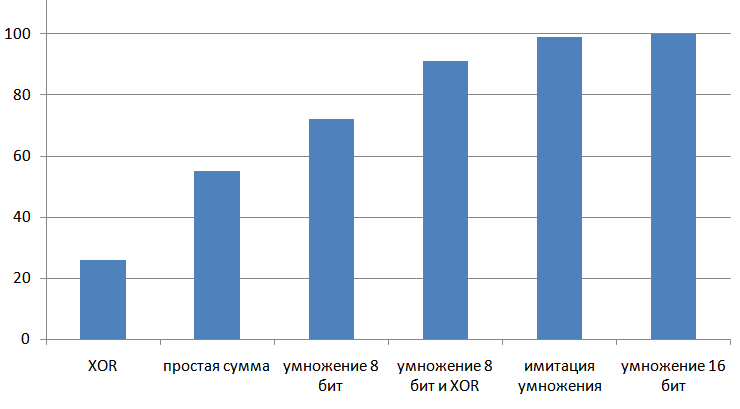
Результат работы рассмотренных алгоритмов, от простых и слабых, к сложным и качественным:
16-битная контрольная сумма
Далее, предположим что нам мало 8 бит для формирования контрольной суммы.
Следующий вариант 16 бит, и теоретическая вероятность ошибки переданных данных 1:65536, что намного лучше. Надежность растет по экспоненте. Но, как побочный эффект, растет количество вспомогательных данных, на примере нашей телеграммы, к 8 байтам полезной информации добавляется 2 байта контрольной суммы.
Простые алгоритмы суммы и XOR, применительно к 16-битной и последующим CRC не рассматриваем вообще, они практически не улучают качество работы, по сравнению с 8-битным вариантов.
Модифицируем алгоритм для обработки контрольной суммы разрядностью 16 бит, надо отметить, что тут так же есть магическое число 8 и 44111, значительное и необоснованное их изменение ухудшает работу алгоритма в разы.
CRC:=CRC + byte16*44111; //все данные 16-битные
CRC:=CRC XOR (CRC SHR 8);
Результат:
Статистика
1: 43478
1: 76923
1: 83333
1: 50000
1: 83333
1: 100000
1: 90909
1: 47619
1: 50000
1: 90909
Что соответствует 109% от теоретического предела. Присутствует ошибка измерений, но это простительно для 10 млн. итераций. Так же сказывается алгоритм создания, и вообще тип ошибок. Для более точного анализа, в любом случае нужно подстраивать условия под ошибки в конкретной линии передачи данных.
Дополнительно отмечу, что можно использовать 32-битные промежуточные переменные для накопления результата, а итоговую контрольную сумму использовать как младшие 16 бит. Во многих случаях, при любой разрядности контрольной суммы, так несколько улучшается качество работы алгоритма.
32-битная контрольная сумма
Перейдем к варианту 32-битной контрольной суммы. Появляется проблема со временем отводимым для анализа статистических данных, так как число переданных телеграмм уже сравнимо с 2^32. Алгоритм такой же, магические числа меняются в сторону увеличения
CRC:=CRC+byte32*$990C9AB5;
CRC:=CRC XOR (CRC SHR 16);
За 10 млн. итераций ошибка не обнаружена. Чтобы ускорить сбор статистики обрезал CRC до 24 бит:
CRC = CRC AND $FFFFFF;
Результат, из 10 млн. итераций ошибка обнаружена 3 раза
Статистика
1: 1000000
1: no
1: no
1: no
1: 1000000
1: no
1: 1000000
1: no
1: no
1: no
Вполне хороший результат и в целом близок к теоретическому пределу для 24 бит контрольной суммы (1:16777216). Тут надо отметить что функция контроля целостности данных равномерно распределена по всем битам CRC, и вполне возможно их отбрасывание с любой стороны, если есть ограничение на размер передаваемой CRC.
Для полноценных 32 бит, достаточно долго ждать результата, ошибок просто нет, за приемлемое время ожидания.
Вариант без умножения:
CRC := (CRC shl 5) + CRC + byte;
CRC := (CRC shl 5) + CRC;
CRC:=CRC xor (CRC shr 16);
Сбоя для полноценной контрольной суммы дождаться не получилось. Контрольная сумма урезанная до 24 бит показывает примерно такие же результаты, 8 ошибок на 100 млн. итераций. Промежуточная переменная CRC 64-битная.
64-битная контрольная сумма
Ну и напоследок 64-битная контрольная сумма, максимальная контрольная сумма, которая имеет смысл при передачи данных на нижнем уровне:
CRC:=CRC+byte64*$5FB7D03C81AE5243;
CRC:=CRC XOR (CRC SHR 8); // магическое число 1..20
Дождаться ошибки передачи данных, до конца существования вселенной, наверное не получится 
Метод аналогичный тому, какой применили для CRC32 показал аналогичные результаты. Больше бит оставляем, выше надежность в полном соответствии с теоретическим пределом. Проверял на младших 20 и 24 битах, этого кажется вполне достаточным, для оценки качества работы алгоритма.
Так же можно применить для 128-битных чисел (и еще больших), главное подобрать корректно 128-битные магические константы. Но это уже явно не для микроконтроллеров, такие числа и компилятор не поддерживает.
Комментарии
В целом метод умножения похож на генерацию псевдослучайной последовательности, только с учетом полезных данных участвующих в процессе.
Рекомендую к использованию в микроконтроллерах, или для проверки целостности любых переданных данных. Вполне рабочий метод, уже как есть, не смотря на простоту алгоритма.
Мой проект по исследованию CRC на гитхаб.
Далее интересно было бы оптимизировать алгоритм на более реальных данных (не псевдослучайные числа по стандартному алгоритму), подобрать более подходящие магические числа под ряд задач и начальных условий, думаю можно еще выиграть доли процента по качеству работы алгоритма. Оптимизировать алгоритм по скорости, читаемости кода (простоте алгоритма), качеству работы. В идеале получить и протестировать образцы кода для всех типов микроконтроллеров, для этого как-раз и нужны примеры с использованием умножения 8, 16, 32 битных данных, и без умножения вообще.
$\begingroup$
I have a table which stores all serial numbers of devices in my system:
|------------------------|--------------------------|
| # | Serial number (4 bytes) |
|------------------------|--------------------------|
| 1 | 0x???????? |
|------------------------|--------------------------|
| 2 | 0x???????? |
|------------------------|--------------------------|
| ... | ... |
|------------------------|--------------------------|
| 31 | 0x???????? |
|------------------------|--------------------------|
If I add a device to the system the position in the table is not predictable. If something in the system changes (e.g. add one or more devices, remove one or more devices, replace a device) I want to detect with a «high» propability that the system change. Therefor I want to use a CRC-32. In my system I have at least always 2 devices but max. 31 devcies. Meaning that the input of the CRC can vary between $2^{64}$ to $2^{992}$ different input streams.
As far as I understand:
- The minimum input should be at least 32 bits
- The most important is to use the right generator polynom. E.g.:
- CRC-32
- CRC-32-IEEE
- CRC-32C
- The selection of generator polynom depends on:
- Input stream length
- Error-detection-feasability
- Collision probablility
- Detection of a single bit error: All CRC’s can do this
- Detection of burst errors: All $n$-bit CRC’s can detect burst errors up to $n$ consecutive bits. Also meaning appending new $n$-bit to the end of the input stream.
My concerns are the collision probability of the CRC32 is to high and due to that I don’t detect a change in the configuration. Therefor I want to calcualte this probabilities and my questions are:
-
Is CRC the right method to use for my use case? If not what would be the best?
-
What is the «best» generator polynom for my use case?
-
How to cacluate the error-detection-feasability or collision probability if more then 32 consecutive bits change?
-
How to cacluate the error-detection-feasability or collision probability if $x$ not consecutive (different locations in the complete input stream) bits change?
Raphael♦
71.9k28 gold badges177 silver badges384 bronze badges
asked Jan 10, 2018 at 17:52
$\endgroup$
$\begingroup$
There’s nothing in your requirements that forces you to use a CRC32. You could use any checksum. If the collision probability for a CRC32seems too high, use a different checksum.
For instance, if you use SHA256, you will never have to worry about collisions — for all engineering purposes, you can treat them as impossible (something that will never happen in your lifetime). And then you won’t need to worry about selecting generator polynomials or anything like that; someone else has done all that work for you. You just use the standard SHA256 algorithm.
P.S. Using a basic checksum algorithm will require you to recompute the checksum on the entire table any time you insert or delete one row. If that’s too slow, there are a number of schemes to speed that up, such as a Merkle hash tree.
answered Jan 10, 2018 at 22:16
D.W.♦D.W.
154k19 gold badges219 silver badges451 bronze badges
$\endgroup$
2
Аннотация: Контроль по четности, CRC, алгоритм Хэмминга. Введение в коды Рида-Соломона: принципы, архитектура и реализация. Метод коррекции ошибок FEC (Forward Error Correction).
Каналы передачи данных ненадежны (шумы, наводки и т.д.), да и само оборудование обработки информации работает со сбоями. По этой причине важную роль приобретают механизмы детектирования ошибок. Ведь если ошибка обнаружена, можно осуществить повторную передачу данных и решить проблему. Если исходный код по своей длине равен полученному коду, обнаружить ошибку передачи не предоставляется возможным. Можно, конечно, передать код дважды и сравнить, но это уже двойная избыточность.
Простейшим способом обнаружения ошибок является контроль по четности. Обычно контролируется передача блока данных ( М бит). Этому блоку ставится в соответствие кодовое слово длиной N бит, причем N>M. Избыточность кода характеризуется величиной 1-M/N. Вероятность обнаружения ошибки определяется отношением M/N (чем меньше это отношение, тем выше вероятность обнаружения ошибки, но и выше избыточность).
При передаче информации она кодируется таким образом, чтобы с одной стороны характеризовать ее минимальным числом символов, а с другой – минимизировать вероятность ошибки при декодировании получателем. Для выбора типа кодирования важную роль играет так называемое расстояние Хэмминга.
Пусть А и Б — две двоичные кодовые последовательности равной длины. Расстояние Хэмминга между двумя этими кодовыми последовательностями равно числу символов, которыми они отличаются. Например, расстояние Хэмминга между кодами 00111 и 10101 равно 2.
Можно показать, что для детектирования ошибок в n битах схема кодирования требует применения кодовых слов с расстоянием Хэмминга не менее N + 1. Можно также показать, что для исправления ошибок в N битах необходима схема кодирования с расстоянием Хэмминга между кодами не менее 2N + 1. Таким образом, конструируя код, мы пытаемся обеспечить расстояние Хэмминга между возможными кодовыми последовательностями большее, чем оно может возникнуть из-за ошибок.
Широко распространены коды с одиночным битом четности. В этих кодах к каждым М бит добавляется 1 бит, значение которого определяется четностью (или нечетностью) суммы этих М бит. Так, например, для двухбитовых кодов 00, 01, 10, 11 кодами с контролем четности будут 000, 011, 101 и 110. Если в процессе передачи один бит будет передан неверно, четность кода из М+1 бита изменится.
Предположим, что частота ошибок ( BER – Bit Error Rate) равна р = 10-4. В этом случае вероятность передачи 8 бит с ошибкой составит 1 – (1 – p)8 = 7,9 х 10-4. Добавление бита четности позволяет детектировать любую ошибку в одном из переданных битах. Здесь вероятность ошибки в одном из 9 битов равна 9p(1 – p)8. Вероятность же реализации необнаруженной ошибки составит 1 – (1 – p)9 – 9p(1 – p)8 = 3,6 x 10-7. Таким образом, добавление бита четности уменьшает вероятность необнаруженной ошибки почти в 1000 раз. Использование одного бита четности типично для асинхронного метода передачи. В синхронных каналах чаще используется вычисление и передача битов четности как
для строк, так и для столбцов передаваемого массива данных. Такая схема позволяет не только регистрировать, но и исправлять ошибки в одном из битов переданного блока.
Контроль по четности достаточно эффективен для выявления одиночных и множественных ошибок в условиях, когда они являются независимыми. При возникновении ошибок в кластерах бит метод контроля четности неэффективен, и тогда предпочтительнее метод вычисления циклических сумм ( CRC — Cyclic Redundancy Check). В этом методе передаваемый кадр делится на специально подобранный образующий полином. Дополнение остатка от деления и является контрольной суммой.
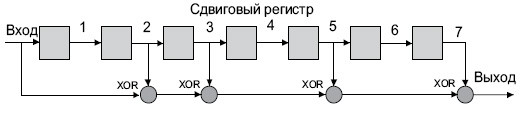
В Ethernet вычисление CRC производится аппаратно. На
рис.
4.1 показан пример реализации аппаратного расчета CRC для образующего полинома R(x) = 1 + x2 + x3 + x5 + x7. В этой схеме входной код приходит слева.
Рис.
4.1.
Схема реализации расчета CRC
Эффективность CRC для обнаружения ошибок на многие порядки выше простого контроля четности. В настоящее время стандартизовано несколько типов образующих полиномов. Для оценочных целей можно считать, что вероятность невыявления ошибки в случае использования CRC, если ошибка на самом деле имеет место, равна (1/2)r, где r — степень образующего полинома.
| CRC -12 | x12 + x11 + x3 + x2 + x1 + 1 |
| CRC -16 | x16 + x15 + x2 + 1 |
| CRC -CCITT | x16 + x12 + x5 + 1 |
4.1. Алгоритмы коррекции ошибок
Исправлять ошибки труднее, чем их детектировать или предотвращать. Процедура коррекции ошибок предполагает два совмещеных процесса: обнаружение ошибки и определение места (идентификации сообщения и позиции в сообщении). После решения этих двух задач исправление тривиально — надо инвертировать значение ошибочного бита. В наземных каналах связи, где вероятность ошибки невелика, обычно используется метод детектирования ошибок и повторной пересылки фрагмента, содержащего дефект. Для спутниковых каналов с типичными для них большими задержками системы коррекции ошибок становятся привлекательными. Здесь используют коды Хэмминга или коды свертки.
Код Хэмминга представляет собой блочный код, который позволяет выявить и исправить ошибочно переданный бит в пределах переданного блока. Обычно код Хэмминга характеризуется двумя целыми числами, например, (11,7), используемыми при передаче 7-битных ASCII-кодов. Такая запись говорит, что при передаче 7-битного кода используется 4 контрольных бита (7 + 4 = 11). При этом предполагается, что имела место ошибка в одном бите и что ошибка в двух или более битах существенно менее вероятна. С учетом этого исправление ошибки осуществляется с определенной вероятностью. Например, пусть возможны следующие правильные коды (все они, кроме первого и последнего, отстоят друг от друга на расстояние Хэмминга 4):
00000000
11110000
00001111
11111111
При получении кода 00000111 нетрудно предположить, что правильное значение полученного кода равно 00001111. Другие коды отстоят от полученного на большее расстояние Хэмминга.
Рассмотрим пример передачи кода буквы s = 0x073 = 1110011 с использованием кода Хэмминга (11,7). Таблица 4.2.
| Позиция бита | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение бита | 1 | 1 | 1 | * | 0 | 0 | 1 | * | 1 | * | * |
Символами * помечены четыре позиции, где должны размещаться контрольные биты. Эти позиции определяются целой степенью 2 (1, 2, 4, 8 и т.д.). Контрольная сумма формируется путем выполнения операции XoR (исключающее ИЛИ) над кодами позиций ненулевых битов. В данном случае это 11, 10, 9, 5 и 3. Вычислим контрольную сумму:
| 11= | 1011 |
| 10= | 1010 |
| 09= | 1001 |
| 05= | 0101 |
| 03= | 0011 |
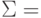 |
1110 |
Таким образом, приемник получит код
| Позиция бита | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение бита | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
Просуммируем снова коды позиций ненулевых битов и получим нуль;
| 11= | 1011 |
| 10= | 1010 |
| 09= | 1001 |
| 08= | 1000 |
| 05= | 0101 |
| 04= | 0100 |
| 03= | 0011 |
| 02= | 0010 |
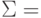 |
0000 |
Ну а теперь рассмотрим два случая ошибок в одном из битов посылки, например в бите 7 (1 вместо 0) и в бите 5 (0 вместо 1). Просуммируем коды позиций ненулевых битов еще раз:
|
|
В обоих случаях контрольная сумма равна позиции бита, переданного с ошибкой. Теперь для исправления ошибки достаточно инвертировать бит, номер которого указан в контрольной сумме. Понятно, что если ошибка произойдет при передаче более чем одного бита, код Хэмминга при данной избыточности окажется бесполезен.
В общем случае код имеет N = M + C бит и предполагается, что не более чем один бит в коде может иметь ошибку. Тогда возможно N+1 состояние кода (правильное состояние и n ошибочных). Пусть М = 4, а N = 7, тогда слово-сообщение будет иметь вид: M4, M3, M2, C3, M1, C2, C1. Теперь попытаемся вычислить значения С1, С2, С3. Для этого используются уравнения, где все операции представляют собой сложение по модулю 2:
С1 = М1 + М2 + М4 С2 = М1 + М3 + М4 С3 = М2 + М3 + М4
Для определения того, доставлено ли сообщение без ошибок, вычисляем следующие выражения (сложение по модулю 2):
С11 = С1 + М4 + М2 + М1 С12 = С2 + М4 + М3 + М1 С13 = С3 + М4 + М3 + М2
Результат вычисления интерпретируется следующим образом:
| C11 | C12 | C13 | Значение |
|---|---|---|---|
| 1 | 2 | 4 | Позиция бит |
| 0 | 0 | 0 | Ошибок нет |
| 0 | 0 | 1 | Бит С3 неверен |
| 0 | 1 | 0 | Бит С2 неверен |
| 0 | 1 | 1 | Бит M3 неверен |
| 1 | 0 | 0 | Бит С1 неверен |
| 1 | 0 | 1 | Бит M2 неверен |
| 1 | 1 | 0 | Бит M1 неверен |
| 1 | 1 | 1 | Бит M4 неверен |
Описанная схема легко переносится на любое число n и М.
Число возможных кодовых комбинаций М помехоустойчивого кода делится на n классов, где N — число разрешенных кодов. Разделение на классы осуществляется так, чтобы в каждый класс вошел один разрешенный код и ближайшие к нему (по расстоянию Хэмминга ) запрещенные коды. В процессе приема данных определяется, к какому классу принадлежит пришедший код. Если код принят с ошибкой, он заменяется ближайшим разрешенным кодом. При этом предполагается, что кратность ошибки не более qm.
В теории кодирования существуют следующие оценки максимального числа N n -разрядных кодов с расстоянием D.
| d=1 | n=2n |
| d=2 | n=2n-1 |
| d=3 | N 2n/(1 + n) |
| d = 2q + 1 | (для кода Хэмминга это неравенство превращается в равенство) |
В случае кода Хэмминга первые k разрядов используются в качестве информационных, причем
K = n – log(n + 1), откуда следует (логарифм по основанию 2), что k может принимать значения 0, 1, 4, 11, 26, 57 и т.д., это и определяет соответствующие коды Хэмминга (3,1); (7,4); (15,11); (31,26); (63,57) и т.д.
Обобщением кодов Хэмминга являются циклические коды BCH (Bose-Chadhuri-hocquenghem). Эти коды имеют широкий выбор длин и возможностей исправления ошибок.
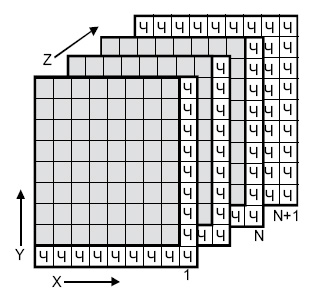
Одной из старейших схем коррекции ошибок является двух-и трехмерная позиционная схема (
рис.
4.2). Для каждого байта вычисляется бит четности (бит <Ч>, направление Х). Для каждого столбца также вычисляется бит четности (направление Y. Производится вычисление битов четности для комбинаций битов с координатами (X,Y) (направление Z, слои с 1 до N ). Если при транспортировке будет искажен один бит, он может быть найден и исправлен по неверным битам четности X и Y. Если же произошло две ошибки в одной из плоскостей, битов четности данной плоскости недостаточно. Здесь поможет плоскость битов четности N+1.
Таким образом, на 512 передаваемых байтов данных пересылается около 200 бит четности.
Рис.
4.2.
Позиционная схема коррекции ошибок
2004 г.
2.7. Обнаружение ошибок
Семёнов Ю.А. (ГНЦ ИТЭФ), book.itep.ru
Каналы передачи данных ненадежны, да и само оборудование обработки информации работает со сбоями. По этой причине важную роль приобретают механизмы детектирования ошибок. Ведь если ошибка обнаружена, можно осуществить повторную передачу данных и решить проблему. Если исходный код по своей длине равен полученному коду, обнаружить ошибку передачи не предоставляется возможным.
Простейшим способом обнаружения ошибок является контроль по четности. Обычно контролируется передача блока данных (М бит). Этому блоку ставится в соответствие кодовое слово длиной N бит, причем N>M. Избыточность кода характеризуется величиной 1-M/N. Вероятность обнаружения ошибки определяется отношением M/N (чем меньше это отношение, тем выше вероятность обнаружения ошибки, но и выше избыточность).
При передаче информации она кодируется таким образом, чтобы с одной стороны характеризовать ее минимальным числом символов, а с другой – минимизировать вероятность ошибки при декодировании получателем. Для выбора типа кодирования важную роль играет так называемое расстояние Хэмминга.
Пусть А и Б две двоичные кодовые последовательности равной длины. Расстояние Хэмминга между двумя этими кодовыми последовательностями равно числу символов, которыми они отличаются. Например, расстояние Хэмминга между кодами 00111 и 10101 равно 2.
Можно показать, что для детектирования ошибок в n битах, схема кодирования требует применения кодовых слов с расстоянием Хэмминга не менее N+1. Можно также показать, что для исправления ошибок в N битах необходима схема кодирования с расстоянием Хэмминга между кодами не менее 2N+1. Таким образом, конструируя код, мы пытаемся обеспечить расстояние Хэмминга между возможными кодовыми последовательностями больше, чем оно может возникнуть из-за ошибок.
Широко распространены коды с одиночным битом четности. В этих кодах к каждым М бит добавляется 1 бит, значение которого определяется четностью (или нечетностью) суммы этих М бит. Так, например, для двухбитовых кодов 00, 01, 10, 11 кодами с контролем четности будут 000, 011, 101 и 110. Если в процессе передачи один бит будет передан неверно, четность кода из М+1 бита изменится.
Предположим, что частота ошибок (BER) равна р=10-4. В этом случае вероятность передачи 8 бит с ошибкой составит 1-(1-p)8=7,9х10-4. Добавление бита четности позволяет детектировать любую ошибку в одном из переданных битах. Здесь вероятность ошибки в одном из 9 бит равна 9p(1-p)8. Вероятность же реализации необнаруженной ошибки составит 1-(1-p)9 – 9p(1-p)8 = 3,6×10-7. Таким образом, добавление бита четности уменьшает вероятность необнаруженной ошибки почти в 1000 раз. Использование одного бита четности типично для асинхронного метода передачи. В синхронных каналах чаще используется вычисление и передача битов четности как для строк, так и для столбцов передаваемого массива данных. Такая схема позволяет не только регистрировать но и исправлять ошибки в одном из битов переданного блока.
Контроль по четности достаточно эффективен для выявления одиночных и множественных ошибок в условиях, когда они являются независимыми. При возникновении ошибок в кластерах бит метод контроля четности неэффективен и тогда предпочтительнее метод вычисления циклических сумм (CRC). В этом методе передаваемый кадр делится на специально подобранный образующий полином. Дополнение остатка от деления и является контрольной суммой.
В Ethernet Вычисление crc производится аппаратно (см. также ethernet). На рис. 2.7.1. показан пример реализации аппаратного расчета CRC для образующего полинома B(x)= 1 + x2 + x3 +x5 + x7. В этой схеме входной код приходит слева.
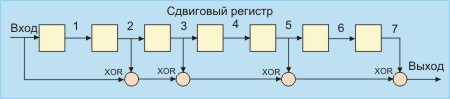
Рис. 2.7.1. Схема реализации расчета CRC
Эффективность CRC для обнаружения ошибок на многие порядки выше простого контроля четности. В настоящее время стандартизовано несколько типов образующих полиномов. Для оценочных целей можно считать, что вероятность невыявления ошибки в случае использования CRC, если ошибка на самом деле имеет место, равна (1/2)r, где r — степень образующего полинома.
| CRC-12 | x12 + x11 + x3 + x2 + x1 + 1 |
| CRC-16 | x16 + x15 + x2 + 1 |
| CRC-CCITT | x16 + x12 + x5 + 1 |
Назад: 2.6.5. Статический алгоритм Хафмана
Оглавление: Телекоммуникационные технологии
Вперёд: 2.8. Коррекция ошибок
Как видно из табл. 2.4, данный матричный код по сравнению с ранее рассмотренными имеет существенное преимущество по обеспечению достоверности передачи данных. Это объясняется его конструктивными особенностями, прежде всего каскадной структурой, и существенно большей избыточностью — 135 бит, по сравнению с ранее рассмотренными, где контрольная сумма составляла всего один байт. Кроме того, из данных табл. 2.4 видно, что для оценки эффективности матричного кода можно ограничиться вероятностью 4-кратной битовой ошибки в реальных каналах ДСК с p = 10 2.
2.3.Методы обнаружения ошибок помехоустойчивыми кодами CRC
Внастоящее время применяют более совершенные методы обнаружения ошибок, основанные на математических алгоритмах высшей алгебры. Наиболее популярными методами обнаружения ошибок в вычислительных сетях и сетях передачи данных являются методы с циклической избыточной суммой CRC (Cyclic Redundancy Check), для вычисления которой используются элементы высшей алгебры — теория групп, теория полей с операциями сложения, умножения и деления по определенным модулям. В большинстве случаев циклическая проверочная сумма, как известно, является остатком от деления одного, скажем, информационного, числа (или многочлена) на другое заданное число (или многочлен). Контроль за ошибками осуществляется сравнением переданной циклической проверочной суммы CRC и суммы, вычисленной на приемной стороне. Несовпадение CRC говорит о наличии (обнаружении) ошибок в принятом сообщении.
Всистемах передачи данных используются различные алгоритмы формирования циклической проверочной суммы CRC. При этом такие коды можно поделить на два класса:
1)с нулевыми начальными состояниями ячеек регистра деления как в кодере, так и в декодере;
2)с ненулевыми начальными состояниями ячеек регистра деления как
вкодере, так и в декодере.
Рассмотрим их более подробно.
2.3.1. Алгоритм с простой CRC
Этот алгоритм, названный «простым», относится к классическим систематическим циклическим (n;k)-кодам с числом избыточных элементов в кодовой комбинации, равным (n k) = m, где m — степень образующего примитивного многочлена P(x).
Рассмотрим, прежде всего, варианты кодов с простой CRC с нулевыми начальными состояниями ячеек регистров деления на многочлен P(x).
44
Напомним, что одним из свойств классического циклического кода является деление без остатка любой разрешенной комбинации кода в виде многочлена f (x) на образующий многочлен P(x).
Общий алгоритм кодирования классическим систематическим (n;k)-кодом состоит из следующих последовательных операций:
|
1) |
умножение исходного информационного многочлена длины k |
|
j(x) = a0 + a1x + a2x2 + ::: + ak 1xk 1 на одночлен xm; |
|
|
2) |
деление произведения xmj(x) на образующий многочлен P(x) степе- |
ни m и определение остатка от деления r(x) = r0 +r1x +r2x2 +::: +rm 1xm 1; 3) формирование разрешенной кодовой комбинации длины n
f (x) = r(x) + xmj(x).
Очевидно, что f (x) = 0 mod P(x) т. е. разрешенная кодовая комбинация f (x) делится на P(x) без остатка.
Алгоритм декодирования сводится к делению принятой комбинации h(x) на образующий многочлен. Если h(x) делится на P(x) без остатка (нулевой синдром), то считается, что в принятой комбинации ошибки отсутствуют и h(x) = f (x). Напротив, если остаток (синдром) не равен нулю, то это свидетельствует о наличии в принятой комбинации ошибок, которые обнаружены кодом. Другой часто используемый алгоритм декодирования сводится к вычислению CRC по принятым информационным элементам и сравнению с принятыми проверочными элементами. Если циклические проверочные элементы CRC совпадают, то считается, что ошибки в комбинации отсутствуют. И наоборот – несовпадение хотя бы в одном разряде сравниваемых контрольных сумм (CRC) будет говорить о наличии в принятой комбинации ошибок.
В литературе циклическую проверку, порожденную многочленом P(x) степени m, часто обозначают CRC-m.
Различают три варианта длин n комбинаций:
оптимальная полная длина n = 2m 1;
укороченный код с длиной комбинации n < 2m 1;
удлиненный код с n > 2m 1.
Рассмотрим особенности кодов CRC-m.
2.3.1.1.Оптимальный полный код CRC
Воптимальном варианте при n = 2m 1 наиболее полно проявляются свойства циклического кода:
деление разрешенных комбинаций f (x) на образующий многочлен P(x) без остатка;
45
поэлементная сумма по mod 2 двух или более разрешенных комбинаций порождает новую разрешенную комбинацию;
циклический сдвиг разрешенной комбинации также порождает другую разрешенную комбинацию;
наиболее оптимальным образом согласуются обнаруживающая способность кода и скорость кода k=n.
Из равенства n = 2m 1 следует равенство Хэмминга (n k) = m = log2(n + 1), доказывающее, что это действительно оптимальный (n;k)-код, имеющий плотную упаковку, минимальное кодовое расстояние Хэмминга dmin = 3 и способный в режиме исправления ошибок исправлять однократные ошибки. Такие циклические коды CRC не являются классическими кодами Хэмминга, их часто не совсем корректно называют кодами Хэмминга.
В режиме обнаружения ошибок такой код может гарантированно обнаруживать все однократные и двукратные ошибки. Кроме того, код сможет обнаруживать многие ошибки большей кратности dmin t n при условии, что комбинации таких ошибок не будут совпадать с разрешенными кодовыми комбинациями.
Вероятность появления необнаруживаемых ошибок в комбинации длины n = 2m 1 для канала ДСК будет определяться выражением
|
n |
|
|
Pно = å A(wi)pwi (1 p)n wi ; |
(2.18) |
|
wi=dmin |
где wi — вес разрешенной комбинации кода; A(wi) — количество разрешенных комбинаций с весом wi (эту характеристику называют еще весовым спектром кода); p — вероятность битовой ошибки в канале ДСК.
Для полных двоичных кодов, для которых n = 2m 1 и dmin = 3, весовой спектр находится как коэффициенты при zwi в разложении по степеням z
|
следующей функции [5]: |
i: |
|||
|
n(z) = n + 1 h(1 + z)n + n(1 + z) |
2 |
1 |
(1 z) 2 |
|
|
1 |
n |
n+1 |
Например, для циклического кода (n;k) = (15;11) с CRC-4 весовой спектр представлен в табл. 2.5.
Таблица 2.5
Весовой спектр циклического кода (15;11)
|
wi |
0 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
15 |
|
A(wi) |
1 |
35 |
105 |
168 |
280 |
435 |
435 |
280 |
168 |
105 |
35 |
1 |
46
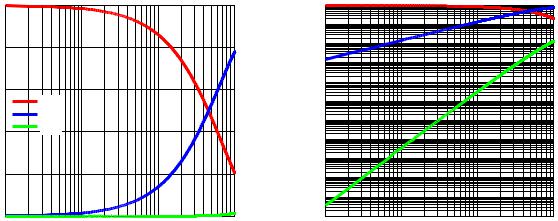
Вероятность приема n-элементной комбинации с обнаруживаемыми ошибками будем определять из выражения: Pоо = 1 Pпп Pно, где Pпп — вероятность правильного приема комбинации, равная Pпп = (1 p)n.
Пример 2.2. Рассчитаем вероятностные характеристики для кода
(n;k) = (15;11) с CRC-4 в канале ДСК с битовой вероятностью ошибки p = 10 3.
Вероятность правильного приема Pпп = (1 p)15 = (0;999)15 = 0;9851. Расчетные вероятности необнаруживаемых ошибок кратности wi и суммарная вероятность Pно в соответствии с формулой (2.18) представлены в
табл. 2.6.
Таблица 2.6 Вероятности необнаруживаемых ошибок для циклического кода (15;11)
|
wi |
3 |
4 |
5 |
6 |
7 |
Pно сумм. |
|
|
Pно(wi) |
3;46 10 8 |
1;04 10 10 |
1;66 10 13 |
2;77 10 16 |
4;31 10 19 |
3;46 10 8 |
Как видно из табл. 2.6, при p = 10 3 в канале ДСК для оценки вероятности необнаруживаемых ошибок можно ограничиться весом wi = 3.
Учитывая вычисленные значения Pпп и Pно, вероятность появления в комбинации обнаруживаемых ошибок будет равна Pоо = 1;5 10 2.
На рис. 2.6 приведены расчетные вероятностные характеристики циклического кода (n;k) = (15;11) с CRC-4 для канала ДСК.
Вероятностные характеристики
1
0.8
0.6
P
пппп
P
оооо
P
0.4 ноно
0.2
Вероятность битовой ошибки, p
Вероятностные характеристики
|
1e+0 |
|||
|
1e-1 |
|||
|
1e-2 |
|||
|
1e-3 |
|||
|
1e-4 |
|||
|
1e-5 |
|||
|
1e-6 |
|||
|
1e-7 |
|||
|
1e-8 |
|||
|
1e-9 |
|||
|
1e-10 |
|||
|
1e-11 |
1e-3 |
1e-2 |
1e-1 |
|
1e-4 |
Вероятность битовой ошибки, p
Рис. 2.6. Вероятностные характеристики циклического кода (n;k) = (15;11) с CRC-4 для канала ДСК
47
2.3.1.2. Укороченные CRC-m коды
При n < 2m 1 получим укороченный код с проверочной контрольной суммой CRC-m и числом информационных элементов k = n m. Такой код имеет меньшую относительную кодовую скорость k=n и, соответственно, большую относительную избыточность. Например, полный код (n;k) = (15;11) имеет скорость k=n = 0;733 и избыточность (n k)=n = 0;266. А укороченный (9;5)-код имеет скорость 0;555, а избыточность — 0;444. При этом минимальное кодовое расстояние остается равным dmin = 3, чем и определяется обнаруживающая способность укороченного кода. Вместе с тем, при оценке вероятностных характеристик необходимо учесть, что для укороченного кода поменяется весовой спектр, который чаще всего определяется путем моделирования.
В укороченном (n;k)-коде свойства циклических кодов сохраняются не полностью. Так, сохраняются свойство делимости разрешенной комбинации в виде многочлена f (x) на образующий многочлен P(x) без остатка и свойство линейности, но не сохраняется свойство циклических сдвигов, так как при-
митивный многочлен P(x) степени m не будет делителем двучлена (xn + 1), если n < 2m 1.
2.3.1.3.Удлиненные CRC-m коды
Вряде систем применяется код с CRC-m при длине комбинации n > 2m 1 при том же числе проверочных элементов m = n k. Такой код, по срав-
нению с оптимальным полным кодом, имеет большую относительную скорость k=n и, соответственно, меньшую относительную избыточность. Например, если взять код (20;16) вместо (15;11), то получим скорость k=n = 0;8 и избыточность 0;2. Особенностью такого кода является то, что у него, по сравнению с полным кодом, увеличится доля необнаруживаемых ошибок. Поясним, чем это вызвано.
Известно, что образующий многочлен P(x) степени m должен быть делителем двучлена (x2m 1 + 1). А так как в удлиненном коде n > 2m 1, то
в комбинации могут возникнуть такие двукратные ошибки с многочленом e(x) = xi(x2m 1 + 1), что i + (2m 1) n 1, а многочлен e(x) будет делиться
на двучлен (x2m 1 + 1) и, следовательно, на образующий многочлен P(x) без остатка. То есть такие двукратные ошибки не будут обнаруживаться кодом с CRC-m при длине комбинации n > 2m 1.
Кодирующее и декодирующее устройства циклического (n;k)-кода с «простой» CRC-m и dmin = 3 реализуются на базе регистра сдвига длиной m ячеек, осуществляющего для систематического кода деление на образующий
48
многочлен P(x) степени m. При этом перед началом процедуры кодирования и декодирования ячейки регистров сдвига должны быть обнулены.
2.3.1.4. Обнаружение ошибок кодами с простой CRC-m
Проанализируем способность циклического кода с простой CRC-m обнаруживать ошибки.
Так как образующий многочлен P(x) степени m > 1 для полного кода является примитивным, то он должен иметь нечетное число слагаемых, включая 1 и xm, т. е. 3, 5, 7 и т. д. Исходя из этого, можно дать оценку обнаруживающей способности такого кода, учитывая, что многочлен обнаруживаемых ошибок e(x) не должен делиться на P(x) без остатка. Начнем с однократной ошибки, многочлен которой будет e(x) = xi, где 0 i n 1. Такой многочлен однократной ошибки не может делиться без остатка на другой многочлен, имеющий более одного члена. Значит, однократные ошибки будут гарантированно обнаруживаться.
Двукратную ошибку с многочленом e(x) = xi + xj, 0 i < j n 1, можно представить произведением двух сомножителей e(x) = xi(1 + xj i) = xi(1 + xv). Такой многочлен двукратных ошибок e(x) не будет делиться на P(x) без остатка в том случае, если ни один из сомножителей не будет делиться на P(x). Одночлен xi не делится на P(x) без остатка. Второй сомножитель (1 + xv) также не будет делиться без остатка на P(x) степени m, так как v n 1 = 2m 2, а примитивный многочлен степени m является делителем двучлена (1 + xi) с наименьшей степенью i = (2m 1). Таким образом, двукратные ошибки код с CRC-m также гарантированно обнаруживает.
Кроме того, будут обнаруживаться и ошибки большей кратности, многочлены которых e(x) не делятся без остатка на P(x).
Наоборот, необнаруживаемыми будут те ошибки, многочлены которых e(x) будут кратны многочлену P(x). Общее количество и вес этих комбинаций ошибок определяется весовым спектром кода A(wi).
2.3.1.5. Варианты кодов с простой CRC-m, применяемых в реальных системах (протоколах)
Напомним, что в этом разделе рассматриваются примеры кодов с простой CRC-m и с нулевыми начальными состояниями ячеек регистра деления как в кодере, так и в декодере.
Наиболее простыми кодами с CRC-m являются коды с малыми значениями m = 4, 6, 7, которые нашли применение в цифровых системах передачи PDH и SDH. Такие коды при низкой избыточности и простой реализации
49
обеспечивают требуемую достоверность в достаточно хороших цифровых каналах.
Так, для контроля за ошибками в цифровом тракте Е1 плезиохронной цифровой иерархии PDH, в соответствии с рекомендацией ITU-T G.704, используется код CRC-4 с образующим многочленом P(x) = 1 + x + x4 [40, 41]. Рассмотрим особенности такого кода.
Информационные последовательности кода в системе PDH представляют собой [40, 41] половины сверхциклов, состоящих из 8 циклов Е1, т. е. содержат 8 8 32 = 2048 бит. Выходная разрешенная комбинация f (x) кода CRC-4 образуется как комбинация систематического кода f (x) = r(x) + x4j(x), где r(x) — остаток от деления x4j(x) на P(x), т. е. контрольная проверочная последовательность CRC-4. Таким образом, комбинация (n;k)-кода на выходе кодера содержит n = 2052 бита. Так как структура цикла цифрового потока Е1 стандартизована и состоит из 32 канальных байтов, то контрольная сумма CRC-4 половины сверхцикла (субсверхцикла), т. е. проверочные элементы (r0;r1;r2;r3), передается на определенных позициях следующего субсверхцикла. Поэтому при декодировании, прежде чем принять решение о наличии ошибок в субсверхцикле, необходимо его сначала принять полностью и вычислить по принятой информации CRC-4 по тому же алгоритму, что и на передаче. Затем, принимая следующий субсверхцикл, выделить из него проверочные элементы (r0;r1;r2;r3) предшествующего субсверхцикла и сверить их с вычисленной на приемной стороне контрольной суммой CRC- 4 в результате декодирования предшествующего субсверхцикла. Если сравниваемые контрольные суммы не совпадают, это говорит о наличии обнаруживаемых ошибок в предшествующем субсверхцикле. Но при этом следует иметь ввиду, что ошибка может иметь место и в самих проверочных элементах (r0;r1;r2;r3), принятых в следующем субсверхцикле, тогда как в самом предшествующем субсверхцикле ошибок нет. Таким образом, одной из особенностей является задержка на приеме длительностью в один субсверхцикл.
Другая особенность рассматриваемого кода CRC-4 заключается в том, что это удлиненный код, так как длина комбинации n = 2052 бит существенно больше 2m 1 = 15. Это, как было сказано выше, ведет к снижению помехоустойчивости кода вследствие появления в комбинации двукратных ошибок, многочлены которых будут делиться на образующий многочлен P(x) без остатка. Действительно, если двукратной ошибке соответствует двучлен e(x) = xi + xj, 0 i < j n 1, который можно представить произведением двух сомножителей e(x) = xi(1 + xj i) = xi(1 + xv), то при v кратном числу 15 примитивный многочлен P(x) будет делителем двучлена (1 + xv), т. е. такие ошибки код не обнаружит.
50
Еще одна особенность кода состоит в том, что при вычислении контрольной суммы субсверхцикла позиции, на которых устанавливают проверочные элементы, как в кодере, так и в декодере, должны считаться нулевыми.
Другими примерами простых кодов с CRC-m являются рекомендованные для цифровых сетей синхронной иерархии SDH код CRC-6 с образующим многочленом P(x) = 1 +x +x6, рекомендация ITU-T G.704 и код CRC-7 с образующим многочленом P(x) = 1 + x3 + x7, рекомендации ITU-T G.704 и G.832 [40].
Но самым простым является код CRC-3 в схеме управления пропускной способностью канала (LCAS — Link Capacity Adjustment Scheme), применяемый для передачи кадров в сети SDH [8] в соответствии с рекомендацией ITU-T G.707. Информационная последовательность, состоящая из 29 бит, кодируется систематическим (n;k)-кодом (32;29) с образующим многочленом P(x) = 1 + x + x3. Очевидно, код является удлиненным, поэтому он гарантированно обнаруживает все однократные и многие двукратные ошибки. В то же время, как было пояснено выше, часть двукратных ошибок он не обнаруживает.
На сегодняшний день, пожалуй, самым сложным является пример кода с CRC-32 стандарта IEEE 802.3, применяемый в кадрах Ethernet на МАС уровне. Образующий многочлен имеет вид:
P(x) = 1 +x +x2 +x4 +x5 +x7 +x8 +x10 +x11 +x12 +x16 +x22 +x23 +x26 +x32:
В кодируемую часть кадра входят МАС-адреса передатчика и приемника кадра по 6 байт, поле длины — 2 байта и поле данных длиной от 42 до 1500 байт. Для контрольной суммы CRC-32 отведено 4-байтовое поле в конце кадра. Таким образом, общая кодируемая часть кодовой комбинации имеет переменную длину в пределах от 56 до 1514 байт.
2.3.2. Алгоритмы обнаружения ошибок двоичными (n, k)-кодами с расширенной CRC и нулевыми состояниями ячеек регистров
Название «расширенная CRC» здесь вводится в связи с тем, что образующий многочлен имеет вид: G(x) = (1 + x)P(x), где P(x) — примитивный многочлен степени m. Варианты таких кодов будут, как и ранее, оптимальные (полные или с плотной упаковкой) при n = 2m 1, укороченные — при n < 2m 1 и удлиненные — при n > 2m 1. В таких (n;k)-кодах с расширенной CRC число проверочных элементов равно (n k) = m + 1, а число информационных элементов — k = n m 1.
Рассмотрим общие свойства (n;k)-кода с расширенной CRC на примере оптимального систематического кода (плотная упаковка) с n = 2m 1.
51
Для большей наглядности будем вести построение такого кода с образую-
щим многочленом G(x) = (1 + x)P(x) в два этапа. На первом этапе информационная k-элементная комбинация j(x) = a0 + a1x + a2x2 + ::: + ak 1xk 1 умножается на xm (m 3) и делится на многочлен P(x). Остаток от деления r(x) = r0 +r1x +::: +rm 1xm 1 добавляется к информационным элементам со стороны младшего разряда. При этом будет получена комбинация из (n 1) элементов:
|
(r0;r1;:::;rm 1;a0;a1;a2;:::;ak 1) |
(2.19) |
с минимальным кодовым расстоянием Хэмминга dmin = 3.
На втором этапе комбинация (2.19) проверяется на четность и к ней со стороны младшего разряда добавляется еще один проверочный элемент «b».
Таким образом, на выходе кодера будет получена n-элементная разрешенная кодовая комбинация: (b;r0;r1;:::;rm 1;a0;a1;a2;:::;ak 1), в которой b = 0, если в комбинации (2.19) четное число «1», и b = 1 при нечетном числе «1». В данном случае контрольной суммой CRC-(m +1) будет комбинация проверочных элементов (b;r0;r1;:::;rm 1).
Следовательно, разрешенные комбинации кода с расширенной CRC будут иметь только четный вес, начиная с wmin = 4 среди ненулевых комбинаций. Отсюда также следует, что минимальное кодовое расстояние кода с расширенной CRC также будет равно dmin = 4. Исходя из этого, такой полный код способен гарантированно обнаруживать однократные, двукратные и трехкратные ошибки. Кроме того, код будет обнаруживать также ошибки более высокой кратности, если многочлен ошибок e(x) не будет делиться на G(x) без остатка. Следовательно, код не сможет обнаружить только те ошибки, многочлен которых e(x) кратен образующему многочлену G(x).
Очевидно, что кодер практически проще реализовать в один этап с помощью одного регистра деления xm+1j(x) на многочлен G(x) = (1 + x)P(x) с нулевыми начальными состоянием ячеек регистра.
Так как код является систематическим, то в декодере информационные элементы xm+1j(x) делятся на образующий многочлен G(x), в результате чего будет получена контрольная сумма CRC-(m + 1), которая, в случае отсутствия ошибок, будет совпадать с принятой, что будет восприниматься как отсутствие ошибок в принятой комбинации. В действительности, на практике чаще вся принятая комбинация h(x) делится на образующий многочлен G(x) и полученный остаток (синдром S(x)) проверяется на равенство нулю. Если S(x) = 0, то считается, что принятая комбинация не содержит ошибки, в противном случае принимается решение об обнаружении ошибок в комбинации.
Еще одной особенностью кода с расширенной CRC является то, что его образующий многочлен G(x) всегда будет иметь четное число слагаемых. Это связано с тем, что примитивный многочлен P(x) степени m > 1 имеет обяза-
52
тельно нечетное число слагаемых, включая xm и 1, а умножение P(x) на (1+x) делает его, соответственно, четным.
Например, для кода (n;k) = (15;10) с CRC-5 и примитивным многочленом P(x) = 1 + x + x4 получим образующий многочлен G(x) = (1 + x)P(x) =
1 + x2 + x4 + x5. Весовой спектр такого кода с n = 24 1 = 15 будет только четным с числами A(wi) комбинаций веса wi, показанным в табл. 2.7.
Таблица 2.7
Весовой спектр кода CRC-5 (15;10)
|
wi |
0 |
4 |
6 |
8 |
10 |
12 |
|
A(wi) |
1 |
105 |
280 |
435 |
168 |
35 |
Исходя из структуры многочлена G(x) = (1 + x)P(x), можно провести оценку обнаруживающей способности кода с расширенной CRC. Очевидно, что однократная ошибка всегда обнаружится, так как одночлен ошибки e(x) = xi не будет делиться без остатка ни на первый, ни на второй сомно-
житель, имеющий также более одного члена. Многочлен двукратной ошибки e(x) = xi + xj = xi(1 + xj i) = xi(1 + xv), 0 i < j n 1 также не делится
без остатка на G(x), так как сомножитель xi не делится без остатка ни на (1 + x), ни на многочлен P(x). Второй сомножитель (1 + xv) может делиться
на примитивный многочлен P(x) степени m только при наименьшем значении v = 2m 1 = n, а в действительности v < n 1.
Многочлен трехкратной ошибки e(x) = xi + xj + xz, имеющий нечетное число слагаемых, не может делиться без остатка на (1 + x). В противном случае элемент поля x = 1 был бы корнем и (1 + x), и многочлена e(x). Но «1» не может быть корнем многочлена e(x), имеющего нечетное число членов. Действительно, подставив в e(x) значение x = 1, получим e(1) = 1(mod 2).
Таким образом, полный (n;k)-код с расширенной CRC и n = 2m 1 будет гарантированно обнаруживать все однократные, двукратные и все другие ошибки нечетной кратности. Это свойство выгодно отличает (n;k)-код с расширенной CRC от кода с простой CRC.
Приведенные выше свойства полного кода с расширенной CRC будут справедливы и для укороченного (n;k)-кода с расширенной CRC с n < 2m 1.
Для удлиненного (n;k)-кода с n > 2m 1 указанные выше свойства пол-
ного кода частично не выполняются. Это вызвано тем, что, как сказано выше, двукратные ошибки e(x) = xi + xj = xi(1 + xj i) = xi(1 + xv), 0 i < j n 1,
для которых величина v кратна 2m 1, не будут обнаружены, так как такой многочлен (1 +xv) делится без остатка и на (1 +x), и на многочлен P(x). Следовательно, такую двукратную ошибку e(x) код не обнаружит.
53
Особенностью кодов с расширенной CRC и dmin = 4 является и то, что такие полные (n;k)-коды с n = 2m 1 могут работать как в режиме только обнаружения ошибок (обнаруживать все однократные, двукратные и все другие ошибки нечетной кратности), так и в режиме исправления однократных ошибок и гарантированного обнаружения всех двукратных ошибок. При этом декодер должен работать по двум этапам. Например, в режиме исправления однократных ошибок факт наличия одной ошибки сначала должен быть обнаружен проверкой на четность, которая покажет, что в комбинации нечетное число двоичных «1», а на втором этапе — делением принятой комбинации на многочлен G(x) (или P(x)), в результате которого при однократной ошибке будет получен ненулевой синдром — ненулевой остаток от деления на многочлен. Далее исправление однократной ошибки происходит либо табличным способом, либо при последовательном считывании комбинации с буферного накопителя по определенной комбинации содержимого в ячейках регистра сдвига. Иногда такую комбинацию называют «замечательной».
Рассмотрим процедуру исправления однократной ошибки на примере
кода (n;k) = (15;10) с CRC-5 и примитивным многочленом P(x) = 1 + x + x4, образующим многочленом G(x) = (1 + x)P(x) = 1 + x2 + x4 + x5 и нулевыми
начальными состояниями ячеек регистра деления на G(x). Для простоты будем считать, что была передана нулевая комбинация, в которой возникла однократная ошибка с одночленом в общем виде e(x) = xi, где 0 i n 1. Проверка на четность указывает на наличие ошибки. При исправлении однократной ошибки табличным способом значение синдрома S(x) 6= 0 укажет на номер ошибочной позиции и ошибка может быть сразу же, без задержек, исправлена. При этом в постоянной памяти должна содержаться таблица синдромов, вид которой для данного примера приведен в табл. 2.8.
Таблица 2.8
Таблица синдромов однократной ошибки кода (15;10) с CRC-5
|
№ п/п |
e(x) = xi |
Si(x)(mod G(x)) |
[Si] = (s0;s1;s2;s3;s4) |
|
0 |
1 |
1 |
(10000) |
|
1 |
x |
x |
(01000) |
|
2 |
x2 |
x2 |
(00100) |
|
3 |
x3 |
x3 |
(00010) |
|
4 |
x4 |
x4 |
(00001) |
|
5 |
x5 |
1 + x2 + x4 |
(10101) |
|
6 |
x6 |
1 + x + x2 + x3 + x4 |
(11111) |
|
7 |
x7 |
1 + x + x3 |
(11010) |
|
8 |
x8 |
x + x2 + x4 |
(01101) |
|
9 |
x9 |
1 + x3 + x4 |
(10011) |
|
10 |
x10 |
1 + x + x2 |
(11100) |
54
Окончание табл. 2.8 Таблица синдромов однократной ошибки кода (15;10) с CRC-5
|
№ п/п |
e(x) = xi |
Si(x)(mod G(x)) |
[Si] = (s0;s1;s2;s3;s4) |
|||||
|
11 |
x11 |
x + x2 + x3 |
(01110) |
|||||
|
12 |
x12 |
x2 + x3 + x4 |
(10111) |
|||||
|
13 |
x13 |
1 + x2 + x3 |
(10110) |
|||||
|
14 |
x14 |
x + x3 + x4 |
(01011) |
|||||
|
Предположим, |
что |
однократная |
ошибка возникла в 8 позиции, |
т. е. e(x) = x8. Записав принятую комбинацию в накопитель и поделив ее на многочлен G(x), получим синдром, равный (x + x2 + x4). Найдя этот синдром в табл. 2.8, определяем, что ошибка возникла в 8 позиции и подлежит исправлению, после чего в накопителе получим исходную кодовую комбинацию.
Другой вариант реализации декодера, исправляющего однократную ошибку, основан на последовательном считывании принятой комбинации с накопителя и исправлении ошибки в момент появления ее из накопителя.
Покажем математику такого исправления однократной ошибки с одночленом e(x) = xi, где 0 i n 1 при оптимальной длине кодовой комбинации n = 2m 1 = 15. Принятой комбинации с однократной ошибкой соответствует многочлен h(x) = f (x) + e(x) xi Si(x)[mod G(x)]. Здесь учтено свойство циклического кода о том, что любая разрешенная комбинация f (x) всегда делится на многочлен G(x) без остатка. Итак, на момент приема всей n-элементной комбинации и записи ее в накопитель на n элементов, в регистре деления будет синдром Si(x) xi[mod G(x)]. Далее, при считывании комбинации с накопителя, каждому такту будет соответствовать один сдвиг содержимого регистра на один шаг, т. е. умножение содержимого ячеек регистра на x и приведение этого произведения по mod G(x). Тогда через (n i) сдвигов на выходе накопителя появится ошибочный элемент hi принятой комбинации h(x). Содержимое регистра также умножится на xn i и станет равным:
xn iSi(x) = xn ixi = xn 1[mod G(x)]:
Таким образом, если к ячейкам регистра деления подключить дешифратор на «1», то он сработает в момент появления из накопителя ошибочного элемента и выдаст «1», которая просуммируется по mod 2 с ошибочным элементом hi и тем самым исправит однократную ошибку. Так, если ошибка была в 8 позиции, т. е. e(x) = x8, то соответствующий такой ошибке синдром, как следует из табл. 2.8, будет S8(x) x+x2 +x4[mod G(x)]. Тогда через (n i) = (15 
x8xn i = x8x7 = x15 1[mod G(x)]:
55
Сработает дешифратор комбинации (10000) в ячейках регистра и выдаст «1», которая суммируется по mod 2 с ошибочным элементом h8 и ошибка будет исправлена.
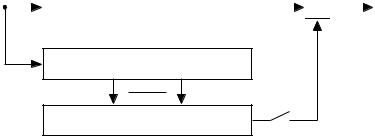
Функциональная схема декодера в общем виде показана на рис. 2.7.
|
Вход |
hi |
||||||||
|
Накопитель на n элементов |
|||||||||
|
h(x) |
f (x) |
||||||||
|
«1» |
Регистр деления на G(x)
Дешифратор «1»
Рис. 2.7. Функциональная схема декодера с исправлением однократной ошибки при последовательном считывании
Отметим, что ключ на выходе дешифратора будет разомкнут, пока поступает на вход комбинация h(x), и замкнут после приема комбинации и записи ее в накопитель, т. е. с первым тактом считывания принятой комбинации из накопителя.
Обнаружение двукратной ошибки может происходить также в два этапа: сначала проверка на четность показывает, что в принятой комбинации ошибок нет, так как в ней будет четное число 1, а на втором этапе деление принятой комбинации на образующий многочлен G(x) (или P(x)) указывает на ненулевой остаток (синдром), что говорит о наличии двукратной ошибки (хотя, как известно, это могут быть и ошибки более высокой четной кратности).
Для укороченного кода с длиной комбинации n1 < 2m 1 дешифратор в схеме на рис. 2.7 должен быть настроен на «замечательную» комбинацию в ячейках регистра, соответствующую одночлену xn1 по mod G(x).
Примеры систем и рекомендаций по использованию (n;k)-кодов с расширенной CRC и с нулевыми начальными состояниями ячеек регистра деления для обнаружения ошибок
Рекомендация ITU-T G.704 1998 г. предписывает применение для обнаружения ошибок кода с CRC-5 и образующим многочленом
G(x) = (1 + x)P(x) = (1 + x)(1 + x + x4) = 1 + x2 + x4 + x5:
Для длины n = 2m 1 = 15, где m — степень примитивного многочлена P(x), получим полный (оптимальный) (n;k) = (15;10) циклический код с dmin = 4. Такой код, как было доказано выше, будет обнаруживать все ошибки
56
нечетной кратности и все двукратные ошибки. В табл. 2.7 приведен весовой спектр разрешенных комбинаций этого кода, из которого следует, что код не будет обнаруживать определенные ошибки четной кратности, начиная с 4. Так, вероятность появления 4-кратной необнаруживаемой ошибки в канале ДСК будет определяться выражением:
P(4;n) = A(4)p4(1 p)n 4;
где p — вероятность битовой ошибки в канале ДСК; A(4) — количество разрешенных комбинаций кода с весом w = 4, число которых для данного кода равно 105 (табл. 2.7).
В реальных системах обычно n > 2m 1, т. е. применяют удлиненный код с расширенной CRC-5. Проведем анализ, насколько ухудшится обнаруживающая способность и общая эффективность кода с расширенной CRC-5 из-за возможных двукратных необнаруживаемых ошибок.
Как известно, примитивный многочлен P(x) = (1 + x + x4) является делителем двучлена (1 + xz) при наименьшем значении z = 2m 1 = 15. Обозначим такое значение z = no и будем считать no оптимальной длиной комбинации, равной no = 2m 1. Тогда, как следует из свойств двучленных уравнений высшей алгебры, любой двучлен (1 +xl no ), где l = 1;2;:::, будет делиться на (1+xno ) без остатка. Из этого также следует, что (1+xl no ) будет делиться без остатка и на (1 + x), и на многочлен P(x). Таким образом, удлиненным кодом
не будут обнаружены двукратные ошибки, многочлен которых будет иметь вид: e(x) = (xi +xj) = xi(1+xl no ), где i и j — целые числа, i 0, l = 1;2;:::;s,
но такие, что i+l no n 1 для всех l . Величина s определяется из равенства
где r — остаток от деления n на no = 2m 1, т. е. n r[mod no].
Для нашего примера с CRC-5 m = 4, следовательно no = 24 1 = 15. Пусть удлиненный (n;k) = (50;45). Найдем количество двукратных необнаруживаемых ошибок в таком удлиненном коде как B(2;n) = B(2;50). При этом n = 50 5(mod 15), т. е. r = 5. Тогда из (2.20) находим s = 3. Анализ конфигураций необнаруживаемых двукратных ошибок, выполненный авторами при подготовке настоящего пособия, а также исследования автора работы [8], показали, что количество таких ошибок точно определяется выражением:
|
B(2;n) = Cs2no + r s: |
(2.21) |
Подставив необходимые величины в (2.21), находим, что B(2;n) = 60.
Тогда вероятность двукратных необнаруживаемых ошибок для данного кода с CRC-5 будет определяться выражением:
P(2;n) = B(2;n)p2(1 p)n 2 = 60p2(1 p)n 2:
57
Как видим, вероятность необнаруженной ошибки для удлиненного кода пропорциональна p2, тогда как для оптимального кода с n = 2m 1 и dmin = 4 эта вероятность пропорциональна p4. Таким образом, эффективность удлиненного кода ухудшится приближенно в p2=p4 = p 2 раз. В то же время, применение удлиненных кодов с расширенной CRC приводит к уменьшению избыточности и, следовательно, к увеличению скорости передачи данных.
Пример 2.3. Рассмотрим в качестве примера код (n;k) = (33;29) с расширенной CRC-4 с образующим многочленом
G(x) = (1 + x)P(x) = (1 + x)(1 + x + x3) = 1 + x2 + x3 + x4:
Этот код образован на базе кода (n;k) = (32;29) с простой CRC-3 и с образующим многочленом P(x) = 1 +x +x3, применяемого для передачи кадров в сети SDH [8] в соответствии с рекомендацией ITU-T G.707. В комбинации к k = 29 информационным элементам добавляются вместо трех четыре проверочных элемента, что вызвано введением сомножителя (1 + x) в образующий многочлен G(x).
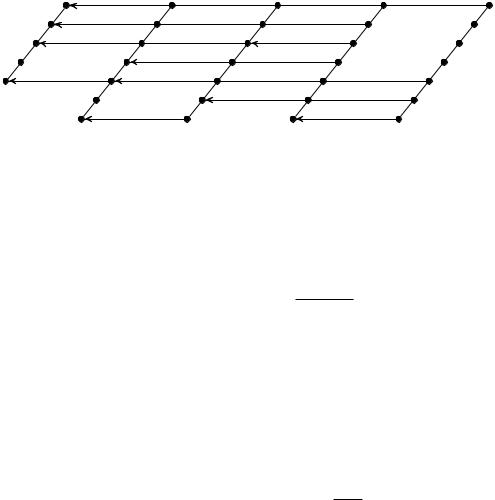
На рис. 2.8 представлена иллюстрация возможных двукратных ошибок, не обнаруживаемых удлиненным кодом с расширенной CRC-4, и поясняющая формулу (2.21). Так как m = 3, то получаем значение no = 2m 1 = 7. Тогда из (2.20) находим, что s = 4, а r = 5. На рис 2.8 условно наклонными линиями показаны s = 4 секции по no = 7 разрядов n-элементной комбинации. Двукратные не обнаруживаемые кодом ошибки располагаются по горизонтальным линиям. Это будут двукратные ошибки (переходы) по горизонтали из точек первого наклонного ряда во второй, как, например, переход x6 ! x13. Таких переходов из первого ряда во второй будет no = 7, и каждому из них соответствует двукратная ошибка с многочленом e(x) = xi(1 + x)7 где i принимает значения от 0 до no 1 = 6. Аналогичные переходы из точек первой наклонной линии в точки третьей и четвертой наклонных линий по no = 7 переходов в каждом случае, как, например, x5 ! x19 и x4 ! x25. Таким переходам соответствуют двукратные ошибки с многочленами e(x) = xi(1 +x)14 и e(x) = xi(1 + x)21. Всего таких двукратных ошибок (переходов) из no = 7 точек первого наклонного ряда в точки 2-го, 3-го и 4-го наклонных рядов будет равно no(s 1) = no 3 = 21.
Такими же необнаруживаемыми будут двукратные ошибки, соответствующие переходам из точек 2-го ряда в 3-й и 4-й, как, например, x9 ! x16 и
x10 ! x24. Таким переходам соответствуют двукратные ошибки с многочленами e(x) = xi(1+x)7 и e(x) = xi(1+x)14 где i меняется от 7 до 2no 1 = 13. Всего количество таких двукратных ошибок будет равно no(s 2) = no 2 = 14.
Не будут обнаружены также двукратные ошибки, соответствующие переходам из 3-го ряда в 4-й, как, например, x20 ! x27. Таким переходам соот-
58
ветствуют двукратные ошибки с многочленами e(x) = xi(1+x)7 где i меняется от 14 до 3no 1 = 20. Всего количество таких двукратных ошибок будет равно no(s 3) = no = 7.
|
s = 5 |
s = 4 |
s = 3 |
s = 2 |
s = 1 |
|
x28 |
x21 |
x14 |
x7 |
1 |
|
x29 |
x8 |
x1 |
||
|
x30 |
x9 |
x2 |
||
|
x31 |
x24 |
x10 |
x3 |
|
|
x32 |
x4 |
|||
|
x26 |
x19 |
x5 |
||
|
x27 |
x20 |
x13 |
x6 |
Рис. 2.8. Иллюстрация к возникновению двукратных необнаруживаемых ошибок в удлиненном коде с расширенной CRC-4 с образующим многочленом
G(x) = (1 + x)(1 + x + x3) и длиной комбинации n = 33
Таким образом, суммарное количество необнаруживаемых двукратных ошибок между разрядами 1-го, 2-го ,3-го и 4-го рядов будет равно
no[1 + 2 + ::: + (s 1)] = no s(s 1) = noC2:
2 s
Наконец, не обнаружатся двукратные ошибки, соответствующие переходам из точек 1-го, 2-го, 3-го и 4-го рядов в r = 5 точек 5-го ряда. Таких двукратных ошибок всего будет s r.
Итого, общее количество двукратных необнаруживаемых ошибок удли-
|
ненным кодом (n;k) = (33;29) с CRC-4 будет равно |
||||||||||
|
B( ;n) = s |
r + n C2 |
= |
4 5 |
+ |
7 |
4 3 |
= |
62 |
: |
|
|
2 |
o s |
2 |
Пример 2.4. Приведем пример кодирования и декодирования, а также схемную реализацию кодера и декодера оптимального систематического (n;k) = (15;10) кода с расширенной CRC-5 с образующим многочленом
G(x) = (1 + x)P(x) = (1 + x)(1 + x + x4) = 1 + x2 + x4 + x5:
Рассмотрим одноэтапный вариант кодирования и декодирования. Пусть входная информационная комбинация имеет вид:
(a0;a1;a2;a3;a4;a5;a6;a7;a8;a9) = (1010010000):
Такой комбинации соответствует многочлен j(x) = 1 + x2 + x5.
59
Процедура кодирования
Операция 1. Умножение j(x) на xm+1 = x5, где m — степень примитивного многочлена P(x):
x5j(x) = x5(1 + x2 + x5) = x5 + x7 + x10:
Операция 2. Деление x5j(x) на образующий многочлен G(x) и получение проверочных элементов (r0;r1;:::;rm+1) = (r0;r1;:::;r4). В результате деления получен следующий многочлен остатка r(x) = 1 + x3 + x4, т. е. проверочные элементы будут равны (r0;r1;:::;r4) = (10011).
Операция 3. Формирование кодовой комбинации
f (x) = r(x) + x5j(x) = 1 + x3 + x4 + x5 + x7 + x10;
которой соответствует двоичный вектор (100111010010000).
Процедура декодирования
Деление принятой комбинации h(x) на образующий многочлен G(x) и проверка на равенство «0» синдрома S(x). Равенство синдрома «0» воспринимается как отсутствие ошибок в принятой комбинации.
Пусть принятая комбинация не содержит ошибок, т. е. h(x) = f (x). Поделив сформированную кодером комбинацию f (x) на G(x), убедимся, что синдром будет нулевым и, следовательно, ошибки в принятой комбинации отсутствуют.
Пусть теперь в принятой комбинации возникли две ошибки с многочленом e(x) = x5 + x8, т. е. h(x) = f (x) + e(x) = 1 + x3 + x4 + x7 + x8 + x10.
Поделив комбинацию h(x) на G(x), получим в остатке ненулевой синдром S(x) = (1 + x), что свидетельствует о наличии ошибок в принятой на вход декодера комбинации.
Схемы кодера и декодера для рассмотренного примера представлены на рис. 2.9.
На вход кодера (рис. 2.9, а) в течение первых k тактов поступает информационная комбинация j(x) со старшего разряда. В течение этого времени ключ «Кл» находится в положении 1. Одновременно информационные элементы через схему «ИЛИ» поступают на выход кодера. После этого ключ переключается в положение 2 и на выход из ячеек регистра последовательно считываются проверочные элементы.
На вход декодера (рис. 2.9, б) в течение первых n тактов поступает комбинация h(x) со старшего разряда. В течение этого времени ключ «Кл» разомкнут. После приема всей комбинации ключ «Кл» замыкается, а в ячейках регистра деления будет находиться синдром S(x), который будет равен нулю, если ошибок в комбинации нет. При этом сработает дешифратор, на-
60
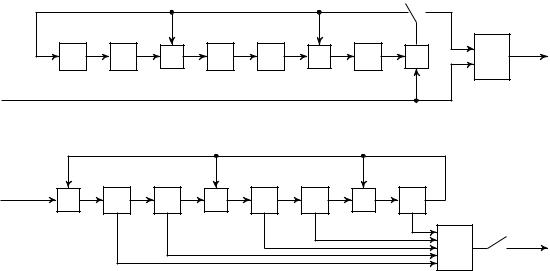
строенный на нулевой синдром, и выдаст сигнал, например «0», свидетельствующий об отсутствии ошибок в принятой комбинации. Напротив, если синдром не равен нулю, то на выходе дешифратора будет противоположный сигнал, указывающий на наличие ошибок в комбинации.
|
1 |
Кл |
2 |
||||||||
|
1 |
x2 |
x4 |
1 |
|||||||
|
j(x) |
R0 |
R1 |
R2 |
R3 |
R4 |
Выход |
||||
|
Вход |
||||||||||
|
(а) |
||||||||||
|
h(x) |
1 |
x2 |
x4 |
x5 |
||||||
|
R0 |
R1 |
R2 |
R3 |
R4 |
||||||
|
Вход |
1 |
|||||||||
|
Кл |
Выход |
|||||||||
|
Дешифратор (00000) |
(б)
Рис. 2.9. Схемы кодера (а) и декодера (б) с расширенной CRC-5 и образующим многочленом G(x) = (1 + x)(1 + x + x4)
Напомним, что в данном случае рассматривается вариант кодера и декодера с начальной установкой «0» в ячейки регистров сдвига с обратной связью.
Рассмотрим потактовую работу декодера при приеме комбинации h(x) со старшего разряда из приведенного выше примера. Так как первые 4 старших разряда комбинации h(x) являются нулями, то начнем рассматривать потактовую работу декодера с 5-го такта, когда на вход поступит «1», соответствующая двоичному коэффициенту при x10 (табл. 2.9).
Таблица 2.9
Потактовая работа декодера
|
№ |
Разряд |
h(x) |
R0 |
R1 |
R2 |
R3 |
R4 |
Выход |
|
такта |
(0) |
(0) |
(0) |
(0) |
(0) |
дешифр. |
||
|
5 |
x10 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
6 |
x9 |
0 |
0 |
1 |
0 |
0 |
0 |
|
|
7 |
x8 |
1 |
1 |
0 |
1 |
0 |
0 |
|
|
8 |
x7 |
1 |
1 |
1 |
0 |
1 |
0 |
|
|
9 |
x6 |
0 |
0 |
1 |
1 |
0 |
1 |
|
|
10 |
x5 |
0 |
1 |
0 |
0 |
1 |
1 |
61
Окончание табл. 2.9
Потактовая работа декодера
|
№ |
Разряд |
h(x) |
R0 |
R1 |
R2 |
R3 |
R4 |
Выход |
|
такта |
(0) |
(0) |
(0) |
(0) |
(0) |
дешифр. |
||
|
11 |
x4 |
1 |
0 |
1 |
1 |
0 |
0 |
|
|
12 |
x3 |
1 |
1 |
0 |
1 |
1 |
0 |
|
|
13 |
x2 |
0 |
0 |
1 |
0 |
1 |
1 |
|
|
14 |
x1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
15 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
1 |
После приема комбинации в ячейках регистра находится ненулевой синдром, равный S(x) = 1 +x, поэтому на выходе дешифратора появится «1», свидетельствующая о наличии ошибок в принятой комбинации.
Приведем другие рекомендации по применению кодов с расширенными CRC и нулевыми начальными состояниями ячеек регистра деления.
В сетях с технологией АТМ заголовки АТМ-ячеек проверяются на наличие в них ошибок, в соответствии с рекомендацией ITU-T I.432, систематическим укороченным кодом (n;k) = (40;32) с расширенной CRC-8 и образующим многочленом G(x) = (1 + x)P(x), где примитивный многочлен P(x) степени 7 имеет вид:
P(x) = 1 + x2 + x3 + x4 + x5 + x6 + x7:
Еще одним широко применяемым кодом с расширенной CRC-16 с образующим многочленом G(x) = 1 + x2 + x15 + x16, который применяется в протоколе бинарной синхронной связи BSC фирмы IBM. Кодирование и декодирование осуществляется по алгоритму систематического циклического (n;k)-кода с нулевыми начальными состояниями ячеек регистра деления.
В виртуальных локальных сетях VLAN в соответствии со стандартом
IEEE 802.1Q применяется (n;k)-код с расширенной CRC-32 c образующим многочленом
G(x) = 1 + x + x3 + x5 + x7 + x8 + x14 + x16 + x22 + x24 + x31 + x32:
Наиболее сложным кодом является (n;k)-код с расширенной CRC-64 стандарта ECMA-182 c образующим многочленом G(x) 64 степени, имеющим вид в шестнадцатеричной форме записи: (142F0E1EBA9EA3693)16, при этом старшая степень слева.
62
2.3.3.Алгоритмы обнаружения ошибок двоичными (n, k)-кодами
сCRC и ненулевыми состояниями ячеек регистров
Для рассмотренного выше алгоритма с нулевыми начальными состояниями ячеек регистра сдвига, реализующего деление на многочлен G(x), решение декодера об отсутствии ошибок в принятой комбинации h(x) выносится по нулевому остатку от деления h(x) на многочлен G(x). В другом, рассматриваемом ниже, алгоритме с ненулевыми состояниями ячеек регистров при отсутствии ошибок в принятой комбинации в результате деления h(x) на многочлен G(x) будет получен вполне определенный, не равный нулю остаток — синдром So(x). Преимущество такого алгоритма в том, что, одновременно с контролем ошибок в принятой комбинации, осуществляется и контроль за исправностью канала. Так, при обрыве канала (или замирании, кратковременном прерывании) в первом алгоритме остаток от деления h(x) на многочлен G(x) будет нулевой, что будет восприниматься как отсутствие ошибок в принятой, в данном случае как бы нулевой, комбинации. Во втором алгоритме с ненулевыми начальными состояниями ячеек регистра сдвига эта ситуация будет обнаруживаться как ошибочная, так как по определению не может быть нулевого синдрома для любой разрешенной, даже нулевой, комбинации.
Как и в предыдущем случае, (n;k)-коды с ненулевыми начальными состояниями ячеек регистра сдвига могут быть как с «простой», так и с расширенной CRC. В приводимых ниже вариантах таких кодов во всех ячейках регистра деления в начальном состоянии установлены «1».
Варианты систематических кодов с «простой» CRC с dmin = 3 и ненулевыми начальными состояниями ячеек регистров деления на образующий многочлен P(x).
1. Широко применяемым таким кодом является код CRC-5 для USB с образующим многочленом
P(x) = 1 + x + x5:
2. Другим примером является код CRC-6 для перспективной технологии CDMA-2000-A с образующим многочленом
P(x) = 1 + x + x2 + x5 + x6:
3. В этой же технологии CDMA-2000 применяется код с CRC-16 с образующим многочленом
P(x) = 1 + x + x2 + x5 + x6 + x11 + x14 + x15 + x16:
4. Во многих современных системах применяется код с «простой» CRC-32 с единичными начальными состояниями ячеек регистра образующего многочлена P(x), имеющего вид в шестнадцатеричной форме записи
63
(104C11DB7)16 со старшим разрядом слева. Одним из них является код с CRC-32 для MPEG-2.
Варианты систематических кодов с расширенной CRC с dmin = 4 и ненулевыми начальными состояниями ячеек регистров деления на образующий многочлен G(x).
1. Одним из примеров является код CRC-6 для перспективной технологии CDMA-2000-В с образующим многочленом
G(x) = 1 + x + x2 + x6 = (1 + x)(1 + x2 + x3 + x4 + x5):
2. Аналогичным примером является код CRC-8 для технологии CDMA-2000 с образующим многочленом
G(x) = 1 + x + x3 + x4 + x7 + x8:
3. Во многих современных системах применяется код с расширенной CRC-16 с единичными начальными состояниями ячеек регистра образующего многочлена G(x) = (1 + x)P(x), P(x) — примитивный многочлен 15 степени. Наиболее популярным является код с образующим многочленом
G(x) = 1 + x5 + x12 + x16;
применяемый в протоколах X.25, HDLC, V.42, XMODEM, Bluetooth и др.
Рассмотрим алгоритмы кодирования и декодирования систематических (n;k)-кодов с CRC и ненулевыми (единичными) состояниями ячеек регистров деления кодера и декодера.
Процедура кодирования.
Шаг 1. Процесс кодирования исходной информационной комбинации в виде многочлена j(x) начинается с ее умножения на xn k.
Шаг 2. Одновременно с началом процесса кодирования во все (n k) ячеек регистра деления на многочлен G(x), как стартовые состояния, записываются «1», т. е. в регистре кодера будет установлен многочлен
L(x) = 1 + x + x2 + x3 + ::: + xn k 1:
Таким образом, этим двум первым шагам будет соответствовать добавление по mod 2 к старшим разрядам информационной комбинации j(x) единичной комбинации, соответствующей многочлену L(x), т. е. получается сумма:
j(x) xn k + xkL(x):
Шаг 3. Последовательно с подачей на вход кодера информационной комбинации, начиная со старшего разряда, происходит потактовое деление
64

суммы j(x) xn k + xkL(x) на образующий многочлен G(x), в результате чего после окончания поступления на вход информационных элементов в ячейках регистра будут получены проверочные элементы
r(x) = r0 + r1x + ::: + rn k 1xn k 1;
при этом будет справедливо следующее сравнение:
|
j(x) xn k + xkL(x) r(x)[mod G(x)]: |
(2.22) |
При этом информационные элементы также последовательно поступают на выход кодера, что соответствует систематическому (n;k)-коду.
Шаг 4. После окончания поступления на вход кодера информационных элементов с ячеек регистра деления последовательно через инвертор считывается остаток от деления r(x), т. е. многочлен r(x).
Шаг 5. Проверочные элементы инвертированного остатка r(x) добавляются к информационным элементам со стороны младших разрядов и в канал отправляется кодовая комбинация
|
f (x) = |
r(x) |
+ j(x) xn k: |
(2.23) |
Процедура декодирования.
Рассмотрим в общем виде процедуру декодирования принятой комбинации h(x) = f (x)+e(x) по шагам, в предположении, что ошибки в ней отсутствуют, т. е. e(x) = 0 и h(x) = f (x).
Шаг 1. С началом поступления на вход декодера принимаемой комбинации в ячейках регистра деления на образующий многочлен G(x) устанавливается стартовая комбинация из всех «1», т. е. параллельным кодом записывается многочлен
L(x) = 1 + x + x2 + x3 + ::: + xn k 1:
Относительно поступающей комбинации h(x) = f (x) эти (n k) единиц
займут k старших разрядов в n-элементной комбинации, т. е. это будет многочлен xkL(x).
Шаг 2. На умножитель на xn k начинает поступать комбинация h(x) = f (x), суммируясь при этом с последовательными элементами, поступающими с выхода регистра деления, т. е. с многочленом xkL(x). При этом происходит потактовое деление получаемой суммы на многочлен G(x). Таким образом, пока на вход декодера потактово поступает кодовая комбинация f (x), начиная со старшего разряда при xn 1, происходит деление суммы xn k[ f (x) + xkL(x)] на образующий многочлен G(x).
65

Шаг 3. После окончания поступления кодовой комбинации в ячейках регистра деления будет содержаться определенный синдром So(x).
Приведем математические выражения работы декодера.
В результате деления будут происходить следующие преобразования:
xn k[ f (x) + xkL(x)] = xn k[xn kj(x) + r(x) + xkL(x)] = = xn k[xn kj(x) + r(x) + L(x) + xkL(x)]:
Подставив вместо r(x) выражение (2.22), получим:
|
xn kL(x) So(x)[mod G(x)]: |
(2.24) |
Таким образом, в случае приема безошибочной кодовой комбинации f (x) в результате ее декодирования в (n k) ячейках регистра деления будет содержаться вполне определенный синдром So(x). Если синдром будет какой-либо другой, то это будет свидетельствовать о наличии в комбинации обнаруживаемых кодом ошибок.
Для приведенного выше примера кода с расширенной CRC-16, применяемого в протоколе HDLC (V.42), образующий многочлен имеет вид:
G(x) = 1 + x5 + x12 + x16:
Тогда, в соответствии с (2.24), синдром безошибочной комбинации So(x) будет иметь вид:
So(x) = x16L(x) = x16(1 + x + x2 + ::: + x15)
x12 + x11 + x10 + x8 + x3 + x2 + x + 1[mod G(x)];
что в двоичной и в 16-ричной форме записи будет равняться
So = (0001110100001111)2 = (1D0F)16:
Покажем, что рассматриваемые (n;k)-коды с CRC и единичными начальными состояниями ячеек регистров деления в кодере и в декодере не являются в полном смысле циклическими даже при n = 2n k 1.
Во-первых, такой систематический код не удовлетворяет свойству линейности, т. е. сумма двух или большего четного числа разрешенных кодовых комбинаций не образует некоторую другую разрешенную кодовую комбинацию. Рассмотрим это на примере двух разрешенных комбинаций f1(x) и f2(x), которые, в соответствии с (2.23), имеют вид:
|
f1(x) = |
r1(x) |
+ j1(x) xn k; |
f2(x) = |
r2(x) |
+ j2(x) xn k: |
66
В приведенных выражениях j1(x) и j2(x) — многочлены исходных информационных элементов соответственно комбинаций f1(x) и f2(x); r1(x) и
r2(x) — инвертированные остатки, которые равны:
|
r1(x) = r1(x) + L(x) |
и |
r2(x) = r2(x) + L(x); |
|
где |
||
|
r1(x) xn kj1(x) + xkL(x) [mod G(x)]; |
r2(x) xn kj2(x) + xkL(x) [mod G(x)]: |
Подставив r1(x), r1(x), r2(x), r2(x) в выражения для разрешенных кодовых комбинаций f1(x) и f2(x), получим следующую сумму:
|
h(x) = f1(x) + f2(x) = xn kj1(x) + r1(x) + L(x) + xn kj2(x) + r2(x) + L(x) = |
||||||||
|
= |
n k |
n k |
HkH |
XnXXk |
XnXXk |
HkH |
||
|
x j1(x) + |
x j1(x) + x LH(x) + x j2(XxX) + x j2(XxX) + x LH(x) = 0: |
|||||||
|
X |
X |
|||||||
|
H |
H |
Таким образом, сумма двух разрешенных комбинаций не является также разрешенной комбинацией, так как среди множества разрешенных комбинаций нулевая отсутствует. Значит, код не удовлетворяет свойству линейности, которое характерно для классических циклических кодов.
Во-вторых, покажем, что также не работает свойство циклического сдвига, порождающего новую разрешенную комбинацию для классического циклического кода.
Пусть имеется разрешенная кодовая комбинация f (x), при декодировании которой получен заранее известный синдром So(x) в соответствии с (2.24).
Произведем теперь циклический сдвиг комбинации f (x) на один шаг, в результате получим произведение x f (x), которое подвергнем декодирова-
|
нию по рассмотренному выше алгоритму: |
||||||||||||||
|
xn k x |
f (x) + xkL(x) = xn k |
x xn k |
(x) + |
+ xkL(x) = |
||||||||||
|
r(x) |
||||||||||||||
|
nnk |
x x |
n k |
o |
n h |
kj |
i |
o |
|||||||
|
= x |
j(x) + r(x) + L(x) + x L(x) = |
|||||||||||||
|
n k n h n k |
n k i k |
o |
k |
|||||||||||
|
= x nx hx j(x) + x |
j(x) + x L(x) + L(x)i+ x L(x)o = |
|||||||||||||
|
= xn kL(x) x + xk + xk+1 |
= S |
(x)[mod G(x)]: |
||||||||||||
|
6 |
o |
Таким образом, циклический сдвиг разрешенной комбинации f (x) на один шаг (умножение f (x) на x) не порождает новую разрешенную комбинацию, т. е. при декодировании описанным выше алгоритмом синдром не равен So(x). Поэтому такой систематический (n;k)-код с CRC не является в полном смысле циклическим и может быть назван псевдоциклическим.
Оценим вероятностные характеристики таких блочных систематических кодов с CRC и ненулевыми (единичными) начальными состояниями ячеек регистра деления на образующий многочлен G(x).
67
Правильное декодирование будет происходить в случае отсутствия ошибок в принятой комбинации, состоящей из n элементов. Вероятность такого события в канале ДСК будет определяться выражением:
Pпп = (1 p0)n;
где p0 — вероятность ошибочного приема сигнального элемента в двоичном симметричном канале.
Определим ситуации, при которых ошибки обнаруживаться не будут. Пусть принимаемая комбинация будет: h(x) = f (x) + e(x), где e(x) — многочлен ошибок. Процедура декодирования в математических операциях будет следующей:
|
nnk n k |
o |
nf x |
k e x |
x |
L x o |
|||||||||
|
xn k |
h(x) + xkL(x) = xn k |
( ) + ( ) + |
k |
( ) = |
||||||||||
|
= xn k nxn kj(x) + |
+ e(x) + x L(x)ok= |
|||||||||||||
|
r(x) |
HkoH |
HkH |
||||||||||||
|
= x |
n k n n k |
n k |
||||||||||||
|
x |
j(x) + r(x) + L(x) + e(x) + x L(x) = |
Ho |
||||||||||||
|
= x |
n k nx |
j x |
x |
n jk x |
L |
n k |
H |
n k |
||||||
|
( ) + |
( ) + |
(x) + e(x) + x LH(x) + x LH(x) = |
||||||||||||
= x [L(x) + e(x)] = x L(x) + x e(x) So(x) + x e(x)[mod G(x)]:
Из полученного выражения следует, что необнаруживаемыми ошибками будут такие, многочлены которых xn ke(x) делятся на G(x) без остатка, т. е.
xn ke(x) 0[mod G(x)]:
Таким образом, для оценки вероятности необнаруживаемых ошибок необходимо знать весовой спектр (n;k)-кода с образующим многочленом G(x). Тогда вероятность необнаруживаемой ошибки Pно в канале ДСК будет определяться выражением:
n
Pно = å A(wi)pw0 i (1 p0)n wi ;
wi=dmin
где A(wi) — число комбинаций классического (n;k)-кода с весом wi, кратным образующему многочлену.
Вероятность приема комбинации с обнаруживаемыми ошибками Pоо, следовательно, будет равна
Pоо = 1 Pпп Pно:
Таким образом, в данном пункте рассмотрен практически весь спектр систематических кодов с CRC, применяемых в различных системах передачи данных для обнаружения ошибок.
68
2.4.Принцип обнаружения ошибок в протоколах межсетевого взаимодействия и транспортного уровня в сети Интернет
В глобальной сети Интернет применяется помехоустойчивый блочный код, предназначенный для обнаружения ошибок на уровне межсетевого взаимодействия в IP-пакетах, а также на транспортном уровне в протоколах TCP и UDP [42–44]. Алгоритмы кодирования и декодирования на различных уровнях одинаковы. При этом, в IP-пакетах код предназначен для контроля за ошибками только в заголовках IP-пакетов, тогда как на транспортном уровне контроль за ошибками осуществляется не только в заголовках, но и в поле данных TCP-сегментов и UDP-датаграмм. Особенности борьбы с ошибками в Интернете отличаются на каждом из уровней. Так, в случае обнаружения ошибок в заголовке IP-пакета весь пакет бракуется и переспрос на повторную передачу пакета не посылается. Обнаружение ошибок в TCP-сегменте приводит к тому, что ошибочный сегмент стирается и к отправителю TCP-сегмента посылается запрос на его повторную передачу. А вот если ошибки будут обнаружены в UDP-датаграмме, то последняя стирается и запрос на повторную передачу этой датаграммы не посылается.
Следующей особенностью (n;k)-кода является то, что длина кодируемой части не является постоянной, но она ограничена максимально возможной в соответствии с документами RFC (Request for Comments — запрос комментариев). Например, длина заголовка в IP-пакете 4 версии обычно равна 20 октетам. Максимальные размеры TCP-сегмента с заголовком без опций и UDP-датаграммы не превышают 65515 байт. Во всех указанных протоколах длина проверочной последовательности (контрольной суммы) равна 16 бит.
Помехоустойчивый код в Интернет не относится к классу CRC, а является кодом с вычислением контрольной суммы по модулю (216 1) с переносом. Рассмотрим этот код подробнее.
2.4.1.Механизм вычисления и проверки контрольной суммы
2.4.1.1.Алгоритм кодирования
Кодируемая часть, длина которой в битах должна быть кратной 16, разбивается на участки по 16 двоичных элементов в каждом. Контрольная сумма формируется путем двоичного суммирования 16-элементных двоичных комбинаций кодируемой части пакета (сегмента, датаграммы) с переносом в следующие старшие разряды. Сложение происходит с приведением суммы 16элементных комбинаций по модулю (216 1). Полученная в результате суммирования 16-элементная двоичная комбинация на передающей стороне инвертируется, т. е. «1» меняется на «0», и наоборот — «0» меняется на «1». Полученная при этом двоичная 16-разрядная комбинация и будет представ-
69

лять собой контрольную сумму, которая записывается в поле контрольной суммы и передается в составе IP-пакета (TCP-сегмента, UDP-датаграммы) на приемную сторону. Следует учесть, что первоначально (до завершения процедуры кодирования) поле контрольной суммы должно быть обнулено. Кроме того, надо иметь ввиду, что в вычислении контрольных сумм TCP-сегмента и UDP-датаграммы как на передающей, так и на приемной стороне должны участвовать псевдозаголовки из 12 байт.
2.4.1.2. Алгоритм декодирования
На приемной стороне в декодере все 16-разрядные двоичные комбинации тех же самых полей, что и в кодере, а также принятая контрольная сумма суммируются по тому же правилу, что и на передаче. Отличие состоит лишь
втом, что полученная после суммирования 16-разрядная двоичная комбинация на приемной стороне не инвертируется. В результате, если в принятом сообщении ошибки отсутствуют, то по окончании процедуры суммирования
вдекодере будет получена контрольная 16-разрядная комбинация, все элементы которой будут равны «1». Этот факт и будет свидетельствовать об отсутствии ошибок в принятом сообщении (заголовке IP-пакета, TCP-сегменте, UDP-датаграмме). Если в контрольной 16-разрядной комбинации будет хотя бы один «0», то это будет говорить о наличии ошибок в принятом сообщении.
На рис. 2.10, 2.11 и 2.12 приведен демонстрационный пример кодирования и декодирования контрольной суммы для трех двоичных 16-разрядных комбинаций с младшими разрядами справа в двоичном и шестнадцатеричном видах соответственно. При этом суммирование шестнадцатеричных чисел производится с переносом по mod 16.
|
15 14 13 12 11 10 9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 (i) |
||||||||||||||
|
1 0 +1 |
+1 +1 +1 +2 +0 +1 +1 +1 |
(a) |
|||||||||||||||||||||
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
||||||||
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
(b) |
|||||||
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
(c) |
|||||||
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
S |
|||||||
|
1 |
0 |
(d) |
|||||||||||||||||||||
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
||||||||
|
2 |
D |
0 |
7 |
||||||||||||||||||||
|
( |
) |
||||||||||||||||||||||
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
d |
|||||||
|
D |
2 |
F |
8 |
КС |
|||||||||||||||||||
Рис. 2.10. Пример кодирования контрольной суммы для трех двоичных 16-разрядных комбинаций с младшими разрядами справа в двоичном виде
70

|
15 14 13 12 11 10 9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 (i) |
||||||||
|
1 0 +1 |
+1 +1 +1 +2 +2 +1 +1 +1 |
(a) |
|||||||||||||||
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
||
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
(b) |
|
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
(c) |
|
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
КС |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
S |
|
|
1 |
0 |
||||||||||||||||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
S |
F F F F
Рис. 2.11. Пример декодирования контрольной суммы для трех двоичных 16-разрядных комбинаций с младшими разрядами слева в двоичном виде
|
3 |
2 |
1 |
0 |
(i) |
3 |
2 |
1 |
0 (i) |
|||||
|
2 |
+2 +1 |
(a) |
2 |
+2 |
+1 |
(a) |
|||||||
|
E 0 E 1 |
E 0 E 1 |
||||||||||||
|
C |
4 |
4 |
8 |
(b) |
C |
4 |
4 |
8 |
(b) |
||||
|
8 |
7 |
D C |
(c) |
8 |
7 |
D C |
(c) |
||||||
|
2 |
D 0 |
5 |
S |
D |
2 |
F |
8 |
КС |
|||||
|
2 |
S |
||||||||||||
|
F |
F |
F |
D |
||||||||||
|
2 |
D |
0 |
7 |
(d) |
2 |
||||||||
|
D |
2 |
F |
8 |
( |
d |
) = КС |
F |
F |
F |
F |
S |
(а) (б)
Рис. 2.12. Пример кодирования (а) и декодирования (б) контрольной суммы для трех двоичных 16-разрядных комбинаций с младшими разрядами слева
вшестнадцатеричном виде
2.4.2.Вероятностная оценка кода по обнаружению ошибок
Обнаружение ошибок в данном коде может быть оценено аналогично рассмотренному в пп. 2.2.1 блочному коду байтовой структуры с длиной блока в 128 байт и вычислением контрольной суммы по mod 255. В частности, при длине блока в N байт вероятность правильного приема блока в канале ДСК с вероятностью битовой ошибки p может быть вычислена в соответствии с выражением Pпп = (1 p)8N.
При вычислении контрольной суммы в Интернет происходит сложение N 16-элементных комбинаций по mod (216 1), поэтому вероятность правильного приема блока будет определяться выражением Pпп = (1 p)16N.
Прием блока с необнаруженной ошибкой возможен из-за возникновения так называемых ошибок замещения. Например, двукратная необнаруживаемая ошибка (t = 2) возникнет в случае, когда в одной из 16 N-элементных комбинаций блока возникнут ошибочные переходы одной «1» в «0» и одного «0» в «1». Вероятность такого события Pно(t = 2;1) в канале ДСК при равно-
71
|
N |
||||||
|
вероятных 0 и 1 и среднем весе N-элементной комбинации w = |
может быть |
|||||
|
2 |
||||||
|
определена по выражению: |
||||||
|
N2 |
||||||
|
P (t = 2;1) = 16 |
p2(1 |
p)16N 2: |
(2.25) |
|||
|
4 |
||||||
|
но |
Аналогично, 4-кратная ошибка (t = 4) не будет обнаружена, если в одной из 16 N-элементных комбинаций блока возникнут ошибочные переходы двух «1» в два «0» и двух «0» в две «1». Вероятность Pно(t = 4;1) такого события оценивается выражением:
|
Pно(t = 4;1) = 16hCN2 |
=2 p2i2 |
(1 p)16N 4: |
(2.26) |
В общем виде вероятность необнаруживаемых ошибок четной кратности t = 2i, (1 i N2 ) типа замещений в одной из 16 N-элементных комбинаций может быть аналитически оценена, при равной вероятности 0 и 1 в сообщении, выражением:
|
Pно(t = 2i;1) = 16hCNi =2 pii2 |
(1 p)16N 2i: |
(2.27) |
Тогда общая вероятность необнаруживаемой ошибки четной кратности типа замещения в одной из 16 N-элементных комбинаций блока может быть определена суммой:
|
N=2 |
N=2 |
i |
2 |
|||||
|
Pно(t = 2;4;8;:::;1) = å Pно(t = 2i) = å |
16 CNi |
=2 pi |
(1 |
p)16N 2i: |
||||
|
i=1 |
i=1 |
h |
Для более полной приближенной оценки вероятности необнаруживаемых ошибок необходимо учесть также необнаруживаемые ошибки кратности 3. Тогда, кроме формул (2.25) и (2.26), следует также получить выражение для 3-кратных необнаруживаемых ошибок типа замещения. К таким ошибкам относятся однократная ошибка в j-й N-элементной комбинации, 1 j 16, и двукратная ошибка в ( j 1)-й комбинации. Причем, ошибки в j-й и в ( j 1)-й комбинациях должны быть в противоположных символах, например, одна ошибка среди «1» в j-й и две ошибки среди «0» в ( j 1)-й комбинации или наоборот. Заметим, при этом, что нулевой строке ( j = 0) соответствуют младшие разряды 16-разрядных комбинаций, участвующих в вычислении контрольной суммы.
При этих условиях вероятность трехкратных необнаруживаемых ошибок, аналогично формуле (2.14), можно определить из выражения:
|
Pно(t = 3;2) = 2 15hCN1 |
=2CN2 |
=2 p3(1 p)16N 3i: |
(2.28) |
72
Кроме того, следует также учесть случай возникновения четырехкратных (t = 4) необнаруживаемых ошибок в двух произвольных N-элементных комбинациях по две ошибки типа замещения в каждой из них. Вероятность Pно(t = 4;2) такого события определяется как
|
Pно(t = 4;2) = C162 (Q1)2(1 p)16N; |
(2.29) |
где Q1 — вероятность (2.30) двукратной необнаруживаемой ошибки типа замещения в отдельно взятой N-элементной комбинации:
|
Q1 = |
N |
2 |
||
|
p2(1 p)N 2: |
(2.30) |
|||
|
2 |
Таким образом, вероятность необнаруживаемых ошибок в протоколах IP, ICMP, TCP и UDP, в соответствии с (2.25), (2.26), (2.28), (2.29) и (2.30), можно приближенно определить выражением:
Pно = Pно(t = 2;1) + Pно(t = 4;1) + Pно(t = 3;2) + Pно(t = 4;2);
где в скобках (t = i; j) обозначено: i — количество ошибок в j N-элементных комбинациях.
Считается, что в случае равномерного распределения, алгоритм контрольной суммы пропускает лишь 1 ошибку из 216 пакетов. Для неравномерно распределенных данных обнаруживающая способность зависит от вида распределения. Так, исследование [45] показало, что в зависимости от вида трафика, используемый в протоколе TCP алгоритм вычисления контроль-
ной суммы обеспечивает вероятность необнаруженной ошибки от 10 10 до
6;25 10 8.
2.4.3. Примеры вычисления контрольной суммы для разных протоколов
2.4.3.1.Контрольная сумма в протоколе IPv4
Впротоколе IPv4 контрольная сумма рассчитывается только для заголовка пакета. Данные не проверяются, поскольку инкапсулируемые в IPv4 протоколы имеют свою контрольную сумму, учитывающую, как их заголовок, так и данные. К тому же, заголовок пакета IPv4 меняется при прохождении маршрутизаторов и, следовательно, контрольная сумма должна вычисляться каждым маршрутизатором заново — если бы она учитывала и данные пакета IPv4, то это бы значительно повысило нагрузку на процессоры маршрутизаторов и увеличило время обработки каждого пакета [46].
Структура заголовка пакета IPv4 приведена на рис. 2.13 [46].
73
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
Версия |
Длина заг. |
Тип сервиса |
Полная длина пакета |
||||||||||||||||||||||||||||
|
Идентификатор пакета |
Флаги |
Смещение фрагмента |
|||||||||||||||||||||||||||||
|
Время жизни |
Тип протокола |
Контрольная сумма |
|||||||||||||||||||||||||||||
|
IPv4-адрес |
отправителя |
||||||||||||||||||||||||||||||
|
IPv4-адрес получателя |
|||||||||||||||||||||||||||||||
|
Опции. . . |
Заполнение |
Рис. 2.13. Структура заголовка пакета IPv4
Контрольная сумма CSIP заголовка передаваемого пакета IPv4 рассчитывается по следующему алгоритму:
1.Заголовок разбивается на слова Wi по 16 бит. При необходимости последнее слово заголовка дополняется нулями справа (биты заполнения), чтобы «выровнять» длину заголовка в битах кратно 16.
2.Значение поля контрольной суммы, которому соответствует слово W6, принимается равным нулю:
W6 = (0000)16:
3. Полученные 16-битные слова Wi поэлементно суммируются между собой, как двоичные числа с переносом в старшие разряды:
Ws = åWi:
i
4. В том случае, если результат сложения Ws в двоичном представлении превышает по длине 16 бит, он разбивается на два 16-битных слова, которые складываются между собой. Эту процедуру называют «круговым переносом», т. е. переполнение старшего разряда переносится в младший, например
если Ws = (2A4E3)16; то Ws = (0002)16 + (A4E3)16 = (A4E5)16:
5.В случае, если результат сложения Ws снова превышает 16 бит, предыдущая операция повторяется.
6.Находится двоичное поразрядное дополнение результата сложения, которое и записывается в поле контрольной суммы:
CSIP = (FFFF)16 Ws:
Для более подробного ознакомления с процедурой вычисления контрольной суммы в протоколах сетевого и транспортного уровня сети Интернет и вариантами ее реализации для различных языков программирования рекомендуется обратиться к RFC 1071 [42].
74
|
0 |
15 16 |
31 |
|
|
4500 |
0076 |
||
|
252D |
4000 |
||
|
4011 |
0000 |
||
|
C0A8 |
010F |
||
|
C1C8 |
B708 |
||
Рис. 2.14. Пример заголовка пакета IPv4 с обнуленным полем контрольной суммы
Для примера рассмотрим расчет контрольной суммы заголовка IPпакета, приведенного на рис. 2.14. Пакет записан в шестнадцатеричной системе счисления. Поле контрольной суммы выделено цветом и обнулено перед началом формирования передаваемого IP-пакета.
1. Разбиваем заголовок с обнуленным полем контрольной суммы на слова по 16 бит и суммируем полученные 16-битные слова между собой:
(4500)16 + (0076)16 + (252D)16 + (4000)16 + (4011)16+ +(0000)16 + (C0A8)16 + (010F)16 + (C1C8)16 + (B708)16 = (3253B)16:
2. Поскольку результат сложения в двоичном представлении превышает 16 разрядов (или 4 шестнадцатеричных цифры), разбиваем его на два слова по 16 бит каждое и снова их суммируем:
(0003)16 + (253B)16 = (253E)16:
3. Находим контрольную сумму, как двоичное поразрядное дополнение результата сложения:
CSIP = (FFFF)16 (253E)16 = (DAC1)16:
Полученное число заносится в поле контрольной суммы заголовка IPпакета (рис. 2.14).
Проверка контрольной суммы при приеме IP-пакета производится по аналогичному алгоритму, отличаясь только тем, что в расчете участвует и контрольная сумма принятого IP-пакета. Если итоговое поразрядное двоичное дополнение полученной суммы равно 0, т. е. (0000)16, то это говорит о корректности контрольной суммы.
Для примера проверим корректность контрольной суммы заголовка IP-пакета, приведенного на рис. 2.14 с учетом значения поля контрольной суммы (DAC1)16.
1. Суммируем все 16-битные слова заголовка между собой:
(4500)16 + (0076)16 + (252D)16 + (4000)16 + (4011)16+ +(DAC1)16 + (C0A8)16 + (010F)16 + (C1C8)16 + (B708)16 = (3FFFC)16:
75
2. Поскольку результат сложения превышает 16 бит, разбиваем его на два слова по 16 бит каждое и снова их суммируем:
(0003)16 + (FFFC)16 = (FFFF)16:
3. Находим двоичное поразрядное дополнение результата сложения:
(FFFF)16 (FFFF)16 = (0000)16:
Таким образом, мы проверили, что приведенная в пакете на рис. 2.14 контрольная сумма верна.
Можно последнюю операцию поразрядного двоичного дополнения не проводить. Тогда правильность контрольной суммы принятого IP-пакета будет подтверждаться результатом суммирования (FFFF)16 на втором шаге алгоритма проверки.
2.4.3.2.Контрольная сумма в протоколе ICMP
Впротоколе ICMP контрольная сумма рассчитывается для всего пакета. Структура пакета ICMP приведена на рис. 2.15 [47].
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
Тип сообщения |
Код сообщения |
Контрольная сумма |
|||||||||||||||||||||||||||||
|
Данные в зависимости от типа и кода сообщения |
Рис. 2.15. Структура пакета ICMP
|
0 |
15 16 |
31 |
|
|
0800 |
7C6B |
||
|
6F83 |
0001 |
||
|
0001 |
0203 |
||
|
0405 |
0607 |
||
Рис. 2.16. Пример пакета ICMP
Алгоритм вычисления контрольной суммы полностью аналогичен таковому для заголовка пакета IP. Рассмотрим вычисление контрольной суммы на примере ICMP-пакета, приведенного на рис. 2.16. Поле контрольной суммы выделено цветом.
1. Разбиваем заголовок на слова по 16 бит, принимаем значение поля контрольной суммы равным нулю и суммируем полученные 16-битные слова между собой:
(0800)16 + (0000)16 + (6F83)16 + (0001)16+ +(0001)16 + (0203)16 + (0405)16 + (0607)16 = (8394)16:
76
2. Находим контрольную сумму, как двоичное поразрядное дополнение результата сложения:
CSICMP = (FFFF)16 (8394)16 = (7C6B)16:
Как можно видеть, результат совпадает со значением поля контрольной суммы, приведенным на рис. 2.16.
Проверка контрольной суммы ICMP-пакета аналогична рассмотренной для протокола IPv4.
2.4.3.3. Контрольная сумма в протоколах TCP и UDP
Алгоритм расчета контрольной суммы пакетов TCP и UDP, структура которых приведена на рис. 2.17 и 2.18 соответственно, практически аналогичен таковому для заголовка пакета IP. Контрольная сумма рассчитывается для всего пакета TCP/UDP, а также учитывает IP-адреса отправителя и получателя. Для этого перед расчетом контрольной суммы формируется специальный псевдозаголовок, структура которого показана на рис. 2.19 [48, 49].
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
Порт отправителя |
Порт получателя |
||||||||||||||||||||||||||||||
|
Номер пакета |
|||||||||||||||||||||||||||||||
|
Номер подтверждения |
|||||||||||||||||||||||||||||||
|
Длина заг. |
Зарезерв. |
Флаги |
Размер окна |
||||||||||||||||||||||||||||
|
Контрольная сумма |
Указатель срочности |
||||||||||||||||||||||||||||||
|
Опции. . . |
Заполнение |
||||||||||||||||||||||||||||||
|
Данные |
|||||||||||||||||||||||||||||||
|
Рис. 2.17. Структура пакета TCP |
|||||||||||||||||||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
Порт отправителя |
Порт получателя |
||||||||||||||||||||||||||||||
|
Длина датаграммы |
Контрольная сумма |
||||||||||||||||||||||||||||||
|
Данные |
|||||||||||||||||||||||||||||||
|
Рис. 2.18. Структура пакета UDP |
|||||||||||||||||||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
IPv4-адрес отправителя |
|||||||||||||||||||||||||||||||
|
IPv4-адрес получателя |
|||||||||||||||||||||||||||||||
|
Нули |
Тип протокола |
Длина пакета TCP/UDP |
Рис. 2.19. Структура псевдозаголовка TCP/UDP
77
Рассмотрим вычисление контрольной суммы TCP/UDP на примере пакета UDP, показанного на рис. 2.20. На рис. 2.20 желтым выделен заголовок IPv4, который необходим для построения псевдозаголовка, а зеленым обозначена контрольная сумма пакета UDP.
|
0 |
15 16 |
31 |
9 |
||
|
DAF5 |
0000 |
||||
|
4500 |
0038 |
> |
|||
|
> |
|||||
|
> |
|||||
|
C0A8 |
010F |
> |
|||
|
= |
|||||
|
4011 |
6537 |
> Заголовок IPv4 |
|||
|
C1C8 |
B708 |
> |
|||
|
> |
|||||
|
> |
|||||
|
E4DD |
0035 |
> |
|||
|
> |
|||||
|
; |
|||||
|
Заголовок UDP |
|||||
|
0024 |
0B54 |
||||
|
9 |
|||||
|
0001 |
0000 |
||||
|
C0FD |
0100 |
> |
|||
|
0000 |
0000 |
||||
|
> |
|||||
|
> |
|||||
|
> |
|||||
|
> |
|||||
|
0667 |
6F6F |
> |
Данные UDP |
||
|
> |
|||||
|
> |
|||||
|
> |
|||||
|
676C |
6503 |
> |
|||
|
= |
|||||
|
636F |
6D00 |
> |
|||
|
> |
|||||
|
> |
|||||
|
0001 |
0001 |
> |
|||
|
> |
|||||
|
> |
|||||
|
> |
|||||
|
> |
|||||
|
> |
|||||
|
> |
|||||
|
; |
Рис. 2.20. Пример пакета UDP с заголовком IPv4
Расчет контрольной суммы происходит в следующем порядке.
1. Формируется псевдозаголовок (рис. 2.21).
|
0 |
15 16 |
31 |
|
|
C0A8 |
010F |
||
|
C1C8 |
B708 |
||
|
0011 |
0024 |
||
Рис. 2.21. Псевдозаголовок для пакета UDP, показанного на рис. 2.20
2. Разбиваем заголовок UDP, блок данных и псевдозаголовок на слова по 16 бит, принимаем значение поля контрольной суммы равным нулю и суммируем полученные 16-битные слова между собой:
|
[(E4DD)16 + (0035)16 + (0024)16 + (0000)16]+ |
|||||||||||||||||||
|
| |
{z |
} |
|||||||||||||||||
|
16 |
|||||||||||||||||||
|
+[(C0FD) |
Заголовок UDP |
||||||||||||||||||
|
+ (0100)16 + (0001)16 + (0000)16+ |
|||||||||||||||||||
|
+(0000)16 + (0000)16 + (0667)16 + (6F6F)16 + (676C)16+ |
|||||||||||||||||||
|
+(6503)16 + (636F)16 + (6D00)16 + (0001)16 + (0001)16]+ |
|||||||||||||||||||
|
| |
{z |
}16 |
16 |
16 |
|||||||||||||||
|
C0A8 16 |
16 |
16 |
16 |
||||||||||||||||
|
+ (010F) |
Данные UDP |
+ (0011) + (0024) |
] = (5F4A6) |
||||||||||||||||
|
+[( |
) |
+ (C1C8) + (B708) |
: |
||||||||||||||||
|
| |
{z |
} |
|||||||||||||||||
|
Псевдозаголовок |
78
Соседние файлы в папке лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #