-
markobes
Только зашел- Регистрация:
- 2 дек 2015
- Сообщения:
- 4
- Имя пользователя:
- владимир
вроде нажимали на кнопку старт и пидаль
-
диагностировал человек который уже делал диагностику меган 2? «вроде нажимали на кнопку и педаль» , ты лучше скажи зажигание при этом включилось или нет? руль разблокировался? приборная панель загорелась?
раз не прочел цепи значит неправильно диагностировал. -
markobes
Только зашел- Регистрация:
- 2 дек 2015
- Сообщения:
- 4
- Имя пользователя:
- владимир
он занимается ремонтом рено. зажигание включилось ,руль разблокировывался ,приборка загорелась.двигатель начел запускаться но не схватывает. клип половина увидел а двигатель, акпп,электроусилитель руля, и подушки не увидел. а всё началось что я приехал заглушил мотор а потом двигатель крутится но не схватывает
Последнее редактирование: 11 окт 2016
-
тогда второй вариант. зажигание значит у тебя включено. при запуске диагностики. ставим галку на пункте повторной идентификации электронных цепей. (или както по другому) находится возле кнопки запуска теста в окне с вводом вин номера
-
markobes
Только зашел- Регистрация:
- 2 дек 2015
- Сообщения:
- 4
- Имя пользователя:
- владимир
я уже не стал его дёргать и так его отрывал два раза от работы. главное obd 2 зашёл в двигатель и увидел ошибку. но это обрыв цепи датчика распредвала. из-за него машина всё равно заводится. а это молчит. может датчик колен вала вышел из строя?
-
Форумчане, выскажите свое мнение пожалуйста.
Проблема — контрольная лампа «Сервис» и сообщение «Check Injection». Двигатель запускается хорошо, с первого раза. Работает устойчиво, обороты не плавают, тянет нормально. Расход бензина тоже в норме.
Диагностика CAN Clip-ом выдала ошибки:
DF602 CO.0 — Силовая цепь подогрева нижн.датчика О2;
DF119 1.DEF — Сигнал датчика распределительного вала;
DF080 CO — Цепь измен. х-ки распределительного вала.
По DF602 в разъеме датчика кислорода после нейтрализатора найден сгнивший контакт. Разъем заменили, но ошибка все равно остается.
Приговор диагностов: под замену датчик кислорода, датчик фаз и фазорегулятор. И, до кучи к фазику, ремень ГРМ с роликами.
Машине 10 лет, пробег 280+ тыс.км, датчики фаз и кислорода родные, поэтому соглашусь что пора их заменить.За фазорегулятор… Нынешний фазик на машине ходит ~70 тыс.км. Прежний (родной) прошел 210 тыс.км и перед заменой при пуске двигателя трещал так, что с первой попытки мотор не заводился. При этом сообщений «Check Injection» и ошибок не было. Отсюда сомнение что фазик зря приговорили, сейчас-то его совсем не слышно.
Может не фазик, а его электромагнитный клапан мозг делает?ЗЫ. Если есть у кого Диалоджис, что означают дополнения к кодам ошибок 1.DEF, CO, CO.0?
Последнее редактирование: 20 ноя 2016
-
Силовая цепь подогрева, такая ошибка была, не работал подогрев ДК, мерил сопротивление — ничего, поставил старый и все пришло в норму. Там сгнивают контакты в самом датчике, так реанимировать смысла нет.
Сигнал с датчика РВ — скорее всего плохой контакт, была данная ошибка, просто снял контакт, промыл карбклинером, силикота капнул и одел обратно, все нормально работает. 1DEF надо было в самом клипе смотреть, он говорит в чем проблема.
Цепь измерения характеристик РВ это все может идти от датчика КВ и клапана фазика, опять же С0 надо было расшифровку смотреть в клипе.Саму ошибку чек инжектор может дубасить лямбда в совокупе с ошибками по впусному валу… У тебя получается лямбда не пашет, корректировка топлива не производится, сигнала о положении впускного вала нет, фосунки не знаю в какую надо прыскать…
-
Рома! Получается,что нижняя лямбда влияет на состав топлива?А то у меня висит Р0141 и есть проблема с оборотами хх при запуске.
-
Скажи какая у тебя система впрыска и я расскажу с чего начинать и что именно обозначают всякие твои co и def.
-
Система впрыска Sagem3000, двигатель K4MD812
-
Да лямбда похоже еще работает, при прогретом двигателе на холостом ходу выходное напряжение медленно меняется около 0.45В (от 0.44 до 0.46В).
-
DF602 вторая лямбда CO.0-обрыв, проверить сопротивление нагревателя лямбды- должно быть порядка 9 Ом. Она и сейчас может давать сигнал, но полноценный сигнал будет только после ее нагрева более 300 градусов, а учитывая что стоит она после катализатора- вряд ли она нагреется от выхлопных газов до рабочей температуры.
DF080 CO- пока на нее не смотрим, т.к. имеется 119 ошибка из-за которой может вываливатся 80я.
DF119-СИГНАЛ ДАТЧИКА ПОЛОЖЕНИЯ РАСПРЕДЕЛИТЕЛЬНОГО ВАЛА , 1.DEF: Пропуск зубца зубчатого шкива распределительного вала- соответственно смотреть почему может мишень не видеть: либо дефект мишени, либо грязь на датчике и его разьеме.
-
Вот почему все пишут номера ошибок, в посмотреть на ее расшифровку всем лениво, это же 1 раз клацнуть мышкой… Если бы я так искал ошибку по ЕСП/АБС то уже все систему бы перебрал впустую… Мне авто написал заднее правое колесо, нажал на расшифровку DEF 1 и там все черным по белому — несоответствие количесво мишеней… С диагностикой впруска все тоже самое… Сколько толдычу людям, никто не воспринимает всерьез…
-
Влияет на образование смеси, первая лямбда выдает значение, топлива в какой то пропорции впрыскивается в горшок и сгорает, если нижняя лямбда фиксирует повышеную токсичность газов, тогда смесь обедняется / обогощается, чтобы она пришла в норму… Насчет плавающих оборотов не скажу, у самого стрелка на хх бегает чуть, не обращаю внимания, клип молчит как партизан.
-
по ошибкам распредвала — вот технота, там всё есть: чтобы приговорить фазик( основываясь на ваших ошибках) нужны дополнительные проверки, одной лиш ошибки DF080 для этого недостаточно, кроме того треск фазика обычно никак не связан с ошибкой DF080.
Вложения:
-
6506A.pdf
- Размер файла:
- 122,6 КБ
- Просмотров:
- 19
-
-
Вот не знаю. как это трактовать. но у меня ошибка по нижней лямбде висит уже давненько. И похоже, что именно на запуск она не влияет. Это мои предположения.! Тут что то другое.
Я так понимаю на запуске нижняя лямбда не опрашивается ЭБУ (именно для коррекции смеси). У неё даже подогрев не сразу включается. А на наших прошивках(как говорят) она вообще не влияет на состав смеси. Тут проверять надо. КЛИП нужен.— Сообщение объединено, 21 ноя 2016 —
На запуске вообще впрыск по программе идёт попарный.
Последнее редактирование: 21 ноя 2016
-
VladimidoFF
Только зашел- Регистрация:
- 27 дек 2016
- Сообщения:
- 5
- Имя пользователя:
- Владимир
Скорее проблема конкретно в датчике, или что-то с гнездом
-
Тоже была недели 3 назад эта проблемка — ошибка по нижней лямбЕ, купил датчик фирмы FAe 77153 у него разъем идентичный нашему,поставил-ошибку сбросил ЕЛМ 327 -неделя полет нормальный! В разделе диагностика с помощью ЕЛМ есть мот фотки работы лямбда на диаграммах!
-
конкретно в каком датчике?
с каким гнездом? …и что за проблема? -
Что было до замены лямды?
Поделиться этой страницей
Господа помогите еще советом, вообщем к одной нестираемой ошибке вчера добавилась уже вторая —
DF199 Датчик давления наддува
1.DEF Проблема питания датчика
2.DEF Соответствие между давлением наддува и атмосферным давлением
СС.01 Короткое замыкание на +12В
СС.00 Обрыв цепи или короткое замыкание на массу
Это я считал ошибки перед тем как вчера ехать надо было, ошибку и стирать пробовал, считывал как при неработающем двигателе так и при работающем, стирал снова — остается, пробовал отсоединять коннектор от датчика опять ошибку стирал, остается, во время езды вроде как все нормально было, ничего плохого не замечал, вернулся из поездки опять стер и перечитал ошибки — она по прежнему остается.
Мне подсказали что с датчиком скорее всего все нормально, надо смотреть проводку к датчику, вероятно где то провод переломался.
И чем чревата езда с этой проблемой? То есть я так понимаю ЭБУ вообще не получает от датчика данных о давлении после турбины? Или получает но неправильные?
1. Что такое Can Clip — это дилерский заточенный под Renault прибор для диагностики автомобилей.
Так он выглядит
2. Что нужно для диагностики: а. Сам прибор б. Ноутбук с установленной программой Renault CAN Clip
3. Где найти программу Renault CAN Clip и какие у нее требования: ссылка на rutracker
Системные требования
4. Что делать, если есть ноутбук только 64 бит: Установить виртуальную машину, поставить на нее Win7 32bit и в нее установить Renault CAN Clip. Все прекрасно работает.
5. Порядок установки программы Renault CAN Clip:
5.1. Запустите файл изменения данных в реестре «Crack Renault CLIP.reg» из каталога «X:…Renault.CAN.Clip.v182Activation (Patch V3)», согласитесь на изменения. Далее запустите установку программы.
5.2. После завершения установки НЕ запускайте CLiP!, сначала замените оригинальный файл RSWin.exe (сделайте резервную копию оригинального файла) файлом Cracked .exe в C: CLIP_X91 Lib Application
5.3. Далее из этого же каталога (C: CLIP_X91 Lib Application ), запустите RSWin.exe, выберите «Зарегистрировать меня сейчас» и в следующем окне выберите «НЕТ»!
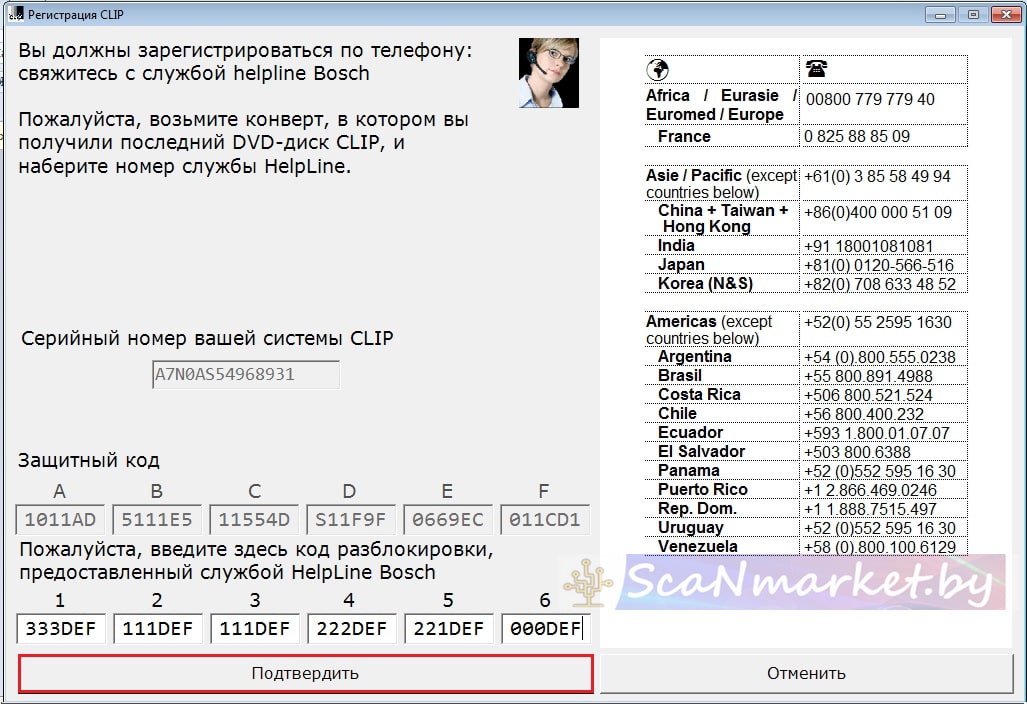
5.4. Используйте этот ключ для регистрации: 333DEF-111DEF-111DEF-222DEF-221DEF-000DEF. Работает до 31.12.2020
5.5. Теперь ВОССТАНОВИТЕ свой оригинальный RSWin.exe и УДАЛИТЕ исправленный!
5.6. На рабочем столе больше запустите CLiP, примите условия и CLiP, который он загрузит.
6. Что из самого популярного можно делать клипом: активировать функции из других комплектаций (противотуманки, парктроники, индикацию круиза и т.д.), производить настройки и адаптации (например, адаптацию ЭУРа), включать бортовой компьютер (где он выключен программно из-за комплектации), менять язык приборки (русского в мегане нет, но часто она на французком или немецком — удобнее на английском!), удалять ошибки, смотреть различные параметры (например, работу фазика, расход топлива на холостых и т.д.) и много чего ещё!
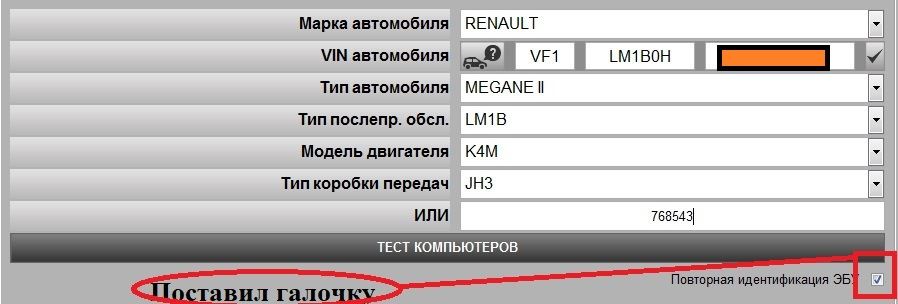
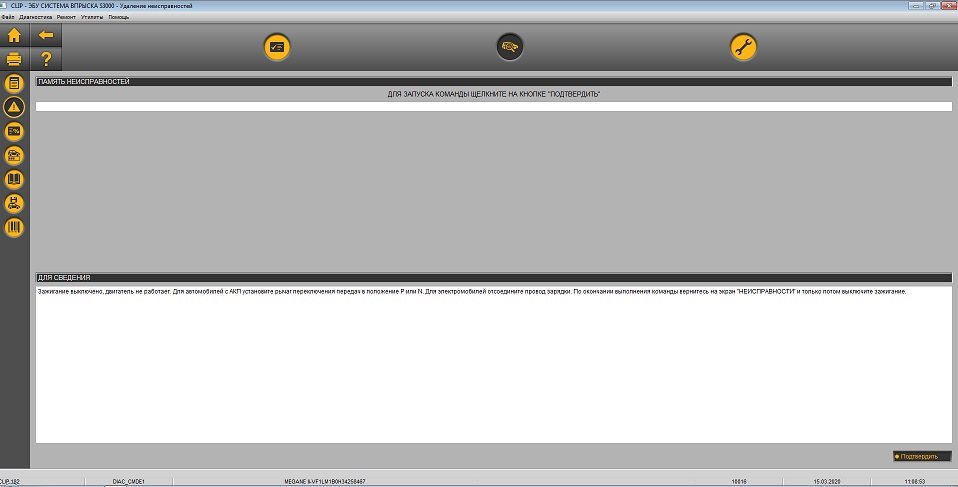
Процесс диагностики:
Если не поставить галочку, выделенную на скрине, то прибор не будет опрашивать заново многие блоки, а будет подтягивать старую информацию от предыдущей диагностики.
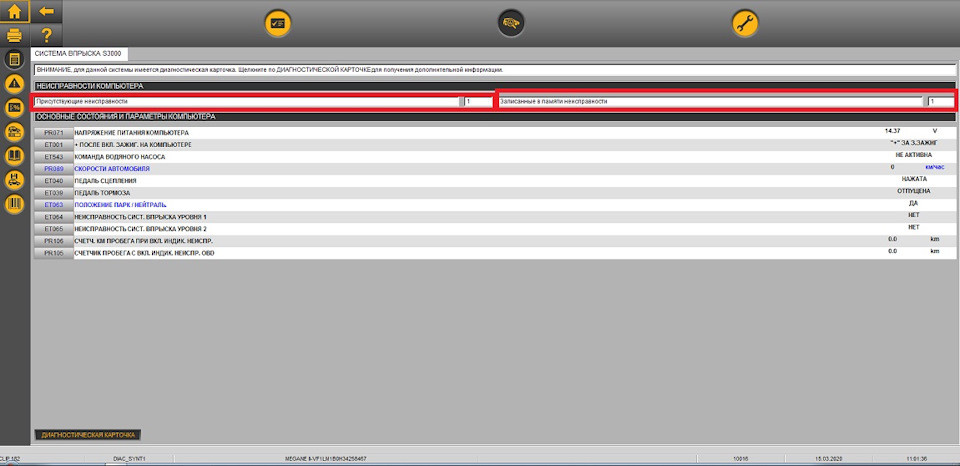
Полный размер
Запчасти на фото: PR105
Запчасти на фото: DF049
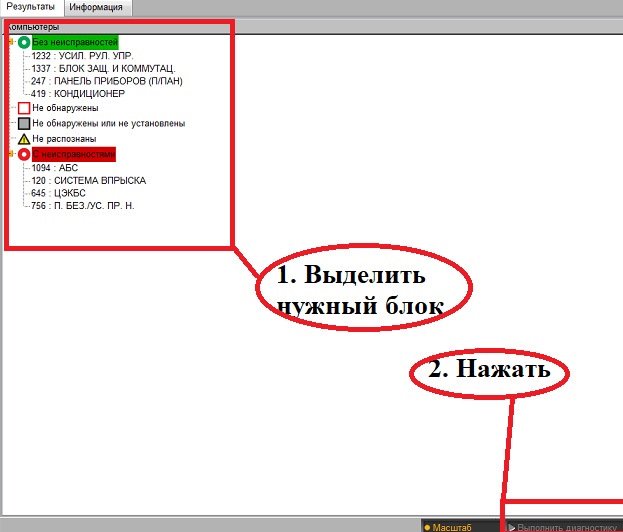
Ошибки могут быть активные (выделяются красным кружком) и запомненные (выделяются желтым мигающим кружком) (на скрине во время принтскрина он как раз моргнул (). Что бы удалить активные надо сначала устранить причину, а запомненные можно просто стереть (когда-то она была активная, затем причину устранили (например, был разрыв цепи и его починили, и ошибка перешла в разряд запомненных).
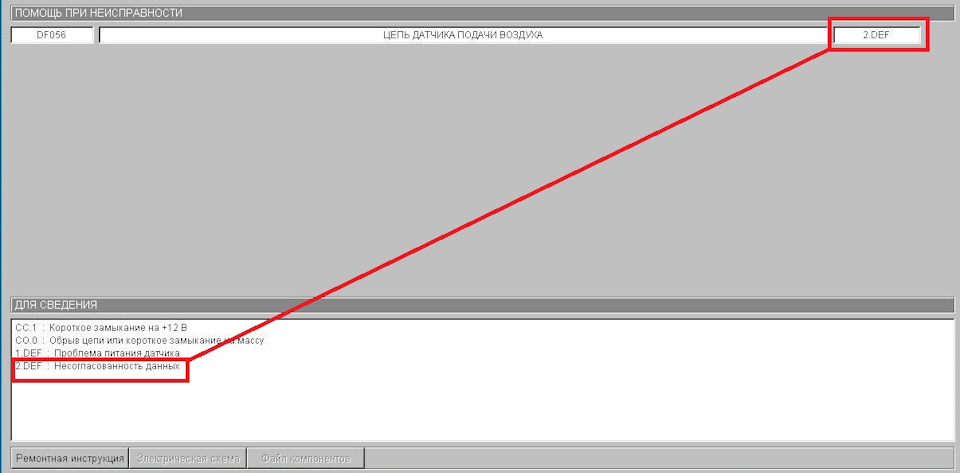
Так же у каждой ошибки может быть под ошибка. На скриншоте номер под ошибки выделен красным. В частности — 1.DEF. Нажимаем на название под ошибки, нас перекидывает на новую страницу, где описание всех под ошибок для данной ошибки. Это необходимо для более точного понимания причины неисправности.
Как это выглядит на примере другой ошибки:
Полный размер
Окно описания под ошибки при нажатии на нее
Для того, что бы удалить ошибки нужно вернуться назад в список ошибок и выполнить действия со скринов ниже:
После процесса удаления осталась только активная ошибка в блоке.
У кого какие есть вопросы — спрашивайте, имею достаточный опыт в данной тематике — попробую и вам помочь!
Сброс адаптаций Renault Can Clip — ChipTuner Forum
Чип-тюнинг коммерческой техники Кама3, ГАЗ от SMS-Soft
| Argutin Motors: VAG Bosch MEDC17 | Прошивки Magneti Marelli VAG от Art-Pro | Прошивки Peugeot/Citroen от Art-Pro | Прошивки Renault от А.Юрлова |
-
Закрытая тема.
-
offline
Начинающий диагност
- Регистрация:
- 17.08.2015
- Сообщений:
- 14
- Адрес:
- Ярославль
Добрый день, уважаемые Коллеги!
Столкнулся с проблемой сброса адаптаций (коррекций топливоподачи) на Логане (3132), ковырялся в Клипе, так и не нашел как это сделать. Подскажите пожалуйста, позволяет ли это сделать Клип, и если позволяет, то где найти этот функционал?
-
offline
Диагностика, ремонт, ГБО, дизели, бензин
- Регистрация:
- 17.02.2006
- Сообщений:
- 12,764
- Адрес:
- г. Пятигорск, лички нет
Тоже не нашёл. Вся надежда на устранение неисправности, и тогда оно само возвращается к норе.
-
offline
Ремонт а/м
- Регистрация:
- 26.02.2006
- Сообщений:
- 327
- Адрес:
- Волжский
Правый-верхний угол программы, кнопка с»гаечным ключем»-ремонтный режим, жмем. Далее слева ряд вертикальных кнопок, самая нижняя «операции удаления»-жмем. В меню выбираем кпопку повторная инициализация параметров-жмем.
-
offline
Начинающий диагност
- Регистрация:
- 17.08.2015
- Сообщений:
- 14
- Адрес:
- Ярославль
Большое спасибо, все именно так.
Не сомневаюсь, просто в данный момент на руках только Клип имеется. Сканматик планируется к приобретению.
Господа, сразу здесь спрошу, дабы тем не плодить. Как-то странно себя ведут коррекции, в т.ч. после сброса. Мультипликатив полез вверх, порядка 140, аддитив при этом лезет вниз около 100… Поясните плз, в чем особенность?
-
Закрытая тема.
Здесь присутствуют: 1 (пользователей: 0 , гостей: 1)
Текущее время: 04:13. Часовой пояс GMT +4.
- Главная
- Установка и настройка Renault CAN CLIP
Как установить Рено Кан Клип
УСТАНОВКА RENAULT CAN CLIP (прибор RLT2002)
Устанавливаем на Windows XP / 7 обязательно 32 бита (драйвера для прибора RLT2002 на 64 битную не установятся).
В win7 все файлы запускаем от имени Администратора (правой кнопкой на файле – запускать от имени администратора)
СКАЧАТЬ ПРОГРАММУ CAN CLIP v200
СКАЧАТЬ ДРАЙВЕРА ДЛЯ CAN CLIP
СКАЧАТЬ ФАЙЛЫ ПАТЧА ДЛЯ RLT2002
СКАЧАТЬ Renault Clip Tool
1.Запускаем файл: Crack RenaultCLIP.reg (если не запустите, система не признает компьютер правильным для Clip)
Далее жмем «Да»:
2. Появится окно, подтверждающее, что данные в реестр внесены:
3. Запускаем Setup.exe в папке с программой
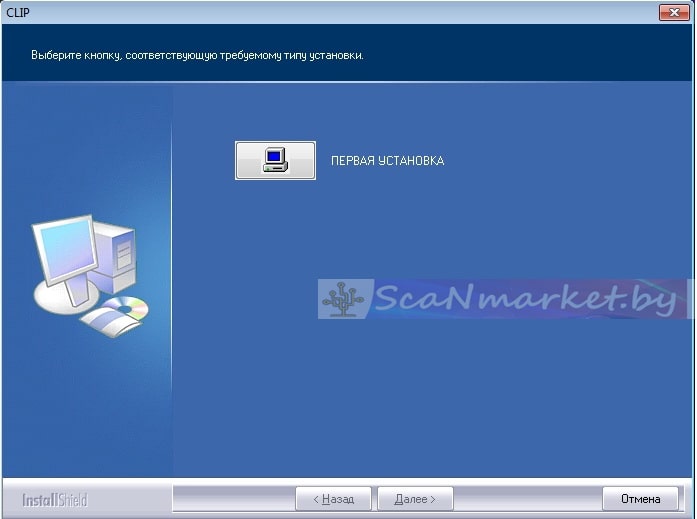
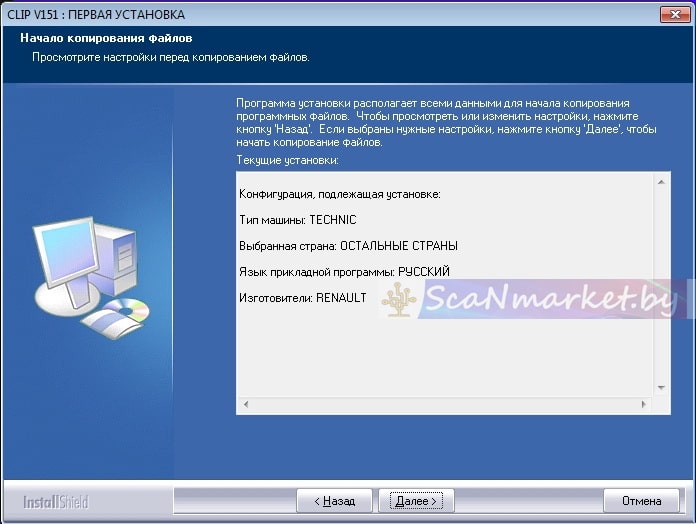
4. Запустится окно установки: жмем «Первая установка»
5. Соглашаемся с условиями лицензионного соглашения и жмем далее:
6. Тут выбираем «Остальные страны» и жмем далее:
7. Нам нужен Русский язык, поэтому «Русский» и жмем далее:
8. Выбираем «Renault» и жмем далее:
9. Тут просто жмем далее:
Наблюдаем за процессом установки программы:
10. После установки компьютер будет автоматически перезапущен:
11. После перезагрузки скопировать файлы из папки «RLT2002 patch files» в папку «C:CLIPConfig» с заменой.
Если этого не сделать RLT2002 не будет определяться в последних версиях CAN CLIP.
РЕГИСТРАЦИЯ ПРОГРАММЫ
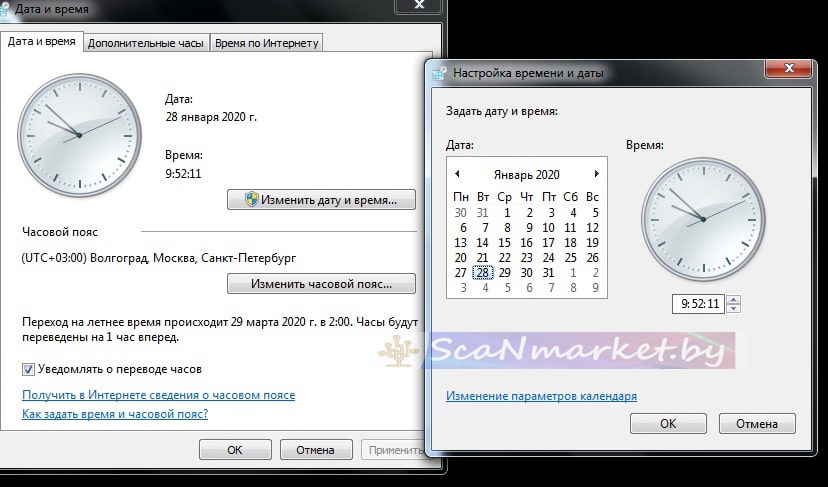
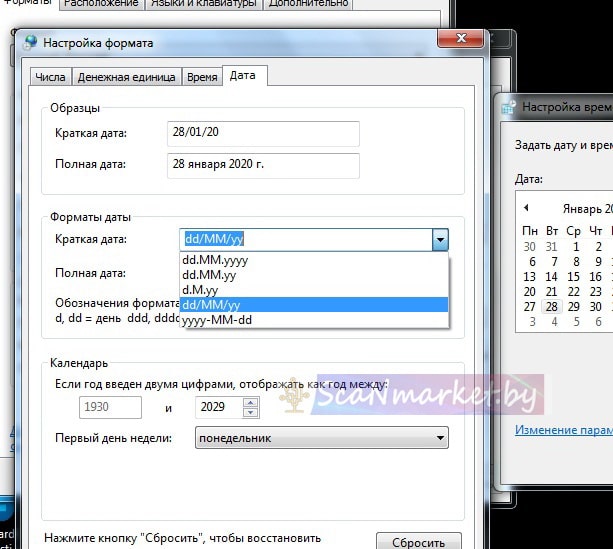
1.Меняем формат отображения даты в компьютере. Чтобы дата отображалась через косую черту:
Для этого нажимаем на часы в углу экрана
2. Нажимаем «Изменение настроек даты и времени»
3. Нажимаем Изменить дату и время и Изменение параметров календаря
4. Во вкладке Дата выбираем нужный формат даты
5. Сохраняем настройки.
6. Запускаем генератор «Renault Clip Tool.exe»
Если выскочит ошибка о необходимости установки Net framework – устанавливаем NET Framework.exe
7. После запуска Renault Clip Tool нажимаем Generate Clip (Manual) и получаем ключ.
8. Не закрывая Renault Clip Tool, запускаем программу Clip с рабочего стола
9. В окне регистрации ставим галочку напротив «Я понимаю и я принимаю изложенное ниже лицензионное соглашение» и жмем «Register me» или «Зарегистрировать меня сейчас»:
10. В окне «Являетесь ли вы участником сети Renault» отвечаем «Нет»:
11. В окне регистрации пишем код полученный ранее и жмём «Подтвердить».
20. Появится сообщение, что программа зарегистрирована. далее «Ok».
Установка драйверов Renault CAN CLIP
1.Подключаем прибор к компьютеру и к разъему автомобиля.
Если загорятся все четыре светодиода, значит драйвера установились автоматически.
2. Если горят только красные, ставим драйвера вручную:
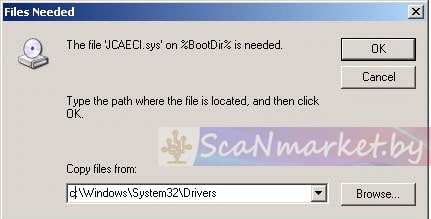
3. Подключаем Clip к компьютеру, появится окно или заходим в Диспетчер Устройств и ищем, не установленные драйвера:
4. Жмем «далее»:
5. Идет поиск драйвера:
6. Появится окно, жмем «далее»:
7. Жмем «ОК»:
8. Указываем путь в папку с нужным драйвером. JCAE CAN AVANT RENUMERATION
9. Драйвер JCAE CAN AVANT RENUMERATION установится.
10. Аналогично устанавливаем 3 оставшихся драйвера: JCAE ISO AVANT RENUMERATION, JCAE CAN APRES RENUMERATION, JCAE ISO APRES RENUMERATION.
11. После установки на приборе загорятся зеленые светодиоды ISO и CAN.
На этом процесс настройки Renault CAN CLIP закончен.
Renault Can Clip 218
Год/Дата Выпуска: 2022
Версия: 218
Язык интерфейса: Многоязычный (русский присутствует)
Таблэтка: отсутствует
Описание: Cофт Renault Can Clip, который является сервисным программным обеспечением, осуществляющим обслуживание и диагностику машин марок Renault, а также Dacia. Использование софта возможно проведение полного диагностирования ЭБУ машин (АКПП, двигатель-инжектора, штатного ксенона, ABS+ESP, климат-контроля, подушек безопасности, приборной панели, ЦКБЭС).
Совместно с адаптером CAN Clip программа способна выполнять такие функции: выводить инфо о машине, выполнять считывание ошибок, тестировать, а также программировать и выполнять другие процедуры с электронными системами авто. Благодаря наличию в интерфейсе нескольких языков, включая и русский, специалист по диагностике сможет с легкостью разобраться и выполнить работу с предлагаемым софтом.
Сама программа может работать как на Win x32, так и на Win x64. Вопрос только в возможности настроить драйвера для прибора диагностики.
Ниже какие приборы поддерживают какие системы:
Renault CAN Clip Alliance работает на Windows 7/10 x64/x32
Renault CAN Clip RLT 2002 работает на Windows 7 x32
Для j2534 — Windows 10 x64
Renault CAN Clip 216
Renault CAN Clip 215
Renault CAN Clip 212
Renault CAN Clip 210
Renault CAN Clip 209
Renault CAN Clip 207
Renault CAN Clip 206
Renault CAN Clip 205
Renault CAN Clip 204
Renault CAN Clip 203
Renault CAN Clip 202
Доп. информация:
Ключ до 2029
333DEF-111DEF-111DEF-222DEF-221DEF-999АВ7
Скриншоты
| [only-soft.org].t168657.torrent | ||
|---|---|---|
| Торрент: |
Зарегистрирован [ 2022-07-26 14:25 ] |
14 KB |
| Статус: |
√ проверено |
|
| Скачан: | 29 раз | |
| Размер: | 2,67 GB | |
| Оценка: |
(Голосов: 1) |
|
| Поблагодарили: | 1  (список) (список) |
|
|
Renault Can Clip 218 [2022] скачать торрент бесплатно и без регистрации |
Перейти к содержанию
На чтение 3 мин Просмотров 188к. Опубликовано 27.11.2019
Обновлено 19.02.2022
Программа Pyclip является почти полным аналогом PyRen и предназначена для диагностики и обслуживания автомобилей Renault. Работает со всеми базами данных и со всеми блоками управления.
Для правильной работы приложения требуется адаптер ELM327 c версией железа 1.5, который обязательно должен поддерживать Flow Control.
Скачать
PyClip v2.2 [Рекомендовано] с Яндекс.Диска или с MY-FILES.
PyClip v3.7 с базами 197 с Яндекс.Диска или с MY-FILES.
Возможности программы
- Чтение всех параметров со всех блоков управления автомобиля — двигателя, трансмиссии и др.
- Чтение, расшифровка всех кодов неисправностей и параметров во время фиксации ошибки.
- Тестирование датчиков и исполнительных механизмов.
- Конфигурирование блоков управления.
Как пользоваться
Чтобы пользоваться приложением понадобится адаптер ELM327 — оригинальный или китайский с версией микросхемы 1,5. На Android 8 и выше возможны разрывы связи с блютуз версией адаптера, в этом случае лучше использовать WI-FI версию. Во время работы с WI-FI ELM327 не будет доступен интернет.
Проверенные продавцы адаптеров ELM327 1.5
Видео о том, как пользоваться программой, активировать бортовой компьютер, часы, температуру и т. д.
Стартовый экран
- START — Запуск программы.
- ELM port — порт адаптера, либо адрес адаптера Wi-Fi. Адрес для Wi-Fi указывается в формате IP:port адаптера.
- Language — язык.
- Demo mode — запуск скрипта в демо-режиме при сохраненном файле savedEcus.p
- DUMP — сохранение дампа блока. Это рекомендуется делать перед любыми изменениями параметров в машине для возможности исправить неожиданные последствия таких изменений.
- Orientation landscape — запуск в портретном режиме.
- Scan vehicle — выбор модели автомобиля.
- Generate logs — включение функции логирования. Лог-файл может быть необходим для анализа ошибки, проверки адреса блока и других случаях.
- Log name — Имя лог-файла.
- CAN2 (Multimedia CAN) — использование шины CAN2 с соответствующим адаптером. На которой находится мультимедиа.
- Font size — Размер шрифта в программе.
- KWP Force Slow lnit — использование параметра slow-init для блоков более старых версий. Если у вас авто до 2009 года при нестабильном подключении — лучше активировать.
- Use CFC0 — программный flow-control, включать в том случае, если адаптер ELM327 не поддерживает аппаратный.
Структура блоков управления
- DE : Device errors — чтение, удаление ошибок.
- ID : Identifications — проверка VIN блока, версии прошивки, оборудования и пр.
- SY : System state — вывод актуальных основных показаний (обороты, напряжение, температура и пр.).
- SP : System parameters — вывод текущих параметров блока, без возможности изменения.
- LC : System configuration — вывод текущей конфигурации, без возможности изменения.
- AC : Executing tests — запуск сценариев тестирования блока (например проверить все лампочки приборки, реле и пр.).
- CF : Changing configuration — Изменение конфигурации блока. ОСТОРОЖНО!
- VP : VIN programming — программирование VIN, зашитого в каждый блок.
- RZ : Resets — Сбрасывает все ошибки блока и калибровки.
- ECM : Extended command set — это конфигурационные сценарии. Большая часть не работает (вероятно пока скрипт дорабатывается), но можно ознакомиться с принципами работы, используя команду «show» и после фразы «There is scenarium. I do not support them!» нажать «ввод» при запросе.
( 13 оценок, среднее 3.69 из 5 )
Помоги нам помогать вам
Вы можете пожертвовать небольшую сумму на поддержание работы и развитие сайта. Оплата происходит через платежную систему ЮМани от Сбербанка.
|
|
Вверх #1 |
|
Новичок Регистрация: 06.08.2012 Адрес: MoscoW Сообщений: 6 Автомобиль: Другой |
Двигатель 1,9DCi
Последний раз редактировалось VladMX; 06.11.2012 в 15:48.
|
|
|
|
|
|
Вверх #2 |
|
Пользователь Только пришёл
Регистрация: 14.03.2011 Адрес: Минск Сообщений: 86 Имя: Дмитрий Автомобиль: Laguna II Ph I |
расшифровку ошибок в нете спокойно найти можно!
__________________
Последний раз редактировалось _Dima_; 06.11.2012 в 21:26.
|
|
|
|
|
|
Вверх #3 |
|
ЛагуноВед Освоился Регистрация: 03.01.2010 Адрес: Литва Сообщений: 1,207 Имя: Aльфонсас Автомобиль: Laguna II Ph II |
DF072 Цепь 1 фронтальной подушки безопасности водителя DF070 Цепь боковой головной подушки безопасности со стороны
__________________ |
|
|
|
|
|
Вверх #4 |
|
Новичок Регистрация: 06.08.2012 Адрес: MoscoW Сообщений: 6 Автомобиль: Другой |
Спасибо за ответы! Пошел читать эспайс-форум. |
|
|
|
|
|
Вверх #5 |
|
Профессор АйБолит Помогу советом
Регистрация: 20.07.2007 Адрес: Минск Сообщений: 5,591 Имя: Дмитрий Автомобиль: Laguna III |
датчик коленвала и распредвала почисти и проверь правильность установки грм
__________________ |
|
|
|
|
|
Вверх #6 |
|
Новичок Регистрация: 06.08.2012 Адрес: MoscoW Сообщений: 6 Автомобиль: Другой |
Цитата:
Сообщение от Smalenski датчик коленвала и распредвала почисти и проверь правильность установки грм Спасибо!, совет — я так понимаю касается ошибки DF 070 5DEF? Цитата:
Сообщение от _Dima_ расшифровку ошибок в нете спокойно найти можно! Спасибо, прочитал. Ситуация похожая. Буду пока поискать донора на регулятор, а для начала завтра проверю сопротивление.
Последний раз редактировалось VladMX; 08.11.2012 в 00:11. Причина: Добавлено сообщение
|
|
|
|
Для того чтобы в принятом сообщении можно было обнаружить ошибку, это сообщение должно обладать некоторой избыточной информацией, позволяющей отличать ошибочный код от правильного. Например, если переданное сообщение состоит из трёх абсолютно одинаковых частей, то в принятом сообщении отделение правильных символов от ошибочных может быть осуществлено по результатам накопления посылок одного вида, например 0 или 1. Для двоичных кодов этот метод можно проиллюстрировать следующим примером:
10110 – переданная кодовая комбинация;
10010 – 1-я принятая комбинация;
10100 – 2-я принятая комбинация;
00110 – 3-я принятая комбинация;
10110 — накопленная комбинация . Как видим, несмотря на то, что во всех трёх принятых комбинациях были ошибки накопленная не содержит ошибок1.
Принятое сообщение может также состоять из кода и его инверсии. Код инверсии посылается в канал связи как одно целое. Ошибка на приёмном конце выделяется при сопоставлении кода и его инверсии (подробнее см. тема 7).
Для того чтобы искажение любого из символов сообщения привело к запрещенной комбинации. Необходимо в коде выделить комбинации, отличающиеся друг от друга в ряде символов, часть из этих комбинаций запретить и тем самым ввести в код избыточность. Например, в равномерном блочном коде считать разрешенными кодовые комбинации с постоянным соотношением нулей и единиц в каждой кодовой комбинации. Такие коды получили название кодов с постоянным весом. Для двоичных кодов число кодовых комбинаций с постоянным весом длиной в n символов равно
, (55)
где l – число единиц в кодовом слове. Если бы не существовало условие постоянного веса, то число комбинаций кода могло бы быть гораздо большим, а именно 2n. Примером кода с постоянным весом может служить стандартный телеграфный код №3 (см. приложение 4). Комбинации этого кода построены таким образом, что на 7 тактов, в течении которых должна быть принята одна комбинация, всегда приходятся три токовые и четыре без токовые посылки. Увеличение или уменьшение количества токовых посылок говорит о наличии ошибок.
Еще одним примером ведения избыточности в код является метод суть которого состоит в том, что к исходным кодам добавляются нули либо единицы таким образом, чтобы сумма их была всегда четной или нечетной. Сбой любого одного символа всегда нарушит условия четности(нечетности), и ошибка будет обнаружена. В этом случае комбинации друг от друга должны отличаться минимум в двух символах (см. задачу 6.9), то есть ровно половина комбинаций кода является запрещенной (запрещенными являются все нечетные комбинации при проверке на четность или наоборот).
Во всех упомянутых выше случаях сообщения обладают избыточной информацией. Избыточность сообщения говорит о том, что оно могло бы содержать большее количество информации, если бы не многократное повторение одного и того же кода не добавления коду его инверсии, не несущей никакой информации, если бы не искусственное запрещение части комбинаций кода и т. д. Но все перечисленные виды избыточности приходиться вводить для того, что бы можно было отличить ошибочную комбинацию от правильной.
Коды без избыточности обнаруживать, а тем более исправлять ошибки не могут1. минимальное количество символов, в которых любые две комбинации кода отличаются друг от друга называются кодовым расстоянием. Минимальное количество символов, в которых все комбинации кода отличаются друг от друга, называются минимальным кодовым расстоянием. Минимальное кодовое расстояние – параметр, определяющий помехоустойчивость кода и заложенную в коде избыточности. Минимальным кодовым расстоянием определяются корректирующие свойства кода.
В общем случае для обнаружения r ошибок минимальное кодовое расстояние
. (56)
Минимальное кодовое расстояние, необходимое для одновременного обнаружения и исправления ошибок,
, (57)
где s – число исправляемых ошибок.
Для кодов, только исправляющих ошибки, . (58)
Для того чтобы определить кодовое расстояние между двумя комбинациями двоичного кода, достаточно просуммировать эти комбинации по модулю 2 и посчитать число единиц в полученной комбинации (см. задачу 6.21).
Понятие кодового расстояния хорошо усваиваются на примере построения геометрических моделей кодов. На геометрических моделях вершинах n – угольников, где n – значность кода, расположены кодовые комбинации, а количества рёбер n угольника, отделяющих одну комбинацию от другой равно кодовому расстоянию (см. задачу 6.19).
Если кодовая комбинация двоичного кода A отстоит от кодовой комбинации B на расстоянии d, то это значит, что в коде A нужно d символов заменить на обратные, чтобы получить код B, но это не означает, что нужно d добавочных символов, чтобы код
обладал данными корректирующими свойствами. В двоичных кодах для обнаружения одиночной ошибки достаточно иметь 1 дополнительный символ независимо от числа информационных разрядов кода, а минимально кодовое расстояние d0=2.
Для обнаружения и исправления одиночной ошибки соотношение между числом информационных разрядов и числом корректирующих разрядов
должно удовлетворять следующим условиям:
, (59)
, (60)
при этом подразумевается, что общая длина кодовой комбинации
. (61)
Для практических расчетов при определении числа контрольных разрядов кодов с минимальным кодовым расстоянием d0 = 3 удобно пользоваться выражениями
, (62)
если известна длина полной кодовой комбинации n, и
, (63)
если при расчетах удобней исходить из заданного числа информационных символов 1.
Для кодов, обнаруживающих трёхкратные ошибки (d0=4),
(64)
или
. (65)
Для кодов длиной в n символов, исправляющих одну или две ошибки (d0=5),
. (66)
Для практических расчетов можно пользоваться выражением
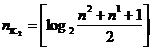
Для кодов, исправляющих 3 ошибки (d0=7),
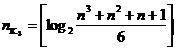
Для кодов, исправляющих s ошибок (d0=2s+1),
. (69)
Выражение слева известно как нижняя граница Хэмминга [16], а выражение справа – как верхняя граница Варшамова – Гильбета [3]1.
Для приближенных расчетов можно пользоваться выражением
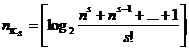
Можно предположить, что значение будет приближаться к верхней или нижней границе в зависимости от того, на сколько выражены выражения под знаком логарифма (см. страницу 7) приближается к целой степени двух.
Линейные групповые коды
Линейными называются коды, в которых проверочные символы представляют собой линейные комбинации информационных символов.
Для двоичных кодов в качестве линейной операции используют сложение по модулю 2.
Правила сложения по модулю 2 определяются следующими равенствами:
Последовательность нулей и единиц, принадлежащих данному коду, будем называть кодовым вектором.
Свойства линейных кодов: сумма (разность) кодовых векторов линейного кода даёт вектор, принадлежащий данному коду.
Линейные коды образуют алгебраическую группу по отношению к операции сложению по модулю 2. в этом смысле они являются групповыми кодами.
Свойства группового кода: минимальное кодовое расстояние между кодовыми векторами группового кода равно минимальному весу ненулевых кодовых векторов.
Вес кодового вектора (кодовой комбинации) равен числу его ненулевых компонентов (см. задачу 6.42).
Расстояние между двумя кодовыми векторами равно весу вектора, полученного в результате сложения исходных векторов по модулю 2 (см. задачу 6.44). Таким образом, для данного группового кода.
Групповые коды удобно задавать матрицам, размерность которых определяется параметрами кода и
. Число строк в матрице равно
, число столбцов матрицы равно
:
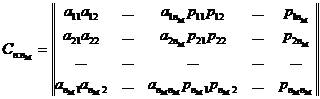
Коды, порождаемые этими матрицами, известны как (n;k) – коды, где k = , а соответствующие им матрицы называются порождающими, производящими, образующими.
Порождающая матрица С может быть представлена двумя матрицами И и П (информационная и проверочная). Число столбцов матрицы П равно nK, число столбцов матрицы И равно nM:
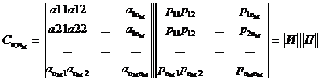
Теорией и практикой установлено [8,9,13], что в качестве матрицы удобно брать единичную матрицу в канонической формуле:
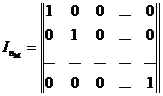
При выборе матрицы П исходят из следующих соображений: чем больше единиц в разрядах проверочной матрицы П, тем ближе соответствующий порождаемый код к оптимальному код к оптимальному1, с другой стороны, число единиц матрицы П определяет число сумматоров по модулю 2 в шифраторе и дешифратор, т. е. Чем больше единиц в матрице П, тем сложнее аппаратура. Вес каждой строки матрицы П должен быть не менее , гдеWИ – вес соответствующей строки матрицы И. Если матрица И – единичная, то WИ = 1 (удобство выбора в количестве матрицы И единичной матрицы очевидно: при WИ > 1 усложнилась бы как построение кодов, так и их технологическая реализация).
При соблюдении перечисленных условий любую порождающую матрицу группового кода можно привести к следующему виду:
…
…
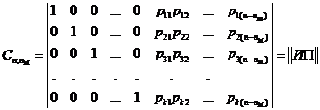
называемому левой канонической формой порождающей матрицы.
Для кодов с производящая матрица С имеет вид:
.
Во всех комбинациях кода, построенного при помощи такой матрицы, четное число единиц.
Для кодов с порождающая матрица не может быть представлена в форме, общей для всех видов с данными
. Вид матрицы зависит от конкретных требований к порождаемому коду (в качестве примера построения некоторого абстрактного группового кода с
может быть предложена задача 6.48). Этим требованиям могут быть либо минимум корректирующих разрядов, либо максимальная простата аппаратуры.
Корректирующие коды с минимальным количеством избыточных разрядов называют плотно упакованными или совершенными кодами.
Для кодов с соотношения n и n0 следующее: (3;1), (7;4), (15;11), (31;26), (63;57) и т. д. (см., например, задачу 6.52).
Плотно упакованные коды, оптимальные с точки зрения минимума избыточных символов, обнаруживающие максимально возможное количество вариантов ошибок кратностью ,
и имеющие
и
, были исследованы Д. Слепяном в работе [10]. Для получения этих кодов матрица П должна иметь
комбинации с максимальным весом. Для этого при построении кодов с последовательно используются векторы длиной
, весом
,
, …,
(см. задачи 6.50; 6.65). Тем же Слепяном в работе[11] были исследованы неплотно упакованные коды с малой плотностью проверок на четность. Эти коды экономны с точки зрения простоты аппаратуры и содержат минимальное число единиц в корректирующих разрядах порождающей матрицы. При построении кодов с максимально простыми шифраторами и дешифраторами последовательно выбираются векторы весом
(см. задачи 6.55; 6.65). если число комбинаций, представляющих собой корректирующие разряды кода и удовлетворяют условию
, больше
, то в первом случае не используют наборы с наименьшим весом, а во втором – с наибольшим.
Строчки образующей матрицы С представляют собой комбинаций искомого кода. Остальные комбинации кода строятся при помощи образующей матрицы по следующему правилу: корректирующие символы, предназначенные для обнаружения или исправления ошибки в информационной части кода, находятся путем суммирования по модулю 2 тех строк матрицы П, номера которых совпадают с номерами разрядов, содержащих единицы в кодовом векторе, представляющем информационную часть кода. Полученную комбинацию приписывают справа к информационной части кода и получают вектор полного корректирующего кода. Аналогичную процедуру проделывают со второй , третьей и последующими информационными кодовыми комбинациями, пока не будет построен корректирующий код для передачи всех символов первичного алфавита (см. задачу 6.57).
Алгоритм образования проверочных символов по известной информационной части кода может быть записан следующим образом:
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
или (73)
В процессе декодирования осуществляются проверки, идея которых в общем виде может быть представлена следующим образом:
, j = 1, 2, …,
. (74) Для каждой конкретной матрицы существует своя, одна-единственная система проверок. Проверки производятся по следующему правилу: в первую проверку вместе с проверочным разрядом p1 входят информационные разряды, которые соответствуют единицам первого столбца проверочной матрицы П; во вторую проверку входит второй проверочный разряд p2 и информационные разряды, соответствующие единицам второго столбца проверочной матрицы, и т. д. Число проверок равно числу проверочных разрядов корректирующего кода
(см. задачу 6.60).
В результате осуществления проверок образуется проверочный вектор,
, …,
, который называют синдромом. Если вес синдрома равен нулю, то принятая комбинация считается безошибочной. Если хотя бы один разряд проверочного вектора содержит единицу, то принятая комбинация содержит ошибку. Исправление ошибки производится по виду синдрома, так как каждому ошибочному разряду соответствует один-единственный проверочный вектор (см. задачи 6.60; 6.62).
Вид синдрома для каждой конкретной матрицы может быть определен при помощи проверочной матрицы Н, которая представляет собой транспонированную матрицу П, дополненную единичной матрицей , число столбцов которой равно числу проверочных разрядов кода:
.
Столбцы такой матрицы представляют собой значение синдрома для разряда, соответствующего номеру столбца матрицы Н (см. задачи 6.60; 6.62).
Процедура исправления ошибок в процессе декодирования групповых кодов сводится к следующему.
Строится кодовая таблица. В первой строке таблицы располагаются все кодовые векторы . В первом столбце второй строки размещается вектор
, вес которого равен 1.
Остальные позиции второй строки заполняются векторами, по лученными в результате суммирования по модулю 2 вектора с вектором
расположенными в соответствующем столбце первой строки. В первом столбце третьей строки записывается вектор
, вес которого также равен 1, однако, если вектор
содержит единицу в первом разряде, то
— во втором. В остальные позиции третьей строки записывают суммы
и
.
Аналогично поступают до тех пор, пока не будут просуммированы с векторами все векторы
, весом 1, с единицами в каждом из n разрядов. Затем суммируются по модулю 2 векторы
, с весом 2, с последовательным перекрытием всех возможных разрядов. Все вектора
определяет число исправляемых ошибок. Число векторов
определяется возможным числом неповторяющихся синдромов и равно
(нулевая комбинация говорит об отсутствии ошибки). Условие неповторяемости синдрома позволяет по его виду определить один-единственный соответствующий ему вектор
. Векторы
есть векторы ошибок, которые могут быть исправлены данным групповым кодом.
По виду синдрома принятая комбинация может быть отнесена к тому или иному смежному классу, образованному сложением по модулю 2 кодовой комбинацией с вектором ошибки
, т. е. к определенной строке кодовой табл. 6.1.
Таблица 6.1.
Ar |
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
Принятая кодовая комбинация сравнивается с векторами, записанными в строке, соответствующей полученному в результате проверок синдрому. Истинный код будет расположен в первой строке той же колонки таблицы (см. задачу 6.68). процесс исправления ошибки заключается в замене на обратное значение разрядов., соответствующих единицам в векторе ошибок
.
Векторы ,
, …,
не должны быть равны ни одному из векторов
,
, …,
в противном случае в таблице появились бы нулевые векторы.
Тривиальные систематические коды. Код Хэмминга.
Систематические коды представляют собой такие коды, в которых информационные и корректирующие разряды расположены по строго определенной системе и всегда занимают строго определенные места в кодовых комбинациях. Систематические коды являются равномерными, т. е. все комбинации кода с заданными корректирующими способностями имеют одинаковую длину. Групповые коды также являются систематическими, но не все систематические коды могут быть отнесены к групповым.
Тривиальные систематические коды могут строиться, как и групповые, на основе производящей матрицы. Обычно производящая матрица строится при помощи матриц единичной, ранг которой определяется числом информационных разрядов, и добавочной, число столбцов которой определяется числом контрольных разрядов кода. Каждая строка добавочной матрицы должна содержать не менее единиц, а сумма по модулю для любых строк не менее
единиц (где
минимальное кодовое расстояние). Производящая матрица позволяет находить все остальные кодовые комбинации суммированием по модулю для строк производящей матрицы во всех возможных сочетаниях (см. например, задачу 6.74).
Код Хэмминга является типичным примером систематического кода. Однако при его построении к матрицам обычно не прибегают. Для вычисления основных параметров кода задается либо количество информационных символов, либо количество информационных символов, либо количество информационных комбинаций . При помощи (59) и (60) вычисляются
и
. Соотношения между n,
, и
для Хэмминга предоставлены в табл. 1 приложения 8. Зная основные параметры корректирующего кода, определяют, какие позиции сигналов будут рабочими, а какие контрольными. Как показала практика, номера контрольных символов удобно выбирать по закону
, где
0, 1, 2 и т. д. — натуральный ряд чисел. Номера контрольных символов в этом случае будут соответственно: 1, 2, 4, 8, 16, 32 и т.д.
Затем определяется значения контрольных коэффициентов (0 или 1), руководствуясь следующим правилом: сумма единиц на контрольных позициях должна быть четной. Если эта сумма четна, то значение контрольного коэффициента — 0, в противно случае — 1.
Проверочные позиции выбираются следующим образом: составляется таблица для ряда натуральных чисел в двоичном коде. Число строк таблицы:
.
Первой строке соответствует проверочный коэффициент , второй
и т. д., как показано в табл. 2 приложения 8. Затем выявляют проверочные позиции, выписывая коэффициенты по следующему принципу: в первую проверку входят коэффициенты, которые содержат в младшем разряде 1, т. е.
,
,
,
,
,
и т. д.; во вторую — коэффициенты, содержащие 1 во втором разряде, т. е.
,
,
,
,
,
и т. д.; в третью проверку — коэффициенты, которые содержат 1 в третьем разряде, и т. д. Номера проверочных коэффициентов соответствует номерам проверочных позиций, что позволяет составить общую таблицу проверок (табл. 3, приложение 8). Старшинство разрядов считается слева направо, а при проверке сверху вниз. Порядок проверок показывает также и порядок следования разрядов в получения разрядов в полученном двоичном коде.
Если в принятом коде есть ошибка, то результат проверок по контрольным позициям образует двоичное число, указывающее номер ошибочной позиции. Исправляют ошибку, изменяя символ ошибочной позиции а обратный (см. задачу 6.78).
Для исправления одиночной и обнаружения двойной ошибки, кроме проверок по контрольным позициям, следует проводить еще одну проверку на четность для каждого кода. Чтобы осуществить такую проверку, следует к каждому коду в конце кодовой комбинации добавить контрольный символ таким образом, чтобы сумма единиц в полученной комбинации всегда была четной. Тогда в случае одиночной ошибки проверки по позициям укажут на наличие ошибки. Если проверки позиций укажут на наличие ошибки, а проверка на четность не фиксирует ошибки, значит в коде две ошибки (см. задачу 6.82).
Циклические коды.
Циклические коды [4, 6, 7, 9, 12, 13] названы так потому, что в них часть комбинаций кода либо все комбинации могут быть получены путем циклического сдвига одной или нескольких комбинацикода. Циклический сдвиг осуществляется справа налево, причем крайний левый символ каждый раз переносится в конец комбинации. Циклические коды, практически1, все относятся к систематическим кодам, в них контрольные и информационные разряды расположены на строго определенных местах. Кроме того, циклические коды относятся к числу блочных кодов. Каждый блок (одна буква является частным случаем блока) кодируется самостоятельно.
Идея построения циклических кодов базируется на использовании неприводимых в поле[1] двоичных чисел многочленов. Неприводимыми называются многочлены, которые не могут быть представлены в виде произведения многочленов низших степеней с коэффициентами из того же поля, так же, как простые числа не могут быть представлены произведением других чисел. Иными словами, неприводимые многочлены делятся без остатка только на себя или на единицу.
Неприводимые многочлены в теории циклических кодов играют роль образующих (генераторных, производящих) многочленов. Если заданную кодовую комбинацию умножить на выбранный неприводимый многочлен, то получим циклический код, корректирующие способности которого определяются неприводимым многочленом.
Предположим, требуется закодировать одну из комбинаций четырехзначного двоичного кода. Предположим также, что эта комбинация . Пока не обосновывая свой выбор, берем из таблицы неприводимых многочленов (табл. 2, приложение 9) в качестве образующего многочлен
. Затем умножим
на одночлен той же степени, что и образующий многочлен. От умножения многочлена на одночлен степени n степень каждого члена многочлена повысится на n, что эквивалентно приписыванию n нулей со стороны младших разрядов многочлена. Так как степень выбранного неприводимого многочлена равна трем, то исходная информационная комбинация умножается на одночлен третьей степени:
Это делается для того, чтобы впоследствии на мест этих нулей можно было бы записать корректирующие разряды.
Значение корректирующих разрядов находят по результату от деления на
:
|
|
|
||||||
|
|
|
||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
или
|
1101000 |
1011 |
|||||||
|
1011 |
1111+ |
|||||||
|
1100 |
||||||||
|
1011 |
||||||||
|
1110 |
||||||||
|
1011 |
||||||||
|
1010 |
||||||||
|
1011 |
||||||||
|
001 |
||||||||
Таким образом,
,
или в общем виде
, (75)
где частное, а
остаток от деления
на
.
Так как в двоичной арифметике , а значит,
, то можно при сложении двоичных чисел переносить слагаемые из одной части равенства в другую без изменения знака (если это удобно), поэтому равенство вида
можно записать и как
, и как
. Все три равенства данном случае означают, что либо a и b равны 0, либо a и b равны 1, т. е. имеют одинаковую четность.
Таким образом, выражение (75) можно записать как
, (76)
что в случае нашего примера даст
или
1 1 1 1
1 0 1 1 = 1 1 0 1 0 0 0 + 0 0 1 =
=1 1 0 1 0 0 1
Многочлен 1101001 и есть искомая комбинация, где 1101 – информационная часть, а 001 – контрольные символы. Заметим, что искомую комбинацию мы получили бы и как в результате умножения одной из комбинаций полного четырехзначного двоичного кода (в двоичном случае 1111) на образующий многочлен, так и умножением заданной комбинации на одночлен, имеющий ту же степень, что и выбранный образующий многочлен (в нашем случае таким образом была получена комбинация 1101000) с последующим добавлением к полученному произведению остатка от деления этого произведения на образующий многочлен (в нашем примере остаток имел вид 001).
Таким образом, мы уже знаем два способа образования комбинаций линейных систематических кодов, к которым относятся и интересующие нас циклические коды. Эти способы явились теоретическим основанием для построения кодирующих и декодирующих устройств.
Шифраторы циклических кодов, в том или ином виде, построены по принципу умножения двоичных многочленов. Кодовые комбинации получаются в результате сложения соседних комбинаций по модулю два, что, как мы увидим ниже, эквивалентно умножению первой комбинации на двучлен .
Итак, комбинации циклических кодов можно представить в виде многочлена, у которых показатели степени x соответствуют номером разрядов, коэффициенты при x равны 0 или 1 в зависимости от того, стоит 0 или 1 в разряде кодовой комбинации , которую представляет данный многочлен. Например,
000101;
001010;
010100;
101000.
Циклический сдвиг кодовой комбинации аналогичен умножению соответствующего многочлена на x:
;
;
.Если степень многочлена достигает разрядности кода, то происходит «перенос» в нулевую степень при x. В шифраторах циклических кодов эта операция осуществляется путем соединения выхода ячейки старшего разряда со входом ячейки нулевого разряда.
Сложение по модулю 2 любых двух соседних комбинаций циклического кода эквивалентного операции умножения многочлена соответствующего комбинации первого слагаемого на многочлен , если приведение подобных членов осуществляется по модулю 2:
|
0 0 0 1 0 1 |
|
|
|||
|
|
|
||||
|
0 0 1 0 1 0 |
|
||||
|
0 0 1 1 1 1 |
|
||||
|
|
|
||||
|
|
|
||||
т. е. существует принципиальная возможность получения любой кодовой комбинации циклического кода путем умножения соответствующим образом подобного образующего многочлена на некоторый другой многочлен.
Однако мало построить циклический код. Надо уметь выделить из него возможные ошибочные разряды, т. е. ввести некоторые опознаватели ошибок, которые выделяли бы ошибочный блок из всех других. Так, как циклические коды – блочные, то каждый блок должен иметь свой опознаватель. И тут решающую роль играют свойства образующего многочлена . Методика построения циклического кода такова, что образующий многочлен принимает участие в образовании каждой кодовой комбинации, поэтому любой многочлен циклического кода делится на образующий без остатка. Но без остатка делятся только те многочлены, которые принадлежат данному коду, т. е. образующий многочлен позволяет выбрать разрешенные комбинации из всех возможных. Если же при делении циклического кода на образующий многочлен будет получен остаток, то значит либо в коде произошла ошибка, либо это комбинация какого-то другого кода (запрещенная комбинация), что для декодирующего устройства не имеет принципиальной разницы. По остатку и обнаруживается наличие запрещенной комбинации, т. е. обнаруживается ошибка. Остатки от деления многочленов являются опознавателями ошибок циклического кодов.
С другой стороны, остатки от деления единицы с нулями на образующий многочлен используются для построения циклических кодов (возможность этого видна из выражения (76)).
При делении единицы с нулями образующих многочлен следует помнить, что длина остатка должна быть не меньше числа контрольных разрядов, поэтому в случае нехватки разрядов в остатке к остатку приписывают справа необходимое число нулейНапример,
|
1 0 0 0 0 0 0 0 0 0 0 |
1 0 1 1 |
||||||||||
|
1 0 1 1 |
1 1 1 1 1 + |
||||||||||
|
0 1 1 0 0 |
|||||||||||
|
1 0 1 1 |
Остатки |
||||||||||
|
1 1 1 0 |
0 1 1 |
||||||||||
|
1 0 1 1 |
1 1 0 |
||||||||||
|
1 0 1 0 |
1 1 1 |
||||||||||
|
1 0 1 1 |
1 0 1 |
||||||||||
|
1 0 0 0 |
0 0 1 |
||||||||||
|
1 0 1 1 |
0 1 0 |
||||||||||
|
1 1 |
1 0 0 |
||||||||||
|
0 1 1 |
|||||||||||
|
1 1 0 |
|||||||||||
|
и т. д., |
|||||||||||
начиная с восьмого, остатки будут повторятся.
Остатки от деления используют для построения образующих матриц, которые, благодоря вой наглядности и удобству получения производных комбинаций, получили широкое распространение для построения циклических кодов. Построение образующей матицы сводится к составлению единичной транспонированной и дополнительной матрицы, элементы которой представляют собой остатки от деления единицы с нулями на образующий многочлен 1. Напомним, что единичная транспонированная матрица представляет собой квадратную матрицу, все элементы которой – нули, кроме элементов, расположенных по диагонали справа на лево сверху вниз (в нетранспонированной матрице диагональ с единичными элементами расположена слева на права сверху вниз). Элементы дополнительной матрицы приписываются справа от единичной транспонированной матрицы.
Однако не все остатки от деления единицы с нулями на образующий многочлен могут быть использованы в качестве элементов дополнительной матрицы. Использоваться могут лишь те остатки вес которых , где
минимальное кодовое расстояние длина остатков должна быть не менее количества контрольных разрядов, а число остатков должно равняться числу информационных разрядов.
Строки образующие матрицы представляют собой первые комбинации искомого кода. Остальные комбинации кода получаются в результате суммирования по модулю 2 всевозможных сочетаний строк образующей матрицы (см. задачу 6.108)1.
Описанный выше метод построения образующих матриц не является единственным. Образующая матрица может быть построена в результате непосредственного умножения элементов единичной матрицы на образующий многочлен. Это часто бывает удобнее чем нахождение остатков от деления. Полученные коды ничем не отличаются от кодов, построенных по образующим матрицам, а которых дополнительная матрица состоит из остатков от деления единицы с нулями на образующий многочлен ( см. задачи 6.103; 6.108; 6.110).
Образующая матрица может быть построена таким путем циклического сдвига комбинации, полученной в результате умножения строки единичной матрицы ранга на образующий многочлен (см. задачу 6.126).
В заключение предлагаем еще один метод построения циклических кодов. Достоинством этого метода является исключительная простота схемных реализаций кодирующих и декодирующих устройств.
Для получения комбинаций циклического кода в этом случае достаточно произвести циклический сдвиг строки образующей матрицы и комбинации, являющейся ее зеркальным отображением (см. задача 6.112). При построении кодов с число комбинаций, получаемых суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы, равно числу комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации (см. задачи 6.103; 6.112). Однако этот способ используется для получения кодов с малым числом информационных разрядов. Уже при
число комбинаций, получаемых в результате циклического сдвига, будет меньше, чем число комбинаций, получаемых в результате суммирования всевозможных сочетаний строк образующей матрицы (см., например, задачи 6.123 и 6.128).
Число ненулевых комбинаций, получаемых в результате суммирования по модулю 2 всевозможных два строк образующей матрицы,
, (77)
где число информационных разрядов кода2.
Число ненулевых комбинаций, получаемых в результате циклического сдвига любой строки образующей матрицы и зеркальной ей комбинации,
, (78)
где n – длина кодовой комбинации.
При числе информационных разрядов число комбинаций от суммирования строк образующей матрицы растет гораздо быстрее, чем число комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации. В последнем случае коды получаются избыточными (так как при той же длине кода можно иным способом передать большее количество сообщений), соответственно, падает относительная скорость передачи информации. В таких случаях целесообразность применения того или иного метода кодирования может быть определена из конкретных технических условий.
Ошибки в циклических кодах обнаруживаются и исправляются при помощи остатков от деления полученной комбинации на образующий многочлен. Остатки от деления являются опознавателями ошибок, но не указывают непосредственно на место ошибки в циклическом коде.
Идея исправления ошибок базируется на том, что ошибочная комбинация после определенного числа циклических сдвигов «подгоняется»под остаток таким образом, что в сумме с остатком она дает исправленную комбинацию. Остаток при этом представляет собой не что иное, как разницу между искаженными и правильными символами, единицы в остатке стоят как раз на местах искаженных разрядов в подогнанной циклическими сдвигами комбинации. Подгоняют искаженную комбинацию до тех пор, пока число единиц в остатке не будет равно числу ошибок в коде. При этом, естественно, число единиц может быть либо равно числу ошибок s; исправляемых данным кодом (код исправляют 3 ошибки и в искаженной комбинации 3 ошибки), либо меньше s (код исправляет 3 ошибки, а в принятой комбинации – 1 ошибка).
Место ошибки в кодовой комбинации не имеет значения. Если , то после определенного количества сдвигов все ошибки окажутся в зоне «разового» действия образующего многочлена, т. е. достаточно получить один остаток, вес которого
, и этого уже будет достаточно для исправления искажаемой комбинации. В смысле коды БЧХ (о них мы будем говорить ниже) могут исправлять пачки ошибок, лишь бы длина пачки не превышала s.
Подробно процесс исправления ошибок рассматривается ниже на примере построения конкретных кодов.
Построение и декодирование конкретных циклических кодов.
I. Коды исправляющие одиночную ошибку, .
1. Расчет соотношения между контрольными и информационными символами кода производятся на основании выражений (59) — (69).
Если задано число информационных разрядов , то число контрольных разрядов
находим из выражения
.
Общее число символов кода
.
Если задана длина кода n, то число контрольных разрядов
.
Соотношение числа контрольных и информационных символов для кодов с приведены в табл. 3 приложения 9.
2. Выбор образующего многочлена производится по таблицам неприводимых двоичных многочленов.
Образующий многочлен следует выбирать как можно более коротким, но степень его должна быть не меньше числа контрольных разрядов
, а число ненулевых членов – не меньше минимального кодового расстояния
.
Выбор параметров единичной транспонированной матрицы происходит из условия, что число столбцов (строк) матрицы определяется числом информационных разрядов, т. е. ранг единичной матрицы равен .
3. Определение элементов дополнительной матрицы производится по остаткам от деления последней строки транспонированной матрицы (единицы с нулями) на образующий многочлен. Полученные остатки должны удовлетворять следующим требованиям:
а) число разрядов каждого остатка должно быть равно числу контрольных символов , следовательно, число разрядов дополнительной матрицы должно быть равно степени образующего многочлена;
б) число остатков должно быть не меньше числа строк единичной транспонированной матрицы, т. е. должно быть равно числу информационных разрядов ;
в) число единиц каждого остатка, т. е . его вес должно быть не менее величены , где
минимальное кодовое расстояние, не меньше числа обнаруженных ошибок;
г) количество нулей, приписанных к единице с нулями в делении ее на выбранный неприводимый многочлен, должно быть таким, чтобы соблюдались условия а), б), в).
4. Образующая матрица составляется дописыванием элементов дополнительной матрицы справа от единичной транспонированной матрицы либо умножением элементов единичной матрицы на образующий многочлен.
5. Комбинациями искомого кода являются строки образующий матрицы и все возможные суммы по модулю 2 различных сочетаний строк образующей матрицы (см. задачу 6.108).
Как видно из решения задач 6.103 и 6.108, коды, получены при использовании неприводимых многочленов и
, подобны друг другу и обладают равноценными корректирующими способностями. Сами же многочлены 1101 и 1011 называют обратными, или двойственными, многочленам. Если данный многочлен неприводимый, то неприводимый будет и двойственный ему многочлен.
6. Обнаружение и исправление ошибок производится по остатку от деления принятой комбинации на образующий многочлен
. Если принятая комбинация делится на образующий многочлен без остатка, то код принят без ошибочно. Остаток от деления свидетельствует о наличии ошибки, но не указывает, какой именно. Для того чтобы найти ошибочный разряд и исправить его в циклических кодах, осуществляют следующие операции:
а) принятую комбинацию делят на образующий многочлен;
б) подсчитывают количество единиц в остатке (вес остатка). Если , где s – допустимое число исправляемых данным кодом ошибок, то принятую комбинацию складывают по модулю 2 с полученным остатком. Сумма даст исправленную комбинацию. Если
, то
в) производят циклический сдвиг принятой комбинация влево на один разряд. Комбинацию, полученную в результате этого повторного деления
, то делимое суммируют с остатком, затем
г) производят циклический сдвиг вправо на один разряд комбинации, полученной в результате суммирования последнего делим, с последним остатком. Полученная в результате комбинация уже не содержит ошибок. Если после первого циклического сдвига последующего деления остаток получается таким, что его вес ,
д) повторяют операцию пункта в) до тех пор, пока не будет . В этом случае комбинацию, полученную в результате последнего циклического сдвига, суммируют с остатка от деления этой комбинации на образующий многочлен, а затем
е) производят циклический сдвиг вправо ровно на столько разрядов, на сколько была сдвинута суммируемая с последним остатком
комбинации относительно принятой комбинации. В результате получим исправленную комбинацию (см. задачи 6.113 – 6.116)1.
II. Коды обнаруживающие трехкратные ошибки. .
1. Выбор числа корректирующих разрядов производится из соотношения
,
или
.
2. Выбор образующего многочлена производят, исходя из следующих соображений: для обнаружения трехкратной ошибки
,
Поэтому степень образующего многочлена не может быть меньше четырех; многочлен третьей степени, имеющий число ненулевых членов больше или равное трем, позволяет обнаруживать все двойные ошибки (см. задачи 6.121; 6.122), многочлен первой степени (х+1) обнаруживает любое количество нечетных ошибок (см. задачи 6.119; 6.120), следовательно, многочлен четвертой степени, получаемый в результате умножения этих многочленов, обладает их корректирующими свойствами: может обнаруживать две ошибки а также одну и три, т. е. все трехкратные ошибки (см. задачу 6.117).
3. Построение образующей матрицы производят либо нахождением остатков от деления единицы с нулями на образующий многочлен, либо умножением строк единичной матрицы на образующий многочлен (си. задачу 6.121).
4. Остальные комбинации корректирующего кода находят суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы.
5. Обнаружение ошибок производится по остаткам от деления принятой комбинации на образующий многочлен
. Если остатка нет, то контрольные разряды отбрасываются и информационная часть кода используется по назначению. Если в результате деления получается остаток, то комбинация бракуется. Заметим, что такие коды могут обнаруживать 75% любого количества ошибок, так как кроме двойной ошибки обнаруживаются все нечетные ошибки, но гарантированное количество ошибок, которое код никогда не пропустит, равно 3.П р и м е р. Исходная кодовая комбинация – 0101111000, принятая – 0001011001 (т. е. произошел тройной сбой). Показать процесс обнаружения ошибки если известно, что комбинации кода были образованы при помощи многочлена 101111.
|
Р е ш е н и е. |
0 0 0 1 0 1 1 0 0 1 |
1 0 1 1 1 1 |
|
|
1 0 1 1 1 1 |
|||
|
0 0 0 0 1 1 1 |
|||
Остаток ненулевой, комбинация бракуется. Указать ошибочные разряды при трехкратных искажениях такие коды не могут.
III. Циклические коды, исправляющие две и большее количество ошибок, .
Методика построения циклических кодов с отличается от методики построения циклических кодов
только в выборе образующего многочлена. В литературе эти коды известны как коды БЧХ (первые буквы фамилий Боуз, Чоудхури, Хоквинхем – авторов методики построения циклических кодов с
).
Построение образующего многочлена зависит в основном, от двух параметров: от длины кодового слова n и от числа исправляемых ошибок s. Остальные параметры, участвующие в построении образующего многочлена в зависимости от заданных n и s могут быть определены при помощи таблиц и вспомогательных соотношений, о которых будет сказано ниже.
Для исправления числа ошибок еще недостаточно условие, что бы между комбинациями кода минимальное кодовое расстояние
, необходимо также чтобы длина кода n удовлетворяла условию
, (79)
при этом n всегда будет нечетным числом. Величина h определяет выбор числа контрольных символов и связанна с
и s следующим соотношением:
. (80)
C другой стороны, число контрольных символов определяется образующим много членом и равно его степени (к этому вопросу мы еще вернемся). При больших значениях h длина кода n становиться очень большой, что вызывает вполне определенные трудности при технической реализации кодирующих и декодирующих устройств. При этом часть информационных разрядов порой остается неиспользованной. В таких случаях для определения h удобно пользоваться выражением
, (81)
где С является одним из сомножителей на которое разлагается число n.
Соотношение между n, С и h могут быть сведены в следующую таблицу:
|
№ п/п |
h |
|
C |
|
1 |
3 |
7 |
1 |
|
2 |
4 |
15 |
5; 3 |
|
3 |
5 |
31 |
1 |
|
4 |
6 |
63 |
7; 3; 3 |
|
5 |
7 |
127 |
1 |
|
6 |
8 |
255 |
17; 5; 3 |
|
7 |
9 |
511 |
7; 3; 7 |
|
8 |
10 |
1023 |
31; 11; 3 |
|
9 |
11 |
2047 |
89; 23 |
|
10 |
12 |
4095 |
3; 3; 5; 7; 13 |
Например, при h=10 длина кодовой комбинации может быть равна и 1023 (C=1) и 341 (С=3), и 33 (С=31), и 31 (С=33), понятно, что n не может быть меньше. Величина С влияет выбор порядковых номеров минимальных многочленов, так как индексы первоначально выбранных многочленов умножаются С. сказанное выше хорошо усваивается на конкретном примере (см. задачу 6.132).
Построение образующего многочлена производится при помощи так называемых минимальных многочленов
, которые являются простыми неприводимыми многочленами (см. табл. 2, приложение 9). Образующий многочлен представляет собой произведение нечетных минимальных многочленов и является их наименьшим общим кратным (НОК). Максимальный порядок
определяет номер последнего из выбираемых табличных минимальных многочленов
, (82)
Порядок многочлена используется при определении числа сомножителей . Например, если s=6, то
. Так как для построения
используются только нечетные многочлены, то ими будут:
;
;
;
;
;
, старший из них имеет порядок
. Как видим число сомножителей
равно 6, т. е. числу исправляемых ошибок. Таким образом, число минимальных многочленов, участвующих в построении образующего многочлена,
, (83)
а старшая степень
(84)
(l указывает колонку в таблице минимальных многочленов, из которой обычно выбирается многочлен для построения ).
Степень образующего многочлена полученного в результате перемножения выбранных минимальных многочленов,
. (85)
В общем виде
, (86)
Декодирование кодов БЧХ производится по той же методике, что и декодирование циклических кодов с . Однако в связи с тем, что практически все коды БЧХ представлены комбинациями с n
15, могут возникнуть весьма сложные варианты, когда для обнаружения и исправления ошибок необходимо производить большое число циклических сдвигов. В этом случае для облегчения можно комбинацию полученную после k-кратного сдвига и суммирования с остатком, сдвигать не вправо, а влево на n – k циклических сдвигов. Это целесообразно делать только при
(см. задачу 6.134).