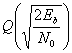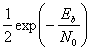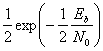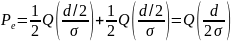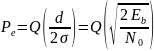Введение
Моя сеть приёма сигналов со спутников r2cloud постепенно растёт. Однако уровень приёма оставляет желать лучшего. Несмотря на то, что на спектограмме виден сигнал, демодулятор не может восстановить его. В попытках найти проблему, я понял, что мне не хватает фундаментальных знаний по теории обработки сигналов и некоторой математики. Дело в том, что в интернете зачастую выкладываются демодуляторы без обоснования их работы. Меня это не устраивает, потому что нужны метрики по которым я буду понимать насколько один алгоритм эффективнее другого. И стал ли новый код лучше, если я добавлю какой-нибудь другой блок в обработку.
Всё это привело меня к \( E_b / N_0 \). Эта метрика показывает отношение энергии сигнала, приходящейся на 1 бит принимаемого сообщения (\( E_b \)), к энергетической спектральной плотности шума (\( N_0 \)). Почему она так важна? Дело в том, что она не зависит от способа модуляции сигнала и пропускной способности канала. Из-за этого её можно использовать, чтобы сравнивать различные модуляции между собой. Обычно строят график отношения \( E_b / N_0 \) к вероятности ошибки (BER). Вот пример графика сравнения BPSK/QPSK/8-PSK/16-PSK:
Что из этого графика можно понять?
- Если увеличивать энергию передаваемого бита, то уменьшается вероятность возникновения ошибки.
- В BPSK/QPSK ошибка возникает значительно реже, чем в 8-PSK и 16-PSK при одинаковых значениях энергии передаваемого бита.
- График, например, читается следующим образом: при \( E_b / N_0 \) равным 4 децибелла и BPSK модуляции можно получить 1 ошибочный бит на каждые 100 полученных.
Мне же график прежде всего нужен:
- Сравнивать теоретические значения с практической реализацией демодулятора. Прямо сейчас я точно знаю, что различия есть из-за ограниченной точности АЦП. Дело в том, что rtl-sdr имеет разрешающую способность 8 бит. А в теории числа могут быть бесконечной точности. Именно эта разница и должна давать ошибку.
- Анализировать улучшится ли демодулятор, если добавить какой-то определённый блок. Как минимум я хочу попробовать различные алгоритмы получения несущего сигнала и компенсации многолучевого распространения.
Ну и для того, чтобы понять математику, я решил проделать выводы сам. Ниже я буду рассчитывать вероятности ошибки для BPSK (см. синий график выше). Вдохновение я черпал у dsplog плюс добавлял свои мысли.
Дано
Прежде всего необходимо описать физику процесса. Схема процесса показана ниже:
- Изначальное сообщение кодируется в аналоговый сигнал. “1” кодируется в \(+\sqrt{E_b}\), “0” кодируется в \(-\sqrt{E_b}\). Почему именно как корень из \(E_b\)? Не знаю. Это единственное место, где я не разобрался.
- После этого сигнал складывается с аддитивным белым гауссовским шумом.
- Далее сигнал демодулируется.
Модулированный BPSK сигнал выглядит следующим образом:
Красными точками обозначается сигнал без шума. Синими — сигнал с добавлением белого гауссовского шума. Как демодулируется этот сигнал? Все точки, которые больше “0” становятся “1”, а те, что меньше “0” становятся “0”. На рисунке выше все синие точки достаточно далеко от “0”, поэтому информацию можно однозначно восстановить. Но что если шум будет сильнее?
Тут уже не всё так однозначно. Видно, что некоторые точки закодированные как “1” на самом деле оказались меньше “0”. И если бы я попытался их демодулировать, то получил бы неправильную информацию.
Решение
Теперь, когда стало понятно влияние шума на результат демодуляции, можно переходить к графику зависимости вероятности от энергии сигнала. Этот график поможет посчитать вероятность ошибок для различных входных значений. Для начала возьмём сигнал без шума. Вероятность получения “0” или “1” всегда 1.
Частота получения ошибочных битов (Bit error rate) будет 0. Т.е. 0 ошибочных битов на бесконечное количество принятых. В случае наличия гауссовского шума, вероятность получения определяется гауссовской функцией вероятности:
Гауссовский шум определяется следующей формулой:
$$
p(x) = \dfrac{1}{\sqrt{2\pi\sigma^2}}e^\dfrac{-(x-\mu)^2}{2\sigma^2}
$$
Где:
- \(\mu=0\),
- \(\sigma^2=N_0/2\)
При передаче “1” \(\mu=+\sqrt{E_b}\), при “0” \(\mu=-\sqrt{E_b}\). Подставляя это в формулу:
$$
\begin{align}
P(x|s_0)=\dfrac{1}{\sqrt{\pi N_0}}e^\dfrac{-(x+\sqrt{E_b})^2}{N_0} \newline
P(x|s_1)=\dfrac{1}{\sqrt{\pi N_0}}e^\dfrac{-(x-\sqrt{E_b})^2}{N_0}
\end{align}
$$
Теперь самое интересное.
На этом рисунке показаны области возникновения ошибки. Зелёная область — это место, где возникает ошибка при передаче “1”, красная — при передаче “0”. Общую вероятность ошибки можно записать с помощью формулы полной вероятности:
$$
P(error)=\dfrac{1}{2}P(error|s_0) + \dfrac{1}{2}P(error|s_1)
$$
После этого необходимо найти каждую из вероятностей:
$$
\begin{align}
P(error|s_0) = \int_{0}^{\infty}P(x|s_0)dx = \dfrac{1}{\sqrt{\pi N_0}}\int_{0}^{\infty}e^\dfrac{-(x+\sqrt{E_b})^2}{N_0}dx \newline
P(error|s_1) = \int_{-\infty}^{0}P(x|s_1)dx = \dfrac{1}{\sqrt{\pi N_0}}\int_{-\infty}^{0}e^\dfrac{-(x-\sqrt{E_b})^2}{N_0}dx
\end{align}
$$
Обычно вероятность ошибки записывают с помощью функции ошибок:
$$
erfc(x)=\dfrac{2}{\sqrt\pi}\int_{0}^{x}e^{-t^2}dt
$$
Для этого необходимо сделать следующее:
$$
z=\dfrac{y+\sqrt{E_b}}{\sqrt{N_0}} => z\sqrt{N_0} = y + \sqrt{E_b}
$$
Заменить пределы интегрирования:
$$
\begin{align}
y=0 => z = \dfrac{\sqrt{E_b}}{\sqrt{N_0}} \newline
y=\infty => z = \infty
\end{align}
$$
Получившаяся ошибка записывается как:
$$
\begin{align}
P(error|s_0)=\dfrac{1}{\sqrt{\pi N_0}}\int_\limits{\sqrt{\dfrac{E_b}{N_0}}}^{\infty}e^{-z^2}\sqrt{N_0}dz
=\dfrac{1}{\sqrt{\pi}}\int_\limits{\sqrt{\dfrac{E_b}{N_0}}}^{\infty}e^{-z^2}dz
=\dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}})
\end{align}
$$
Аналогично можно найти ошибку при передаче “1”:
$$
\begin{align}
P(error|s_1)=1-P(s_1)=1-\dfrac{1}{2}erfc(-\sqrt{\dfrac{E_b}{N_0}})
\end{align}
$$
Можно воспользоваться свойством функции ошибок:
$$
\begin{align}
erfc(-x)=2-erfc(x) => P(error|s_1) = \dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}})
\end{align}
$$
Если подставить в формулу полной вероятности:
$$
P(error)=\dfrac{1}{2}(\dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}})) + \dfrac{1}{2}(\dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}}))=\dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}})
$$
Ответ
Получившийся график:
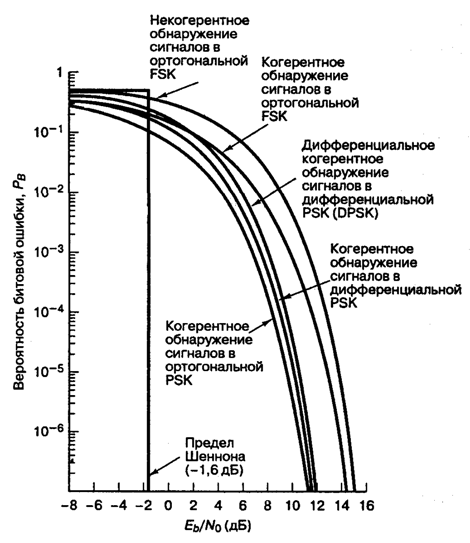
9.8.1. Передача сигналов с модуляцией QPSK и OQPSK
9.8.2. Манипуляция с минимальным сдвигом
9.8.2.1.Вероятность ошибки при модуляциях OQPSK и MSK
9.8.3. Квадратурная амплитудная модуляция
9.8.3.1. Вероятность битовой ошибки при модуляции QAM
9.8.3.2. Компромисс между полосой пропускания и мощностью
Основной задачей спектрально эффективных модуляций является максимизация эффективности использования полосы частот. Увеличение спроса на цифровые каналы передачи привело к исследованиям спектрально эффективных методов модуляции [8, 16], направленных на максимально эффективное использование полосы частот и, следовательно, призванных ослабить проблему спектральной перегрузки каналов связи.
В некоторых системах, помимо требования эффективности использования спектра, имеются и другие. Например, в спутниковых системах с сильно нелинейными транс-пондерами требуется модуляция с постоянной огибающей. Это связано с тем, что при прохождении сигнала с большими флуктуациями амплитуды нелинейные транспондеры создают паразитные боковые полосы (причина — механизм, называемый преобразованием амплитудной модуляции в фазовую). Эти боковые полосы отбирают у информационного сигнала часть мощности транспондера, а также могут интерферировать с сигналами соседних каналов (помеха соседнего канала) или других систем связи (внутриканальная помеха). Двумя примерами модуляций с постоянной огибающей, подходящими для систем с нелинейными транспондерами, являются квадратурная фазовая манипуляция со сдвигом (Offset QPSK — OQPSK) и манипуляция с минимальным сдвигом (minimum shift keying — MSK).
9.8.1. Передача сигналов с модуляцией QPSK и OQPSK
На рис. 9.10 показано разбиение типичного потока импульсов при модуляции QPSK. На рис. 9.10, а представлен исходный поток данных dk(t)=d0,d1,d2, …, состоящий из биполярных импульсов, т.е. dk принимают значения +1 или -1, представляющие двоичную единицу и двоичный нуль. Этот поток импульсов разделяется на синфазный поток, dI(t), и квадратурный, dQ(t), как показано на рис. 9.10, б.
dI(t) = d0, d2, d4, … (четные биты)
dQ(t) = d1, d3, d5, … (нечетные биты)
Отметим, что скорости потоков dI(t) и dQ(t) равны половине скорости передачи потока dk(t). Удобную ортогональную реализацию сигнала QPSK, s(t), можно получить, используя амплитудную модуляцию синфазного и квадратурного потоков на синусной и косинусной функциях от несущей.
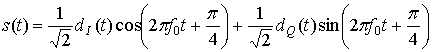
С помощью тригонометрических тождеств (Г.5) и (Г.6) уравнение (9.44) можно представить в следующем виде.
(9.45)
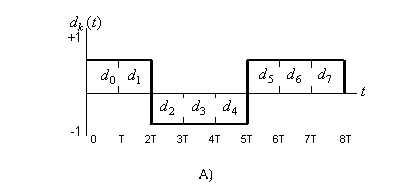
Рис.9.10. Модуляция QPSK
Модулятор QPSK, показанный на рис. 9.10, в, использует сумму синусоидального и косинусоидального слагаемых, тогда как аналогичное устройство, описанное в разделе 4.6, применяет разность таких слагаемых. Материл данного раздела представлен так, как это сделано в работе [17]. Поскольку когерентный приемник должен разрешать любую неопределенность фазы, использование в передатчике иного формата фазы можно рассматривать как часть подобной неопределенности. Поток импульсов dI(t) используется для амплитудной модуляции (с амплитудой +1 или -1) косинусоиды. Это равноценно сдвигу фазы косинусоиды на 0 или ; следовательно, в результате получаем сигнал BPSK. Аналогично поток импульсов dQ(t) модулирует синусоиду, что дает сигнал BPSK, ортогональный предыдущему. При суммировании этих двух ортогог нальных компонентов несущей получается сигнал QPSK. Величина
будет соответствовать одному из четырех возможных сочетаний dI(t) и dQ(t) в уравнении (9.44):
= 0°, ±90° или 180°; результирующие векторы сигналов показаны в сигнальном пространстве на рис. 9.11. Так как cos(
) и sin(
) ортогональны, два сигнала BPSK можно обнаруживать раздельно.
Рис. 9.11. Сигнальное пространство для схем QPSK и OQPSK
Передачу сигналов OQPSK также можно представить формулами (9.44) и (9.45); различие между двумя схемами модуляции, QPSK и OQPSK, состоит только в ориентации двух модулированных сигналов. Как показано на рис. 9.10, длительность каждого исходного импульса равна Т (рис.9.10, а); следовательно, в потоках на рис. 9.10, б длительность каждого импульса равна 2T. В обычной QPSK потоки четных и нечетных импульсов передаются со скоростью 1/(2T) бит/с, причем они синхронизированы так, что их переходы совпадают, как показано на рис. 9.10, б. В OQPSK, которую иногда называют QPSK с разнесением (staggered QPSK — SQPSK), используется также разделение потока данных и ортогональная передача; разница в том, что потоки dI(t) и dQ(t) синхронизированы со сдвигом на Т. Этот сдвиг показан на рис. 9.12.
Рис. 9.12. Потоки данных при модуляции OQPSK
При стандартной QPSK из-за синхронизации dI(t) и dQ(t) за промежуток 2Т фаза несущей может изменяться только раз. В зависимости от значений dI(t) и dQ(t) в любом промежутке 2Т, фаза несущей на этом промежутке может принимать одно из четырех значений, показанных на рис. 9.11. В течение следующего интервала 2T фаза несущей остается такой же, если ни один из потоков не меняет знака. Если только один из потоков импульсов изменит знак, происходит сдвиг фазы на ±90°. Изменение знака у обоих потоков приводит к сдвигу фазы на 180°. На- рис. 9.13, а изображен типичный сигнал QPSK для последовательности dI(t) и dQ(t), показанной на рис. 9.10.
Рис. 9.13. Сигналы: a) QPSK; 6) OQPSK. (Перепечатано с разрешения автора из работы Pasupathy S. «Minimum Shift Keying: A Spectrally Efficient Modulation,» IEEE Commun. Mag., July, 1979, Fig. 4, p. 17. © 1979, IEEE.)
Если сигнал, модулированный QPSK, подвергается фильтрации для уменьшения побочных максимумов спектра, результирующий сигнал больше не будет иметь постоянной огибающей и, фактически, случайный фазовый сдвиг на 180° вызовет моментальное обращение огибающей в нуль (рис. 9.13, а). Если эти сигналы применяются в спутниковых каналах, где используются нелинейные усилители, постоянная огибающая будет восстанавливаться. Однако в то же время восстанавливаться будут и все нежелательные частотные боковые максимумы, которые могут интерферировать с сигналами соседних каналов и других систем связи.
При модуляции QPSK потоки импульсов dI(t) и dQ(t) разнесены и, следовательно, не могут одновременно изменить состояние. Несущая не может изменять фазу на 180°, поскольку за один раз переход может сделать только один из компонентов. За каждые Т секунд фаза может измениться только на 0° или ±90°. На рис. 9.13, б показан типичный сигнал OQPSK для последовательности, представленной на рис. 9.12. Если сигнал OQPSK становится сигналом с ограниченной полосой, возникающая межсимвольная интерференция приводит к легкому спаду огибающей в области переходов фазы на ±90°, но поскольку переходов на 180° при OQPSK нет, огибающая не обращается в нуль, как это происходит при QPSK. Если сигнал OQPSK с ограниченной полосой проходит через нелинейный транспондер, спад огибающей устраняется; в то же время высокочастотные компоненты, связанные с исчезновением огибающей, не усиливаются. Таким образом, отсутствует внеполосная интерференция [17].
9.8.2. Манипуляция с минимальным сдвигом
Главное преимущество OQPSK перед QPSK. (устранение внеполосной интерференции) наводит на мысль, что можно дополнительно усилить формат OQPSK, устранив разрывные переходы фазы. Это стало мотивацией разработки схем модуляции без разрыва фазы (continuous phase modulation — СРМ). Одной из таких схем является манипуляция с минимальным сдвигом (minimum shift keying — MSK) [17, 20]. MSK можно рассматривать как частный случай частотной манипуляции без разрыва фазы (continuous-phase frequency shift keying — CPFSK) или как частный случай OQPSK с синусоидальным взвешиванием символов. В первом случае сигнал MSK можно представить следующим образом [18].
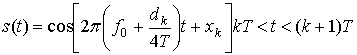
Здесь f0— несущая частота, dk=±1 представляет биполярные данные,* которые передаются со скоростью R = 1|T, a xk — это фазовая постоянная для k—го интервала передачи двоичных данных. Отметим, что при dk=1 передаваемая частота — это f0+1/4T, а при dk=-1 — этоf0-1/4T. Следовательно, разнесение тонов в MSK составляет половину от используемого при ортогональной FSK с некогерентной демодуляцией, откуда и название — манипуляция с минимальным сдвигом. В течение каждого Т-секундного интервала передачи данных значение xk постоянно, т.е. xk=0 или , что диктуется требованием непрерывности фазы сигнала в моменты t=kT. Это требование накладывает ограничение на фазу, которое можно представить следующим рекурсивным соотношением для xk.
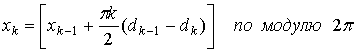
С помощью тождеств (Г.5) и (Г.6) уравнение (9.46) можно переписать в квадратурном представлении.
(9.48)
где
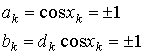
Синфазный компонент обозначается как , где
— несущая,
— синусоидальное взвешивание символов, ak — информационно-зависимый член. Подобным образом квадратурный компонент — это
, где
— квадратурное слагаемое несущей,
— такое же синусоидальное взвешивание символов, a bk — информационно-зависимый член. Может показаться, что величины ak и bk могут изменять свое значение каждые Т секунд. Однако из-за требования непрерывности фазы величина ak может измениться лишь при переходе функции
через нуль; — a bk — только при переходе через нуль
. Следовательно, взвешивание символов в синфазном или квадратурном канале — это синусоидальный импульс с периодом 2Т и переменным знаком. Как и в случае OQPSK, синфазный и квадратурный компоненты сдвинуты относительно друг друга на Т секунд.
Отметим, что xk в уравнении (9.46) — это функция разности между прежним и текущим информационными битами (дифференциальное кодирование). Таким образом, величины ak и bk в уравнении (9.48) можно рассматривать как дифференциально кодированные компоненты исходных данных dk — Однако чтобы биты данных dk были независимы между собой, знаки последовательных импульсов квадратурного и синфазного каналов различных интервалов, длительностью, 2Т секунд, должны быть случайными импульсами. Таким образом, если уравнение (9.48) рассматривать как частный случай модуляции OQPSK, его можно переписать в иной (недифференциальной) форме [18].
(9.50)
Здесь dI(t) и dQ(t) имеют такой же смысл синфазного и квадратурного потоков данных, как и в уравнении (9.43). Схема MSK, записанная в форме (9.50), иногда называется MSK с предварительным кодированием (preceded MSK). Графическое представление уравнения (9.50) дано на рис. 9.14. На рис. 9.14, а и в показано синусоидальное взвешивание импульсов синфазного и квадратурного каналов. Эти последовательности представляют собой те же информационные последовательности, что и на рис. 9.12, но здесь умножение на синусоиду дает более плавные переходы фазы, чем в исходном представлении данных. На рис. 9.14, б и г показана модуляция ортогональных компонентов и
синусоидальными потоками данных. На рис. 9.14, д представлено суммирование ортогональных компонентов, изображенных на рис. 9.14, б и г. Итак, из уравнения (9.50) и рис. 9.14 можно заключить следующее: 1) сигнал s(t) имеет постоянную огибающую; 2) фаза радиочастотной несущей непрерывна при битовых переходах; 3) сигнал s(t) можно рассматривать как сигнал, модулированный FSK, с частотами передачи f0+1/4T и f0-1/4T. Таким образом, минимальное разнесение тонов, требуемое при модуляции MSK, можно записать следующим образом.
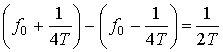
что равно половине скорости передачи битов. Отметим, что разнесение тонов, требуемое для MSK, — это половина (1/T) разнесения, необходимого при некогерентном обнаружении сигналов, модулированных FSK (см. раздел 4.5.4). Это объясняется тем, что фаза несущей известна и непрерывна, что позволяет осуществить когерентную демодуляцию сигнала.
Спектральная плотность мощности G(f) дляQPSK и OQPSK имеет следующий вид [18].
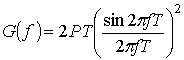
где Р — средняя мощность модулированного сигнала. При MSK G(f) будет иметь следующий вид [18].
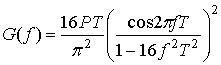
Рис. 9.14. Манипуляция с минимальным сдвигом (minimum shift keying — MSK): а) модифицированный синфазный поток битов; 6) произведение синфазного потока битов и несущей; в) модифицированный квадратурный поток битов; г) произведение квадратурного потока битов и несущей; д) сигнал MSK. (Перепечатано с разрешения автора из работы Pasupathy S. «Minimum Shift Keying: A Spectrally Efficient Modulation,» IEEE Common. Mag., July, 1979, Fig. 5, p. 18. © 1979, IEEE.)
Нормированная спектральная плотность мощности (P=1Вт) для QPSK, OQPSK и MSK изображена на рис. 9.15. Для сравнения здесь же приводится спектральный график BPSK. Не должно удивлять, что BPSK требует большей полосы пропускания, чем другие типы модуляции, при том же уровне спектральной плотности. В разделе 9.5.1 и на рис. 9.6 было показано, что теоретическая эффективность использования полосы частот схемы BPSK вдвое меньше, чем схемы QPSK. Из рис. 9.15 видно, что боковые максимумы графика MSK ниже, чем графика QPSK или OQPSK. Это является следствием умножения потока данных на синусоиду и дает большое количество плавных фазовых переходов. Чем плавнее переход, тем быстрее спектральные хвосты стремятся к нулю. Модуляция MSK спектрально эффективнее QPSK или OQPSK; тем не менее, как видно из рис. 9.15, спектр MSK имеет более широкий основной максимум, чем спектр QPSK или OQPSK. Следовательно, MSK нельзя назвать удачным выбором при наличии узкополосных линий связи. В то же время MSK стоит использовать в системах с несколькими несущими, поскольку ее относительно малые побочные максимумы спектра позволяют избежать значительных помех соседних каналов (adjacent channel interference — ACI). To, что спектр QPSK имеет более узкий основной максимум, чем MSK, объясняется тем, что при данной скорости передачи битов скорость передачи символов QPSK вдвое меньше скорости передачи символов MSK.
Рис. 9.15. Нормированная спектральная плотность мощности для BPSK, QPSK, OQPSK и MSK. (Перепечатано с разрешения автора из работы Amoroso F. «The Bandwidth of Digital Data Signals, » IEEE Commun. Mag., vol. 18, n. 6, November, 1980, Fig. 24, p. 16. © 1980, IEEE.)
9.8.2.1. Вероятность ошибки при модуляциях OQPSK и MSK
Ранее говорилось, что BPSK и QPSK имеют одинаковую вероятность появления битовой ошибки, поскольку QPSK сконфигурирована как два сигнала BPSK на ортогональных компонентах несущей. Так как разнесение потоков данных не меняет ортогональности несущих, схема OQPSK имеет ту же теоретическую вероятность появления битовой ошибки, что и BPSK и QPSK.
Для модуляции двух квадратурных компонентов несущей манипуляция с минимальным сдвигом использует сигналы антиподной формы, и
, с периодом 2Т. Следовательно, если для независимого восстановления данных из каждого ортогонального компонента используются согласованные фильтры, то модуляция MSK, определенная в формуле (9.50), имеет ту же вероятность появления ошибки, что и BPSK, QPSK и OQPSK [17]. Однако если сигнал, модулированный MSK, когерентно обнаруживается в интервале Т секунд как сигнал, модулированный FSK, то эта вероятность будет ниже, чем у BPSK, на 3дБ [17]. У MSK с дифференциально кодированными данными, определенной в выражении (9.46), вероятность появления ошибки будет такой же, как и при когерентном обнаружении дифференциально кодированных данных в модуляции PSK. Сигналы MSK также можно обнаруживать некогерентно [19]. Это позволяет осуществлять дешевую демодуляцию (если это позволяет величина принятого Eb/N0).
9.8.3. Квадратурная амплитудная модуляция
Когерентная М-арная фазовая манипуляция (M-ary phase shift keying — MPSK) — Это хорошо известный метод, позволяющий сузить полосу пропускания. Здесь используется не бинарный алфавит с передачей одного информационного бита за период передачи канального символа, а алфавит из М символов, что позволяет передавать k=log2M битов за каждый символьный интервал. Поскольку использование M-арных символов в k раз повышает скорость передачи информации при той же полосе пропускания, то при фиксированной скорости применение М-арной PSK сужает необходимую полосу пропускания в k раз (см. раздел 4.8.3).
Из уравнения (9.44) можно видеть, что модуляция QPSK состоит из двух независимых потоков. Один поток модулирует амплитуду косинусоидальной функции несущей на уровни +1 и -1, а другой — аналогичным образом синусоидальную функцию. Результирующий сигнал называется двухполосным сигналом с подавлением несущей (double-sideband suppressed-carrier — DSB-SC), поскольку полоса радиочастот вдвое больше полосы немодулированного сигнала (см. раздел 1.7.1) и не содержит выделенной несущей. Квадратурную амплитудную модуляцию (quadrature amplitude modulation — QAM) можно считать логическим продолжением QPSK, поскольку сигнал QAM также состоит из двух независимых амплитудно-модулированных несущих. Каждый блок из k бит (k полагается четным) можно разделить на два блока из k/2 бит, подаваемых на цифро-аналоговые преобразователи (ЦАП), которые обеспечивают требующее модулирующее напряжение для несущих. В приемнике оба сигнала обнаруживаются независимо с помощью согласованных фильтров. Передачу сигналов, модулированных QAM, можно также рассматривать как комбинацию амплитудной (amplitude shift keying — ASK) и фазовой (phase shift keying — PSK) манипуляций, откуда альтернативное название амплитудно-фазовая манипуляция (amplitude phase keying — АРК). И наконец, ее можно считать двухмерной амплитудной манипуляцией, откуда еще одно название — квадратурная амплитудная манипуляция (quadrature amplitude shift keying — QASK).
На рис. 9.16, а показано двухмерное пространство сигналов и набор векторов сигналов, модулированных 16-ричной QAM и изображенных точками, которые расположены в виде прямоугольной совокупности. На рис. 9.16, б показан канонический модулятор QAM. На рис. 9.16, в изображен пример модели канала, в которой предполагается наличие лишь гауссова шума. Сигналы передаются в виде пары (x, у). На модели показано, что координаты сигнальной точки (x, у) передаются по раздельным каналам и независимо возмущаются переменными гауссова шума (пx,nу), каждый компонент которого имеет нулевое среднее и дисперсию N. Можно также сказать, что двухмерная точка сигнала возмущается двухмерной переменной гауссова шума. Если средняя энергия сигнала (среднеквадратическое значение координат сигнала) равна S, тогда отношение сигнал/шум равно S/N. Простейший метод цифровой передачи сигналов через подобные системы — это применение одномерной амплитудно-импульсной модуляции (pulse amplitude modulation — РАМ) независимо к каждой координате сигнала. При модуляции РАМ для передачи k битов/размерность по гауссову каналу каждая точка сигнала принимает значение одной из 2k равновероятных эквидистантных амплитуд. Точки сигналов принято группировать в окрестности пространства на амплитудах ±1, ±3, …, ±(2k — 1).
Рис. 9.16. Схема модуляции QAM: а) 16-ричное пространство сигналов; б) канонический модулятор QAM; в) модель канала QAM
9.8.3.1. Вероятность битовой ошибки при модуляции QAM
Для прямоугольной совокупности, гауссова канала и приема с помощью согласованных фильтров, вероятность появления битовой ошибки выражается следующим образом [12].
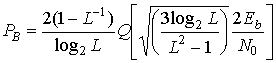
Здесь Q(x) определено в формуле (3.43), a L представляет количество уровней амплитуды в одном измерении. Предполагается, что при отображении последовательности log2 L бит в L-арный символ используется код Грея (см. раздел 4.9.4).
9.8.3.2. Компромисс между полосой пропускания и мощностью
На рис. 9.6 представлена плоскость эффективности использования полосы частот, на которой показан компромисс между полосой пропускания и мощностью при Л/арной модуляции QAM, если вероятность битовой ошибки равна 10-5, а значения на оси абсцисс измеряются в среднем отношении Eb/N0. Предполагается, что немодулированные импульсы фильтруются по Найквисту, так что двусторонняя полоса пропускания на промежуточной частоте (Intermediate Frequency — IF) равна WIF =1/Т, где Т — длительность передачи символа. Следовательно, эффективность использования полосы частот равна R/W= log2 М, где М — размер набора символов. Для реальных каналов и сигналов достоверность передачи ниже указанной, поскольку для реализации реальных фильтров требуется большая полоса пропускания. Из рис. 9.6 видно, что QAM — это метод снижения требований к полосе пропускания при передаче цифровых данных. Как и при M-арной PSK, за счет снижения эффективности использования полосы частот можно получить выигрыш в мощности или Eb/N0; однако при QAM можно реализовать более выгодный компромисс, чем при М-арной PSK.
Пример 9.5. Выбор схемы модуляции
Пусть поток данных со скоростью R=144 Мбит/с передается по радиочастотному каналу с использованием двухполосной схемы модуляции. Предполагается фильтрация по Найквисту и наличие двусторонней полосы 36 МГц. Какую модуляцию стоит выбрать при данных требованиях? Если доступное Eb/N0, равно 20, какой будет вероятность битовой ошибки?
Решение
Запишем требуемую спектральную эффективность.
Из рис. 9.6 видно, что 16-ричная QAM с теоретической спектральной эффективностью 4 бит/с/Гц требует более низкого значения Eb|N0, чем 16-арная PSK, при том же значении рв . Исходя из этого выбираем модем QAM.
Считая Eb|N0 равным 20 и используя формулу (9.54), вычисляем ожидаемую вероятность битовой ошибки.
Пример 9.6. Спектральная эффективность
а) Объясните схему расчета спектральной эффективности схемы QAM в примере 9.5, считая что сигнал, модулированный QAM, передается на ортогональных компонентах несущей.
б) Поскольку двусторонняя полоса пропускания в примере 9.5 равна 36 МГц, рассмотрим использование половины этого значения для передачи потока данных со скоростью 144 Мбит/с при многоуровневой схеме РАМ. Какая спектральная эффективность нужна для осуществления этого и какое количество уровней необходимо в схеме РАМ? Предполагается фильтрация по Найквисту.
Решение
а) Полосовой канал с использованием схемы QAM: поток данных со скоростью 144 Мбит/с разделяется на синфазный поток со скоростью 72 Мбит/с и квадратурный поток с такой же скоростью (72 Мбит/с); один поток модулирует амплитуду косинусоидальной функции несущей в полосе пропускания 36 МГц, а другой поток аналогичным образом модулирует синусоидальную функцию. Поскольку каждый поток со скоростью 72 Мбит/с модулирует ортогональный компонент несущей, 36 МГц достаточно для обоих потоков или для передачи со скоростью 144 Мбит/с. Следовательно, спектральная эффективность равна (144 Мбит/с)/36 МГц =4 бит/с/Гц.
б) Требуемая спектральная эффективность при узкополосной передаче равна следующему.
Если предполагается фильтрация по Найквисту, полоса пропускания 18 МГц поддерживает максимальную скорость передачи символов RS=2W=3106 символ/с (см. уравнение (3.80)). Следовательно, каждый импульс, модулированный РАМ, должен иметь l-битовое значение.
Откуда
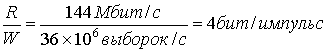
где l = log2 L, a L=16 уровней.
Phase-shift keying (PSK) is a digital modulation process which conveys data by changing (modulating) the phase of a constant frequency reference signal (the carrier wave). The modulation is accomplished by varying the sine and cosine inputs at a precise time. It is widely used for wireless LANs, RFID and Bluetooth communication.
Any digital modulation scheme uses a finite number of distinct signals to represent digital data. PSK uses a finite number of phases, each assigned a unique pattern of binary digits. Usually, each phase encodes an equal number of bits. Each pattern of bits forms the symbol that is represented by the particular phase. The demodulator, which is designed specifically for the symbol-set used by the modulator, determines the phase of the received signal and maps it back to the symbol it represents, thus recovering the original data. This requires the receiver to be able to compare the phase of the received signal to a reference signal – such a system is termed coherent (and referred to as CPSK).
CPSK requires a complicated demodulator, because it must extract the reference wave from the received signal and keep track of it, to compare each sample to. Alternatively, the phase shift of each symbol sent can be measured with respect to the phase of the previous symbol sent. Because the symbols are encoded in the difference in phase between successive samples, this is called differential phase-shift keying (DPSK). DPSK can be significantly simpler to implement than ordinary PSK, as it is a ‘non-coherent’ scheme, i.e. there is no need for the demodulator to keep track of a reference wave. A trade-off is that it has more demodulation errors.
Introduction[edit]
There are three major classes of digital modulation techniques used for transmission of digitally represented data:
- Amplitude-shift keying (ASK)
- Frequency-shift keying (FSK)
- Phase-shift keying (PSK)
All convey data by changing some aspect of a base signal, the carrier wave (usually a sinusoid), in response to a data signal. In the case of PSK, the phase is changed to represent the data signal. There are two fundamental ways of utilizing the phase of a signal in this way:
- By viewing the phase itself as conveying the information, in which case the demodulator must have a reference signal to compare the received signal’s phase against; or
- By viewing the change in the phase as conveying information – differential schemes, some of which do not need a reference carrier (to a certain extent).
A convenient method to represent PSK schemes is on a constellation diagram. This shows the points in the complex plane where, in this context, the real and imaginary axes are termed the in-phase and quadrature axes respectively due to their 90° separation. Such a representation on perpendicular axes lends itself to straightforward implementation. The amplitude of each point along the in-phase axis is used to modulate a cosine (or sine) wave and the amplitude along the quadrature axis to modulate a sine (or cosine) wave. By convention, in-phase modulates cosine and quadrature modulates sine.
In PSK, the constellation points chosen are usually positioned with uniform angular spacing around a circle. This gives maximum phase-separation between adjacent points and thus the best immunity to corruption. They are positioned on a circle so that they can all be transmitted with the same energy. In this way, the moduli of the complex numbers they represent will be the same and thus so will the amplitudes needed for the cosine and sine waves. Two common examples are «binary phase-shift keying» (BPSK) which uses two phases, and «quadrature phase-shift keying» (QPSK) which uses four phases, although any number of phases may be used. Since the data to be conveyed are usually binary, the PSK scheme is usually designed with the number of constellation points being a power of two.
Binary phase-shift keying (BPSK)[edit]
BPSK (also sometimes called PRK, phase reversal keying, or 2PSK) is the simplest form of phase shift keying (PSK). It uses two phases which are separated by 180° and so can also be termed 2-PSK. It does not particularly matter exactly where the constellation points are positioned, and in this figure they are shown on the real axis, at 0° and 180°. Therefore, it handles the highest noise level or distortion before the demodulator reaches an incorrect decision. That makes it the most robust of all the PSKs. It is, however, only able to modulate at 1 bit/symbol (as seen in the figure) and so is unsuitable for high data-rate applications. Yet there is the possibility of extending this bit/symbol, given the modulators symbol encryption / decryption logic system.
In the presence of an arbitrary phase-shift introduced by the communications channel, the demodulator (see, e.g. Costas loop) is unable to tell which constellation point is which. As a result, the data is often differentially encoded prior to modulation.
BPSK is functionally equivalent to 2-QAM modulation.
Implementation[edit]
The general form for BPSK follows the equation:
This yields two phases, 0 and π.
In the specific form, binary data is often conveyed with the following signals:[citation needed]
for binary «0»
for binary «1»
where f is the frequency of the base band.
Hence, the signal space can be represented by the single basis function
where 1 is represented by 

This use of this basis function is shown at the end of the next section in a signal timing diagram. The topmost signal is a BPSK-modulated cosine wave that the BPSK modulator would produce. The bit-stream that causes this output is shown above the signal (the other parts of this figure are relevant only to QPSK). After modulation, the base band signal will be moved to the high frequency band by multiplying 
Bit error rate[edit]
The bit error rate (BER) of BPSK under additive white Gaussian noise (AWGN) can be calculated as:[1]
or
Since there is only one bit per symbol, this is also the symbol error rate.
Quadrature phase-shift keying (QPSK)[edit]
Constellation diagram for QPSK with Gray coding. Each adjacent symbol only differs by one bit.
Sometimes this is known as quadriphase PSK, 4-PSK, or 4-QAM. (Although the root concepts of QPSK and 4-QAM are different, the resulting modulated radio waves are exactly the same.) QPSK uses four points on the constellation diagram, equispaced around a circle. With four phases, QPSK can encode two bits per symbol, shown in the diagram with Gray coding to minimize the bit error rate (BER) – sometimes misperceived as twice the BER of BPSK.
The mathematical analysis shows that QPSK can be used either to double the data rate compared with a BPSK system while maintaining the same bandwidth of the signal, or to maintain the data-rate of BPSK but halving the bandwidth needed. In this latter case, the BER of QPSK is exactly the same as the BER of BPSK – and believing differently is a common confusion when considering or describing QPSK. The transmitted carrier can undergo numbers of phase changes.
Given that radio communication channels are allocated by agencies such as the Federal Communications Commission giving a prescribed (maximum) bandwidth, the advantage of QPSK over BPSK becomes evident: QPSK transmits twice the data rate in a given bandwidth compared to BPSK — at the same BER. The engineering penalty that is paid is that QPSK transmitters and receivers are more complicated than the ones for BPSK. However, with modern electronics technology, the penalty in cost is very moderate.
As with BPSK, there are phase ambiguity problems at the receiving end, and differentially encoded QPSK is often used in practice.
Implementation[edit]
The implementation of QPSK is more general than that of BPSK and also indicates the implementation of higher-order PSK. Writing the symbols in the constellation diagram in terms of the sine and cosine waves used to transmit them:
This yields the four phases π/4, 3π/4, 5π/4 and 7π/4 as needed.
This results in a two-dimensional signal space with unit basis functions
The first basis function is used as the in-phase component of the signal and the second as the quadrature component of the signal.
Hence, the signal constellation consists of the signal-space 4 points
The factors of 1/2 indicate that the total power is split equally between the two carriers.
Comparing these basis functions with that for BPSK shows clearly how QPSK can be viewed as two independent BPSK signals. Note that the signal-space points for BPSK do not need to split the symbol (bit) energy over the two carriers in the scheme shown in the BPSK constellation diagram.
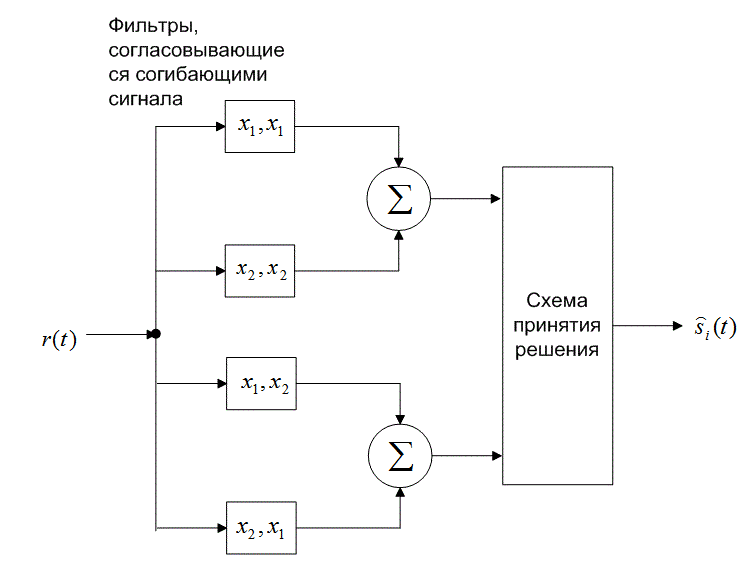
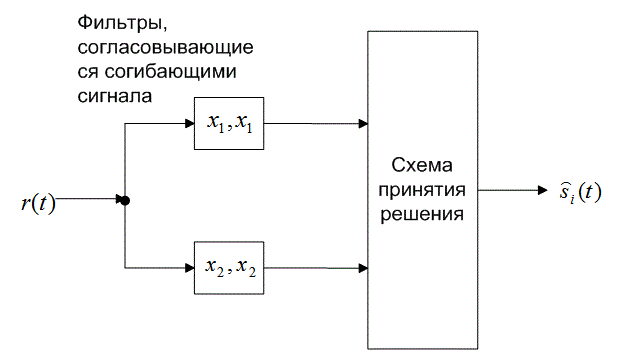
QPSK systems can be implemented in a number of ways. An illustration of the major components of the transmitter and receiver structure are shown below.
Conceptual transmitter structure for QPSK. The binary data stream is split into the in-phase and quadrature-phase components. These are then separately modulated onto two orthogonal basis functions. In this implementation, two sinusoids are used. Afterwards, the two signals are superimposed, and the resulting signal is the QPSK signal. Note the use of polar non-return-to-zero encoding. These encoders can be placed before for binary data source, but have been placed after to illustrate the conceptual difference between digital and analog signals involved with digital modulation.
Receiver structure for QPSK. The matched filters can be replaced with correlators. Each detection device uses a reference threshold value to determine whether a 1 or 0 is detected.
Probability of error[edit]
Although QPSK can be viewed as a quaternary modulation, it is easier to see it as two independently modulated quadrature carriers. With this interpretation, the even (or odd) bits are used to modulate the in-phase component of the carrier, while the odd (or even) bits are used to modulate the quadrature-phase component of the carrier. BPSK is used on both carriers and they can be independently demodulated.
As a result, the probability of bit-error for QPSK is the same as for BPSK:
However, in order to achieve the same bit-error probability as BPSK, QPSK uses twice the power (since two bits are transmitted simultaneously).
The symbol error rate is given by:
If the signal-to-noise ratio is high (as is necessary for practical QPSK systems) the probability of symbol error may be approximated:
The modulated signal is shown below for a short segment of a random binary data-stream. The two carrier waves are a cosine wave and a sine wave, as indicated by the signal-space analysis above. Here, the odd-numbered bits have been assigned to the in-phase component and the even-numbered bits to the quadrature component (taking the first bit as number 1). The total signal – the sum of the two components – is shown at the bottom. Jumps in phase can be seen as the PSK changes the phase on each component at the start of each bit-period. The topmost waveform alone matches the description given for BPSK above.
Timing diagram for QPSK. The binary data stream is shown beneath the time axis. The two signal components with their bit assignments are shown at the top, and the total combined signal at the bottom. Note the abrupt changes in phase at some of the bit-period boundaries.
The binary data that is conveyed by this waveform is: 11000110.
- The odd bits, highlighted here, contribute to the in-phase component: 11000110
- The even bits, highlighted here, contribute to the quadrature-phase component: 11000110
Variants[edit]
Offset QPSK (OQPSK)[edit]
Signal doesn’t pass through the origin, because only one bit of the symbol is changed at a time.
Offset quadrature phase-shift keying (OQPSK) is a variant of phase-shift keying modulation using four different values of the phase to transmit. It is sometimes called staggered quadrature phase-shift keying (SQPSK).
Difference of the phase between QPSK and OQPSK
Taking four values of the phase (two bits) at a time to construct a QPSK symbol can allow the phase of the signal to jump by as much as 180° at a time. When the signal is low-pass filtered (as is typical in a transmitter), these phase-shifts result in large amplitude fluctuations, an undesirable quality in communication systems. By offsetting the timing of the odd and even bits by one bit-period, or half a symbol-period, the in-phase and quadrature components will never change at the same time. In the constellation diagram shown on the right, it can be seen that this will limit the phase-shift to no more than 90° at a time. This yields much lower amplitude fluctuations than non-offset QPSK and is sometimes preferred in practice.
The picture on the right shows the difference in the behavior of the phase between ordinary QPSK and OQPSK. It can be seen that in the first plot the phase can change by 180° at once, while in OQPSK the changes are never greater than 90°.
The modulated signal is shown below for a short segment of a random binary data-stream. Note the half symbol-period offset between the two component waves. The sudden phase-shifts occur about twice as often as for QPSK (since the signals no longer change together), but they are less severe. In other words, the magnitude of jumps is smaller in OQPSK when compared to QPSK.
Timing diagram for offset-QPSK. The binary data stream is shown beneath the time axis. The two signal components with their bit assignments are shown the top and the total, combined signal at the bottom. Note the half-period offset between the two signal components.
SOQPSK[edit]
The license-free shaped-offset QPSK (SOQPSK) is interoperable with Feher-patented QPSK (FQPSK), in the sense that an integrate-and-dump offset QPSK detector produces the same output no matter which kind of transmitter is used.[2]
These modulations carefully shape the I and Q waveforms such that they change very smoothly, and the signal stays constant-amplitude even during signal transitions. (Rather than traveling instantly from one symbol to another, or even linearly, it travels smoothly around the constant-amplitude circle from one symbol to the next.) SOQPSK modulation can be represented as the hybrid of QPSK and MSK: SOQPSK has the same signal constellation as QPSK, however the phase of SOQPSK is always stationary.[3][4]
The standard description of SOQPSK-TG involves ternary symbols.[5] SOQPSK is one of the most spread modulation schemes in application to LEO satellite communications.[6]
π/4-QPSK[edit]
Dual constellation diagram for π/4-QPSK. This shows the two separate constellations with identical Gray coding but rotated by 45° with respect to each other.
This variant of QPSK uses two identical constellations which are rotated by 45° (

One property this modulation scheme possesses is that if the modulated signal is represented in the complex domain, transitions between symbols never pass through 0. In other words, the signal does not pass through the origin. This lowers the dynamical range of fluctuations in the signal which is desirable when engineering communications signals.
On the other hand, 
The modulated signal is shown below for a short segment of a random binary data-stream. The construction is the same as above for ordinary QPSK. Successive symbols are taken from the two constellations shown in the diagram. Thus, the first symbol (1 1) is taken from the «blue» constellation and the second symbol (0 0) is taken from the «green» constellation. Note that magnitudes of the two component waves change as they switch between constellations, but the total signal’s magnitude remains constant (constant envelope). The phase-shifts are between those of the two previous timing-diagrams.
Timing diagram for π/4-QPSK. The binary data stream is shown beneath the time axis. The two signal components with their bit assignments are shown the top and the total, combined signal at the bottom. Note that successive symbols are taken alternately from the two constellations, starting with the «blue» one.
DPQPSK[edit]
Dual-polarization quadrature phase shift keying (DPQPSK) or dual-polarization QPSK — involves the polarization multiplexing of two different QPSK signals, thus improving the spectral efficiency by a factor of 2. This is a cost-effective alternative to utilizing 16-PSK, instead of QPSK to double the spectral efficiency.j
Higher-order PSK[edit]
Constellation diagram for 8-PSK with Gray coding
Any number of phases may be used to construct a PSK constellation but 8-PSK is usually the highest order PSK constellation deployed. With more than 8 phases, the error-rate becomes too high and there are better, though more complex, modulations available such as quadrature amplitude modulation (QAM). Although any number of phases may be used, the fact that the constellation must usually deal with binary data means that the number of symbols is usually a power of 2 to allow an integer number of bits per symbol.
Bit error rate[edit]
For the general M-PSK there is no simple expression for the symbol-error probability if 
where
and 

Bit-error rate curves for BPSK, QPSK, 8-PSK and 16-PSK, additive white Gaussian noise channel
This may be approximated for high 

The bit-error probability for 
(Using Gray coding allows us to approximate the Lee distance of the errors as the Hamming distance of the errors in the decoded bitstream, which is easier to implement in hardware.)
The graph on the right compares the bit-error rates of BPSK, QPSK (which are the same, as noted above), 8-PSK and 16-PSK. It is seen that higher-order modulations exhibit higher error-rates; in exchange however they deliver a higher raw data-rate.
Bounds on the error rates of various digital modulation schemes can be computed with application of the union bound to the signal constellation.
Spectral efficiency[edit]
Bandwidth (or spectral) efficiency of M-PSK modulation schemes increases with increasing of modulation order M (unlike, for example, M-FSK):[7]
The same relationship holds true for M-QAM.[8]
Differential phase-shift keying (DPSK)[edit]
Differential encoding[edit]
Differential phase shift keying (DPSK) is a common form of phase modulation that conveys data by changing the phase of the carrier wave. As mentioned for BPSK and QPSK there is an ambiguity of phase if the constellation is rotated by some effect in the communications channel through which the signal passes. This problem can be overcome by using the data to change rather than set the phase.
For example, in differentially encoded BPSK a binary «1» may be transmitted by adding 180° to the current phase and a binary «0» by adding 0° to the current phase.
Another variant of DPSK is Symmetric Differential Phase Shift keying, SDPSK, where encoding would be +90° for a «1» and −90° for a «0».
In differentially encoded QPSK (DQPSK), the phase-shifts are 0°, 90°, 180°, −90° corresponding to data «00», «01», «11», «10». This kind of encoding may be demodulated in the same way as for non-differential PSK but the phase ambiguities can be ignored. Thus, each received symbol is demodulated to one of the 
The modulated signal is shown below for both DBPSK and DQPSK as described above. In the figure, it is assumed that the signal starts with zero phase, and so there is a phase shift in both signals at 
Timing diagram for DBPSK and DQPSK. The binary data stream is above the DBPSK signal. The individual bits of the DBPSK signal are grouped into pairs for the DQPSK signal, which only changes every Ts = 2Tb.
Analysis shows that differential encoding approximately doubles the error rate compared to ordinary 

One of the most popular applications of DPSK is the Bluetooth standard where 
Demodulation[edit]
BER comparison between DBPSK, DQPSK and their non-differential forms using Gray coding and operating in white noise
For a signal that has been differentially encoded, there is an obvious alternative method of demodulation. Instead of demodulating as usual and ignoring carrier-phase ambiguity, the phase between two successive received symbols is compared and used to determine what the data must have been. When differential encoding is used in this manner, the scheme is known as differential phase-shift keying (DPSK). Note that this is subtly different from just differentially encoded PSK since, upon reception, the received symbols are not decoded one-by-one to constellation points but are instead compared directly to one another.
Call the received symbol in the 



The decision variable for the 





where superscript * denotes complex conjugation. In the absence of noise, the phase of this is 
The probability of error for DPSK is difficult to calculate in general, but, in the case of DBPSK it is:
[9]
which, when numerically evaluated, is only slightly worse than ordinary BPSK, particularly at higher 
Using DPSK avoids the need for possibly complex carrier-recovery schemes to provide an accurate phase estimate and can be an attractive alternative to ordinary PSK.
In optical communications, the data can be modulated onto the phase of a laser in a differential way. The modulation is a laser which emits a continuous wave, and a Mach–Zehnder modulator which receives electrical binary data. For the case of BPSK, the laser transmits the field unchanged for binary ‘1’, and with reverse polarity for ‘0’. The demodulator consists of a delay line interferometer which delays one bit, so two bits can be compared at one time. In further processing, a photodiode is used to transform the optical field into an electric current, so the information is changed back into its original state.
The bit-error rates of DBPSK and DQPSK are compared to their non-differential counterparts in the graph to the right. The loss for using DBPSK is small enough compared to the complexity reduction that it is often used in communications systems that would otherwise use BPSK. For DQPSK though, the loss in performance compared to ordinary QPSK is larger and the system designer must balance this against the reduction in complexity.
Example: Differentially encoded BPSK[edit]
Differential encoding/decoding system diagram
At the 



where 
BER comparison between BPSK and differentially encoded BPSK operating in white noise
So 

The received signal is demodulated to yield 
since binary subtraction is the same as binary addition.
Therefore, 






Differential schemes for other PSK modulations may be devised along similar lines. The waveforms for DPSK are the same as for differentially encoded PSK given above since the only change between the two schemes is at the receiver.
The BER curve for this example is compared to ordinary BPSK on the right. As mentioned above, whilst the error rate is approximately doubled, the increase needed in 

Definitions[edit]
For determining error-rates mathematically, some definitions will be needed:


.
The error rates quoted here are those in additive white Gaussian noise (AWGN). These error rates are lower than those computed in fading channels, hence, are a good theoretical benchmark to compare with.
Applications[edit]
Owing to PSK’s simplicity, particularly when compared with its competitor quadrature amplitude modulation, it is widely used in existing technologies.
The wireless LAN standard, IEEE 802.11b-1999,[10][11] uses a variety of different PSKs depending on the data rate required. At the basic rate of 1 Mbit/s, it uses DBPSK (differential BPSK). To provide the extended rate of 2 Mbit/s, DQPSK is used. In reaching 5.5 Mbit/s and the full rate of 11 Mbit/s, QPSK is employed, but has to be coupled with complementary code keying. The higher-speed wireless LAN standard, IEEE 802.11g-2003,[10][12] has eight data rates: 6, 9, 12, 18, 24, 36, 48 and 54 Mbit/s. The 6 and 9 Mbit/s modes use OFDM modulation where each sub-carrier is BPSK modulated. The 12 and 18 Mbit/s modes use OFDM with QPSK. The fastest four modes use OFDM with forms of quadrature amplitude modulation.
Because of its simplicity, BPSK is appropriate for low-cost passive transmitters, and is used in RFID standards such as ISO/IEC 14443 which has been adopted for biometric passports, credit cards such as American Express’s ExpressPay, and many other applications.[13]
Bluetooth 2 uses 
Both QPSK and 8PSK are widely used in satellite broadcasting. QPSK is still widely used in the streaming of SD satellite channels and some HD channels. High definition programming is delivered almost exclusively in 8PSK due to the higher bitrates of HD video and the high cost of satellite bandwidth.[14] The DVB-S2 standard requires support for both QPSK and 8PSK. The chipsets used in new satellite set top boxes, such as Broadcom’s 7000 series support 8PSK and are backward compatible with the older standard.[15]
Historically, voice-band synchronous modems such as the Bell 201, 208, and 209 and the CCITT V.26, V.27, V.29, V.32, and V.34 used PSK.[16]
Mutual information with additive white Gaussian noise[edit]
Mutual information of PSK over the AWGN channel
The mutual information of PSK can be evaluated in additive Gaussian noise by numerical integration of its definition.[17] The curves of mutual information saturate to the number of bits carried by each symbol in the limit of infinite signal to noise ratio 
At intermediate values of signal to noise ratios the mutual information (MI) is well approximated by:[17]
The mutual information of PSK over the AWGN channel is generally farther to the AWGN channel capacity than QAM modulation formats.
See also[edit]
- Binary offset carrier modulation
- Differential coding
- Modulation – for an overview of all modulation schemes
- Phase modulation (PM) – the analogue equivalent of PSK
- Polar modulation
- PSK31
- PSK63
Notes[edit]
- ^ Communications Systems, H. Stern & S. Mahmoud, Pearson Prentice Hall, 2004, p. 283.
- ^
Tom Nelson, Erik Perrins, and Michael Rice.
«Common detectors for Tier 1 modulations» Archived 2012-09-17 at the Wayback Machine.T. Nelson, E. Perrins, M. Rice.
«Common detectors for shaped offset QPSK (SOQPSK) and Feher-patented QPSK (FQPSK)»
Nelson, T.; Perrins, E.; Rice, M. (2005). «Common detectors for shaped offset QPSK (SOQPSK) and Feher-patented QPSK (FQPSK)». GLOBECOM ’05. IEEE Global Telecommunications Conference, 2005. pp. 5 pp. doi:10.1109/GLOCOM.2005.1578470. ISBN 0-7803-9414-3. S2CID 11020777.
ISBN 0-7803-9414-3 - ^ Hill, Terrance J. «A non-proprietary, constant envelope, variant of shaped offset QPSK (SOQPSK) for improved spectral containment and detection efficiency.» MILCOM 2000. 21st Century Military Communications Conference Proceedings. Vol. 1. IEEE, 2000.
- ^ Li, Lifang, and M. K. Simon. «Performance of coded offset quadrature phase-shift keying (OQPSK) and MIL-STD shaped OQPSK (SOQPSK) with iterative decoding.» Interplanetary Network Prog. Rep. 42 (2004).
- ^ Sahin, C. and Perrins, E., 2011, November. The capacity of SOQPSK-TG. In 2011-MILCOM 2011 Military Communications Conference (pp. 555-560). IEEE.
- ^ Saeed, N., Elzanaty, A., Almorad, H., Dahrouj, H., Al-Naffouri, T.Y. and Alouini, M.S., 2020. Cubesat communications: Recent advances and future challenges. IEEE Communications Surveys & Tutorials.
- ^ Haykin, S., 2001. Communication Systems, John Wiley&Sons. Inc. — p. 368
- ^ Link Budget Analysis: Digital Modulation, Part 3 (www.AtlantaRF.com)
- ^ G.L. Stüber, “Soft Decision Direct-Sequence DPSK Receivers,” IEEE Transactions on Vehicular Technology, vol. 37, no. 3, pp. 151–157, August 1988.
- ^ a b IEEE Std 802.11-1999: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications – the overarching IEEE 802.11 specification. Archived August 28, 2007, at the Wayback Machine
- ^ IEEE Std 802.11b-1999 (R2003) – the IEEE 802.11b specification.
- ^ IEEE Std 802.11g-2003 – the IEEE 802.11g specification.
- ^ Understanding the Requirements of ISO/IEC 14443 for Type B Proximity Contactless Identification Cards, Application Note, Rev. 2056B–RFID–11/05, 2005, ATMEL.
- ^ «How Communications Satellites Work». Planet Fox. 2014.
- ^ «Low-Cost Satellite Set-top Box SoC — BCM7325 | Broadcom». Archived from the original on 2015-09-15. Retrieved 2015-09-08.
- ^ «Local and Remote Modems» (PDF). Black Box. Black Box Network Services. Archived from the original (PDF) on December 22, 2015. Retrieved December 20, 2015.
- ^ a b Blahut, R. E. (1988). Principles and Practice of Information Theory. Boston, MA, USA: Addison Wesley Publishing Company. ISBN 0-201-10709-0.
References[edit]
The notation and theoretical results in this article are based on material presented in the following sources:
- Proakis, John G. (1995). Digital Communications. Singapore: McGraw Hill. ISBN 0-07-113814-5.
- Couch, Leon W. II (1997). Digital and Analog Communications. Upper Saddle River, NJ: Prentice-Hall. ISBN 0-13-081223-4.
- Haykin, Simon (1988). Digital Communications. Toronto, Canada: John Wiley & Sons. ISBN 0-471-62947-2.
Phase-shift keying (PSK) is a digital modulation process which conveys data by changing (modulating) the phase of a constant frequency reference signal (the carrier wave). The modulation is accomplished by varying the sine and cosine inputs at a precise time. It is widely used for wireless LANs, RFID and Bluetooth communication.
Any digital modulation scheme uses a finite number of distinct signals to represent digital data. PSK uses a finite number of phases, each assigned a unique pattern of binary digits. Usually, each phase encodes an equal number of bits. Each pattern of bits forms the symbol that is represented by the particular phase. The demodulator, which is designed specifically for the symbol-set used by the modulator, determines the phase of the received signal and maps it back to the symbol it represents, thus recovering the original data. This requires the receiver to be able to compare the phase of the received signal to a reference signal – such a system is termed coherent (and referred to as CPSK).
CPSK requires a complicated demodulator, because it must extract the reference wave from the received signal and keep track of it, to compare each sample to. Alternatively, the phase shift of each symbol sent can be measured with respect to the phase of the previous symbol sent. Because the symbols are encoded in the difference in phase between successive samples, this is called differential phase-shift keying (DPSK). DPSK can be significantly simpler to implement than ordinary PSK, as it is a ‘non-coherent’ scheme, i.e. there is no need for the demodulator to keep track of a reference wave. A trade-off is that it has more demodulation errors.
Introduction[edit]
There are three major classes of digital modulation techniques used for transmission of digitally represented data:
- Amplitude-shift keying (ASK)
- Frequency-shift keying (FSK)
- Phase-shift keying (PSK)
All convey data by changing some aspect of a base signal, the carrier wave (usually a sinusoid), in response to a data signal. In the case of PSK, the phase is changed to represent the data signal. There are two fundamental ways of utilizing the phase of a signal in this way:
- By viewing the phase itself as conveying the information, in which case the demodulator must have a reference signal to compare the received signal’s phase against; or
- By viewing the change in the phase as conveying information – differential schemes, some of which do not need a reference carrier (to a certain extent).
A convenient method to represent PSK schemes is on a constellation diagram. This shows the points in the complex plane where, in this context, the real and imaginary axes are termed the in-phase and quadrature axes respectively due to their 90° separation. Such a representation on perpendicular axes lends itself to straightforward implementation. The amplitude of each point along the in-phase axis is used to modulate a cosine (or sine) wave and the amplitude along the quadrature axis to modulate a sine (or cosine) wave. By convention, in-phase modulates cosine and quadrature modulates sine.
In PSK, the constellation points chosen are usually positioned with uniform angular spacing around a circle. This gives maximum phase-separation between adjacent points and thus the best immunity to corruption. They are positioned on a circle so that they can all be transmitted with the same energy. In this way, the moduli of the complex numbers they represent will be the same and thus so will the amplitudes needed for the cosine and sine waves. Two common examples are «binary phase-shift keying» (BPSK) which uses two phases, and «quadrature phase-shift keying» (QPSK) which uses four phases, although any number of phases may be used. Since the data to be conveyed are usually binary, the PSK scheme is usually designed with the number of constellation points being a power of two.
Binary phase-shift keying (BPSK)[edit]
BPSK (also sometimes called PRK, phase reversal keying, or 2PSK) is the simplest form of phase shift keying (PSK). It uses two phases which are separated by 180° and so can also be termed 2-PSK. It does not particularly matter exactly where the constellation points are positioned, and in this figure they are shown on the real axis, at 0° and 180°. Therefore, it handles the highest noise level or distortion before the demodulator reaches an incorrect decision. That makes it the most robust of all the PSKs. It is, however, only able to modulate at 1 bit/symbol (as seen in the figure) and so is unsuitable for high data-rate applications. Yet there is the possibility of extending this bit/symbol, given the modulators symbol encryption / decryption logic system.
In the presence of an arbitrary phase-shift introduced by the communications channel, the demodulator (see, e.g. Costas loop) is unable to tell which constellation point is which. As a result, the data is often differentially encoded prior to modulation.
BPSK is functionally equivalent to 2-QAM modulation.
Implementation[edit]
The general form for BPSK follows the equation:
This yields two phases, 0 and π.
In the specific form, binary data is often conveyed with the following signals:[citation needed]
for binary «0»
for binary «1»
where f is the frequency of the base band.
Hence, the signal space can be represented by the single basis function
where 1 is represented by 

This use of this basis function is shown at the end of the next section in a signal timing diagram. The topmost signal is a BPSK-modulated cosine wave that the BPSK modulator would produce. The bit-stream that causes this output is shown above the signal (the other parts of this figure are relevant only to QPSK). After modulation, the base band signal will be moved to the high frequency band by multiplying 
Bit error rate[edit]
The bit error rate (BER) of BPSK under additive white Gaussian noise (AWGN) can be calculated as:[1]
or
Since there is only one bit per symbol, this is also the symbol error rate.
Quadrature phase-shift keying (QPSK)[edit]
Constellation diagram for QPSK with Gray coding. Each adjacent symbol only differs by one bit.
Sometimes this is known as quadriphase PSK, 4-PSK, or 4-QAM. (Although the root concepts of QPSK and 4-QAM are different, the resulting modulated radio waves are exactly the same.) QPSK uses four points on the constellation diagram, equispaced around a circle. With four phases, QPSK can encode two bits per symbol, shown in the diagram with Gray coding to minimize the bit error rate (BER) – sometimes misperceived as twice the BER of BPSK.
The mathematical analysis shows that QPSK can be used either to double the data rate compared with a BPSK system while maintaining the same bandwidth of the signal, or to maintain the data-rate of BPSK but halving the bandwidth needed. In this latter case, the BER of QPSK is exactly the same as the BER of BPSK – and believing differently is a common confusion when considering or describing QPSK. The transmitted carrier can undergo numbers of phase changes.
Given that radio communication channels are allocated by agencies such as the Federal Communications Commission giving a prescribed (maximum) bandwidth, the advantage of QPSK over BPSK becomes evident: QPSK transmits twice the data rate in a given bandwidth compared to BPSK — at the same BER. The engineering penalty that is paid is that QPSK transmitters and receivers are more complicated than the ones for BPSK. However, with modern electronics technology, the penalty in cost is very moderate.
As with BPSK, there are phase ambiguity problems at the receiving end, and differentially encoded QPSK is often used in practice.
Implementation[edit]
The implementation of QPSK is more general than that of BPSK and also indicates the implementation of higher-order PSK. Writing the symbols in the constellation diagram in terms of the sine and cosine waves used to transmit them:
This yields the four phases π/4, 3π/4, 5π/4 and 7π/4 as needed.
This results in a two-dimensional signal space with unit basis functions
The first basis function is used as the in-phase component of the signal and the second as the quadrature component of the signal.
Hence, the signal constellation consists of the signal-space 4 points
The factors of 1/2 indicate that the total power is split equally between the two carriers.
Comparing these basis functions with that for BPSK shows clearly how QPSK can be viewed as two independent BPSK signals. Note that the signal-space points for BPSK do not need to split the symbol (bit) energy over the two carriers in the scheme shown in the BPSK constellation diagram.
QPSK systems can be implemented in a number of ways. An illustration of the major components of the transmitter and receiver structure are shown below.
Conceptual transmitter structure for QPSK. The binary data stream is split into the in-phase and quadrature-phase components. These are then separately modulated onto two orthogonal basis functions. In this implementation, two sinusoids are used. Afterwards, the two signals are superimposed, and the resulting signal is the QPSK signal. Note the use of polar non-return-to-zero encoding. These encoders can be placed before for binary data source, but have been placed after to illustrate the conceptual difference between digital and analog signals involved with digital modulation.
Receiver structure for QPSK. The matched filters can be replaced with correlators. Each detection device uses a reference threshold value to determine whether a 1 or 0 is detected.
Probability of error[edit]
Although QPSK can be viewed as a quaternary modulation, it is easier to see it as two independently modulated quadrature carriers. With this interpretation, the even (or odd) bits are used to modulate the in-phase component of the carrier, while the odd (or even) bits are used to modulate the quadrature-phase component of the carrier. BPSK is used on both carriers and they can be independently demodulated.
As a result, the probability of bit-error for QPSK is the same as for BPSK:
However, in order to achieve the same bit-error probability as BPSK, QPSK uses twice the power (since two bits are transmitted simultaneously).
The symbol error rate is given by:
If the signal-to-noise ratio is high (as is necessary for practical QPSK systems) the probability of symbol error may be approximated:
The modulated signal is shown below for a short segment of a random binary data-stream. The two carrier waves are a cosine wave and a sine wave, as indicated by the signal-space analysis above. Here, the odd-numbered bits have been assigned to the in-phase component and the even-numbered bits to the quadrature component (taking the first bit as number 1). The total signal – the sum of the two components – is shown at the bottom. Jumps in phase can be seen as the PSK changes the phase on each component at the start of each bit-period. The topmost waveform alone matches the description given for BPSK above.
Timing diagram for QPSK. The binary data stream is shown beneath the time axis. The two signal components with their bit assignments are shown at the top, and the total combined signal at the bottom. Note the abrupt changes in phase at some of the bit-period boundaries.
The binary data that is conveyed by this waveform is: 11000110.
- The odd bits, highlighted here, contribute to the in-phase component: 11000110
- The even bits, highlighted here, contribute to the quadrature-phase component: 11000110
Variants[edit]
Offset QPSK (OQPSK)[edit]
Signal doesn’t pass through the origin, because only one bit of the symbol is changed at a time.
Offset quadrature phase-shift keying (OQPSK) is a variant of phase-shift keying modulation using four different values of the phase to transmit. It is sometimes called staggered quadrature phase-shift keying (SQPSK).
Difference of the phase between QPSK and OQPSK
Taking four values of the phase (two bits) at a time to construct a QPSK symbol can allow the phase of the signal to jump by as much as 180° at a time. When the signal is low-pass filtered (as is typical in a transmitter), these phase-shifts result in large amplitude fluctuations, an undesirable quality in communication systems. By offsetting the timing of the odd and even bits by one bit-period, or half a symbol-period, the in-phase and quadrature components will never change at the same time. In the constellation diagram shown on the right, it can be seen that this will limit the phase-shift to no more than 90° at a time. This yields much lower amplitude fluctuations than non-offset QPSK and is sometimes preferred in practice.
The picture on the right shows the difference in the behavior of the phase between ordinary QPSK and OQPSK. It can be seen that in the first plot the phase can change by 180° at once, while in OQPSK the changes are never greater than 90°.
The modulated signal is shown below for a short segment of a random binary data-stream. Note the half symbol-period offset between the two component waves. The sudden phase-shifts occur about twice as often as for QPSK (since the signals no longer change together), but they are less severe. In other words, the magnitude of jumps is smaller in OQPSK when compared to QPSK.
Timing diagram for offset-QPSK. The binary data stream is shown beneath the time axis. The two signal components with their bit assignments are shown the top and the total, combined signal at the bottom. Note the half-period offset between the two signal components.
SOQPSK[edit]
The license-free shaped-offset QPSK (SOQPSK) is interoperable with Feher-patented QPSK (FQPSK), in the sense that an integrate-and-dump offset QPSK detector produces the same output no matter which kind of transmitter is used.[2]
These modulations carefully shape the I and Q waveforms such that they change very smoothly, and the signal stays constant-amplitude even during signal transitions. (Rather than traveling instantly from one symbol to another, or even linearly, it travels smoothly around the constant-amplitude circle from one symbol to the next.) SOQPSK modulation can be represented as the hybrid of QPSK and MSK: SOQPSK has the same signal constellation as QPSK, however the phase of SOQPSK is always stationary.[3][4]
The standard description of SOQPSK-TG involves ternary symbols.[5] SOQPSK is one of the most spread modulation schemes in application to LEO satellite communications.[6]
π/4-QPSK[edit]
Dual constellation diagram for π/4-QPSK. This shows the two separate constellations with identical Gray coding but rotated by 45° with respect to each other.
This variant of QPSK uses two identical constellations which are rotated by 45° (

One property this modulation scheme possesses is that if the modulated signal is represented in the complex domain, transitions between symbols never pass through 0. In other words, the signal does not pass through the origin. This lowers the dynamical range of fluctuations in the signal which is desirable when engineering communications signals.
On the other hand, 
The modulated signal is shown below for a short segment of a random binary data-stream. The construction is the same as above for ordinary QPSK. Successive symbols are taken from the two constellations shown in the diagram. Thus, the first symbol (1 1) is taken from the «blue» constellation and the second symbol (0 0) is taken from the «green» constellation. Note that magnitudes of the two component waves change as they switch between constellations, but the total signal’s magnitude remains constant (constant envelope). The phase-shifts are between those of the two previous timing-diagrams.
Timing diagram for π/4-QPSK. The binary data stream is shown beneath the time axis. The two signal components with their bit assignments are shown the top and the total, combined signal at the bottom. Note that successive symbols are taken alternately from the two constellations, starting with the «blue» one.
DPQPSK[edit]
Dual-polarization quadrature phase shift keying (DPQPSK) or dual-polarization QPSK — involves the polarization multiplexing of two different QPSK signals, thus improving the spectral efficiency by a factor of 2. This is a cost-effective alternative to utilizing 16-PSK, instead of QPSK to double the spectral efficiency.j
Higher-order PSK[edit]
Constellation diagram for 8-PSK with Gray coding
Any number of phases may be used to construct a PSK constellation but 8-PSK is usually the highest order PSK constellation deployed. With more than 8 phases, the error-rate becomes too high and there are better, though more complex, modulations available such as quadrature amplitude modulation (QAM). Although any number of phases may be used, the fact that the constellation must usually deal with binary data means that the number of symbols is usually a power of 2 to allow an integer number of bits per symbol.
Bit error rate[edit]
For the general M-PSK there is no simple expression for the symbol-error probability if 
where
and 

Bit-error rate curves for BPSK, QPSK, 8-PSK and 16-PSK, additive white Gaussian noise channel
This may be approximated for high 

The bit-error probability for 
(Using Gray coding allows us to approximate the Lee distance of the errors as the Hamming distance of the errors in the decoded bitstream, which is easier to implement in hardware.)
The graph on the right compares the bit-error rates of BPSK, QPSK (which are the same, as noted above), 8-PSK and 16-PSK. It is seen that higher-order modulations exhibit higher error-rates; in exchange however they deliver a higher raw data-rate.
Bounds on the error rates of various digital modulation schemes can be computed with application of the union bound to the signal constellation.
Spectral efficiency[edit]
Bandwidth (or spectral) efficiency of M-PSK modulation schemes increases with increasing of modulation order M (unlike, for example, M-FSK):[7]
The same relationship holds true for M-QAM.[8]
Differential phase-shift keying (DPSK)[edit]
Differential encoding[edit]
Differential phase shift keying (DPSK) is a common form of phase modulation that conveys data by changing the phase of the carrier wave. As mentioned for BPSK and QPSK there is an ambiguity of phase if the constellation is rotated by some effect in the communications channel through which the signal passes. This problem can be overcome by using the data to change rather than set the phase.
For example, in differentially encoded BPSK a binary «1» may be transmitted by adding 180° to the current phase and a binary «0» by adding 0° to the current phase.
Another variant of DPSK is Symmetric Differential Phase Shift keying, SDPSK, where encoding would be +90° for a «1» and −90° for a «0».
In differentially encoded QPSK (DQPSK), the phase-shifts are 0°, 90°, 180°, −90° corresponding to data «00», «01», «11», «10». This kind of encoding may be demodulated in the same way as for non-differential PSK but the phase ambiguities can be ignored. Thus, each received symbol is demodulated to one of the 
The modulated signal is shown below for both DBPSK and DQPSK as described above. In the figure, it is assumed that the signal starts with zero phase, and so there is a phase shift in both signals at 
Timing diagram for DBPSK and DQPSK. The binary data stream is above the DBPSK signal. The individual bits of the DBPSK signal are grouped into pairs for the DQPSK signal, which only changes every Ts = 2Tb.
Analysis shows that differential encoding approximately doubles the error rate compared to ordinary 

One of the most popular applications of DPSK is the Bluetooth standard where 
Demodulation[edit]
BER comparison between DBPSK, DQPSK and their non-differential forms using Gray coding and operating in white noise
For a signal that has been differentially encoded, there is an obvious alternative method of demodulation. Instead of demodulating as usual and ignoring carrier-phase ambiguity, the phase between two successive received symbols is compared and used to determine what the data must have been. When differential encoding is used in this manner, the scheme is known as differential phase-shift keying (DPSK). Note that this is subtly different from just differentially encoded PSK since, upon reception, the received symbols are not decoded one-by-one to constellation points but are instead compared directly to one another.
Call the received symbol in the 



The decision variable for the 





where superscript * denotes complex conjugation. In the absence of noise, the phase of this is 
The probability of error for DPSK is difficult to calculate in general, but, in the case of DBPSK it is:
[9]
which, when numerically evaluated, is only slightly worse than ordinary BPSK, particularly at higher 
Using DPSK avoids the need for possibly complex carrier-recovery schemes to provide an accurate phase estimate and can be an attractive alternative to ordinary PSK.
In optical communications, the data can be modulated onto the phase of a laser in a differential way. The modulation is a laser which emits a continuous wave, and a Mach–Zehnder modulator which receives electrical binary data. For the case of BPSK, the laser transmits the field unchanged for binary ‘1’, and with reverse polarity for ‘0’. The demodulator consists of a delay line interferometer which delays one bit, so two bits can be compared at one time. In further processing, a photodiode is used to transform the optical field into an electric current, so the information is changed back into its original state.
The bit-error rates of DBPSK and DQPSK are compared to their non-differential counterparts in the graph to the right. The loss for using DBPSK is small enough compared to the complexity reduction that it is often used in communications systems that would otherwise use BPSK. For DQPSK though, the loss in performance compared to ordinary QPSK is larger and the system designer must balance this against the reduction in complexity.
Example: Differentially encoded BPSK[edit]
Differential encoding/decoding system diagram
At the 



where 
BER comparison between BPSK and differentially encoded BPSK operating in white noise
So 

The received signal is demodulated to yield 
since binary subtraction is the same as binary addition.
Therefore, 






Differential schemes for other PSK modulations may be devised along similar lines. The waveforms for DPSK are the same as for differentially encoded PSK given above since the only change between the two schemes is at the receiver.
The BER curve for this example is compared to ordinary BPSK on the right. As mentioned above, whilst the error rate is approximately doubled, the increase needed in 

Definitions[edit]
For determining error-rates mathematically, some definitions will be needed:


.
The error rates quoted here are those in additive white Gaussian noise (AWGN). These error rates are lower than those computed in fading channels, hence, are a good theoretical benchmark to compare with.
Applications[edit]
Owing to PSK’s simplicity, particularly when compared with its competitor quadrature amplitude modulation, it is widely used in existing technologies.
The wireless LAN standard, IEEE 802.11b-1999,[10][11] uses a variety of different PSKs depending on the data rate required. At the basic rate of 1 Mbit/s, it uses DBPSK (differential BPSK). To provide the extended rate of 2 Mbit/s, DQPSK is used. In reaching 5.5 Mbit/s and the full rate of 11 Mbit/s, QPSK is employed, but has to be coupled with complementary code keying. The higher-speed wireless LAN standard, IEEE 802.11g-2003,[10][12] has eight data rates: 6, 9, 12, 18, 24, 36, 48 and 54 Mbit/s. The 6 and 9 Mbit/s modes use OFDM modulation where each sub-carrier is BPSK modulated. The 12 and 18 Mbit/s modes use OFDM with QPSK. The fastest four modes use OFDM with forms of quadrature amplitude modulation.
Because of its simplicity, BPSK is appropriate for low-cost passive transmitters, and is used in RFID standards such as ISO/IEC 14443 which has been adopted for biometric passports, credit cards such as American Express’s ExpressPay, and many other applications.[13]
Bluetooth 2 uses 
Both QPSK and 8PSK are widely used in satellite broadcasting. QPSK is still widely used in the streaming of SD satellite channels and some HD channels. High definition programming is delivered almost exclusively in 8PSK due to the higher bitrates of HD video and the high cost of satellite bandwidth.[14] The DVB-S2 standard requires support for both QPSK and 8PSK. The chipsets used in new satellite set top boxes, such as Broadcom’s 7000 series support 8PSK and are backward compatible with the older standard.[15]
Historically, voice-band synchronous modems such as the Bell 201, 208, and 209 and the CCITT V.26, V.27, V.29, V.32, and V.34 used PSK.[16]
Mutual information with additive white Gaussian noise[edit]
Mutual information of PSK over the AWGN channel
The mutual information of PSK can be evaluated in additive Gaussian noise by numerical integration of its definition.[17] The curves of mutual information saturate to the number of bits carried by each symbol in the limit of infinite signal to noise ratio 
At intermediate values of signal to noise ratios the mutual information (MI) is well approximated by:[17]
The mutual information of PSK over the AWGN channel is generally farther to the AWGN channel capacity than QAM modulation formats.
See also[edit]
- Binary offset carrier modulation
- Differential coding
- Modulation – for an overview of all modulation schemes
- Phase modulation (PM) – the analogue equivalent of PSK
- Polar modulation
- PSK31
- PSK63
Notes[edit]
- ^ Communications Systems, H. Stern & S. Mahmoud, Pearson Prentice Hall, 2004, p. 283.
- ^
Tom Nelson, Erik Perrins, and Michael Rice.
«Common detectors for Tier 1 modulations» Archived 2012-09-17 at the Wayback Machine.T. Nelson, E. Perrins, M. Rice.
«Common detectors for shaped offset QPSK (SOQPSK) and Feher-patented QPSK (FQPSK)»
Nelson, T.; Perrins, E.; Rice, M. (2005). «Common detectors for shaped offset QPSK (SOQPSK) and Feher-patented QPSK (FQPSK)». GLOBECOM ’05. IEEE Global Telecommunications Conference, 2005. pp. 5 pp. doi:10.1109/GLOCOM.2005.1578470. ISBN 0-7803-9414-3. S2CID 11020777.
ISBN 0-7803-9414-3 - ^ Hill, Terrance J. «A non-proprietary, constant envelope, variant of shaped offset QPSK (SOQPSK) for improved spectral containment and detection efficiency.» MILCOM 2000. 21st Century Military Communications Conference Proceedings. Vol. 1. IEEE, 2000.
- ^ Li, Lifang, and M. K. Simon. «Performance of coded offset quadrature phase-shift keying (OQPSK) and MIL-STD shaped OQPSK (SOQPSK) with iterative decoding.» Interplanetary Network Prog. Rep. 42 (2004).
- ^ Sahin, C. and Perrins, E., 2011, November. The capacity of SOQPSK-TG. In 2011-MILCOM 2011 Military Communications Conference (pp. 555-560). IEEE.
- ^ Saeed, N., Elzanaty, A., Almorad, H., Dahrouj, H., Al-Naffouri, T.Y. and Alouini, M.S., 2020. Cubesat communications: Recent advances and future challenges. IEEE Communications Surveys & Tutorials.
- ^ Haykin, S., 2001. Communication Systems, John Wiley&Sons. Inc. — p. 368
- ^ Link Budget Analysis: Digital Modulation, Part 3 (www.AtlantaRF.com)
- ^ G.L. Stüber, “Soft Decision Direct-Sequence DPSK Receivers,” IEEE Transactions on Vehicular Technology, vol. 37, no. 3, pp. 151–157, August 1988.
- ^ a b IEEE Std 802.11-1999: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications – the overarching IEEE 802.11 specification. Archived August 28, 2007, at the Wayback Machine
- ^ IEEE Std 802.11b-1999 (R2003) – the IEEE 802.11b specification.
- ^ IEEE Std 802.11g-2003 – the IEEE 802.11g specification.
- ^ Understanding the Requirements of ISO/IEC 14443 for Type B Proximity Contactless Identification Cards, Application Note, Rev. 2056B–RFID–11/05, 2005, ATMEL.
- ^ «How Communications Satellites Work». Planet Fox. 2014.
- ^ «Low-Cost Satellite Set-top Box SoC — BCM7325 | Broadcom». Archived from the original on 2015-09-15. Retrieved 2015-09-08.
- ^ «Local and Remote Modems» (PDF). Black Box. Black Box Network Services. Archived from the original (PDF) on December 22, 2015. Retrieved December 20, 2015.
- ^ a b Blahut, R. E. (1988). Principles and Practice of Information Theory. Boston, MA, USA: Addison Wesley Publishing Company. ISBN 0-201-10709-0.
References[edit]
The notation and theoretical results in this article are based on material presented in the following sources:
- Proakis, John G. (1995). Digital Communications. Singapore: McGraw Hill. ISBN 0-07-113814-5.
- Couch, Leon W. II (1997). Digital and Analog Communications. Upper Saddle River, NJ: Prentice-Hall. ISBN 0-13-081223-4.
- Haykin, Simon (1988). Digital Communications. Toronto, Canada: John Wiley & Sons. ISBN 0-471-62947-2.
Тип кодирования данных
Фазовая манипуляция (PSK ) — это цифровая модуляция процесс, который передает данные путем изменения (модуляции) фазы постоянного частоты эталонного сигнала ( несущая ). Модуляция осуществляется путем изменения входных сигналов синус и косинус в точное время. Он широко используется для беспроводных локальных сетей, RFID и Bluetooth связи.
Любая схема цифровой модуляции использует конечное количество различных сигналов для представления цифровых данных. PSK использует конечное количество фаз, каждой из которых назначен уникальный шаблон из двоичных цифр. Обычно каждая фаза кодирует равное количество битов. Каждый набор битов образует символ , который представлен конкретной фазой. Демодулятор , который разработан специально для набора символов, используемого модулятором, определяет фазу принятого сигнала и отображает ее обратно в символ, который он представляет, таким образом восстанавливая исходные данные. Для этого приемник должен иметь возможность сравнивать фазу принятого сигнала с опорным сигналом — такая система называется когерентной (и упоминается как CPSK).
CPSK требует сложного демодулятора, поскольку он должен извлекать опорную волну из принятого сигнала и отслеживать ее, чтобы сравнивать каждую выборку. В качестве альтернативы, фазовый сдвиг каждого отправленного символа можно измерить относительно фазы предыдущего отправленного символа. Поскольку символы кодируются с разностью фаз между последовательными выборками, это называется дифференциальной фазовой манипуляцией (DPSK) . DPSK может быть значительно проще в реализации, чем обычный PSK, поскольку это «некогерентная» схема, то есть демодулятору не нужно отслеживать опорную волну. Компромисс в том, что он имеет больше ошибок демодуляции.
Содержание
- 1 Введение
- 1.1 Определения
- 2 Приложения
- 3 Двоичная фазовая манипуляция (BPSK)
- 3.1 Реализация
- 3.2 Частота битовых ошибок
- 4 Квадратурная фаза- Shift-манипуляция (QPSK)
- 4.1 Реализация
- 4.2 Вероятность ошибки
- 4.3 Варианты
- 4.3.1 Смещение QPSK (OQPSK)
- 4.3.2 SOQPSK
- 4.3.3 π / 4- QPSK
- 4.3.4 DPQPSK
- 5 PSK высшего порядка
- 5.1 Частота битовых ошибок
- 5.2 Спектральная эффективность
- 6 Дифференциальная фазовая манипуляция (DPSK)
- 6.1 Дифференциальное кодирование
- 6.2 Демодуляция
- 6.3 Пример: дифференциально-кодированная BPSK
- 7 Взаимная информация с аддитивным белым гауссовским шумом
- 8 См. Также
- 9 Примечания
- 10 Ссылки
Введение
Есть три основных класса методов цифровой модуляции, используемых для передачи представленных в цифровом виде данных:
- Амплитудно-сдвигающая манипуляция (ASK)
- Частотная манипуляция (FSK)
- Фазовая манипуляция (PSK)
Все передают данные, изменяя какой-либо аспект основного знака al, несущая (обычно синусоида ) в ответ на сигнал данных. В случае PSK фаза изменяется для представления сигнала данных. Существует два основных способа использования фазы сигнала таким образом:
- путем рассмотрения самой фазы как передачи информации, и в этом случае демодулятор должен иметь опорный сигнал. сигнал для сравнения фазы принятого сигнала; или
- При просмотре изменения в фазе, как транспортирующая информация -. дифференциального схема, некоторые из которых не нужен опорный носителя (в определенную степень)
Удобный способ представления схем PSK — это диаграмма созвездия . Здесь показаны точки на комплексной плоскости , где в данном контексте оси действительная и мнимая называются синфазной и квадратурной осями соответственно из-за их Разделение на 90 °. Такое представление на перпендикулярных осях легко реализуется. Амплитуда каждой точки вдоль синфазной оси используется для модуляции косинусной (или синусоидальной) волны, а амплитуда вдоль квадратурной оси — для модуляции синусоидальной (или косинусной) волны. По соглашению синфазная модуляция модулирует косинус, а квадратурная модуляция синуса.
В PSK выбранные точки созвездия обычно располагаются с равномерным угловым интервалом вокруг окружности. Это обеспечивает максимальное разделение фаз между соседними точками и, следовательно, лучшую защиту от повреждений. Они расположены по кругу, поэтому все они могут передаваться с одинаковой энергией. Таким образом, модули комплексных чисел, которые они представляют, будут такими же, как и амплитуды, необходимые для косинусной и синусоидальной волн. Двумя распространенными примерами являются «двоичная фазовая манипуляция» (BPSK), которая использует две фазы, и «квадратурная фазовая манипуляция» (QPSK), которая использует четыре фазы, хотя любое количество фаз могут быть использованы. Поскольку данные, которые должны быть переданы, обычно являются двоичными, схема PSK обычно разрабатывается с количеством точек совокупности, равным степени двух.
Определения
Для математического определения частоты ошибок потребуются некоторые определения:
Q (x) { displaystyle Q (x)}

- Q (x) = 1 2 π ∫ x ∞ e — 1 2 t 2 dt = 1 2 erfc (x 2), x ≥ 0 { displaystyle Q (x) = { frac {1} { sqrt {2 pi}}} int _ {x} ^ { infty} e ^ {- { frac {1} {2}} t ^ { 2}} , dt = { frac {1} {2}} operatorname {erfc} left ({ frac {x} { sqrt {2}}} right), x geq 0}
.
Приведенные здесь коэффициенты ошибок соответствуют аддитивному белому гауссовскому шуму (AWGN). Эти коэффициенты ошибок ниже, чем вычисленные в каналах с замираниями, следовательно, они являются хорошим теоретическим эталоном для сравнения.
Приложения
Благодаря простоте PSK, особенно по сравнению с его конкурентом квадратурной амплитудной модуляцией, он широко используется в существующих технологиях.
Стандарт беспроводной локальной сети, IEEE 802.11b-1999, использует различные PSK в зависимости от требуемой скорости передачи данных. При базовой скорости 1 Мбит / с он использует DBPSK (дифференциальный BPSK). Для обеспечения расширенной скорости 2 Мбит / с используется DQPSK. При достижении 5,5 Мбит / с и полной скорости 11 Мбит / с используется QPSK, но он должен сочетаться с вводом дополнительного кода. Стандарт высокоскоростной беспроводной локальной сети, IEEE 802.11g-2003, имеет восемь скоростей передачи данных: 6, 9, 12, 18, 24, 36, 48 и 54 Мбит / с. В режимах 6 и 9 Мбит / с используется модуляция OFDM, где каждая поднесущая модулируется BPSK. В режимах 12 и 18 Мбит / с используется OFDM с QPSK. Четыре самых быстрых режима используют OFDM с формами квадратурной амплитудной модуляции.
Из-за своей простоты BPSK подходит для недорогих пассивных передатчиков и используется в стандартах RFID, таких как ISO / IEC 14443, который был принят для биометрических паспортов, кредитных карт, таких как American Express, ExpressPay, и многих других приложений.
Bluetooth 2 использует π / 4 { displaystyle pi / 4}
И QPSK, и 8PSK широко используются в спутниковом вещании. QPSK по-прежнему широко используется при потоковой передаче спутниковых каналов SD и некоторых каналов HD. Программы высокого разрешения передаются почти исключительно в 8PSK из-за более высоких битрейтов HD-видео и высокой стоимости спутниковой полосы пропускания. Стандарт DVB-S2 требует поддержки как QPSK, так и 8PSK. Наборы микросхем, используемые в новых спутниковых приставках, таких как серия 7000 компании Broadcom, поддерживают 8PSK и обратно совместимы со старым стандартом.
Исторически сложилось так, что модемы с синхронизацией голосового диапазона , например, Bell 201, 208 и 209 и CCITT V.26, V.27, V.29, V.32 и V.34 использовали PSK.
Двоичная фазовая манипуляция (BPSK)

BPSK (также иногда называемый PRK, фазовой манипуляцией или 2PSK) — это простейшая форма фазовой манипуляции (PSK). В нем используются две фазы, разделенные на 180 °, поэтому их также можно назвать 2-PSK. Не имеет особого значения, где именно расположены точки созвездия, и на этом рисунке они показаны на действительной оси в точках 0 ° и 180 °. Следовательно, он обрабатывает самый высокий уровень шума или искажения до того, как демодулятор примет неверное решение. Это делает его самым надежным из всех PSK. Однако он может модулировать только со скоростью 1 бит / символ (как показано на рисунке) и поэтому не подходит для приложений с высокой скоростью передачи данных.
При наличии произвольного фазового сдвига, вносимого каналом связи, демодулятор (см., Например, цикл Костаса ) не может определить, какая точка совокупности который. В результате данные часто дифференциально кодируются перед модуляцией.
BPSK функционально эквивалентен модуляции 2-QAM.
Реализация
Общая форма для BPSK следует уравнению:
- sn (t) = 2 E b T b cos (2 π ft + π (1 — n)), п = 0, 1. { displaystyle s_ {n} (t) = { sqrt { frac {2E_ {b}} {T_ {b}}}} cos (2 pi ft + pi (1-n)), quad n = 0,1.}
Это дает две фазы, 0 и π. В особой форме двоичные данные часто передаются с помощью следующих сигналов:
- s 0 (t) = 2 E b T b cos (2 π ft + π) = — 2 E b T b cos (2 π фут) { displaystyle s_ {0} (t) = { sqrt { frac {2E_ {b}} {T_ {b}}}} cos (2 pi ft + pi) = — { sqrt { frac {2E_ {b}} {T_ {b}}}} cos (2 pi ft)}
для двоичного «0»
- s 1 (t) = 2 E b T b cos (2 π фут) { displaystyle s_ {1} (t) = { sqrt { frac {2E_ {b}} {T_ {b}}}} cos (2 pi ft)}
для двоичной «1»
, где f — частота основной полосы частот.
Следовательно, пространство сигналов может быть представлено единственной базисной функцией
- ϕ (t) = 2 T b cos (2 π ft) { displaystyle phi (t) = { sqrt { frac {2} {T_ {b}}}} cos (2 pi ft)}
где 1 представлено как E b ϕ (t) { displaystyle { sqrt {E_ {b}}} phi (t)}

Это использование этой базовой функции показано в конце следующего раздела на временной диаграмме сигнала. Самый верхний сигнал — это косинусоидальная волна, модулированная BPSK, которую будет производить модулятор BPSK. Битовый поток, который вызывает этот вывод, показан над сигналом (другие части этого рисунка относятся только к QPSK). После модуляции сигнал основной полосы будет перемещен в полосу высоких частот путем умножения cos (2 π fct) { displaystyle cos (2 pi f_ {c} t)}
Коэффициент битовых ошибок
коэффициент битовых ошибок (BER) BPSK при аддитивном белом гауссовском шуме (AWGN) можно рассчитать как:
- P b = Q (2 E b N 0) { displaystyle P_ {b} = Q left ({ sqrt { frac {2E_ {b}} {N_ {0}}}} right)}
или P е = 1 2 erfc (E b N 0) { displaystyle P_ {e} = { frac {1} {2}} operatorname {erfc} left ({ sqrt { frac {E_ {b}}) {N_ {0}}}} right)}
Поскольку на каждый символ приходится только один бит, это также частота ошибок символа.

Иногда это называется четырехфазным PSK, 4-PSK или 4- QAM. (Хотя основные концепции QPSK и 4-QAM различны, результирующие модулированные радиоволны точно такие же.) QPSK использует четыре точки на диаграмме созвездия, равномерно распределенные по кругу. С четырьмя фазами QPSK может кодировать два бита на символ, показанные на диаграмме с кодированием Грея, чтобы минимизировать коэффициент ошибок по битам (BER) — иногда ошибочно воспринимается как удвоенный BER, чем BPSK.
Математический анализ показывает, что QPSK может использоваться либо для удвоения скорости передачи данных по сравнению с системой BPSK при сохранении той же полосы пропускания сигнала, либо для поддержания скорости передачи данных BPSK. но необходимо сократить вдвое полосу пропускания. В последнем случае BER QPSK в точности совпадает с BER BPSK — и полагать иначе — это обычная путаница при рассмотрении или описании QPSK. Переданная несущая может претерпевать ряд фазовых изменений.
Учитывая, что каналы радиосвязи распределяются такими агентствами, как Федеральная комиссия по связи, что дает предписанную (максимальную) полосу пропускания, преимущество QPSK над BPSK становится очевидным: QPSK передает в два раза большую скорость передачи данных в заданной полосе пропускания по сравнению с BPSK — при том же BER. Плата за техническое обслуживание состоит в том, что передатчики и приемники QPSK сложнее, чем передатчики для BPSK. Однако с современной технологией электроники снижение стоимости очень умеренное.
Как и в случае с BPSK, на принимающей стороне возникают проблемы с фазовой неоднозначностью, и на практике часто используется дифференциально кодированный QPSK.
Реализация
Реализация QPSK является более общей, чем реализация BPSK, а также указывает на реализацию PSK более высокого порядка. Записывая символы на диаграмме созвездия в виде синусоидальных и косинусоидальных волн, используемых для их передачи:
- sn (t) = 2 E s T s cos (2 π fct + (2 n — 1) π 4), n = 1, 2, 3, 4. { displaystyle s_ {n} (t) = { sqrt { frac {2E_ {s}} {T_ {s}}}} cos left (2 pi f_ {c} t + (2n-1) { frac { pi} {4}} right), quad n = 1,2,3,4.}
Это дает четыре фазы π / 4, 3π / 4, 5π / 4 и 7π / 4 по мере необходимости.
Это приводит к двумерному сигнальному пространству с единицами базисных функций
- ϕ 1 (t) = 2 T s cos (2 π fct) ϕ 2 (t) = 2 T s грех (2 π fct) { displaystyle { begin {align} phi _ {1} (t) = { sqrt { frac {2} {T_ {s}}}} cos left (2 pi f_ {c} t right) \ phi _ {2} (t) = { sqrt { frac {2} {T_ {s}}}} sin left (2 pi f_ { c} t right) end {align}}}
Первая базовая функция используется как синфазная составляющая сигнала, а вторая как квадратурная составляющая сигнала.
Следовательно, совокупность сигналов состоит из 4 точек
- пространства сигнала (± E s 2 ± E s 2). { displaystyle { begin {pmatrix} pm { sqrt { frac {E_ {s}} {2}}} pm { sqrt { frac {E_ {s}} {2}}} end {pmatrix}}.}
Коэффициент 1/2 показывает, что общая мощность поровну делится между двумя несущими.
Сравнение этих базовых функций с функциями для BPSK ясно показывает, как QPSK можно рассматривать как два независимых сигнала BPSK. Обратите внимание, что точки пространства сигнала для BPSK не нуждаются в разделении энергии символа (бита) по двум несущим в схеме, показанной на диаграмме созвездия BPSK.
Системы QPSK могут быть реализованы несколькими способами. Ниже показаны основные компоненты конструкции передатчика и приемника.


Вероятность ошибки
Хотя QPSK можно рассматривать как четвертичную модуляцию, его легче рассматривать как две независимо модулированные квадратурные носители. При такой интерпретации четные (или нечетные) биты используются для модуляции синфазной составляющей несущей, в то время как нечетные (или четные) биты используются для модуляции квадратурной составляющей несущей. BPSK используется на обеих несущих, и их можно независимо демодулировать.
В результате вероятность битовой ошибки для QPSK такая же, как для BPSK:
- P b = Q (2 E b N 0) { displaystyle P_ {b} = Q left ({ sqrt { frac {2E_ {b}} {N_ {0}}}} right)}
Однако для достижения той же вероятности битовой ошибки, что и BPSK, QPSK использует вдвое большую мощность (поскольку два бита передаются одновременно).
Коэффициент ошибок символа определяется следующим образом:
- P s = 1 — (1 — P b) 2 = 2 Q (E s N 0) — [Q (E s N 0)] 2. { displaystyle { begin {align} P_ {s} = 1- left (1-P_ {b} right) ^ {2} \ = 2Q left ({ sqrt { frac {E_ { s}} {N_ {0}}}} right) — left [Q left ({ sqrt { frac {E_ {s}} {N_ {0}}}} right) right] ^ { 2}. End {align}}}
Если отношение сигнал / шум высокое (что необходимо для практических систем QPSK), вероятность ошибки символа может быть приблизительно равна:
- P s ≈ 2 Q (E s N 0) = erfc (E s 2 N 0) = erfc (E b N 0) { displaystyle P_ {s} приблизительно 2Q left ({ sqrt { frac { E_ {s}} {N_ {0}}}} right) = operatorname {erfc} left ({ sqrt { frac {E_ {s}} {2N_ {0}}}} right) = operatorname {erfc} left ({ sqrt { frac {E_ {b}} {N_ {0}}}} right)}
Модулированный сигнал показан ниже для короткого сегмента случайных двоичных данных — поток. Две несущие волны представляют собой косинусоидальную и синусоидальную волну, как показывает анализ пространства сигналов выше. Здесь биты с нечетными номерами назначены синфазному компоненту, а биты с четными номерами — квадратурному компоненту (принимая первый бит за номер 1). Общий сигнал — сумма двух компонентов — показан внизу. Скачки по фазе можно увидеть, поскольку PSK изменяет фазу на каждом компоненте в начале каждого битового периода. Самая верхняя форма волны соответствует описанию, данному для BPSK выше.
.
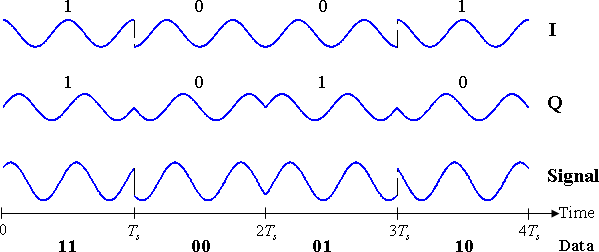
Двоичные данные, которые передаются этим сигналом: 11000110.
- Нечетные биты, выделенные здесь, вносят вклад в синфазную составляющую: 11000110
- Четные биты, выделенные здесь, вносят вклад в квадратурно-фазовую составляющую: 11000110
Варианты
QPSK смещения (OQPSK)
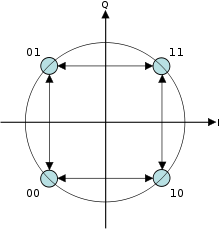
Квадратурная фазовая манипуляция со смещением (OQPSK) — это вариант модуляции с фазовой манипуляцией, использующий четыре различных значения фазы для передачи. Иногда это называют ступенчатой квадратурной фазовой манипуляцией (SQPSK).

Одновременное использование четырех значений фазы (два бита ) для построения символа QPSK может позволить фазе сигнала прыгнуть на столько же как 180 ° за раз. Когда сигнал фильтруется нижними частотами (как это обычно бывает в передатчике), эти фазовые сдвиги приводят к большим колебаниям амплитуды, что является нежелательным качеством в системах связи. При смещении синхронизации нечетных и четных битов на один битовый период или половину периода символа синфазная и квадратурная составляющие никогда не изменятся одновременно. На диаграмме созвездия, показанной справа, можно увидеть, что это ограничит фазовый сдвиг не более чем на 90 ° за раз. Это дает гораздо меньшие колебания амплитуды, чем QPSK без смещения, и иногда это предпочтительнее на практике.
На рисунке справа показана разница в поведении фазы между обычным QPSK и OQPSK. Видно, что на первом графике фаза может измениться сразу на 180 °, а в OQPSK изменения никогда не превышают 90 °.
Модулированный сигнал показан ниже для короткого сегмента случайного потока двоичных данных. Обратите внимание на сдвиг на половину периода символа между двумя составляющими волнами. Внезапные сдвиги фазы происходят примерно в два раза чаще, чем при QPSK (поскольку сигналы больше не изменяются вместе), но они менее серьезны. Другими словами, величина скачков меньше в OQPSK по сравнению с QPSK.

SOQPSK
Безлицензионный сформированный -смещение QPSK (SOQPSK) совместим с Feher- запатентованный QPSK (FQPSK ) в том смысле, что детектор QPSK с интегрированием и сбросом смещения дает одинаковый выходной сигнал независимо от типа используемого передатчика.
Эти модуляции тщательно формируют I и формы волны Q, так что они изменяются очень плавно, и сигнал остается постоянной амплитуды даже во время переходов сигнала. (Вместо мгновенного перехода от одного символа к другому или даже линейного, он плавно перемещается по кругу с постоянной амплитудой от одного символа к другому.) Модуляция SOQPSK может быть представлена как гибрид QPSK и MSK : SOQPSK имеет ту же совокупность сигналов, что и QPSK, однако фаза SOQPSK всегда стационарна.
Стандартное описание SOQPSK-TG включает троичные символы. SOQPSK — одна из наиболее распространенных схем модуляции в применении к спутниковой связи LEO.
π / 4-QPSK

В этом варианте QPSK используются два идентичных созвездия, повернутых на 45 ° (π / 4 { displaystyle pi / 4}

Одно свойство, которым обладает эта схема модуляции, заключается в том, что если модулированный сигнал представлен в комплексной области, переходы между символами никогда не проходят через 0. Другими словами, сигнал не проходит через начало координат. Это снижает динамический диапазон колебаний сигнала, что желательно при разработке сигналов связи.
С другой стороны, π / 4 { displaystyle pi / 4}
Модулированный сигнал показан ниже для короткого сегмента случайного потока двоичных данных. Конструкция такая же, как и для обычного QPSK. Последовательные символы взяты из двух созвездий, показанных на схеме. Таким образом, первый символ (11) взят из «синего» созвездия, а второй символ (0 0) взят из «зеленого» созвездия. Обратите внимание, что величины двух составляющих волн изменяются при переключении между созвездиями, но общая величина сигнала остается постоянной (постоянная огибающая ). Фазовые сдвиги находятся между двумя предыдущими временными диаграммами.

DPQPSK
Квадратурная фазовая манипуляция с двойной поляризацией (DPQPSK) или QPSK с двойной поляризацией — включает поляризационное мультиплексирование двух разных сигналов QPSK, таким образом улучшая спектральную эффективность в 2 раза. Это экономичная альтернатива использованию 16-PSK вместо QPSK для удвоения спектральной эффективности.
PSK высшего порядка
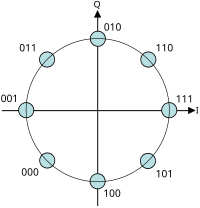
Для построения совокупности PSK можно использовать любое количество фаз, но 8-PSK обычно является развернутой совокупностью PSK высшего порядка. При более чем 8 фазах частота ошибок становится слишком высокой, и доступны более качественные, хотя и более сложные модуляции, такие как квадратурная амплитудная модуляция (QAM). Хотя может использоваться любое количество фаз, тот факт, что совокупность обычно должна иметь дело с двоичными данными, означает, что количество символов обычно является степенью 2, чтобы обеспечить целое число битов на символ.
Коэффициент битовых ошибок
Для общего M-PSK не существует простого выражения для вероятности ошибки символа, если M>4 { displaystyle M>4}
- P s = 1 — ∫ — π / M π / M p θ r (θ r) d θ r, { displaystyle P_ {s} = 1- int _ {- pi / M } ^ { pi / M} p _ { theta _ {r}} left ( theta _ {r} right) d theta _ {r},}
где
- p θ r (θ r) = 1 2 π e — 2 γ s sin 2 θ r ∫ 0 ∞ V e — 1 2 (V — 2 γ s cos θ r) 2 d V, V = r 1 2 + r 2 2, θ р знак равно загар — 1 (р 2 р 1), γ s знак равно Е s N 0 { Displaystyle { begin {align} p _ { theta _ {r}} left ( theta _ {r} right) = { frac {1} {2 pi}} e ^ {- 2 gamma _ {s} sin ^ {2} theta _ {r}} int _ {0} ^ { infty} Ve ^ {- { frac {1} {2}} left (V-2 { sqrt { gamma _ {s}}} cos theta _ {r} right) ^ {2}} , dV, \ V = { sqrt {r_ {1} ^ {2} + r_ {2} ^ {2}}}, \ theta _ {r} = tan ^ {- 1} left ({ frac {r_ {2}} {r_ {1}}} r ight), \ gamma _ {s} = { frac {E_ {s}} {N_ {0}}} end {align}}}
и r 1 ∼ N (E s, 1 2 N 0) { displaystyle r_ {1} sim N left ({ sqrt {E_ {s}}}, { frac {1} {2}} N_ {0} right)}


Это может быть приблизительно для высокого M { displaystyle M}

- P s ≈ 2 Q (2 γ s sin π M). { displaystyle P_ {s} приблизительно 2Q left ({ sqrt {2 gamma _ {s}}} sin { frac { pi} {M}} right).}
Бит- вероятность ошибки для M { displaystyle M}
- P b ≈ 1 k P s. { displaystyle P_ {b} приблизительно { frac {1} {k}} P_ {s}.}
(Использование кодирования Грея позволяет нам приблизить расстояние Ли ошибок как Расстояние Хэмминга ошибок в декодированном потоке битов, которое легче реализовать аппаратно.)
На графике слева сравниваются коэффициенты битовых ошибок BPSK, QPSK (которые являются то же, что и отмечалось выше), 8-PSK и 16-PSK. Видно, что модуляция более высокого порядка демонстрирует более высокие коэффициенты ошибок; однако взамен они обеспечивают более высокую скорость необработанных данных.
Границы частоты ошибок для различных схем цифровой модуляции могут быть вычислены с применением объединения к сигнальной совокупности.
Спектральная эффективность
Ширина полосы (или спектральная) эффективность схем модуляции M-PSK увеличивается с увеличением порядка модуляции M (в отличие, например, от M-FSK ):
- ρ = журнал 2 M 2 [бит / с ⋅ Гц] { displaystyle rho = { frac { log _ {2} M} {2}} quad [{ text {bits}} / { text {s }} cdot { text {Hz}}]}
То же соотношение сохраняется и для M-QAM.
Дифференциальная фазовая манипуляция (DPSK)
Дифференциальное кодирование
Дифференциальная фазовая манипуляция (DPSK) — это распространенная форма фазовой модуляции, которая передает данные путем изменения фазы несущей волны. Как упоминалось для BPSK и QPSK, существует неоднозначность фазы, если совокупность поворачивается некоторым эффектом в канал связи, через который проходит сигнал. Эту проблему можно решить, используя данные для изменения, а не для установки фазы.
Например, в дифференциально-кодированной BPSK двоичной «1» может быть передан путем добавления 180 ° к текущей фазе и двоичного «0» путем добавления 0 ° к текущей фазе. Другой вариант DPSK — это симметричная дифференциальная фазовая манипуляция, SDPSK, где кодирование будет составлять + 90 ° для «1» и -90 ° для «0».
В дифференциально кодированной QPSK (DQPSK) фазовые сдвиги составляют 0 °, 90 °, 180 °, -90 °, что соответствует данным «00», «01», «11», «10». Этот вид кодирования может быть демодулирован таким же образом, как и для недифференциальной PSK, но фазовые неоднозначности можно игнорировать. Таким образом, каждый принятый символ демодулируется в одну из точек M { displaystyle M}
Модулированный сигнал показан ниже как для DBPSK, так и для DQPSK, как описано выше. На рисунке предполагается, что сигнал начинается с нулевой фазы, и поэтому в обоих сигналах есть фазовый сдвиг в t = 0 { displaystyle t = 0}

Анализ показывает, что дифференциальное кодирование примерно вдвое увеличивает количество ошибок по сравнению с обычным M { displaystyle M}

Одно из самых популярных приложений DPSK — это стандарт Bluetooth, где π / 4 { displaystyle pi / 4}
Демодуляция

Для сигнала, который был закодирован дифференциально, существует очевидный альтернативный метод демодуляции. Вместо обычной демодуляции и игнорирования неоднозначности фазы несущей сравнивается фаза между двумя последовательными принятыми символами и используется для определения того, какими должны были быть данные. Когда дифференциальное кодирование используется таким образом, схема известна как дифференциальная фазовая манипуляция (DPSK). Обратите внимание, что это немного отличается от просто дифференциально кодированной PSK, поскольку при приеме принятые символы не декодируются один за другим в точки совокупности, а вместо этого напрямую сравниваются друг с другом.
Вызвать полученный символ в k { displaystyle k}



- r k = E s e j ϕ k + n k. { displaystyle r_ {k} = { sqrt {E_ {s}}} e ^ {j phi _ {k}} + n_ {k}.}
Переменная решения для k — 1 { displaystyle k-1}





- rkrk — 1 ∗ = E sej (φ k — φ k — 1) + E sej φ knk — 1 ∗ + E se — j φ k — 1 nk + nknk — 1 * { displaystyle r_ {k} r_ {k-1} ^ {*} = E_ {s} e ^ {j left ( varphi _ {k} — varphi _ {k-1} right) } + { sqrt {E_ {s}}} e ^ {j varphi _ {k}} n_ {k-1} ^ {*} + { sqrt {E_ {s}}} e ^ {- j varphi _ {k-1}} n_ {k} + n_ {k} n_ {k-1} ^ {*}}
где верхний индекс * обозначает комплексное сопряжение. В отсутствие шума фаза этого сигнала равна ϕ k — ϕ k — 1 { displaystyle phi _ {k} — phi _ {k-1}}
Вероятность ошибки для DPSK в целом трудно вычислить, но в случае DBPSK это:
- P b = 1 2 e — E b N 0, { displaystyle P_ {b } = { frac {1} {2}} e ^ {- { frac {E_ {b}} {N_ {0}}}},}
который при численной оценке лишь немного хуже обычного BPSK, особенно при более высоких значениях E b / N 0 { displaystyle E_ {b} / N_ {0}}
Использование DPSK устраняет необходимость в возможных сложных схемах восстановления несущей для обеспечения точной оценки фазы и может быть привлекательной альтернативой обычному PSK.
В оптической связи данные могут быть модулированы по фазе лазера дифференциальным способом. Модуляция представляет собой лазер, который излучает непрерывную волну, и модулятор Маха – Цендера, который принимает электрические двоичные данные. В случае BPSK лазер передает поле без изменений для двоичной «1» и с обратной полярностью для «0». Демодулятор состоит из интерферометра линии задержки, который задерживает один бит, поэтому два бита можно сравнивать за один раз. При дальнейшей обработке используется фотодиод для преобразования оптического поля в электрический ток, так что информация возвращается в исходное состояние.
Коэффициенты ошибок по битам DBPSK и DQPSK сравниваются с их недифференциальными аналогами на графике справа. Потери при использовании DBPSK достаточно малы по сравнению с уменьшением сложности, которое часто используется в системах связи, которые иначе использовали бы BPSK. Однако для DQPSK потеря производительности по сравнению с обычным QPSK больше, и разработчик системы должен сбалансировать это с уменьшением сложности.
Пример: BPSK с дифференциальным кодированием
Схема системы дифференциального кодирования / декодирования
В k th { displaystyle k ^ { textrm {th}}}



- ek = ek — 1 ⊕ bk { displaystyle , e_ {k} = e_ {k-1} oplus b_ {k}}
где ⊕ { displaystyle oplus {}}

Итак, ek { displaystyle e_ {k}}

Полученный сигнал демодулируется для получения ek = ± 1 { displaystyle e_ {k} = pm 1}
- bk = ek ⊕ ek — 1, { displaystyle b_ {k} = e_ {k} oplus e_ {k-1},}
поскольку двоичное вычитание аналогично двоичному сложению.
Следовательно, bk = 1 { displaystyle b_ {k} = 1}






Дифференциальные схемы для других модуляций PSK могут быть разработаны аналогичным образом. Формы сигналов для DPSK такие же, как для PSK с дифференциальным кодированием, приведенные выше, поскольку единственное изменение между двумя схемами — на приемнике.
Кривая BER для этого примера сравнивается с обычным BPSK справа. Как упоминалось выше, хотя частота ошибок увеличивается примерно вдвое, увеличение E b / N 0 { displaystyle E_ {b} / N_ {0}}

Взаимная информация с аддитивным белым гауссовским шумом

взаимная информация PSK может быть оценена в аддитивном гауссовском шуме посредством численного интегрирования его определения. Кривые взаимной информации насыщаются до количества битов, переносимых каждым символом в пределе бесконечного отношения сигнал / шум E s / N 0 { displaystyle E_ {s} / N_ {0}}
При промежуточных значениях отношения сигнал / шум взаимная информация (MI) хорошо аппроксимируется следующим образом:
- MI ≃ log 2 (4 π e E s N 0). { displaystyle { textrm {MI}} simeq log _ {2} left ({ sqrt {{ frac {4 pi} {e}} { frac {E_ {s}} {N_ {0) }}}}} right).}
Взаимная информация PSK по каналу AWGN обычно находится дальше от пропускной способности канала AWGN, чем форматы модуляции QAM.
См. Также
- Двоичная модуляция несущей со смещением
- Дифференциальное кодирование
- Модуляция — для обзора все схемы модуляции
- Фазовая модуляция (PM) — аналог эквивалент PSK
- Полярная модуляция
- PSK31
- PSK63
Примечания
Ссылки
Обозначения и теоретические результаты в этой статье основаны на материалах, представленных в следующих источниках:
- Proakis, John G. (1995). Цифровая связь. Сингапур: Макгроу Хилл. ISBN 0-07-113814-5.
- Диван, Леон В. II (1997). Цифровая и аналоговая связь. Река Аппер Сэдл, Нью-Джерси: Прентис-Холл. ISBN 0-13-081223-4.
- Хайкин, Саймон (1988). Цифровые коммуникации. Торонто, Канада: John Wiley Sons. ISBN 0-471-62947-2.
350 руб
Журнал «Радиотехника» №8 за 2022 г.
Статья в номере:
Методика расчета вероятностей битовых ошибок приема радиосигналов с QPSK-модуляцией при нескольких гармонических помехах
Тип статьи:
научная статья
DOI: https://doi.org/10.18127/j00338486-202208-09
УДК: 623.612
Авторы:
В.В. Звонарев1, А.С. Попов2, А.В. Питрин3
1-3 Военно-космическая академия имени А.Ф. Можайского (Санкт-Петербург, Россия)
Аннотация:
Постановка проблемы. На обеспечение устойчивости передачи информации с использованием радиоканала большое влияние оказывают шумы и помехи. При этом результат одновременного применения нескольких структурных помех существенно отличается от результата воздействия одной помехи. Необходимость компенсации нескольких помех на приеме приводит к усложнению и удорожанию оборудования приемной системы. Кроме того, в ряде случаев полное подавление группы помех может оказаться недостижимым. Учет наличия нескольких помех вносит заметные принципиальные и технические трудности при выводе формул для анализа помехоустойчивости приема полезного радиосигнала. Методика расчета вероятностей битовых ошибок для радиосигналов с QPSK-модуляцией при наличии структурных помех, основанная на построении вероятностного пространства на множестве совместных событий, предложена и рассмотрена в [1]. Необходимо на основе применения условных вероятностей получить формулы для расчета средних вероятностей битовых ошибок когерентного приема радиосигнала с QPSK-модуляцией в присутствии нескольких помех.
Цель. Предложить методику расчета вероятностей битовых ошибок приема радиосигналов с QPSK-модуляцией при нескольких гармонических помехах на основе применения условных вероятностей, а также вывести формулы для расчета средних вероятностей битовых ошибок когерентного приема радиосигнала с QPSK-модуляцией в присутствии нескольких помех.
Результаты. Представлена методика расчета вероятностей битовых ошибок приема радиосигналов в различных условиях электромагнитной обстановки, позволяющая с высокой точностью и надежным прогнозированием рассчитать (обосновать) достоверность передаваемой информации в радиоканале с учетом применения нескольких помех. Получены формулы для расчета средних вероятностей битовых ошибок когерентного приема радиосигнала с QPSK-модуляцией в присутствии нескольких помех. Выполнен расчет вероятности битовой ошибки радиосигналов с QPSK-модуляцией при нескольких гармонических помехах с применением условных вероятностей перехода номеров позиций символов в созвездии передаваемого радиосигнала в номера позиций символов созвездия принятого (детектированного).
Практическая значимость. Данная методика позволяет с высокой точностью и надежным прогнозированием рассчитать (обосновать) достоверность передаваемой информации в радиоканале с учетом применения нескольких помех.
Страницы: 84-95
Для цитирования
Звонарев В.В., Попов А.С., Питрин А.В. Методика расчета вероятностей битовых ошибок приема радиосигналов с QPSK-модуляцией при нескольких гармонических помехах // Радиотехника. 2022. Т. 86. № 8. С. 84-95. DOI: https://doi.org/10.18127/j00338486-202208-09
Список источников
- Бродский М. С., Звонарев В. В., Попов А. С. Метод построения вероятностного пространства на множестве совместных событий для расчета вероятностей битовых ошибок приема радиосигналов с QPSK-модуляцией при наличии помех // Труды Военно-космической академии им. А.Ф. Можайского. 2021. Вып. № 678. С. 43–50.
- Волхонская Е. В., Коротей Е. В., Власова К. В., Рушко М. В. Модельное исследование помехоустойчивости приема радиосигналов с QPSK, BPSK, 8PSK и DBPSK // Известия КГТУ. 2017. № 46. С. 165–174.
- Михайлов Р. Л. Радиоэлектронная борьба в Вооруженных силах США: военно-теоретический труд. СПб: Наукоемкие технологии. 2018. 131 с.
- Зубарев А. Е., Позов А. В., Приходько А. И. Анализ методов расчета битовой вероятности ошибки при когерентном приеме сигналов с M-ичной фазовой манипуляцией // Международный научно-исследовательский журнал. Екатеринбург. 2019.
№ 1(79). Ч. 1. С. 53–59. - Куприянов А. И. Основы радиоэлектронной борьбы. М.: Факториал. 2022. 382 с.
- Михайлов Р. Л. Помехозащищенность транспортных сетей связи специального назначения. Монография. Череповец: РИО ЧВВИУРЭ. 2016. 128 с.
- Чиров Д. С., Лобов Е. М. Выбор сигнально-кодовой конструкции для командно-телеметрической линии радиосвязи с беспилотными летательными аппаратами средней и большой дальности // Телекоммуникации и транспорт. 2017. Т. 11. № 10. С. 21–28.
- Савищенко Н. В. Многомерные сигнальные конструкции: их частотная эффективность и потенциальная помехоустойчивость приема. СПб: СПбГПУ. 2005. 420 с.
- Звонарев В. В., Попов А. С. Потенциальная помехоустойчивость когерентного приема четырехпозиционного фазоманипулированного радиосигнала в присутствии когерентной гармонической помехи // Информационно-управляющие системы. 2021. № 1. С. 45–54.
- Звонарев В. В., Пименов В. Ф., Попов А. С. Методика вычисления вероятностей символьных и битовых ошибок для QPSK-сигналов при наличии гармонической помехи со сдвигом частоты // Труды Военно-космической академии им. А.Ф. Можайского. Вып. № 677. 2021. С. 50–61.
- Беккиев А. Ю., Борисов В. И. Оценка помехозащищенности каналов радиосвязи в условиях действия помех от средств радиоэлектронной борьбы // Радиотехника и электроника. 2019. Т. 64. № 9. С. 891–901.
- Бучинский Д. И., Вознюк В. В., Фомин А. В. Исследование помехоустойчивости приемника сигналов с многопозиционной фазовой манипуляцией к воздействию помех с различной структурой // Труды Военно-космической академии им. А.Ф. Можайского. 2019. Вып. № 671. С. 120–127.
- Зубарев А.Е., Позов А.В., Приходько А.И. Анализ методов расчета битовой вероятности ошибки при когерентном приеме сигналов с M-ичной фазовой манипуляцией // Международный научно-исследовательский журнал. Екатеринбург. 2019.
№ 1(79). Ч. 1, С. 53–59. - Финк Л. М. Теория передачи дискретных сообщений. М.: Советское радио. 1979. 728 с.
- Ковальский А. А., Митряев Г. А., Питрин А. В. Управление орбитальным канальным ресурсом на основе немарковских приоритетных систем массового обслуживания. Ч. 1. Модель оперативного распределения // Труды учебных заведений связи. 2021. Т. 7. № 3. С. 36–46.
- Кузовникова А. В. Космические системы ретрансляции. М.: Радиотехника. 2017. 448 с.
- Бродский М. С., Розганов М. В., Уткин Д.Р. Обоснование технических требований к земным станциям спутниковых связных комплексов на основе модели функционирования активных фазированных антенных решеток // Известия института инженерной физики. 2021. № 1(59). С. 24–28.
- Ерохин Г.А., Мандель В.И., Нестеркин Ю.А., Струков А.П. Методика расчета энергетического запаса радиолинии «космический аппарат – станция» // Ракетно-космическое приборостроение и информационные системы. 2018. Т. 5. Вып. 1.С. 65-74.
- Ложкин К. Ю. Помехоустойчивость приема OFDM-сигнала с однократной фазовой манипуляцией и корректирующим кодированием на фоне полигармонической помехи // Информация и космос. 2018. № 2. С. 37–43.
- Вознюк В.В., Куценко Е.В. Помехоустойчивость систем радиосвязи с бинарными фазоманипулированными шумоподобными сигналами при воздействии ретранслированных компенсационных помех типа инверсии, огибающей сигнала // Журнал радиоэлектроники. 2018. № 2. С. 1–16.
Дата поступления: 20.06.2022
Одобрена после рецензирования: 01.07.2022
Принята к публикации: 25.07.2022
Двоичная
фазовая манипуляция (англ. BPSK — binary
phase-shift keying)
— самая простая форма фазовой манипуляции.
Работа схемы двоичной ФМн заключается
в смещении фазы несущего колебания на
одно из двух значений, нуль или π (180°).
Двоичную фазовую манипуляцию можно
также рассматривать как частный случай
квадратурной манипуляции (QAM-2).
При
квадратурной фазовой манипуляции (англ.
QPSK — Quadrature Phase Shift Keying или 4-PSK)
используется созвездие из четырёх
точек, размещённых на равных расстояниях
на окружности. Используя 4 фазы, в QPSK на
символ приходится два бита, как показано
на рисунке. Анализ показывает, что
скорость может быть увеличена в два
раза относительно BPSK при той же полосе
сигнала, либо оставить скорость прежней,
но уменьшить полосу вдвое.
Хотя
QPSK можно считать квадратурной манипуляцией
(QAM-4), иногда её проще рассматривать в
виде двух независимых модулированных
несущих, сдвинутых на 90°. При таком
подходе чётные (нечётные) биты используются
для модуляции синфазной составляющей
I, а нечётные (чётные) — квадратурной
составляющей несущей Q. Так как BPSK
используется для обеих составляющих
несущей, то они могут быть демодулированы
независимо.
Когерентное
детектирование
При
когерентном детектировании вероятность
ошибки на бит для QPSK такая же, как и для
BPSK:
Однако,
так как в символе два бита, то значение
символьной ошибки возрастает:
При
высоком отношении сигнал/шум (это
необходимо для реальных QPSK систем)
вероятность символьной ошибки может
быть оценена приблизительно по следующей
формуле:
Некогерентное
детектирование
Как
и при BPSK, существует проблема
неопределённости начальной фазы в
приёмнике. Поэтому при некогерентном
детектировании QPSK с дифференциальным
кодированием на практике используется
чаще.
Отличие
QPSK от первых видов модуляции (АМн, ЧМн)
в том, что плотность передаваемой
информации в расчёте на частотную ширину
канала (на символ, на герц) выше единицы.
27. Система кодирования с адаптивной модуляцией
Главные
задачи адаптивной модуляции и кодирования
— это компенсация нестабильности
радиоканала и точная подстройка
параметров передачи. Для этого существуют
различные методы и средства, улучшающие
адаптацию радиоканала, как, например,
регулировка мощности, адаптивные
антенны, динамическое кодирование,
размещение каналов и т. д. Хотя все эти
методы преследуют в конечном итоге одну
цель, реализация их различна и поэтому
они могут использоваться как дополнительные
средства достижения положительного
эффекта.
В
отношении метода AMC можно сказать, что
его основная функция состоит в подстройке
характеристик модуляции и кодирования
для того, чтобы компенсировать изменения
в канале физического слоя.
Преимущества
системы АМС хорошо известны, но ее
характеристики сильно зависят от
измерений в радиоканале, получаемых в
оконечном оборудовании, а цикл измерений
может не совпадать с периодами обычных
изменений в канале во время быстрых
замираний. Кроме того, такие измерения
не лишены ошибок. Ненадежная сводка о
состоянии канала может привести к
принятию ошибочных решений при
планировании пакетов, установке мощности
передачи, а также выборе вида модуляции
и кодирования.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Phase-shift keying (PSK) is a digital modulation process which conveys data by changing (modulating) the phase of a constant frequency carrier wave. The modulation is accomplished by varying the sine and cosine inputs at a precise time. It is widely used for wireless LANs, RFID and Bluetooth communication.
Any digital modulation scheme uses a finite number of distinct signals to represent digital data. PSK uses a finite number of phases, each assigned a unique pattern of binary digits. Usually, each phase encodes an equal number of bits. Each pattern of bits forms the symbol that is represented by the particular phase. The demodulator, which is designed specifically for the symbol-set used by the modulator, determines the phase of the received signal and maps it back to the symbol it represents, thus recovering the original data. This requires the receiver to be able to compare the phase of the received signal to a reference signal – such a system is termed coherent (and referred to as CPSK).
CPSK requires a complicated demodulator, because it must extract the reference wave from the received signal and keep track of it, to compare each sample to. Alternatively, the phase shift of each symbol sent can be measured with respect to the phase of the previous symbol sent. Because the symbols are encoded in the difference in phase between successive samples, this is called differential phase-shift keying (DPSK). DPSK can be significantly simpler to implement than ordinary PSK, as it is a ‘non-coherent’ scheme, i.e. there is no need for the demodulator to keep track of a reference wave. A trade-off is that it has more demodulation errors.
Introduction[edit]
There are three major classes of digital modulation techniques used for transmission of digitally represented data:
- Amplitude-shift keying (ASK)
- Frequency-shift keying (FSK)
- Phase-shift keying (PSK)
All convey data by changing some aspect of a base signal, the carrier wave (usually a sinusoid), in response to a data signal. In the case of PSK, the phase is changed to represent the data signal. There are two fundamental ways of utilizing the phase of a signal in this way:
- By viewing the phase itself as conveying the information, in which case the demodulator must have a reference signal to compare the received signal’s phase against; or
- By viewing the change in the phase as conveying information – differential schemes, some of which do not need a reference carrier (to a certain extent).
A convenient method to represent PSK schemes is on a constellation diagram. This shows the points in the complex plane where, in this context, the real and imaginary axes are termed the in-phase and quadrature axes respectively due to their 90° separation. Such a representation on perpendicular axes lends itself to straightforward implementation. The amplitude of each point along the in-phase axis is used to modulate a cosine (or sine) wave and the amplitude along the quadrature axis to modulate a sine (or cosine) wave. By convention, in-phase modulates cosine and quadrature modulates sine.
In PSK, the constellation points chosen are usually positioned with uniform angular spacing around a circle. This gives maximum phase-separation between adjacent points and thus the best immunity to corruption. They are positioned on a circle so that they can all be transmitted with the same energy. In this way, the moduli of the complex numbers they represent will be the same and thus so will the amplitudes needed for the cosine and sine waves. Two common examples are «binary phase-shift keying» (BPSK) which uses two phases, and «quadrature phase-shift keying» (QPSK) which uses four phases, although any number of phases may be used. Since the data to be conveyed are usually binary, the PSK scheme is usually designed with the number of constellation points being a power of two.
Binary phase-shift keying (BPSK)[edit]
BPSK (also sometimes called PRK, phase reversal keying, or 2PSK) is the simplest form of phase shift keying (PSK). It uses two phases which are separated by 180° and so can also be termed 2-PSK. It does not particularly matter exactly where the constellation points are positioned, and in this figure they are shown on the real axis, at 0° and 180°. Therefore, it handles the highest noise level or distortion before the demodulator reaches an incorrect decision. That makes it the most robust of all the PSKs. It is, however, only able to modulate at 1 bit/symbol (as seen in the figure) and so is unsuitable for high data-rate applications.
In the presence of an arbitrary phase-shift introduced by the communications channel, the demodulator (see, e.g. Costas loop) is unable to tell which constellation point is which. As a result, the data is often differentially encoded prior to modulation.
BPSK is functionally equivalent to 2-QAM modulation.
Implementation[edit]
The general form for BPSK follows the equation:
This yields two phases, 0 and π.
In the specific form, binary data is often conveyed with the following signals:[citation needed]
for binary «0»
for binary «1»
where f is the frequency of the base band.
Hence, the signal space can be represented by the single basis function
where 1 is represented by 

This use of this basis function is shown at the end of the next section in a signal timing diagram. The topmost signal is a BPSK-modulated cosine wave that the BPSK modulator would produce. The bit-stream that causes this output is shown above the signal (the other parts of this figure are relevant only to QPSK). After modulation, the base band signal will be moved to the high frequency band by multiplying 
Bit error rate[edit]
The bit error rate (BER) of BPSK under additive white Gaussian noise (AWGN) can be calculated as:[1]
or
Since there is only one bit per symbol, this is also the symbol error rate.
Quadrature phase-shift keying (QPSK)[edit]
Sometimes this is known as quadriphase PSK, 4-PSK, or 4-QAM. (Although the root concepts of QPSK and 4-QAM are different, the resulting modulated radio waves are exactly the same.) QPSK uses four points on the constellation diagram, equispaced around a circle. With four phases, QPSK can encode two bits per symbol, shown in the diagram with Gray coding to minimize the bit error rate (BER) – sometimes misperceived as twice the BER of BPSK.
The mathematical analysis shows that QPSK can be used either to double the data rate compared with a BPSK system while maintaining the same bandwidth of the signal, or to maintain the data-rate of BPSK but halving the bandwidth needed. In this latter case, the BER of QPSK is exactly the same as the BER of BPSK – and believing differently is a common confusion when considering or describing QPSK. The transmitted carrier can undergo numbers of phase changes.
Given that radio communication channels are allocated by agencies such as the Federal Communications Commission giving a prescribed (maximum) bandwidth, the advantage of QPSK over BPSK becomes evident: QPSK transmits twice the data rate in a given bandwidth compared to BPSK — at the same BER. The engineering penalty that is paid is that QPSK transmitters and receivers are more complicated than the ones for BPSK. However, with modern electronics technology, the penalty in cost is very moderate.
As with BPSK, there are phase ambiguity problems at the receiving end, and differentially encoded QPSK is often used in practice.
Implementation[edit]
The implementation of QPSK is more general than that of BPSK and also indicates the implementation of higher-order PSK. Writing the symbols in the constellation diagram in terms of the sine and cosine waves used to transmit them:
This yields the four phases π/4, 3π/4, 5π/4 and 7π/4 as needed.
This results in a two-dimensional signal space with unit basis functions
The first basis function is used as the in-phase component of the signal and the second as the quadrature component of the signal.
Hence, the signal constellation consists of the signal-space 4 points
The factors of 1/2 indicate that the total power is split equally between the two carriers.
Comparing these basis functions with that for BPSK shows clearly how QPSK can be viewed as two independent BPSK signals. Note that the signal-space points for BPSK do not need to split the symbol (bit) energy over the two carriers in the scheme shown in the BPSK constellation diagram.
QPSK systems can be implemented in a number of ways. An illustration of the major components of the transmitter and receiver structure are shown below.
Probability of error[edit]
Although QPSK can be viewed as a quaternary modulation, it is easier to see it as two independently modulated quadrature carriers. With this interpretation, the even (or odd) bits are used to modulate the in-phase component of the carrier, while the odd (or even) bits are used to modulate the quadrature-phase component of the carrier. BPSK is used on both carriers and they can be independently demodulated.
As a result, the probability of bit-error for QPSK is the same as for BPSK:
However, in order to achieve the same bit-error probability as BPSK, QPSK uses twice the power (since two bits are transmitted simultaneously).
The symbol error rate is given by:
If the signal-to-noise ratio is high (as is necessary for practical QPSK systems) the probability of symbol error may be approximated:
The modulated signal is shown below for a short segment of a random binary data-stream. The two carrier waves are a cosine wave and a sine wave, as indicated by the signal-space analysis above. Here, the odd-numbered bits have been assigned to the in-phase component and the even-numbered bits to the quadrature component (taking the first bit as number 1). The total signal – the sum of the two components – is shown at the bottom. Jumps in phase can be seen as the PSK changes the phase on each component at the start of each bit-period. The topmost waveform alone matches the description given for BPSK above.
The binary data that is conveyed by this waveform is: 11000110.
- The odd bits, highlighted here, contribute to the in-phase component: 11000110
- The even bits, highlighted here, contribute to the quadrature-phase component: 11000110
Variants[edit]
Offset QPSK (OQPSK)[edit]
Offset quadrature phase-shift keying (OQPSK) is a variant of phase-shift keying modulation using four different values of the phase to transmit. It is sometimes called staggered quadrature phase-shift keying (SQPSK).
Taking four values of the phase (two bits) at a time to construct a QPSK symbol can allow the phase of the signal to jump by as much as 180° at a time. When the signal is low-pass filtered (as is typical in a transmitter), these phase-shifts result in large amplitude fluctuations, an undesirable quality in communication systems. By offsetting the timing of the odd and even bits by one bit-period, or half a symbol-period, the in-phase and quadrature components will never change at the same time. In the constellation diagram shown on the right, it can be seen that this will limit the phase-shift to no more than 90° at a time. This yields much lower amplitude fluctuations than non-offset QPSK and is sometimes preferred in practice.
The picture on the right shows the difference in the behavior of the phase between ordinary QPSK and OQPSK. It can be seen that in the first plot the phase can change by 180° at once, while in OQPSK the changes are never greater than 90°.
The modulated signal is shown below for a short segment of a random binary data-stream. Note the half symbol-period offset between the two component waves. The sudden phase-shifts occur about twice as often as for QPSK (since the signals no longer change together), but they are less severe. In other words, the magnitude of jumps is smaller in OQPSK when compared to QPSK.
SOQPSK[edit]
The license-free shaped-offset QPSK (SOQPSK) is interoperable with Feher-patented QPSK (FQPSK), in the sense that an integrate-and-dump offset QPSK detector produces the same output no matter which kind of transmitter is used.[2]
These modulations carefully shape the I and Q waveforms such that they change very smoothly, and the signal stays constant-amplitude even during signal transitions. (Rather than traveling instantly from one symbol to another, or even linearly, it travels smoothly around the constant-amplitude circle from one symbol to the next.) SOQPSK modulation can be represented as the hybrid of QPSK and MSK: SOQPSK has the same signal constellation as QPSK, however the phase of SOQPSK is always stationary.[3][4]
The standard description of SOQPSK-TG involves ternary symbols.[5] SOQPSK is one of the most spread modulation schemes in application to LEO satellite communications.[6]
π/4-QPSK[edit]
This variant of QPSK uses two identical constellations which are rotated by 45° (

One property this modulation scheme possesses is that if the modulated signal is represented in the complex domain, transitions between symbols never pass through 0. In other words, the signal does not pass through the origin. This lowers the dynamical range of fluctuations in the signal which is desirable when engineering communications signals.
On the other hand, 
The modulated signal is shown below for a short segment of a random binary data-stream. The construction is the same as above for ordinary QPSK. Successive symbols are taken from the two constellations shown in the diagram. Thus, the first symbol (1 1) is taken from the «blue» constellation and the second symbol (0 0) is taken from the «green» constellation. Note that magnitudes of the two component waves change as they switch between constellations, but the total signal’s magnitude remains constant (constant envelope). The phase-shifts are between those of the two previous timing-diagrams.
DPQPSK[edit]
Dual-polarization quadrature phase shift keying (DPQPSK) or dual-polarization QPSK — involves the polarization multiplexing of two different QPSK signals, thus improving the spectral efficiency by a factor of 2. This is a cost-effective alternative to utilizing 16-PSK, instead of QPSK to double the spectral efficiency.
Higher-order PSK[edit]
Any number of phases may be used to construct a PSK constellation but 8-PSK is usually the highest order PSK constellation deployed. With more than 8 phases, the error-rate becomes too high and there are better, though more complex, modulations available such as quadrature amplitude modulation (QAM). Although any number of phases may be used, the fact that the constellation must usually deal with binary data means that the number of symbols is usually a power of 2 to allow an integer number of bits per symbol.
Bit error rate[edit]
For the general M-PSK there is no simple expression for the symbol-error probability if 
where
and 

This may be approximated for high 

The bit-error probability for 
(Using Gray coding allows us to approximate the Lee distance of the errors as the Hamming distance of the errors in the decoded bitstream, which is easier to implement in hardware.)
The graph on the right compares the bit-error rates of BPSK, QPSK (which are the same, as noted above), 8-PSK and 16-PSK. It is seen that higher-order modulations exhibit higher error-rates; in exchange however they deliver a higher raw data-rate.
Bounds on the error rates of various digital modulation schemes can be computed with application of the union bound to the signal constellation.
Spectral efficiency[edit]
Bandwidth (or spectral) efficiency of M-PSK modulation schemes increases with increasing of modulation order M (unlike, for example, M-FSK):[7]
The same relationship holds true for M-QAM.[8]
Differential phase-shift keying (DPSK)[edit]
Differential encoding[edit]
Differential phase shift keying (DPSK) is a common form of phase modulation that conveys data by changing the phase of the carrier wave. As mentioned for BPSK and QPSK there is an ambiguity of phase if the constellation is rotated by some effect in the communications channel through which the signal passes. This problem can be overcome by using the data to change rather than set the phase.
For example, in differentially encoded BPSK a binary «1» may be transmitted by adding 180° to the current phase and a binary «0» by adding 0° to the current phase.
Another variant of DPSK is Symmetric Differential Phase Shift keying, SDPSK, where encoding would be +90° for a «1» and −90° for a «0».
In differentially encoded QPSK (DQPSK), the phase-shifts are 0°, 90°, 180°, −90° corresponding to data «00», «01», «11», «10». This kind of encoding may be demodulated in the same way as for non-differential PSK but the phase ambiguities can be ignored. Thus, each received symbol is demodulated to one of the 
The modulated signal is shown below for both DBPSK and DQPSK as described above. In the figure, it is assumed that the signal starts with zero phase, and so there is a phase shift in both signals at 
Analysis shows that differential encoding approximately doubles the error rate compared to ordinary 

One of the most popular applications of DPSK is the Bluetooth standard where 
Demodulation[edit]
For a signal that has been differentially encoded, there is an obvious alternative method of demodulation. Instead of demodulating as usual and ignoring carrier-phase ambiguity, the phase between two successive received symbols is compared and used to determine what the data must have been. When differential encoding is used in this manner, the scheme is known as differential phase-shift keying (DPSK). Note that this is subtly different from just differentially encoded PSK since, upon reception, the received symbols are not decoded one-by-one to constellation points but are instead compared directly to one another.
Call the received symbol in the 



The decision variable for the 





where superscript * denotes complex conjugation. In the absence of noise, the phase of this is 
The probability of error for DPSK is difficult to calculate in general, but, in the case of DBPSK it is:
[9]
which, when numerically evaluated, is only slightly worse than ordinary BPSK, particularly at higher 
Using DPSK avoids the need for possibly complex carrier-recovery schemes to provide an accurate phase estimate and can be an attractive alternative to ordinary PSK.
In optical communications, the data can be modulated onto the phase of a laser in a differential way. The modulation is a laser which emits a continuous wave, and a Mach–Zehnder modulator which receives electrical binary data. For the case of BPSK, the laser transmits the field unchanged for binary ‘1’, and with reverse polarity for ‘0’. The demodulator consists of a delay line interferometer which delays one bit, so two bits can be compared at one time. In further processing, a photodiode is used to transform the optical field into an electric current, so the information is changed back into its original state.
The bit-error rates of DBPSK and DQPSK are compared to their non-differential counterparts in the graph to the right. The loss for using DBPSK is small enough compared to the complexity reduction that it is often used in communications systems that would otherwise use BPSK. For DQPSK though, the loss in performance compared to ordinary QPSK is larger and the system designer must balance this against the reduction in complexity.
Example: Differentially encoded BPSK[edit]
At the 



where 
So 

The received signal is demodulated to yield 
since binary subtraction is the same as binary addition.
Therefore, 






Differential schemes for other PSK modulations may be devised along similar lines. The waveforms for DPSK are the same as for differentially encoded PSK given above since the only change between the two schemes is at the receiver.
The BER curve for this example is compared to ordinary BPSK on the right. As mentioned above, whilst the error rate is approximately doubled, the increase needed in 

Definitions[edit]
For determining error-rates mathematically, some definitions will be needed:


.
The error rates quoted here are those in additive white Gaussian noise (AWGN). These error rates are lower than those computed in fading channels, hence, are a good theoretical benchmark to compare with.
Applications[edit]
Owing to PSK’s simplicity, particularly when compared with its competitor quadrature amplitude modulation, it is widely used in existing technologies.
The wireless LAN standard, IEEE 802.11b-1999,[10][11] uses a variety of different PSKs depending on the data rate required. At the basic rate of 1 Mbit/s, it uses DBPSK (differential BPSK). To provide the extended rate of 2 Mbit/s, DQPSK is used. In reaching 5.5 Mbit/s and the full rate of 11 Mbit/s, QPSK is employed, but has to be coupled with complementary code keying. The higher-speed wireless LAN standard, IEEE 802.11g-2003,[10][12] has eight data rates: 6, 9, 12, 18, 24, 36, 48 and 54 Mbit/s. The 6 and 9 Mbit/s modes use OFDM modulation where each sub-carrier is BPSK modulated. The 12 and 18 Mbit/s modes use OFDM with QPSK. The fastest four modes use OFDM with forms of quadrature amplitude modulation.
Because of its simplicity, BPSK is appropriate for low-cost passive transmitters, and is used in RFID standards such as ISO/IEC 14443 which has been adopted for biometric passports, credit cards such as American Express’s ExpressPay, and many other applications.[13]
Bluetooth 2 uses 
Both QPSK and 8PSK are widely used in satellite broadcasting. QPSK is still widely used in the streaming of SD satellite channels and some HD channels. High definition programming is delivered almost exclusively in 8PSK due to the higher bitrates of HD video and the high cost of satellite bandwidth.[14] The DVB-S2 standard requires support for both QPSK and 8PSK. The chipsets used in new satellite set top boxes, such as Broadcom’s 7000 series support 8PSK and are backward compatible with the older standard.[15]
Historically, voice-band synchronous modems such as the Bell 201, 208, and 209 and the CCITT V.26, V.27, V.29, V.32, and V.34 used PSK.[16]
Mutual information with additive white Gaussian noise[edit]
The mutual information of PSK can be evaluated in additive Gaussian noise by numerical integration of its definition.[17] The curves of mutual information saturate to the number of bits carried by each symbol in the limit of infinite signal to noise ratio 
At intermediate values of signal to noise ratios the mutual information (MI) is well approximated by:[17]
The mutual information of PSK over the AWGN channel is generally lower than that of QAM modulation formats.
See also[edit]
- Binary offset carrier modulation
- Differential coding
- Modulation – for an overview of all modulation schemes
- Phase modulation (PM) – the analogue equivalent of PSK
- Polar modulation
- PSK31
- PSK63
Notes[edit]
- ^ Communications Systems, H. Stern & S. Mahmoud, Pearson Prentice Hall, 2004, p. 283.
- ^
Tom Nelson, Erik Perrins, and Michael Rice.
«Common detectors for Tier 1 modulations» Archived 2012-09-17 at the Wayback Machine.T. Nelson, E. Perrins, M. Rice.
«Common detectors for shaped offset QPSK (SOQPSK) and Feher-patented QPSK (FQPSK)»
Nelson, T.; Perrins, E.; Rice, M. (2005). «Common detectors for shaped offset QPSK (SOQPSK) and Feher-patented QPSK (FQPSK)». GLOBECOM ’05. IEEE Global Telecommunications Conference, 2005. pp. 5 pp. doi:10.1109/GLOCOM.2005.1578470. ISBN 0-7803-9414-3. S2CID 11020777.
ISBN 0-7803-9414-3 - ^ Hill, Terrance J. «A non-proprietary, constant envelope, variant of shaped offset QPSK (SOQPSK) for improved spectral containment and detection efficiency.» MILCOM 2000. 21st Century Military Communications Conference Proceedings. Vol. 1. IEEE, 2000.
- ^ Li, Lifang, and M. K. Simon. «Performance of coded offset quadrature phase-shift keying (OQPSK) and MIL-STD shaped OQPSK (SOQPSK) with iterative decoding.» Interplanetary Network Prog. Rep. 42 (2004).
- ^ Sahin, C. and Perrins, E., 2011, November. The capacity of SOQPSK-TG. In 2011-MILCOM 2011 Military Communications Conference (pp. 555-560). IEEE.
- ^ Saeed, N., Elzanaty, A., Almorad, H., Dahrouj, H., Al-Naffouri, T.Y. and Alouini, M.S., 2020. Cubesat communications: Recent advances and future challenges. IEEE Communications Surveys & Tutorials.
- ^ Haykin, S., 2001. Communication Systems, John Wiley&Sons. Inc. — p. 368
- ^ Link Budget Analysis: Digital Modulation, Part 3 (www.AtlantaRF.com)
- ^ G.L. Stüber, “Soft Decision Direct-Sequence DPSK Receivers,” IEEE Transactions on Vehicular Technology, vol. 37, no. 3, pp. 151–157, August 1988.
- ^ a b IEEE Std 802.11-1999: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications – the overarching IEEE 802.11 specification. Archived August 28, 2007, at the Wayback Machine
- ^ IEEE Std 802.11b-1999 (R2003) – the IEEE 802.11b specification.
- ^ IEEE Std 802.11g-2003 – the IEEE 802.11g specification.
- ^ Understanding the Requirements of ISO/IEC 14443 for Type B Proximity Contactless Identification Cards, Application Note, Rev. 2056B–RFID–11/05, 2005, ATMEL.
- ^ «How Communications Satellites Work». Planet Fox. 2014.
- ^ «Low-Cost Satellite Set-top Box SoC — BCM7325 | Broadcom». Archived from the original on 2015-09-15. Retrieved 2015-09-08.
- ^ «Local and Remote Modems» (PDF). Black Box. Black Box Network Services. Archived from the original (PDF) on December 22, 2015. Retrieved December 20, 2015.
- ^ a b Blahut, R. E. (1988). Principles and Practice of Information Theory. Boston, MA, USA: Addison Wesley Publishing Company. ISBN 0-201-10709-0.
References[edit]
The notation and theoretical results in this article are based on material presented in the following sources:
- Proakis, John G. (1995). Digital Communications. Singapore: McGraw Hill. ISBN 0-07-113814-5.
- Couch, Leon W. II (1997). Digital and Analog Communications. Upper Saddle River, NJ: Prentice-Hall. ISBN 0-13-081223-4.
- Haykin, Simon (1988). Digital Communications. Toronto, Canada: John Wiley & Sons. ISBN 0-471-62947-2.
4.7.1. Вероятность появления ошибочного бита при когерентном обнаружении сигнала BPSK
4.7.2. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в дифференциальной модуляции BPSK
4.7.3. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
4.7.4. Вероятность появления ошибочного бита при некогерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
4.7.5. Вероятность появления ошибочного бита для бинарной модуляции DPSK
4.7.6. Вероятность ошибки для различных модуляций
4.7.1. Вероятность появления ошибочного бита при когерентном обнаружении сигнала BPSK
Важной мерой производительности, используемой для сравнения цифровых схем модуляции, является вероятность ошибки, РЕ Для коррелятора или согласованного фильтра вычисление РЕ можно представить геометрически (см. рис. 4.6). Расчет РЕ включает нахождение вероятности того, что при данном векторе переданного сигнала, скажем si вектор шума n выведет сигнал из области 1. Вероятность принятия детектором неверного решения называется вероятностью символьной ошибки, рE. Несмотря на то что решения принимаются на символьном уровне, производительность системы часто удобнее задавать через вероятность битовой ошибки (Ps). Связь РВ и РЕ рассмотрена в разделе 4.9.3 для ортогональной передачи сигналов и в разделе 4.9.4 для многофазной передачи сигналов.
Для удобства изложения в данном разделе мы ограничимся когерентным обнаружением сигналов BPSK. В этом случае вероятность символьной ошибки — это то же самое, что и вероятность битовой ошибки. Предположим, что сигналы равновероятны. Допустим также, что при передаче сигнала принятый сигнал r(t) равен
, где n(t) — процесс AWGN; кроме того, мы пренебрегаем ухудшением качества вследствие введенной каналом или схемой межсимвольной интерференции. Как показывалось в разделе 4.4.1, антиподные сигналы
и
можно описать в одномерном сигнальном пространстве, где
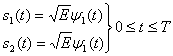
Детектор выбирает с наибольшим выходом коррелятора
; или, в нашем случае антиподных сигналов с равными энергиями, детектор, используя формулу (4.20), принимает решение следующего вида.
(4.74)
Как видно из рис. 4.9, возможны ошибки двух типов: шум так искажает переданный сигнал , что измерения в детекторе дают отрицательную величину z(T), и детектор выбирает гипотезу H2, что был послан сигнал s2(t). Возможна также обратная ситуация: шум искажает переданный сигнал
, измерения в детекторе дают положительную величину z(T), и детектор выбирает гипотезу Н1, соответствующую предположению о передаче сигнала
.
В разделе 3.2.1.1 была выведена формула (3.42), описывающая вероятность битовой ошибки РB для детектора, работающего по принципу минимальной вероятности ошибки.
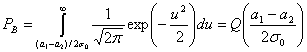
Здесь σ0 — среднеквадратическое отклонение шума вне коррелятора. Функция Q(x), называемая гауссовым интегралом ошибок, определяется следующим образом.
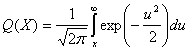
Эта функция подробно описывается в разделах 3.2 и Б.3.2.
Для передачи антиподных сигналов с равными энергиями, таких как сигналы в формате BPSK, приведенные в выражении (4.74), на выход приемника поступают следующие компоненты: , при переданном сигнале
, и
, при переданном сигнале s2(t), где Еь — энергия сигнала, приходящаяся на двоичный символ. Для процесса AWGN дисперсию шума
вне коррелятора можно заменить N0/2 (см. приложение В), так что формулу (4.76) можно переписать следующим образом.
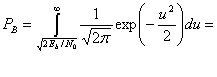
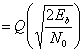
Данный результат для полосовой передачи антиподных сигналов BPSK совпадает с полученными ранее формулами для обнаружения антиподных сигналов с использованием согласованного фильтра (формула (3.70)) и обнаружения узкополосных антиподных сигналов с применением согласованного фильтра (формула (3.76)). Это является примером описанной ранее теоремы эквивалентности. Для линейных систем теорема эквивалентности утверждает, что на математическое описание процесса обнаружения не влияет сдвиг частоты. Как следствие, использование согласованных фильтров или корреляторов для обнаружения полосовых сигналов (рассмотренное в данной главе) дает те же соотношения, что были выведены ранее для сопоставимых узкополосных сигналов.
4.7.2. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в дифференциальной модуляции BPSK
Сигналы в канале иногда инвертируются; например, при использовании когерентного опорного сигнала, генерируемого контуром ФАПЧ, фаза может быть неоднозначной. Если фаза несущей была инвертирована при использовании схемы DPSK, как это скажется на сообщении? Поскольку информация сообщения кодируется подобием или отличием соседних символов, единственным следствием может быть ошибка в бите, который инвертируется, или в бите, непосредственно следующим за инвертированным. Точность определения подобия или отличия символов не меняется при инвертировании несущей. Иногда сообщения (и кодирующие их сигналы) дифференциально кодируются и когерентно обнаруживаются, чтобы просто избежать неопределенности в определении фазы.
Вероятность появления ошибочного бита при когерентном обнаружении сигналов в дифференциальной модуляции PSK (DPSK) дается выражением [5].
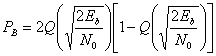
Это соотношение изображено на рис. 4.25. Отметим, что существует незначительное ухудшение достоверности обнаружения по сравнению с когерентным обнаружением сигналов в модуляции PSK. Это вызвано дифференциальным кодированием, поскольку любая отдельная ошибка обнаружения обычно приводит к принятию двух ошибочных решений. Подробно вероятность ошибки при использовании наиболее популярной схемы — когерентного обнаружения сигналов в модуляции DPSK — рассмотрена в разделе 4.7.5.
Рис. 4.25. Вероятность появления ошибочного бита для бинарных систем нескольких типов
4.7.3. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
Формулы (4.78) и (4.79) описывают вероятность появления ошибочного бита для когерентного обнаружения антиподных сигналов. Более общую трактовку для когерентного обнаружения бинарных сигналов (не ограничивающихся антиподными сигналами) дает следующее выражение для РВ [6].
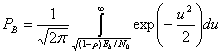
Из формулы (3.64,б) — временной коэффициент взаимной корреляций между
и
, где θ — угол между векторами сигналов
и s2 (см. рис. 4.6). Для антиподных сигналов, таких как сигналы BPSK, θ = π, поэтому ρ = -1.
Для ортогональных сигналов, таких как сигналы бинарной FSK (BFSK), θ = π/2, поскольку векторы и s2 перпендикулярны; следовательно, ρ = 0, что можно доказать с помощью формулы (3.64,а), поэтому выражение (4.81) можно переписать следующим образом.
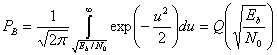
Здесь Q(x) — дополнительная функция ошибок, подробно описанная в разделах 3.2 и Б.3.2. Зависимость (4.82) для когерентного обнаружения ортогональных сигналов BFSK, показанная на рис. 4.25, аналогична зависимости, полученной для обнаружения ортогональных сигналов с помощью согласованного фильтра (формула (3.71)) и узкополосных ортогональных сигналов (униполярных импульсов) с использованием согласованного фильтра (формула (3.73)). В данной книге мы не рассматриваем амплитудную манипуляцию ООК (on-off keying), но соотношение (4.82 применимо к обнаружению с помощью согласованного фильтра сигналов ООК, так же как и к когерентному обнаружению любых ортогональных сигналов.
Справедливость соотношения (4.82) подтверждает и то, что разность энергий между ортогональными векторами сигналов и s2 с амплитудой
, как показано на рис. 3.10, б, равна квадрату расстояния между концами ортогональных векторов Ed = 2Eb. Подстановка этого результата в формулу (3.63) также дает формулу (4.82). Сравнивая формулы (4.82) и (4.79), видим, что, по сравнению со схемой BPSK, схема BFSK требует на 3 дБ большего отношения E/N0 для обеспечения аналогичной достоверности передачи. Этот результат не должен быть неожиданным, поскольку при данной мощности сигнала квадрат расстояния между ортогональными векторами вдвое (на 3 дБ) больше квадрата расстояния между антиподными векторами.
4.7.4. Вероятность появления ошибочного бита при некогерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
Рассмотрим бинарное ортогональное множество равновероятных сигналов FSK , определенное формулой (4.8).
Фаза φ неизвестна и предполагается постоянной. Детектор описывается М = 2 каналами, состоящими, как показано на рис. 4.19, из полосовых фильтров и детекторов огибающей. На вход детектора поступает принятый сигнал r(t) = si(t) + n(t), где n(i) — гауссов шум с двусторонней спектральной плотностью мощности No/2. Предположим, что и
достаточно разнесены по частоте, чтобы их перекрытием можно было пренебречь. Вычисление вероятности появления ошибочного бита для равновероятных сигналов
и
начнем, как и в случае узкополосной передачи, с уравнения (3.38).
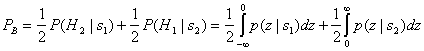
Для бинарного случая тестовая статистика z(T) определена как . Предположим, что полоса фильтра Wf равна 1/T, так что огибающая сигнала FSK (приблизительно) сохраняется на выходе фильтра. При отсутствии шума в приемнике значение z(T) равно
при передаче s1(t) и —
— при передаче s2(t). Вследствие такой симметрии оптимальный порог γ0=0. Плотность вероятности
подобна плотности вероятности
.
(4.84)
Таким образом, можем записать
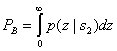
или
(4.86)
где z1 и z2 обозначают выходы z1(T) и z2(T) детекторов огибающей, показанных на рис.4.19. При передаче тона , т.е. когда r(t) = s2(t) + n(t), выход z1(T) состоит исключительно из случайной переменной гауссового шума; он не содержит сигнального компонента. Распределение Гаусса в нелинейном детекторе огибающей дает распределение Релея на выходе [6], так что
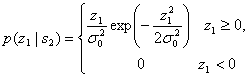
где — шум на выходе фильтра. С другой стороны, z2(T) имеет распределение Раиса, поскольку на вход нижнего детектора огибающей подается синусоида плюс шум [6]. Плотность вероятности p(z2\s2) записывается как
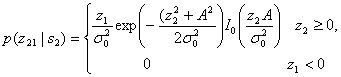
где и, как и ранее,
— шум на выходе фильтра. Функция 10(х), известная как модифицированная функция Бесселя первого рода нулевого порядка [7], определяется следующим образом.
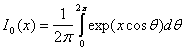
Ошибка при передаче s2(t) происходит, если выборка огибающей z1(T), полученная из верхнего канала (по которому проходит шум), больше выборки огибающей z2(T), полученной из нижнего канала (по которому проходит сигнал и шум). Таким образом, вероятность этой ошибки можно получить, проинтегрировав до бесконечности с последующим усреднением результата по всем возможным z2.
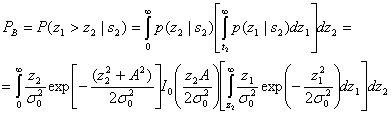
Здесь , внутренний интеграл — условная вероятность ошибки, при фиксированном значении z2, если был передан сигнал s2(1), а внешний интеграл усредняет условную вероятность по всем возможным значениям z2. Данный интеграл можно вычислить аналитически [8], и его значение равно следующему.
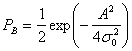
С помощью формулы (1.19) шум на выходе фильтра можно выразить как
(4.93)
где a Wf — ширина полосы фильтра. Таким образом, формула (4.92) приобретает следующий вид.
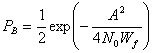
Выражение (4.94) показывает, что вероятность ошибки зависит от ширины полосы полосового фильтра и РB уменьшается при снижении Wf. Результат справедлив только при пренебрежении межсимвольной интерференцией (intersymbol interference — ISI). Минимальная разрешенная Wf (т.е. не дающая межсимвольной интерференции) получается из уравнения (3.81) при коэффициенте сглаживания г = 0. Следовательно, Wf= R бит/с =1/T, и выражение (4.94) можно переписать следующим образом.
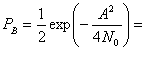
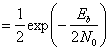
Здесь Еь= (1/2)А2Т — энергия одного бита. Если сравнить вероятность ошибки схем некогерентной и когерентной FSK (см. рис. 4.25), можно заметить, что при равных РB некогерентная FSK требует приблизительно на 1 дБ большего отношения Eb/N0, чем когерентная FSK (для РB < 10-4). При этом некогерентный приемник легче реализуется, поскольку не требуется генерировать когерентные опорные сигналы. По этой причине практически все приемники FSK используют некогерентное обнаружение. В следующем разделе будет показано, что при сравнении когерентной ортогональной схемы FSK с нёкогерентной схемой DPSK имеет место та же разница в 3 дБ, что и при сравнении когерентной ортогональной FSK и когерентной PSK. Как указывалось ранее, в данной книге не рассматривается амплитудная манипуляция ООК (on-off keying). Все же отметим, что вероятность появления ошибочного бита РB, выраженная в формуле (4.96), идентична РB для некогерентного обнаружения сигналов ООК.
4.7.5. Вероятность появления ошибочного бита для бинарной модуляции DPSK
Определим набор сигналов BPSK следующим образом.
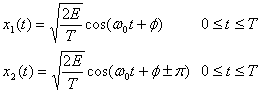
Особенностью схемы DPSK является отсутствие в сигнальном пространстве четко определенных областей решений. В данном случае решение основывается на разности фаз между принятыми сигналами. Таким образом, при передаче сигналов DPSK каждый бит в действительности передается парой двоичных сигналов.
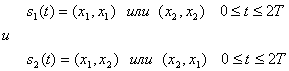
Здесь обозначает сигнал
, за которым следует сигнал
. Первые Т секунд каждого сигнала — это в действительности последние Т секунд предыдущего. Отметим, что оба сигнала s1(t) и s2(t) могут принимать любую из возможных форм и что
и
— это антиподные сигналы. Таким образом, корреляцию между
и s2(t) для любой комбинации сигналов можно записать следующим образом.
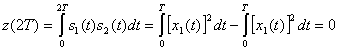
Следовательно, каждую пару сигналов DPSK можно представить как ортогональный сигнал длительностью 2Т секунд. Обнаружение может соответствовать некогерентному обнаружению огибающей с помощью четырех каналов, согласованных с каждым возможным выходом огибающей, как показано на рис. 4.26. Поскольку два детектора огибающей, представляющих каждый символ, обратны друг другу, выборки их огибающих будут совпадать. Значит, мы можем реализовать детектор как один канал для , согласовывающегося с
или
, и один канал для
, согласовывающегося с
или
, как показано на рис. 4.26. Следовательно, детектор DPSK сокращается до стандартного двухканального некогерентного детектора. В действительности фильтр может согласовываться с разностным сигналом; так что необходимым является всего один канал. На рис. 4.26 показаны фильтры, которые согласовываются с огибающими сигнала (в течение двух периодов передачи символа). Что это означает, если вспомнить, что DPSK — это схема передачи сигналов с постоянной огибающей? Это означает, что нам требуется реализовать детектор энергии, подобный квадратурному приемнику на рис. 4.18, где каждый сигнал в течение периода
представляется синфазным и квадратурным опорными сигналами.
синфазный опорный сигнал квадратурный опорный сигнал
синфазный опорный сигнал
квадратурный опорный сигнал
Поскольку пары сигналов DPSK ортогональны, вероятность ошибки при подобном некогерентном обнаружении дается выражением (4.96). Впрочем, поскольку сигналы DPSK длятся 2Т секунд, энергия сигналов , определенных в формуле (4.98), равна удвоенной энергии сигнала, определенного в течение одного периода передачи символа.
а)
б)
Рис. 4.26. Обнаружение в схеме DPSK: а) четырехканальное дифференциально-когерентное обнаружение сигналов в бинарной модуляции DPSK; б) эквивалентный двухканальный детектор сигналов в бинарной модуляции DPSK
Таким образом, РВможно записать в следующем виде.
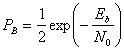
Зависимость (4.100), изображенная на рис. 4.25, представляет собой дифференциальное когерентное обнаружение сигналов в дифференциальной модуляции PSK, или просто DPSK. Выражение справедливо для оптимального детектора DPSK (рис. 4.17, в). Для детектора, показанного на рис. 4.17, б, вероятность ошибки будет несколько выше приведенной в выражении (4.100) [3]. Если сравнить вероятность ошибки, приведенную в формуле (4.100), с вероятностью ошибки когерентной схемы PSK (см. рис. 4.25), видно, что при равных РB схема DPSK требует приблизительно на 1 дБ большего отношения E^N0, чем схема BPSK (для ). Систему DPSK реализовать легче, чем систему PSK, поскольку приемник DPSK не требует фазовой синхронизации. По этой причине иногда предпочтительнее использовать менее эффективную схему DPSK, чем более сложную схему PSK.
4.7.6. Вероятность ошибки для различных модуляций
В табл. 4.1 и на рис. 4.25 приведены аналитические выражения и графики РB для наиболее распространенных схем модуляции, описанных выше. Для РB = 10-4 можно видеть, что разница между лучшей (когерентной PSK) и худшей (некогерентной ортогональной FSK) из рассмотренных схем равна приблизительно 4 дБ. В некоторых случаях 4 дБ — это небольшая цена за простоту реализации, увеличивающуюся от когерентной схемы PSK до некогерентной FSK (рис. 4.25); впрочем, в других случаях ценным является даже выигрыш в 1 дБ. Помимо сложности реализации и вероятности РB существуют и другие факторы, влияющие на выбор модуляции; например, в некоторых случаях (в каналах со случайным затуханием) желательными являются некогерентные системы, поскольку иногда когерентные опорные сигналы затруднительно определять и использовать. В военных и космических приложениях весьма желательны сигналы, которые могут противостоять значительному ухудшению качества, сохраняя возможность обнаружения.
Таблица 4.1. Вероятность ошибки для различных бинарных модуляций
|
Модуляция |
PB |
|
PSK (когерентное обнаружение) |
|
|
DPSK (дифференциальное когерентное обнаружение) |
|
|
Ортогональная FSK (когерентное обнаружение) |
|
|
Ортогональная FSK (некогерентное обнаружение) |
|
-
Среды
-
Согласованная
фильтрация и -
фильтрация
по Найквисту -
Полная
система передачи данных -
Вероятности
символьной и битовой -
ошибки
для модуляционных схем -
Синхронизация
элементов сети
Согласованная
фильтрация и фильтрация по Найквисту.
фильтрация
по Найквисту
-
Временной
критерий Найквиста:
-
Частотный
критерий Найквиста:
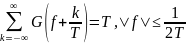
-
Для
простоты реализации, в качестве ФН
применяют т.н. фильтр «с приподнятым
косинусом»
(англ. raised cosine), имеющий полосу пропускания,
полосу задержки и спад между ними по 1
+ cos(f) (отсюда название)
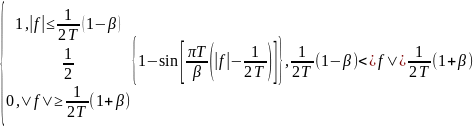
-
Коэффициент
β в диапазоне 0..1 определяет крутизну
перехода от полосы пропускания к полосе
задержки. Для
телефонных
модемов обычно β = 0.75
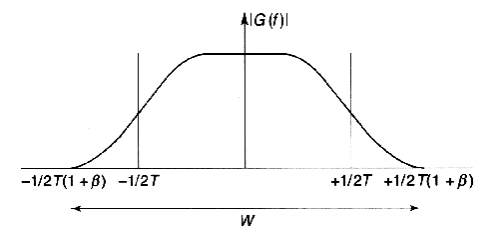
-
Занимаемая
сигналом полоса определяется β и:
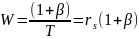
Согласованная
фильтрация
-
Для
верного обнаружения переданного
символа, на приемной стороне необходимо
максимизировать отношение сигнал/шум
для моментов измерения параметров
сигнала t
= i*T
(используем равенство Парсевал)
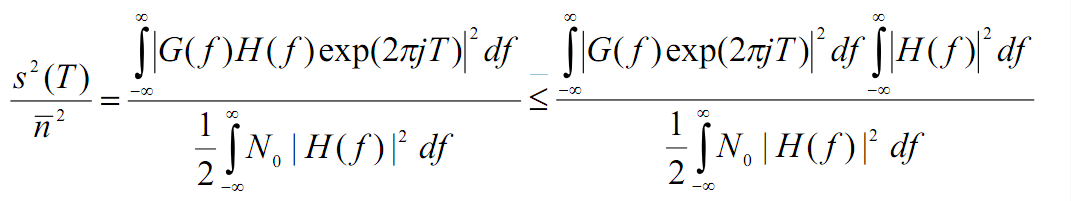
-
Здесь
используется неравенство Коши-Шварца,
которое в нашем случае становится
равенством при условии:
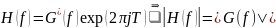
Согласованный
фильтр (СФ)
-
Фильтр
с частотной характеристикой, совпадающей
(согласованной) со спектром входного
сигнала называется СФ. Отношение
сигнал/шум на выходе СФ:
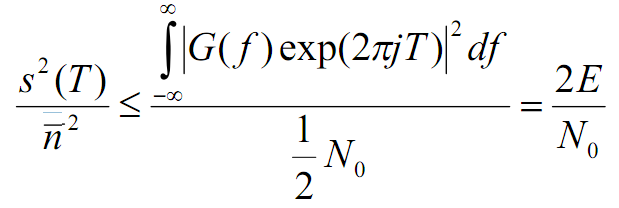
-
Импульсная
характеристика СФ обратна повремени
импульсу сигнала
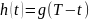
Полная
система передачи
-
Система
передачи данных, состоящая из приемника,
передатчика и линии связи, должна в
целом удовлетворять обоим критериям:
Найквиста и согласованной фильтрации -
Обозначая
частотные характеристики передатчика
и приемника T(f), R(f), и используя фильтр
«с приподнятым косинусом», получим
T(f) и R(f):
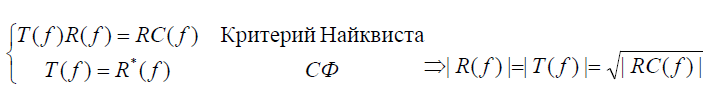
-
Полная
мощность принятого шума при использовании
такого фильтра для rb = 1/T:
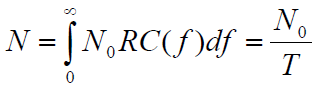
9) Расчет вероятностей символьной и битовой ошибки для модуляционных схем (bpsk, mpsk, qam). Основной подход, примеры.
Вероятность
битовой ошибки для BPSK
модуляции
Ошибка
возникает, когда np
> d/2
(см.созвездие). Тогда вероятность ошибки
определяется как:
n(t)
— гаус. сл. процесс: µ=0, P{n(t)>d/2}=Q
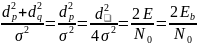
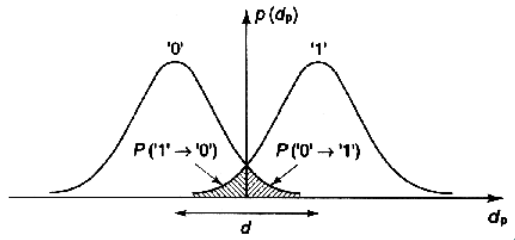
Вероятность
битовой ошибки для QPSK
модуляции
-
Энергетическая
эффективность QPSK аналогична BPSK, а
спектральная эффективность в 2 раза
выше.
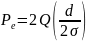
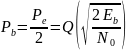
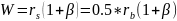
Вероятность
битовой ошибки для МPSK
модуляци
-
MPSK
модуляция определяет более 4-х фазовых
состояний (см. рис). -
Количество
состояний– степени 2, следовательно
символьная скорость в
k=log2M
меньше битовой
-
Определите
Pe
и Pb
для M=16, а также W для маркировки состояний
по Грею
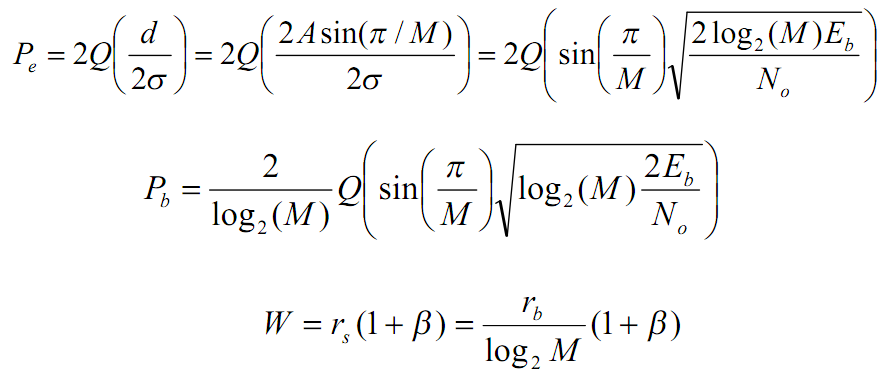
-
Энергетическая
эффективность MPSK
меньше BPSK,QPSK,
а спектральная эффективность выше.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


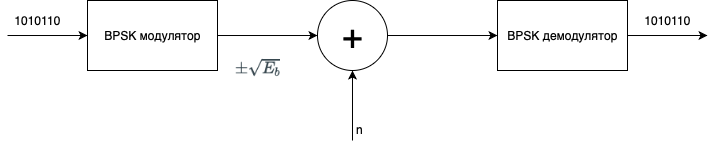
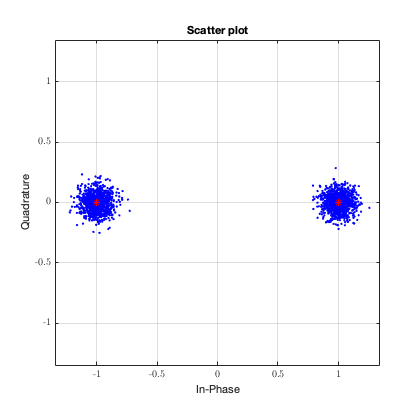
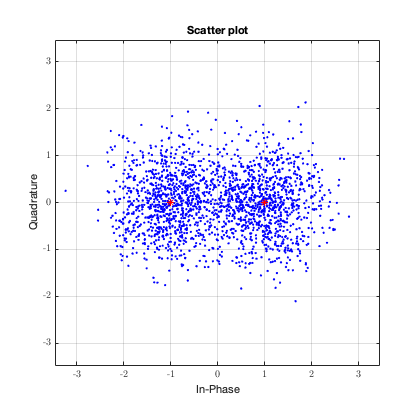
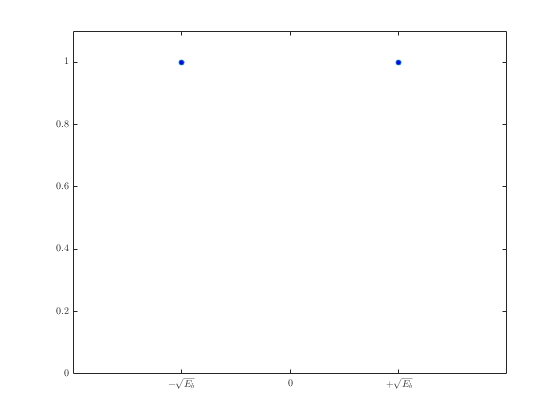
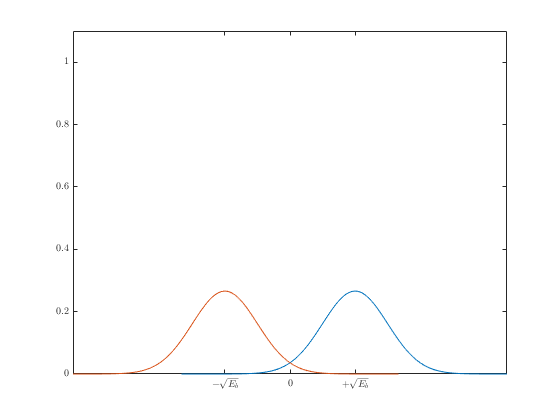
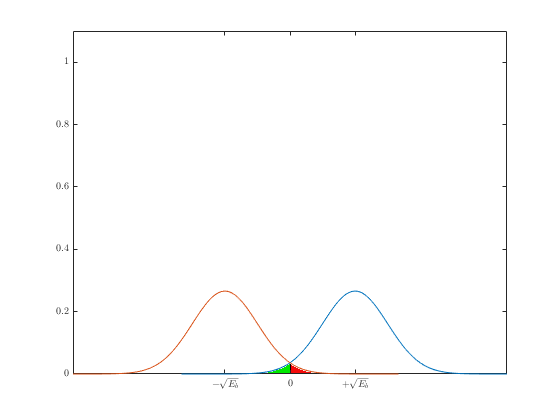
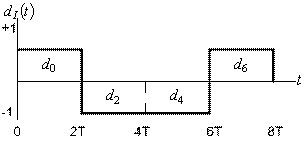
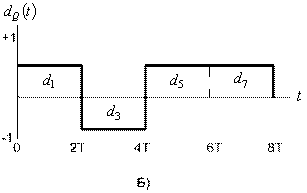
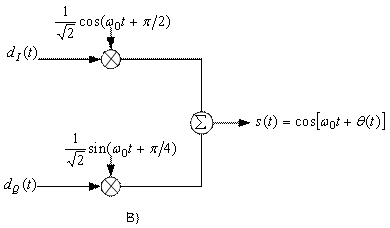
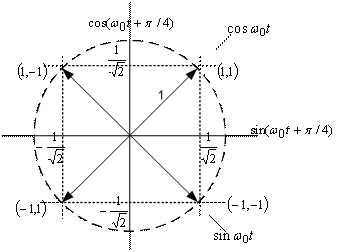
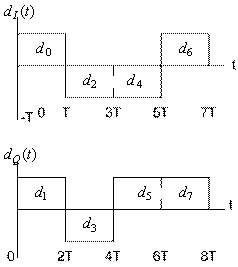
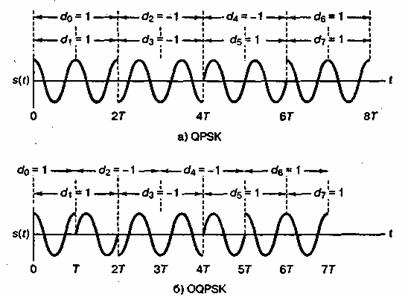
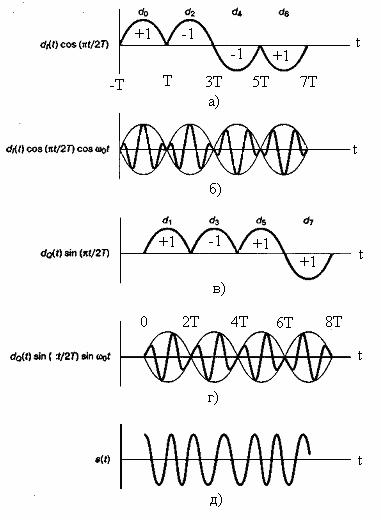
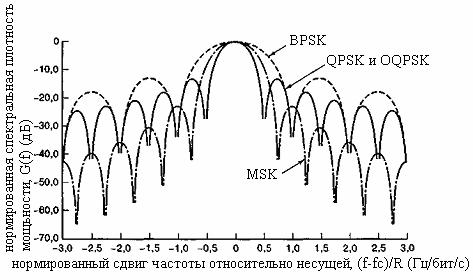
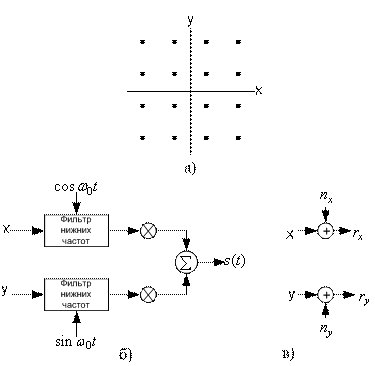
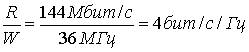
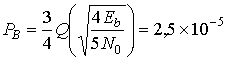
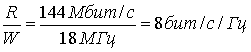









![{displaystyle {begin{aligned}P_{s}&=1-left(1-P_{b}right)^{2}\&=2Qleft({sqrt {frac {E_{s}}{N_{0}}}}right)-left[Qleft({sqrt {frac {E_{s}}{N_{0}}}}right)right]^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f83586ff4bc11f3ac6369902becbeba4313b675a)





![{displaystyle rho ={frac {log _{2}M}{2}}quad [({text{bits}}/{text{s}})/{text{Hz}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a61e49e0f629d1a571189de0c9b559a9273d777)







![{ displaystyle rho = { frac { log _ {2} M} {2}} quad [{ text {bits}} / { text {s}} cdot { текст {Гц}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0750a97fea3020cd5bc401183d6ceb8b35dc51a3)