Введение
При решении задач сейсмического анализа зданий и сооружений чаще всего применяется линейно-спектральный метод. Значительной по трудоемкости составляющей этого подхода является определение частот и форм собственных колебаний. При этом возникает вопрос: а сколько частот и форм собственных колебаний следует удерживать, чтобы результат был достоверным? В сейсмических нормах многих стран (Еврокод 8, UBC-97, сейсмические нормы Украины и др.) принято, что сумма модальных масс по каждому из направлений сейсмического воздействия должна быть не менее установленной границы. Обычно для горизонтальной составляющей сейсмического воздействия принимается 85−90%, для вертикальной — 70−90%. Под направлением сейсмического воздействия понимается направление, совпадающее с одной из осей глобальной системы координат OXYZ расчетной модели сооружения. Считается, что сейсмическое воздействие поочередно прикладывается вдоль каждой оси, причем принимается гипотеза об их статистической независимости [5, 8].
Модальной массой при сейсмическом воздействии в направлении dir (dir = OX, OY, OZ) называется величина
, где Гidir = (Mψi, Idir), M — матрица масс, ψi — собственный вектор (форма колебаний, отвечающая i-й частоте), Idir — вектор, компоненты которого равны 1, если соответствуют степени свободы сейсмического входа по направлению dir, и нулю в противном случае,
— общая масса, участвующая в движении по направлению dir.
Суммой модальных масс по направлению dir называется величина
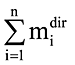
, где N — количество степеней свободы дискретной модели [3, 5, 8], n — количество удерживаемых собственных форм, n < < N.
В [3] на примере простой задачи показана зависимость некоторых внутренних усилий от суммы модальных масс (рис. 1).
Рис. 1
Здесь NΛ = NA ⁄ NA100; VΛ = V ⁄ V100; MΛ = Mov ⁄ Mov100, NA — продольная сила в стержне А, V — суммарная сдвигающая сила в основании, Mov — опрокидывающий момент. Символ 100 означает, что этот фактор получен при удержании в решении всех собственных форм дискретной модели (100% модальных масс).
Рис. 1 иллюстрирует тот факт, что для получения достоверной сейсмической реакции сооружения необходимо удерживать такое количество собственных форм, чтобы обеспечить высокий процент модальных масс (не менее 80%). При этом, разумеется, расчетная модель должна достаточно достоверно описывать поведение системы.
Таким образом, сумма модальных масс в сейсмическом анализе используется как индикатор достаточного количества удерживаемых форм колебаний.
При решении ряда задач было обнаружено, что суммы модальных масс сходятся крайне неравномерно и очень медленно [2]. При работе с расчетными моделями, содержащими большое количество степеней свободы (несколько сот тысяч), возникает серьезная проблема определения большого количества частот и форм собственных колебаний (порядка нескольких тысяч), представляющая собой сложную вычислительную задачу.
В этой работе представлен один из методов решения — блочный метод Ланцоша со сдвигами, реализованный автором в программном комплексе SCAD.
Блочный метод Ланцоша со сдвигами
В основу этой статьи положена работа Р. Граймса, Дж. Льюиса и Г. Саймона «A shifted block Lanczos algorithm for solving sparse symmetric generalized eigenproblems» [7]. Алгоритм данной реализации метода приведен в [4], а ее внедрение в программный комплекс SCAD представлено в [1]. Отметим, что блочная версия алгоритма позволяет сократить медленные операции ввода-вывода по сравнению с классической (неблочной) версией. Введение сдвигов существенно улучшает сходимость, а в случае определения большого количества собственных пар разделяет длинный частотный интервал на относительно короткие подинтервалы, ограничивая тем самым размерность пространства Крылова и заменяя экспоненциальный рост количества вычислений квазилинейным. Если исходная задача на собственные значения представляется как
, где K, M — соответственно положительно определенная разреженная матрица жесткости и полуопределенная матрица масс, {λ, ψ} — собственная пара. Вводя сдвиги σ1,σ2,…,σk, разбиваем этот частотный интервал на к+1 подинтервалов, на каждом из которых решаем задачу
где Kσ = K — σkM, λk = 1 ⁄ (ω2 — σk).
Таким образом, на каждом частотном подинтервале решается отдельная задача (4). Алгоритм выглядит так: при отсутствии какой-либо информации о спектре собственных частот полагаем σ1 = 0. Затем выполняем L шагов блочного метода Ланцоша и определяем сошедшиеся собственные пары. Далее анализируется сумма модальных масс для сошедшихся собственных пар. Если хотя бы по одному из направлений сейсмического входа сумма модальных масс меньше указанной, осуществляется переход к новому частотному интервалу. Кроме сошедшихся собственных пар имеются приближения собственных частот, которые еще не сошлись. Именно они используются для прогнозирования нового значения параметра сдвига σ2. Приняв сдвиг на основе такого прогноза, продолжаем вычисления на новом частотном интервале до тех пор, пока не определим все собственные числа, лежащие слева от сдвига и справа от последнего собственного числа, соответствующего сошедшейся собственной паре с предыдущего частотного интервала. Затем снова определяем суммы модальных масс. И так до тех пор, пока не будет достигнута достаточная сумма модальных масс.
Пример расчета
На рис. 2 приведена расчетная модель здания, включающая 8937 узлов, 9073 конечных элементов и 52 572 уравнения.
Рис. 2. Расчетная модель здания
По количеству уравнений эта задача на сегодняшний день относится к классу средних, однако по сложности решения обобщенной проблемы собственных значений она очень трудна, так как вследствие значительной жесткости несущих конструкций в нижней части спектра расположены локальные формы колебаний (рис. 3, 4), и только форма колебаний, соответствующая 522-й частоте (рис. 5), существенно влияет на сейсмическую реакцию сооружения (m522ox = 29%, тогда как
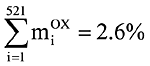
Рис. 3. Первая форма колебаний, частота 4,183 Гц
Рис. 4. Четвертая форма колебаний, частота 4,365 Гц
Наибольший вклад дает 523-я форма колебаний, представленная на рис. 5.
Рис. 5. 523-я форма колебаний, частота 5,756 Гц
Для обеспечения требуемых сумм модальных масс пришлось определить 2398 собственных пар.
Спектр собственных частот для этой задачи очень густой — в интервале [4.183, 5.756] Гц лежит 523 собственных частоты.
Зависимость сумм модальных масс от количества удерживаемых собственных форм приведена на рис. 6.
Рис. 6. Зависимость сумм модальных масс (Mx, My, Mz) от количества удерживаемых собственных форм
Выводы
При расчетах зданий и сооружений на сейсмику периодически встречаются задачи, в которых в нижней части спектра лежит большое количество локальных форм колебаний, причем спектр собственных частот является очень густым. Такие задачи создают серьезные проблемы, поскольку вычислительные алгоритмы, реализованные в современных компьютерных системах МКЭ-анализа, как правило, в таких случаях оказываются малоэффективными. Разработанный в программном комплексе SCAD алгоритм блочного метода Ланцоша со сдвигами, реализующий сейсмический режим, позволяет значительно продвинуться в решении этой проблемы.
Литература
- Карпиловский В.С., Криксунов Э.З., Фиалко С.Ю. Блочный метод Ланцоша со спектральными трансформациями для решения больших МКЭ задач собственных колебаний. — Вісник Одеського національного морського університету. — 2003, № 10, с. 93−99.
- Перельмутер А.В., Карпиловский В.С., Фиалко С.Ю., Егупов К.В. Опыт реализации проекта МСН СНГ «Строительство в сейсмических районах» в программной системе SCAD. — Вісник Одеської державної академії будівництва та архітектури. — 2003, випуск 9, с. 147−159.
- Фиалко С.Ю. Некоторые особенности анализа частот и форм собственных колебаний при расчете сооружений на сейсмические воздействия. — Вісник Одеської державної академії будівництва та архітектури. — 2002, випуск 8, с. 193−201.
- Фиалко С.Ю. О решении обобщенной проблемы собственных значений. — В кн. Перельмутер А.В., Сливкер В.И. Расчетные модели сооружений и возможность их анализа. — Издание второе. К.: Сталь, 2002, с. 570−597.
- Clough R., Penzien J. Dynamics of structures. — New York: McGraw-Hill, Inc., 1975. — 527 p.
- Fialko S.Yu., Kriksunov E.Z. and Karpilovskyy V.S. A block Lanczos method with spectral transformations for natural vibrations and seismic analysis of large structures in SCAD software. Proceedings of the CMM-2003 — Computer Methods in Mechanics, June 3−6, 2003. Gliwice, Poland, р. 129−130.
- Grimes R.G., Lewis J.G., Simon H.D. A shifted block Lanczos algorithm for solving sparse symmetric generalized eigenproblems. SIAM J. Matrix Anal. Appl. V. 15, 1: pp. 1−45, 1994.
- Wilson E.L. Three dimensional dynamic analysis of structures. California, Computers and Structures, Inc., Berkeley, USA, 1996. — 261 p.
Сергей Фиалко
д.т.н., с.н.с., проф.
Киевский национальный университет
строительства и архитектуры
Алгоритм Ланцоша — это прямой алгоритм, поиск Корнелиусом Ланцошем, который является адаптацией методов мощности для нахождения m { displaystyle m}



В 1970 году Ойалво и Ньюман показали, как сделать метод численно устойчивым, и применили его к решению очень больших инженерных задач. конструкции, подверженные динамическому нагружению. Это было достигнуто с использованием метода очистки векторов Ланцоша (т.е. путем многократной реортогонализации каждого вновь сгенерированного объекта с помощью всех ранее сгенерированных) с любой степенью точности, которая, если не выполнялась, давала серию векторов, которые были сильно загрязнены теми, которые связаны с самыми низкими собственными частотами.
В своей первоначальной работе эти авторы также предложили, как выбрать начальный вектор (т. Е. Использовать генератор случайных чисел для выбора каждого элемента начального события), и предложили эмпирический метод определения m { displaystyle m }
Содержание
- 1 Алгоритм
- 1.1 Применение к задаче собственных значений
- 1.2 Применение к тридиагонализации
- 2 Вывод алгоритм
- 2.1 Более предусмотрительный степенной метод
- 2.2 Одновременная аппроксимация крайних собственных значений
- 3 Сходимость и другая динамика
- 3.1 Теория сходимости Каниэля — Пейджа
- 4 Числовая устойчивость
- 5 Вариации
- 5.1 Пустое пространство над конечным полем
- 6 Приложения
- 7 Реализации
- 8 Примечания
- 9 Ссылки
- 10 Дополнительная литература
Алгоритм
- Вход a Эрмитов матрица A { displaystyle A}
размера n × n { displaystyle n times n}
и, необязательно, количество итераций m { displaystyle m}
(по умолчанию пусть m = n { displaystyle m = n}
).
- Вывод an n × m { displaystyle n times m}
матрица V { displaystyle V}
с ортонормированными столбцами и трехдиагональной действительной симметричной матрицей T = V ∗ AV { displaystyle T = V ^ {*} AV}
размером m × m { displaystyle м раз м}
. Если m = n { displaystyle m = n}
, то V { displaystyle V}
является унитарным и A = VTV ∗ { displaystyle A = VTV ^ {*}}
.
- Предупреждение Итерация Ланцоша подвержена числовой нестабильности. При выполнении неточной арифметики необходимо выполнить дополнительные меры (как в следующих разделах) для достоверности результатов.
- Пусть v 1 ∈ C n { displaystyle v_ {1} in mathbb {C} ^ {n}}
— произвольный вектор с евклидовой нормой. 1 { displaystyle 1}
.
- Сокращенный шаг начальной итерации:
- Пусть w 1 ′ = A v 1 { displaystyle w_ {1} ‘= Av_ {1} }
.
- Пусть α 1 = вес 1 ′ ∗ v 1 { displaystyle alpha _ {1} = w_ {1} ‘^ {*} v_ {1}}
.
- w 1 знак равно w 1 ′ — α 1 v 1 { displaystyle w_ {1} = w_ {1} ‘- alpha _ {1} v_ {1}}
.
- Пусть w 1 ′ = A v 1 { displaystyle w_ {1} ‘= Av_ {1} }
- Для j = 2,…, m { displaystyle j = 2, dots, m}
do:
- Пусть β j = ‖ wj — 1 ‖ { displaystyle beta _ {j} = | w_ {j-1} |}
(также Евклидова норма ).
- Если β j ≠ 0 { displaystyle beta _ {j} neq 0}
, тогда пусть vj = wj — 1 / β j { displaystyle v_ {j} = w_ {j-1} / beta _ {j}}
,
- иначе выберет как vj { displaystyle v_ {j}}
произвольный вектор с евклидовой нормой 1 { displaystyle 1}
, который ортогонален всем v 1,…, vj — 1 { displaystyle v_ {1}, dots, v_ {j-1}}
.
- иначе выберет как vj { displaystyle v_ {j}}
- Пусть wj ′ = A vj { disp laystyle w_ {j} ‘= Av_ {j}}
.
- Пусть α j = wj ′ ∗ vj { displaystyle alpha _ {j} = w_ {j} ‘^ {*} v_ {j}}
.
- Пусть wj = wj ′ — α jvj — β jvj — 1 { displaystyle w_ {j} = w_ {j} ‘- alpha _ {j} v_ {j} — beta _ {j} v_ {j-1}}
.
- Пусть β j = ‖ wj — 1 ‖ { displaystyle beta _ {j} = | w_ {j-1} |}
- Пусть V { displaystyle V}
будет матрицей со столбцами v 1,…, vm { displaystyle v_ {1}, dots, v_ {m}}
. Пусть T = (α 1 β 2 0 β 2 α 2 β 3 β 3 α 3 ⋱ ⋱ ⋱ β м — 1 β м — 1 α м — 1 β м 0 β м α м) { displaystyle T = { begin {pmatrix} alpha _ {1} beta _ {2} 0 \ beta _ {2} alpha _ {2} beta _ {3} \ beta _ {3} alpha _ {3 } ddots \ ddots ddots beta _ {m-1} \ beta _ {m-1} alpha _ {m-1} beta _ {m} \ 0 beta _ {m} alpha _ {m} \ end {pmatrix}}}
.
- Пусть v 1 ∈ C n { displaystyle v_ {1} in mathbb {C} ^ {n}}
- ПримечаниеA vj = wj ′ = β j + 1 vj + 1 + α jvj + β jvj — 1 { displaystyle Av_ {j} = w_ {j} ‘= beta _ {j + 1} v_ {j + 1} + alpha _ {j} v_ {j} + beta _ {j} v_ {j-1}}
для 1 < j < m {displaystyle 1
.
В принципе существует четыре способа написать итерационные полномочия. Пейдж и другие работы показывают, что приведенный выше порядок наиболее устойчиво устойчивым. На практике начальный вектор v 1 { displaystyle v_ {1}}

Не считая умножения матрицы на вектор, каждая итерация действия O (n) { displaystyle O (n)}





Векторы v j { displaystyle v_ {j}}








Применение к задаче собственных значений
Алгоритм Ланцоша чаще всего используется в контексте поиска собственные значения и собственных векторов матрицы, но в то время как обычная диагонализация матрицы сделала бы трех проверенные конструкции и собственные значения очевидными прике, это не верно для выполняемой алгоритмом Ланцоша; Для вычисления даже одного собственного значения или вектора необходимы нетривиальные дополнительные шаги. Тем не менее, применение алгоритма Ланцоша часто является значительным шагом вперед в вычислении собственного разложения. Если λ { displaystyle lambda}









- Для трехдиагональных матриц существует ряд специализированных алгоритмов, часто с большей вычислительной сложностью, чем алгоритмы общего назначения. Например, если T { displaystyle T}
представляет собой трехдиагональную симметричную матрицу m × m { displaystyle m times m}
, тогда:
- Известно, некоторые общие алгоритмы разложения на собственные числа, в частности, QR-алгоритм, сход быстрее для трехдиагональных матриц, чем для обычных матриц. Асимптотическая сложность трехдиагонального QR составляет O (m 2) { displaystyle O (m ^ {2})}
, как и для алгоритма «разделяй и властвуй» (хотя постоянный множитель может быть другим.) ; так как собственные конструкции вместе имеют m 2 { displaystyle m ^ {2}}
элементов, это асимптотически оптимально.
- Даже алгоритмы, скорость сходимости которых не зависит от унитарных преобразователей, таких как метод мощности и обратная итерация, может иметь преимущества на низком уровне производительности от применения к трехдиагональной матрице T { displaystyle T}
чем скорее исходная матрица A { displaystyle A}
. Время T { displaystyle T}
очень разрежен, все ненулевые элементы находятся в хорошо предсказуемых позициях, обеспечивает компактное хранение с превосходной производительностью по сравнению с кэшированием. Аналогично, T { displaystyle T}
— это вещественная матрица со всеми собственными объектами и собственными значениями действительными, тогда как A { displaystyle A}
как правило, может иметь сложные элементы и существующие, поэтому достаточно вещественной арифметики для собственных векторов и собственных значений T { displaystyle T}
.
- Если n { displaystyle n}
равно очень большой, то уменьшение m { displaystyle m}
так, чтобы T { displaystyle T}
имел управляемый размер, все равно позволит найти более экстремальные собственные значения и конструктивные элементы A { displaystyle A}
; в области m ≪ n { displaystyle m ll n}
алгоритм Ланцоша можно рассматривать как схему сжатие с потерянными для эрмитовых матриц, которая подчеркивает сохранение крайних собственных значений.
Сочетание хорошей производительности для разреженных матриц и способности вычислять несколько (без всех вычислений) значений собственных показателей использования алгоритма Ланцоша.
Применение к трехдиагонализации
Хотя проблема собственных значений часто является мотивацией для применения алгоритма Ланцоша, операция, которая в первую очередь выполняет алгоритм, представляет собой трехдиагонализацию матрицы, для которой численно стабильны преобразования Хаусхолдера Популярностью с 1950-х годов. В 60-е годы алгоритм Ланцоша не принимался во внимание. Интерес к нему был возрожден теорией конвергенции Каниэля — Пейджа и разработала методы предотвращения числовой нестабильности, но алгоритм Ланцоша является альтернативным алгоритмом, который можно пробовать только в том случае, если Хаусхолдер не удовлетворителен.
два алгоритма различаются: использует
- Ланцош то, что A { displaystyle A}
является разреженным матрицей, тогда как Хаусхолдер этого не делает, и генерирует заполнение.
- Ланцоша работает с исходной матрицей A { displaystyle A}
(и не имеет проблем с тем, что она известна только неявно), тогда как необработанный Хаусхолдер хочет изменить матрицу во время вычислений (хотя это может быть
- Каждая итера алгоритма Ланцоша создает другой столбец матрицы окончательного преобразования V { displaystyle V}
, тогда итерация Хаусхолдера еще один множитель в унитарной факторизации Q 1 Q 2… Q n { displaystyle Q_ {1} Q_ {2} dots Q_ {n}}
из V { displaystyle V}
. Однако каждый фактор определяется одним вектором, поэтому требования к памяти одинаковы для обоих алгоритмов, и V = Q 1 Q 2… Q n { displaystyle V = Q_ {1} Q_ {2} dots Q_ {n}}
можно вычислить в O (n 3) { displaystyle O (n ^ {3})}
time.
- Домохозяин — это численно стабильный, тогда как исходный Ланцош — нет.
- Ланцош очень параллелен, только с O (n) { displaystyle O (n)}
точками синхронизации (вычисления α j { displaystyle alpha _ {j}}
и β j { displaystyle beta _ {j}}
). Хаусхолдер менее параллелен, поскольку имеет последовательность O (n 2) { displaystyle O (n ^ {2})}
вычисленных скалярных величин, каждая из которых зависит от предыдущей величины в последовательности.
Вывод алгоритма
Есть несколько аргументов, которые приводят к алгоритму Ланцоша.
Более предусмотрительный метод мощности
Метод мощности для нахождения собственного значения наибольшей величины и соответствующей матрицы матрицы A { displaystyle A}
-
- Выберите случайный вектор u 1 ≠ 0 { displaystyle u_ {1} neq 0}
.
- для j ⩾ 1 { displaystyle j geqslant 1}
(пока направление uj { displaystyle u_ {j}}
не сойдется) do:
- Пусть uj + 1 ′ = A uj. { displaystyle u_ {j + 1} ‘= Au_ {j}.}
- Пусть u j + 1 = u j + 1 ′ / ‖ u j + 1 ′ ‖. { displaystyle u_ {j + 1} = u_ {j + 1} ‘/ | u_ {j + 1} ‘ |.}
- Пусть uj + 1 ′ = A uj. { displaystyle u_ {j + 1} ‘= Au_ {j}.}
- Выберите случайный вектор u 1 ≠ 0 { displaystyle u_ {1} neq 0}
Этот метод может быть подвергнут критике за его расточительность: он тратит много работы (произведение матрица-вектор на шаге 2.1), извлекая информация из матрицы A { displaystyle A}

Одна часть информации, которая тривиально доступна из векторов u j { displaystyle u_ {j}}
- подмножество {vj} j = 1 m { displaystyle {v_ {j} } _ {j = 1} ^ { m}}
основы C n { displaystyle mathbb {C} ^ {n}}
такой, что A x ∈ span (v 1,…, vj + 1) { displaystyle Ax in operatorname {span} (v_ {1}, dotsc, v_ {j + 1})}
для каждого x ∈ span (v 1,…, vj) { displaystyle x in operatorname {span} (v_ {1}, dotsc, v_ {j})}
и все 1 ⩽ j < m ; {displaystyle 1leqslant j
это тривиально удовлетворяется vj = uj { displaystyle v_ {j} = u_ {j}}






-
- Выберите случайный вектор u 1 { displaystyle u_ {1}}
евклидовой нормы 1 { displaystyle 1}
. Пусть v 1 = u 1 { displaystyle v_ {1} = u_ {1}}
.
- для j = 1,…, m — 1 { displaystyle j = 1, dotsc, m- 1}
do:
- Пусть uj + 1 ′ = A uj { displaystyle u_ {j + 1} ‘= Au_ {j}}
.
- Для всех к = 1,…, j { displaystyle k = 1, dotsc, j}
пусть gk, j = vk ∗ uj + 1 ′ { displaystyle g_ {k, j} = v_ {k} ^ {*} u_ {j + 1} ‘}
. (Это координаты A uj = uj + 1 ′ { displaystyle Au_ {j} = u_ {j + 1} ‘}
относительно базисных векторов v 1,…, Vj { displaystyle v_ {1}, dotsc, v_ {j}}
.)
- Пусть wj + 1 = uj + 1 ′ — ∑ k = 1 jgk, jvk { displaystyle w_ {j + 1} = u_ {j + 1} ‘- sum _ {k = 1} ^ {j} g_ {k, j} v_ {k}}
. (Отменить компонент uj + 1 ′ { displaystyle u_ {j + 1} ‘}
, который находится в span (v 1,…, vj) { displaystyle operatorname {span} (v_ {1}, dotsc, v_ {j}) }
.)
- Если wj + 1 ≠ 0 { displaystyle w_ {j + 1} neq 0}
, тогда пусть uj + 1 = uj + 1 ′ / ‖ uj + 1 ′ ‖ { displaystyle u_ {j + 1} = u_ {j + 1} ‘/ | u_ {j + 1}’ |}
и vj + 1 = wj + 1 / ‖ Wj + 1 ‖ { displaystyle v_ {j + 1} = w_ {j + 1} / | w_ {j + 1} |}
,
- в случае опасности uj + 1 = vj + 1 { displaystyle u_ {j + 1} = v_ {j + 1}}
произвольный вектор евклидовой нормы 1 { displaystyle 1}
который ортогонал ен всем из v 1,…, vj { displaystyle v_ {1}, dotsc, v_ {j}}
.
- в случае опасности uj + 1 = vj + 1 { displaystyle u_ {j + 1} = v_ {j + 1}}
- Пусть uj + 1 ′ = A uj { displaystyle u_ {j + 1} ‘= Au_ {j}}
- Выберите случайный вектор u 1 { displaystyle u_ {1}}
соотношение между вектором степенных итераций uj { displaystyle u_ {j}}

- A uj знак равно ‖ uj + 1 ′ ‖ uj + 1 = uj + 1 ′ = wj + 1 + ∑ К знак равно 1 jgk, jvk = ‖ wj + 1 ‖ vj + 1 + ∑ k = 1 jgk, jvk { displaystyle Au_ {j} = | u_ {j + 1} ‘ | u_ {j + 1} = u_ {j + 1} ‘= w_ {j + 1} + sum _ {k = 1} ^ {j} g_ {k, j} v_ {k} = | w_ {j + 1} | v_ {j + 1} + sum _ {k = 1} ^ {j} g_ {k, j} v_ {k}}
.
Здесь можно заметить, что нам на самом деле не нужна конструкция uj { displaystyle u_ {j}}





-
- Выбрать случайный вектор v 1 { displaystyle v_ {1}}
евклидовой нормы 1 { displaystyle 1}
.
- Для j = 1,…, m — 1 { displaystyle j = 1, dotsc, m-1}
do:
- Пусть wj + 1 ′ = A vj { displaystyle w_ {j + 1} ‘= Av_ {j}}
.
- Для всех k = 1,…, j { displaystyle k = 1, dotsc, j}
пусть hk, j = vk ∗ wj + 1 ′ { displaystyle h_ {k, j} = v_ {k} ^ {*} w_ {j + 1} ‘}
.
- Пусть wj + 1 = wj + 1 ′ — ∑ К = 1 jhk, jvk { displaystyle w_ {j + 1} = w_ {j + 1} ‘- sum _ {k = 1} ^ {j} h_ {k, j} v_ {k}}
.
- Пусть hj + 1, j = ‖ wj + 1 ‖ { displaystyle h_ {j + 1, j} = | w_ {j + 1} |}
.
- Если hj + 1, j ≠ 0 { displaystyle h_ {j + 1, j} neq 0}
, тогда пусть vj + 1 = wj + 1 / hj + 1, j { displaystyle v_ {j + 1} = w_ {j + 1} / h_ {j + 1, j}}
,
- в противном случае получить как vj + 1 { displaystyle v_ {j + 1}}
произвольный вектор евклидовой нормы 1 { displaystyle 1}
, который ортогонален всем из v 1,…, vj { displaystyle v_ {1}, dotsc, v_ {j}}
.
- в противном случае получить как vj + 1 { displaystyle v_ {j + 1}}
- Пусть wj + 1 ′ = A vj { displaystyle w_ {j + 1} ‘= Av_ {j}}
- Выбрать случайный вектор v 1 { displaystyle v_ {1}}
Априори коэффициенты hk, j { displaystyle h_ {k, j}}
- A vj знак равно ∑ К знак равно 1 j + 1 hk, jvk { displaystyle Av_ {j} = sum _ {k = 1} ^ {j + 1} h_ {k, j} v_ {k}}
для всех j < m {displaystyle j
;
определение hj + 1, j = ‖ wj + 1 ‖ { displaystyle h_ {j + 1, j} = | w_ {j + 1} |}

- vj + 1 ∗ wj + 1 ′ = vj + 1 ∗ wj + 1 = ‖ wj + 1 ‖ vj + 1 ∗ vj + 1 = ‖ Wj + 1 ‖. { Displaystyle v_ {j + 1} ^ {*} w_ {j + 1} ‘= v_ {j + 1} ^ {*} w_ {j + 1} = | w_ {j + 1} | v_ {j + 1} ^ {*} v_ {j + 1} = | w_ {j + 1} |.}
Технических степенных итераций uj { displaystyle u_ {j}}





Эта последняя процедура является итерацией Арнольди. Алгоритм Ланцоша возникает как упрощение, которое можно получить за счет исключения этапов вычисления, которые оказываются тривиальными, когда A { displaystyle A}

Элементарно, если A { displaystyle A}
- hk, j = vk ∗ wj + 1 ′ = vk ∗ A vj = vk ∗ A ∗ vj = (A vk) ∗ vj. { displaystyle h_ {k, j} = v_ {k} ^ {*} w_ {j + 1} ‘= v_ {k} ^ {*} Av_ {j} = v_ {k} ^ {*} A ^ { *} v_ {j} = (Av_ {k}) ^ {*} v_ {j}.}
Для k < j − 1 {displaystyle k



- hj — 1, j = (A vj — 1) ∗ vj = vj ∗ A vj — 1 ¯ = hj, j — 1 ¯ = hj, j — 1 { displaystyle h_ {j -1, j} = (Av_ {j-1}) ^ {*} v_ {j} = { overline {v_ {j} ^ {*} Av_ {j-1}}} = { overline {h_ { j, j-1}}} = h_ {j, j-1}}
, поскольку последний является действительным, поскольку является нормой вектора. Для k = j { displaystyle k = j}
- hj, j = (A vj) ∗ vj = vj ∗ A vj ¯ = hj, j ¯, { displaystyle h_ {j, j} = (Av_ {j}) ^ {*} v_ {j} = { overline {v_ {j} ^ {*} Av_ {j}}} = { overline {h_ {j, j }}},}
означает, что это тоже реально.
Более абстрактно, если V { displaystyle V}




матрица H { displaystyle H}

- H ∗ = (V ∗ AV) * = V * A * V = V * AV = H { Displaystyle H ^ {*} = left (V ^ {*} AV right) ^ {*} = V ^ {*} A ^ {*} V = V ^ {*} AV = H}
матрица H { displaystyle H}



Одновременное приближение экстремальных значений собственные значения
Один из способов охарактеризовать собственные векторы эрмитова матрица A { displaystyle A}
- r (x) = x ∗ A xx ∗ x, x ∈ C n. { displaystyle r (x) = { frac {x ^ {*} Ax} {x ^ {*} x}}, qquad x in mathbb {C} ^ {n}.}
В частности, наибольшее собственное значение λ max { displaystyle lambda _ { max}}



в подпространстве низкой размерности L { displaystyle { mathcal {L}}}








- r (x 1) ⩽ r (x 2) ⩽ ⋯ ⩽ λ max r (y 1) ⩾ r (y 2) ⩾ ⋯ ⩾ λ мин { Displaystyle { begin {align} r (x_ {1}) leqslant r (x_ {2}) leqslant cdots leqslant lambda _ { max} \ r (y_ {1 }) geqslant r (y_ {2}) geqslant cdots geqslant lambda _ { min} end {align}}}
Тогда возникает вопрос, как выбрать подпространства, чтобы эти последовательности сходились в оптимальная скорость.
Из xj { displaystyle x_ {j}}





- ∇ r (x) = 2 x ∗ x (A x — r (x) x) { displaystyle nabla r (x) = { frac {2} {x ^ {*} x}} (Ax-r (x) x)}
,
поэтому интересующие направления достаточно легко вычислить в матричной арифметике, но если кто-то хочет улучшить оба, xj { displaystyle x_ {j}}














Другими словами, мы можем начать с некоторого произвольного начального вектора x 1 = y 1, { displaystyle x_ {1} = y_ {1},}
- L j = span (x 1, A x 1,…, A j — 1 x 1) { displaystyle { mathcal {L}} _ {j} = operatorname {span} (x_ {1}, Ax_ {1}, ldots, A ^ {j-1} x_ {1})}
и затем искать xj, yj ∈ L j { displaystyle x_ {j}, y_ {j} in { mathcal {L}} _ {j}}
- r (xj) = max z ∈ L jr (z) и r (yj) = min z ∈ L jr (z). { displaystyle r (x_ {j}) = max _ {z in { mathcal {L}} _ {j}} r (z) qquad { text {and}} qquad r (y_ {j }) = min _ {z in { mathcal {L}} _ {j}} r (z).}
Поскольку j { displaystyle j}







Сходимость и другая динамика
При анализе динамики алгоритма удобно брать собственные значения и собственные векторы A { displaystyle A}




Также удобно зафиксировать обозначение для коэффициентов исходного вектора Ланцоша v 1 { displaystyle v_ {1 }}











The fact that the Lanczos algorithm is coordinate-agnostic – operations only look at inner products of vectors, never at individual elements of vectors – makes it easy to construct examples with known eigenstructure to run the algorithm on: make A {displaystyle A}


Теория сходимости Каниэля – Пейдж
После m { displaystyle m}













Границы для θ 1 { displaystyle theta _ {1}}












Размер m { displaystyle m}
- span {v 1, A v 1, A 2 v 1,…, A m — 1 v 1}, { displayst yle operatorname {span} left {v_ {1}, Av_ {1}, A ^ {2} v_ {1}, ldots, A ^ {m-1} v_ {1} right },}
, поэтому любой его элемент может быть выражен как p (A) v 1 { displaystyle p (A) v_ {1}}





- r (p (A) v 1) = (p (A) v 1) ∗ A p (A) v 1 (p (A) v 1) ∗ p (A) v 1 = v 1 ∗ p (A) ∗ A p (A) v 1 v 1 ∗ p (A) ∗ p (A) v 1 = v 1 ∗ p ∗ (A ∗) A p (A) v 1 v 1 ∗ p * (A *) p (A) v 1 знак равно v 1 * p * (A) A p (A) v 1 v 1 * p * (A) p (A) v 1 { displaystyle r (p ( A) v_ {1}) = { frac {(p (A) v_ {1}) ^ {*} Ap (A) v_ {1}} {(p (A) v_ {1}) ^ {*} p (A) v_ {1}}} = { frac {v_ {1} ^ {*} p (A) ^ {*} Ap (A) v_ {1}} {v_ {1} ^ {*} p (A) ^ {*} p (A) v_ {1}}} = { frac {v_ {1} ^ {*} p ^ {*} (A ^ {*}) Ap (A) v_ {1} } {v_ {1} ^ {*} p ^ {*} (A ^ {*}) p (A) v_ {1}}} = { frac {v_ {1} ^ {*} p ^ {*} (A) Ap (A) v_ {1}} {v_ {1} ^ {*} p ^ {*} (A) p (A) v_ {1}}}}
Используя теперь выражение для v 1 { displaystyle v_ {1}}
- A v 1 = A ∑ k = 1 ndkzk = ∑ k = 1 ndk λ kzk { displaystyle Av_ {1 } = A sum _ {k = 1} ^ {n} d_ {k} z_ {k} = sum _ {k = 1} ^ {n} d_ {k} lambda _ {k} z_ { k}}
и в более общем плане
- q (A) v 1 = ∑ k = 1 ndkq (λ k) zk { displaystyle q (A) v_ {1} = sum _ {k = 1 } ^ {n} d_ {k} q ( lambda _ {k}) z_ {k}}
для любого полинома q { displaystyle q}
Таким образом,
- λ 1 — r (p (A) v 1) = λ 1 — v 1 ∗ ∑ k = 1 ndkp ∗ (λ k) λ kp (λ k) zkv 1 ∗ ∑ k = 1 ndkp ∗ (λ k) p (λ k) zk = λ 1 — ∑ k = 1 n | d k | 2 λ k p (λ k) ∗ p (λ k) ∑ k = 1 n | d k | 2 p (λ k) ∗ p (λ k) = ∑ k = 1 n | d k | 2 (λ 1 — λ k) | p (λ k) | 2 ∑ k = 1 n | d k | 2 | p (λ k) | 2. { displaystyle lambda _ {1} -r (p (A) v_ {1}) = lambda _ {1} — { frac {v_ {1} ^ {*} sum _ {k = 1 } ^ {n} d_ {k} p ^ {*} ( lambda _ {k}) lambda _ {k} p ( lambda _ {k}) z_ {k}} {v_ {1} ^ {* } сумма _ {k = 1} ^ {n} d_ {k} p ^ {*} ( lambda _ {k}) p ( lambda _ {k}) z_ {k}}} = lambda _ { 1} — { frac { sum _ {k = 1} ^ {n} | d_ {k} | ^ {2} lambda _ {k} p ( lambda _ {k}) ^ {*} p ( lambda _ {k})} { sum _ {k = 1} ^ {n} | d_ {k} | ^ {2} p ( lambda _ {k}) ^ {*} p ( lambda _ {k})}} = { frac { sum _ {k = 1} ^ {n} | d_ {k} | ^ {2} ( lambda _ {1} — lambda _ {k}) left | p ( lambda _ {k}) right | ^ {2}} { sum _ {k = 1} ^ {n} | d_ {k} | ^ {2} left | p ( lambda _ {k}) right | ^ {2}}}.}
Ключевое различие между числителем и знаменателем в том, что член k = 1 { displaystyle k = 1}



Бук A { displaystyle A}





![[-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
![[-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)

![[-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
- p (x) = см — 1 (2 x — λ 2 — λ n λ 2 — λ n) { displaystyle p (x) = c_ {m-1} left ({ frac {2x- lambda _ {2} — lambda _ {n}} { lambda _ {2} — lambda _ {n}}} right)}
(в случае λ 2 = λ 1 { displaystyle lambda _ {2} = lambda _ {1}}





- λ 1 — θ 1 ⩽ λ 1 — r (p (A) v 1) = ∑ k = 2 n | d k | 2 (λ 1 — λ k) | p (λ k) | 2 ∑ k = 1 n | d k | 2 | p (λ k) | 2 ⩽ ∑ k = 2 n | d k | 2 (λ 1 — λ k) | d 1 | 2 | p (λ 1) | 2 ⩽ (λ 1 — λ n) ∑ k = 2 n | d k | 2 | p (λ 1) | 2 | d 1 | 2. { displaystyle lambda _ {1} — theta _ {1} leqslant lambda _ {1} -r (p (A) v_ {1}) = { frac { sum _ {k = 2 } ^ {n} | d_ {k} | ^ {2} ( lambda _ {1} — lambda _ {k}) | p ( lambda _ {k}) | ^ {2}} { sum _ {k = 1} ^ {n} | d_ {k} | ^ {2} | p ( lambda _ {k}) | ^ {2}}} leqslant { frac { sum _ {k = 2} ^ {n} | d_ {k} | ^ {2} ( lambda _ {1} — lambda _ {k})} {| d_ {1} | ^ {2} | p ( lambda _ {1}) | ^ {2}}} leqslant { frac {( lambda _ {1} — lambda _ {n}) sum _ {k = 2} ^ {n} | d_ {k} | ^ {2}} {| p ( lambda _ {1}) | ^ {2} | d_ {1} | ^ {2}}}.}
Кроме того,
- p (λ 1) = см — 1 (2 λ 1 — λ 2 — λ n λ 2 — λ n) = см — 1 (2 λ 1 — λ 2 λ 2 — λ n + 1); { displaystyle p ( lambda _ {1}) = c_ {m-1} left ({ frac {2 lambda _ {1} — lambda _ {2} — lambda _ {n}} { lambda _ {2} — lambda _ {n}}} right) = c_ {m-1} left (2 { frac { lambda _ {1} — lambda _ {2}} { lambda _ {2} — lambda _ {n}}} + 1 right);}
величина
- ρ = λ 1 — λ 2 λ 2 — λ n { displaystyle rho = { frac { lambda _ {1} — lambda _ {2}} { lambda _ {2} — lambda _ {n}}}}
(т. Е. Отношение первой собственной щели к диаметру остальной части тип ), таким образом, имеет значение для скорости сходимости здесь. Также пишем
- R = e arcosh (1 + 2 ρ) = 1 + 2 ρ + 2 ρ 2 + ρ, { displaystyle R = e ^ { operatorname {arcosh} (1 + 2 rho)} = 1 + 2 rho +2 { sqrt { rho ^ {2} + rho}},}
мы можем заключить, что
- λ 1 — θ 1 ⩽ (λ 1 — λ n) (1 — | d 1 | 2) см — 1 (2 ρ + 1) 2 | d 1 | 2 = 1 — | d 1 | 2 | d 1 | 2 (λ 1 — λ n) 1 ch 2 ((m — 1) arcosh (1 + 2 ρ)) = 1 — | d 1 | 2 | d 1 | 2 (λ 1 — λ n) 4 (R m — 1 + R — (m — 1)) 2 ⩽ 4 1 — | d 1 | 2 | d 1 | 2 (λ 1 — λ N) р — 2 (м — 1) { displaystyle { begin {выровнено} lambda _ {1} — theta _ {1} leqslant { frac {( lambda _ { 1} — lambda _ {n}) left (1- | d_ {1} | ^ {2} right)} {c_ {m-1} (2 rho +1) ^ {2} | d_ {1} | ^ {2}}} \ [6pt] = { frac {1- | d_ {1} | ^ {2}} {| d_ {1} | ^ {2}}} ( lambda _ {1} — lambda _ {n}) { frac {1} { cosh ^ {2} ((m-1) operatorname {arcosh} (1 + 2 rho))}} \ [6pt] = { frac {1- | d_ {1} | ^ {2}} {| d_ {1} | ^ {2}}} ( lambda _ {1} — lambda _ {n}) { frac {4} { left (R ^ {m-1} + R ^ {- (m-1)} справа) ^ {2}}} \ [6pt] leqslant 4 { frac {1- | d_ {1} | ^ {2}} {| d_ {1} | ^ {2}}} ( lambda _ {1} — lambda _ {n}) R ^ {- 2 (m-1)} end {align}}}
Таким образом, скорость сходимости контролируется главным образом R { displaystyle R}

Для сравнения можно рассмотреть, как скорость сходимости степенного метода зависит от ρ { displaystyle rho}




- u = (1 — t 2) 1/2 z 1 + tz 2 ≈ z 1 + tz 2, { displaystyle u = (1-t ^ {2}) ^ {1 / 2} z_ {1} + tz_ {2} приблизительно z_ {1} + tz_ {2},}
, каждая где новая итерация эффективно умножает z 2 { displaystyle z_ {2}}

- λ 2 λ 1 = λ 2 λ 2 + (λ 1 — λ 2) = 1 1 + λ 1 — λ 2 λ 2 знак равно 1 1 + 2 ρ. { displaystyle { frac { lambda _ {2}} { lambda _ {1}}} = { frac { lambda _ {2}} { lambda _ {2} + ( lambda _ {1} — lambda _ {2})}} = { frac {1} {1 + { frac { lambda _ {1} — lambda _ {2}} { lambda _ {2}}}}} = { frac {1} {1 + 2 rho}}.}
Тогда оценка наибольшего собственного значения будет
- u ∗ A u = (1 — t 2) λ 1 + t 2 λ 2, { displaystyle u ^ {*} Au = (1-t ^ {2}) lambda _ {1} + t ^ {2} lambda _ {2},}
, поэтому указанная выше граница сходимости алгоритма Ланцоша скорость следует сравнить с
- λ 1 — u ∗ A U знак равно (λ 1 — λ 2) t 2, { displaystyle lambda _ {1} -u ^ {*} Au = ( lambda _ {1} — lambda _ {2}) t ^ {2},}
, который сжимается в (1 + 2 ρ) — 2 { displaystyle (1 + 2 rho) ^ {- 2}}







Числовая стабильность
Стабильность означает, насколько будет значительный алгоритм (т.е. будет ли он приблизительный результат, близкий к исходному), если будут внесены и накоплены небольшие числовые ошибки. Числовая стабильность — это центральный критерий оценки полезности реализации алгоритма на компьютере с округлением.
Для алгоритма Ланцоша можно доказать, что с помощью точной арифметики векторов наборов v 1, v 2, ⋯, vm + 1 { displaystyle v_ {1}, v_ {2}, cdots, v_ {m + 1}}
Пользователи этого алгоритма должны иметь возможность находить и удалить эти «ложные» собственные значения. Практические алгоритмы реализации Ланцоша идут в трех направлениях для борьбы с этой проблемой стабильности:
- Предотвратить потерю ортогональности,
- Восстановить ортогональность после создания основы.
- После Все «ложные» собственные значения идентифицируют, ложные удаляются.
Варианты
Существуют варианты алгоритма Ланцоша, которые задействованные обеспечивают высокие узкие матрицы вместо векторов, а нормализующие константы представляют собой небольшие квадратные матрицы. Они называются «блочными» алгоритмами Ланцоша и могут быть намного быстрее на компьютере с большим количеством регистров и длительным временем выборки из памяти.
Многие реализации алгоритма Ланцоша перезапускаются после определенного количества итераций. Одним из наиболее важных вариантов перезапуска является неявно перезапускаемый метод Ланцоша, который реализован в ARPACK. Это привело к ряду других перезапущенных вариаций, таких как перезапуск бидиагонализации Ланцоша. Другой успешный вариант с перезапуском — это метод Ланцоша с толстым перезапуском, который был реализован в программном пакете под названием TRLan.
Пустое пространство над конечным полем
В 1995 году Питер Монтгомери опубликовал алгоритм, основанный на алгоритме Ланцоша, для поиска элементов нулевого пространства большой разреженной матрицы над GF (2) ; как множество людей, интересующихся большими разреженными матрицами над конечными полями и множеством людей, интересующимися большими проблемами собственных значений, почти не пересекаются, это часто также называют блочным алгоритмом Ланцоша, не вызывая необоснованной путаницы.
Приложения
Алгоритмы Ланцоша очень привлекательны, потому что умножение на A { displaystyle A ,}
Алгоритмы Ланцоша также используются в Физике конденсированных сред как методы решения гамильтонианов сильно коррелированных электронных систем, а также в модели оболочки коды в ядерной физике.
Реализации
Библиотека NAG содержит несколько процедур для решения крупномасштабных линейных систем и собственных задач, использующих метод Ланцоша. алгоритм.
MATLAB и GNU Octave поставляются со встроенным ARPACK. Как сохраненные, так и неявные матрицы могут быть проанализированы с помощью функций eigs () (Matlab / Octave ).
Реализация алгоритма Ланцоша в Matlab (обратите внимание на проблемы с точностью) доступна как часть пакета Matlab для распространения веры по Гауссу. Библиотека совместной фильтрации GraphLab включает крупномасштабную параллельную реалима Ланцоша (на C ++) для многоядерных процессоров.
Библиотека PRIMME также реализует алгоритм типа Ланцоша.
Примечания
Ссылки
Дополнительная литература
- Голуб, Джин Х. ; Ван Лоан, Чарльз Ф. (1996). «Методы Ланцоша». Матричные вычисления. Балтимор: Издательство Университета Джона Хопкинса. С. 470–507. ISBN 0-8018-5414-8.
- Нг, Эндрю Ю. ; Чжэн, Алиса X.; Джордан, Майкл И. (2001). «Анализ связи, собственные основы и стабильность» (PDF). IJCAI’01 Труды 17-й международной совместной конференции по искусственному интеллекту. Том 2: 903–910.
В Алгоритм Ланцоша это прямой алгоритм разработан Корнелиус Ланцош это адаптация силовые методы найти 



В 1970 году Оялво и Ньюман показали, как сделать метод численно устойчивым, и применили его к решению очень больших инженерных сооружений, подвергающихся динамической нагрузке.[2] Это было достигнуто с использованием метода очистки векторов Ланцоша (т.е. путем многократной реортогонализации каждого вновь созданного вектора с помощью все ранее созданные)[2] с любой степенью точности, которая, если ее не выполнять, давала серию векторов, которые были сильно загрязнены векторами, связанными с самыми низкими собственными частотами.
В своей первоначальной работе эти авторы также предложили, как выбрать начальный вектор (т.е. использовать генератор случайных чисел для выбора каждого элемента начального вектора), и предложили эмпирически определенный метод определения 
Алгоритм
- Вход а Эрмитова матрица
размера
, и, возможно, несколько итераций
(по умолчанию пусть
).
- Выход ан
матрица
с ортонормированный колонны и трехдиагональный вещественная симметричная матрица
размера
. Если
, тогда
является унитарный, и
.
- Предупреждение Итерация Ланцоша подвержена численной нестабильности. При выполнении неточной арифметики необходимо принять дополнительные меры (как описано в следующих разделах) для обеспечения достоверности результатов.
- Позволять
— произвольный вектор с Евклидова норма
.
- Сокращенный этап начальной итерации:
- Позволять
.
- Позволять
.
- Позволять
.
- Позволять
- За
делать:
- Позволять
(также Евклидова норма ).
- Если
, тогда пусть
,
- иначе выберите как
произвольный вектор с евклидовой нормой
что ортогонально всем
.
- иначе выберите как
- Позволять
.
- Позволять
.
- Позволять
.
- Позволять
- Позволять
матрица со столбцами
. Позволять
.
- Позволять
- Примечание
за
.
В принципе, существует четыре способа написать итерационную процедуру. Пейдж и другие работы показывают, что приведенный выше порядок операций является наиболее численно устойчивым.[6][7]На практике начальный вектор 

Не считая умножения матрицы на вектор, каждая итерация делает 





Векторы 








Приложение к проблеме собственных значений
Алгоритм Ланцоша чаще всего упоминается в контексте поиска собственные значения и собственные векторы матрицы, но в то время как обычный диагонализация матрицы сделает собственные векторы и собственные значения очевидными при проверке, этого нельзя сказать о трехдиагонализации, выполняемой алгоритмом Ланцоша; Для вычисления даже одного собственного значения или собственного вектора необходимы нетривиальные дополнительные шаги. Тем не менее, применение алгоритма Ланцоша часто является значительным шагом вперед в вычислении собственного разложения. Если 









- Для трехдиагональных матриц существует ряд специализированных алгоритмов, часто с большей вычислительной сложностью, чем алгоритмы общего назначения. Например, если
является
трехдиагональная симметричная матрица, тогда:
- Некоторые общие алгоритмы разложения на собственные числа, в частности QR-алгоритм, как известно, сходятся быстрее для трехдиагональных матриц, чем для обычных матриц. Асимптотическая сложность трехдиагонального QR равна
точно так же, как для алгоритма «разделяй и властвуй» (хотя постоянный коэффициент может быть другим); так как собственные векторы вместе имеют
элементов, это асимптотически оптимально.
- Даже алгоритмы, скорость сходимости которых не зависит от унитарных преобразований, таких как силовой метод и обратная итерация, может обладать низкими преимуществами производительности от применения к трехдиагональной матрице
а не исходная матрица
. С
очень разреженный, со всеми ненулевыми элементами в хорошо предсказуемых положениях, он обеспечивает компактное хранение с отличной производительностью по сравнению с кеширование. Так же,
это настоящий матрица со всеми собственными векторами и собственными значениями действительными, тогда как
в общем, может иметь комплексные элементы и собственные векторы, поэтому вещественной арифметики достаточно для нахождения собственных векторов и собственных значений
.
- Если
очень большой, то уменьшение
так что
имеет управляемый размер, но позволит находить наиболее экстремальные собственные значения и собственные векторы
; в
области алгоритм Ланцоша можно рассматривать как сжатие с потерями схема для эрмитовых матриц, подчеркивающая сохранение крайних собственных значений.
Сочетание хорошей производительности для разреженных матриц и способности вычислять несколько (без вычисления всех) собственных значений являются основными причинами использования алгоритма Ланцоша.
Применение к тридиагонализации
Хотя проблема собственных значений часто является мотивацией для применения алгоритма Ланцоша, операция, которую в первую очередь выполняет алгоритм, — это трехдиагонализация матрицы, для которой численно стабильная Преобразования домовладельцев пользуются популярностью с 1950-х годов. В 60-е годы алгоритм Ланцоша не принимался во внимание. Интерес к нему был возрожден теорией сходимости Каниэля – Пейджа и развитием методов предотвращения числовой нестабильности, но алгоритм Ланцоша остается альтернативным алгоритмом, который можно пробовать только в том случае, если Хаусхолдер не удовлетворителен.[9]
Аспекты, в которых различаются два алгоритма, включают:
- Ланцош пользуется
будучи разреженной матрицей, тогда как Хаусхолдер нет и будет генерировать заполните.
- Ланцош полностью работает с исходной матрицей
(и не имеет проблем с тем, что он известен только неявно), тогда как необработанный Хаусхолдер хочет изменить матрицу во время вычисления (хотя этого можно избежать).
- Каждая итерация алгоритма Ланцоша создает еще один столбец окончательной матрицы преобразования.
, тогда как итерация Хаусхолдера дает еще один фактор в унитарной факторизации
из
. Однако каждый фактор определяется одним вектором, поэтому требования к памяти одинаковы для обоих алгоритмов, и
можно вычислить в
время.
- Домохозяин численно стабилен, тогда как сырой Ланцош — нет.
- Ланцош очень параллелен, только
точки синхронизация (вычисления
и
). Домохозяин менее параллелен, имея последовательность
вычисляются скалярные величины, каждая из которых зависит от предыдущей величины в последовательности.
Вывод алгоритма
Есть несколько аргументов, которые приводят к алгоритму Ланцоша.
Более предусмотрительный метод силы
Степенной метод нахождения наибольшего собственного значения и соответствующего собственного вектора матрицы 
-
- Выберите случайный вектор
.
- За
(до направления
сошлась) делать:
- Позволять
- Позволять
- Позволять
- Выберите случайный вектор
Этот метод можно критиковать за то, что он расточителен: он тратит много работы (произведение матрица-вектор на шаге 2.1), извлекая информацию из матрицы. 

Одна часть информации, которую легко получить из векторов 
- подмножество
основы
такой, что
для каждого
и все
это тривиально удовлетворяется 






-
- Выберите случайный вектор
евклидовой нормы
. Позволять
.
- За
делать:
- Позволять
.
- Для всех
позволять
. (Это координаты
относительно базисных векторов
.)
- Позволять
. (Отменить компонент
это в
.)
- Если
тогда пусть
и
,
- в противном случае выберите как
произвольный вектор евклидовой нормы
что ортогонально всем
.
- в противном случае выберите как
- Позволять
- Выберите случайный вектор
Связь между векторами степенных итераций 

.
Здесь можно заметить, что на самом деле нам не нужен 





-
- Выберите случайный вектор
евклидовой нормы
.
- За
делать:
- Позволять
.
- Для всех
позволять
.
- Позволять
.
- Позволять
.
- Если
тогда пусть
,
- в противном случае выберите как
произвольный вектор евклидовой нормы
что ортогонально всем
.
- в противном случае выберите как
- Позволять
- Выберите случайный вектор
Априори коэффициенты 
для всех
;
Определение 

Поскольку векторы степенной итерации 





Эта последняя процедура является Итерация Арнольди. Алгоритм Ланцоша возникает как упрощение, получаемое от исключения этапов вычислений, которые оказываются тривиальными, когда 

Элементарно, если 
За 



поскольку последний реален в силу того, что является нормой вектора. За 
это значит, что это тоже реально.
Более абстрактно, если 






матрица 



Одновременное приближение крайних собственных значений
Один из способов характеризации собственных векторов эрмитовой матрицы 
В частности, наибольшее собственное значение 



В подпространстве малой размерности 








Тогда возникает вопрос, как выбрать подпространства, чтобы эти последовательности сходились с оптимальной скоростью.
Из 





,
так что интересующие направления достаточно легко вычислить в матричной арифметике, но если кто-то хочет улучшить оба 














Другими словами, мы можем начать с произвольного начального вектора 
а затем искать 
Поскольку 







Конвергенция и другая динамика
При анализе динамики алгоритма удобно брать собственные значения и собственные векторы 




Также удобно зафиксировать обозначения для коэффициентов исходного вектора Ланцоша 











Тот факт, что алгоритм Ланцоша не зависит от координат — операции смотрят только на внутренние произведения векторов, а не на отдельные элементы векторов, — позволяет легко создавать примеры с известной собственной структурой для запуска алгоритма: make 


Теория сходимости Кэниела – Пейджа
После 













Границы для 












Измерение 
так что любой его элемент может быть выражен как 





Используя теперь выражение для 
и вообще
для любого полинома 
Таким образом
Ключевое различие между числителем и знаменателем заключается в том, что 



С 





![[-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
![[-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)

![[-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
(в случае 





более того
количество
(т. е. отношение первых собственная щель к диаметру остальной части спектр ) имеет ключевое значение для скорости сходимости здесь. Также пишу
мы можем сделать вывод, что
Таким образом, скорость сходимости определяется главным образом 

Для сравнения можно рассмотреть, как скорость сходимости степенного метода зависит от 




[примечание 1]
где каждая новая итерация эффективно умножает 

Тогда оценка наибольшего собственного значения имеет вид
поэтому приведенную выше оценку скорости сходимости алгоритма Ланцоша следует сравнить с
который сжимается в раз 







Численная стабильность
Стабильность означает, насколько сильно будет затронут алгоритм (то есть будет ли он давать приблизительный результат, близкий к исходному), если будут внесены и накоплены небольшие численные ошибки. Числовая стабильность — это центральный критерий оценки полезности реализации алгоритма на компьютере с округлением.
Для алгоритма Ланцоша можно доказать, что с точная арифметика, множество векторов 
Пользователи этого алгоритма должны иметь возможность находить и удалять эти «ложные» собственные значения. Практические реализации алгоритма Ланцоша идут в трех направлениях для борьбы с этой проблемой стабильности:[6][7]
- Предотвратить потерю ортогональности,
- Восстановите ортогональность после создания основы.
- После того, как все хорошие и «ложные» собственные значения определены, удалите ложные.
Вариации
Существуют вариации алгоритма Ланцоша, где задействованные векторы представляют собой высокие узкие матрицы вместо векторов, а нормализующие константы представляют собой небольшие квадратные матрицы. Они называются «блочными» алгоритмами Ланцоша и могут быть намного быстрее на компьютерах с большим количеством регистров и длительным временем выборки из памяти.
Многие реализации алгоритма Ланцоша перезапускаются после определенного количества итераций. Одним из наиболее важных вариантов перезапуска является неявно перезапускаемый метод Ланцоша,[10] который реализован в ARPACK.[11] Это привело к ряду других перезапущенных вариаций, таких как перезапуск бидиагонализации Ланцоша.[12] Другой успешный вариант перезапуска — метод Ланцоша с толстым перезапуском,[13] который был реализован в программном пакете под названием TRLan.[14]
Нулевое пространство над конечным полем
В 1995 г. Питер Монтгомери опубликовал алгоритм, основанный на алгоритме Ланцоша, для поиска элементов пустое пространство большой разреженной матрицы над GF (2); поскольку множество людей, интересующихся большими разреженными матрицами над конечными полями, и множество людей, интересующихся большими проблемами собственных значений, почти не пересекаются, это часто также называют блочный алгоритм Ланцоша не вызывая необоснованной путаницы.[нужна цитата ]
Приложения
Алгоритмы Ланцоша очень привлекательны тем, что умножение на 
Алгоритмы Ланцоша также используются в Физика конденсированного состояния как метод решения Гамильтонианы из сильно коррелированные электронные системы,[15] а также в модель оболочки коды в ядерная физика.[16]
Реализации
В Библиотека NAG содержит несколько процедур[17] для решения крупномасштабных линейных систем и собственных задач, использующих алгоритм Ланцоша.
MATLAB и GNU Octave поставляются со встроенным ARPACK. Как хранимые, так и неявные матрицы можно анализировать с помощью eigs () функция (Matlab /Октава ).
Реализация алгоритма Ланцоша в Matlab (проблемы с точностью примечания) доступна как часть Пакет Matlab для распространения веры по Гауссу. В GraphLab[18] Библиотека совместной фильтрации включает крупномасштабную параллельную реализацию алгоритма Ланцоша (на C ++) для многоядерных процессоров.
В ПРИММ библиотека также реализует алгоритм, подобный Ланцошу.
Примечания
Рекомендации
- ^ Ланцош, К. (1950). «Итерационный метод решения задачи на собственные значения линейных дифференциальных и интегральных операторов» (PDF). Журнал исследований Национального бюро стандартов. 45 (4): 255–282. Дои:10.6028 / jres.045.026.
- ^ а б Ojalvo, I.U .; Ньюман, М. (1970). «Режимы вибрации крупногабаритных конструкций методом автоматического уменьшения матриц». Журнал AIAA. 8 (7): 1234–1239. Bibcode:1970AIAAJ … 8.1234N. Дои:10.2514/3.5878.
- ^ Пейдж, К. С. (1971). Вычисление собственных значений и собственных векторов очень больших разреженных матриц (Кандидатская диссертация). Лондонский университет. OCLC 654214109.
- ^ Пейдж, К. С. (1972). «Вычислительные варианты метода Ланцоша для задачи собственных значений». J. Inst. Приложения по математике. 10 (3): 373–381. Дои:10.1093 / imamat / 10.3.373.
- ^ Оялво, И. У. (1988). «Происхождение и преимущества векторов Ланцоша для больших динамических систем». Proc. 6-я Конференция по модальному анализу (IMAC), Киссимми, Флорида. С. 489–494.
- ^ а б Cullum; Уиллоби. Алгоритмы Ланцоша для вычисления больших симметричных собственных значений. 1. ISBN 0-8176-3058-9.
- ^ а б Юсеф Саад (1992-06-22). Численные методы решения больших задач на собственные значения. ISBN 0-470-21820-7.
- ^ Coakley, Ed S .; Рохлин, Владимир (2013). «Быстрый алгоритм« разделяй и властвуй »для вычисления спектров вещественных симметричных трехдиагональных матриц». Прикладной и вычислительный гармонический анализ. 34 (3): 379–414. Дои:10.1016 / j.acha.2012.06.003.
- ^ а б Golub, Gene H .; Ван Лоан, Чарльз Ф. (1996). Матричные вычисления (3-е изд.). Балтимор: Johns Hopkins Univ. Нажмите. ISBN 0-8018-5413-X.
- ^ Д. Кальветти; Л. Райхель; Д.К. Соренсен (1994). «Неявно перезапущенный метод Ланцоша для больших симметричных задач на собственные значения». Электронные транзакции по численному анализу. 2: 1–21.
- ^ Р. Б. Лехук; Д. К. Соренсен; К. Ян (1998). Руководство пользователя ARPACK: решение крупномасштабных проблем собственных значений с помощью неявно перезапускаемых методов Арнольди. СИАМ. Дои:10.1137/1.9780898719628. ISBN 978-0-89871-407-4.
- ^ Э. Кокиопулу; К. Бекас; Э. Галлопулос (2004). «Вычисление наименьших сингулярных троек с неявно перезапущенной бидиагонализацией Ланцоша» (PDF). Appl. Нумер. Математика. 49: 39–61. Дои:10.1016 / j.apnum.2003.11.011.
- ^ Кешенг Ву; Хорст Саймон (2000). «Толстый перезапуск метода Ланцоша для больших симметричных задач на собственные значения». Журнал SIAM по матричному анализу и приложениям. СИАМ. 22 (2): 602–616. Дои:10.1137 / S0895479898334605.
- ^ Кешенг Ву; Хорст Саймон (2001). «Программный комплекс TRLan». Архивировано из оригинал на 2007-07-01. Получено 2007-06-30.
- ^ Чен, HY; Аткинсон, W.A .; Уортис, Р. (июль 2011 г.). «Вызванная беспорядком аномалия нулевого смещения в модели Андерсона-Хаббарда: численные и аналитические расчеты». Физический обзор B. 84 (4): 045113. arXiv:1012.1031. Bibcode:2011PhRvB..84d5113C. Дои:10.1103 / PhysRevB.84.045113.
- ^ Симидзу, Норитака (21 октября 2013 г.). «Код модели ядерной оболочки для массовых параллельных вычислений», KSHELL««. arXiv:1310.5431 [ядерный ].
- ^ Группа численных алгоритмов. «Указатель ключевых слов: Ланцош». Руководство библиотеки NAG, Mark 23. Получено 2012-02-09.
- ^ GraphLab В архиве 2011-03-14 на Wayback Machine
дальнейшее чтение
- Голуб, Джин Х.; Ван Лоан, Чарльз Ф. (1996). «Методы Ланцоша». Матричные вычисления. Балтимор: Издательство Университета Джона Хопкинса. С. 470–507. ISBN 0-8018-5414-8.
- Нг, Эндрю Ю.; Чжэн, Алиса X .; Джордан, Майкл И. (2001). «Анализ связей, собственные векторы и стабильность» (PDF). IJCAI’01 Труды 17-й международной совместной конференции по искусственному интеллекту. Том 2: 903–910.
Часто при получении технического задания на проведение расчета фигурирует условие, согласно которому проектируемую конструкцию необходимо подобрать или проверить по прочности, деформативности и устойчивости с учетом сейсмического воздействия. В текущей постановке задачи, сделать это совсем несложно, например, используя в качестве расчетного программный комплекс SCAD. Ранее уже была представлена статья с аналогичной тематикой, но в рамках программного комплекса ЛИРА-САПР. О том, как осуществить задание сейсмики в SCAD, пойдет речь в текущей статье.
Нюансы в подготовке расчетной схемы
Чтобы правильно применить сейсмику к расчетной схеме, необходимо уточнить несколько нюансов, касаемых граничных условий.
- Если в расчетной схеме отражен свайный фундамент с помощью конечных элементов №51, которые их моделируют, то такие элементы следует заменить на жесткие связи во всех направлениях, ограничив так же и углы поворота.
- Если же в расчетной схеме здания или сооружения присутствуют модель фундамента на естественном основании, то в этом случае следует увеличить в 10 раз модули деформации грунтов при назначении коэффициентов постели (например, в программе КРОСС).
Назначение к расчетной схеме сейсмического загружения
Сейсмику в SCAD можно задавать уже тогда, когда набрана геометрия расчетной схемы, установлены связи и назначены все остальные загружения на рассматриваемый объект. Так как сейсмика представляет из себя динамическое загружение, то активация окна настройки осуществляется по кнопке «Динамические воздействия» — «Создание нового загружения» (рис. 1).
В новом окне в левом верхнем углу следует поставить галочку напротив «Сейсмические воздействия», затем появится перечень норм, согласно которым нужно делать расчет (рис. 2). На счет остальных настроек стоит остановиться поподробнее, чтобы более корректно осуществить задание сейсмики в SCAD.
Вкладка «Общие данные» при задании сейсмики в SCAD
- Преобразование статических нагрузок в массы – следует активировать этот пункт. Из-за того, что сейсмика учитывается только в особых сочетаниях, то от каждого типа нагрузок задается коэффициент пересчета, согласно следующим коэффициентам:
- Постоянные — 0.9.
- Длительные — 0.8.
- Кратковременные — 0.5. Причем кратковременные нагрузки, не имеющие длительной части
(например, ветровая нагрузка), не входят в особые сочетания.
2. Определение собственных форм и частот выполняется методом Ланцоша, согласно кеоторому происходит автоматическое определение количества форм, пока не наберется требуемая в СП 14.13330.2018, п.5.9 общая сумма масс системы по направлениям X=90% Y=90% Z=75%.
Вкладка с настройками, согласно выбранным нормам в SCAD
Остальные настройки назначаются во второй вкладке текущего окна (рис. 3).
- Число учитываемых частот колебаний определяется модальным анализом.
- Ориентация высоты здания на схеме – по оси Z.
- Категория грунта определяется из отчета по инженерно-геологическим изысканиям (СП 14.13330.2018, табл. 1).
- Сейсмичность — требуемая балльность, согласно техническому заданию или району предполагаемого размещению объекта.
- Поправочный коэффициент — обычно, 1. Можно усиливать влияние сейсмики на конструкцию, вплоть до назначения 10 баллов, введя коэффициент 2.
- Тип сооружения, назначается согласно СП14.13330.2018, табл. 5.3.
- Коэффициент допускаемых повреждений, назначается согласно СП14.13330.2018, табл. 5.4.
- Характеристика сооружения, назначается согласно СП14.13330.2018, табл. 5.5.
После нажатия «ОК» новое сейсмическое воздействие появится в общем списке загружений.
Чтобы задать сейсмику в SCAD в РСУ, нужно в дереве проекта нажать на соответствующую кнопку, после чего в появившейся таблице отредактировать список загружений, согласно ниженаписанным параметрам:
- У сейсмического загружения задать тип — особая нагрузка, а вид — сейсмическое воздействие.
- Сейсмика строго знакопеременна, отметить этот пункт галочкой.
- Сейсмика может входить в сочетание только с теми нагрузками, которые были пересчитаны при задании самого воздействия (постоянные и временные нагрузки, которые имеют длительную часть). Напротив сейсмического воздействия ставим галочку в желтом столбце; для постоянных и временных нагрузок с длительной частью (за исключением нагрузок, которые не имеют длительной составляющей, например ветровая нагрузка) – галочку в зеленном столбце напротив каждого загружения.
- При задании двух и более сейсмических воздействий необходимо задать взаимоисключение данных нагрузок.
- В области «Связи загружений» необходимо зайти в «Сопутствия» и поставить галочки по всем ячейкам.
Задание сейсмики в SCAD завершается на этапе получения результатов расчета. Анализ результатов от сейсмического воздействия в режиме «Графический анализ», во вкладке «Деформации» выполняется по нагрузке «SD –амплитуда от суммарной динамической нагрузки». Значение суммарной амплитуды в среде SCAD всегда несколько завышено в силу того, что программный комплекс складывает значения амплитуд по модулю, без учета знака. Следует учитывать, что при больших значениях перемещений узлов от сейсмического воздействия, результат может быть обусловлен наличием некоторых отдельных частей расчетной схемы (консольный стержень и т.п.). При удалении данных элементов перемещения, вероятнее всего, будут на порядок ниже.
Результаты армирования проводятся аналогичным образом, как и при решении стандартной классической задачи.
vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1
•Элементы “узел-поверхность”
•Элементы “узел-узел”
•Контакт деформируемых тел
•Контакт деформируемого тела с жестким
9 Граничные условия
•Для геометрической и для КЭ-моделей (заданные перемещения и кинематические связи групп узлов)
•Начальные условия
•Ввод нагрузок в форме таблиц или функций
•Тепловые нагрузки
•Преднапряжение
9Модели материалов
•Упругие изотропные, трансверсально-изотропные, ортотропные
•Пластичность металлов (теория течения с различными упрочнениями)
•Гиперупругость (несжимаемые резиноподобные)
•Вязкопластичность металлов
•Ползучесть металлов
•Образование трещин в бетоне и железобетоне
•Нелинейная модель грунта (Друкера-Прагера)
•Пользовательские материалы (нелинейная модель кирпичной кладки, деревянные клееные)
9Конечные элементы
•Объемные КЭ (“солиды”)
•Оболочечные элементы
•Балочные КЭ
•Трубы
•2D и 3D гиперупругие
•2D и 3D оболочки и “солиды” для тепловых задач
•Многоточечные MPC
•2D и 3D контактные
•2D и 3D поверхностного эффекта
•Опция “рождение-смерть”
9Теплопередача
•Стационарные и нестационарные задачи
•Теплопроводность
•Теплообмен конвекцией
9Многодисциплинарные связанные задачи
•Теплообмен + Прочность
9Оптимизация
•Оптимизация параметров
•Параметрическое моделирование
9Дополнительные возможности
•Циклическая симметрия
•Субмоделирование (дополнительный анализ зон конструкции)
•Модальный синтез
•Суперэлементы/подконструкции
9Методы решения
•СЛАУ
•Прямой разреженный метод (Sparse)
•Итерационный метод сопряженных градиентов с предобуславливанием
(PCG)
•Решение задач на собственные значения
|
ЗАО НИЦ СтаДиО (www.stadyo.ru stadyo@stadyo.ru), МГСУ (niccm@mgsu.ru), 2009 |
12 |
vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1
•Блочный метод Ланцоша
•Метод Ланцоша-PCG
•Метод итераций в подпространстве
•Решение нелинейных задач
•Метод Ньютона-Рафсона
•Метод окаймляющих дуг (Arc-length)
•Интегрирование нестационарных уравнений теории поля (теплопроводность и т.п.)
•“Метод трапеций” (Hughes)
•Интегрирование уравнений динамики
•Метод Ньюмарка
•Метод HHT (Hilbert-Hughes-Taylor)
•Спектральный расчет
•Суперэлементные алгоритмы
•Контактные взаимодействия
•Метод штрафных функций
•Метод множителей Лагранжа
•Расширенный метод множителей Лагранжа
•Оптимизация
•Метод аппроксимации подзадачи
•Метод 1-го порядка
4.3Реализация верифицируемых типов решаемых задач (виды расчетов) в ПК
ANSYS Mechanical
Численное моделирование статического, температурного и динамического напряженно-деформированного состояния зданий, сооружений и конструкций без какихлибо существенных ограничений в ПК ANSYS основано на реализации метода конечных элементов (МКЭ) в форме перемещений. Для решения основной системы уравнений формируются глобальные матрицы жесткости [K], демпфирования [C] и матрицы масс [M], а также вектор внешней узловой нагрузки {F}.
4.3.1Линейная статика
Для задач линейной статики решается следующая система линейных алгебраических уравнений (СЛАУ):
или
|
[K ] {u}= {F a }+{F r }, |
(2) |
где:
[K] – глобальная матрица жесткости
N
[K ]= ∑[Ke ];
m=1
{u} – вектор узловых перемещений; N – количество элементов;
[Ke] – элементная матрица жесткости;
|
ЗАО НИЦ СтаДиО (www.stadyo.ru stadyo@stadyo.ru), МГСУ (niccm@mgsu.ru), 2009 |
13 |
vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1
{Fr} – вектор реакций от нагрузки;
{Fa} – вектор глобальной внешней нагрузки,
{F a }= {F nd }+{F ac }+ ∑N ({Feth }+{Fepr })
m=1
где:
{Fnd} – вектор приложенной узловой нагрузки; {Fac} – вектор инерционных сил,
{F ac }= [M ] {ac }
где:
[M] – глобальная матрица масс,
N
[M ]= ∑[Me ]
m=1
[Me] – элементная матрица масс; {ac} – глобальный вектор ускорений;
{Feth} – вектор температурной нагрузки в пределах одного элемента; {Fepr} – вектор давлений в пределах одного элемента.
Решение системы линейных уравнений (1) или (2) в программе осуществляется прямыми (Разреженный Sparse, Фронтальный Frontal) или итерационными (Сопряженных градиентов с предобуславливанием PCG, Сопряженных градиентов Якоби JCG, Сопряженных градиентов с неполным разложением Холецкого ICCG) методами.
В рамках верификации были рассмотрены наиболее эффективные универсальные схемы:
1)прямой разреженный метод (Sparse)
2)итерационный метод сопряженных градиентов с предобуславливанием (PCG).
4.3.1.1Прямой разреженный метод (Sparse Direct Solver)
Линейные матричные уравнения (1) решаются триангуляцией матрицы жесткости [K] для получения следующего уравнения:
|
[L] [U ] {u}= {F} |
(3) |
|
где: |
|
|
[L] – нижняя матрица треугольного вида |
|
|
[U] – верхняя матрица треугольного вида |
|
|
Обозначим |
|
|
[U ] {u}= {w} |
(4) |
Искомый вектор узловых перемещений {u} определяем, предварительно решив СЛАУ относительно {w}:
а затем
|
ЗАО НИЦ СтаДиО (www.stadyo.ru stadyo@stadyo.ru), МГСУ (niccm@mgsu.ru), 2009 |
14 |
|
ANSYS Mechanical. Верификационный отчет. Том 1 |
|
|
vk.com/club152685050 | vk.com/id446425943 |
|
|
[U ] {u}= {w} |
(6) |
|
Когда матрица жесткости [K] симметрична, ее можно записать в виде: |
|
|
[K ]= [L] [L]T |
(7) |
в свою очередь
|
[K ]= [L |
] [D][L ] |
(8) |
|
′ |
′ T |
где [D] – диагональная матрица, члены которой могут быть отрицательными для некоторых нелинейных задач, что позволяет сформировать матрицу [L′] без учета квадратного корня из отрицательного числа. Поэтому уравнения (3)-(6) можно представить в виде:
|
[L ] [D] [L ] |
{u}= {F} |
(9) |
|
|
′ |
′ T |
||
|
′ T |
{u} |
(10) |
|
|
{w}= [D] [L ] |
|||
|
′ |
(11) |
||
|
[L ] {w}= {F} |
|||
|
′ T |
{u}= {F} |
(12) |
|
|
[D] [L ] |
В том случае, когда матрица [K] редкозаполненная с коэффициентами, расположенными, в основном, вокруг главной диагонали, прямой разреженный метод предназначен для обработки только ненулевых элементов матрицы [K]. В целом, в ходе разложения Холецкого матрицы [K], (3) или (9), матрицы [L] или [L’] заполняются ненулевыми коэффициентами, расположенными на нулевых позициях матрицы [K]. Эффективность прямого разреженного метода определяется максимальной оптимизацией вышеописанного процесса.
4.3.1.2Итерационный метод сопряженных градиентов с предобуславливанием
(Preconditioned Conjugate Gradient)
Итерационный метод сопряженных градиентов с предобуславливанием (PCG) является эффективным и надежным для всех типов расчетов. PCG метод применим только для симметричных матриц жесткости.
Решается основная система линейных уравнений (1). Вектор узловых перемещений ищется в виде:
|
{u}=α1 {p1 }+α2 {p2 }+…+αm {pm } |
(13) |
где m ≤ n, где n – размер матрицы.
Алгоритм метода сопряженных градиентов реализован следующим образом (14):
{u0 }= {0} {R0 }= {F}
{z0 }= [Q]−1 {F}
Do i = 1, n
If(Norm (R)≤ ε 2 ) then
Set {u}={ui-1} Quit loop
Else
|
ЗАО НИЦ СтаДиО (www.stadyo.ru stadyo@stadyo.ru), МГСУ (niccm@mgsu.ru), 2009 |
15 |

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1
|
If(i=1)then |
|
|
β1=0 |
|
|
{p1}={R0} |
|
|
α1 = |
{z0 }T {R0 } |
|
{p1 }T [K ] {p1 } |
{R1 }={R0 }+α1 [K ] {p1 }
Else
Applying preconditioning:{zi-1}=[Q]-1{Ri-1}
|
β |
= |
{zi−1 }T {Ri−1 } |
||||
|
i |
{zi−2 }T {Ri−2 } |
|||||
|
{pi }= {zi−1 }+ βi {pi−1 } |
||||||
|
α |
= |
{zi−1 }T {Ri−1 } |
||||
|
i |
{pi }T [K ] {pi } |
|||||
{Ri }= {Ri−1 }+αi [K ] {pi }
Endif
Endif
End loop
Условие сходимости:
|
{Ri }T {Ri } |
≤ ε 2 |
(15) |
|
{F}T {F} |
где:
ε – точность, заданная пользователем;
{Ri }= {F}−[K ] {ui }
{ui} – вектор решений на i-ой итерации. Вектор {u0} может быть нулевым.
4.3.2 Стационарные задачи теплопроводности (фильтрации)
Для стационарных задач теплопроводности (фильтрации) решаем СЛАУ (1) или (2), подставляя вместо глобальной матрицы [K ] матрицу теплопроводности, вместо вектора
перемещений {u} – искомый вектор узловых температур {T}, а вместо вектора приложенной глобальной внешней нагрузки {F a }– {Qa }, где
{Qa }= {Qnd }+ ∑N ({Qe }+{Qeg }+{Qec }), m=1
4.3.3Собственные частоты и формы колебаний
Уравнение движения для задач определения собственных частот и форм колебаний без учета демпфирования имеет вид:
|
[M ] {u}+[K ] {u}= {0} |
(16) |
Эффекты преднапряженного состояния могут быть учтены в матрице жесткости [K ]
(команда PSTRES,ON).
|
ЗАО НИЦ СтаДиО (www.stadyo.ru stadyo@stadyo.ru), МГСУ (niccm@mgsu.ru), 2009 |
16 |
|
ANSYS Mechanical. Верификационный отчет. Том 1 |
|||||
|
vk.com/club152685050 | vk.com/id446425943 |
|||||
|
Для линейных систем свободные колебания являются гармоническими: |
|||||
|
{u}= {φ}i cosωi t |
(17) |
||||
|
где: |
|||||
|
{φ}i – собственный вектор, соответствующий i-ой собственной частоте; |
|||||
|
ωi – i-я собственная круговая частота (радиан в единицу времени); |
|||||
|
t – время. |
|||||
|
Таким образом, уравнение (16) примет вид: |
|||||
|
(−ω2 [M ]+[K ]) |
{φ} = {0} |
(18) |
|||
|
i |
i |
||||
|
Нетривиальным решением (18) является: |
|||||
|
[K ]−ω2 [M ] |
= 0 |
(19) |
|||
Через полученные значения круговых частот собственных колебаний {ω} можно выразить частоты собственных колебаний {f}:
|
fi |
= |
ωi |
(20) |
|
|
2π |
||||
Проблема собственных частот и форм колебаний может быть решена одним из методов, реализованных в ПК ANSYS Mechanical:
•Редуцированный метод;
•Метод итераций в подпространстве;
•Прямой блочный метод Ланцоша;
•Метод Ланцоша–PCG;
•Несимметричный метод;
•Метод демпфирования;
•QR-разложение для задач с демпфированием.
Врамках настоящей верификации рассмотрены наиболее эффективные для задач большой размерности:
1) метод итераций в подпространстве;
2) прямой блочный метод Ланцоша;
3) метод Ланцоша-PCG.
4.3.3.1Метод итераций в подпространстве
Основной алгоритм метода итераций в подпространстве выглядит следующим образом:
1.Определение так называемых «сдвигов» s. В случае частотного анализа (ANTYPE,MODAL),) s = FREQB – низшая частота в частотном диапазоне.
2.Инициализация начальных векторов [X 0 ].
Количество начальных векторов (итераций) определяется равенством
где:
p – необходимое количество вычисляемых форм;
d – дополнительное число итерируемых векторов (по умолчанию d = 4)
|
ЗАО НИЦ СтаДиО (www.stadyo.ru stadyo@stadyo.ru), МГСУ (niccm@mgsu.ru), 2009 |
17 |

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1
|
3. |
Триангуляция “сдвинутой” матрицы |
|
|
[K ]= [K ]+ s [M ] |
(22) |
[K ] – глобальная матрица жесткости системы;
[M ] – глобальная матрица масс (для модального анализа).
В качестве проверки используется свойство последовательности Штурма со сдвигом
s.
4.Для каждой итерации в подпространстве n от 1 до NM выполняются нижеследующие пункты 5-14. NM – максимальное количество итераций в подпространстве.
5.Формируется
[F ]масштабируется по {λn−1}, где {λn−1} – предварительно оцениваемый вектор собственных значений.
6.Прямым фронтальным методом (EQSLV,FRONT) решается система уравнений
(29)относительно [X n ]:
7.Вектор [X n ] масштабируется {(λn−1 − s) / λn−1}.
8.Для сохраниения численной устойчивости проводится ортогонализация по Граму-Шмидту.
9.Определяются матрицы подпространства [K ] и [M ]:
|
[ |
]= [ |
n ]T [K ] [ |
n ] |
(25) |
||||||||||||||||||||
|
K |
X |
X |
||||||||||||||||||||||
|
[ |
]= [ |
n ]T [M ] [ |
n ] |
(26) |
||||||||||||||||||||
|
M |
X |
X |
||||||||||||||||||||||
|
10. |
С учетом сдвига, получается |
|||||||||||||||||||||||
|
[ |
]= [ |
]+ s [ |
] |
(27) |
||||||||||||||||||||
|
K |
K |
M |
||||||||||||||||||||||
|
11. |
Вычисляются собственные значения и векторы |
подпространства с |
||||||||||||||||||||||
|
применением обобщенного метода Якоби: |
||||||||||||||||||||||||
|
[K ] [Q]= [ |
] [Q] {λn } |
(28) |
||||||||||||||||||||||
|
M |
||||||||||||||||||||||||
|
где: |
||||||||||||||||||||||||
|
[Q] – собственные вектора подпространства; |
||||||||||||||||||||||||
|
{λn } – обновленные собственные значения. |
||||||||||||||||||||||||
|
12. |
Обновление приближения к собственным векторам: |
|||||||||||||||||||||||
|
[X n ]= [ |
n ] [Q] |
(29) |
||||||||||||||||||||||
|
X |
13.Если найдены отрицательные или лишние формы колебаний, их нужно удалить
исоздать новый случайный вектор.
14.Анализ сходимости полученных приближений:
• Если для всех форм сходимость достигается:
|
ЗАО НИЦ СтаДиО (www.stadyo.ru stadyo@stadyo.ru), МГСУ (niccm@mgsu.ru), 2009 |
18 |
vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1
|
ei |
= |
(λi )n −(λi )n−1 |
< tol |
(30) |
|
|
B |
|||||
где:
(λi )n – i-е собственное значение, вычисленное на n-ой итерации;
(λi )n−1 – i-е собственное значение, вычисленное на (n-1)-ой итерации;
1.0
B = ( ) – выбирается наибольшее значение;
λi n
tol – предел сходимости, равный 10-5, то переходим к пункту 15.
•Если требуется задать новый сдвиг, возвращаемся к пункту 3.
•Для перехода на следующую итерацию, переходим к пункту 4.
15.Выполняется последняя необходимая проверка с использованием свойства последовательности Штурма.
4.3.3.2Прямой блочный метод Ланцоша
Для решения большой симметричной проблемы собственных значений помимо метода итераций в подпространстве применяют прямой блочный метод Ланцоша, имеющий более быструю сходимость.
Алгоритм блочного метода Ланцоша со сдвигом подробно описан в [194]. Для получения требуемого количества собственных векторов в модальном анализе блочный метод Ланцоша применяется совместно с проверкой последовательности Штурма.
Отметим, что блочная версия алгоритма позволяет сократить медленные операции ввода-вывода по сравнению с классической (неблочной) версией. Введение сдвигов существенно улучшает сходимость.
Альтернативой блочному методу Ланцоша является метод Ланцоша-PCG, требующий меньше вычислительных затрат.
4.3.3.3 Метод Ланцоша-PCG
Теоретические выкладки по реализации метода Ланцоша-PCG можно также найти в работе [194].
Несмотря на то, что данный метод основан на блочном методе Ланцоша, их реализация несколько отличается:
•Значение сдвига в ходе вычислений остается неизменным;
•Для решения уравнения (24) применяется метод PCG;
•По умолчанию не выполняется проверка последовательности Штурма;
•Не применим к задачам на устойчивость.
4.3.4Линейная устойчивость
Расчет на устойчивость в линейной постановке (частичная проблема собственных
значений) формулируется следующим образом:
|
([K ]+ λi [S]) {ψ}i ={0} |
(31) |
где:
[K ] – матрица жесткости системы;
[S] – матрица геометрической жесткости (stress stiffness matrix);
|
ЗАО НИЦ СтаДиО (www.stadyo.ru stadyo@stadyo.ru), МГСУ (niccm@mgsu.ru), 2009 |
19 |

vk.com/club152685050ANSYS Mechanical. Верификационный| vk.com/id446425943отчет. Том 1
λi – i-е собственное значение (критическая нагрузка);
{ψ}i – i-й собственный вектор перемещений (форма потери устойчивости).
Методы решения проблемы собственных значений, реализованных в ПК ANSYS Mechanical, перечислены в п. 3.3.3.
В рамках настоящей верификации применительно к задачам на линейную устойчивость рассмотрен прямой блочный метод Ланцоша (см. п. 3.3.3.2).
4.3.5Гармонический анализ (установившиеся вибрации)
При гармоническом анализе линейных систем с установившимися вибрациями решаются уравнения движения во времени:
|
[M ] {u}+[C] {u}+[K ] {u}= {F a } |
(32) |
где:
[M ] – матрица масс системы;
[C] – матрица демпфирования (диссипации) системы; [K ]– матрица жесткости системы;
{u} — вектор узловых ускорений; {u} — вектор узловых скоростей; {u} — вектор узловых перемещений;
{F a }— функция нагрузки, зависящая от времени.
Известно, что все точки системы движутся с одной частотой, но необязательно в одной фазе. Сдвиг по фазе объясняется наличием демпфирования. Поэтому перемещения могут быть представлены следующим образом:
|
{u}= {umax eiφ } eiΩt |
(33) |
|
|
где: |
||
|
umax |
– максимальные перемещения; |
|
|
i = |
−1 ; |
Ω –круговая частота внешней нагрузки (радианы в единицу времени), Ω = 2πf ; f – вынуждающая частота;
t– время;
φ– сдвиг по фазе для перемещений (радианы).
Вкомплексной форме перемещения можно записать следующим образом:
|
{u}={umax (cosφ +isinφ)} eiΩt |
(34) |
||||
|
или |
|||||
|
{u}={{u |
}+i{u |
2 |
}} eiΩt |
(35) |
|
|
1 |
|||||
|
где: |
|||||
|
{u1 |
}={umax cosφ} – вектор действительных значений перемещений; |
||||
|
{u2 }={umax sinφ} – вектор мнимых значений перемещений. |
|||||
|
Вектор нагрузки может быть представлен по аналогии: |
|||||
|
{F}={Fmax eiψ }eiΩt |
(36) |
||||
|
{F}={F |
(cosψ +isinψ )} eiΩt |
(37) |
|||
|
max |
|
ЗАО НИЦ СтаДиО (www.stadyo.ru stadyo@stadyo.ru), МГСУ (niccm@mgsu.ru), 2009 |
20 |
|
ANSYS Mechanical. Верификационный отчет. Том 1 |
|||
|
vk.com/club152685050 | vk.com/id446425943 |
|||
|
{F}={{F |
}+i{F }} eiΩt |
(38) |
|
|
1 |
2 |
||
|
где: |
|||
|
Fmax – амплитуда приложенной силы; |
|||
|
Ψ – сдвиг по фазе для нагрузки (радианы); |
|||
|
{F1}={Fmax cosψ} – вектор действительных значений нагрузки; |
|||
|
{F2 }={Fmax sinψ} – вектор мнимых значений нагрузки. |
|||
|
Подставив выражения (35) и (38) в (32), получим: |
|||
|
(−Ω2 [M ]+iΩ [C]+[K ]) ({u1}+i{u2 }) eiΩt = ({F1}+i{F2 }) eiΩt |
(39) |
||
|
Выполнив необходимые преобразования, представим уравнение (39) в виде: |
|||
|
(− Ω2 [M ]+iΩ [C]+[K ]) ({u1}+i{u2 })= ({F1}+ i{F2 }) |
(40) |
Существует четыре метода решения представленной выше системы уравнений (40):
•Полный метод решения (Full Solution Method);
•Редуцированный метод решения (Reduced Solution Method);
•Метод суперпозиций форм колебаний;
•Вариационный метод решения (Variational Technology).
Врамках данной верификации остановимся на методе суперпозиций форм колебаний.
4.3.5.1Метод суперпозиций форм колебаний
Уравнение движения (32) в частотной (модальной) форме записывается следующим образом (подробнее см. “Documentation for ANSYS, Theory Reference, Chapter 15. Analysis Tools, 15.10 Mode Superposition Method”):
|
y j + 2ωjξj y j +ω2j y j = f j |
(41) |
|
|
где: |
||
|
y j |
– модальная (нормальная) координата (modal coordinate); |
|
|
ωj |
– собственная круговая частота j-й формы колебаний; |
|
|
ξj |
– коэффициент затухания для j-й формы колебаний; |
|
|
fi – нагрузка в модальных координатах. |
||
|
Вектор нагрузки в модальных координатах: |
||
|
{F}= {F nd }+ s{F s } |
(42) |
где:
{F nd }– вектор узловых сил;
s – масштабный коэффициент нагрузки;
{F s } – вектор нагрузки из модального анализа (подробнее см. “Documentation for ANSYS,
Theory Reference, Chapter 15. Analysis Tools, 15.10 Mode Superposition Method” []).
Для установившихся гармонических колебаний
|
ЗАО НИЦ СтаДиО (www.stadyo.ru stadyo@stadyo.ru), МГСУ (niccm@mgsu.ru), 2009 |
21 |
Соседние файлы в предмете Информатика
- #
- #
- #
- #
- #
- #
- #
- #
The Lanczos algorithm is an iterative method devised by Cornelius Lanczos that is an adaptation of power methods to find the 



In 1970, Ojalvo and Newman showed how to make the method numerically stable and applied it to the solution of very large engineering structures subjected to dynamic loading.[2] This was achieved using a method for purifying the Lanczos vectors (i.e. by repeatedly reorthogonalizing each newly generated vector with all previously generated ones)[2] to any degree of accuracy, which when not performed, produced a series of vectors that were highly contaminated by those associated with the lowest natural frequencies.
In their original work, these authors also suggested how to select a starting vector (i.e. use a random-number generator to select each element of the starting vector) and suggested an empirically determined method for determining 
The algorithm[edit]
- Input a Hermitian matrix
of size
, and optionally a number of iterations
(as default, let
).
- Output an
matrix
with orthonormal columns and a tridiagonal real symmetric matrix
of size
. If
, then
is unitary, and
.
- Warning The Lanczos iteration is prone to numerical instability. When executed in non-exact arithmetic, additional measures (as outlined in later sections) should be taken to ensure validity of the results.
- Let
be an arbitrary vector with Euclidean norm
.
- Abbreviated initial iteration step:
- Let
.
- Let
.
- Let
.
- Let
- For
do:
- Let
(also Euclidean norm).
- If
, then let
,
- else pick as
an arbitrary vector with Euclidean norm
that is orthogonal to all of
.
- else pick as
- Let
.
- Let
.
- Let
.
- Let
- Let
be the matrix with columns
. Let
.
- Let
- Note
for
.
There are in principle four ways to write the iteration procedure. Paige and other works show that the above order of operations is the most numerically stable.[6][7]
In practice the initial vector 

Not counting the matrix–vector multiplication, each iteration does 





The vectors 
The vector 







Application to the eigenproblem[edit]
The Lanczos algorithm is most often brought up in the context of finding the eigenvalues and eigenvectors of a matrix, but whereas an ordinary diagonalization of a matrix would make eigenvectors and eigenvalues apparent from inspection, the same is not true for the tridiagonalization performed by the Lanczos algorithm; nontrivial additional steps are needed to compute even a single eigenvalue or eigenvector. Nonetheless, applying the Lanczos algorithm is often a significant step forward in computing the eigendecomposition. If 









- For tridiagonal matrices, there exist a number of specialised algorithms, often with better computational complexity than general-purpose algorithms. For example, if
is an
tridiagonal symmetric matrix then:
- Some general eigendecomposition algorithms, notably the QR algorithm, are known to converge faster for tridiagonal matrices than for general matrices. Asymptotic complexity of tridiagonal QR is
just as for the divide-and-conquer algorithm (though the constant factor may be different); since the eigenvectors together have
elements, this is asymptotically optimal.
- Even algorithms whose convergence rates are unaffected by unitary transformations, such as the power method and inverse iteration, may enjoy low-level performance benefits from being applied to the tridiagonal matrix
rather than the original matrix
. Since
is very sparse with all nonzero elements in highly predictable positions, it permits compact storage with excellent performance vis-à-vis caching. Likewise,
is a real matrix with all eigenvectors and eigenvalues real, whereas
in general may have complex elements and eigenvectors, so real arithmetic is sufficient for finding the eigenvectors and eigenvalues of
.
- If
is very large, then reducing
so that
is of a manageable size will still allow finding the more extreme eigenvalues and eigenvectors of
; in the
region, the Lanczos algorithm can be viewed as a lossy compression scheme for Hermitian matrices, that emphasises preserving the extreme eigenvalues.
The combination of good performance for sparse matrices and the ability to compute several (without computing all) eigenvalues are the main reasons for choosing to use the Lanczos algorithm.
Application to tridiagonalization[edit]
Though the eigenproblem is often the motivation for applying the Lanczos algorithm, the operation the algorithm primarily performs is tridiagonalization of a matrix, for which numerically stable Householder transformations have been favoured since the 1950s. During the 1960s the Lanczos algorithm was disregarded. Interest in it was rejuvenated by the Kaniel–Paige convergence theory and the development of methods to prevent numerical instability, but the Lanczos algorithm remains the alternative algorithm that one tries only if Householder is not satisfactory.[9]
Aspects in which the two algorithms differ include:
Derivation of the algorithm[edit]
There are several lines of reasoning which lead to the Lanczos algorithm.
A more provident power method[edit]
The power method for finding the eigenvalue of largest magnitude and a corresponding eigenvector of a matrix 
-
- Pick a random vector
.
- For
(until the direction of
has converged) do:
- Let
- Let
- Let
- Pick a random vector
A critique that can be raised against this method is that it is wasteful: it spends a lot of work (the matrix–vector products in step 2.1) extracting information from the matrix 

One piece of information that trivially is available from the vectors 
- a subset
of a basis of
such that
for every
and all
this is trivially satisfied by 






- Pick a random vector
of Euclidean norm
. Let
.
- For
do:
- Let
.
- For all
let
. (These are the coordinates of
with respect to the basis vectors
.)
- Let
. (Cancel the component of
that is in
.)
- If
then let
and
,
- otherwise pick as
an arbitrary vector of Euclidean norm
that is orthogonal to all of
.
- otherwise pick as
- Let
The relation between the power iteration vectors 

.
Here it may be observed that we do not actually need the 





- Pick a random vector
of Euclidean norm
.
- For
do:
- Let
.
- For all
let
.
- Let
.
- Let
.
- If
then let
,
- otherwise pick as
an arbitrary vector of Euclidean norm
that is orthogonal to all of
.
- otherwise pick as
- Let
A priori the coefficients 
for all
;
the definition 

Because the power iteration vectors 





This last procedure is the Arnoldi iteration. The Lanczos algorithm then arises as the simplification one gets from eliminating calculation steps that turn out to be trivial when 

Elementarily, if 
For 



since the latter is real on account of being the norm of a vector. For 
meaning this is real too.
More abstractly, if 






the matrix 



Simultaneous approximation of extreme eigenvalues[edit]
One way of characterising the eigenvectors of a Hermitian matrix 
In particular, the largest eigenvalue 



Within a low-dimensional subspace 








The question then arises how to choose the subspaces so that these sequences converge at optimal rate.
From 





so the directions of interest are easy enough to compute in matrix arithmetic, but if one wishes to improve on both 














In other words, we can start with some arbitrary initial vector 
and then seek 
Since the 







Convergence and other dynamics[edit]
When analysing the dynamics of the algorithm, it is convenient to take the eigenvalues and eigenvectors of 




It is also convenient to fix a notation for the coefficients of the initial Lanczos vector 











The fact that the Lanczos algorithm is coordinate-agnostic – operations only look at inner products of vectors, never at individual elements of vectors – makes it easy to construct examples with known eigenstructure to run the algorithm on: make 


Kaniel–Paige convergence theory[edit]
After 













The bounds for 












The dimension 
so any element of it can be expressed as 





Using now the expression for 
and more generally
for any polynomial 
Thus
A key difference between numerator and denominator here is that the 



Since 





![[-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
![[-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)

![[-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
(in case 





Furthermore
the quantity
(i.e., the ratio of the first eigengap to the diameter of the rest of the spectrum) is thus of key importance for the convergence rate here. Also writing
we may conclude that
The convergence rate is thus controlled chiefly by 

For comparison, one may consider how the convergence rate of the power method depends on 




[note 1]
where each new iteration effectively multiplies the 

The estimate of the largest eigenvalue is then
so the above bound for the Lanczos algorithm convergence rate should be compared to
which shrinks by a factor of 







Numerical stability[edit]
Stability means how much the algorithm will be affected (i.e. will it produce the approximate result close to the original one) if there are small numerical errors introduced and accumulated. Numerical stability is the central criterion for judging the usefulness of implementing an algorithm on a computer with roundoff.
For the Lanczos algorithm, it can be proved that with exact arithmetic, the set of vectors 
Users of this algorithm must be able to find and remove those «spurious» eigenvalues. Practical implementations of the Lanczos algorithm go in three directions to fight this stability issue:[6][7]
- Prevent the loss of orthogonality,
- Recover the orthogonality after the basis is generated.
- After the good and «spurious» eigenvalues are all identified, remove the spurious ones.
Variations[edit]
Variations on the Lanczos algorithm exist where the vectors involved are tall, narrow matrices instead of vectors and the normalizing constants are small square matrices. These are called «block» Lanczos algorithms and can be much faster on computers with large numbers of registers and long memory-fetch times.
Many implementations of the Lanczos algorithm restart after a certain number of iterations. One of the most influential restarted variations is the implicitly restarted Lanczos method,[10] which is implemented in ARPACK.[11] This has led into a number of other restarted variations such as restarted Lanczos bidiagonalization.[12] Another successful restarted variation is the Thick-Restart Lanczos method,[13] which has been implemented in a software package called TRLan.[14]
Nullspace over a finite field[edit]
In 1995, Peter Montgomery published an algorithm, based on the Lanczos algorithm, for finding elements of the nullspace of a large sparse matrix over GF(2); since the set of people interested in large sparse matrices over finite fields and the set of people interested in large eigenvalue problems scarcely overlap, this is often also called the block Lanczos algorithm without causing unreasonable confusion.[citation needed]
Applications[edit]
Lanczos algorithms are very attractive because the multiplication by 
Lanczos algorithms are also used in condensed matter physics as a method for solving Hamiltonians of strongly correlated electron systems,[15] as well as in shell model codes in nuclear physics.[16]
Implementations[edit]
The NAG Library contains several routines[17] for the solution of large scale linear systems and eigenproblems which use the Lanczos algorithm.
MATLAB and GNU Octave come with ARPACK built-in. Both stored and implicit matrices can be analyzed through the eigs() function (Matlab/Octave).
Similarly, in Python, the SciPy package has scipy.sparse.linalg.eigsh which is also a wrapper for the SSEUPD and DSEUPD functions functions from ARPACK which use the Implicitly Restarted Lanczos Method.
A Matlab implementation of the Lanczos algorithm (note precision issues) is available as a part of the Gaussian Belief Propagation Matlab Package. The GraphLab[18] collaborative filtering library incorporates a large scale parallel implementation of the Lanczos algorithm (in C++) for multicore.
The PRIMME library also implements a Lanczos-like algorithm.
Notes[edit]
References[edit]
- ^ Lanczos, C. (1950). «An iteration method for the solution of the eigenvalue problem of linear differential and integral operators» (PDF). Journal of Research of the National Bureau of Standards. 45 (4): 255–282. doi:10.6028/jres.045.026.
- ^ a b Ojalvo, I. U.; Newman, M. (1970). «Vibration modes of large structures by an automatic matrix-reduction method». AIAA Journal. 8 (7): 1234–1239. Bibcode:1970AIAAJ…8.1234N. doi:10.2514/3.5878.
- ^ Paige, C. C. (1971). The computation of eigenvalues and eigenvectors of very large sparse matrices (Ph.D. thesis). U. of London. OCLC 654214109.
- ^ Paige, C. C. (1972). «Computational Variants of the Lanczos Method for the Eigenproblem». J. Inst. Maths Applics. 10 (3): 373–381. doi:10.1093/imamat/10.3.373.
- ^ Ojalvo, I. U. (1988). «Origins and advantages of Lanczos vectors for large dynamic systems». Proc. 6th Modal Analysis Conference (IMAC), Kissimmee, FL. pp. 489–494.
- ^ a b Cullum; Willoughby (1985). Lanczos Algorithms for Large Symmetric Eigenvalue Computations. Vol. 1. ISBN 0-8176-3058-9.
- ^ a b Yousef Saad (1992-06-22). Numerical Methods for Large Eigenvalue Problems. ISBN 0-470-21820-7.
- ^ Coakley, Ed S.; Rokhlin, Vladimir (2013). «A fast divide-and-conquer algorithm for computing the spectra of real symmetric tridiagonal matrices». Applied and Computational Harmonic Analysis. 34 (3): 379–414. doi:10.1016/j.acha.2012.06.003.
- ^ a b Golub, Gene H.; Van Loan, Charles F. (1996). Matrix computations (3. ed.). Baltimore: Johns Hopkins Univ. Press. ISBN 0-8018-5413-X.
- ^ D. Calvetti; L. Reichel; D.C. Sorensen (1994). «An Implicitly Restarted Lanczos Method for Large Symmetric Eigenvalue Problems». Electronic Transactions on Numerical Analysis. 2: 1–21.
- ^ R. B. Lehoucq; D. C. Sorensen; C. Yang (1998). ARPACK Users Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM. doi:10.1137/1.9780898719628. ISBN 978-0-89871-407-4.
- ^ E. Kokiopoulou; C. Bekas; E. Gallopoulos (2004). «Computing smallest singular triplets with implicitly restarted Lanczos bidiagonalization» (PDF). Appl. Numer. Math. 49: 39–61. doi:10.1016/j.apnum.2003.11.011.
- ^ Kesheng Wu; Horst Simon (2000). «Thick-Restart Lanczos Method for Large Symmetric Eigenvalue Problems». SIAM Journal on Matrix Analysis and Applications. SIAM. 22 (2): 602–616. doi:10.1137/S0895479898334605.
- ^ Kesheng Wu; Horst Simon (2001). «TRLan software package». Archived from the original on 2007-07-01. Retrieved 2007-06-30.
- ^ Chen, HY; Atkinson, W.A.; Wortis, R. (July 2011). «Disorder-induced zero-bias anomaly in the Anderson-Hubbard model: Numerical and analytical calculations». Physical Review B. 84 (4): 045113. arXiv:1012.1031. Bibcode:2011PhRvB..84d5113C. doi:10.1103/PhysRevB.84.045113. S2CID 118722138.
- ^ Shimizu, Noritaka (21 October 2013). «Nuclear shell-model code for massive parallel computation, «KSHELL»«. arXiv:1310.5431 [nucl-th].
- ^ The Numerical Algorithms Group. «Keyword Index: Lanczos». NAG Library Manual, Mark 23. Retrieved 2012-02-09.
- ^ GraphLab Archived 2011-03-14 at the Wayback Machine
Further reading[edit]
- Golub, Gene H.; Van Loan, Charles F. (1996). «Lanczos Methods». Matrix Computations. Baltimore: Johns Hopkins University Press. pp. 470–507. ISBN 0-8018-5414-8.
- Ng, Andrew Y.; Zheng, Alice X.; Jordan, Michael I. (2001). «Link Analysis, Eigenvectors and Stability» (PDF). IJCAI’01 Proceedings of the 17th International Joint Conference on Artificial Intelligence. 2: 903–910.
Введение
При решении задач сейсмического анализа зданий и сооружений чаще всего применяется линейно-спектральный метод. Значительной по трудоемкости составляющей этого подхода является определение частот и форм собственных колебаний. При этом возникает вопрос: а сколько частот и форм собственных колебаний следует удерживать, чтобы результат был достоверным? В сейсмических нормах многих стран (Еврокод 8, UBC-97, сейсмические нормы Украины и др.) принято, что сумма модальных масс по каждому из направлений сейсмического воздействия должна быть не менее установленной границы. Обычно для горизонтальной составляющей сейсмического воздействия принимается 85−90%, для вертикальной — 70−90%. Под направлением сейсмического воздействия понимается направление, совпадающее с одной из осей глобальной системы координат OXYZ расчетной модели сооружения. Считается, что сейсмическое воздействие поочередно прикладывается вдоль каждой оси, причем принимается гипотеза об их статистической независимости [5, 8].
Модальной массой при сейсмическом воздействии в направлении dir (dir = OX, OY, OZ) называется величина
, где Гidir = (Mψi, Idir), M — матрица масс, ψi — собственный вектор (форма колебаний, отвечающая i-й частоте), Idir — вектор, компоненты которого равны 1, если соответствуют степени свободы сейсмического входа по направлению dir, и нулю в противном случае,
— общая масса, участвующая в движении по направлению dir.
Суммой модальных масс по направлению dir называется величина
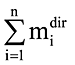
, где N — количество степеней свободы дискретной модели [3, 5, 8], n — количество удерживаемых собственных форм, n < < N.
В [3] на примере простой задачи показана зависимость некоторых внутренних усилий от суммы модальных масс (рис. 1).
Рис. 1
Здесь NΛ = NA ⁄ NA100; VΛ = V ⁄ V100; MΛ = Mov ⁄ Mov100, NA — продольная сила в стержне А, V — суммарная сдвигающая сила в основании, Mov — опрокидывающий момент. Символ 100 означает, что этот фактор получен при удержании в решении всех собственных форм дискретной модели (100% модальных масс).
Рис. 1 иллюстрирует тот факт, что для получения достоверной сейсмической реакции сооружения необходимо удерживать такое количество собственных форм, чтобы обеспечить высокий процент модальных масс (не менее 80%). При этом, разумеется, расчетная модель должна достаточно достоверно описывать поведение системы.
Таким образом, сумма модальных масс в сейсмическом анализе используется как индикатор достаточного количества удерживаемых форм колебаний.
При решении ряда задач было обнаружено, что суммы модальных масс сходятся крайне неравномерно и очень медленно [2]. При работе с расчетными моделями, содержащими большое количество степеней свободы (несколько сот тысяч), возникает серьезная проблема определения большого количества частот и форм собственных колебаний (порядка нескольких тысяч), представляющая собой сложную вычислительную задачу.
В этой работе представлен один из методов решения — блочный метод Ланцоша со сдвигами, реализованный автором в программном комплексе SCAD.
Блочный метод Ланцоша со сдвигами
В основу этой статьи положена работа Р. Граймса, Дж. Льюиса и Г. Саймона «A shifted block Lanczos algorithm for solving sparse symmetric generalized eigenproblems» [7]. Алгоритм данной реализации метода приведен в [4], а ее внедрение в программный комплекс SCAD представлено в [1]. Отметим, что блочная версия алгоритма позволяет сократить медленные операции ввода-вывода по сравнению с классической (неблочной) версией. Введение сдвигов существенно улучшает сходимость, а в случае определения большого количества собственных пар разделяет длинный частотный интервал на относительно короткие подинтервалы, ограничивая тем самым размерность пространства Крылова и заменяя экспоненциальный рост количества вычислений квазилинейным. Если исходная задача на собственные значения представляется как
, где K, M — соответственно положительно определенная разреженная матрица жесткости и полуопределенная матрица масс, {λ, ψ} — собственная пара. Вводя сдвиги σ1,σ2,…,σk, разбиваем этот частотный интервал на к+1 подинтервалов, на каждом из которых решаем задачу
где Kσ = K — σkM, λk = 1 ⁄ (ω2 — σk).
Таким образом, на каждом частотном подинтервале решается отдельная задача (4). Алгоритм выглядит так: при отсутствии какой-либо информации о спектре собственных частот полагаем σ1 = 0. Затем выполняем L шагов блочного метода Ланцоша и определяем сошедшиеся собственные пары. Далее анализируется сумма модальных масс для сошедшихся собственных пар. Если хотя бы по одному из направлений сейсмического входа сумма модальных масс меньше указанной, осуществляется переход к новому частотному интервалу. Кроме сошедшихся собственных пар имеются приближения собственных частот, которые еще не сошлись. Именно они используются для прогнозирования нового значения параметра сдвига σ2. Приняв сдвиг на основе такого прогноза, продолжаем вычисления на новом частотном интервале до тех пор, пока не определим все собственные числа, лежащие слева от сдвига и справа от последнего собственного числа, соответствующего сошедшейся собственной паре с предыдущего частотного интервала. Затем снова определяем суммы модальных масс. И так до тех пор, пока не будет достигнута достаточная сумма модальных масс.
Пример расчета
На рис. 2 приведена расчетная модель здания, включающая 8937 узлов, 9073 конечных элементов и 52 572 уравнения.
Рис. 2. Расчетная модель здания
По количеству уравнений эта задача на сегодняшний день относится к классу средних, однако по сложности решения обобщенной проблемы собственных значений она очень трудна, так как вследствие значительной жесткости несущих конструкций в нижней части спектра расположены локальные формы колебаний (рис. 3, 4), и только форма колебаний, соответствующая 522-й частоте (рис. 5), существенно влияет на сейсмическую реакцию сооружения (m522ox = 29%, тогда как
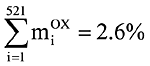
Рис. 3. Первая форма колебаний, частота 4,183 Гц
Рис. 4. Четвертая форма колебаний, частота 4,365 Гц
Наибольший вклад дает 523-я форма колебаний, представленная на рис. 5.
Рис. 5. 523-я форма колебаний, частота 5,756 Гц
Для обеспечения требуемых сумм модальных масс пришлось определить 2398 собственных пар.
Спектр собственных частот для этой задачи очень густой — в интервале [4.183, 5.756] Гц лежит 523 собственных частоты.
Зависимость сумм модальных масс от количества удерживаемых собственных форм приведена на рис. 6.
Рис. 6. Зависимость сумм модальных масс (Mx, My, Mz) от количества удерживаемых собственных форм
Выводы
При расчетах зданий и сооружений на сейсмику периодически встречаются задачи, в которых в нижней части спектра лежит большое количество локальных форм колебаний, причем спектр собственных частот является очень густым. Такие задачи создают серьезные проблемы, поскольку вычислительные алгоритмы, реализованные в современных компьютерных системах МКЭ-анализа, как правило, в таких случаях оказываются малоэффективными. Разработанный в программном комплексе SCAD алгоритм блочного метода Ланцоша со сдвигами, реализующий сейсмический режим, позволяет значительно продвинуться в решении этой проблемы.
Литература
- Карпиловский В.С., Криксунов Э.З., Фиалко С.Ю. Блочный метод Ланцоша со спектральными трансформациями для решения больших МКЭ задач собственных колебаний. — Вісник Одеського національного морського університету. — 2003, № 10, с. 93−99.
- Перельмутер А.В., Карпиловский В.С., Фиалко С.Ю., Егупов К.В. Опыт реализации проекта МСН СНГ «Строительство в сейсмических районах» в программной системе SCAD. — Вісник Одеської державної академії будівництва та архітектури. — 2003, випуск 9, с. 147−159.
- Фиалко С.Ю. Некоторые особенности анализа частот и форм собственных колебаний при расчете сооружений на сейсмические воздействия. — Вісник Одеської державної академії будівництва та архітектури. — 2002, випуск 8, с. 193−201.
- Фиалко С.Ю. О решении обобщенной проблемы собственных значений. — В кн. Перельмутер А.В., Сливкер В.И. Расчетные модели сооружений и возможность их анализа. — Издание второе. К.: Сталь, 2002, с. 570−597.
- Clough R., Penzien J. Dynamics of structures. — New York: McGraw-Hill, Inc., 1975. — 527 p.
- Fialko S.Yu., Kriksunov E.Z. and Karpilovskyy V.S. A block Lanczos method with spectral transformations for natural vibrations and seismic analysis of large structures in SCAD software. Proceedings of the CMM-2003 — Computer Methods in Mechanics, June 3−6, 2003. Gliwice, Poland, р. 129−130.
- Grimes R.G., Lewis J.G., Simon H.D. A shifted block Lanczos algorithm for solving sparse symmetric generalized eigenproblems. SIAM J. Matrix Anal. Appl. V. 15, 1: pp. 1−45, 1994.
- Wilson E.L. Three dimensional dynamic analysis of structures. California, Computers and Structures, Inc., Berkeley, USA, 1996. — 261 p.
Сергей Фиалко
д.т.н., с.н.с., проф.
Киевский национальный университет
строительства и архитектуры
Особенности задания данных сейсмических воздействий
Поправочный коэффициент
задается в данных всех сейсмических загружений для корректировки исходных
данных, если имеется необходимость полнее учесть требования норм. Этот
коэффициент может принимать любое положительное значение, и на него умножаются
результаты расчета инерционных сил от сейсмического воздействия. В качестве
примеров можно рассмотреть следующие случаи использования значения поправочного
коэффициента, отличного от единицы:
- категория грунта требует изменения сейсмичности площадки (например,
уменьшения ее на один балл), что приводит к необходимости задания
6-балльной сейсмики (см., например, таблицу 1 СП 14.13330.2014).
Учитывая то, что повышение сейсмичности на 1 балл приводит к удвоению
результата, можно указать сейсмичность площадки как 7-балльную и
задать значение поправочного коэффициента равным 0,5; - необходимо проверить расчетом реально существующую конструкцию
на воздействие землетрясения интенсивностью 8,5 баллов. Достаточно
указать сейсмичность площадки в 8 баллов и задать значение поправочного
коэффициента равным 20,5 = 1,414, т.к. значение ускорения
грунта вычисляется по формуле K*2N
и (K*28,5)/(K*28) = 1,414.
Требование об учете
крутящего сейсмического момента в актуализированной редакции
российских норм «Строительство в сейсмических районах» (СП 14.13330.2014)
формулируется следующим образом:
«5.16 При расчете зданий и сооружений длиной
или шириной более 30 м по консольной
РДМ помимо сейсмической нагрузки, определяемой по 5.5, необходимо
учитывать крутящий момент относительно вертикальной оси здания или сооружения,
проходящей через его центр жесткости. Значение расчетного эксцентриситета
между центрами жесткостей и масс зданий или сооружений в рассматриваемом
уровне следует принимать не менее 0,1B, где B – размер здания или сооружения
в плане в направлении, перпендикулярном к действию силы Sk».
Аналогичные требования имеются в нормах Украины — ДБН В.1.1-12:2006,
Казахстана — РК 2.03-30-2006 и ряда других стран.
При использовании SCAD обычно
применяются расчетные динамические модели (РДМ) плоского или
пространственного типов и указанная рекомендация, относящаяся к консольным
РДМ теряет свою силу. Однако расчет на условный крутящий момент может
потребоваться в тех случаях, когда регулярная конструктивная схема под
действием сейсмики претерпевает только поступательные перемещения.
Типичным примером может служить каркас с рядами одинаковых поперечных
рам, которые синхронно изгибаются и все диски перекрытий получают линейные
смещения.
Если рассчитываемый объект именно таков и закручивание дисков перекрытий
нет, то рекомендуется искусственно ввести несимметрию в схему. Это можно
сделать, взяв собственный вес (следовательно, и массу) в одной половине
здания с коэффициентом надежности по нагрузке, а в другой половине — без
этого коэффициента. Тогда появится естественное закручивание и не потребуется
использовать рекомендацию п. 5.15 СНиП.
Можно также использовать описанное ниже смещение центров масс этажей.
Сдвиг центров масс
Реальное сейсмическое воздействие отличается тем, что ускорения грунтового
основания под сооружением не являются строго синхронными и за счет этой
неравномерности могут проявляться эффекты закручивания сооружения.
Для учета пространственных изменений движения грунта и погрешностей,
возможных при определении центра масс, в Еврокоде и в нормах республики
Казахстан предлагается расчетный центр масс на каждом этаже
сместить от своего номинального положения на величину случайного эксцентриситета:
ek=Lkhek,
hek=±0,05fek
где Lk – размер
перекрытия, перпендикулярного к направлению действия сейсмической нагрузки,
fek – коэффициент
учитывающий нерегулярность здания в уровне k-го
этажа (указан в нормах Казахстана).
Для сдвижки центра масс относительно вертикальной плоскости, проходящей
через центр масс и параллельной заданному направлению сейсмического воздействия
S, используется прием увеличения
масс с одной стороны и уменьшения с другой таким способом, что бы суммарная
масса оставалась неизменной. При этом для каждого этажа рассматриваются
массы расположенные в уровне его перекрытия, поскольку именно здесь находятся
основные нагрузки обладающие массой (собственный вес и все полезные).
При заданном направлении сейсмического воздействия размер Lk
определяется автоматически как расстояние между наиболее удаленными друг
от друга узлами, в которых имеются приведенные массы. Поэтому в расчетной
схеме в виде консольного стержня с единственной массой на этаже Lk=0 и никакого смещения
не будет.
Для задания данных о смещении центров масс этажей следует воспользоваться
одноименной кнопкой (предполагается, что предварительно созданы группы
элементов, которые соответствуют различным этажам). Нажатие кнопки приводит
к появлению диалогового окна, в котором с помощью кнопок Добавить и Удалить
можно создать таблицу с данными о требуемых сдвигах центров масс. В первом
столбце этой таблицы из списка имеющихся групп элементов выбирается нужная
группа (этаж), а во втором столбце следует задать описанный выше коэффициент
hek.
Сдвиг центров масс выполняется только для тех загружений, в которых
учитывается (задано) направление воздействия.
Число учитываемых
форм задается во всех диалогах. Однако если заданы проценты модальных
масс, которые необходимо достигнуть для каждого направления, и выбран
метод Ланцоша вычисления собственных чисел и форм колебаний, то будет
найдено не меньше заданного числа
форм.
Учет вертикальной
составляющей сейсмической нагрузки требуется для ряда случаев сейсмической
нагрузки. Но она не может быть учтена автоматически, поскольку в описании
расчетной схемы, принятом в комплексе SCAD
и многих других программах, использующих метод конечных элементов, отсутствуют
такие понятия, как «горизонтальная или наклонная консольная конструкция»,
«пролетное строение моста» или «…пролет более 24 метров». Эти и другие
случаи рассчитываются на действие вертикальной сейсмической нагрузки,
если при задании исходных данных указать ее направление вдоль оси Z.
Расчетные значения
НДС, например, в соответствии с формулой (8) СП 14.13330.2014,
компоненты сейсмической реакции вычисляются как корень квадратный из суммы
квадратов значений, соответствующих различным формам собственных колебаний.
Это нелинейное преобразование (оценка Розенблюма) приводит к тому, что
перемещения и внутренние усилия не соответствуют друг другу и не удовлетворяют
условиям равновесия, поскольку для разных форм собственных колебаний они
реализуются в различные моменты времени. Этот факт следует учитывать при
анализе результатов расчета. Соответствие указанных компонентов гарантируется
лишь для каждой формы в отдельности.
При расчете симметричных в плане конструкций может возникнуть ситуация,
когда появляются перемещения (и соответствующие им усилия) не только по
направлению действия сейсмической силы, но и в ортогональном направлении,
хотя, исходя из условий симметрии, этого, казалось бы, не должно быть.
Происходит это вследствие реализации формулировок норм, что можно показать
на простейшем примере.
Пример.
Пусть вертикально стоящая консоль с массой на вершине имеет формы колебаний
(векторы записаны в строку) f1(1)={1;
0} и f2(1)={0; 1}.
Тогда при направляющих косинусах {1; 0} мы получим полный учет первой
формы, а вторая форма не сработает, и ответ в некоторых условных единицах
будет {1; 0}. Но, если эта же пара кратных форм определится как f1(2)={0,707; 0,707}
и f2(2) ={0,707; -0,707},
то мы получим ответ {1; 1}. Разнозначные компоненты не уничтожат
друг друга, так как суммируются квадраты (!)
компонент и затем извлекается корень из суммы.
Остается только заметить, что для кратных собственных значений, характерных
для симметричных конструкций, когда все направления равноправны, решение
f1(1), f2(1)
и решение f1(2), f2(2) абсолютно равноправны.
Какое из них выберет программа (любая, а не только SCAD),
определяется такими неуправляемыми деталями, как ошибки округления чисел
с плавающей запятой.
Проблема исчезает при расчете по акселерограммам, поскольку там нет
операции «корень из суммы квадратов».
Учет близости частот.
Например, в соответствии с формулой (9) СП 14.13330.2014 компоненты сейсмической
реакции необходимо вычислять с учетом взаимной корреляции близких частот.
При расчете по некоторым нормативным документам можно выбрать способ корреляции,
если разрешено несколько вариантов.
Вычисление остаточных
членов. Данный маркер указывает программе на необходимость добавить
к множеству собственных форм колебаний «остаточные формы», которые дополнят
сумму модальных масс по соответствующим направлениям до 100%. Этим формам
«приписывается» частота, равная частоте последней формы, которая определена
на основании стандартного модального анализа. Здесь следует обратить внимание
на то, что даже если не определено ни одной собственной пары, то остаточные
формы все равно обеспечат 100% модальных масс (в нормативных документах
вводится следующее требование: определенный процент модальных масс необходимо
набрать «честно» и только остаток разрешается покрыть за счет остаточных
форм). Предполагается, что взаимной корреляции остаточных форм нет.
Графики коэффициентов
динамичности — некоторые нормы допускают использование специальных
форм графика (спектра) коэффициентов динамичности. График может быть задан
в виде кусочно-линейной функции и сохраняться в файле с расширением .spd. Кроме единого графика предусмотрена
возможность задания до шести графиков — отдельно для каждого направления
воздействия.
Ниже приведен формат файла с описанием графика коэффициентов динамичности.
Аналогичный по формату файл может быть получен с использованием программы-сателлита
Редактор
графика коэффициентов динамичности, входящей в комплект поставки
системы SCAD Office. Если файл
с графиком выбран, то кнопка 
для просмотра графика.
Спектр
коэффициентов динамичности
#
0.030 1.030 0.060 1.45 0.100 2.500 0.147 3.100
0.202 2.820 0.261 2.64 0.359 2.560 0.464 2.030
0.681 1.400 1.000 1.06 1.565 0.650 0.966 0.390
До символа # идет комментарий, затем описываются вершины ломаной, аппроксимирующей
график, где последовательно для каждой точки задаются период в секундах
и значение соответствующего ему коэффициента.
Файлы акселлерограмм
(расширение .spc) используются
при расчетах по акселерограммах. Они должны находиться в том же каталоге,
что и данные задачи. Вместе с комплексом поставляется несколько стандартных
акселлерограмм, которые находятся в каталоге программ. Приведем пример
одной из них, имеющей имя 1m1-z.spc:
Расчетная акселерограмма в cм/(c*c) для MPЗ на
площадке атомного реактора.
Компонента — Z. Mодель
— M1c. Amax = 42.2 cм/(c*c).
Количество
точек N = 2047; Шаг по времени Dt = 0.05000
c.
#
0.01 2047 0.05
0.0 0.0 -0.0 -0.3 -0.6 -0.4 0.8 1.8 1.9 0.3
-1.6 -2.5 -3.5 -2.7
-1.7 -1.3 2.0 3.6 0.1 -0.6
…
Ординаты акселлерограммы могут быть заданы в любых единицах измерения.
Первое число после символа # — коэффициент перевода используемых единиц,
на который умножаются заданные значения для получения данных в м/с2.
В данном случае этот коэффициент равен 0,01. Затем следуют количество
точек (2047), шаг по времени (0.05 сек) и последовательно значения ординат.
В качестве разделителя целой и дробной частей используется десятичная
точка. На странице предусмотрено задание масштабного множителя к ординатам
акселлерограммы.
Для упрощения процесса подготовки акселерограмм в SCAD
Office включена специальная программа Редактор Акселерограмм.
Если файл с акселерограммой выбран, то кнопка 
позволяет вызвать Редактор Акселерограмм
для просмотра акселерограммы и ее параметров.
Недостаточное количество итераций при определении собственных векторов скад
Да, в новом так не работает, но легко решается через «Спектр жесткостных характеристик».
При возможности посмотрю на очередном расчёте. Не пытались писать письма в SCAD?
Собственно, справка скада:
В случаях, когда выполняется проверка устойчивости по комбинациям загружений, среди которых имеются динамические, требуется проявить некоторую осторожность, связанную с двумя обстоятельствами:
результаты динамического нагружения являются знакопеременными;
в тех случаях, когда результаты динамического расчета сформированы как корень квадратный из суммы квадратов (ККСК) модальных вкладов, нарушены условия равновесия и геометрической связности узловых перемещений.
Рассмотрим эти обстоятельства порознь.
Поскольку заранее неизвестно, какой знак результата динамического расчета является более опасным с точки зрения проверки устойчивости, то следует рассмотреть обе возможности. Так, например, если при расчете устойчивости рассматривается комбинация (L1)*1+(L2)*0.9+(L3)*0.7+(L4)*0.8, в которой нагружение (L3) является динамическим, то следует также выполнить проверку на комбинацию (L1)*1+(L2)*0.9+(L3)*(-0.7)+(L4)*0.8. При наличии нескольких динамических нагружений приходится перебирать все варианты знаков для их результатов.
Несовместность усилий связанная с использованием ККСК (естественно, если учтена не только одна форма собственных колебаний), вообще говоря, никаких неприятностей не вызывает. Просто проверяется коэффициент запаса устойчивости при пропорциональном росте всех внутренних усилий, игнорируя тот факт, что эти усилия нарушают условия равновесия.
Но несовместность узловых перемещений приводит к тому, что имеющиеся в схеме абсолютно жесткие тела получают искажения (по сути, они деформируются, что не соответствует их физической природе). Сложность состоит в том, что для этих элементов матрица К1(λ), не определяется внутренними силами или напряжениями, а вычисляется по значениям узловых перемещений, которые определяют изменение пространственной ориентации бесконечно жесткого конечного элемента (см. 9.5.1 в работе [3]). Несовместность узловых перемещений может привести к фатальной ошибке при вычислении К1(λ).
В связи с этим программа предусматривает обнуление матрицы К1(λ) при проверке устойчивости для комбинаций содержащих динамическое нагружение с более чем одной учитываемой формой собственных колебаний. Об этом в протоколе расчета появляется соответствующее предупреждение.
Источник
CADmaster
Реализация в программном комплексе SCAD блочного метода Ланцоша со сдвигами применительно к сейсмическому анализу сооружений
Как избежать проблем, возникающих из-за большого количества локальных форм колебаний при расчетах зданий и сооружений на сейсмику? Разработанный в программном комплексе SCAD алгоритм блочного метода Ланцоша со сдвигами, реализующий сейсмический режим, позволяет значительно продвинуться в решении этой задачи.
Скачать статью в формате PDF — 793.8 Кбайт
Главная » CADmaster №5(40) 2007 » Архитектура и строительство Реализация в программном комплексе SCAD блочного метода Ланцоша со сдвигами применительно к сейсмическому анализу сооружений
Введение
Суммой модальных масс по направлению dir называется величина 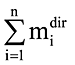
Рис. 1 иллюстрирует тот факт, что для получения достоверной сейсмической реакции сооружения необходимо удерживать такое количество собственных форм, чтобы обеспечить высокий процент модальных масс (не менее 80%). При этом, разумеется, расчетная модель должна достаточно достоверно описывать поведение системы.
Таким образом, сумма модальных масс в сейсмическом анализе используется как индикатор достаточного количества удерживаемых форм колебаний.
При решении ряда задач было обнаружено, что суммы модальных масс сходятся крайне неравномерно и очень медленно [2]. При работе с расчетными моделями, содержащими большое количество степеней свободы (несколько сот тысяч), возникает серьезная проблема определения большого количества частот и форм собственных колебаний (порядка нескольких тысяч), представляющая собой сложную вычислительную задачу.
В этой работе представлен один из методов решения — блочный метод Ланцоша со сдвигами, реализованный автором в программном комплексе SCAD.
Блочный метод Ланцоша со сдвигами
, где K, M — соответственно положительно определенная разреженная матрица жесткости и полуопределенная матрица масс, <λ, ψ>— собственная пара. Вводя сдвиги σ1,σ2,…,σk, разбиваем этот частотный интервал на к+1 подинтервалов, на каждом из которых решаем задачу
Таким образом, на каждом частотном подинтервале решается отдельная задача (4). Алгоритм выглядит так: при отсутствии какой-либо информации о спектре собственных частот полагаем σ1 = 0. Затем выполняем L шагов блочного метода Ланцоша и определяем сошедшиеся собственные пары. Далее анализируется сумма модальных масс для сошедшихся собственных пар. Если хотя бы по одному из направлений сейсмического входа сумма модальных масс меньше указанной, осуществляется переход к новому частотному интервалу. Кроме сошедшихся собственных пар имеются приближения собственных частот, которые еще не сошлись. Именно они используются для прогнозирования нового значения параметра сдвига σ2. Приняв сдвиг на основе такого прогноза, продолжаем вычисления на новом частотном интервале до тех пор, пока не определим все собственные числа, лежащие слева от сдвига и справа от последнего собственного числа, соответствующего сошедшейся собственной паре с предыдущего частотного интервала. Затем снова определяем суммы модальных масс. И так до тех пор, пока не будет достигнута достаточная сумма модальных масс.
Пример расчета
По количеству уравнений эта задача на сегодняшний день относится к классу средних, однако по сложности решения обобщенной проблемы собственных значений она очень трудна, так как вследствие значительной жесткости несущих конструкций в нижней части спектра расположены локальные формы колебаний (рис. 3, 4), и только форма колебаний, соответствующая 522-й частоте (рис. 5), существенно влияет на сейсмическую реакцию сооружения (m522 ox = 29%, тогда как 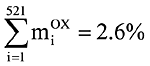
Реальный размер: 1344×1014. Рис. 3. Первая форма колебаний, частота 4,183 Гц’>)» title=»Рис. 3. Первая форма колебаний, частота 4,183 Гц»> 

Наибольший вклад дает 523-я форма колебаний, представленная на рис. 5.
Для обеспечения требуемых сумм модальных масс пришлось определить 2398 собственных пар.
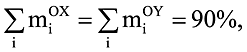
Спектр собственных частот для этой задачи очень густой — в интервале [4.183, 5.756] Гц лежит 523 собственных частоты.
Зависимость сумм модальных масс от количества удерживаемых собственных форм приведена на рис. 6.
Источник
Методы решения задач о собственных
значениях и векторах матриц
Постановка задачи
Равенство (2.1) равносильно однородной относительно [math]X[/math] системе:
являются собственными векторами.
Требуется найти собственные значения и собственные векторы заданной матрицы. Поставленная задача часто именуется второй задачей линейной алгебры.
Проблема собственных значений (частот) возникает при анализе поведения мостов, зданий, летательных аппаратов и других конструкций, характеризующихся малыми смещениями от положения равновесия, а также при анализе устойчивости численных схем. Характеристическое уравнение вместе с его собственными значениями и собственными векторами является основным в теории механических или электрических колебаний на макроскопическом или микроскопическом
уровнях.
2. Попарно различным собственным значениям соответствуют линейно независимые собственные векторы; k-кратному корню характеристического уравнения соответствует не более [math]k[/math] линейно независимых собственных векторов.
3. Симметрическая матрица имеет полный спектр [math]\lambda_i,
4. Положительно определенная симметрическая матрица имеет полный спектр действительных положительных собственных значений.
Метод непосредственного развертывания
Полную проблему собственных значений для матриц невысокого порядка [math](n\leqslant10)[/math] можно решить методом непосредственного развертывания. В этом случае будем иметь
Алгоритм метода непосредственного развертывания
3. Для каждого собственного значения составить систему (2.4):
Замечание. Каждому собственному значению соответствует один или несколько векторов. Поскольку определитель [math]|A-\lambda_iE|[/math] системы равен нулю, то ранг матрицы системы меньше числа неизвестных: [math]\operatorname(A-\lambda_iE)=r и в системе имеется ровно [math]r[/math] независимых уравнений, а [math](n-r)[/math] уравнений являются зависимыми. Для нахождения решения системы следует выбрать [math]r[/math] уравнений с [math]r[/math] неизвестными так, чтобы определитель составленной системы был отличен от нуля. Остальные [math](n-r)[/math] неизвестных следует перенести в правую часть и считать параметрами. Придавая параметрам различные значения, можно получить различные решения системы. Для простоты, как правило, попеременно полагают значение одного параметра равным 1, а остальные равными 0.
2. Находим его корни (собственные значения): [math]\lambda_1=5,
3. Составим систему [math](A-\lambda_iE)X^i=0,
Для [math]\lambda_2=-1[/math] имеем
1. Запишем характеристическое уравнение (2.5):
2. Корни характеристического уравнения: [math]\lambda_<1,2>=1[/math] (кратный корень), [math]\lambda_3=3[/math] — собственные значения матрицы.
3. Найдем собственные векторы.
Для [math]\lambda_<1,2>=1[/math] запишем систему [math](A-\lambda_<1,2>E)\cdot X^<1,2>=0\colon[/math]
Для собственного значения [math]\lambda_3=3[/math] запишем систему [math](A-\lambda_3E)\cdot X^3=0\colon[/math]
Метод итераций для нахождения собственных значений и векторов
Пусть матрица [math]A[/math] имеет [math]n[/math] линейно независимых собственных векторов [math]X^i,
Алгоритм метода итераций
1. Процесс последовательных приближений
2. Вместо применяемой в пункте 4 алгоритма формулы для [math]\lambda_1^<(k+1)>[/math] можно взять среднее арифметическое соответствующих отношений для разных координат.
3. Метод может использоваться и в случае, если наибольшее по модулю собственное значение матрицы [math]A[/math] является кратным, т.е.
4. При неудачном выборе начального приближения [math]X^<1(0)>[/math] предел отношения [math]\frac>>[/math] может не существовать. В этом случае следует задать другое начальное приближение.
5. Рассмотренный итерационный процесс для [math]\lambda_1[/math] сходится линейно, с параметром [math]c=\frac<\lambda_2><\lambda_1>[/math] и может быть очень медленным. Для его ускорения используется алгоритм Эйткена.
6. Если [math]A=A^T[/math] (матрица [math]A[/math] симметрическая), то сходимость процесса при определении [math]\rho(A)[/math] может быть ускорена.
Так как собственный вектор определяется с точностью до постоянного множителя, то [math]X^1[/math] лучше пронормировать, т.е. поделить все его компоненты на величину нормы. Для рассматриваемого примера получим
Согласно замечаниям, в качестве собственного значения [math]\lambda_1[/math] матрицы можно взять не только отношение
Выполним расчеты согласно методике (табл. 10.11).
В результате получено собственное значение [math]\lambda_1\cong 3,\!00003[/math] и собственный вектор [math]X^1= \begin 88573&-88573&1\end^T[/math] или после нормировки
Метод вращений для нахождения собственных значений
При реализации метода вращений преобразование подобия применяется к исходной матрице [math]A[/math] многократно:
Угол поворота [math]\varphi^<(k)>[/math] определяется по формуле
где [math]|2\varphi^<(k)>|\leqslant \frac<\pi><2>,
i ( [math]a_[/math] выбирается в верхней треугольной наддиагональной части матрицы [math]A[/math] ).
Замечание. В двумерном пространстве с введенной в нем системой координат [math]Oxy[/math] с ортонормированным базисом [math]\<\vec,\vec\>[/math] матрица вращения легко получается из рис. 2.1, где система координат [math]Ox’y'[/math] повернута на угол [math]\varphi\colon[/math]
Алгоритм метода вращений
2. Выделить в верхней треугольной наддиагональной части матрицы [math]A^<(k)>[/math] максимальный по модулю элемент [math]a_^<(k)>,
Собственные векторы [math]X^i[/math] находятся как i-e столбцы матрицы, получающейся в результате перемножения:
2. Контроль правильности выполнения действий по каждому повороту осуществляется путем проверки сохранения следа преобразуемой матрицы.
3. При [math]n=2[/math] для решения задачи требуется одна итерация.
Пример 2.5. Для матрицы [math]A=\begin 2&1\\1&3 \end[/math] методом вращений найти собственные значения и собственные векторы.
3°. Находим угол поворота матрицы по формуле (2.7), используя в расчетах 11 цифр после запятой в соответствии с заданной точностью:
4°. Сформируем матрицу вращения:
5°. Выполним первую итерацию:
2. Максимальный по модулю наддиагональный элемент [math]|a_<12>|= 4,\!04620781325\cdot10^ <-12>. Для решения задачи (подчеркнем, что [math]n=2[/math] ) с принятой точностью потребовалась одна итерация, полученную матрицу можно считать диагональной. Найдены следующие собственные значения и собственные векторы:
3°. Находим угол поворота:
3(1). Найдем угол поворота:
3(2). Найдем угол поворота:
5(2). Выполним третью итерацию и положим [math]k=3[/math] и перейдем к пункту 2:
3(3). Найдем угол поворота:
5(3). Выполним четвертую итерацию и положим [math]k=4[/math] и перейдем к пункту 2:
3(4). Найдем угол поворота
5(4). Выполним пятую итерацию и положим [math]k=5[/math] и перейдем к пункту 2:
Собственные значения: [math]\lambda_1\cong a_<11>^<(5)>= 6,\!895\,,
X^3=\begin-0,\!473\\-0,\!171\\0,\!864 \end[/math] или после нормировки
Источник
n17.doc
6. Управление расчетом
В главе 1 уже отмечалось, что выполнение расчета возможно только при условии, когда исходные данные текущего проекта содержат обязательный минимум информации, т.е. геометрию расчетной схемы, описание жесткостных характеристик всех элементов и, по крайней мере, одно загружение. Так как полный контроль исходных данных выполняется на первом шаге расчета, то при наличии этой информации процессор стартует.
Р
Активизация расчета выполняется из соответствующего раздела Дерева проекта. После чего появляется диалоговое окно Параметры расчета (рис. 6.1), в котором следует выбрать режим работы процессора (Полный расчет или Продолжение расчета) и нажать кнопку Выполнить расчет. Как правило, режим Продолжение расчета используется в тех случаях, когда по какой-либо причине был прерван расчет задачи. Им можно воспользоваться и после модификации исходных данных, которые не затрагивали узлы, связи и элементы (например, после корректировки нагрузок).
Для изменения параметров настройки вычислительного процесса используется кнопка Параметры, после нажатия которой в диалоговом окне становятся доступными поля ввода данных и опции управления расчетом (рис. 6.2).

Параметры расчета с доступными полями ввода данных и опциями управления расчетом
Параметры настройки условно можно разделить на шесть групп.
В первой находятся параметры управления процессом оптимизации матрицы жесткости.
Вторая содержит информацию, определяющую точность, с которой выполняется разложение матрицы, а также вычисляются собственные формы и частоты при решении задач динамики.
В третьей сосредоточены параметры настройки процесса анализа устойчивости.
Пятую составляют параметры управления ходом вычислений.
В шестой находятся параметры управления протоколом выполнения расчета.
Значения параметров управления расчетом, используемые по умолчанию, соответствуют значениям, заданным при настройке комплекса (пункт меню Параметры расчета в разделе Опции окна управления проектом). Изменения, вносимые в эти данные при запуске на расчет конкретной задачи, запоминаются только для этой задачи.
Рассмотрим назначение основных параметров управления расчетом.
Точность разложения матрицы – определяет минимальную величину по диагонали треугольного разложения матрицы жесткости, появление которой следует рассматривать как признак геометрической изменяемости системы.
Точность решения собственной проблемы – определяет точность решения задачи на собственные значения.
Допустимая погрешность при решении системы уравнений – определяет допустимую погрешность в режиме контроля решения системы уравнений.
Масштабный множитель – используется для ограничения интервала поиска коэффициента запаса устойчивости. Если значение коэффициента больше заданного значения параметра, система считается устойчивой.
Точность вычислений – параметр задает критерий окончания итерационного процесса поиска коэффициента запаса устойчивости. При очень малых значениях этого параметра время расчета может существенно увеличиться.
Последние два параметра имеют приоритет перед аналогичными параметрами, заданными при подготовке исходных данных для постпроцессора анализа устойчивости.
Точность определения формы потери устойчивости – допустимая погрешность при определении формы потери устойчивости.
Кроме того могут быть заданы метод оптимизации матрицы жесткости, ширина ленты и порядок системы, при которых не выполняется оптимизация матрицы жесткости и максимальное количество итераций при определении форм потери устойчивости.
Три параметра используются для управления формированием протокола выполнения расчета:
Максимальное количество ошибок – количество ошибок в исходных данных, сообщения о которых попадают в протокол.
Максимальное количество предупреждений – количество предупреждений о возможных ошибках в исходных данных, сообщения о которых попадает в протокол.
Учет нагрузок в связях – при активизации этой опции в протокол попадают значения суммарных нагрузок в узлах с учетом нагрузок, приходящих в узлы с наложенными связями.
Опция Автоматический вызов расчетных постпроцессоров позволяет включить или отключить вычисление расчетных сочетаний усилий, комбинаций загружений, анализ устойчивости и другие задачи, для которых подготовлены исходные данные, после выполнения статического и динамического расчетов.
Источник
Результаты расчета в SCAD: инструменты анализа
После проведения любого расчета, необходимо увидеть результаты расчета в SCAD и проанализировать полученные данные. В обозначенном программном комплексе реализованы удобные инструменты отображения проверки используемых жесткостей у стержней в расчетной схеме.
Цветовая шкала проверки элементов в SCAD.
Для всех заданных в расчете конструктивных элементов (тех, у кого задан материал) могут отображаться результаты проверки несущей способности. Чтобы произвести визульный просмотр результатов, необходимо в дереве управления проектом перейти в раздел «Графический анализ» (рис. 1).
В появившемся окне будет доступна так же расчетная схема. Например, чтобы наглядно увидеть проходит сечение или нет, нужно сделать расчет профилей, щелкнув по одноименной кнопке (рис. 2).
После расчета появится возможность отображения степени использования элементов по множеству параметров. Этот режим открывается нажатием кнопки «Отображение результатов проверки на схеме» (рис. 3). Конструктивные элементы отображаются на схеме тремя цветами: зеленым, если несущая способность достаточна, красным — в противном случае или желтым, если несущая способность находится вблизи критического значения (фактор близок к 1,0), а красным — если элемент не проходит.
В случае, если проверяемый элемент красного цвета, то чтобы проверить причину его неудовлетворительного назначения, следует воспользоваться инструментом «Информация об элементе» — «Сталь. Факторы» — «Диаграмма факторов». В этом окне представлены всевозможные проверки действия назначенного сечения, а так же комбинация нагрузок, при котором достигаются наивысшие значения каждой из проверок (рис. 4.)
Анализ деформаций и перемещений в SCAD
Анализ перемещений в SCAD выполняется с помощью операций одноименного раздела (рис. 5) инструментальной панели. Для этого необходимо выполнить следующие действия:
Набор операций отображения позволяет получить различные формы представления результатов расчета перемещений. Каждой форме соответствует кнопка в инструментальной панели. При анализе перемещений от статических нагрузок в стержневых конструкциях можно воспользоваться кнопками:
При этом допускается совместное отображение деформированной схемы и одного из видов цветовой индикации. Узлы имеют цветовую идентификацию согласно определенному промежутку перемещений при выбранном направлении.
Эпюры усилий в SCAD
Поскольку независимо от режима в комплексе сохраняется преемственность функций управления, то анализ силовых факторов (в данном случае — построение эпюр) выполняется по тем же правилам, что и анализ перемещений (рис. 6).
Таким образом можно осуществлять анализ перемещений в SCAD.
Источник
Понравилась статья? Поделить с друзьями:
Become a DeepAI PRO

500 AI generator calls per month + $5 per 500 more (includes images)
1750 AI Chat messages per month + $5 per 1750 more
60 Genius Mode messages per month + $5 per 60 more
HD image generator access
Private image generation
Complete styles library
API access
Ad-free experience
*
This is a recurring payment that will happen monthly
*
If you exceed number of images or messages listed, they will be charged at a rate of $5
Pay as you go
100 AI Generator Calls (includes images)
350 AI Chat messages
Does not include Genius Mode
Private image generation
Complete styles library
API access
Ad-free experience

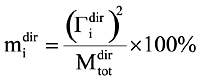
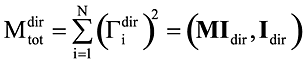
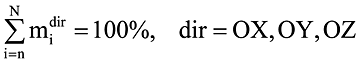
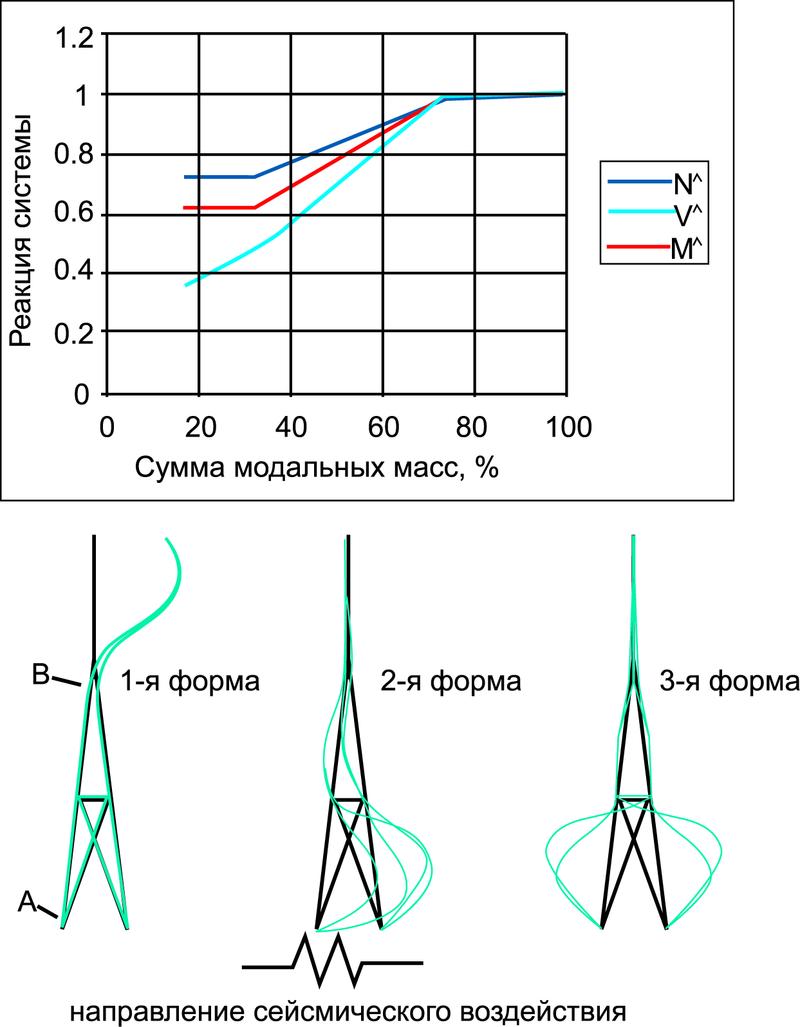
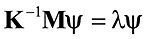
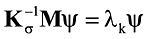
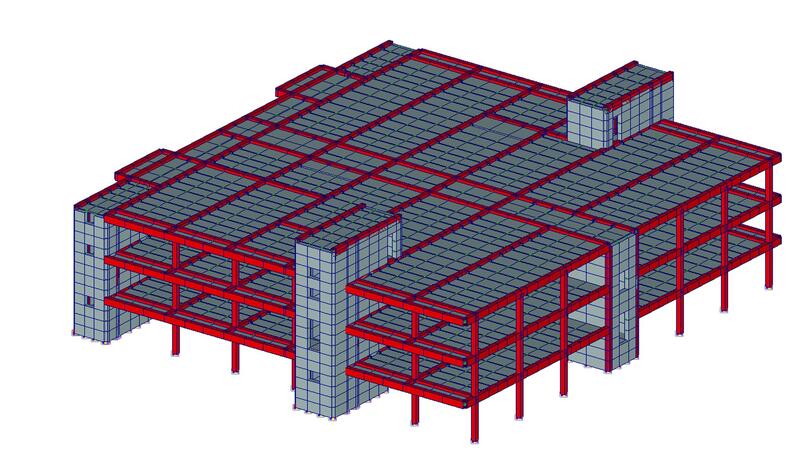
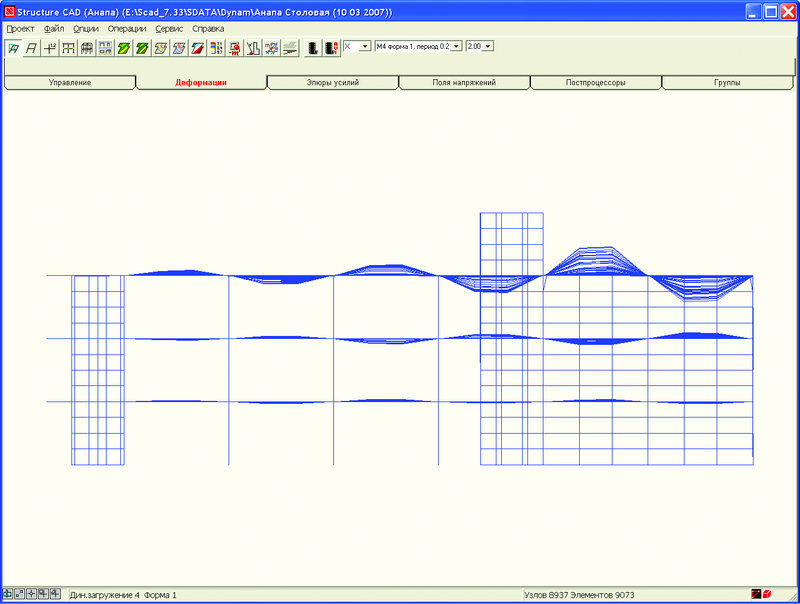
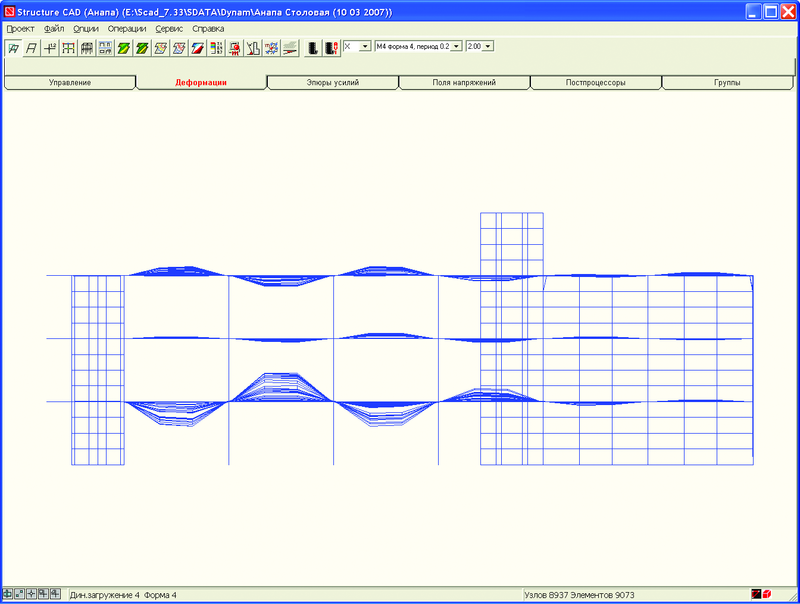
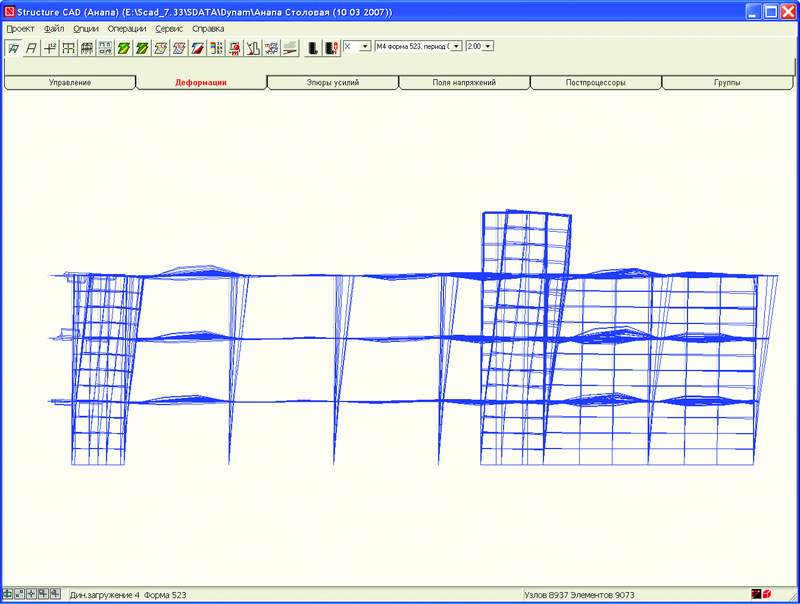
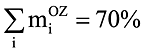
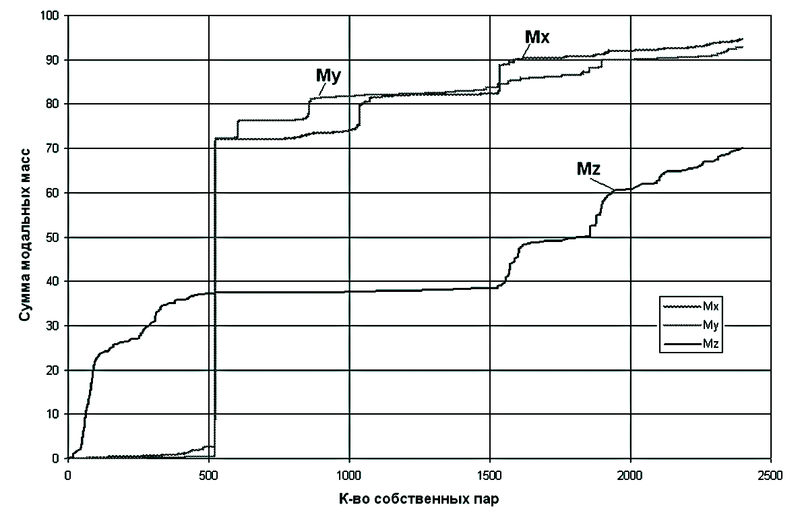
 матрица V { displaystyle V}
матрица V { displaystyle V} размером m × m { displaystyle м раз м}
размером m × m { displaystyle м раз м} .
. — произвольный вектор с евклидовой нормой. 1 { displaystyle 1}
— произвольный вектор с евклидовой нормой. 1 { displaystyle 1} .
. .
. .
. do:
do:
 (также Евклидова норма ).
(также Евклидова норма ). , тогда пусть vj = wj — 1 / β j { displaystyle v_ {j} = w_ {j-1} / beta _ {j}}
, тогда пусть vj = wj — 1 / β j { displaystyle v_ {j} = w_ {j-1} / beta _ {j}} ,
,
 .
. .
. .
. .
. . Пусть T = (α 1 β 2 0 β 2 α 2 β 3 β 3 α 3 ⋱ ⋱ ⋱ β м — 1 β м — 1 α м — 1 β м 0 β м α м) { displaystyle T = { begin {pmatrix} alpha _ {1} beta _ {2} 0 \ beta _ {2} alpha _ {2} beta _ {3} \ beta _ {3} alpha _ {3 } ddots \ ddots ddots beta _ {m-1} \ beta _ {m-1} alpha _ {m-1} beta _ {m} \ 0 beta _ {m} alpha _ {m} \ end {pmatrix}}}
. Пусть T = (α 1 β 2 0 β 2 α 2 β 3 β 3 α 3 ⋱ ⋱ ⋱ β м — 1 β м — 1 α м — 1 β м 0 β м α м) { displaystyle T = { begin {pmatrix} alpha _ {1} beta _ {2} 0 \ beta _ {2} alpha _ {2} beta _ {3} \ beta _ {3} alpha _ {3 } ddots \ ddots ddots beta _ {m-1} \ beta _ {m-1} alpha _ {m-1} beta _ {m} \ 0 beta _ {m} alpha _ {m} \ end {pmatrix}}} .
. для 1 < j < m {displaystyle 1
для 1 < j < m {displaystyle 1 .
. , как и для алгоритма «разделяй и властвуй» (хотя постоянный множитель может быть другим.) ; так как собственные конструкции вместе имеют m 2 { displaystyle m ^ {2}}
, как и для алгоритма «разделяй и властвуй» (хотя постоянный множитель может быть другим.) ; так как собственные конструкции вместе имеют m 2 { displaystyle m ^ {2}} элементов, это асимптотически оптимально.
элементов, это асимптотически оптимально. алгоритм Ланцоша можно рассматривать как схему сжатие с потерянными для эрмитовых матриц, которая подчеркивает сохранение крайних собственных значений.
алгоритм Ланцоша можно рассматривать как схему сжатие с потерянными для эрмитовых матриц, которая подчеркивает сохранение крайних собственных значений. из V { displaystyle V}
из V { displaystyle V} можно вычислить в O (n 3) { displaystyle O (n ^ {3})}
можно вычислить в O (n 3) { displaystyle O (n ^ {3})} time.
time. и β j { displaystyle beta _ {j}}
и β j { displaystyle beta _ {j}} ). Хаусхолдер менее параллелен, поскольку имеет последовательность O (n 2) { displaystyle O (n ^ {2})}
). Хаусхолдер менее параллелен, поскольку имеет последовательность O (n 2) { displaystyle O (n ^ {2})} вычисленных скалярных величин, каждая из которых зависит от предыдущей величины в последовательности.
вычисленных скалярных величин, каждая из которых зависит от предыдущей величины в последовательности. .
. (пока направление uj { displaystyle u_ {j}}
(пока направление uj { displaystyle u_ {j}}

 для каждого x ∈ span (v 1,…, vj) { displaystyle x in operatorname {span} (v_ {1}, dotsc, v_ {j})}
для каждого x ∈ span (v 1,…, vj) { displaystyle x in operatorname {span} (v_ {1}, dotsc, v_ {j})} и все 1 ⩽ j < m ; {displaystyle 1leqslant j
и все 1 ⩽ j < m ; {displaystyle 1leqslant j
 евклидовой нормы 1 { displaystyle 1}
евклидовой нормы 1 { displaystyle 1} .
. do:
do:
 пусть gk, j = vk ∗ uj + 1 ′ { displaystyle g_ {k, j} = v_ {k} ^ {*} u_ {j + 1} ‘}
пусть gk, j = vk ∗ uj + 1 ′ { displaystyle g_ {k, j} = v_ {k} ^ {*} u_ {j + 1} ‘} . (Это координаты A uj = uj + 1 ′ { displaystyle Au_ {j} = u_ {j + 1} ‘}
. (Это координаты A uj = uj + 1 ′ { displaystyle Au_ {j} = u_ {j + 1} ‘} относительно базисных векторов v 1,…, Vj { displaystyle v_ {1}, dotsc, v_ {j}}
относительно базисных векторов v 1,…, Vj { displaystyle v_ {1}, dotsc, v_ {j}} .)
.) . (Отменить компонент uj + 1 ′ { displaystyle u_ {j + 1} ‘}
. (Отменить компонент uj + 1 ′ { displaystyle u_ {j + 1} ‘} , который находится в span (v 1,…, vj) { displaystyle operatorname {span} (v_ {1}, dotsc, v_ {j}) }
, который находится в span (v 1,…, vj) { displaystyle operatorname {span} (v_ {1}, dotsc, v_ {j}) } , тогда пусть uj + 1 = uj + 1 ′ / ‖ uj + 1 ′ ‖ { displaystyle u_ {j + 1} = u_ {j + 1} ‘/ | u_ {j + 1}’ |}
, тогда пусть uj + 1 = uj + 1 ′ / ‖ uj + 1 ′ ‖ { displaystyle u_ {j + 1} = u_ {j + 1} ‘/ | u_ {j + 1}’ |} и vj + 1 = wj + 1 / ‖ Wj + 1 ‖ { displaystyle v_ {j + 1} = w_ {j + 1} / | w_ {j + 1} |}
и vj + 1 = wj + 1 / ‖ Wj + 1 ‖ { displaystyle v_ {j + 1} = w_ {j + 1} / | w_ {j + 1} |} ,
,
 произвольный вектор евклидовой нормы 1 { displaystyle 1}
произвольный вектор евклидовой нормы 1 { displaystyle 1} .
. .
. , тогда пусть vj + 1 = wj + 1 / hj + 1, j { displaystyle v_ {j + 1} = w_ {j + 1} / h_ {j + 1, j}}
, тогда пусть vj + 1 = wj + 1 / hj + 1, j { displaystyle v_ {j + 1} = w_ {j + 1} / h_ {j + 1, j}} ,
,
 для всех j < m {displaystyle j
для всех j < m {displaystyle j ;
;






 ,
,











![{ displaystyle { begin {align} lam bda _ {1} - theta _ {1} leqslant { frac {( lambda _ {1} - lambda _ {n}) left (1- | d_ {1} | ^ {2} справа)} {c_ {m -1} (2 rho +1) ^ {2} | d_ {1} | ^ {2}}} \ [6pt] = { frac {1- | d_ {1} | ^ {2}} {| d_ {1} | ^ {2}}} ( lambda _ {1} - lambda _ {n}) { frac {1} { cosh ^ {2} ((m-1) operatorname {arcosh} (1 + 2 rho))}} \ [6pt] = { frac {1- | d_ {1} | ^ {2}} {| d_ {1} | ^ {2}}} ( lambda _ {1} - lambda _ {n}) { frac {4} { left (R ^ {m-1} + R ^ {- (m-1)} справа) ^ {2}}} \ [6pt] leqslant 4 { frac {1- | d_ {1} | ^ {2}} {| d_ {1} | ^ {2}}} ( lambda _ {1} - lambda _ {n}) R ^ {- 2 (m-1)} end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a971e473f56e04b8e556a5085f49a1025a08878)