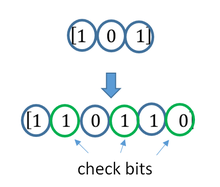
Коды
Боуза-Чоудхури-Хоквингема (БЧХ) –класс
циклических кодов, исправляющих кратные
ошибки, т. е. две и более (d0
5).
Теоретически
коды БЧХ могут исправлять произвольное
количество ошибок, но при этом существенно
увеличивается длительность кодовой
комбинации, что приводит к уменьшению
скорости передачи данных и усложнению
приемо-передающей аппаратуры (схем
кодеров и декодеров).
Методика
построения кодов БЧХ отличается от
обычных циклических, в основном, выбором
определяющего полинома P(х). Коды БЧХ
строятся по заданной длине кодового
слова n и числа исправляемых ошибок
S , при этом количество информационных
разрядов k не известно пока не выбран
определяющий полином.
Рассмотрим
процедуру кодирования с использованием
кода БЧХ на конкретных примерах.
Пример
1. Построить 15-разрядный код БЧХ,
исправляющий две ошибки в кодовой
комбинации (т. е. n = 15, S = 2).
Решение:
1.
Определим количество контрольных m и
информационных разрядов k
m
h S .
Определим
параметр h из формулы
n
= 2h-1,
h = log2(n+1)
= log216
= 4,
при
этом: m h
S = 42 = 8;
k = n-m = 15-8 = 7.
Таким
образом, получили (15, 7)-код.
2.
Определим параметры образующего
полинома:
—
количество минимальных многочленов,
входящих в образующий
L
= S = 2;
—
порядок старшего (все минимальные —
нечетные) минимального многочлена
= 2S-1 = 3;
—
степень образующего многочлена
= m 8.
3.
Выбор образующего многочлена.
Из
таблицы для минимальных многочленов
для кодов БЧХ (см. приложение 4) из колонки
4 (т. к. l = h = 4) выбираем два минимальных
многочлена 1 и 3 (т. к.
= 3):
M1(x)
= 10011;
M2(x)
= 11111.
При
этом
P(x)
=M1(x)M2(x)=1001111111=111010001=
x8+ x7+
x6+ x4+1.
4.
Строим образующую матрицу. Записываем
первую строку образующей матрицы,
которая состоит из образующего полинома
с предшествующими нулями, при этом
общая длина кодовой комбинации равна
n = 15. Остальные строки матрицы
получаем в результате k-кратного
циклического сдвига справа налево
первой строки матрицы.

Строки
образующей матрицы представляют собой
7 кодовых комбинаций кода БЧХ, а остальные
могут быть получены путем суммирования
по модулю 2 всевозможных сочетаний строк
матрицы.
Процедура
декодирования, обнаружения и исправления
ошибок в принятой кодовой комбинации
такая же, как и для циклических кодов с
d0 < 5
Пример
2. Построить 31-разрядный код БЧХ,
исправляющий три ошибки в кодовой
комбинации (т. е. n = 31, S = 3).
Решение:
1.
Определим количество контрольных
разрядов m и информационных разрядов
k.
m
h S.
Определим
параметр h из формулы
n
= 2h-1,h
= log2(n+1)
= log232
= 5,
при
этом: m h
S = 53 = 15;
k = n-m = 31-15 = 16.
Таким
образом, получили (31, 16)-код.
2.Определим
параметры образующего полинома:
—
количество минимальных многочленов,
входящих в образующий
L
= S = 3;
-
порядок
старшего минимального многочлена
=
3S-1 = 5;
-
степень
образующего многочлена
=
m 15.
-
Выбор
образующего многочлена.
Из
таблицы для минимальных многочленов
для кодов БЧХ ( приложение 4) из колонки
5 (т. к. l = h = 5) выбираем три минимальных
многочлена 1, 3 и 5 (т. к.
= 5):
M1(x)
=100101;
M2(x)
=111101;
M3(x)
=110111.
При
этом
P(x)
= M1(x)
M2(x)
M3(x)
=1000111110101111=
= x15+
x11 +x10+
x9+ x8+
x7+ x5+
x3 + x2+x+
1.
4.
Строим образующую матрицу. Записываем
первую строку образующей матрицы,
которая состоит из образующего полинома
с предшествующими нулями, при этом
общая длина кодовой комбинации равна
n = 31. Остальные строки матрицы
получаем в результате k-кратного
циклического сдвига справа налево
первой строки матрицы.
000000000000000100011111011111
G(31,16)=
000000000000001000111110111110
.
. .
100011111011111000000000000000
Строки
образующей матрицы представляют собой
16 кодовых комбинации кода БЧХ, а
остальные могут быть получены путем
суммирования по модулю 2 всевозможных
сочетаний строк матрицы.
Декодирование
кодов БЧХ. Коды БЧХ представляют собой
циклические коды и, следовательно, к
ним применимы любые методы декодирования
циклических кодов. Открытие кодов БЧХ
привело к необходимости поиска новых
алгоритмов и методов реализации кодеров
и декодеров. Получены существенно лучшие
алгоритмы, специально разработанные
для кодов БЧХ. Это алгоритмы Питерсона,
Бэрлекэмпа и др.
Применение
кодов БЧХ. Коды БЧХ используются для
защиты данных в ОП, лентах и дисках
контроля логических устройств и т. д.
Использование кодов БЧХ позволяет
снизить мощность передаваемых сигналов
(например через спутники, где увеличение
сигнала обходится дорого), позволяет
использовать более плотную запись на
магнитные носители и т. д. Коды БЧХ
используются для защиты данных в ОП, а
также на дисках и лентах, контроля работы
логических устройств, сжатия данных.
Коды
Рида –Соломона. Широко используемым
подмножеством кодов БЧХ являются коды
Рида-Соломона, которые позволяют
исправлять пакеты ошибок. Пакет
ошибок длины b представляет
собой последовательность из таких b
ошибочных символов, что первый и
последний из них отличны от нуля.
Существуют классы кодов Рида-Соломона,
позволяющие исправлять многократные
пакеты ошибок.
Коды Рида-Соломона
широко используются в устройствах
цифровой записи звука, в том числе на
компакт-диски. Данные, состоящие из
отсчетов объединяются в кадр, представляющий
кодовое слово. Кадры разбиваются на
блоки по 8 бит. Часть блоков являются
контрольными.
Обычно 1 кадр
(кодовое слово) = 32 символа данных +24
сигнальных символа +8 контрольных бит
= 256 бит.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
17.03.201529.7 Mб45Тимонин А.С. — Инж-эко справочник т 1.djvu
- #
17.03.201527.65 Mб39Тимонин А.С. — Инж-эко справочник т 3.djvu
- #
- #
- #
4. Циклические коды
4.1 Основные понятия
Циклическим кодом
называется линейный блоковый (n,k)-код, который характеризуется свойством
цикличности, т.е. сдвиг влево на один шаг любого разрешенного кодового слова
дает также разрешенное кодовое слово, принадлежащее этому же коду и у которого,
множество кодовых слов представляется совокупностью многочленов степени (n-1) и
менее, делящихся на некоторый многочлен g(x) степени r = n-k, являющийся
сомножителем двучлена xn+1.
Многочлен g(x) называется
порождающим.
Как следует из определения, в циклическом коде кодовые слова
представляются в виде многочленов 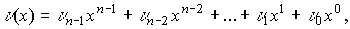
где n — длина кода;
— коэффициенты из поля GF(q).
Если код построен над полем GF(2), то
коэффициенты принимают значения 0 или 1 и код называется двоичным.
Пример. Если кодовое слово циклического кода 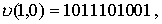
то соответствующий
ему многочлен 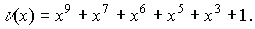
Например, если код
построен над полем GF(q)=GF(23), которое является расширением GF(2)
по модулю неприводимого многочлена f(z)=z3+z+1, а элементы этого поля
имеют вид, представленный в таблице 3,
| 0 | 000 | 0 | a3 | 011 | Z+1 |
| a0 | 001 | 1 | a4 | 110 | Z2+Z |
| a1 | 010 | Z | a5 | 111 | Z2+Z+1 |
| a2 | 100 | Z2 | a6 | 101 | Z2+1 |
то
коэффициенты 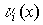
элементов этого поля и поэтому они сами отображаются в виде многочленов
следующего вида
где m — степень многочлена, по которому получено расширение поля GF(2);
ai — коэффициенты, принимающие значение элементов GF(2), т.е. 0 и
1.
Такой код называется q-ным.
Длина циклического кода
называется примитивной и сам код называется примитивным, если его длина
n=qm-1 над GF(q).
Если длина кода меньше длины примитивного кода,
то код называется укороченным или непримитивным.
Как следует
из определения общее свойство кодовых слов циклического кода — это их делимость
без остатка на некоторый многочлен g(x), называемый порождающим.
Результатом деления двучлена xn+1 на многочлен g(x)
является проверочный многочлен h(x).
При декодировании
циклических кодов используются многочлен ошибок e(x) и синдромный многочлен
S(x).
Многочлен ошибок степени не более (n-1) определяется из выражения
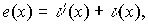
где 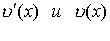
многочлены, отображающие соответственно принятое (с ошибкой) и переданное
кодовые слова.
Ненулевые коэффициенты в е(x) занимают позиции, которые
соответствуют ошибкам.
Пример.
Синдромный многочлен, используемый при декодировании циклического
кода, определяется как остаток от деления принятого кодового слова на
порождающий многочлен, т.е. 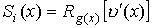
или
Следовательно, синдромный многочлен зависит непосредственно от многочлена
ошибок е(х).Это положение используется при построении таблицы
синдромов, применяемой в процессе декодирования. Эта таблица содержит список
многочленов ошибок (см. первый столбец стандартного расположения кода в разделе
2.4) и список соответствующих синдромов, определяемых из выражения 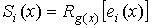
таблицу 4).
| (x) | S(x) |
| 1 | Rg(x)[1] |
| X | Rg(x)[x] |
| X2 | Rg(x)[x2] |
| · | · |
| · | · |
| · | · |
| X+1 | Rg(x)[x+1] |
| X2+1 | Rg(x)[x2+1] |
| · | · |
| · | · |
| · | · |
В процессе
декодирования по принятому кодовому слову вычисляется синдром, затем в таблице
находится соответствующий многочлен е(х), суммирование которого с принятым
кодовым словом дает исправленное кодовое слово, т.е. 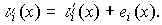
Перечисленные
многочлены 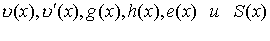
умножать и делить, используя известные правила алгебры, но с приведением
результата по mod 2, а затем по mod xn+1, если степень результата
превышает степень (n-1).
Примеры.
Допустим,
что длина кода n=7, то результат приводим по mod x7+1.
При
построении и декодировании циклических кодов в результате деления многочленов
обычно необходимо иметь не частное, а остаток от деления.
Поэтому
рекомендуется более простой способ деления, используя не многочлены, а только
его коэффициенты (вариант 2 в примере).
- Пример.
- 1.
- 2.
4.2 Матричное задание кодов
Циклический
код может быть задан порождающей и проверочной матрицами. Для их построения
достаточно знать порождающий g(x) и проверочный h(x) многочлены.
Для несистематического циклического кода матрицы строятся
циклическим сдвигом порождающего и проверочного многочленов, т.е. путем их
умножения на x 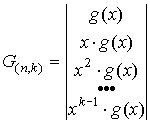
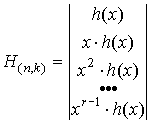
При построении
матрицы H(n,k) старший коэффициент многочлена h(x) располагается
справа.
Пример. Для циклического (7,4)-кода с порождающим многочленом
g(x)=x3+x+1 матрицы G(n,k) и H(n,k) имеют вид:
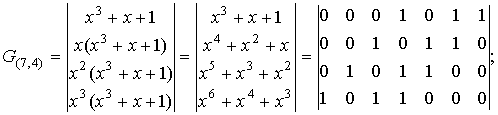
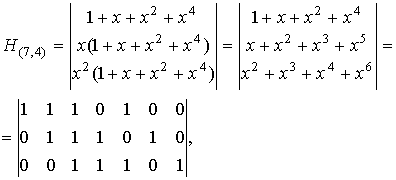
где 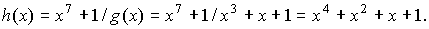
Для систематического циклического кода матрица G(n,k)
определяется из выражения 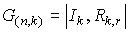
где
Ik — единичная матрица;
Rk,r — прямоугольная
матрица.
Строки матрицы Rk,r определяются из выражений 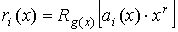
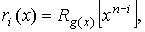
где
ai(x) — значение i-той строки матрицы Ik;
i — номер
строки матрицы Rk,r.
Пример. Матрица G(n,k) для
(7,4)-кода на основе порождающего многочлена g(x)=x3+x+1, строится в
следующей последовательности 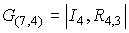
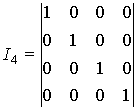
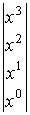
Определяется
R4,3, используя 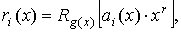
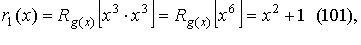
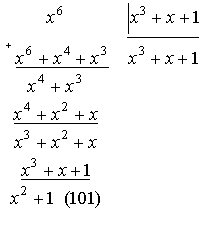
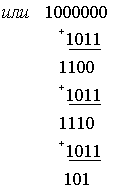
Аналогичным способом
определяется
В результате получаем 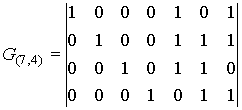
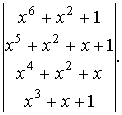
Используя выражение
получим тот же результат.
Строки матрицы G(n,k) можно определить
непосредственно из выражения 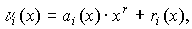
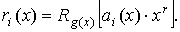
Проверочная матрица в систематическом виде строится на основе
матрицы G(n,k), а именно: 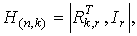
где
Ir — единичная матрица; 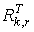
G(n,k) в транспонированном виде.
Пример. Для (7,4)-кода
матрица H(n,k) будет иметь вид: 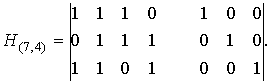
Одна из основных
задач, стоящих перед разработчиками устройств защиты от ошибок при передаче
дискретных сообщений по каналам связи является выбор порождающего многочлена
g(x) для построения циклического кода, обеспечивающего требуемое минимальное
кодовое расстояние для гарантийного обнаружения и исправления t-кратных ошибок.
Существуют специальные таблицы по выбору g(x) в зависимости от предъявляемых
требований к корректирующим возможностям кода. Однако у каждого циклического
кода имеются свои особенности формирования g(x). Поэтому при изучении конкретных
циклических кодов будут рассматриваться соответствующие способы построения g(x).
4.3 Коды БЧХ
Одним из классов
циклических кодов, способных исправлять многократные ошибки, являются коды БЧХ.
Примитивным кодом БЧХ, исправляющим tu ошибок,
называется код длиной n=qm-1 над GF(q), для которого элементы 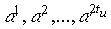
корнями порождающего многочлена.
Здесь a —
примитивный элемент GF(qm).
Порождающий многочлен
определяется из выражения 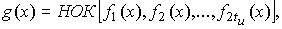
f1(x),f2(x)…- минимальные многочлены корней g(x).
Число проверочных элементов кода БЧХ удовлетворяет соотношению
Пример. Определить значение порождающего многочлена для построения
примитивного кода БЧХ над GF(2) длины 31, исправляющего двух кратные ошибки
(tu=2).
Исходя из определения кода БЧХ корнями многочлена g(x)
являются: 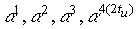
Порождающий многочлен определяется из выражения 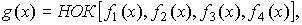
f2(x), f3(x), f4(x) — минимальные многочлены
корней соответственно 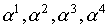
Примечание.
Минимальный многочлен элемента b поля
GF(qm) определяется из выражения 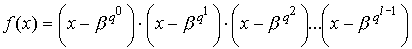
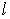
число, при котором 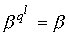
Значения
минимальных многочленов будут следующими: 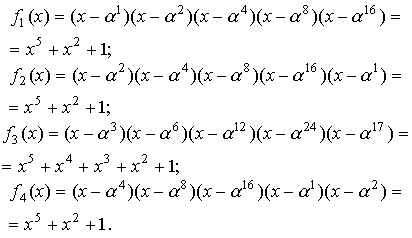
Так как f1(x)=
f2(x)= f4(x), то 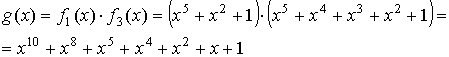
На
практике при определении значений порождающего многочлена пользуются специальной
таблицей минимальных многочленов (см. таблицу 8 приложения), и выражением для
порождающего многочлена 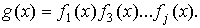
осуществляется в следующей последовательности.
По заданной длине кода n и
кратности исправляемых ошибок tu определяют:
— из выражения
n=2m-1 значение параметра m, который является максимальной степенью
сомножителей g(x);
— из выражения j=2tu-1 максимальный порядок
минимального многочлена, входящего в число сомножителей g(x).
— пользуясь
таблицей минимальных многочленов, определяется выражение для g(x) в зависимости
от m и j. Для этого из колонки, соответствующей параметру m, выбираются
многочлены с порядками от 1 до j, которые в результате перемножения дают
значение g(x).
Примечание.
В выражении для g(x) содержаться минимальные
многочлены только для нечетных степеней a, так как
обычно соответствующие им минимальные многочлены четных степеней a имеют аналогичные выражения.
Например, минимальные
многочлены элементов 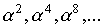
минимальному многочлену элемента a1,
минимальные многочлены элементов 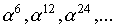
минимальному многочлену a3 и т.п.
Пример. Определить значение порождающего многочлена для построения
примитивного кода БЧХ над GF(2) длины 31, обеспечивающего tu=3.
Определяем значения m и j. 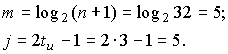
Из таблицы
минимальных многочленов в соответствии с m=5 и j=5 получаем 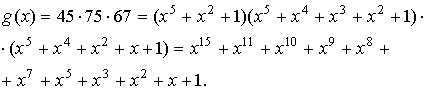
Заданные исходные
данные: n и tu или k и tu для построения циклического кода
часто приводят к выбору завышенного значения m и как следствие этого к
неоправданному увеличению длины кода. Такое положение снижает эффективность
полученного кода, так как часть информационных разрядов вообще не используется.
Пример. Требуется построить циклический код, исправляющий двух
кратные ошибки, если длина информационной части кода k=40.
Согласно
выражению для примитивного кода n=2m-1, ближайшая длина кода равна
63, для которой m=6, а r=mtu=12. Следовательно, код будет иметь n=63,
k=51. Неиспользованных информационных разрядов будет 11(51-40).
Подобное
несоответствие в ряде случаев можно устранить, применяя непримитивный код БЧХ.
Непримитивным кодом БЧХ, исправляющим tu ошибок,
называется код длины n над GF(q), для которого элементы 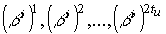
порождающего многочлена.
Здесь bi-непримитивный элемент GF(qm), а
длина кода n равна порядку элемента bi.
Примечание.
Порядком элемента bi
является наименьшее n, для которого 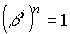
Пример.
Порядок элемента b3 поля GF(26)
равен 21, так как 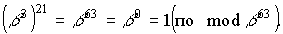
Порождающий многочлен непримитивного кода БЧХ, по аналогии с
примитивным кодом, определяется из выражения 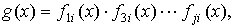
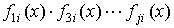
элементов 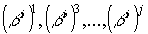
GF(qm), которые являются корнями g(x); i — степень непримитивного
элемента b.
Пример. Определить значение g(x)
для построения непримитивного кода БЧХ над GF(2) длины n=20, исправляющего двух
кратные ошибки.
Из таблицы непримитивных элементов GF(2m) (см.
таблицу 7 приложения) выбираем поле, элемент b которого
имеет порядок больший, но близкий к заданному n.
Такими являются
GF(26) и b3, порядок которого
n=21.
Так как j=2tu-1=2(2-1=3, то выражение для g(x) будет иметь
вид
где f3(x) и f9(x) — минимальные многочлены элементов
b3 и b9
поля GF(26).
Значения этих многочленов следующие: 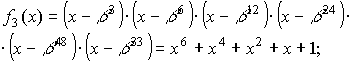
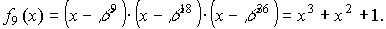
Выражения для
f3(x) и f9(x) можно определить из таблицы минимальных
многочленов, используя для этого параметр m выбранного поля GF(2m) и
порядковые номера сомножителей g(x).
Для рассмотренного примера m=6, а
порядковые номера равны 3 и 9. Поэтому 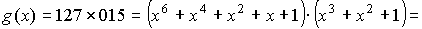
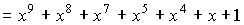
4.4 Способы кодирования
Задача кодирования
заключается в формировании по информационным словам a(x) кодовых слов u(x) циклического (n,k)-кода, который по своей структуре
может быть несистематическим и систематическим.
Формирование
кодовых слов несистематического кода заключается в умножении многочлена a(x),
отображающего информационную последовательность длины k, на порождающий
многочлен, т.е. u(x)=a(x)(g(x). Формирование кодовых
слов систематического кода заключается в преобразовании информационной
последовательности a(x) в соответствии с выражением u(x)=a(x)·xr+r(x).
Проверочная последовательность r(x) определяется двумя способами:
при использовании «классического» способа кодирования 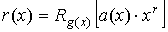
при использовании
способа кодирования, рекомендованного МККТТ 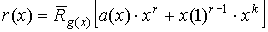
где
x(1)r-1 — единичный многочлен степени (r-1).
Указанные выше
математические операции выполняют кодеры несистематического и систематического
кодов.
4.5 Способы декодирования с обнаружением ошибок
Процедура декодирования
циклического кода с обнаружением ошибок, по аналогии с процессом кодирования,
использует два способа:
— при кодировании «классическим»
способом декодирование основано на использовании свойства делимости без остатка
кодового многочлена u(x) циклического (n,k)-кода на
порождающий многочлен g(x). Поэтому алгоритм декодирования включает в себя
деление принятого кодового слова, описываемого многочленом 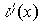
анализ остатка r(x). Если r(x)=0, то принятое кодовое слово считается
неискаженным. Если r(x)№0, то принятое кодовое слово
стирается и формируется сигнал «ошибка».
— при кодировании
способом МККТТ декодирование основано на свойстве получения определенного
контрольного остатка R0(x) при делении принятого кодового многочлена
u(x) на порождающий многочлен. Поэтому, если полученный
при делении остаток 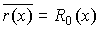
слово считается неискаженным. Если остаток 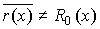
слово стирается и формируется сигнал «ошибка».
Значение контрольного остатка
определяется из выражения 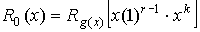
4.6 Способы декодирования с исправлением ошибок
и схемная реализация декодирующих устройств
и схемная реализация декодирующих устройств
Декодирование циклического
кода в режиме исправления ошибок можно осуществлять различными способами. Ниже
излагаются два способа, являющиеся наиболее простыми.
В
основу первого способа положено использование таблицы синдромов (декодирования),
в которой каждому многочлену или образцу ошибок ei(x), соответствует
определенный синдром Si(x), представляющий остаток от деления
принятого кодового слова 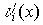
ei(x) на g(x). Процедура декодирования следующая. Принятое кодовое
слово 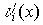
определяется Si(x) и соответствующий ему многочлен ei(x),
а затем 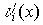
ei(x). В результате получаем исправленное кодовое слово, т.е. 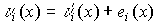
В состав декодера входят: вычислитель
синдрома (ВС), два регистра сдвига RG1 и RG2, постоянное запоминающее устройство
(ПЗУ), котороесодержит 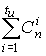
соответствующие многочленам ошибок ei(x).
Принятое кодовое слово
поступает на вход вычислителя синдрома, где осуществляется деление его на g(x) и
формирование Si(x), и одновременно — на вход RG2, где
накапливается. Синдром Si(x) используется в качестве адреса, по
которому из ПЗУ в регистр RG1 записывается ei(x), соответствующий
синдрому Si(x). Перечисленные операции завершаются за n тактов. В
течение последующих n тактов происходит поэлементное суммирование содержимого
RG2 и RG1, т.е. операция 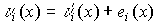
В основе второго способа исправления ошибок, позволяющего
значительно сократить объем используемых табличных синдромов и существенно
упростить схему декодера, лежат следующие положения:
1. Синдром
Si(x), соответствующий принятому кодовому слову равен остатку от
деления 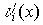
от деления соответствующего многочлена ошибок ei(x) на g(x), т.е. 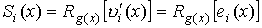
2.
Если Si(x) соответствует 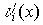
x( Si(x) является синдромом, который соответствует 

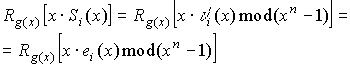
3.
При исправлении ошибок используются синдромы образцов ошибок только с ненулевым
коэффициентом в старшем разряде.
Поэтому при реализации
этого способа множество всех образцов ошибок разбивается на классы
эквивалентности. Каждый класс представляет циклический сдвиг одного образца
ошибок, а синдром этого класса соответствует образцу ошибок с ненулевым старшим
разрядом. Если вычисленный синдром принадлежит одному из классов эквивалентности
образцов исправляемых ошибок, то старший символ кодового слова исправляется.
Затем принятое слово и синдром циклически сдвигается, а процесс нахождения в
предыдущей по старшинству позиции повторяется.
Для исправления ошибок,
принадлежащих данному классу эквивалентности, нужно произвести n циклических
сдвигов.
Простейшим является декодер Меггитта. В состав декодера
входят: вычислитель синдрома, осуществляющий деление кодового слова 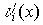
и формирование соответствующего синдрома; блок декодеров (ДК), который настроен
на синдромы всех образцов исправляемых ошибок с ненулевыми старшими разрядами;
регистр сдвига RG.
При поступлении на вход схемы кодового слова 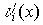
символы заполняют регистр RG, а в вычислителе формируется соответствующий
синдром Si(x). Вычисленный синдром сравнивается со всеми табличными
синдромами, заложенными в схему блока ДК, и в случае совпадения с одним из них
на его выходе формируется сигнал, который исправляет ошибочный символ,
находящийся в старшем разряде регистра. После этого содержимое вычислителя и RG
циклически сдвигается на один шаг. Этот сдвиг реализует операции 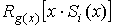

новый синдром совпадает с одним из табличных синдромов, то это означает, что
произошла ошибка во втором по старшинству символе кодового слова, который,
перейдя в старший разряд RG, исправляется. Затем производится новый циклический
сдвиг на одну позицию и новая проверка на совпадение синдромов. После повторения
этого процесса n раз в RG будет сформировано исправленное кодовое слово.
Введение обратной связи для RG не обязательно, так как в процессе исправления
ошибок символы кодового слова поступают на выход декодера.
Пример. Рассмотрим схему и работу декодера Меггитта
циклического (15,7)-кода, обеспечивающего исправление одиночных и двойных
ошибок, с g(x)=x8+ x7+ x6+ x4+1 (см.
рисунок 8).
Блок декодеров настраивается на 15 синдромов, которые
представлены в таблице 5 и соответствуют классам эквивалентности с образцами
ошибок в старшем разряде.
| № | е(х) | S(x) | № | е(х) | S(x) |
|---|---|---|---|---|---|
| 1 | x14 | x7+ x6+x5+ x3 |
9 | x14+ x6 | |
| 2 | x14+ x13 | x7+ x4+x3+ x2 |
10 | x14+ x5 | x7+ x6+x3 |
| 3 | x14+ x12 | x7+ x6+x4+ x |
11 | x14+ x4 | x7+ x6+x5+ x4+x3 |
| 4 | x14+ x11 | 12 | x14+ x3 | x7+ x6+x5 |
|
| 5 | x14+ x10 | 13 | x14+ x2 | x7+ x6+x5+ x3+x2 |
|
| 6 | x14+ x9 | 14 | x14+ x1 | x7+ x6+x5+ x3+x |
|
| 7 | x14+ x8 | 15 | x14+ x0 | x7+ x6+x5+ x3+0 |
|
| 8 | x14+ x7 |
Допустим, что
ошибки в 3 и 5 разрядах, т.е. им соответствует многочлен ошибки
e(x)=x12+x10.
При поступлении на вход декодера
искаженного кодового слова он заполняет регистр и в вычислителе формируется
синдром 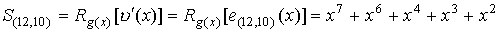
Блок декодеров не
реагирует на этот синдром.
Затем происходит сдвиг кодового слова в RG, а в
BC формируется новый синдром 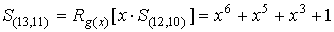
Блок декодеров и в
этом случае не срабатывает.
При следующем сдвиге кодового слова в RG первый
искаженный разряд занимает старшую позицию в RG, а в BC формируется синдром 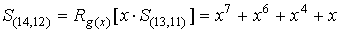
которого срабатывает БДК. В результате исправляется первая ошибка.
Следующим
сдвиг приводит к формированию синдрома 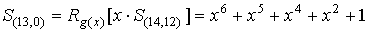
Этот синдром
соответствует многочлену ошибки e(x)=x13+x0, т.к. первый
искаженный разряд по обратной связи должен занять младшую позицию RG.
На
синдром S(13,0) блок декодеров не реагирует.
При следующем сдвиге
кодового слова в RG второй искаженный разряд занимает старшую позицию в RG, а в
BC формируется синдром 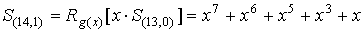
БДК. В результате исправляется вторая ошибка в кодовом слове.
4.7 Коды Рида-Соломона (РС)
Коды РС
являются недвоичными циклическими кодами, символы кодовых слов которых берутся
из конечного поля GF(q). Здесь q степень некоторого простого числа, например
q=2m.
Допустим, что РС-код построен над GF(8), которое является
расширением поля GF(2) по модулю примитивного многочлена f(z)=z3+z+1.
В этом случае символы кодовых слов кода будут иметь значения, представленные в
таблице 6.
| 000 | 0 | 0 | 011 | z+1 | a3 |
| 001 | 1 | a0 | 110 | z2+z | a4 |
| 010 | z | a1 | 111 | z2+z+1 | a5 |
| 100 | z2 | a2 | 101 | z2+1 | a6 |
Кодовые слова РС-кода
отображаются в виде многочленов 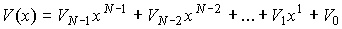
где N — длина кода;
Vi — q-ичные коэффициенты (символы кодовых слов), которые могут
принимать любое значение из GF(q).
Эти коэффициенты как это следует из
таблицы, также отображаются многочленами с двоичными коэффициентами 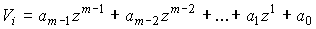
информационной последовательности k они обладают наибольшим кодовым расстоянием
d=N-k+1.
Порождающим многочленом g(x) РС-кода является делитель двучлена
xN+1 степени меньшей N с коэффициентами из GF(q) при условии, что
элементы 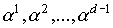
корнями g(x). Здесь 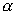
GF(q).
На основе этого определения, а также теоремы Безу,
выражение для порождающего многочлена РС-кода будет иметь вид 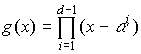
Степень g(x) равна d-1=N-k=R.
В РС-кодах принадлежность кодовых слов
данному коду определяется выполнением d-1 уравнений в соответствии с выражением
(*),
где Vi — символы-коэффициенты из GF(q);
z0,
z1… zN-1 — ненулевые элементы GF(q).
Элементы
z0, z1… zN-1 называются локаторами, т.е.
указывающими на номер позиции символа кодового слова.
Например, указателем i
— позиции является локатор zi или элемент ai
GF(q).
Так как все локаторы должны быть различны и причем ненулевыми, то их
число в GF(q) равно q-1. Следовательно, такое количество символов должно быть в
кодовых словах кода.Поэтому обычно длина РС-кода определяется из
выражения N=q-1.
Пример. Допустим, что длина РС-кода равна N, кодовое
расстояние d=3, то в соответствии с (*) проверочными уравнениями будут 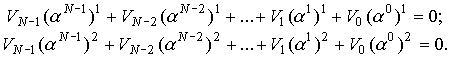
Свойства РС-кодов.
1. Циклический сдвиг кодовых слов, символы которых принимают значение из
GF(q), порождает новые кодовые слова этого же кода.
2. Сумма по mod2 двух и
более кодовых слов дает кодовое слово, принадлежащее этому же коду.
3.
Кодовое расстояние РС-кода определяется не по двоичным элементам, а по q-ичным
символам.
4. В РС-коде, исправляющем tu ошибок порождающий
многочлен определяется из выражения 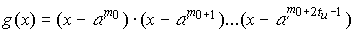
принимают равным 1. Однако, с помощью разумного выбора значения m0,
иногда можно упростить схему кодера.
5. Корректирующие способности РС-кода
определяются его кодовым расстоянием. 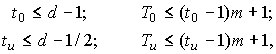
где T0 и
Tu — длина пакетов, в которых обнаруживаются и исправляются ошибки.
Обнаружение ошибок в кодовых словах состоит в проверке условий ((), т.е.
определении синдрома 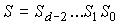
определяются из выражения 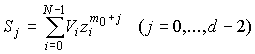
Пример. Требуется сформировать кодовое слово РС-кода над
GF(23), соответствующее двоичной информационной последовательности
a(1,0)=000000011100101.
Так как m=3, то каждый q-ичный символ кода состоит
из трех двоичных элементов. Поэтому с учетом таблицы 6 a(x)=a3x2+ a2x+a6.
Определяем параметры кода.
N=q-1=7; k=5; R=2; d=N-k+1=3; 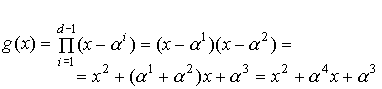
Кодовое слово формируется в соответствии с выражением. 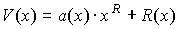
где
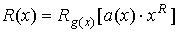
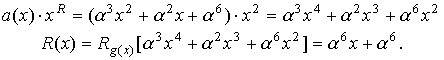
В
результате 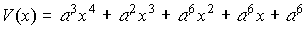
V(1,0)=000.000.011.100.101.101.101.
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
Коды
Боуза—Чоудхури—Хоквингема
(БЧХ-коды)
представляют собой большой класс
циклических кодов, исправляющих
независимые
ошибки кратности t
и
менее.
Для кодов БЧХ характерны
все основные свойства циклических
кодов. Чаще всего
коды БЧХ описывают с помощью корней
порождающего многочлена
Р
(х) степени
2t.
В качестве корней Р
(х) выбирают
2t
последовательных
элементов аj,aj+1
…, аj+2i-1поля
Галуа GF
(р’п),
где
1≤ j≤pm—
1. Если при этом элемент а
является примитивным
(первообразным) в поле GF(pm),
то
такой код БЧХ
называют примитивным с длиной кодовой
комбинации п=рт—1
над полем GF
(р). Для
двоичных примитивных кодов
БЧХ п
=
2n
— 1 над полем GF
(2).
В случае, если ряд корней
многочлена Р(х)
для
кода БЧХ начинается с j=1,
т. е. а,
а2,
…. а2t,
то
такой код называют кодом БЧХ в узком
смысле.
Код
БЧХ, у которого корень
а
не является примитивным элементом
поля GF
(рm),
т.
е. имеет
порядок
d
<
рт
—1,
называют
непримитивным
с
длиной
комбинации
п
=d.
Пусть
аj—элемент
расширения
простого числового поля. Тогда по
определению, данному в [7], некоторый
нормированный
многочлен
т(х)
наименьшей
степени, для
которого т(аj
)
=
0, называют минимальной
функцией
для аi.
Отметим,
что
минимальные
функции m(х)
являются
непри-водимыми
многочленами.
Если предположить, что каждому из корней
аi
производящего
многочлена Р
(х) соответствует
своя минимальная
функция
тi
(х), то
производящий многочлен Р
(х) должен
быть наименьшим общим
кратным
всех
минимальных
функций,
т. е.
P(x)=НОК[m1(x),m2(x),
…
m2t(x)]. (51)
Таким
образом,
вектор,
представленный многочленом
f
(x),будет
кодовым тогда и только тогда, когда он
делится без остатка
как на каждую из минимальных функций
т1
(х), m2(x),
…, т2t
(х), так
и на их наименьшее общее кратное.
Тогда
для любого из корней а, а2,
….a2t
справедливо уравнение
f
(аi)
=
с0
+ с1
аi
+с2(аi
)2+…cn-1
(ai)n-1
= 0, которое
можно записать в виде произведения двух
матриц (coc1c2…cn-1)*[lai(ai)2…(ai)n-1]T=0.
Но
так как корнями
f(х)
должны
быть все элементы a,
a2
…,a2t,
то можно
сделать вывод, что вектор (c0c1…cn-1_)
будет
кодовым тогда
и только тогда, когда он принадлежит
нулевому пространству
матрицы
Может
оказаться, что элементы аi
и аj
из совокупности а, а2,
…, а2t
соответствуют одной и той же минимальной
функции,
т. е. тi
(х) = mj(х).
Вследствие
того, что производящий многочлен
Р(х) равен
наименьшему общему кратному всех
минимальных
функций mj(х),
в качестве
сомножителя в разложении многочлена
Р(х) следует
взять только одну из нескольких равных
между собой минимальных функций.
Из
свойства 1.6 полей следует, что если аi
корень
какой-либо
минимальной неприводимой по модулю 2
функции mi
(х)степени
к,
то
остальными корнями будут
(аi)2,((аi)2)2,…,(ai)2^(k-1).Следовательно,
в разложении многочлена Р
(х) каждая
из
различных минимальных функций mi
(х)
должна
входить
только один раз, а для построения матрицы
(5.2) нужно использовать
только по одному корню каждой из
минимальных функций,
входящих в разложение многочлена Р
(х). Таким
образом,
если в качестве совокупности корней
многочлена Р
(х) выбраны
элементы поля Галуа GF
(2m)
а, а2,
а3,
…, а2t,
то при
построении матрицы Н
должны
быть использованы только нечетные
степени а, а3,
…, а2t-1,
а многочлен Р
(х) будет
иметь
вид
P(x)=m1(x)m3(x)
… m2t-1(x). (5.3)
Рассмотрим
следующий пример.
Пример
5.1. Пусть
имеем двоичный циклический код БЧХ. к
которому
вектор {f
(х)}
будет
принадлежать только тогда, когда элементы
а, a2,
а3,
а4,
а5,
а6
будут корнями многочлена f
(х). Кроме
того, предполагается, что a
— примитивный элемент
поля Галуа GF
(24).
Тогда а15
= 1 и тi
(х) обозначает
минимальную
функцию для аj
.
В
соответствие со свойством 1.6 элементы
a,
а2,
а4
и а8
— корни
одной
и той же минимальной функции четвертой
степени,
следовательно, m1(х)
=
т2
(х)= т4
(х) =
т8
(х). Аналогично,
а3,
а6,
а12
и
а24
= а9
— корни минимальной функции четвертой
степени и m3
(х) = т6
(х) =
m9
(х) = т12(х),
а
элементы
a5
и а10
являются корнями минимальной функции
второй степени
и, следовательно, т5
(х)=т10(х).
Отсюда,
Р
(х) является
многочленом
P(x)=
ml(x)m3(x)m5(x)
(5.4)
степень
которого равна 10.
Таким
образом, к искомому циклическому коду
БЧХ будет принадлежать
любой вектор {f
(х)},
если
f
(х) делится
на Р(х).
В
то же время циклический код будет нулевым
пространством матрицы
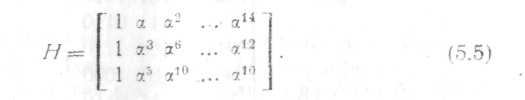
Так
как аj
является элементом поля GF
(2т
)
и представляет собой
вектор из т
двоичных
элементов 0 и I,
то матрица HT
имеет
размерность
п
*
mt.
Из
свойства 2.2 следует, что многочлен Р
(х) является
делителем
многочлена F
(х) = хn
—
1, где п
=
2m—1.
В то же время,
многочлен Р
(х) для
кодов БЧХ равен произведению минимальных
функций. Следовательно, любая из
минимальных функций,
входящих в разложение многочлена
Р(х),
должна
быть
делителем функции F
(х) =
хn—
1 = х2^m-1—
1. При этом, как
следует из высшей алгебры [4, 7], степень
каждой минимальной
функции не может быть больше т.
А
так как таких функций
t,
то
степень многочлена Р
(х) не
превосходит mt.
Отсюда
каждая комбинация циклического
примитивного кода
БЧХ при длине, равной n
= 2m—1,
имеет число информационных
разрядов, равное k≥2m—
1—mt.
Рассмотрим
конкретный пример построения циклического
кода
БЧХ.
Пример
5.2.
Построить двоичный примитивный
циклический код
БЧХ для т
=
4 и t=
3.
В
этом случае длина кодовой комбинации
равна п
=
2m—
1 = 15, а вектор {f
(х)}
будет
принадлежать этому циклическому
коду, если элементы поля GF
(24)
а, a2,
…, а6
будут корнями
многочлена f(х).
Кроме
того, отметим, что а — примитивный
элемент поля, а минимальной функцией
для него пусть
будет примитивный неприводимый
многочлен т1
(х) =
1 +x+x4.
Как
видим, этот пример является непосредственным
продолжением
примера 5.1, из которого следует, что
производящий многочлен
Р
(х) имеет
вид Р
(х) =
m1(х)
т3
(х) т5
(х), где
т1
(х) и
m3
(х)
—
минимальные многочлены четвертой
степени, а
т5
(х) —
минимальный многочлен второй степени,
вследствие чего
степень
многочлена Р
(х) равна
10. Кроме того, было показано,
что матрица Н
имеет
вид (5.5).
Т
ак
как примитивный элемент а — корень
минимального многочлена тх(х)=1
+ х
+
х4,
то,
подставив вместо каждого элемента
матрицы H
его
значение из табл. 1.1,
получим транспонированную
матрицу НТ;
В [7] показано, что
m3(x)=1+x+x2+x3+x4,
m5(x)=1+x+x2,
тогда степень многочлена P(x)
равна 10, что не превышает mt.
В рассмотренном
примере
Т
огда
производящая матрица G
искомого систематического кода
имеет вид :
Образованный таким
образом циклический (n,k)=(15,5)
код БЧХ позволяет исправить любую
совокупность ошибок кратности t=3
и менее.
Принципы
исправления ошибок кодами БЧХ
Предположим, что
передавая кодовый вектор {f(x)},
представление которого в виде многочлена
будет иметь вид: f(x)=c0+c1x+…+cn-1xn-1.
Пусть далее вследствие ошибок вместо
вектора {f(x)}
принят вектор {f(x)+e(x)}=
{f(x)}+
{e(x)},
где {e(x)}-вектор
ошибок.
Обозначим принятый
с ошибками вектор {f(x)+e(x)}
через вектор {h(x)}=(h0h1h2…hn-1).Принятую
комбинацию можно представить в виде
многочлена степени n-1,
т.е. h(x)=h0+h1x+h2x2+…+hn-1xn-1.
В результате умножения вектора {h(x)}
на матрицу (5.2) получим вектор из t
компонент [h(a),
h(a3),…h(a2t-1)],где
h(a)=h0+h1a+h2a2+…+hn-1an-1;
h(a3)=h0+h1a3+h2(a3)2+…+hn-1(a3)n-1
И т.д.
В то же время
{h(x)}=
{f(x)+e(x)},
следовательно, h(x)=
f(x)+e(x).
Тогда h(ai)=f(ai)+e(ai),
где i=1,3,…,2t-1,
но так как f(x)
делится на P(x)
без остатка, то f(a)=f(a3)=…=f(a2t-1)≡0,
так что h(ai)≡e(ai).
При умножении
вектора {h(x)}
на первый столбец матрицы HT
, образованной из (5.5), получаем элемент
Отсюда следует,
что имеется взаимнооднозначное
соответствие между элементами вектора
ошибок и элементами поля GF(2m).
Каждому ошибочному элементу ei
соответствует элемент i-й
строки (i=0,1,2,…,n-1)
первого столбца транспонированной
матрицы HT,
т.е. элемент поля ai.
Предположим,
что ошибки произошли на позициях
i1,i2,…,it,
для которых ei=1,
а для всех остальных ej=0,
тогда (5.8) может быть переписана следующим
образом:
Обозначим
каждый из элементов аk
через Хk
(k
= 1, 2, …it)
и назовем
их локаторами ошибок, тогда (5.9) может
быть переписана
так:
Умножив
вектор {h(x)}
на
какой-либо другой j-й
столбец матрицы
HTполучим
h(aj)=e(aj)=(aj)i1+(aj)i2+…+(aj)it=
где j=
1, 3, ….
2t—
1.
Выражения
(5.11) представляют t
симметрических
функций
Sj
от
нечетных
степеней элементов Х1,
Х2 Xt,
которые
имеют вид
Функции
Sj
называют
синдромами.
Таким
образом, функции Sj
дают t
уравнений
вида (5.12) с t
неизвестными
Х1,
Х2…,
Xt.
Кроме
того, из (5.12) можно найти
также симметрические функции для четных
j
= 2, 4, .., 2t,
т. е. можно получить дополнительно t
уравнений
вида (5.12) с
теми же неизвестными. Действительно,
учитывая свойство 1.4 для
р
=
2, получим
Решение
указанных уравнений относительно Хk
определит
номера
ошибочных позиций. Поскольку имеется
конечное число решений,
то значения Хk
могут
быть найдены путем подстановок
в эти уравнения различных элементов
поля GF
(2m).
Но
подстановка
всех комбинаций no
t
из 2m
— 1
ненулевых элементов
поля требует большого числа вычислений.
Для
кодов БЧХ имеются более эффективные
алгебраические алгоритмы
декодирования. Рассмотрим один из них.
Так
как суммы j—x
степеней
элементов Х1,Х2,
...,
Xt
представляют
собой симметрические функции Sj,
то
эти элементы могут
рассматриваться
[8] как корни некоторого многочлена
степени
t
Xt+p1Xt-1+p2Xt-2+…+pt (5.I4)
разложение
которого на линейные множители дает
уравнение
(X-X1)(Х-Х2)
…
(X—Xt)=0. (5.16)
Коэффициенты
р1,
р2,
…,
рt
являются
простейшими
симметрическими
функциями,
которые связаны с симметрическими
функциями
Sj
тождествами
Ньютона [1, 7]:
S3-p1S2+p2S1-3p3=0
S4-p1S3+p2S2-p3S1+4p4=0
и
т.
д.
При
операциях по
модулю
2 тождества Ньютона выписываются по
формуле
где
δ = 0 при i—четном
и
δ=1-
при
нечетном.
С
учетом последнего тождества Ньютона
можно переписать
так:
St=p1St-1+p2St-2+…+pt-1S1+
δpt
Если
тождества (5.16) решить относительно
простейших симметрических
функций pi
и
найденные значения рi,
подставить
в
(5.14),
то корни этого многочлена Х1,
Х2,
…, Xt
можно
определить
последовательной подстановкой в него
каждого из п
=
2m
—
1 элементов поля. Если подставленный
вместо X
элемент
аi
не является корнем, то соответствующий
символ вектора {h
(x)}
принят
правильно. Если же элемент ai
является
корнем,
то соответствующий i-й
символ вектора {h
(х)} принят
ошибочным
и должен быть исправлен.
Однако
в силу зависимости (5.13) следует
рассматривать не
все тождества (5.16), а лишь те, которые
определяют Sj
для
нечетных
j,
т. е.
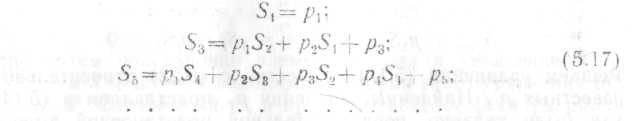
St-1=p1St-2+p2St-3+…+pt-2S1+pt-1
(при
t
—четном)
или
St=p1St-1+p2St-2+…pt-1S1+pt
(при
t—
нечетном).
Отсюда
видно, что имеется i/2
(при t—четном)
или (t+1)/2
(при
t
— нечетном) уравнений, которых
недостаточно для
определения t
неизвестных
р1,
р2,
…, рi.
Однако
в результате умножения {h(x)}*HT
можно
определить все симметрические
функции S1,
S3,…,S2t-1.
Знание симметрических функций
Sj
с
нечетными значениями j’
вплоть до 2t—1позволяет
составить
дополнительные уравнения, которые
вместе с (5.17)
дадут
t
независимых
уравнений с t
неизвестными
р1,р2,
….
рt
Эти
уравнения можно уже решить относительно
pt.
Выше
было показано, как составить тождества
Ньютона, когда
j
при Sj
принимает
целые значения, не превосходящие
t,
т.
е. степени многочлена (5.14).
Можно показать, что аналогично
можно составить тождества Ньютона для
значений j
> t.
Действительно,
если обозначить многочлен (5.14)
через ψ(X)
и
подставить
вместо X
какой-либо
из корней Х1,
X2
…. Xt,
то
получим уравнение
Умножение обоих
частей уравнения (5.18) на Xic—t
дает
Где c>t.
Если теперь просуммируем (5.19) по всем
корням, т.е.
То получим
Решаем
уравнения (5.17) совместно с (5.22) относительно
неизвестных
рi
Найденные
значения рi
подставляем
в (5.14) и, как
было указано, последовательной
подстановкой вместо X
элементов
поля GF
(2m)
находим корни этого многочлена. Этим
самым
мы устанавливаем ошибочные позиции
принятого вектора
{h
(х)}.
Если
произошло в действительности t
—
1 ошибок, то один из
корней Х1,
Х2,…Xt
должен
быть равен нулю. Следовательно,
при решении уравнений (5.17) и (5.22) мы должны
получить pt
=0.
Если произошло t
—
2 ошибки, то два корня равны
нулю и, следовательно, pt=
рt-1=
0
и так далее.
Пример
5.3. Рассмотрим
процесс исправления тройных ошибок
(t
=
3) циклическим кодом БЧХ, построение
которого рассматривалось
в примере 5.2. Многочлен (5.14) для такого
кода будет
иметь вид Х3
+
р1Х2
+
р2Х
+
р3
На основании (5.17)
и (5.22) составляем уравнения:
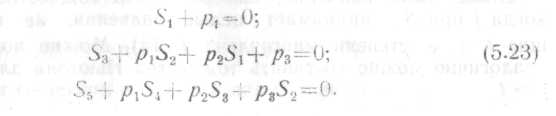
Сложение
по модулю 2 соответствующих столбцов
матрицы HT(5.6)
позволяет найти значения S1,S3,
S5.
Кроме
того, при операциях
по модулю 2 S2
= S12,
a
S4
= S14
Решая уравнения относительно
рt,
находим
[7]:
при условии, что
S13+S3≠0.
Рассмотрим случай,
когда ошибки появляются на 2, 5 и 7-м
местах, т.е. {e(x)}=(010010100000000),
тогда {h(x)}HT=(1011,1111,1000),
т.е. S1=(1011),
S3=(1111),
S5=(1000).
Теперь найдем S2
и S4,
обращаясь к табл. 1.1,
По формулам (5.24)
находим p1=S1=a13,
Теперь
путем подстановки элементов поля в
уравнение X3+
+
а13X2+
а9X
+a11=
0 находим, что корни этого уравнения
будут
а, а4
а6.
Следовательно, в принятом векторе {h
(x)}
ошибки
находятся
на 2, 5 и 7-м местах. Если произошла только
одна ошибка,
то р2
= р3
= 0, а из
уравнений (5.23) pi=S1.
Следовательно,
номер ошибочной позиции можно определить,
решая, уравнение
X
+р1=
0.
Содержание
- 1 Исправление ошибок в помехоустойчивом кодировании
- 2 Параметры помехоустойчивого кодирования
- 3 Контроль чётности
- 4 Классификация помехоустойчивых кодов
- 5 Код Хэмминга
- 5.1 Декодирование кода Хэмминга
- 5.2 Расстояние Хэмминга
- 6 Помехоустойчивые коды
- 6.1 Компромиссы при использовании помехоустойчивых кодов
- 6.2 Необходимость чередования (перемежения)
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
Коды Боуза — Чоудхури — Хоквингхема (БЧХ-коды) — в теории кодирования это широкий класс циклических кодов, применяемых для защиты информации от ошибок (см. Обнаружение и исправление ошибок). Отличается возможностью построения кода с заранее определенными корректирующими свойствами, а именно, минимальным кодовым расстоянием. Коды Рида — Соломона являются частным случаем БЧХ-кодов.
Содержание
- 1 Формальное описание
- 2 Построение
- 3 Примеры кодов
- 3.1 Примитивный 2-ичный (15,7,5) код
- 3.2 16-ричный (15,11,5) код (код Рида — Соломона)
- 4 Кодирование
- 5 Методы декодирования
- 5.1 Алгоритм Питерсона — Горенстейна — Цирлера (ПГЦ)
- 6 См. также
- 7 Литература
Формальное описание
БЧХ-код является циклическим кодом, который можно задать порождающим полиномом. Для его нахождения в случае БЧХ-кода необходимо заранее определить длину кода n (она не может быть произвольной) и требуемое минимальное расстояние 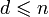
Пусть α — примитивный элемент поля GF(qm) (то есть 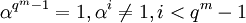
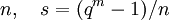
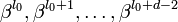
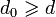
Число проверочных символов r равно степени g(x), число информационных символов k = n − r, величина d называется конструктивным расстоянием БЧХ-кода. Если n = qm − 1, то код называется примитивным, иначе непримитивным.
Так же, как и для циклического кода, кодовый полином c(x) может быть получен из информационного полинома m(x), степени не больше k − 1, путем перемножения m(x) и g(x):
c(x) = m(x)g(x).
Построение
Для нахождения порождающего полинома необходимо выполнить несколько этапов:
- выбрать q, то есть поле GF(q), над которым будет построен код;
- выбрать длину n кода из условия n = (qm − 1) / s, где m,s — целые положительные числа;
- задать величину d конструктивного расстояния;
1) построить циклотомические классы элемента β = αs поля GF(qm) над полем GF(q), где α — примитивный элемент GF(qm);
2) поскольку каждому такому циклотомическому классу соответвует неприводимый полином над GF(q), корнями которого являются элементы этого и только этого класса, со степенью равной количеству элементов в классе, то выбрать 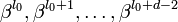
3) вычислить порождающий полином 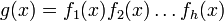
Примеры кодов
Примитивный 2-ичный (15,7,5) код
Пусть q = 2, требуемая длина кода n = 24 − 1 = 15 и минимальное расстояние 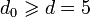
g(x) = f1(x)f2(x) = x8 + x7 + x6 + x4 + 1
имеет в качестве корней элементы α,α2,α3,α4 и является порождающим полиномом БЧХ-кода с параметрами (15,7,5).
16-ричный (15,11,5) код (код Рида — Соломона)
Пусть n = q − 1 = 15 и α — примитивный элемент GF(16). Тогда
g(x) = (x − α)(x − α2)(x − α3)(x − α4) = x4 + α13x3 + α6x2 + α3x + α10
.
Каждому элементу поля GF(16) можно сопоставить 4 битам, поэтому одно кодовое слово эквивалентно 60=15*4 битам, таким образом набору из 44 бит ставится в соответствие набор из 60 бит. Можно сказать, что такой код работает с полубайтами информации.
Кодирование
Для кодирования кодами БЧХ применяются те же методы, что и для кодирования циклическими кодами.
Методы декодирования
Коды БЧХ являются циклическими кодами, поэтому к ним применимы все методы, используемые для декодирования циклических кодов. Однако существуют гораздо лучшие алгоритмы, разработанные именно для БЧХ-кодов.
Исторически первым методом декодирования был найден Питерсоном для двоичного случая (q = 2), затем Горенстейном и Цирлером для общего случая. Упрощение алгоритма было найдено Берлекэмпом, а затем усовершенствовано Месси (алгоритм Берлекэмпа — Месси). Существует отличный от этих методов декдирования — метод основанный на алгоритме Евклида.
Алгоритм Питерсона — Горенстейна — Цирлера (ПГЦ)
Пусть БЧХ код над полем GF(q) длины n и с конструктивным расстоянием d задается порождающим полиномом g(x), который имеет среди своих корней элементы 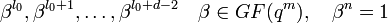
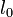
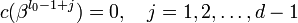
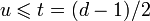
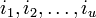
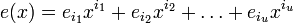
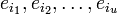
Можно составить j-ый синдром Sj принятого слова r(x):
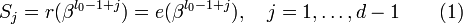
Задача состоит в нахождений числа ошибок u, их позиций 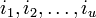
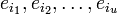
Предположим, для начала, что u в точности равно t. Запишем (1) в виде системы нелинейных(!) уравнений в явном виде:
Обозначим через 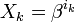
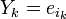
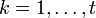
Составим полином локаторов ошибок:
Корнями этого полинома являются элементы, обратные локаторам ошибок. Помножим обе части этого полинома на 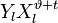
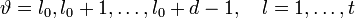
Положим 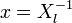
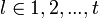
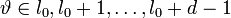
Таким образом для каждого l можно записать свое равенство. Если их просуммировать по l, то получиться равенство, справедливое для каждого 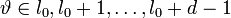
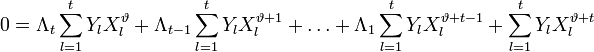
.
Учитывая (2) и то, что 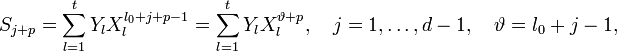
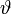
.
Или в матричной форме
,
где
Если число ошибок и в самом деле равно t, то система (4) разрешима, и можно найти значения коэффициентов 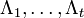
После этого можно решить систему (4) и получить коэффициенты полинома локаторов ошибок. Его корни (элементы, обратные локаторам ошибок) можно найти простым перебором по всем элементам поля GF(qm). К ним найти элементы, обратные по умножению, — это локаторы ошибок 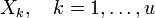
См. также
- Обнаружение и исправление ошибок
- Конечное поле
- Многочлен над конечным полем
- Матрица Вандермонда
- Линейный код
- Циклический код
- Код Рида — Соломона
Литература
- Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and practice of error control codes. — М.: Мир, 1986. — С. 576.
- Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. — М.: Мир, 1976. — С. 596.
Wikimedia Foundation.
2010.
3.1. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ (I)
Известно из гл. 1, что коды Хэмминга исправляют одиночные ошибки. В этой главе будут введены коды, которые в определенном смысле обобщают их на случай 
Попытаемся вначале найти обобщение кодов Хэмминга, позволяющее исправлять две ошибки.
Двоичный код Хэмминга длины 





В качестве примера возьмем 



что мы сокращенно обозначим как

где через число 


где значением функции 



представляет собой вектор-столбец длины 8.
Как выбрать функцию 


Необходимо выбрать 



относительно 



Для того чтобы решить эти уравнения, нам хотелось бы уметь складывать, вычитать, умножать и делить эти 

Определение. Поле — это множество элементов в котором определены операции сложения, вычитания, умножения и деления (за исключением деления на 0, которое не определено). Сложение и умножение должны удовлетворять коммутативному, ассоциативному и дистрибутивному законам: для любых элементов 


кроме того, должны существовать элементы 0, 1 (и для любого а) 

Конечное поле содержит конечное число элементов, и это число называется порядком поля.
Конечные поля называются полями Галуа по имени их первого исследователя Эвариста Галуа.
Содержание
Раздел создан при поддержке компании RAIDIX
Для понимания материалов настоящего раздела крайне желательно ознакомиться с разделом Циклические коды.
Коды Боуза-Чоудхури-Хоквингема
Идея
Для ее пояснения обратимся к материалам
☞
ПУНКТА и рассмотрим циклические коды в $ mathbb Z^n $. Принадлежность кодового слова $ (b_0,b_1,dots,b_{n-1}) $ циклическому коду $ C_{} $, порождаемому полиномом
$$ g(x)=a_0+a_1x+a_2x^2+dots+a_{r}x^{r}, (r<n,a_{r}ne 0) , ,$$
равносильна тому, что полином
$$ G(x)=b_0+b_1x+b_2x^2+dots+b_{n-1}x^{n-1} $$
делится на $ g_{}(x) $. Предположим теперь, что при передаче по зашумленному каналу связи кодовый полином (кодовое слово) исказился и на выходе мы получили полином
$$ tilde G(x)= G(x)+E_jx^j+E_kx^k quad npu quad {j,k} subset {0,1,2,dots,n-1}, j < k, {E_j,E_k} subset mathbb Z .$$
В
☞
ПУНКТЕ предлагался метод нахождения ошибок в случае, когда они соседствуют, т.е. $ k=j+1 $. Фактически, задача в такой постановке оказывалась задачей с тремя неизвестными: требовалось найти место ошибки $ j_{} $ и величины ошибок $ E_j,E_{j+1} $. Теперь мы рассмотреть общий случай, когда неизвестными являются четыре величины $ j,k,E_j,E_k $. Интуитивно понятно, что для нахождения этих четырех неизвестных требуется, по меньшей мере, такое же количество условий. По аналогии с рассмотренным в
☞
ПУНКТЕ подходом, будем пытаться найти эти условия виде $ tilde G(lambda_{ell})=0 $, где $ lambda_{ell} $ — корень порождающего код полинома $ g_{}(x) $, т.е. $ g_{}(lambda_{ell})=0 $ и $ G(lambda_{ell})=0 $. Если $ lambda_1,lambda_2,lambda_3,lambda_4 $ — различные корни полинома $ g_{}(x) $, то подстановка их в «зашумленный» полином $ tilde G(x) $ приведет к системе уравнений
$$ E_jlambda_1^j+E_klambda_1^k= tilde G(lambda_1), E_jlambda_2^j+E_klambda_2^k= tilde G(lambda_2), E_jlambda_3^j+E_klambda_3^k= tilde G(lambda_3), E_jlambda_4^j+E_klambda_4^k= tilde G(lambda_4) , $$
линейной по неизвестным $ E_j $ и $ E_k $, но нелинейной по значениям индексов $ j_{} $ и $ k_{} $. Эту систему требуется решить в целых числах. Можно попробовать осуществить поиск решений перебором вариантов (например, положив гипотезой что величины ошибок $ E_j $ и $ E_k $ невелики); однако этот подход не кажется конструктивным если оценить число потенциально возможных комбинаций в зависимости от $ n_{} $.
Допустим теперь, что порождающий $ n_{} $-код полином $ g_{}(x) $ удается подобрать так, чтобы его корнями оказались бы величины
$$ lambda_1=varepsilon_1, lambda_2=varepsilon_1^2, lambda_3=varepsilon_1^3, lambda_4=varepsilon_1^4 quad npu quad varepsilon_1=cos frac{2pi}{n}+mathbf i sin frac{2pi}{n} $$
— корне степени n из единицы. Посмотрим как можно использовать эту возможность для решения задачи исправления ошибок. Подставим корни в предыдущую систему, воспользовавшись равенствами
$$ varepsilon_1^j = varepsilon_j=cos frac{2pi,j}{n}+mathbf i sin frac{2pi , j}{n} , varepsilon_1^k=varepsilon_k= cos frac{2pi,k}{n}+mathbf i sin frac{2pi,k}{n} , $$
получим «систему ошибок»1)
$$
left{ begin{array}{rrl}
E_j varepsilon_j & + E_k varepsilon_k & = tilde G(varepsilon_1), \
E_j varepsilon_j^2 & + E_k varepsilon_k^2 & = tilde G(varepsilon_1^2), \
E_j varepsilon_j^3& + E_k varepsilon_k^3 & = tilde G(varepsilon_1^3), \
E_j varepsilon_j^4 & + E_k varepsilon_k^4 & = tilde G(varepsilon_1^4).
end{array}
right.
$$
Попробуем на основе этих равенств сконструировать новое — квадратное:
$$ sigma_2+sigma_1x+sigma_0x^2=0 , $$
которому должны удовлетворять обе величины $ varepsilon_j $ и $ varepsilon_k $. С этой целью умножим первое из этих разыскиваемых уравнений на $ E_j varepsilon_j $, второе — на $ E_k varepsilon_k $
$$
left{ begin{array}{rl|lc|lc}
sigma_2+sigma_1varepsilon_j+sigma_0varepsilon_j^2&=0, & times E_j varepsilon_j & & times E_j varepsilon_j^2 & \
& & & + & & + \
sigma_2+sigma_1varepsilon_k+sigma_0varepsilon_k^2&=0 & times E_k varepsilon_k & & times E_k varepsilon_k^2. &
end{array}
right.
$$
и сложим:
$$ sigma_2 (E_j varepsilon_j +E_k varepsilon_k)+sigma_1(E_j varepsilon_j^2 +E_k varepsilon_k^2)+sigma_0(E_j varepsilon_j^3 +E_k varepsilon_k^3)=0 ;
$$
аналогичным образом, домножим первое из равенств на $ E_j varepsilon_j^2 $, второе — на $ E_k varepsilon_k^2 $ и сложим:
$$ sigma_2 (E_j varepsilon_j^2 +E_k varepsilon_k^2)+sigma_1(E_j varepsilon_j^3 +E_k varepsilon_k^3)+sigma_0(E_j varepsilon_j^4 +E_k varepsilon_k^4)=0 .
$$
Обратим теперь внимание на то, что все величины, стоящие в полученных формулах в круглых скобках, нам известны из приведенной выше системы:
$$
left{ begin{array}{rl}
sigma_2tilde G(varepsilon_1)+sigma_1tilde G(varepsilon_1^2)+sigma_0tilde G(varepsilon_1^3)&=0, \
sigma_2tilde G(varepsilon_1^2)+sigma_1tilde G(varepsilon_1^3)+sigma_0tilde G(varepsilon_1^4)&=0.
end{array}
right.
$$
Эта система линейна относительно неизвестных коэффициентов $ sigma_0, sigma_1,sigma_2 $. Возникает вопрос о ее разрешимости.
Т
Теорема.
Пусть порождающий код полином обладает корнями $ varepsilon_1,varepsilon_1^2,varepsilon_1^3,varepsilon_1^4 $. Если при передаче кодового полинома
$$ G(x)=b_0+b_1x+b_2x^2+dots+b_{n-1}x^{n-1} $$
произошли ровно две ошибки в $ j_{} $-м и $ k_{} $-м коэффициентах, и на выходе канала связи получен полином $ tilde G(x) $, то корни степени $ n_{} $ из единицы, обозначенные $ varepsilon_j $ и $ varepsilon_k $, удовлетворяют «уравнению ошибочных позиций»2)
$$
left| begin{array}{ccc}
tilde G(varepsilon_1) & tilde G(varepsilon_1^2) & tilde G(varepsilon_1^3) \
tilde G(varepsilon_1^2) & tilde G(varepsilon_1^3) & tilde G(varepsilon_1^4) \
1 & x & x^2
end{array}
right|=0 .
$$
Доказательство. Фактически к двум линейным уравнениям мы приписываем $ sigma_2+sigma_1x+sigma_0x^2=0 $, и к получившейся линейной однородной системе относительно неизвестных $ sigma_2,sigma_1,sigma_0 $ применяем критерий существования нетривиального решения: определитель этой системы должен быть равен нулю.
♦
В следующем пункте я часто буду употреблять подобные детерминантные представления, нетрадиционные для теории кодирования. В последней обычно разыскивают полином ошибочных позиций в виде нормализованного полинома — со старшим коэффициентом равным $ 1_{} $.
Разрешив уравнение ошибочных позиций, мы определим величины $ varepsilon_j $ и $ varepsilon_k $, и, следовательно, сможем восстановить значения соответствующих индексов $ {j,k} subset {0,1,2,dots,n-1} $, т.е. номеров коэффициентов полинома, в которых произошли ошибки. Величины же $ E_j $ и $ E_k $ этих ошибок восстанавливаются из первых двух уравнений системы ошибок:
$$
left{ begin{array}{rrl}
E_j varepsilon_j & + E_k varepsilon_k & = tilde G(varepsilon_1), \
E_j varepsilon_j^2 & + E_k varepsilon_k^2 & = tilde G(varepsilon_1^2)
end{array}
right.
$$
Впрочем, как правило, величины $ E_j $ и $ E_k $ можно установить только из первого уравнения — если воспользоваться условием их вещественности.
Остался открытым вопрос о возможности выбора порождающего циклический код полинома $ g_{}(x) $, имеющего одновременно корнями $ varepsilon_1, varepsilon_1^2,varepsilon_1^3,varepsilon_1^4 $. При этом полином $ g_{}(x) $ должен иметь целочисленные коэффициенты — иначе мы не сможем организовать выбор кодовых слов в пространстве $ mathbb Z^n $. По аналогии с подходом
☞
ПУНКТА можно попробовать выбрать полином $ g_{}(x) $ как произведение полиномов деления круга $ X_j(x) $. Действительно, при любом $ nin mathbb N $ полином $ X_n(x) $ будет иметь корнем $ varepsilon_1 $, равно как и любой другой первообразный корень степени $ n_{} $. Тогда при $ nge 5 $ и $ n_{} $ — простом, все степени $ {varepsilon_1^j}_{j=1}^{n-1} $ будут первообразными корнями степени $ n_{} $, и, следовательно, будут корнями полинома $ X_n(x) $. В этом случае можно было бы взять $ g(x)equiv X_n(x) $, однако, хотя с формальной точки зрения это и допустимо, тем не менее, с точки зрения практической пользы такой вариант бессмыслен: при любом способе кодирования в циклическом коде размерность кодового пространства $ mathbb U $ становится равной $ 1_{} $, т.е. в $ n_{} $-кодовом слове остается единственный свободный разряд, который можно использовать в качестве информационного.
Итак, число $ nge 5 $ должно быть составным. Пусть $ n_{} $— нечетно. Тогда (см.
☞
ЗДЕСЬ) величины $ varepsilon_1, varepsilon_1^2,varepsilon_1^4 $ будут все первообразными корнями и, следовательно,
корнями полинома $ X_n(x) $. Если $ n_{} $ не делится на $ 3_{} $, то и $ varepsilon_1^3 $ будет первообразным корнем, т.е. корнем $ X_n(x) $. Обобщим эти рассуждения: если $ n_{}ge 5 $ — составное и $ operatorname{HOD}(n,6)=1 $, то можно взять $ g(x)equiv X_n(x) $. Если $ operatorname{HOD}(n,6)>1 $, то полином $ g_{}(x) $ можно построить в виде произведения полиномов $ X_j(x) $. Так,
при $ operatorname{HOD}(n,6)=2 $ можно взять $ g(x)equiv X_n(x)X_{n/2}(x) $ в случае когда $ n_{} $ не делится на $ 4_{} $ и $ g(x)equiv X_n(x)X_{n/2}(x)X_{n/4}(x) $ в случае когда $ n_{} $ делится на $ 4_{} $
П
Пример. Пусть $ n=15 $ и порождающий циклический код полином выбран в виде
$$ g(x)equiv X_5(x)X_{15}(x)equiv (1+x+x^2+x^3+x^4)(1-x+x^3-x^4+x^5-x^7+x^8) equiv $$
$$ equiv 1+x^3+x^6+x^9+x^{12} . $$
Пусть при передаче некоторого кодового полинома $ G_{}(x) $ на выходе канала получен полином
$$ tilde G(x)=-1+5,x+2,x^2-x^3+3,x^4+2,x^5-x^6+5,x^7+2,x^8-x^9+5,x^{10}+2,x^{11}-x^{12}+2,x^{13}+2,x^{14} . $$
Требуется восстановить кодовый полином $ G_{}(x) $, основываясь на гипотезе, что при передаче произошло ровно две ошибки.
Решение. Порождающий код полином $ g_{}(x) $ удовлетворяет условиям теоремы: его корнями являются
величины $ varepsilon_1, varepsilon_1^2,varepsilon_1^3,varepsilon_1^4 $ при
$$ varepsilon_1=cos frac{2pi}{15}+mathbf i sin frac{2pi}{15} approx 0.913545+0.406736, mathbf i . $$
Вычисляем $ tilde G(varepsilon_1) approx -1.798335+0.240391 , mathbf i $. Поскольку $ tilde G(varepsilon_1) ne 0 $, то заключаем, что хотя бы одна ошибка при передаче по каналу произошла. Вычисляем дополнительно $ tilde G(varepsilon_1^2), tilde G(varepsilon_1^3), tilde G(varepsilon_1^4) $ и составляем уравнение ошибочных позиций из теоремы:
$$
left| begin{array}{rrr}
-1.798335+0.240391 , mathbf i & 2.269881+3.399389 , mathbf i & 1.809017+3.665469 , mathbf i \
2.269881+3.399389 , mathbf i & 1.809017+3.665469 , mathbf i & 1.107352-1.437208 , mathbf i \
1 & x & x^2
end{array}
right|=0
$$
или
$$
(17.562306-12.759762, mathbf i) +(-6.708203964+11.618950, mathbf i)x+(2.269125-21.589284, mathbf i)x^2=0 .
$$
Решаем его и находим
$$ mu_1 approx -0.104528+0.994522, mathbf i, mu_2approx 0.669131-0.743145, mathbf i . $$
Если при передаче по каналу произошли — как утверждается в условии — ровно две ошибки, то получившиеся значения должны быть корнями $ 15 $-й степени из единицы. Это немедленно проверяется. Остается выяснить каким значениям показателей $ varepsilon_j $ и $ varepsilon_k $ соответствуют эти числа.
$$ 15 arccos(-0.104528)/(2pi) approx 4 quad mbox{ и } quad 0.994522>0 quad Rightarrow j=4 . $$
$$ 15 arccos(0.669131)/(2pi) approx 2 quad mbox{ и } quad -0.743145<0 quad Rightarrow k=15-2=13 . $$
Итак, полином $ tilde G(x) $ имеет ошибочные коэффициенты при $ x^{4} $ и $ x^{13} $. Для нахождения величин этих ошибок имеем уравнение
$$ E_4 mu_1 + E_{13} mu_2 = tilde G(varepsilon_1) quad iff quad
left{ begin{array}{rrr}
-0.104528 E_4 &+0.669131 E_{13} & = -1.798335, \
0.994522 E_4 &-0.743145 E_{13} & = 0.240391.
end{array} right. $$
Откуда получаем $ E_4approx -1.999997, E_{13} approx -2.999997 $. Заключаем, что $ G(x)equiv tilde G(x) +2,x^4+3,x^{13} $.
Теперь проверим насколько «устойчив» алгоритм к истинному количеству ошибок. Допустим, что вместо предполагаемых двух ошибок произошла одна и на выходе канала получен полином $ tilde G(x)equiv G(x)-4,x^7 $. Уравнение ошибочных позиций из теоремы
$$
left| begin{array}{rrr}
3.912590-0.831647 , mathbf i & -3.654182+1.626946 , mathbf i & 3.236068-2.351141 , mathbf i \
-3.654182+1.626946 , mathbf i & 3.236068-2.351141 , mathbf i & -2.676522+2.972579 , mathbf i \
1 & x & x^2
end{array}
right|=0
$$
вырождается в тождество $ 0equiv 0 $. С формальной точки зрения, истинность уравнения сохраняется, только информации из него не извлечь… Модифицируем метод, играя на понижение количества ошибок — составим уравнение
$$
left| begin{array}{cc}
tilde G(varepsilon_1) & tilde G(varepsilon_1^2) \
1 & x
end{array}
right|=0 quad iff
$$
$$
iff quad
(3.654181840-1.626946579, mathbf i )+(3.912590396-.8316467668, mathbf i )x=0 quad iff muapprox -0.978148+0.207912 , mathbf i .
$$
Далее идем как в предыдущем случае: действительно, $ mu^{15} = 1 $ и
$$ 15 arccos(-0.978148)/(2pi) approx 7 quad mbox{ и } quad 0.207912 >0 quad Rightarrow j=7 . $$
Место ошибки обнаружено верно. Ее величину определяем из условия $ tilde G(varepsilon_1)=E_7 mu $.
♦
Распространение идеи подхода для случая трех и более ошибок очевидно. Так, если порождающий $ n_{} $-код полином $ g_{}(x) $ имеет корнями $ {varepsilon_1^j}_{j=1}^6 $, то это даст возможность исправления не менее трех ошибок. Соответствующее уравнение ошибочных позиций для определения номеров испорченных коэффициентов:
$$
left| begin{array}{cccc}
tilde G(varepsilon_1) & tilde G(varepsilon_1^2) & tilde G(varepsilon_1^3) & tilde G(varepsilon_1^4) \
tilde G(varepsilon_1^2) & tilde G(varepsilon_1^3) & tilde G(varepsilon_1^4) & tilde G(varepsilon_1^5)\
tilde G(varepsilon_1^3) & tilde G(varepsilon_1^4) & tilde G(varepsilon_1^5) & tilde G(varepsilon_1^6) \
1 & x & x^2 & x^3
end{array}
right|=0
$$
строится по аналогии со случаем двух ошибок. Покажем здесь, что при наличии ровно трех ошибок в полиноме $ tilde G(x) $, явившихся результатом передачи кодового полинома $ G_{}(x) $, построенное уравнение нетривиально. Итак, пусть $ tilde G(x)equiv G(x)+E_jx^j+E_kx^k+E_sx^s $. Рассмотрим коэффициент при $ x^{3} $ в уравнении ошибок:
$$
left| begin{array}{ccc}
tilde G(varepsilon_1) & tilde G(varepsilon_1^2) & tilde G(varepsilon_1^3) \
tilde G(varepsilon_1^2) & tilde G(varepsilon_1^3) & tilde G(varepsilon_1^4) \
tilde G(varepsilon_1^3) & tilde G(varepsilon_1^4) & tilde G(varepsilon_1^5)
end{array}
right|=
left| begin{array}{ccc}
E_jvarepsilon_j+E_kvarepsilon_k+E_svarepsilon_s & E_jvarepsilon_j^2+E_kvarepsilon_k^2+E_svarepsilon_s^2 &
E_jvarepsilon_j^3+E_kvarepsilon_k^3+E_svarepsilon_s^3 \
E_jvarepsilon_j^2+E_kvarepsilon_k^2+E_svarepsilon_s^2 &
E_jvarepsilon_j^3+E_kvarepsilon_k^3+E_svarepsilon_s^3 &
E_jvarepsilon_j^4+E_kvarepsilon_k^4+E_svarepsilon_s^4 \
E_jvarepsilon_j^3+E_kvarepsilon_k^3+E_svarepsilon_s^3 &
E_jvarepsilon_j^4+E_kvarepsilon_k^4+E_svarepsilon_s^4 &
E_jvarepsilon_j^5+E_kvarepsilon_k^5+E_svarepsilon_s^5
end{array}
right|
.
$$
Этот определитель относится к типу ганкелевых; для его вычисления представим его в виде определителя произведения трех матриц
$$
det left{
left(
begin{array}{ccc}
1 & 1 & 1 \
varepsilon_j & varepsilon_k & varepsilon_s \
varepsilon_j^2 & varepsilon_k^2 & varepsilon_s^2
end{array}
right)
left(
begin{array}{ccc}
E_j & 0 & 0 \
0& E_k & 0 \
0 & 0 & E_s
end{array}
right)
left(
begin{array}{ccc}
varepsilon_j & varepsilon_j^2 & varepsilon_j^3 \
varepsilon_k & varepsilon_k^2 & varepsilon_k^3 \
varepsilon_s & varepsilon_s^2 & varepsilon_s^3
end{array}
right)
right} .
$$
Применение теоремы Бине-Коши сводит вычисление этого определителя к произведению определителей составляющих матриц. Определитель первой матрицы является определителем Вандермонда —
$$
left|
begin{array}{ccc}
1 & 1 & 1 \
varepsilon_j & varepsilon_k & varepsilon_s \
varepsilon_j^2 & varepsilon_k^2 & varepsilon_s^2
end{array}
right|=(varepsilon_k -varepsilon_j)(varepsilon_s-varepsilon_j)(varepsilon_s-varepsilon_k),
$$
он
отличен от нуля, поскольку, по предположению, числа $ varepsilon_j, varepsilon_k, varepsilon_s $ все различны. Далее, определитель третьей матрицы
$$
left|
begin{array}{ccc}
varepsilon_j & varepsilon_j^2 & varepsilon_j^3 \
varepsilon_k & varepsilon_k^2 & varepsilon_k^3 \
varepsilon_s & varepsilon_s^2 & varepsilon_s^3
end{array}
right|=varepsilon_jvarepsilon_kvarepsilon_s left|
begin{array}{ccc}
1 & 1 & 1 \
varepsilon_j & varepsilon_k & varepsilon_s \
varepsilon_j^2 & varepsilon_k^2 & varepsilon_s^2
end{array}
right|=varepsilon_jvarepsilon_kvarepsilon_s(varepsilon_k -varepsilon_j)(varepsilon_s-varepsilon_j)(varepsilon_s-varepsilon_k) ,
$$
также отличен от нуля, поскольку все числа $ varepsilon_j,varepsilon_k,varepsilon_s $ еще и ненулевые.
Определитель средней матрицы равен $ E_jE_kE_s $ и отличен от нуля по предположению, что величины ошибок — ненулевые. Следовательно, коэффициент при $ x^{3} $ в уравнении ошибочных позиций отличен от нуля и уравнение не обращается в тривиальное тождество $ 0equiv 0 $.
Хочется развить этот успех на случай произвольного количества ошибок. К сожалению, на пути исполнения этого желания стоит препятствием уже упомянутое ранее ограничение на степень $ n_{} $. При фиксировании этого числа, добавление в состав кодового полинома $ g_{}(x) $ новых сомножителей из числа полиномов $ X_{ell} (x) $ уменьшает количество информационных разрядов.
Двоичные БЧХ-коды
Будем строить двоичный циклический $ n_{} $-разрядный код для случая $ n=2^M-1, Min mathbb N $. Основываясь на идее предыдущего пункта, будем строить его на основе порождающего полинома $ g_{}(x) $, имеющего корнями последовательные степени примитивного элемента поля Галуа $ mathfrak A in mathbf{GF}(2^M) $:
$$ mathfrak A, mathfrak A^2, mathfrak A^3,dots,mathfrak A^{2tau} quad npu quad tau ge 2 . $$
Как построить такой полином? Примитивный элемент $ mathfrak A $ поля $ mathbf{GF}(2^M) $ является корнем неприводимого полинома степени $ m_{} $ над $ mathbf{GF}(2) $ — который также называется примитивным. Выражения для примитивных полиномов берутся из заранее составленных таблиц. Обозначим этот полином $ f_{1}(x) $. Тогда, в соответствии с теоремой 1, приведенной ☞ ЗДЕСЬ, корнями этого же полинома будут и величины $ mathfrak A^2, mathfrak A^4,dots, mathfrak A^{2^{m-1}} $. Но вот величина $ mathfrak A^3 $ не будет корнем $ f_{1}(x) $. С другой стороны, она будет корнем некоторого другого неприводимого полинома $ f_3(x) $. Поэтому интересующий нас полином $ g_{}(x) $ должен иметь представление в виде произведения примитивных полиномов
$$ g(x)equiv f_1(x)f_3(x)times dots , $$
каждый из которых имеет корнем определенную величину из множества $ { mathfrak A^{j}}_{j=1}^{2tau} $. Строго говоря, определим $ g_{}(x) $ равенством
$$ g(x)equiv operatorname{HOK}(f_1,f_2,dots,f_{2tau}) , $$
где $ operatorname{HOK} $ означает наименьшее общее кратное неприводимых над $ mathbf{GF}(2) $ полиномов $ f_{j}(x) $, таких, что $ f_{j}(mathfrak A^{j})=mathfrak o $. Такое представление позволяет, во-первых, обеспечить выполнение требования к структуре множества корней полинома $ g_{}(x) $, а, во-вторых, отбросить «дублирующие» полиномы.
П
Пример. Пусть $ M=4 $. Построить полином, корнями которого являются
$ mathfrak A, mathfrak A^2, mathfrak A^3, mathfrak A^4 $, где $ mathfrak A $ означает примитивный элемент поля $ mathbf{GF}(16) $.
Решение. Примитивный элемент поля $ mathbf{GF}(16) $ является корнем одного из неприводимых над $ mathbf{GF}(2) $ полиномов: $ x^4+x+1 $ или $ x^4+x^3+1 $ (см. разбор
☞
ЗДЕСЬ). Возьмем $ f_1(x)=x^4+x+1 $. Корнями этого полинома будут также $ mathfrak A^2 $ и $ mathfrak A^4 $. Величина $ mathfrak A^3 $ будет корнем полинома $ f_3(x)=x^4+x^3+x^2+x+1 $. Таким образом,
$$ g(x)equiv (x^4+x+1)(x^4+x^3+x^2+x+1) pmod{2} equiv x^8+x^7+x^6+x^4+1 . $$
Кодовое пространство, порождаемое этим полиномом, имеет размерность $ k=15-8=7 $, т.е. на $ 7_{} $ информационных битов приходится $ 8_{} $ проверочных. Иными словами, этот линейный код является $ (15,7) $-кодом.
Если бы мы поставили задачу нахождения полинома $ g_{}(x) $ с корнями $ mathfrak A, mathfrak A^2, mathfrak A^3, mathfrak A^4,mathfrak A^5,mathfrak A^6 $, то для нам пришлось бы домножить предыдущий полином на $ x^2+x+1 $, поскольку именно его корнем является $ mathfrak A^5 $ (в то время как $ mathfrak A^6 $ является корнем уже используемого полинома $ f_3 $):
$$ g(x)equiv (x^4+x+1)(x^4+x^3+x^2+x+1)(x^2+x+1) pmod{2} equiv x^{10}+x^8+x^5+x^4+x^2+x+1 . $$
Код, порождаемый этим полиномом, является $ (15,5) $-кодом, т.е. на $ 5_{} $ информационных битов приходится $ 10_{} $ проверочных.
♦
Итак, допустим нам удалось построить циклический код на основе порождающего полинома $ g_{}(x) $, имеющего корнями $ { mathfrak A^{j}}_{j=1}^{2tau} $, где $ mathfrak A $ — примитивный элемент поля $ mathbf{GF}(2^M) $. Кодирование передаваемой информации производится любым из способов, принятых в циклических кодах.
Покажем, что такой код способен исправить от одной до $ tau_{} $ ошибок при передаче по каналу связи. Пусть при передаче кодового полинома $ G_{}(x) $ произошло ровно $ ell_{} $ ошибок в коэффициентах при $ x^{j_1},x^{j_2},dots,x^{j_{ell}} $:
$$ tilde G(x) equiv G(x)+E_{j_1} x^{j_1}+E_{j_2} x^{j_2}+dots+ E_{j_{ell}} x^{j_{ell}} pmod{2} . $$
Заметим, что для двоичного кода ошибка — это либо $ 0 to 1 $, либо $ 1 to 0 $, и, следовательно, величина ошибки $ E_{j} $ всегда равна $ 1_{} $. Подставляем в полином $ tilde G(x) $ корни $ { mathfrak A^{j}}_{j=1}^{2tau} $ полинома $ g_{}(x) $. Кодовый полином обращается на них в нуль, так что получаем:
$$left{begin{array}{lllll}
tilde G(mathfrak A)&= mathfrak A^{j_1}&+mathfrak A^{j_2}&+dots& + mathfrak A^{j_{ell}}, \
tilde G(mathfrak A^2)&= mathfrak A^{2j_1}&+mathfrak A^{2j_2}&+dots& + mathfrak A^{2j_{ell}}, \
tilde G(mathfrak A^3)&= mathfrak A^{3j_1}&+mathfrak A^{3j_2}&+dots& + mathfrak A^{3j_{ell}}, \
dots & & & dots \
tilde G(mathfrak A^{2tau})&= mathfrak A^{2tau j_1}&+mathfrak A^{2 tau j_2}&+dots& + mathfrak A^{2 tau j_{ell}}.
end{array}
right.
$$
Величины $ mathfrak A^{j_1},mathfrak A^{j_2},dots,mathfrak A^{j_{ell}} $ называются локаторами ошибок. Система уравнений для их определения — существенно нелинейная. Однако, благодаря наработанному в предыдущем пункте, у нас имеется конструктивный подход к ее решению. Именно, мы разыскиваем полином
$$ L(x)=sigma_{0}x^{ell}+ sigma_1x^{ell-1}+dots+sigma_{ell} $$
имеющий корнями локаторы ошибок, т.е. такой, что
$$ L(mathfrak A^{j_1})=mathfrak o,L(mathfrak A^{j_2})=mathfrak o,dots, L(mathfrak A^{j_{ell}})=mathfrak o .
$$
Полином $ L(x) $ называется полиномом локаторов ошибок. Подчеркнем, что его коэффициенты являются элементами поля Галуа: $ {sigma_j}_{j=0}^{ell} subset mathbf{GF}(2^M) $.
Т
Теорема. Пусть порождающий код полином обладает корнями $ { mathfrak A^{j}}_{j=1}^{2tau} $, где $ mathfrak A $ — примитивный элемент поля $ mathbf{GF}(2^M) $. Если при передаче кодового полинома
$$ G(x)=b_0+b_1x+b_2x^2+dots+b_{n-1}x^{n-1}, (n=2^M-1) $$
произошли ровно $ ell $ ошибок в коэффициентах с номерами $ {j_k}_{k=1}^{ell} $, и на выходе канала связи получен полином $ tilde G(x) $, то при $ tau ge ell $ локаторы ошибок $ {mathfrak A^{j_k}}_{k=1}^{ell} $ удовлетворяют уравнению
$$
L(x)=
left|
begin{array}{lllcl}
tilde G(mathfrak A) & tilde G(mathfrak A^2) & tilde G(mathfrak A^3) & dots & tilde G(mathfrak A^{ell+1}) \
tilde G(mathfrak A^2) & tilde G(mathfrak A^3) & tilde G(mathfrak A^4) & dots & tilde G(mathfrak A^{ell+2}) \
tilde G(mathfrak A^3) & tilde G(mathfrak A^4) & tilde G(mathfrak A^5) & dots & tilde G(mathfrak A^{ell+3}) \
dots & & & & dots \
tilde G(mathfrak A^{ell}) & tilde G(mathfrak A^{ell+1}) & tilde G(mathfrak A^{ell+2}) & dots & tilde G(mathfrak A^{2ell}) \
1 & x & x^2 & dots & x^{ell}
end{array}
right|=mathfrak o
$$
и это уравнение имеет степень $ ell_{} $. Если же произошло меньше чем $ ell_{} $ ошибок, то это уравнение обращается в тождество $ mathfrak o = mathfrak o $.
П
Пример. Рассмотрим $ (15,5) $-код из предыдущего примера — пусть порождающий его полином имеет вид
$$ g(x)= x^{10}+x^8+x^5+x^4+x^2+x+1 . $$
Пусть при передаче некоторого кодового полинома $ G_{}(x) $ произошло некоторое количество ошибок, и на выходе канала связи оказался полином
$$ tilde G(x)= 1+x^3+x^4+x^7+x^{10}+x^{12}+x^{13}+x^{14} .
$$
Попробуем исправить эти ошибки, основываясь на предыдущем результате. Максимально возможное количество ошибок, которых потенциально возможно «отловить» с его помощью, равно $ 3_{} $. Положив эту оценку стартовой гипотезой, строим детерминантное представление для полинома локаторов ошибок:
$$
L(x)=
left|
begin{array}{lllcl}
tilde G(mathfrak A) & tilde G(mathfrak A^2) & tilde G(mathfrak A^3) & tilde G(mathfrak A^4) \
tilde G(mathfrak A^2) & tilde G(mathfrak A^3) & tilde G(mathfrak A^4) & tilde G(mathfrak A^5) \
tilde G(mathfrak A^3) & tilde G(mathfrak A^4) & tilde G(mathfrak A^5) & tilde G(mathfrak A^6) \
1 & x & x^2 & x^{3}
end{array}
right| .
$$
Здесь через $ mathfrak A $ обозначен корень полинома $ x^4+x+1 $; он является примитивным элементом поля $ mathbf{GF}(16) $. Вычисляем элементы определителя, пользуясь таблицей для степеней $ mathfrak A^j $, приведенной
☞
ЗДЕСЬ.
$$
begin{array}{rccccccc}
tilde G(mathfrak A) =& 1 +mathfrak A^3 &+ mathfrak A^4 &+mathfrak A^7&+mathfrak A^{10}& +mathfrak A^{12}& +mathfrak A^{13}& +mathfrak A^{14}= \
=&1+mathfrak A^3&+(mathfrak A+1)& +(mathfrak A^3+mathfrak A+1) &+(mathfrak A^2+mathfrak A+1)&+(mathfrak A^3+mathfrak A^2+mathfrak A+1)&+(mathfrak A^3+mathfrak A^2+1)&+(mathfrak A^3+1)=
end{array}
$$
$$
{}_{} qquad =mathfrak A^3+mathfrak A^2+1=mathfrak A^{13} .
$$
Поскольку $ tilde G(mathfrak A) ne mathfrak o $, то хотя бы одна ошибка при передаче произошла.
Далее,
$$
tilde G(mathfrak A^2)=mathfrak A^3+mathfrak A^2+mathfrak A=mathfrak A^{11}, tilde G(mathfrak A^3)=mathfrak o, tilde G(mathfrak A^4)=mathfrak A^3+mathfrak A +1=mathfrak A^7,
tilde G(mathfrak A^5)=mathfrak A^2+mathfrak A=mathfrak A^5, tilde G(mathfrak A^6)=mathfrak o .
$$
Разложение определителя по последней строке, начинаем с правого угла: коэффициент при $ x^{3} $ равен3)
$$
left|
begin{array}{ccc}
mathfrak A^3+mathfrak A^2+1 & mathfrak A^3+mathfrak A^2+mathfrak A & mathfrak o \
mathfrak A^3+mathfrak A^2+mathfrak A & mathfrak o & mathfrak A^3+mathfrak A +1 \
mathfrak o & mathfrak A^3+mathfrak A +1 & mathfrak A^2+mathfrak A
end{array}
right| =
left|
begin{array}{ccc}
mathfrak A^{13} & mathfrak A^{11} & mathfrak o \
mathfrak A^{11} & mathfrak o & mathfrak A^7 \
mathfrak o & mathfrak A^7 & mathfrak A^5
end{array}
right|=mathfrak o .
$$
Следовательно, $ deg L(x)le 3 $, и это4) свидетельствует о том, что количество ошибок не может равняться $ 3_{} $.
Выдвигаем гипотезу о том, что количество ошибок передачи равно $ 2_{} $. Уменьшаем размерность соответствующего определителя:
$$
L(x)=
left|
begin{array}{lll}
tilde G(mathfrak A) & tilde G(mathfrak A^2) & tilde G(mathfrak A^3) \
tilde G(mathfrak A^2) & tilde G(mathfrak A^3) & tilde G(mathfrak A^4) \
1 & x & x^2
end{array}
right| =
left|
begin{array}{ccc}
mathfrak A^{13} & mathfrak A^{11} & mathfrak o \
mathfrak A^{11} & mathfrak o & mathfrak A^7 \
1 & x & x^2
end{array}
right|=mathfrak A^{22}x^2+mathfrak A^{20}x+mathfrak A^{18}=mathfrak A^{7}x^2+mathfrak A^{5}x+mathfrak A^{3} .
$$
В этом случае полином $ L(x) $ нетривиален. Непосредственной проверкой убеждаемся, что корнями полинома являются элементы поля $ mathfrak A^{3} $ и $ mathfrak A^{8} $. Это — локаторы ошибок, они указывают на позиции ошибок в $ 3_{} $-м и $ 8 $-м коэффициентах полинома $ tilde G(x) $. Кодовым является полином
$$ G(x)= 1+x^4+x^7+x^8+x^{10}+x^{12}+x^{13}+x^{14} . $$
♦
Построенный выше двоичный код является примером кода Боуза-Чоудхури-Хоквингема5) или БЧХ-кода. Его кодовое расстояние не превосходит величины
$$ d_0=1+2tau , $$
которая называется конструктивным расстоянием БЧХ-кода. Число $ k_{} $ информационных символов БЧХ-кода и, соответственно, число $ n-k=2^M-k-1 $ проверочных символов зависит от степеней множителей полинома $ g_{}(x) $ — неприводимых по модулю $ 2_{} $ полиномов.
=>
Код Хэмминга является частным случаем БЧХ-кода, он соответствует случаю $ tau=1 $. В этом случае кодовым полиномом берется просто произвольный примитивный полином — поскольку его корнями обязательно будут две последовательные степени $ mathfrak A $ и $ mathfrak A^2 $ (см. теорему $ 1 $
☞
ЗДЕСЬ ) примитивного элемента поля $ mathbf{GF}(2^M) $, то, в соответствии с теоремой, он способен исправлять одну ошибку линейного $ (2^M-1,2^M-M-1) $-кода.
Теперь сделаем несколько комментариев, позволяющих упростить вычисление полинома локаторов ошибок, а также «развить успех» в разных направлениях.
1.
В соответствии с теоремой Шёнеманна, для любого полинома $ F_{}(x) $ над $ mathbf{GF}(2) $ имеет место сравнение $ left[F(x)right]^2 equiv F(x^2) pmod{2} $. Тогда
$$ tilde G(mathfrak A^2)=left(tilde G(mathfrak A)right)^2, tilde G(mathfrak A^4)=left(tilde G(mathfrak A^2)right)^2, tilde G(mathfrak A^6)=left(tilde G(mathfrak A^3)right)^2,dots
$$
Таким образом, вычислив значения $ tilde G(mathfrak A^j) $ для нечетных показателей $ j_{} $,
значения $ tilde G ( mathfrak A^{2j}) $ получим возведением в квадрат уже вычисленного $ tilde G(mathfrak A^j) $. (Понаблюдайте проявление этого свойства в предыдущем примере).
2.
Полином $ L_{}(x) $ раскладывается на линейные множители над полем $ mathbf{GF}(2^M) $:
$$ L(x) equiv sigma_{ell}(x-mathfrak A^{j_1})(x-mathfrak A^{j_2})timesdots times (x-mathfrak A^{j_{ell}}) . $$
Величины $ tilde G(mathfrak A),tilde G(mathfrak A^2),tilde G(mathfrak A^3),dots, tilde G(mathfrak A^{2tau}) $ представляют суммы степеней его корней; такие суммы — в случае полинома над $ mathbb Q,mathbb R $ или $ mathbb C_{} $ — называются суммами Ньютона. Известно, что над этими полями коэффициенты полинома рационально выражаются через суммы Ньютона: если обозначить корни нормализованного полинома
$$ L(x)=x^{ell}+sigma_{1}x^{ell-1}+sigma_{2}x^{ell-2}+dots+sigma_{ell} $$
через $ lambda_1,dots,lambda_{ell} $, а его $ k_{} $-ю сумму Ньютона через $ s_k=lambda_1^k+dots+lambda_{ell}^k $, то коэффициенты полинома $ L(x) $ выражаются через суммы Ньютона по следующим рекурсивным формулам Ньютона:
$$
sigma_{1}=-s_1, 2sigma_2=-(s_2+sigma_1s_1), 3sigma_3=-(s_3+sigma_1s_2+sigma_2s_1),dots,
$$
$$
ksigma_k=-(s_{k}+sigma_1s_{k-1}+sigma_2s_{k-2}+dots+sigma_{k-1}s_1) npu k le ell.
$$
В случае полинома $ L_{}(x) $ над $ mathbf{GF}(2) $ эти формулы следует рассматривать по модулю $ 2_{} $ и формулы с четными номерами отбрасываются потому как являются следствиями предыдущих, а также комментария
1
. Следующее детерминантное представление полинома аналогично приведенному в конце
☞
ПУНКТА для полинома над бесконечными полями;
для наглядности я приведу его для случая $ ell = 4 $:
$$
L(x)=
left|
begin{array}{lllll}
tilde G(mathfrak A) & 1 & 0 & 0 & 0 \
tilde G(mathfrak A^3) & tilde G(mathfrak A^2) & tilde G(mathfrak A) & 1 & 0 \
tilde G(mathfrak A^5) & tilde G(mathfrak A^4) & tilde G(mathfrak A^3) & tilde G(mathfrak A^2) & tilde G(mathfrak A) \
tilde G(mathfrak A^7) & tilde G(mathfrak A^6) & tilde G(mathfrak A^5) & tilde G(mathfrak A^4) & tilde G(mathfrak A^3) \
x^4 & x^3 & x^2 & x & 1
end{array}
right|
$$
П
Пример. Рассмотрим $ (15,5) $-код из предыдущего примера с порождающим полиномом
$$ g(x)= x^{10}+x^8+x^5+x^4+x^2+x+1 . $$
Пусть при передаче некоторого кодового полинома на выходе канала связи оказался полином
$$ tilde G(x)= 1+x+x^4+x^7+x^8+x^9+x^{11}+x^{14} .
$$
Примитивный элемент поля $ mathbf{GF}(16) $ выбираем тем же, что и ранее: пусть $ mathfrak A $ является корнем полинома $ x^4+x+1 $, входящего сомножителем в $ g_{}(x) $. Поскольку
$$ tilde G(mathfrak A)=mathfrak A+1 ne mathfrak o , $$
то при передаче по каналу произошла хотя бы одна ошибка. Положив начальной гипотезой наличие $ ell=2 $ ошибок, строим полином:
$$ L(x)=
left|
begin{array}{lll}
tilde G(mathfrak A) & 1 & 0 \
tilde G(mathfrak A^3) & tilde G(mathfrak A^2) & tilde G(mathfrak A) \
x^2 & x & 1
end{array}
right| =left|
begin{array}{ccc}
mathfrak A+1 & 1 & 0 \
mathfrak A^3 & mathfrak A^2+1 & mathfrak A+1 \
x^2 & x & 1
end{array}
right|=(mathfrak A+1)x^2+(mathfrak A^2+1)x+(mathfrak A^2+mathfrak A+1)
$$
Этот полином не имеет корней среди $ {mathfrak A^j}_{j=0}^{14} $.
Положив гипотезой наличие $ ell=3 $ ошибок (максимального количества ошибок, возможного для исправления настоящим кодом), строим полином
$$ L(x)=
left|
begin{array}{llll}
tilde G(mathfrak A) & 1 & 0 & 0 \
tilde G(mathfrak A^3) & tilde G(mathfrak A^2) & tilde G(mathfrak A) & 1 \
tilde G(mathfrak A^5) & tilde G(mathfrak A^4) & tilde G(mathfrak A^3) & tilde G(mathfrak A^2) \
x^3 & x^2 & x & 1
end{array}
right| =left|
begin{array}{cccc}
mathfrak A+1 & 1 & 0 & 0 \
mathfrak A^3 & mathfrak A^2+1 & mathfrak A+1 & 1 \
1 & mathfrak A & mathfrak A^3 & mathfrak A^2+1 \
x^3 & x^2 & x & 1
end{array}
right|=
$$
$$
=(mathfrak A^2+mathfrak A+1)x^3+(mathfrak A^3+1)x^2+(mathfrak A^3+mathfrak A^2+mathfrak A+1)x+mathfrak A^2 .
$$
Полином имеет корнями $ mathfrak A^3, mathfrak A^8,mathfrak A^{11} $, следовательно ошибки произошли в коэффициентах при $ x^3, x^8 $ и $ x^{11} $, и кодовым полиномом является
$$ G(x)=1+x+x^3+x^4+x^7+x^9+x^{14} . $$
♦
3.
Основное требование к порождающему код полиному иметь корнями последовательность первых степеней примитивного элемента поля допускает модификации. Эти модификации касаются двух выражений: «первых степеней» и «примитивного элемента». Так, с одной стороны, можно потребовать от порождающего код полинома $ g_{}(x) $ обращения в нуль на последовательности степеней примитивного элемента поля
$$ mathfrak A^{m_0}, mathfrak A^{m_0+1}, mathfrak A^{m_0+2},dots,mathfrak A^{m_0+2tau-1} quad npu quad m_0ge 1, tau ge 2 , $$
не обязательно начинающейся с первой его степени.
Небольшая модификация приведенного выше алгоритма исправления ошибок позволит применять его.
С другой стороны, можно отказаться от требования примитивности элемента $ mathfrak A $. Пусть порядок элемента $ mathfrak B in mathbf{GF}(2^M) $ равен $ n_{} $. Тогда все его степени
$$ mathfrak B^0,mathfrak B^1,mathfrak B^2,dots,mathfrak B^{n-1} $$
будут различными элементами поля и локаторы ошибок $ n_{} $-разрядного кода позволят однозначно установить места ошибок. Таким образом, в этом случае мы уменьшаем количество разрядов кода с максимально возможного $ 2^M-1 $ до некоторого делителя этого числа.
П
Пример. Пусть $ M=6 $. Построить $ 21 $-разрядный код, исправляющий две ошибки.
Решение. Поле $ mathbf{GF}(2^6) $ исследовано
☞
ЗДЕСЬ.
Число $ 2^6-1=63 $ делится на $ 21 $, следовательно в $ mathbf{GF}(2^6) $ существует элемент порядка $ 21 $, в качестве этого элемента можно взять произвольный корень полинома $ f_{6,2}(x)=x^6+x^5+x^4+x^2+1 $. Если обозначить корень этого полинома через $ mathfrak B_{} $, то найдется такой примитивный элемент $ mathfrak A in mathbf{GF}(2^6) $, что $ mathfrak B =mathfrak A^3 $. Если мы ставим целью подобрать полином $ g_{}(x) $ с корнями, среди которых имеются $ mathfrak B, mathfrak B^2, mathfrak B^3,mathfrak B^4 $, то все эти корни, кроме $ mathfrak B^3 $, будут корнями $ f_{6,2}(x) $. Корень же $ mathfrak B^3=mathfrak A^9 $ будет корнем полинома $ x^3+x+1 $ (проверьте что именно его, а не двойственного ему $ x^3+x^2+1 $). Таким образом, полином $ g(x)=(x^6+x^5+x^4+x^2+1)(x^3+x+1)=x^9+x^8+x^5+x^4+x^2+x+1 $ порождает $ (21,12) $-циклический код, исправляющий две ошибки.
♦
Коды Рида-Соломона
В предыдущем пункте мы столкнулись с необходимостью рассмотрения полиномов относительно переменной $ x_{} $, коэффициентами которых оказывались не числа, а элементы поля Галуа $ mathbf{GF}(2^M) $. Нам даже пришлось решать алгебраические уравнения, содержащие подобные полиномы6). Если первоначальный шок от использования подобных объектов преодолен, то попробуем пойти и дальше — допустим к рассмотрению в качестве порождающего циклический код полинома $ g_{}(x) $ не только полиномы с двоичными коэффициентами, но также и с коэффициентами из $ mathbf{GF}(2^M) $.
Начнем с формального обобщения БЧХ-кода, а уж практическое применение этого обобщения обсудим позже.
П
Пример 1. Рассмотрим код с порождающим полиномом равным
$$ g(x)=(x-mathfrak A)(x-mathfrak A^2)(x-mathfrak A^3)(x-mathfrak A^4)
$$
при $ mathfrak A $ — корне полинома $ f(x)= x^4+x+1 $.
Перемножив линейные сомножители по модулю $ 2,f(x) $, получим представление порождающего полинома в виде
$$ g(x)=x^4+(mathfrak A^3+mathfrak A^2+1)x^3+(mathfrak A^3+mathfrak A^2)x^2+mathfrak A^3,x+(mathfrak A^2+mathfrak A+1) ,
$$
которое — с помощью таблицы, приведенной
☞
ЗДЕСЬ — можно преобразовать к виду, когда коэффициентами мономов становятся степени примитивного элемента:
$$
g(x)=x^4+mathfrak A^{13}x^3+mathfrak A^6,x^2+mathfrak A^3,x+mathfrak A^{10} ;
$$
однако в дальнейших рассчетах более удобно именно первое представление.
Пусть для передачи некоторого информационного вектора $ (x_1,x_2,dots,x_{11}) in mathbb V^{11} $ используется несистематическое кодирование и кодовым полиномом является
$$ G(x)equiv (x_1x^{10}+x_2,x^9+dots+x_{11}) g(x) pmod{2} , $$
который при передаче по каналу связи преобразуется в
$$ tilde G(x) = x^{14}+(mathfrak A^3+mathfrak A^2+1)x^{13}+(mathfrak A^3+mathfrak A^2+1)x^{12}+(mathfrak A^3+1)x^{11}+
$$
$$
+(mathfrak A^2+mathfrak A+1)x^{10}+(mathfrak A^3+1)x^9+(mathfrak A+1)x^8
+(mathfrak A^3+mathfrak A^2+mathfrak A)x^7+
$$
$$
+(mathfrak A^3+mathfrak A+1)x^6+x^5+(mathfrak A^2+1)x^4+(mathfrak A^3+1)x^3+(mathfrak A^3+mathfrak A+1)x^2+mathfrak A^3x+
$$
$$
+(mathfrak A^2+mathfrak A+1) ,
$$
предположительно содержащий две ошибки в коэффициентах, т.е.
$$ tilde G(x) equiv G(x)+E_jx^j + E_kx^k quad npu quad {j,k} subset {0,1,2,dots,14}, {E_j,E_k} subset mathbf{GF}(16) . $$
Акцентируем, что в данном случае, в отличие от предыдущего пункта, величины ошибок $ E_j $ и $ E_k $ являются элементами поля $ mathbf{GF}(16) $, т.е. представляют собой выражения $ B_0+B_1mathfrak A+B_2mathfrak A^2+B_3mathfrak A^3 $ при $ {B_0,B_1,B_2,B_3} subset {0,1} $.
Требуется восстановить информационный вектор.
Действуя по сценарию
☞
ПУНКТА и руководствуясь гипотезой о двух ошибках, составляем систему уравнений
$$
left{ begin{array}{lll}
E_j mathfrak A^j & + E_k mathfrak A^k & = tilde G(mathfrak A), \
E_j mathfrak A^{2j} & + E_k mathfrak A^{2k} & = tilde G(mathfrak A^2), \
E_j mathfrak A^{3j} & + E_k mathfrak A^{3k} & = tilde G(mathfrak A^3), \
E_j mathfrak A^{4j} & + E_k mathfrak A^{4k} & = tilde G(mathfrak A^4).
end{array}
right.
$$
которую пытаемся решить относительно локаторов ошибок $ mathfrak A^j, mathfrak A^k $ и величин ошибок $ E_j, E_k $. Уравнение локаторов ошибок разыскивается в виде:
$$
left| begin{array}{lll}
tilde G(mathfrak A) & tilde G(mathfrak A^2) & tilde G(mathfrak A^3) \
tilde G(mathfrak A^2) & tilde G(mathfrak A^3) & tilde G(mathfrak A^4) \
1 & x & x^2
end{array}
right|=
left| begin{array}{ccc}
mathfrak A^3+mathfrak A^2+1 & mathfrak A^3+mathfrak A+1 & mathfrak o \
mathfrak A^3+mathfrak A+1 & mathfrak o & mathfrak A^3+mathfrak A^2 \
1 & x & x^2
end{array}
right|= mathfrak o .
$$
Поскольку $ tilde G(mathfrak A)ne mathfrak o $, то, крайней мере, одна ошибка имеется. Раскладываем определитель по последней строке:
$$
(mathfrak A^3+1)x^2+(mathfrak A+1)x+(mathfrak A^3+mathfrak A^2+1) = mathfrak o .
$$
Корнями этого уравнения оказываются $ mathfrak A^3 $ и $ mathfrak A^{11} $. Таким образом, $ j=3, k=11 $, т.е. ошибки передачи по каналу содержатся в коэффициентах при $ x^{3} $ и $ x^{11} $. Величины ошибок $ E_3 $ и $ E_{11} $ находим из приведенной выше системы линейных уравнений, в которой коэффициенты нами теперь установлены:
$$left{
begin{array}{lllll}
E_3 mathfrak A^3&+E_{11}mathfrak A^{11}&=tilde G(mathfrak A)&= mathfrak A^3+mathfrak A^2+1&=mathfrak A^{13}, \
E_3 mathfrak A^6&+E_{11}mathfrak A^{22}&=tilde G(mathfrak A^2)&= mathfrak A^3+mathfrak A+1&=mathfrak A^{7},
end{array}
right .
$$
Решаем эту систему по формулам Крамера:
$$
E_3=frac{ left| begin{array}{ll} mathfrak A^{13} & mathfrak A^{11} \ mathfrak A^7 & mathfrak A^{22}
end{array}
right| }{
left| begin{array}{ll} mathfrak A^{3} & mathfrak A^{11} \ mathfrak A^6 & mathfrak A^{22}
end{array}
right|
}=frac{mathfrak A^{35}+mathfrak A^{18}}{mathfrak A^{25}+mathfrak A^{17}}=frac{mathfrak A^{5}+mathfrak A^{3}}{mathfrak A^{10}+mathfrak A^{2}}=frac{mathfrak A^{11}}{mathfrak A^{4}}=mathfrak A^{7}=mathfrak A^{3}+mathfrak A+1 ,
$$
$$
E_{11}=
frac{left| begin{array}{ll} mathfrak A^{3} & mathfrak A^{13} \ mathfrak A^6 & mathfrak A^{7}
end{array}
right| }{
left| begin{array}{ll} mathfrak A^{3} & mathfrak A^{11} \ mathfrak A^6 & mathfrak A^{22}
end{array}
right|
}=mathfrak A^{3}+mathfrak A^2+1 .
$$
Таким образом, кодовый полином равен
$$ G(x)equiv tilde G(x)+(mathfrak A^{3}+mathfrak A+1)x^3+(mathfrak A^{3}+mathfrak A^2+1)x^{11} , $$
его частное от деления на порождающий полином $ g_{}(x) $ равно $ x^{10}+x^8+x^7+x^6+x^3+x^2+1 $, т.е. информационным вектором является $ (10111001101) $.
♦
Итак, формальное обобщение двоичного БЧХ-кода из предыдущего пункта произведено. Порождающий код полином $ g_{}(x) $ оказывается делителем полинома $ x^{2^M-1} — 1 $, но только делителем не с двоичными коэффициентами, а с коэффициентами из $ mathbf{GF}(2^M) $. Этот полином правильно исправляет ошибки, а его степень существенно меньше степени порождающего полинома двоичного БЧХ-кода, решающего ту же задачу. Правда, выражения для коэффициентов полинома становятся более сложными, но если уж мы принципиально решили связываться с формализмом полей Галуа, то упомянутое усложнение не кажется существенным.
Коды, построенные по аналогии с разобранным в примере 1 случаем, также относят к БЧХ-кодам, но они имеют специальное название — это коды Рида-Соломона7).
В примере $ 1 $ в качестве порождающего код полинома рассматривался полином над полем $ mathbf{GF}(16) $, в то время как собственно информационный полином, который был вычислен на последнем шаге, оказался полиномом над $ mathbf{GF}(2) $. А что будет, если взять и в качестве информационного полинома не полином над $ mathbf{GF}(2) $, а полином над $ mathbf{GF}(16) $
?
П
Пример 2. Рассмотрим код из предыдущего примера. Пусть информационный полином равен
$$ P(x)=(mathfrak A^3+mathfrak A^2+1)x^{10}+(mathfrak A^2+1)x^9+(mathfrak A^3+mathfrak A^2+mathfrak A+1)x^8+mathfrak A,x^7+(mathfrak A^2+mathfrak A+1)x^6+
$$
$$
+(mathfrak A^3+mathfrak A^2+1)x^3
+(mathfrak A+1)x^2+(mathfrak A^3+1) .
$$
Далее идем по проложенному в предыдущем примере пути. Используем несистематическое кодирование, получаем кодовый полином
$$ G(x)equiv P(x)g(x) pmod{2} = $$
$$
=(mathfrak A^3+mathfrak A^2+1)x^{14}+(mathfrak A^3+mathfrak A+1)x^{13}+ dots+ x^3+(mathfrak A^3+mathfrak A^2+mathfrak A+1)x^2+mathfrak A^2,x+
$$
$$
+(mathfrak A^3+mathfrak A) , $$
пересылаем по каналу, на выходе получаем испорченный полином
$$ tilde G(x)equiv G(x)+(mathfrak A^2+1),x^{13}+mathfrak A^3,x^3 =
$$
$$
=(mathfrak A^3+mathfrak A^2+1)x^{14}+(mathfrak A^3+mathfrak A^2)x^{13}+ dots+ (mathfrak A^3+1)x^3+(mathfrak A^3+mathfrak A^2+mathfrak A+1)x^2+mathfrak A^2,x+
$$
$$
+(mathfrak A^3+mathfrak A) , $$
т.е. снова оказываемся в ситуации наличия двух ошибок в коэффициентах при степенях $ x_{} $.
Уравнение синдромов ошибок:
$$
left| begin{array}{ccc}
mathfrak o & mathfrak A^3+1 & mathfrak A^3+mathfrak A+1 \
mathfrak A^3+1 & mathfrak A^3+mathfrak A+1 & mathfrak o \
1 & x & x^2
end{array}
right|= mathfrak o iff (mathfrak A^3+mathfrak A^2+1)x^2+(mathfrak A^3+mathfrak A^2)x+(mathfrak A^3+1) = mathfrak o
$$
имеет корнями правильные значения синдромов $ mathfrak A^3 $ и $ mathfrak A^{13} $. Величины ошибок
системе уравнений
$$left{
begin{array}{llll}
E_3 mathfrak A^3&+E_{13}mathfrak A^{13}&=tilde G(mathfrak A)&= mathfrak o , \
E_3 mathfrak A^6&+E_{13}mathfrak A^{26}&=tilde G(mathfrak A^2)&= mathfrak A^3+1
end{array}
right .
$$
удовлетворяют.
♦
Теперь попробуем придать «физический смысл» приведенным примерам. Что такое информационный полином $ P(x) $ из примера 2? Если в примере 1 нас интересовали только коэффициенты подобного полинома — именно эти двоичные цифры несли информацию, а собственно степени переменной $ x_{} $ нужны были исключительно для удобства преобразований — то коэффициенты полинома $ P(x) $ из примера 2 являются не цифрами, а совсем даже готичными выражениями… Реально мы имеем дело с полиномом от двух величин — $ x_{} $ и $ mathfrak A $. В общем случае полинома нескольких переменных над произвольным полем (не обязательно полем Галуа) — его можно задать набором коэффициентов — см.
☞
ЗДЕСЬ. Что можно сказать о потенциально возможном виде полинома $ P(x,mathfrak A) $, который можно было взять в качестве информационного в примере 2? Он подчиняется следующим ограничениям на степени:
$$ deg_x P< 15, deg_{mathfrak A} P< 4 ; $$
последняя оценка накладывается степенью порождающего код полинома $ g(x,mathfrak A) $. Для однозначного задания полинома при таких ограничениях требуются $ 15 times 4=60 $ коэффициентов — и этими коэффициентами являются числа $ 0_{} $ и $ 1_{} $. Кое-что начинает проясняться : нас интересуют не коэффициенты при степенях $ x_{} $, а при степенях мономов $ x^k mathfrak A^{ell} $! Таким образом, в информационном полиноме $ P(x,mathfrak A) $ заложена информация о $ 60 $ его коэффициентах. Эти коэффициенты можно записать в последовательность (договорившись предварительно о способе упорядочения мономов ). Представим этот массив не одномерным:
$$
begin{array}{ccccccc}
x^{10} mathfrak A^{3} & x^{10} mathfrak A^{2} & x^{10} mathfrak A & x^{10} & x^{9} mathfrak A^{3} & x^{9} mathfrak A^{2} & dots \
1 & 1 & 0 & 1 & 0 & 1 & dots ,
end{array}
$$
а двумерным — т.е. рассмотрим матрицу. Фактически, полином уже представлен в виде, из которого матрица извлекается мгновенно:
$$
begin{array}{cc}
&
x^{10}, x^9 x^8 x^7 x^6 x^5 x^4 x^3 x^2 x 1 \
& downarrow downarrow downarrow downarrow downarrow downarrow downarrow downarrow downarrow downarrow downarrow \
begin{array}{ll}
mathfrak A^{3} & rightarrow \
mathfrak A^{2} & rightarrow \
mathfrak A^{3} & rightarrow \
1 & rightarrow \
end{array}
&
left[
begin{array}{ccccccccccc}
1 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \
1&1&1&0&1&0&0&1&0&0&0 \
0&0&1&1&1&0&0&0&1&0&0 \
1&1&1&0&1&0&0&1&1&0&1
end{array}
right]
end{array}
$$
Кодовый полином $ G_{}(x) $ и результат его передачи по каналу связи — полином $ tilde G(x) $ также можно представить в аналогичном виде:
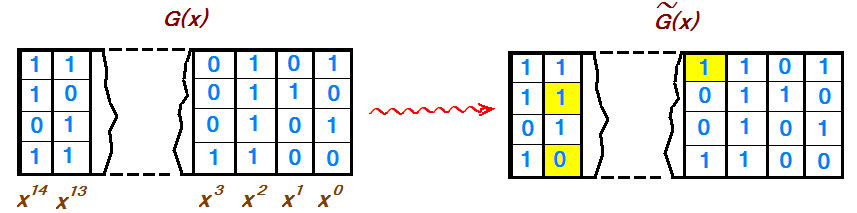
В $ 60 $-битном кодовом слове при передаче произошли три ошибки, но в примере 2 они исправлялись по алгоритму, который изначально «заточен» под ситуацию двух ошибок! Почему этот алгоритм отработал правильно? Объяснение заключается в том, что две из трех произошедших ошибок оказались компактно расположенными в одном столбце информационной таблицы
Такая возможность «упаковки» ошибок весьма существенна для практики: дело в том, что ошибки передачи часто имеют обыкновение происходить серией9). Поэтому применение кодов Рида-Соломона очень распространено — причем не только в задачах исправления ошибок, но и восстановления потерянных данных; подробнее см.
☞
ЗДЕСЬ.
Источники
[1]. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.Мир. 1976.
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
In computing, telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding[1][2][3] is a technique used for controlling errors in data transmission over unreliable or noisy communication channels.
The central idea is that the sender encodes the message in a redundant way, most often by using an error correction code or error correcting code, (ECC).[4][5] The redundancy allows the receiver not only to detect errors that may occur anywhere in the message, but often to correct a limited number of errors. Therefore a reverse channel to request re-transmission may not be needed. The cost is a fixed, higher forward channel bandwidth.
The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code.[5]
FEC can be applied in situations where re-transmissions are costly or impossible, such as one-way communication links or when transmitting to multiple receivers in multicast.
Long-latency connections also benefit; in the case of a satellite orbiting Uranus, retransmission due to errors can create a delay of five hours. FEC is widely used in modems and in cellular networks, as well.
FEC processing in a receiver may be applied to a digital bit stream or in the demodulation of a digitally modulated carrier. For the latter, FEC is an integral part of the initial analog-to-digital conversion in the receiver. The Viterbi decoder implements a soft-decision algorithm to demodulate digital data from an analog signal corrupted by noise. Many FEC decoders can also generate a bit-error rate (BER) signal which can be used as feedback to fine-tune the analog receiving electronics.
FEC information is added to mass storage (magnetic, optical and solid state/flash based) devices to enable recovery of corrupted data, and is used as ECC computer memory on systems that require special provisions for reliability.
The maximum proportion of errors or missing bits that can be corrected is determined by the design of the ECC, so different forward error correcting codes are suitable for different conditions. In general, a stronger code induces more redundancy that needs to be transmitted using the available bandwidth, which reduces the effective bit-rate while improving the received effective signal-to-noise ratio. The noisy-channel coding theorem of Claude Shannon can be used to compute the maximum achievable communication bandwidth for a given maximum acceptable error probability. This establishes bounds on the theoretical maximum information transfer rate of a channel with some given base noise level. However, the proof is not constructive, and hence gives no insight of how to build a capacity achieving code. After years of research, some advanced FEC systems like polar code[3] come very close to the theoretical maximum given by the Shannon channel capacity under the hypothesis of an infinite length frame.
How it works[edit]
ECC is accomplished by adding redundancy to the transmitted information using an algorithm. A redundant bit may be a complex function of many original information bits. The original information may or may not appear literally in the encoded output; codes that include the unmodified input in the output are systematic, while those that do not are non-systematic.
A simplistic example of ECC is to transmit each data bit 3 times, which is known as a (3,1) repetition code. Through a noisy channel, a receiver might see 8 versions of the output, see table below.
| Triplet received | Interpreted as |
|---|---|
| 000 | 0 (error-free) |
| 001 | 0 |
| 010 | 0 |
| 100 | 0 |
| 111 | 1 (error-free) |
| 110 | 1 |
| 101 | 1 |
| 011 | 1 |
This allows an error in any one of the three samples to be corrected by «majority vote», or «democratic voting». The correcting ability of this ECC is:
- Up to 1 bit of triplet in error, or
- up to 2 bits of triplet omitted (cases not shown in table).
Though simple to implement and widely used, this triple modular redundancy is a relatively inefficient ECC. Better ECC codes typically examine the last several tens or even the last several hundreds of previously received bits to determine how to decode the current small handful of bits (typically in groups of 2 to 8 bits).
Averaging noise to reduce errors[edit]
ECC could be said to work by «averaging noise»; since each data bit affects many transmitted symbols, the corruption of some symbols by noise usually allows the original user data to be extracted from the other, uncorrupted received symbols that also depend on the same user data.
- Because of this «risk-pooling» effect, digital communication systems that use ECC tend to work well above a certain minimum signal-to-noise ratio and not at all below it.
- This all-or-nothing tendency – the cliff effect – becomes more pronounced as stronger codes are used that more closely approach the theoretical Shannon limit.
- Interleaving ECC coded data can reduce the all or nothing properties of transmitted ECC codes when the channel errors tend to occur in bursts. However, this method has limits; it is best used on narrowband data.
Most telecommunication systems use a fixed channel code designed to tolerate the expected worst-case bit error rate, and then fail to work at all if the bit error rate is ever worse.
However, some systems adapt to the given channel error conditions: some instances of hybrid automatic repeat-request use a fixed ECC method as long as the ECC can handle the error rate, then switch to ARQ when the error rate gets too high;
adaptive modulation and coding uses a variety of ECC rates, adding more error-correction bits per packet when there are higher error rates in the channel, or taking them out when they are not needed.
Types of ECC[edit]
A block code (specifically a Hamming code) where redundant bits are added as a block to the end of the initial message
A continuous code convolutional code where redundant bits are added continuously into the structure of the code word
The two main categories of ECC codes are block codes and convolutional codes.
- Block codes work on fixed-size blocks (packets) of bits or symbols of predetermined size. Practical block codes can generally be hard-decoded in polynomial time to their block length.
- Convolutional codes work on bit or symbol streams of arbitrary length. They are most often soft decoded with the Viterbi algorithm, though other algorithms are sometimes used. Viterbi decoding allows asymptotically optimal decoding efficiency with increasing constraint length of the convolutional code, but at the expense of exponentially increasing complexity. A convolutional code that is terminated is also a ‘block code’ in that it encodes a block of input data, but the block size of a convolutional code is generally arbitrary, while block codes have a fixed size dictated by their algebraic characteristics. Types of termination for convolutional codes include «tail-biting» and «bit-flushing».
There are many types of block codes; Reed–Solomon coding is noteworthy for its widespread use in compact discs, DVDs, and hard disk drives. Other examples of classical block codes include Golay, BCH, Multidimensional parity, and Hamming codes.
Hamming ECC is commonly used to correct NAND flash memory errors.[6]
This provides single-bit error correction and 2-bit error detection.
Hamming codes are only suitable for more reliable single-level cell (SLC) NAND.
Denser multi-level cell (MLC) NAND may use multi-bit correcting ECC such as BCH or Reed–Solomon.[7][8] NOR Flash typically does not use any error correction.[7]
Classical block codes are usually decoded using hard-decision algorithms,[9] which means that for every input and output signal a hard decision is made whether it corresponds to a one or a zero bit. In contrast, convolutional codes are typically decoded using soft-decision algorithms like the Viterbi, MAP or BCJR algorithms, which process (discretized) analog signals, and which allow for much higher error-correction performance than hard-decision decoding.
Nearly all classical block codes apply the algebraic properties of finite fields. Hence classical block codes are often referred to as algebraic codes.
In contrast to classical block codes that often specify an error-detecting or error-correcting ability, many modern block codes such as LDPC codes lack such guarantees. Instead, modern codes are evaluated in terms of their bit error rates.
Most forward error correction codes correct only bit-flips, but not bit-insertions or bit-deletions.
In this setting, the Hamming distance is the appropriate way to measure the bit error rate.
A few forward error correction codes are designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.
The Levenshtein distance is a more appropriate way to measure the bit error rate when using such codes.
[10]
Code-rate and the tradeoff between reliability and data rate[edit]
The fundamental principle of ECC is to add redundant bits in order to help the decoder to find out the true message that was encoded by the transmitter. The code-rate of a given ECC system is defined as the ratio between the number of information bits and the total number of bits (i.e., information plus redundancy bits) in a given communication package. The code-rate is hence a real number. A low code-rate close to zero implies a strong code that uses many redundant bits to achieve a good performance, while a large code-rate close to 1 implies a weak code.
The redundant bits that protect the information have to be transferred using the same communication resources that they are trying to protect. This causes a fundamental tradeoff between reliability and data rate.[11] In one extreme, a strong code (with low code-rate) can induce an important increase in the receiver SNR (signal-to-noise-ratio) decreasing the bit error rate, at the cost of reducing the effective data rate. On the other extreme, not using any ECC (i.e., a code-rate equal to 1) uses the full channel for information transfer purposes, at the cost of leaving the bits without any additional protection.
One interesting question is the following: how efficient in terms of information transfer can an ECC be that has a negligible decoding error rate? This question was answered by Claude Shannon with his second theorem, which says that the channel capacity is the maximum bit rate achievable by any ECC whose error rate tends to zero:[12] His proof relies on Gaussian random coding, which is not suitable to real-world applications. The upper bound given by Shannon’s work inspired a long journey in designing ECCs that can come close to the ultimate performance boundary. Various codes today can attain almost the Shannon limit. However, capacity achieving ECCs are usually extremely complex to implement.
The most popular ECCs have a trade-off between performance and computational complexity. Usually, their parameters give a range of possible code rates, which can be optimized depending on the scenario. Usually, this optimization is done in order to achieve a low decoding error probability while minimizing the impact to the data rate. Another criterion for optimizing the code rate is to balance low error rate and retransmissions number in order to the energy cost of the communication.[13]
Concatenated ECC codes for improved performance[edit]
Classical (algebraic) block codes and convolutional codes are frequently combined in concatenated coding schemes in which a short constraint-length Viterbi-decoded convolutional code does most of the work and a block code (usually Reed–Solomon) with larger symbol size and block length «mops up» any errors made by the convolutional decoder. Single pass decoding with this family of error correction codes can yield very low error rates, but for long range transmission conditions (like deep space) iterative decoding is recommended.
Concatenated codes have been standard practice in satellite and deep space communications since Voyager 2 first used the technique in its 1986 encounter with Uranus. The Galileo craft used iterative concatenated codes to compensate for the very high error rate conditions caused by having a failed antenna.
Low-density parity-check (LDPC)[edit]
Low-density parity-check (LDPC) codes are a class of highly efficient linear block
codes made from many single parity check (SPC) codes. They can provide performance very close to the channel capacity (the theoretical maximum) using an iterated soft-decision decoding approach, at linear time complexity in terms of their block length. Practical implementations rely heavily on decoding the constituent SPC codes in parallel.
LDPC codes were first introduced by Robert G. Gallager in his PhD thesis in 1960,
but due to the computational effort in implementing encoder and decoder and the introduction of Reed–Solomon codes,
they were mostly ignored until the 1990s.
LDPC codes are now used in many recent high-speed communication standards, such as DVB-S2 (Digital Video Broadcasting – Satellite – Second Generation), WiMAX (IEEE 802.16e standard for microwave communications), High-Speed Wireless LAN (IEEE 802.11n),[14] 10GBase-T Ethernet (802.3an) and G.hn/G.9960 (ITU-T Standard for networking over power lines, phone lines and coaxial cable). Other LDPC codes are standardized for wireless communication standards within 3GPP MBMS (see fountain codes).
Turbo codes[edit]
Turbo coding is an iterated soft-decoding scheme that combines two or more relatively simple convolutional codes and an interleaver to produce a block code that can perform to within a fraction of a decibel of the Shannon limit. Predating LDPC codes in terms of practical application, they now provide similar performance.
One of the earliest commercial applications of turbo coding was the CDMA2000 1x (TIA IS-2000) digital cellular technology developed by Qualcomm and sold by Verizon Wireless, Sprint, and other carriers. It is also used for the evolution of CDMA2000 1x specifically for Internet access, 1xEV-DO (TIA IS-856). Like 1x, EV-DO was developed by Qualcomm, and is sold by Verizon Wireless, Sprint, and other carriers (Verizon’s marketing name for 1xEV-DO is Broadband Access, Sprint’s consumer and business marketing names for 1xEV-DO are Power Vision and Mobile Broadband, respectively).
Local decoding and testing of codes[edit]
Sometimes it is only necessary to decode single bits of the message, or to check whether a given signal is a codeword, and do so without looking at the entire signal. This can make sense in a streaming setting, where codewords are too large to be classically decoded fast enough and where only a few bits of the message are of interest for now. Also such codes have become an important tool in computational complexity theory, e.g., for the design of probabilistically checkable proofs.
Locally decodable codes are error-correcting codes for which single bits of the message can be probabilistically recovered by only looking at a small (say constant) number of positions of a codeword, even after the codeword has been corrupted at some constant fraction of positions. Locally testable codes are error-correcting codes for which it can be checked probabilistically whether a signal is close to a codeword by only looking at a small number of positions of the signal.
Interleaving[edit]
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
A short illustration of interleaving idea
Interleaving is frequently used in digital communication and storage systems to improve the performance of forward error correcting codes. Many communication channels are not memoryless: errors typically occur in bursts rather than independently. If the number of errors within a code word exceeds the error-correcting code’s capability, it fails to recover the original code word. Interleaving alleviates this problem by shuffling source symbols across several code words, thereby creating a more uniform distribution of errors.[15] Therefore, interleaving is widely used for burst error-correction.
The analysis of modern iterated codes, like turbo codes and LDPC codes, typically assumes an independent distribution of errors.[16] Systems using LDPC codes therefore typically employ additional interleaving across the symbols within a code word.[17]
For turbo codes, an interleaver is an integral component and its proper design is crucial for good performance.[15][18] The iterative decoding algorithm works best when there are not short cycles in the factor graph that represents the decoder; the interleaver is chosen to avoid short cycles.
Interleaver designs include:
- rectangular (or uniform) interleavers (similar to the method using skip factors described above)
- convolutional interleavers
- random interleavers (where the interleaver is a known random permutation)
- S-random interleaver (where the interleaver is a known random permutation with the constraint that no input symbols within distance S appear within a distance of S in the output).[19]
- a contention-free quadratic permutation polynomial (QPP).[20] An example of use is in the 3GPP Long Term Evolution mobile telecommunication standard.[21]
In multi-carrier communication systems, interleaving across carriers may be employed to provide frequency diversity, e.g., to mitigate frequency-selective fading or narrowband interference.[22]
Example[edit]
Transmission without interleaving:
Error-free message: aaaabbbbccccddddeeeeffffgggg Transmission with a burst error: aaaabbbbccc____deeeeffffgggg
Here, each group of the same letter represents a 4-bit one-bit error-correcting codeword. The codeword cccc is altered in one bit and can be corrected, but the codeword dddd is altered in three bits, so either it cannot be decoded at all or it might be decoded incorrectly.
With interleaving:
Error-free code words: aaaabbbbccccddddeeeeffffgggg Interleaved: abcdefgabcdefgabcdefgabcdefg Transmission with a burst error: abcdefgabcd____bcdefgabcdefg Received code words after deinterleaving: aa_abbbbccccdddde_eef_ffg_gg
In each of the codewords «aaaa», «eeee», «ffff», and «gggg», only one bit is altered, so one-bit error-correcting code will decode everything correctly.
Transmission without interleaving:
Original transmitted sentence: ThisIsAnExampleOfInterleaving Received sentence with a burst error: ThisIs______pleOfInterleaving
The term «AnExample» ends up mostly unintelligible and difficult to correct.
With interleaving:
Transmitted sentence: ThisIsAnExampleOfInterleaving... Error-free transmission: TIEpfeaghsxlIrv.iAaenli.snmOten. Received sentence with a burst error: TIEpfe______Irv.iAaenli.snmOten. Received sentence after deinterleaving: T_isI_AnE_amp_eOfInterle_vin_...
No word is completely lost and the missing letters can be recovered with minimal guesswork.
Disadvantages of interleaving[edit]
Use of interleaving techniques increases total delay. This is because the entire interleaved block must be received before the packets can be decoded.[23] Also interleavers hide the structure of errors; without an interleaver, more advanced decoding algorithms can take advantage of the error structure and achieve more reliable communication than a simpler decoder combined with an interleaver[citation needed]. An example of such an algorithm is based on neural network[24] structures.
Software for error-correcting codes[edit]
Simulating the behaviour of error-correcting codes (ECCs) in software is a common practice to design, validate and improve ECCs. The upcoming wireless 5G standard raises a new range of applications for the software ECCs: the Cloud Radio Access Networks (C-RAN) in a Software-defined radio (SDR) context. The idea is to directly use software ECCs in the communications. For instance in the 5G, the software ECCs could be located in the cloud and the antennas connected to this computing resources: improving this way the flexibility of the communication network and eventually increasing the energy efficiency of the system.
In this context, there are various available Open-source software listed below (non exhaustive).
- AFF3CT(A Fast Forward Error Correction Toolbox): a full communication chain in C++ (many supported codes like Turbo, LDPC, Polar codes, etc.), very fast and specialized on channel coding (can be used as a program for simulations or as a library for the SDR).
- IT++: a C++ library of classes and functions for linear algebra, numerical optimization, signal processing, communications, and statistics.
- OpenAir: implementation (in C) of the 3GPP specifications concerning the Evolved Packet Core Networks.
List of error-correcting codes[edit]
| Distance | Code |
|---|---|
| 2 (single-error detecting) | Parity |
| 3 (single-error correcting) | Triple modular redundancy |
| 3 (single-error correcting) | perfect Hamming such as Hamming(7,4) |
| 4 (SECDED) | Extended Hamming |
| 5 (double-error correcting) | |
| 6 (double-error correct-/triple error detect) | Nordstrom-Robinson code |
| 7 (three-error correcting) | perfect binary Golay code |
| 8 (TECFED) | extended binary Golay code |
- AN codes
- BCH code, which can be designed to correct any arbitrary number of errors per code block.
- Barker code used for radar, telemetry, ultra sound, Wifi, DSSS mobile phone networks, GPS etc.
- Berger code
- Constant-weight code
- Convolutional code
- Expander codes
- Group codes
- Golay codes, of which the Binary Golay code is of practical interest
- Goppa code, used in the McEliece cryptosystem
- Hadamard code
- Hagelbarger code
- Hamming code
- Latin square based code for non-white noise (prevalent for example in broadband over powerlines)
- Lexicographic code
- Linear Network Coding, a type of erasure correcting code across networks instead of point-to-point links
- Long code
- Low-density parity-check code, also known as Gallager code, as the archetype for sparse graph codes
- LT code, which is a near-optimal rateless erasure correcting code (Fountain code)
- m of n codes
- Nordstrom-Robinson code, used in Geometry and Group Theory[25]
- Online code, a near-optimal rateless erasure correcting code
- Polar code (coding theory)
- Raptor code, a near-optimal rateless erasure correcting code
- Reed–Solomon error correction
- Reed–Muller code
- Repeat-accumulate code
- Repetition codes, such as Triple modular redundancy
- Spinal code, a rateless, nonlinear code based on pseudo-random hash functions[26]
- Tornado code, a near-optimal erasure correcting code, and the precursor to Fountain codes
- Turbo code
- Walsh–Hadamard code
- Cyclic redundancy checks (CRCs) can correct 1-bit errors for messages at most
bits long for optimal generator polynomials of degree
, see Mathematics of cyclic redundancy checks#Bitfilters
See also[edit]
- Code rate
- Erasure codes
- Soft-decision decoder
- Burst error-correcting code
- Error detection and correction
- Error-correcting codes with feedback
References[edit]
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
How Forward Error-Correcting Codes Work]
- ^ a b Maunder, Robert (2016). «Overview of Channel Coding».
- ^ Glover, Neal; Dudley, Trent (1990). Practical Error Correction Design For Engineers (Revision 1.1, 2nd ed.). CO, USA: Cirrus Logic. ISBN 0-927239-00-0.
- ^ a b Hamming, Richard Wesley (April 1950). «Error Detecting and Error Correcting Codes». Bell System Technical Journal. USA: AT&T. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773.
- ^ «Hamming codes for NAND flash memory devices» Archived 21 August 2016 at the Wayback Machine. EE Times-Asia. Apparently based on «Micron Technical Note TN-29-08: Hamming Codes for NAND Flash Memory Devices». 2005. Both say: «The Hamming algorithm is an industry-accepted method for error detection and correction in many SLC NAND flash-based applications.»
- ^ a b «What Types of ECC Should Be Used on Flash Memory?» (Application note). Spansion. 2011.
Both Reed–Solomon algorithm and BCH algorithm are common ECC choices for MLC NAND flash. … Hamming based block codes are the most commonly used ECC for SLC…. both Reed–Solomon and BCH are able to handle multiple errors and are widely used on MLC flash.
- ^ Jim Cooke (August 2007). «The Inconvenient Truths of NAND Flash Memory» (PDF). p. 28.
For SLC, a code with a correction threshold of 1 is sufficient. t=4 required … for MLC.
- ^ Baldi, M.; Chiaraluce, F. (2008). «A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions». International Journal of Digital Multimedia Broadcasting. 2008: 1–12. doi:10.1155/2008/957846.
- ^ Shah, Gaurav; Molina, Andres; Blaze, Matt (2006). «Keyboards and covert channels». USENIX. Retrieved 20 December 2018.
- ^ Tse, David; Viswanath, Pramod (2005), Fundamentals of Wireless Communication, Cambridge University Press, UK
- ^ Shannon, C. E. (1948). «A mathematical theory of communication» (PDF). Bell System Technical Journal. 27 (3–4): 379–423 & 623–656. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:11858/00-001M-0000-002C-4314-2.
- ^ Rosas, F.; Brante, G.; Souza, R. D.; Oberli, C. (2014). «Optimizing the code rate for achieving energy-efficient wireless communications». Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). pp. 775–780. doi:10.1109/WCNC.2014.6952166. ISBN 978-1-4799-3083-8.
- ^ IEEE Standard, section 20.3.11.6 «802.11n-2009» Archived 3 February 2013 at the Wayback Machine, IEEE, 29 October 2009, accessed 21 March 2011.
- ^ a b Vucetic, B.; Yuan, J. (2000). Turbo codes: principles and applications. Springer Verlag. ISBN 978-0-7923-7868-6.
- ^ Luby, Michael; Mitzenmacher, M.; Shokrollahi, A.; Spielman, D.; Stemann, V. (1997). «Practical Loss-Resilient Codes». Proc. 29th Annual Association for Computing Machinery (ACM) Symposium on Theory of Computation.
- ^ «Digital Video Broadcast (DVB); Second generation framing structure, channel coding and modulation systems for Broadcasting, Interactive Services, News Gathering and other satellite broadband applications (DVB-S2)». En 302 307. ETSI (V1.2.1). April 2009.
- ^ Andrews, K. S.; Divsalar, D.; Dolinar, S.; Hamkins, J.; Jones, C. R.; Pollara, F. (November 2007). «The Development of Turbo and LDPC Codes for Deep-Space Applications». Proceedings of the IEEE. 95 (11): 2142–2156. doi:10.1109/JPROC.2007.905132. S2CID 9289140.
- ^ Dolinar, S.; Divsalar, D. (15 August 1995). «Weight Distributions for Turbo Codes Using Random and Nonrandom Permutations». TDA Progress Report. 122: 42–122. Bibcode:1995TDAPR.122…56D. CiteSeerX 10.1.1.105.6640.
- ^ Takeshita, Oscar (2006). «Permutation Polynomial Interleavers: An Algebraic-Geometric Perspective». IEEE Transactions on Information Theory. 53 (6): 2116–2132. arXiv:cs/0601048. Bibcode:2006cs……..1048T. doi:10.1109/TIT.2007.896870. S2CID 660.
- ^ 3GPP TS 36.212, version 8.8.0, page 14
- ^ «Digital Video Broadcast (DVB); Frame structure, channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2)». En 302 755. ETSI (V1.1.1). September 2009.
- ^ Techie (3 June 2010). «Explaining Interleaving». W3 Techie Blog. Retrieved 3 June 2010.
- ^ Krastanov, Stefan; Jiang, Liang (8 September 2017). «Deep Neural Network Probabilistic Decoder for Stabilizer Codes». Scientific Reports. 7 (1): 11003. arXiv:1705.09334. Bibcode:2017NatSR…711003K. doi:10.1038/s41598-017-11266-1. PMC 5591216. PMID 28887480.
- ^ Nordstrom, A.W.; Robinson, J.P. (1967), «An optimum nonlinear code», Information and Control, 11 (5–6): 613–616, doi:10.1016/S0019-9958(67)90835-2
- ^ Perry, Jonathan; Balakrishnan, Hari; Shah, Devavrat (2011). «Rateless Spinal Codes». Proceedings of the 10th ACM Workshop on Hot Topics in Networks. pp. 1–6. doi:10.1145/2070562.2070568. hdl:1721.1/79676. ISBN 9781450310598.
Further reading[edit]
- MacWilliams, Florence Jessiem; Sloane, Neil James Alexander (2007) [1977]. Written at AT&T Shannon Labs, Florham Park, New Jersey, USA. The Theory of Error-Correcting Codes. North-Holland Mathematical Library. Vol. 16 (digital print of 12th impression, 1st ed.). Amsterdam / London / New York / Tokyo: North-Holland / Elsevier BV. ISBN 978-0-444-85193-2. LCCN 76-41296. (xxii+762+6 pages)
- Clark, Jr., George C.; Cain, J. Bibb (1981). Error-Correction Coding for Digital Communications. New York, USA: Plenum Press. ISBN 0-306-40615-2.
- Arazi, Benjamin (1987). Swetman, Herb (ed.). A Commonsense Approach to the Theory of Error Correcting Codes. MIT Press Series in Computer Systems. Vol. 10 (1 ed.). Cambridge, Massachusetts, USA / London, UK: Massachusetts Institute of Technology. ISBN 0-262-01098-4. LCCN 87-21889. (x+2+208+4 pages)
- Wicker, Stephen B. (1995). Error Control Systems for Digital Communication and Storage. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-200809-2.
- Wilson, Stephen G. (1996). Digital Modulation and Coding. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-210071-1.
- «Error Correction Code in Single Level Cell NAND Flash memories» 2007-02-16
- «Error Correction Code in NAND Flash memories» 2004-11-29
- Observations on Errors, Corrections, & Trust of Dependent Systems, by James Hamilton, 2012-02-26
- Sphere Packings, Lattices and Groups, By J. H. Conway, Neil James Alexander Sloane, Springer Science & Business Media, 2013-03-09 – Mathematics – 682 pages.
External links[edit]
- Morelos-Zaragoza, Robert (2004). «The Correcting Codes (ECC) Page». Retrieved 5 March 2006.
- lpdec: library for LP decoding and related things (Python)
Содержание
Раздел создан при поддержке компании RAIDIX
Для понимания материалов настоящего раздела крайне желательно ознакомиться с разделом Циклические коды.
Коды Боуза-Чоудхури-Хоквингема
Идея
Для ее пояснения обратимся к материалам
☞
ПУНКТА и рассмотрим циклические коды в $ \mathbb Z^n $. Принадлежность кодового слова $ (b_0,b_1,\dots,b_{n-1}) $ циклическому коду $ C_{} $, порождаемому полиномом
$$ g(x)=a_0+a_1x+a_2x^2+\dots+a_{r}x^{r}, (r<n,a_{r}\ne 0) \, ,$$
равносильна тому, что полином
$$ G(x)=b_0+b_1x+b_2x^2+\dots+b_{n-1}x^{n-1} $$
делится на $ g_{}(x) $. Предположим теперь, что при передаче по зашумленному каналу связи кодовый полином (кодовое слово) исказился и на выходе мы получили полином
$$ \tilde G(x)= G(x)+E_jx^j+E_kx^k \quad npu \quad \{j,k\} \subset \{0,1,2,\dots,n-1\},\ j < k,\ \{E_j,E_k\} \subset \mathbb Z \ .$$
В
☞
ПУНКТЕ предлагался метод нахождения ошибок в случае, когда они соседствуют, т.е. $ k=j+1 $. Фактически, задача в такой постановке оказывалась задачей с тремя неизвестными: требовалось найти место ошибки $ j_{} $ и величины ошибок $ E_j,E_{j+1} $. Теперь мы рассмотреть общий случай, когда неизвестными являются четыре величины $ j,k,E_j,E_k $. Интуитивно понятно, что для нахождения этих четырех неизвестных требуется, по меньшей мере, такое же количество условий. По аналогии с рассмотренным в
☞
ПУНКТЕ подходом, будем пытаться найти эти условия виде $ \tilde G(\lambda_{\ell})=0 $, где $ \lambda_{\ell} $ — корень порождающего код полинома $ g_{}(x) $, т.е. $ g_{}(\lambda_{\ell})=0 $ и $ G(\lambda_{\ell})=0 $. Если $ \lambda_1,\lambda_2,\lambda_3,\lambda_4 $ — различные корни полинома $ g_{}(x) $, то подстановка их в «зашумленный» полином $ \tilde G(x) $ приведет к системе уравнений
$$ E_j\lambda_1^j+E_k\lambda_1^k= \tilde G(\lambda_1),\ E_j\lambda_2^j+E_k\lambda_2^k= \tilde G(\lambda_2),\ E_j\lambda_3^j+E_k\lambda_3^k= \tilde G(\lambda_3),\ E_j\lambda_4^j+E_k\lambda_4^k= \tilde G(\lambda_4) \ , $$
линейной по неизвестным $ E_j $ и $ E_k $, но нелинейной по значениям индексов $ j_{} $ и $ k_{} $. Эту систему требуется решить в целых числах. Можно попробовать осуществить поиск решений перебором вариантов (например, положив гипотезой что величины ошибок $ E_j $ и $ E_k $ невелики); однако этот подход не кажется конструктивным если оценить число потенциально возможных комбинаций в зависимости от $ n_{} $.
Допустим теперь, что порождающий $ n_{} $-код полином $ g_{}(x) $ удается подобрать так, чтобы его корнями оказались бы величины
$$ \lambda_1=\varepsilon_1,\ \lambda_2=\varepsilon_1^2,\ \lambda_3=\varepsilon_1^3,\ \lambda_4=\varepsilon_1^4 \quad npu \quad \varepsilon_1=\cos \frac{2\pi}{n}+\mathbf i \sin \frac{2\pi}{n} $$
— корне степени n из единицы. Посмотрим как можно использовать эту возможность для решения задачи исправления ошибок. Подставим корни в предыдущую систему, воспользовавшись равенствами
$$ \varepsilon_1^j = \varepsilon_j=\cos \frac{2\pi\,j}{n}+\mathbf i \sin \frac{2\pi \, j}{n} ,\ \varepsilon_1^k=\varepsilon_k= \cos \frac{2\pi\,k}{n}+\mathbf i \sin \frac{2\pi\,k}{n} \ , $$
получим «систему ошибок»1)
$$
\left\{ \begin{array}{rrl}
E_j \varepsilon_j & + E_k \varepsilon_k & = \tilde G(\varepsilon_1), \\
E_j \varepsilon_j^2 & + E_k \varepsilon_k^2 & = \tilde G(\varepsilon_1^2), \\
E_j \varepsilon_j^3& + E_k \varepsilon_k^3 & = \tilde G(\varepsilon_1^3), \\
E_j \varepsilon_j^4 & + E_k \varepsilon_k^4 & = \tilde G(\varepsilon_1^4).
\end{array}
\right.
$$
Попробуем на основе этих равенств сконструировать новое — квадратное:
$$ \sigma_2+\sigma_1x+\sigma_0x^2=0 \ , $$
которому должны удовлетворять обе величины $ \varepsilon_j $ и $ \varepsilon_k $. С этой целью умножим первое из этих разыскиваемых уравнений на $ E_j \varepsilon_j $, второе — на $ E_k \varepsilon_k $
$$
\left\{ \begin{array}{rl|lc|lc}
\sigma_2+\sigma_1\varepsilon_j+\sigma_0\varepsilon_j^2&=0, & \times E_j \varepsilon_j & & \times E_j \varepsilon_j^2 & \\
& & & + & & + \\
\sigma_2+\sigma_1\varepsilon_k+\sigma_0\varepsilon_k^2&=0 & \times E_k \varepsilon_k & & \times E_k \varepsilon_k^2. &
\end{array}
\right.
$$
и сложим:
$$ \sigma_2 (E_j \varepsilon_j +E_k \varepsilon_k)+\sigma_1(E_j \varepsilon_j^2 +E_k \varepsilon_k^2)+\sigma_0(E_j \varepsilon_j^3 +E_k \varepsilon_k^3)=0 \ ;
$$
аналогичным образом, домножим первое из равенств на $ E_j \varepsilon_j^2 $, второе — на $ E_k \varepsilon_k^2 $ и сложим:
$$ \sigma_2 (E_j \varepsilon_j^2 +E_k \varepsilon_k^2)+\sigma_1(E_j \varepsilon_j^3 +E_k \varepsilon_k^3)+\sigma_0(E_j \varepsilon_j^4 +E_k \varepsilon_k^4)=0 \ .
$$
Обратим теперь внимание на то, что все величины, стоящие в полученных формулах в круглых скобках, нам известны из приведенной выше системы:
$$
\left\{ \begin{array}{rl}
\sigma_2\tilde G(\varepsilon_1)+\sigma_1\tilde G(\varepsilon_1^2)+\sigma_0\tilde G(\varepsilon_1^3)&=0, \\
\sigma_2\tilde G(\varepsilon_1^2)+\sigma_1\tilde G(\varepsilon_1^3)+\sigma_0\tilde G(\varepsilon_1^4)&=0.
\end{array}
\right.
$$
Эта система линейна относительно неизвестных коэффициентов $ \sigma_0, \sigma_1,\sigma_2 $. Возникает вопрос о ее разрешимости.
Т
Теорема.
Пусть порождающий код полином обладает корнями $ \varepsilon_1,\varepsilon_1^2,\varepsilon_1^3,\varepsilon_1^4 $. Если при передаче кодового полинома
$$ G(x)=b_0+b_1x+b_2x^2+\dots+b_{n-1}x^{n-1} $$
произошли ровно две ошибки в $ j_{} $-м и $ k_{} $-м коэффициентах, и на выходе канала связи получен полином $ \tilde G(x) $, то корни степени $ n_{} $ из единицы, обозначенные $ \varepsilon_j $ и $ \varepsilon_k $, удовлетворяют «уравнению ошибочных позиций»2)
$$
\left| \begin{array}{ccc}
\tilde G(\varepsilon_1) & \tilde G(\varepsilon_1^2) & \tilde G(\varepsilon_1^3) \\
\tilde G(\varepsilon_1^2) & \tilde G(\varepsilon_1^3) & \tilde G(\varepsilon_1^4) \\
1 & x & x^2
\end{array}
\right|=0 \ .
$$
Доказательство. Фактически к двум линейным уравнениям мы приписываем $ \sigma_2+\sigma_1x+\sigma_0x^2=0 $, и к получившейся линейной однородной системе относительно неизвестных $ \sigma_2,\sigma_1,\sigma_0 $ применяем критерий существования нетривиального решения: определитель этой системы должен быть равен нулю.
♦
В следующем пункте я часто буду употреблять подобные детерминантные представления, нетрадиционные для теории кодирования. В последней обычно разыскивают полином ошибочных позиций в виде нормализованного полинома — со старшим коэффициентом равным $ 1_{} $.
Разрешив уравнение ошибочных позиций, мы определим величины $ \varepsilon_j $ и $ \varepsilon_k $, и, следовательно, сможем восстановить значения соответствующих индексов $ \{j,k\} \subset \{0,1,2,\dots,n-1\} $, т.е. номеров коэффициентов полинома, в которых произошли ошибки. Величины же $ E_j $ и $ E_k $ этих ошибок восстанавливаются из первых двух уравнений системы ошибок:
$$
\left\{ \begin{array}{rrl}
E_j \varepsilon_j & + E_k \varepsilon_k & = \tilde G(\varepsilon_1), \\
E_j \varepsilon_j^2 & + E_k \varepsilon_k^2 & = \tilde G(\varepsilon_1^2)
\end{array}
\right.
$$
Впрочем, как правило, величины $ E_j $ и $ E_k $ можно установить только из первого уравнения — если воспользоваться условием их вещественности.
Остался открытым вопрос о возможности выбора порождающего циклический код полинома $ g_{}(x) $, имеющего одновременно корнями $ \varepsilon_1, \varepsilon_1^2,\varepsilon_1^3,\varepsilon_1^4 $. При этом полином $ g_{}(x) $ должен иметь целочисленные коэффициенты — иначе мы не сможем организовать выбор кодовых слов в пространстве $ \mathbb Z^n $. По аналогии с подходом
☞
ПУНКТА можно попробовать выбрать полином $ g_{}(x) $ как произведение полиномов деления круга $ X_j(x) $. Действительно, при любом $ n\in \mathbb N $ полином $ X_n(x) $ будет иметь корнем $ \varepsilon_1 $, равно как и любой другой первообразный корень степени $ n_{} $. Тогда при $ n\ge 5 $ и $ n_{} $ — простом, все степени $ \{\varepsilon_1^j\}_{j=1}^{n-1} $ будут первообразными корнями степени $ n_{} $, и, следовательно, будут корнями полинома $ X_n(x) $. В этом случае можно было бы взять $ g(x)\equiv X_n(x) $, однако, хотя с формальной точки зрения это и допустимо, тем не менее, с точки зрения практической пользы такой вариант бессмыслен: при любом способе кодирования в циклическом коде размерность кодового пространства $ \mathbb U $ становится равной $ 1_{} $, т.е. в $ n_{} $-кодовом слове остается единственный свободный разряд, который можно использовать в качестве информационного.
Итак, число $ n\ge 5 $ должно быть составным. Пусть $ n_{} $— нечетно. Тогда (см.
☞
ЗДЕСЬ) величины $ \varepsilon_1, \varepsilon_1^2,\varepsilon_1^4 $ будут все первообразными корнями и, следовательно,
корнями полинома $ X_n(x) $. Если $ n_{} $ не делится на $ 3_{} $, то и $ \varepsilon_1^3 $ будет первообразным корнем, т.е. корнем $ X_n(x) $. Обобщим эти рассуждения: если $ n_{}\ge 5 $ — составное и $ \operatorname{HOD}(n,6)=1 $, то можно взять $ g(x)\equiv X_n(x) $. Если $ \operatorname{HOD}(n,6)>1 $, то полином $ g_{}(x) $ можно построить в виде произведения полиномов $ X_j(x) $. Так,
при $ \operatorname{HOD}(n,6)=2 $ можно взять $ g(x)\equiv X_n(x)X_{n/2}(x) $ в случае когда $ n_{} $ не делится на $ 4_{} $ и $ g(x)\equiv X_n(x)X_{n/2}(x)X_{n/4}(x) $ в случае когда $ n_{} $ делится на $ 4_{} $
П
Пример. Пусть $ n=15 $ и порождающий циклический код полином выбран в виде
$$ g(x)\equiv X_5(x)X_{15}(x)\equiv (1+x+x^2+x^3+x^4)(1-x+x^3-x^4+x^5-x^7+x^8) \equiv $$
$$ \equiv 1+x^3+x^6+x^9+x^{12} \ . $$
Пусть при передаче некоторого кодового полинома $ G_{}(x) $ на выходе канала получен полином
$$ \tilde G(x)=-1+5\,x+2\,x^2-x^3+3\,x^4+2\,x^5-x^6+5\,x^7+2\,x^8-x^9+5\,x^{10}+2\,x^{11}-x^{12}+2\,x^{13}+2\,x^{14} \ . $$
Требуется восстановить кодовый полином $ G_{}(x) $, основываясь на гипотезе, что при передаче произошло ровно две ошибки.
Решение. Порождающий код полином $ g_{}(x) $ удовлетворяет условиям теоремы: его корнями являются
величины $ \varepsilon_1, \varepsilon_1^2,\varepsilon_1^3,\varepsilon_1^4 $ при
$$ \varepsilon_1=\cos \frac{2\pi}{15}+\mathbf i \sin \frac{2\pi}{15} \approx 0.913545+0.406736\, \mathbf i \ . $$
Вычисляем $ \tilde G(\varepsilon_1) \approx -1.798335+0.240391 \, \mathbf i $. Поскольку $ \tilde G(\varepsilon_1) \ne 0 $, то заключаем, что хотя бы одна ошибка при передаче по каналу произошла. Вычисляем дополнительно $ \tilde G(\varepsilon_1^2), \tilde G(\varepsilon_1^3), \tilde G(\varepsilon_1^4) $ и составляем уравнение ошибочных позиций из теоремы:
$$
\left| \begin{array}{rrr}
-1.798335+0.240391 \, \mathbf i & 2.269881+3.399389 \, \mathbf i & 1.809017+3.665469 \, \mathbf i \\
2.269881+3.399389 \, \mathbf i & 1.809017+3.665469 \, \mathbf i & 1.107352-1.437208 \, \mathbf i \\
1 & x & x^2
\end{array}
\right|=0
$$
или
$$
(17.562306-12.759762\, \mathbf i) +(-6.708203964+11.618950\, \mathbf i)x+(2.269125-21.589284\, \mathbf i)x^2=0 \ .
$$
Решаем его и находим
$$ \mu_1 \approx -0.104528+0.994522\, \mathbf i,\ \mu_2\approx 0.669131-0.743145\, \mathbf i \ . $$
Если при передаче по каналу произошли — как утверждается в условии — ровно две ошибки, то получившиеся значения должны быть корнями $ 15 $-й степени из единицы. Это немедленно проверяется. Остается выяснить каким значениям показателей $ \varepsilon_j $ и $ \varepsilon_k $ соответствуют эти числа.
$$ 15 \arccos(-0.104528)/(2\pi) \approx 4 \quad \mbox{ и } \quad 0.994522>0 \quad \Rightarrow j=4 \ . $$
$$ 15 \arccos(0.669131)/(2\pi) \approx 2 \quad \mbox{ и } \quad -0.743145<0 \quad \Rightarrow k=15-2=13 \ . $$
Итак, полином $ \tilde G(x) $ имеет ошибочные коэффициенты при $ x^{4} $ и $ x^{13} $. Для нахождения величин этих ошибок имеем уравнение
$$ E_4 \mu_1 + E_{13} \mu_2 = \tilde G(\varepsilon_1) \quad \iff \quad
\left\{ \begin{array}{rrr}
-0.104528 E_4 &+0.669131 E_{13} & = -1.798335, \\
0.994522 E_4 &-0.743145 E_{13} & = 0.240391.
\end{array} \right. $$
Откуда получаем $ E_4\approx -1.999997, E_{13} \approx -2.999997 $. Заключаем, что $ G(x)\equiv \tilde G(x) +2\,x^4+3\,x^{13} $.
Теперь проверим насколько «устойчив» алгоритм к истинному количеству ошибок. Допустим, что вместо предполагаемых двух ошибок произошла одна и на выходе канала получен полином $ \tilde G(x)\equiv G(x)-4\,x^7 $. Уравнение ошибочных позиций из теоремы
$$
\left| \begin{array}{rrr}
3.912590-0.831647 \, \mathbf i & -3.654182+1.626946 \, \mathbf i & 3.236068-2.351141 \, \mathbf i \\
-3.654182+1.626946 \, \mathbf i & 3.236068-2.351141 \, \mathbf i & -2.676522+2.972579 \, \mathbf i \\
1 & x & x^2
\end{array}
\right|=0
$$
вырождается в тождество $ 0\equiv 0 $. С формальной точки зрения, истинность уравнения сохраняется, только информации из него не извлечь… Модифицируем метод, играя на понижение количества ошибок — составим уравнение
$$
\left| \begin{array}{cc}
\tilde G(\varepsilon_1) & \tilde G(\varepsilon_1^2) \\
1 & x
\end{array}
\right|=0 \ \quad \iff
$$
$$
\iff \quad
(3.654181840-1.626946579\, \mathbf i )+(3.912590396-.8316467668\, \mathbf i )x=0 \quad \iff \mu\approx -0.978148+0.207912 \, \mathbf i \ .
$$
Далее идем как в предыдущем случае: действительно, $ \mu^{15} = 1 $ и
$$ 15 \arccos(-0.978148)/(2\pi) \approx 7 \quad \mbox{ и } \quad 0.207912 >0 \quad \Rightarrow j=7 \ . $$
Место ошибки обнаружено верно. Ее величину определяем из условия $ \tilde G(\varepsilon_1)=E_7 \mu $.
♦
Распространение идеи подхода для случая трех и более ошибок очевидно. Так, если порождающий $ n_{} $-код полином $ g_{}(x) $ имеет корнями $ \{\varepsilon_1^j\}_{j=1}^6 $, то это даст возможность исправления не менее трех ошибок. Соответствующее уравнение ошибочных позиций для определения номеров испорченных коэффициентов:
$$
\left| \begin{array}{cccc}
\tilde G(\varepsilon_1) & \tilde G(\varepsilon_1^2) & \tilde G(\varepsilon_1^3) & \tilde G(\varepsilon_1^4) \\
\tilde G(\varepsilon_1^2) & \tilde G(\varepsilon_1^3) & \tilde G(\varepsilon_1^4) & \tilde G(\varepsilon_1^5)\\
\tilde G(\varepsilon_1^3) & \tilde G(\varepsilon_1^4) & \tilde G(\varepsilon_1^5) & \tilde G(\varepsilon_1^6) \\
1 & x & x^2 & x^3
\end{array}
\right|=0
$$
строится по аналогии со случаем двух ошибок. Покажем здесь, что при наличии ровно трех ошибок в полиноме $ \tilde G(x) $, явившихся результатом передачи кодового полинома $ G_{}(x) $, построенное уравнение нетривиально. Итак, пусть $ \tilde G(x)\equiv G(x)+E_jx^j+E_kx^k+E_sx^s $. Рассмотрим коэффициент при $ x^{3} $ в уравнении ошибок:
$$
\left| \begin{array}{ccc}
\tilde G(\varepsilon_1) & \tilde G(\varepsilon_1^2) & \tilde G(\varepsilon_1^3) \\
\tilde G(\varepsilon_1^2) & \tilde G(\varepsilon_1^3) & \tilde G(\varepsilon_1^4) \\
\tilde G(\varepsilon_1^3) & \tilde G(\varepsilon_1^4) & \tilde G(\varepsilon_1^5)
\end{array}
\right|=
\left| \begin{array}{ccc}
E_j\varepsilon_j+E_k\varepsilon_k+E_s\varepsilon_s & E_j\varepsilon_j^2+E_k\varepsilon_k^2+E_s\varepsilon_s^2 &
E_j\varepsilon_j^3+E_k\varepsilon_k^3+E_s\varepsilon_s^3 \\
E_j\varepsilon_j^2+E_k\varepsilon_k^2+E_s\varepsilon_s^2 &
E_j\varepsilon_j^3+E_k\varepsilon_k^3+E_s\varepsilon_s^3 &
E_j\varepsilon_j^4+E_k\varepsilon_k^4+E_s\varepsilon_s^4 \\
E_j\varepsilon_j^3+E_k\varepsilon_k^3+E_s\varepsilon_s^3 &
E_j\varepsilon_j^4+E_k\varepsilon_k^4+E_s\varepsilon_s^4 &
E_j\varepsilon_j^5+E_k\varepsilon_k^5+E_s\varepsilon_s^5
\end{array}
\right|
\ .
$$
Этот определитель относится к типу ганкелевых; для его вычисления представим его в виде определителя произведения трех матриц
$$
\det \left\{
\left(
\begin{array}{ccc}
1 & 1 & 1 \\
\varepsilon_j & \varepsilon_k & \varepsilon_s \\
\varepsilon_j^2 & \varepsilon_k^2 & \varepsilon_s^2
\end{array}
\right)
\left(
\begin{array}{ccc}
E_j & 0 & 0 \\
0& E_k & 0 \\
0 & 0 & E_s
\end{array}
\right)
\left(
\begin{array}{ccc}
\varepsilon_j & \varepsilon_j^2 & \varepsilon_j^3 \\
\varepsilon_k & \varepsilon_k^2 & \varepsilon_k^3 \\
\varepsilon_s & \varepsilon_s^2 & \varepsilon_s^3
\end{array}
\right)
\right\} \ .
$$
Применение теоремы Бине-Коши сводит вычисление этого определителя к произведению определителей составляющих матриц. Определитель первой матрицы является определителем Вандермонда —
$$
\left|
\begin{array}{ccc}
1 & 1 & 1 \\
\varepsilon_j & \varepsilon_k & \varepsilon_s \\
\varepsilon_j^2 & \varepsilon_k^2 & \varepsilon_s^2
\end{array}
\right|=(\varepsilon_k -\varepsilon_j)(\varepsilon_s-\varepsilon_j)(\varepsilon_s-\varepsilon_k),
$$
он
отличен от нуля, поскольку, по предположению, числа $ \varepsilon_j, \varepsilon_k, \varepsilon_s $ все различны. Далее, определитель третьей матрицы
$$
\left|
\begin{array}{ccc}
\varepsilon_j & \varepsilon_j^2 & \varepsilon_j^3 \\
\varepsilon_k & \varepsilon_k^2 & \varepsilon_k^3 \\
\varepsilon_s & \varepsilon_s^2 & \varepsilon_s^3
\end{array}
\right|=\varepsilon_j\varepsilon_k\varepsilon_s \left|
\begin{array}{ccc}
1 & 1 & 1 \\
\varepsilon_j & \varepsilon_k & \varepsilon_s \\
\varepsilon_j^2 & \varepsilon_k^2 & \varepsilon_s^2
\end{array}
\right|=\varepsilon_j\varepsilon_k\varepsilon_s(\varepsilon_k -\varepsilon_j)(\varepsilon_s-\varepsilon_j)(\varepsilon_s-\varepsilon_k) \ ,
$$
также отличен от нуля, поскольку все числа $ \varepsilon_j,\varepsilon_k,\varepsilon_s $ еще и ненулевые.
Определитель средней матрицы равен $ E_jE_kE_s $ и отличен от нуля по предположению, что величины ошибок — ненулевые. Следовательно, коэффициент при $ x^{3} $ в уравнении ошибочных позиций отличен от нуля и уравнение не обращается в тривиальное тождество $ 0\equiv 0 $.
Хочется развить этот успех на случай произвольного количества ошибок. К сожалению, на пути исполнения этого желания стоит препятствием уже упомянутое ранее ограничение на степень $ n_{} $. При фиксировании этого числа, добавление в состав кодового полинома $ g_{}(x) $ новых сомножителей из числа полиномов $ X_{\ell} (x) $ уменьшает количество информационных разрядов.
Двоичные БЧХ-коды
Будем строить двоичный циклический $ n_{} $-разрядный код для случая $ n=2^M-1, M\in \mathbb N $. Основываясь на идее предыдущего пункта, будем строить его на основе порождающего полинома $ g_{}(x) $, имеющего корнями последовательные степени примитивного элемента поля Галуа $ \mathfrak A \in \mathbf{GF}(2^M) $:
$$ \mathfrak A, \mathfrak A^2, \mathfrak A^3,\dots,\mathfrak A^{2\tau} \quad npu \quad \tau \ge 2 \ . $$
Как построить такой полином? Примитивный элемент $ \mathfrak A $ поля $ \mathbf{GF}(2^M) $ является корнем неприводимого полинома степени $ m_{} $ над $ \mathbf{GF}(2) $ — который также называется примитивным. Выражения для примитивных полиномов берутся из заранее составленных таблиц. Обозначим этот полином $ f_{1}(x) $. Тогда, в соответствии с теоремой 1, приведенной ☞ ЗДЕСЬ, корнями этого же полинома будут и величины $ \mathfrak A^2, \mathfrak A^4,\dots, \mathfrak A^{2^{m-1}} $. Но вот величина $ \mathfrak A^3 $ не будет корнем $ f_{1}(x) $. С другой стороны, она будет корнем некоторого другого неприводимого полинома $ f_3(x) $. Поэтому интересующий нас полином $ g_{}(x) $ должен иметь представление в виде произведения примитивных полиномов
$$ g(x)\equiv f_1(x)f_3(x)\times \dots \ , $$
каждый из которых имеет корнем определенную величину из множества $ \{ \mathfrak A^{j}\}_{j=1}^{2\tau} $. Строго говоря, определим $ g_{}(x) $ равенством
$$ g(x)\equiv \operatorname{HOK}(f_1,f_2,\dots,f_{2\tau}) \ , $$
где $ \operatorname{HOK} $ означает наименьшее общее кратное неприводимых над $ \mathbf{GF}(2) $ полиномов $ f_{j}(x) $, таких, что $ f_{j}(\mathfrak A^{j})=\mathfrak o $. Такое представление позволяет, во-первых, обеспечить выполнение требования к структуре множества корней полинома $ g_{}(x) $, а, во-вторых, отбросить «дублирующие» полиномы.
П
Пример. Пусть $ M=4 $. Построить полином, корнями которого являются
$ \mathfrak A, \mathfrak A^2, \mathfrak A^3, \mathfrak A^4 $, где $ \mathfrak A $ означает примитивный элемент поля $ \mathbf{GF}(16) $.
Решение. Примитивный элемент поля $ \mathbf{GF}(16) $ является корнем одного из неприводимых над $ \mathbf{GF}(2) $ полиномов: $ x^4+x+1 $ или $ x^4+x^3+1 $ (см. разбор
☞
ЗДЕСЬ). Возьмем $ f_1(x)=x^4+x+1 $. Корнями этого полинома будут также $ \mathfrak A^2 $ и $ \mathfrak A^4 $. Величина $ \mathfrak A^3 $ будет корнем полинома $ f_3(x)=x^4+x^3+x^2+x+1 $. Таким образом,
$$ g(x)\equiv (x^4+x+1)(x^4+x^3+x^2+x+1) \pmod{2} \equiv x^8+x^7+x^6+x^4+1 \ . $$
Кодовое пространство, порождаемое этим полиномом, имеет размерность $ k=15-8=7 $, т.е. на $ 7_{} $ информационных битов приходится $ 8_{} $ проверочных. Иными словами, этот линейный код является $ (15,7) $-кодом.
Если бы мы поставили задачу нахождения полинома $ g_{}(x) $ с корнями $ \mathfrak A, \mathfrak A^2, \mathfrak A^3, \mathfrak A^4,\mathfrak A^5,\mathfrak A^6 $, то для нам пришлось бы домножить предыдущий полином на $ x^2+x+1 $, поскольку именно его корнем является $ \mathfrak A^5 $ (в то время как $ \mathfrak A^6 $ является корнем уже используемого полинома $ f_3 $):
$$ g(x)\equiv (x^4+x+1)(x^4+x^3+x^2+x+1)(x^2+x+1) \pmod{2} \equiv x^{10}+x^8+x^5+x^4+x^2+x+1 \ . $$
Код, порождаемый этим полиномом, является $ (15,5) $-кодом, т.е. на $ 5_{} $ информационных битов приходится $ 10_{} $ проверочных.
♦
Итак, допустим нам удалось построить циклический код на основе порождающего полинома $ g_{}(x) $, имеющего корнями $ \{ \mathfrak A^{j}\}_{j=1}^{2\tau} $, где $ \mathfrak A $ — примитивный элемент поля $ \mathbf{GF}(2^M) $. Кодирование передаваемой информации производится любым из способов, принятых в циклических кодах.
Покажем, что такой код способен исправить от одной до $ \tau_{} $ ошибок при передаче по каналу связи. Пусть при передаче кодового полинома $ G_{}(x) $ произошло ровно $ \ell_{} $ ошибок в коэффициентах при $ x^{j_1},x^{j_2},\dots,x^{j_{\ell}} $:
$$ \tilde G(x) \equiv G(x)+E_{j_1} x^{j_1}+E_{j_2} x^{j_2}+\dots+ E_{j_{\ell}} x^{j_{\ell}} \pmod{2} \ . $$
Заметим, что для двоичного кода ошибка — это либо $ 0 \to 1 $, либо $ 1 \to 0 $, и, следовательно, величина ошибки $ E_{j} $ всегда равна $ 1_{} $. Подставляем в полином $ \tilde G(x) $ корни $ \{ \mathfrak A^{j}\}_{j=1}^{2\tau} $ полинома $ g_{}(x) $. Кодовый полином обращается на них в нуль, так что получаем:
$$\left\{\begin{array}{lllll}
\tilde G(\mathfrak A)&= \mathfrak A^{j_1}&+\mathfrak A^{j_2}&+\dots& + \mathfrak A^{j_{\ell}}, \\
\tilde G(\mathfrak A^2)&= \mathfrak A^{2j_1}&+\mathfrak A^{2j_2}&+\dots& + \mathfrak A^{2j_{\ell}}, \\
\tilde G(\mathfrak A^3)&= \mathfrak A^{3j_1}&+\mathfrak A^{3j_2}&+\dots& + \mathfrak A^{3j_{\ell}}, \\
\dots & & & \dots \\
\tilde G(\mathfrak A^{2\tau})&= \mathfrak A^{2\tau j_1}&+\mathfrak A^{2 \tau j_2}&+\dots& + \mathfrak A^{2 \tau j_{\ell}}.
\end{array}
\right.
$$
Величины $ \mathfrak A^{j_1},\mathfrak A^{j_2},\dots,\mathfrak A^{j_{\ell}} $ называются локаторами ошибок. Система уравнений для их определения — существенно нелинейная. Однако, благодаря наработанному в предыдущем пункте, у нас имеется конструктивный подход к ее решению. Именно, мы разыскиваем полином
$$ L(x)=\sigma_{0}x^{\ell}+ \sigma_1x^{\ell-1}+\dots+\sigma_{\ell} $$
имеющий корнями локаторы ошибок, т.е. такой, что
$$ L(\mathfrak A^{j_1})=\mathfrak o,L(\mathfrak A^{j_2})=\mathfrak o,\dots, L(\mathfrak A^{j_{\ell}})=\mathfrak o \ .
$$
Полином $ L(x) $ называется полиномом локаторов ошибок. Подчеркнем, что его коэффициенты являются элементами поля Галуа: $ \{\sigma_j\}_{j=0}^{\ell} \subset \mathbf{GF}(2^M) $.
Т
Теорема. Пусть порождающий код полином обладает корнями $ \{ \mathfrak A^{j}\}_{j=1}^{2\tau} $, где $ \mathfrak A $ — примитивный элемент поля $ \mathbf{GF}(2^M) $. Если при передаче кодового полинома
$$ G(x)=b_0+b_1x+b_2x^2+\dots+b_{n-1}x^{n-1}, \ (n=2^M-1) $$
произошли ровно $ \ell $ ошибок в коэффициентах с номерами $ \{j_k\}_{k=1}^{\ell} $, и на выходе канала связи получен полином $ \tilde G(x) $, то при $ \tau \ge \ell $ локаторы ошибок $ \{\mathfrak A^{j_k}\}_{k=1}^{\ell} $ удовлетворяют уравнению
$$
L(x)=
\left|
\begin{array}{lllcl}
\tilde G(\mathfrak A) & \tilde G(\mathfrak A^2) & \tilde G(\mathfrak A^3) & \dots & \tilde G(\mathfrak A^{\ell+1}) \\
\tilde G(\mathfrak A^2) & \tilde G(\mathfrak A^3) & \tilde G(\mathfrak A^4) & \dots & \tilde G(\mathfrak A^{\ell+2}) \\
\tilde G(\mathfrak A^3) & \tilde G(\mathfrak A^4) & \tilde G(\mathfrak A^5) & \dots & \tilde G(\mathfrak A^{\ell+3}) \\
\dots & & & & \dots \\
\tilde G(\mathfrak A^{\ell}) & \tilde G(\mathfrak A^{\ell+1}) & \tilde G(\mathfrak A^{\ell+2}) & \dots & \tilde G(\mathfrak A^{2\ell}) \\
1 & x & x^2 & \dots & x^{\ell}
\end{array}
\right|=\mathfrak o
$$
и это уравнение имеет степень $ \ell_{} $. Если же произошло меньше чем $ \ell_{} $ ошибок, то это уравнение обращается в тождество $ \mathfrak o = \mathfrak o $.
П
Пример. Рассмотрим $ (15,5) $-код из предыдущего примера — пусть порождающий его полином имеет вид
$$ g(x)= x^{10}+x^8+x^5+x^4+x^2+x+1 \ . $$
Пусть при передаче некоторого кодового полинома $ G_{}(x) $ произошло некоторое количество ошибок, и на выходе канала связи оказался полином
$$ \tilde G(x)= 1+x^3+x^4+x^7+x^{10}+x^{12}+x^{13}+x^{14} \ .
$$
Попробуем исправить эти ошибки, основываясь на предыдущем результате. Максимально возможное количество ошибок, которых потенциально возможно «отловить» с его помощью, равно $ 3_{} $. Положив эту оценку стартовой гипотезой, строим детерминантное представление для полинома локаторов ошибок:
$$
L(x)=
\left|
\begin{array}{lllcl}
\tilde G(\mathfrak A) & \tilde G(\mathfrak A^2) & \tilde G(\mathfrak A^3) & \tilde G(\mathfrak A^4) \\
\tilde G(\mathfrak A^2) & \tilde G(\mathfrak A^3) & \tilde G(\mathfrak A^4) & \tilde G(\mathfrak A^5) \\
\tilde G(\mathfrak A^3) & \tilde G(\mathfrak A^4) & \tilde G(\mathfrak A^5) & \tilde G(\mathfrak A^6) \\
1 & x & x^2 & x^{3}
\end{array}
\right| \ .
$$
Здесь через $ \mathfrak A $ обозначен корень полинома $ x^4+x+1 $; он является примитивным элементом поля $ \mathbf{GF}(16) $. Вычисляем элементы определителя, пользуясь таблицей для степеней $ \mathfrak A^j $, приведенной
☞
ЗДЕСЬ.
$$
\begin{array}{rccccccc}
\tilde G(\mathfrak A) =& 1 +\mathfrak A^3 &+ \mathfrak A^4 &+\mathfrak A^7&+\mathfrak A^{10}& +\mathfrak A^{12}& +\mathfrak A^{13}& +\mathfrak A^{14}= \\
=&1+\mathfrak A^3&+(\mathfrak A+1)& +(\mathfrak A^3+\mathfrak A+1) &+(\mathfrak A^2+\mathfrak A+1)&+(\mathfrak A^3+\mathfrak A^2+\mathfrak A+1)&+(\mathfrak A^3+\mathfrak A^2+1)&+(\mathfrak A^3+1)=
\end{array}
$$
$$
{}_{} \qquad =\mathfrak A^3+\mathfrak A^2+1=\mathfrak A^{13} \ .
$$
Поскольку $ \tilde G(\mathfrak A) \ne \mathfrak o $, то хотя бы одна ошибка при передаче произошла.
Далее,
$$
\tilde G(\mathfrak A^2)=\mathfrak A^3+\mathfrak A^2+\mathfrak A=\mathfrak A^{11},\ \tilde G(\mathfrak A^3)=\mathfrak o,\ \tilde G(\mathfrak A^4)=\mathfrak A^3+\mathfrak A +1=\mathfrak A^7,\
\tilde G(\mathfrak A^5)=\mathfrak A^2+\mathfrak A=\mathfrak A^5,\ \tilde G(\mathfrak A^6)=\mathfrak o \ .
$$
Разложение определителя по последней строке, начинаем с правого угла: коэффициент при $ x^{3} $ равен3)
$$
\left|
\begin{array}{ccc}
\mathfrak A^3+\mathfrak A^2+1 & \mathfrak A^3+\mathfrak A^2+\mathfrak A & \mathfrak o \\
\mathfrak A^3+\mathfrak A^2+\mathfrak A & \mathfrak o & \mathfrak A^3+\mathfrak A +1 \\
\mathfrak o & \mathfrak A^3+\mathfrak A +1 & \mathfrak A^2+\mathfrak A
\end{array}
\right| =
\left|
\begin{array}{ccc}
\mathfrak A^{13} & \mathfrak A^{11} & \mathfrak o \\
\mathfrak A^{11} & \mathfrak o & \mathfrak A^7 \\
\mathfrak o & \mathfrak A^7 & \mathfrak A^5
\end{array}
\right|=\mathfrak o \ .
$$
Следовательно, $ \deg L(x)\le 3 $, и это4) свидетельствует о том, что количество ошибок не может равняться $ 3_{} $.
Выдвигаем гипотезу о том, что количество ошибок передачи равно $ 2_{} $. Уменьшаем размерность соответствующего определителя:
$$
L(x)=
\left|
\begin{array}{lll}
\tilde G(\mathfrak A) & \tilde G(\mathfrak A^2) & \tilde G(\mathfrak A^3) \\
\tilde G(\mathfrak A^2) & \tilde G(\mathfrak A^3) & \tilde G(\mathfrak A^4) \\
1 & x & x^2
\end{array}
\right| =
\left|
\begin{array}{ccc}
\mathfrak A^{13} & \mathfrak A^{11} & \mathfrak o \\
\mathfrak A^{11} & \mathfrak o & \mathfrak A^7 \\
1 & x & x^2
\end{array}
\right|=\mathfrak A^{22}x^2+\mathfrak A^{20}x+\mathfrak A^{18}=\mathfrak A^{7}x^2+\mathfrak A^{5}x+\mathfrak A^{3} \ .
$$
В этом случае полином $ L(x) $ нетривиален. Непосредственной проверкой убеждаемся, что корнями полинома являются элементы поля $ \mathfrak A^{3} $ и $ \mathfrak A^{8} $. Это — локаторы ошибок, они указывают на позиции ошибок в $ 3_{} $-м и $ 8 $-м коэффициентах полинома $ \tilde G(x) $. Кодовым является полином
$$ G(x)= 1+x^4+x^7+x^8+x^{10}+x^{12}+x^{13}+x^{14} \ . $$
♦
Построенный выше двоичный код является примером кода Боуза-Чоудхури-Хоквингема5) или БЧХ-кода. Его кодовое расстояние не превосходит величины
$$ d_0=1+2\tau \ , $$
которая называется конструктивным расстоянием БЧХ-кода. Число $ k_{} $ информационных символов БЧХ-кода и, соответственно, число $ n-k=2^M-k-1 $ проверочных символов зависит от степеней множителей полинома $ g_{}(x) $ — неприводимых по модулю $ 2_{} $ полиномов.
=>
Код Хэмминга является частным случаем БЧХ-кода, он соответствует случаю $ \tau=1 $. В этом случае кодовым полиномом берется просто произвольный примитивный полином — поскольку его корнями обязательно будут две последовательные степени $ \mathfrak A $ и $ \mathfrak A^2 $ (см. теорему $ 1 $
☞
ЗДЕСЬ ) примитивного элемента поля $ \mathbf{GF}(2^M) $, то, в соответствии с теоремой, он способен исправлять одну ошибку линейного $ (2^M-1,2^M-M-1) $-кода.
Теперь сделаем несколько комментариев, позволяющих упростить вычисление полинома локаторов ошибок, а также «развить успех» в разных направлениях.
1.
В соответствии с теоремой Шёнеманна, для любого полинома $ F_{}(x) $ над $ \mathbf{GF}(2) $ имеет место сравнение $ \left[F(x)\right]^2 \equiv F(x^2) \pmod{2} $. Тогда
$$ \tilde G(\mathfrak A^2)=\left(\tilde G(\mathfrak A)\right)^2,\ \tilde G(\mathfrak A^4)=\left(\tilde G(\mathfrak A^2)\right)^2, \tilde G(\mathfrak A^6)=\left(\tilde G(\mathfrak A^3)\right)^2,\dots
$$
Таким образом, вычислив значения $ \tilde G(\mathfrak A^j) $ для нечетных показателей $ j_{} $,
значения $ \tilde G ( \mathfrak A^{2j}) $ получим возведением в квадрат уже вычисленного $ \tilde G(\mathfrak A^j) $. (Понаблюдайте проявление этого свойства в предыдущем примере).
2.
Полином $ L_{}(x) $ раскладывается на линейные множители над полем $ \mathbf{GF}(2^M) $:
$$ L(x) \equiv \sigma_{\ell}(x-\mathfrak A^{j_1})(x-\mathfrak A^{j_2})\times\dots \times (x-\mathfrak A^{j_{\ell}}) \ . $$
Величины $ \tilde G(\mathfrak A),\tilde G(\mathfrak A^2),\tilde G(\mathfrak A^3),\dots, \tilde G(\mathfrak A^{2\tau}) $ представляют суммы степеней его корней; такие суммы — в случае полинома над $ \mathbb Q,\mathbb R $ или $ \mathbb C_{} $ — называются суммами Ньютона. Известно, что над этими полями коэффициенты полинома рационально выражаются через суммы Ньютона: если обозначить корни нормализованного полинома
$$ L(x)=x^{\ell}+\sigma_{1}x^{\ell-1}+\sigma_{2}x^{\ell-2}+\dots+\sigma_{\ell} $$
через $ \lambda_1,\dots,\lambda_{\ell} $, а его $ k_{} $-ю сумму Ньютона через $ s_k=\lambda_1^k+\dots+\lambda_{\ell}^k $, то коэффициенты полинома $ L(x) $ выражаются через суммы Ньютона по следующим рекурсивным формулам Ньютона:
$$
\sigma_{1}=-s_1, 2\sigma_2=-(s_2+\sigma_1s_1), 3\sigma_3=-(s_3+\sigma_1s_2+\sigma_2s_1),\dots,
$$
$$
k\sigma_k=-(s_{k}+\sigma_1s_{k-1}+\sigma_2s_{k-2}+\dots+\sigma_{k-1}s_1) \ npu \ k \le \ell.
$$
В случае полинома $ L_{}(x) $ над $ \mathbf{GF}(2) $ эти формулы следует рассматривать по модулю $ 2_{} $ и формулы с четными номерами отбрасываются потому как являются следствиями предыдущих, а также комментария
1
. Следующее детерминантное представление полинома аналогично приведенному в конце
☞
ПУНКТА для полинома над бесконечными полями;
для наглядности я приведу его для случая $ \ell = 4 $:
$$
L(x)=
\left|
\begin{array}{lllll}
\tilde G(\mathfrak A) & 1 & 0 & 0 & 0 \\
\tilde G(\mathfrak A^3) & \tilde G(\mathfrak A^2) & \tilde G(\mathfrak A) & 1 & 0 \\
\tilde G(\mathfrak A^5) & \tilde G(\mathfrak A^4) & \tilde G(\mathfrak A^3) & \tilde G(\mathfrak A^2) & \tilde G(\mathfrak A) \\
\tilde G(\mathfrak A^7) & \tilde G(\mathfrak A^6) & \tilde G(\mathfrak A^5) & \tilde G(\mathfrak A^4) & \tilde G(\mathfrak A^3) \\
x^4 & x^3 & x^2 & x & 1
\end{array}
\right|
$$
П
Пример. Рассмотрим $ (15,5) $-код из предыдущего примера с порождающим полиномом
$$ g(x)= x^{10}+x^8+x^5+x^4+x^2+x+1 \ . $$
Пусть при передаче некоторого кодового полинома на выходе канала связи оказался полином
$$ \tilde G(x)= 1+x+x^4+x^7+x^8+x^9+x^{11}+x^{14} \ .
$$
Примитивный элемент поля $ \mathbf{GF}(16) $ выбираем тем же, что и ранее: пусть $ \mathfrak A $ является корнем полинома $ x^4+x+1 $, входящего сомножителем в $ g_{}(x) $. Поскольку
$$ \tilde G(\mathfrak A)=\mathfrak A+1 \ne \mathfrak o \ , $$
то при передаче по каналу произошла хотя бы одна ошибка. Положив начальной гипотезой наличие $ \ell=2 $ ошибок, строим полином:
$$ L(x)=
\left|
\begin{array}{lll}
\tilde G(\mathfrak A) & 1 & 0 \\
\tilde G(\mathfrak A^3) & \tilde G(\mathfrak A^2) & \tilde G(\mathfrak A) \\
x^2 & x & 1
\end{array}
\right| =\left|
\begin{array}{ccc}
\mathfrak A+1 & 1 & 0 \\
\mathfrak A^3 & \mathfrak A^2+1 & \mathfrak A+1 \\
x^2 & x & 1
\end{array}
\right|=(\mathfrak A+1)x^2+(\mathfrak A^2+1)x+(\mathfrak A^2+\mathfrak A+1)
$$
Этот полином не имеет корней среди $ \{\mathfrak A^j\}_{j=0}^{14} $.
Положив гипотезой наличие $ \ell=3 $ ошибок (максимального количества ошибок, возможного для исправления настоящим кодом), строим полином
$$ L(x)=
\left|
\begin{array}{llll}
\tilde G(\mathfrak A) & 1 & 0 & 0 \\
\tilde G(\mathfrak A^3) & \tilde G(\mathfrak A^2) & \tilde G(\mathfrak A) & 1 \\
\tilde G(\mathfrak A^5) & \tilde G(\mathfrak A^4) & \tilde G(\mathfrak A^3) & \tilde G(\mathfrak A^2) \\
x^3 & x^2 & x & 1
\end{array}
\right| =\left|
\begin{array}{cccc}
\mathfrak A+1 & 1 & 0 & 0 \\
\mathfrak A^3 & \mathfrak A^2+1 & \mathfrak A+1 & 1 \\
1 & \mathfrak A & \mathfrak A^3 & \mathfrak A^2+1 \\
x^3 & x^2 & x & 1
\end{array}
\right|=
$$
$$
=(\mathfrak A^2+\mathfrak A+1)x^3+(\mathfrak A^3+1)x^2+(\mathfrak A^3+\mathfrak A^2+\mathfrak A+1)x+\mathfrak A^2 \ .
$$
Полином имеет корнями $ \mathfrak A^3, \mathfrak A^8,\mathfrak A^{11} $, следовательно ошибки произошли в коэффициентах при $ x^3, x^8 $ и $ x^{11} $, и кодовым полиномом является
$$ G(x)=1+x+x^3+x^4+x^7+x^9+x^{14} \ . $$
♦
3.
Основное требование к порождающему код полиному иметь корнями последовательность первых степеней примитивного элемента поля допускает модификации. Эти модификации касаются двух выражений: «первых степеней» и «примитивного элемента». Так, с одной стороны, можно потребовать от порождающего код полинома $ g_{}(x) $ обращения в нуль на последовательности степеней примитивного элемента поля
$$ \mathfrak A^{m_0}, \mathfrak A^{m_0+1}, \mathfrak A^{m_0+2},\dots,\mathfrak A^{m_0+2\tau-1} \quad npu \quad m_0\ge 1,\ \tau \ge 2 \ , $$
не обязательно начинающейся с первой его степени.
Небольшая модификация приведенного выше алгоритма исправления ошибок позволит применять его.
С другой стороны, можно отказаться от требования примитивности элемента $ \mathfrak A $. Пусть порядок элемента $ \mathfrak B \in \mathbf{GF}(2^M) $ равен $ n_{} $. Тогда все его степени
$$ \mathfrak B^0,\mathfrak B^1,\mathfrak B^2,\dots,\mathfrak B^{n-1} $$
будут различными элементами поля и локаторы ошибок $ n_{} $-разрядного кода позволят однозначно установить места ошибок. Таким образом, в этом случае мы уменьшаем количество разрядов кода с максимально возможного $ 2^M-1 $ до некоторого делителя этого числа.
П
Пример. Пусть $ M=6 $. Построить $ 21 $-разрядный код, исправляющий две ошибки.
Решение. Поле $ \mathbf{GF}(2^6) $ исследовано
☞
ЗДЕСЬ.
Число $ 2^6-1=63 $ делится на $ 21 $, следовательно в $ \mathbf{GF}(2^6) $ существует элемент порядка $ 21 $, в качестве этого элемента можно взять произвольный корень полинома $ f_{6,2}(x)=x^6+x^5+x^4+x^2+1 $. Если обозначить корень этого полинома через $ \mathfrak B_{} $, то найдется такой примитивный элемент $ \mathfrak A \in \mathbf{GF}(2^6) $, что $ \mathfrak B =\mathfrak A^3 $. Если мы ставим целью подобрать полином $ g_{}(x) $ с корнями, среди которых имеются $ \mathfrak B, \mathfrak B^2, \mathfrak B^3,\mathfrak B^4 $, то все эти корни, кроме $ \mathfrak B^3 $, будут корнями $ f_{6,2}(x) $. Корень же $ \mathfrak B^3=\mathfrak A^9 $ будет корнем полинома $ x^3+x+1 $ (проверьте что именно его, а не двойственного ему $ x^3+x^2+1 $). Таким образом, полином $ g(x)=(x^6+x^5+x^4+x^2+1)(x^3+x+1)=x^9+x^8+x^5+x^4+x^2+x+1 $ порождает $ (21,12) $-циклический код, исправляющий две ошибки.
♦
Коды Рида-Соломона
В предыдущем пункте мы столкнулись с необходимостью рассмотрения полиномов относительно переменной $ x_{} $, коэффициентами которых оказывались не числа, а элементы поля Галуа $ \mathbf{GF}(2^M) $. Нам даже пришлось решать алгебраические уравнения, содержащие подобные полиномы6). Если первоначальный шок от использования подобных объектов преодолен, то попробуем пойти и дальше — допустим к рассмотрению в качестве порождающего циклический код полинома $ g_{}(x) $ не только полиномы с двоичными коэффициентами, но также и с коэффициентами из $ \mathbf{GF}(2^M) $.
Начнем с формального обобщения БЧХ-кода, а уж практическое применение этого обобщения обсудим позже.
П
Пример 1. Рассмотрим код с порождающим полиномом равным
$$ g(x)=(x-\mathfrak A)(x-\mathfrak A^2)(x-\mathfrak A^3)(x-\mathfrak A^4)
$$
при $ \mathfrak A $ — корне полинома $ f(x)= x^4+x+1 $.
Перемножив линейные сомножители по модулю $ 2,f(x) $, получим представление порождающего полинома в виде
$$ g(x)=x^4+(\mathfrak A^3+\mathfrak A^2+1)x^3+(\mathfrak A^3+\mathfrak A^2)x^2+\mathfrak A^3\,x+(\mathfrak A^2+\mathfrak A+1) \ ,
$$
которое — с помощью таблицы, приведенной
☞
ЗДЕСЬ — можно преобразовать к виду, когда коэффициентами мономов становятся степени примитивного элемента:
$$
g(x)=x^4+\mathfrak A^{13}x^3+\mathfrak A^6\,x^2+\mathfrak A^3\,x+\mathfrak A^{10} ;
$$
однако в дальнейших рассчетах более удобно именно первое представление.
Пусть для передачи некоторого информационного вектора $ (x_1,x_2,\dots,x_{11}) \in \mathbb V^{11} $ используется несистематическое кодирование и кодовым полиномом является
$$ G(x)\equiv (x_1x^{10}+x_2\,x^9+\dots+x_{11}) g(x) \pmod{2} , $$
который при передаче по каналу связи преобразуется в
$$ \tilde G(x) = x^{14}+(\mathfrak A^3+\mathfrak A^2+1)x^{13}+(\mathfrak A^3+\mathfrak A^2+1)x^{12}+(\mathfrak A^3+1)x^{11}+
$$
$$
+(\mathfrak A^2+\mathfrak A+1)x^{10}+(\mathfrak A^3+1)x^9+(\mathfrak A+1)x^8
+(\mathfrak A^3+\mathfrak A^2+\mathfrak A)x^7+
$$
$$
+(\mathfrak A^3+\mathfrak A+1)x^6+x^5+(\mathfrak A^2+1)x^4+(\mathfrak A^3+1)x^3+(\mathfrak A^3+\mathfrak A+1)x^2+\mathfrak A^3x+
$$
$$
+(\mathfrak A^2+\mathfrak A+1) \ ,
$$
предположительно содержащий две ошибки в коэффициентах, т.е.
$$ \tilde G(x) \equiv G(x)+E_jx^j + E_kx^k \quad npu \quad \{j,k\} \subset \{0,1,2,\dots,14\},\ \{E_j,E_k\} \subset \mathbf{GF}(16) \ . $$
Акцентируем, что в данном случае, в отличие от предыдущего пункта, величины ошибок $ E_j $ и $ E_k $ являются элементами поля $ \mathbf{GF}(16) $, т.е. представляют собой выражения $ B_0+B_1\mathfrak A+B_2\mathfrak A^2+B_3\mathfrak A^3 $ при $ \{B_0,B_1,B_2,B_3\} \subset \{0,1\} $.
Требуется восстановить информационный вектор.
Действуя по сценарию
☞
ПУНКТА и руководствуясь гипотезой о двух ошибках, составляем систему уравнений
$$
\left\{ \begin{array}{lll}
E_j \mathfrak A^j & + E_k \mathfrak A^k & = \tilde G(\mathfrak A), \\
E_j \mathfrak A^{2j} & + E_k \mathfrak A^{2k} & = \tilde G(\mathfrak A^2), \\
E_j \mathfrak A^{3j} & + E_k \mathfrak A^{3k} & = \tilde G(\mathfrak A^3), \\
E_j \mathfrak A^{4j} & + E_k \mathfrak A^{4k} & = \tilde G(\mathfrak A^4).
\end{array}
\right.
$$
которую пытаемся решить относительно локаторов ошибок $ \mathfrak A^j, \mathfrak A^k $ и величин ошибок $ E_j, E_k $. Уравнение локаторов ошибок разыскивается в виде:
$$
\left| \begin{array}{lll}
\tilde G(\mathfrak A) & \tilde G(\mathfrak A^2) & \tilde G(\mathfrak A^3) \\
\tilde G(\mathfrak A^2) & \tilde G(\mathfrak A^3) & \tilde G(\mathfrak A^4) \\
1 & x & x^2
\end{array}
\right|=
\left| \begin{array}{ccc}
\mathfrak A^3+\mathfrak A^2+1 & \mathfrak A^3+\mathfrak A+1 & \mathfrak o \\
\mathfrak A^3+\mathfrak A+1 & \mathfrak o & \mathfrak A^3+\mathfrak A^2 \\
1 & x & x^2
\end{array}
\right|= \mathfrak o \ .
$$
Поскольку $ \tilde G(\mathfrak A)\ne \mathfrak o $, то, крайней мере, одна ошибка имеется. Раскладываем определитель по последней строке:
$$
(\mathfrak A^3+1)x^2+(\mathfrak A+1)x+(\mathfrak A^3+\mathfrak A^2+1) = \mathfrak o \ .
$$
Корнями этого уравнения оказываются $ \mathfrak A^3 $ и $ \mathfrak A^{11} $. Таким образом, $ j=3, k=11 $, т.е. ошибки передачи по каналу содержатся в коэффициентах при $ x^{3} $ и $ x^{11} $. Величины ошибок $ E_3 $ и $ E_{11} $ находим из приведенной выше системы линейных уравнений, в которой коэффициенты нами теперь установлены:
$$\left\{
\begin{array}{lllll}
E_3 \mathfrak A^3&+E_{11}\mathfrak A^{11}&=\tilde G(\mathfrak A)&= \mathfrak A^3+\mathfrak A^2+1&=\mathfrak A^{13}, \\
E_3 \mathfrak A^6&+E_{11}\mathfrak A^{22}&=\tilde G(\mathfrak A^2)&= \mathfrak A^3+\mathfrak A+1&=\mathfrak A^{7},
\end{array}
\right .
$$
Решаем эту систему по формулам Крамера:
$$
E_3=\frac{ \left| \begin{array}{ll} \mathfrak A^{13} & \mathfrak A^{11} \\ \mathfrak A^7 & \mathfrak A^{22}
\end{array}
\right| }{
\left| \begin{array}{ll} \mathfrak A^{3} & \mathfrak A^{11} \\ \mathfrak A^6 & \mathfrak A^{22}
\end{array}
\right|
}=\frac{\mathfrak A^{35}+\mathfrak A^{18}}{\mathfrak A^{25}+\mathfrak A^{17}}=\frac{\mathfrak A^{5}+\mathfrak A^{3}}{\mathfrak A^{10}+\mathfrak A^{2}}=\frac{\mathfrak A^{11}}{\mathfrak A^{4}}=\mathfrak A^{7}=\mathfrak A^{3}+\mathfrak A+1 ,
$$
$$
E_{11}=
\frac{\left| \begin{array}{ll} \mathfrak A^{3} & \mathfrak A^{13} \\ \mathfrak A^6 & \mathfrak A^{7}
\end{array}
\right| }{
\left| \begin{array}{ll} \mathfrak A^{3} & \mathfrak A^{11} \\ \mathfrak A^6 & \mathfrak A^{22}
\end{array}
\right|
}=\mathfrak A^{3}+\mathfrak A^2+1 \ .
$$
Таким образом, кодовый полином равен
$$ G(x)\equiv \tilde G(x)+(\mathfrak A^{3}+\mathfrak A+1)x^3+(\mathfrak A^{3}+\mathfrak A^2+1)x^{11} \ , $$
его частное от деления на порождающий полином $ g_{}(x) $ равно $ x^{10}+x^8+x^7+x^6+x^3+x^2+1 $, т.е. информационным вектором является $ (10111001101) $.
♦
Итак, формальное обобщение двоичного БЧХ-кода из предыдущего пункта произведено. Порождающий код полином $ g_{}(x) $ оказывается делителем полинома $ x^{2^M-1} — 1 $, но только делителем не с двоичными коэффициентами, а с коэффициентами из $ \mathbf{GF}(2^M) $. Этот полином правильно исправляет ошибки, а его степень существенно меньше степени порождающего полинома двоичного БЧХ-кода, решающего ту же задачу. Правда, выражения для коэффициентов полинома становятся более сложными, но если уж мы принципиально решили связываться с формализмом полей Галуа, то упомянутое усложнение не кажется существенным.
Коды, построенные по аналогии с разобранным в примере 1 случаем, также относят к БЧХ-кодам, но они имеют специальное название — это коды Рида-Соломона7).
В примере $ 1 $ в качестве порождающего код полинома рассматривался полином над полем $ \mathbf{GF}(16) $, в то время как собственно информационный полином, который был вычислен на последнем шаге, оказался полиномом над $ \mathbf{GF}(2) $. А что будет, если взять и в качестве информационного полинома не полином над $ \mathbf{GF}(2) $, а полином над $ \mathbf{GF}(16) $
?
П
Пример 2. Рассмотрим код из предыдущего примера. Пусть информационный полином равен
$$ P(x)=(\mathfrak A^3+\mathfrak A^2+1)x^{10}+(\mathfrak A^2+1)x^9+(\mathfrak A^3+\mathfrak A^2+\mathfrak A+1)x^8+\mathfrak A\,x^7+(\mathfrak A^2+\mathfrak A+1)x^6+
$$
$$
+(\mathfrak A^3+\mathfrak A^2+1)x^3
+(\mathfrak A+1)x^2+(\mathfrak A^3+1)\ .
$$
Далее идем по проложенному в предыдущем примере пути. Используем несистематическое кодирование, получаем кодовый полином
$$ G(x)\equiv P(x)g(x) \pmod{2} = $$
$$
=(\mathfrak A^3+\mathfrak A^2+1)x^{14}+(\mathfrak A^3+\mathfrak A+1)x^{13}+ \dots+ x^3+(\mathfrak A^3+\mathfrak A^2+\mathfrak A+1)x^2+\mathfrak A^2\,x+
$$
$$
+(\mathfrak A^3+\mathfrak A) \, $$
пересылаем по каналу, на выходе получаем испорченный полином
$$ \tilde G(x)\equiv G(x)+(\mathfrak A^2+1)\,x^{13}+\mathfrak A^3\,x^3 =
$$
$$
=(\mathfrak A^3+\mathfrak A^2+1)x^{14}+(\mathfrak A^3+\mathfrak A^2)x^{13}+ \dots+ (\mathfrak A^3+1)x^3+(\mathfrak A^3+\mathfrak A^2+\mathfrak A+1)x^2+\mathfrak A^2\,x+
$$
$$
+(\mathfrak A^3+\mathfrak A) \ , $$
т.е. снова оказываемся в ситуации наличия двух ошибок в коэффициентах при степенях $ x_{} $.
Уравнение синдромов ошибок:
$$
\left| \begin{array}{ccc}
\mathfrak o & \mathfrak A^3+1 & \mathfrak A^3+\mathfrak A+1 \\
\mathfrak A^3+1 & \mathfrak A^3+\mathfrak A+1 & \mathfrak o \\
1 & x & x^2
\end{array}
\right|= \mathfrak o \ \iff \ (\mathfrak A^3+\mathfrak A^2+1)x^2+(\mathfrak A^3+\mathfrak A^2)x+(\mathfrak A^3+1) = \mathfrak o
$$
имеет корнями правильные значения синдромов $ \mathfrak A^3 $ и $ \mathfrak A^{13} $. Величины ошибок
системе уравнений
$$\left\{
\begin{array}{llll}
E_3 \mathfrak A^3&+E_{13}\mathfrak A^{13}&=\tilde G(\mathfrak A)&= \mathfrak o , \\
E_3 \mathfrak A^6&+E_{13}\mathfrak A^{26}&=\tilde G(\mathfrak A^2)&= \mathfrak A^3+1
\end{array}
\right .
$$
удовлетворяют.
♦
Теперь попробуем придать «физический смысл» приведенным примерам. Что такое информационный полином $ P(x) $ из примера 2? Если в примере 1 нас интересовали только коэффициенты подобного полинома — именно эти двоичные цифры несли информацию, а собственно степени переменной $ x_{} $ нужны были исключительно для удобства преобразований — то коэффициенты полинома $ P(x) $ из примера 2 являются не цифрами, а совсем даже готичными выражениями… Реально мы имеем дело с полиномом от двух величин — $ x_{} $ и $ \mathfrak A $. В общем случае полинома нескольких переменных над произвольным полем (не обязательно полем Галуа) — его можно задать набором коэффициентов — см.
☞
ЗДЕСЬ. Что можно сказать о потенциально возможном виде полинома $ P(x,\mathfrak A) $, который можно было взять в качестве информационного в примере 2? Он подчиняется следующим ограничениям на степени:
$$ \deg_x P< 15, \deg_{\mathfrak A} P< 4 \ ; $$
последняя оценка накладывается степенью порождающего код полинома $ g(x,\mathfrak A) $. Для однозначного задания полинома при таких ограничениях требуются $ 15 \times 4=60 $ коэффициентов — и этими коэффициентами являются числа $ 0_{} $ и $ 1_{} $. Кое-что начинает проясняться : нас интересуют не коэффициенты при степенях $ x_{} $, а при степенях мономов $ x^k \mathfrak A^{\ell} $! Таким образом, в информационном полиноме $ P(x,\mathfrak A) $ заложена информация о $ 60 $ его коэффициентах. Эти коэффициенты можно записать в последовательность (договорившись предварительно о способе упорядочения мономов ). Представим этот массив не одномерным:
$$
\begin{array}{ccccccc}
x^{10} \mathfrak A^{3} & x^{10} \mathfrak A^{2} & x^{10} \mathfrak A & x^{10} & x^{9} \mathfrak A^{3} & x^{9} \mathfrak A^{2} & \dots \\
1 & 1 & 0 & 1 & 0 & 1 & \dots ,
\end{array}
$$
а двумерным — т.е. рассмотрим матрицу. Фактически, полином уже представлен в виде, из которого матрица извлекается мгновенно:
$$
\begin{array}{cc}
&
x^{10}\, x^9 \ x^8 \ x^7 \ x^6 \ x^5 \ x^4 \ x^3 \ \ x^2 \ x \ 1 \\
& \downarrow \ \ \downarrow \ \ \ \downarrow \ \ \downarrow \ \ \downarrow \ \ \ \downarrow \ \ \ \downarrow \ \ \downarrow \ \ \ \downarrow \ \ \downarrow \ \ \downarrow \\
\begin{array}{ll}
\mathfrak A^{3} & \rightarrow \\
\mathfrak A^{2} & \rightarrow \\
\mathfrak A^{3} & \rightarrow \\
1 & \rightarrow \\
\end{array}
&
\left[
\begin{array}{ccccccccccc}
1 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\
1&1&1&0&1&0&0&1&0&0&0 \\
0&0&1&1&1&0&0&0&1&0&0 \\
1&1&1&0&1&0&0&1&1&0&1
\end{array}
\right]
\end{array}
$$
Кодовый полином $ G_{}(x) $ и результат его передачи по каналу связи — полином $ \tilde G(x) $ также можно представить в аналогичном виде:

В $ 60 $-битном кодовом слове при передаче произошли три ошибки, но в примере 2 они исправлялись по алгоритму, который изначально «заточен» под ситуацию двух ошибок! Почему этот алгоритм отработал правильно? Объяснение заключается в том, что две из трех произошедших ошибок оказались компактно расположенными в одном столбце информационной таблицы 
Такая возможность «упаковки» ошибок весьма существенна для практики: дело в том, что ошибки передачи часто имеют обыкновение происходить серией9). Поэтому применение кодов Рида-Соломона очень распространено — причем не только в задачах исправления ошибок, но и восстановления потерянных данных; подробнее см.
☞
ЗДЕСЬ.
Источники
[1]. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.Мир. 1976.


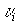
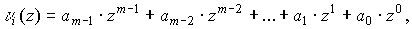
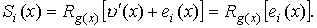
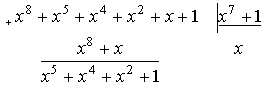
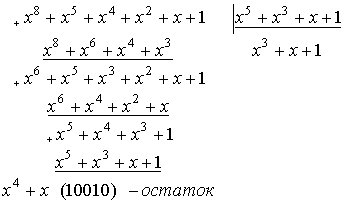

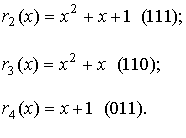
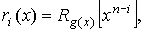
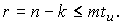
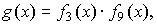
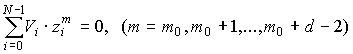














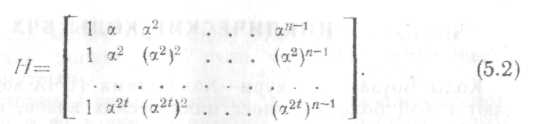


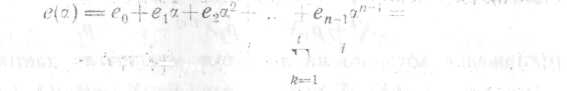
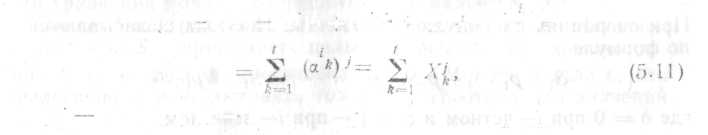
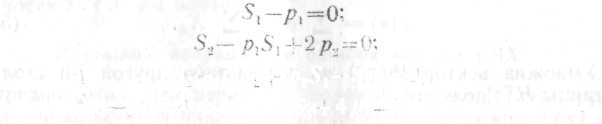
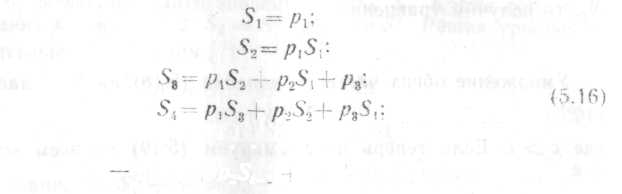

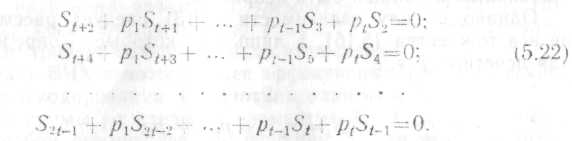
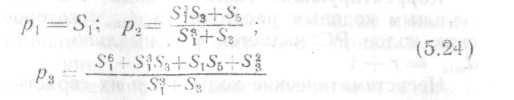

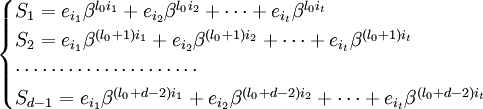
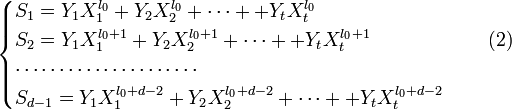
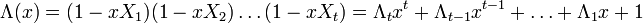
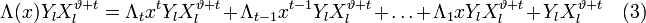
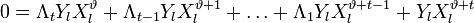
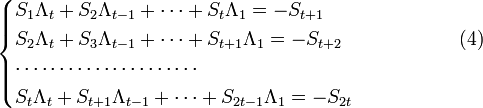
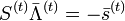
![S^{(t)}={ left[ begin{matrix}
S_1 &amp; S_2 &amp; dots &amp; S_t \
S_2 &amp; S_3 &amp; dots &amp; S_{t+1} \
cdots &amp; cdots &amp; cdots &amp; \
S_t &amp; S_{t+1} &amp; dots &amp; S_{2t-1}
end{matrix} right] }, quad quad quad quad quadquad(5)](https://dic.academic.ru/pictures/wiki/files/99/cb1fb0775da4988ff94bb8f82afbb614.png)
![barLambda^{(t)} =
{ left[ begin{matrix}
Lambda_t \
Lambda_{t-1} \
cdots \
Lambda_1
end{matrix} right] },
quad quad
bar s^{(t)}
{ left[ begin{matrix}
S_{t+1} \
S_{t+2} \
cdots \
S_{2t}
end{matrix} right] }](https://dic.academic.ru/pictures/wiki/files/102/fb3abb36e14beb74ecaab8e8af0df01e.png)