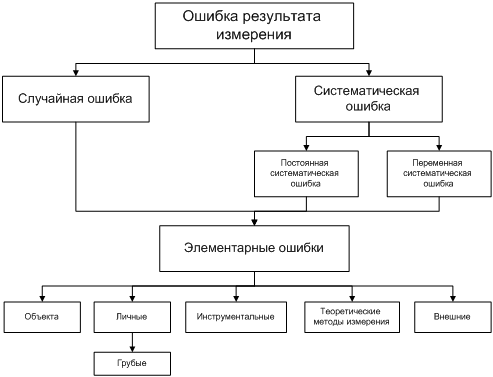
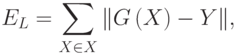более высокочастотный диапазон радиоволн, в котором увеличивается поглощение энергии радиоволн в среде и, следовательно, уменьшается дальность действия системы; разрешение данного противоречия было найдено при использовании так называемых сложных сигналов).
Физические противоречия состоят в наличии у одного и того же элемента системы противоположных физических свойств или функций (например, элемент электронной схемы должен быть проводником при протекании тока в одном направлении и диэлектриком при другом направлении тока, это противоречие разрешает такой элемент как диод).
Путь к созданию качественно новой технической системы лежит через выявление все более глубоких противоречий и нахождение способов их разрешения. В этом состоит одно из проявлений закона перехода количественных изменений в качественные. В то же время новая техническая система представляет собой синтез нового и некоторых элементов прежних решений, демонстрируя этим действие закона отрицания отрицания.
Вопросы для самоконтроля:
Каково соотношение терминов «понятие», «суждение», «умозаключение»? Каким образом происходит эволюция научной идеи в гипотезу и, далее, в закон?
Какова структура научной теории?
В чем различие диалектического и метафизического подхода к процессу познания?
Перечислите общенаучные эмпирические методы исследований и приведите примеры их использования для получения нового научного знания. Перечислите общенаучные теоретические методы исследований и приведите примеры их использования в процессе обучения по специальности радиотехника.
Каково содержание и методы решения задачи анализа структурной схемы устройства?
Каково содержание и методы решения задачи параметрического синтеза?
Эксперимент – основной общенаучный эмпирический метод исследования, научно поставленный опыт с точно учитываемыми условиями. Эксперимент обобщает ряд сопряженных понятий: опыт, целенаправленное наблюдение, воспроизведение объекта познания, организация особых условий осуществления, проверка предсказаний. Основная цель эксперимента: выявление свойств исследуемых объектов, проверка справедливости гипотез. Различают эксперименты по отраслям науки (физический, химический, социальный и т.п.), по способу формирования условий (естественный, искусственный), по целям исследования (преобразующий, констатирующий, контролирующий, поисковый, решающий), по месту проведения (лабораторный, натурный, полевой, производственный), по структуре (простой, сложный), по характеру внешних воздействий (вещественный,
энергетический, информационный), по типу моделей (материальный, мысленный), по числу варьируемых факторов (одно- и многофакторный). Методика эксперимента – это совокупность мыслительных и физических операций, размещенных в определенной последовательности, в соответствии с которой достигается цель исследований. Необходимо также обосновать набор средств измерений (приборов), машин, аппаратов. Методы измерений должны базироваться на законах метрологии, изучающей средства и методы измерений.
Получив результаты эксперимента, исследователь должен извлечь из них полезную информацию или, другими словами, провести обработку и анализ экспериментальных данных. Мы рассмотрим несколько широко используемых методов обработки и анализа экспериментальных данных, а именно: графическое представление, аппроксимацию и статистическую обработку.
2.1. Графическое представление экспериментальных данных
Графическое представление экспериментальных данных является наиболее наглядным (например, по сравнению с табличным или аналитическим), позволяет выявить общий характер функциональной зависимости изучаемых физических величин, сравнительно легко установить наличие экстремумов функции, пределов увеличения (уменьшения) функций.
|
z |
y=y1 |
|
y=y2 |
|
|
y=y3 |
|
|
x |
|
|
Рис.2.2 |
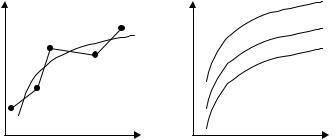
Обычно при графическом представлении применяют прямоугольную систему координат. На плоскости наносят точки, отображающие экспериментальные данные (рис. 2.1). Если попытаться провести линию через все точки (в предельном случае – соединить точки отрезками прямых), то она будет иметь резкие искривления (в предельном случае – это будет ломаная линия). В естественных процессах такие искривления (на математическом языке – быстрые изменения первой производной) встречаются редко. Поскольку в экспериментальных данных всегда присутствуют ошибки измерения, график, проведенный через все экспериментальные точки, фактически отражает воздействие случайных мешающих факторов на результат измерения, а не исследуемое физическое явление. Поэтому при построении графика стараются провести плавную линию, как можно ближе проходящую ко всем экспериментальным точкам (см. раздел 2.2).
Иногда при построении графика выясняется, что некоторые точки резко удалены от кривой. В этих случаях, если нет оснований предполагать наличие скачка функции, резкое отклонение, скорее всего, объясняется грубой ошибкой измерения или промахом. Эксперимент следует повторить в диапазоне резкого отклонения данных.
Графики функций, имеющие сложный немонотонный вид (например, имеющие экстремумы), требуют тщательного вычерчивания в зонах изгибов и перегибов. На этих участках шаг изменения независимой переменой в эксперименте должен быть значительно меньше, чем на плавных участках.
Часто при проведении экспериментальных измерений приходится иметь дело с функцией двух переменных z=f (x,y). В этом случае одну из переменных, например y, при построении используют в качестве параметра. В результате график (рис. 2.2) представляет собой семейство кривых z=f(x) при y=y1 , y=y2 ,
…, y=yn .
Еще одна проблема при построении графика – рациональный выбор масштаба. Для увеличения точности построения необходимо, чтобы график заполнял всю площадь листа. Поэтому следует определить диапазон изменений переменных по координатным осям и соответствующим образом выбрать шкалы осей (не обязательно вести отсчет от нуля!). Масштаб осей, таким образом, получится автоматически.
Приведенные рекомендации могут оказаться недостаточными, если одна или обе переменные имеют большой диапазон изменений, например, несколько порядков. В этом случае применяют полулогарифмический y = f (lgx) или логарифмический
lg y = f (lgx) масштабы. Например, при построении частотной характеристики радиотехнического устройства широко применяется следующая разновидность логарифмического масштаба: по оси абсцисс откладывается частота в декадах lgω, а по оси ординат – амплитуда в децибелах 20 lgA.
2.2. Аппроксимация экспериментальных данных 2.2.1 Задача аппроксимации
Термин аппроксимация (от латинского approximo) означает замену одних математических объектов другими, более простыми и в том или ином смысле близкими к исходным.
Задача аппроксимации может возникнуть, например, при обработке экспериментальных данных, когда в результате некоторых измерений получена связь независимой переменной x и зависимой переменной y в виде таблицы значений (табл. 2.1).
Таблица 2.1
|
x |
x1 |
x2 |
x3 |
… |
xk |
|
y |
y1 |
y2 |
y3 |
… |
yk |
Простейший пример такого эксперимента – измерение напряжения на выходе электрической цепи при различных значениях какого-либо параметра цепи или параметров входного воздействия. В результате процедуры аппроксимации должна быть получена аналитическая связь – функция y=f(x),
которая в дальнейшем может быть использована в расчетах как характеристика электрической цепи в целом.
Задача аппроксимации возникает также и в случае, когда для относительно сложной функции требуется получить более простое выражение, которое легко интегрируется или анализируется тем или иным стандартным методом. Например, разложение функции в ряд Тейлора (2.1) и использование в качестве аппроксимирующей функции только нескольких первых членов этого ряда (2.2) позволяет существенно упростить исходную функцию для дальнейшего анализа (2.3):
|
f (x)= f (x0 )+ |
x − x0 |
f ′(x0 )+ |
(x − x0 )2 |
f ′′(x0 )+ |
(x − x0 )3 |
f ′′′(x0 )+… (2.1) |
|
|
1 2 3 |
|||||||
|
1 |
1 2 |
||||||
|
f (x)≈ f (x0 )+ |
x − x0 |
f ′(x0 ) |
при x − x0 <<1 |
(2.2) |
|||
|
1 |
|||||||
|
(1+ x)n ≈1+nx; ln(1+ x)≈ x; sin x ≈ x; cos x ≈1 при x <<1. |
(2.3) |
Очевидно, что качество аппроксимации может быть оценено двумя показателями: точность аппроксимации и простота аппроксимирующей функции, причем эти показатели противоречивы.
Процедура аппроксимации включает два этапа:
выбор типа аппроксимирующей функции (это может быть многочлен степени n, в частности, при n=1 и n=2 это соответственно прямая и парабола, экспонента, синусоида, гипербола, логарифмическая функция и другие функции); выбор параметров аппроксимирующей функции (коэффициентов
многочлена, показателя экспоненты, амплитуды, частоты и фазы синусоиды и т.д.), обеспечивающих наилучшее приближение аппроксимирующей функции к исходным данным. При этом обязательно должен быть заранее сформулирован критерий оценки качества приближения.
Если исходная экспериментальная или расчетная зависимость задана в виде набора точек (xi, yi), i=1,2,…, k, где k — количество точек, то при аппроксимации возникает естественное желание наиболее полно использовать имеющуюся информацию: то есть подобрать такую функцию, значения которой во всех точках xi совпадают со значениями yi. Эта задача была решена во второй половине XVIII века французским математиком
|
Лагранжем, который предложил так называемый «интерполяционный |
||||||||||||||||||||||||
|
многочлен n-го порядка» в виде суммы (n+1) слагаемых: |
||||||||||||||||||||||||
|
P |
(x)= y |
(x − x2 )(x − x3 ) … (x − xn+1 ) |
+ |
|||||||||||||||||||||
|
) |
||||||||||||||||||||||||
|
n |
1 |
(x |
− x |
2 |
)(x |
− x |
) … (x |
− x |
n+1 |
|||||||||||||||
|
1 |
1 |
3 |
1 |
|||||||||||||||||||||
|
+ y2 |
(x − x1 )(x − x3 ) … (x − xn+1 ) |
+… |
+ |
|||||||||||||||||||||
|
(x |
2 |
− x |
)(x |
2 |
− x |
) … |
(x |
2 |
− x |
n+1 |
) |
|||||||||||||
|
1 |
3 |
|||||||||||||||||||||||
|
+ yn+1 |
(x − x1 )(x − x2 ) … (x − xn ) |
. |
(2.4) |
|||||||||||||||||||||
|
(x |
n+1 |
− x |
)(x |
n+1 |
− x |
) … (x |
n+1 |
− x |
n |
) |
||||||||||||||
|
1 |
2 |
Интерполяционный многочлен (2.4) – частный случай аппроксимирующей функции – позволяет вычислить значение f(x)=Pn(x) для любого x (interpole – между точками), причем в узлах интерполяции – точках (xi, yi) выполняется
условие
Pn(xi ) = yi , i = 1,…,n+1.
Интерполяционный многочлен n-го порядка проходит через k = n +1 исходных точек. Если точек достаточно много, то и многочлен будет иметь высокую степень, то есть аппроксимирующая функция получится сложной. Кроме того, стремление провести аппроксимирующую функцию через исходные точки, особенно при их экспериментальном происхождении, не разумно из-за наличия ошибок измерения. Поэтому следует ограничиться невысокой степенью многочлена n =1,2,3, так, чтобы график аппроксимирующей функции, соответственно прямая, парабола или кубическая парабола, адекватно отражал общий ход экспериментальной зависимости.
При таком подходе количество определяемых параметров аппроксимирующей функции меньше количества точек k, используемых для этого. Поэтому необходимо выбрать специальные критерии качества аппроксимирующей функции. На практике чаще других используются следующие два критерия: критерий равномерного приближения и критерий наименьших квадратов.
2.2.2. Критерий равномерного приближения
Предположим, что тип аппроксимирующей функции выбран, и теперь необходимо определить ее параметры. Критерий равномерного приближения означает минимизацию наибольшего отклонения f(x) в точках x = xi от исходных значений yi
|
max |
f (xi ) − yi |
→ min . |
(2.5) |
||
|
1≤i ≤k |
Для аппроксимирующей функции – степенного многочлена
n
f (x) = a0 + a1x + a2 x2 +… + an xn = ∑a j x j ,
j=0
сформулируем оптимизационную задачу в соответствии с выбранным критерием (2.5) следующим образом
|
n |
||||
|
yi −∑a j xij |
≤ z, i =1,2,…, k; n < k |
(2.6) |
||
|
j=0 |
||||
|
z ≥ 0 → min , |
где переменными являются z и aj.
Если каждое из неравенств в (2.6), содержащее знак абсолютной величины, представить в виде двух обычных неравенств, то задача сводится к варианту задачи линейного программирования и может быть решена с помощью симплекс-метода [1].
Пример 2.1. Для результатов измерений, приведенных в табл.2.2 найти равномерное приближение для аппроксимирующей функции вида f(x)= a0+ a1x.
Таблица 2.2
|
i |
1 |
2 |
3 |
4 |
|||||||||||||||
|
xi |
1 |
2 |
3 |
4 |
|||||||||||||||
|
Запишем |
yi |
2,0 |
1,5 |
2,0 |
3,5 |
||||||||||||||
|
оптимизационную задачу (2.6) для k = 4, n = 1. |
|||||||||||||||||||
|
2 −a0 −a1 |
≤ z , |
1,5 −a0 −2a1 |
≤ z , |
2 −a0 −3a1 |
≤ z , |
3,5 −a0 −4a1 |
≤ z , |
||||||||||||
z ≥ 0 → min
и представим каждое из неравенств, содержащее знак абсолютной величины, в виде двух обычных неравенств
|
a0 +a1 + z −2 ≥ 0 |
−a0 −a1 + z +2 ≥ 0 |
|
|
a0 + 2a1 + z −1,5 ≥ 0 |
−a0 −2a1 + z +1,5 ≥ 0 |
|
|
a0 +3a1 + z −2 ≥ 0 |
−a0 −3a1 + z + 2 ≥ 0 |
(2.7) |
|
a0 +4a1 + z −3,5 ≥ 0 |
−a0 −4a1 + z +3,5 ≥0 |
Для того, чтобы качественно описать решение задачи (2.7) – задачи линейного программирования – воспользуемся пространственным представлением. В трехмерном пространстве неизвестных (a0 , a1 , z) каждое их восьми неравенств определяет полупространство, находящееся над соответствующей плоскостью. Например, для первого неравенства – такую плоскость описывает уравнение z = – a0 – a1 + 2 . Полупространство над этой плоскостью, с учетом условия z ≥ 0, есть область возможных значений неизвестных, удовлетворяющих первому неравенству. Построив все восемь плоскостей, получим некоторую причудливую область пространства в форме многогранника, находящуюся над всеми этими плоскостями. Самая нижняя точка этой области, ближайшая к плоскости z = 0, и будет решением задачи
(2.7).
К сожалению, графическое изображение описанной процедуры на плоском листе бумаги практически невозможно было бы воспринять. Рекомендуем читателю попробовать самостоятельно решить задачу в двумерном представлении по следующему алгоритму, используя неизвестное z в качестве параметра. Запишем восемь исходных неравенств в несколько ином виде
|
a1 ≥ −a0 + 2 − z (1) |
a1 ≤ −a0 + 2 + z |
(2) |
||||||||||||||||||||
|
a ≥ − |
a0 |
+ 3 |
− |
z |
(3) |
a ≤ − |
a0 |
+ 3 |
+ |
z |
(4) |
|||||||||||
|
1 |
2 |
4 |
2 |
1 |
2 |
4 |
2 |
|||||||||||||||
|
a ≥ − |
a0 |
+ 2 |
− |
z |
(5) |
a ≤ − |
a0 |
+ 2 |
+ |
z |
(6) |
|||||||||||
|
1 |
3 |
3 |
3 |
1 |
3 |
3 |
3 |
|||||||||||||||
|
(7) |
a ≤ − |
a0 |
+ 7 + |
z |
(8) |
|||||||||||||||||
|
1 |
4 |
8 |
4 |
|||||||||||||||||||
y4
3
2
1
|
0 |
x |
|||||
|
0 |
1 |
2 |
3 |
4 |
Рис. 2.3
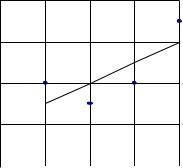
При некотором значении параметра z, например z = 1, каждое из неравенств определяет полуплоскость, находящуюся над или под соответствующей прямой. Построив все восемь прямых, можно определить область плоскости (a0,a1) в форме многоугольника, которая удовлетворяет всем восьми неравенствам. Эта область в нашем примере будет ограничена прямыми 1,4,6 и 7. Если далее уменьшать значение параметра z, то площадь области будет уменьшаться и при z = 0,5 окажется, что область пространства стянется в точку с координатами a0=1, a1=0,5.
Таким образом, искомое равномерное приближение есть f(x)=1 + 0,5x. На рис. 2.3 изображены точки, отражающие исходные данные табл. 2.2, и график аппроксимирующей функции.
2.2.3. Критерий наименьших квадратов
Критерий наименьших квадратов означает минимизацию суммы V квадратов отклонений значений аппроксимирующей функции в точках xi от экспериментальных значений yi
k
V = ∑( yi − f (xi ))2 → min
i=1
или, для аппроксимирующей функции – степенного многочлена,
|
k |
n |
|
V = ∑( yi −∑a j xij )2 → min; n < k , |
|
|
i=1 |
j=0 |
где переменными являются коэффициенты многочлена aj. Требуемый минимум имеет место, при равенстве нулю всех (n+1) частных производных функции V , т.е. при ∂V
Частная производная при j=m имеет вид
|
∂V |
k |
n |
j |
m |
||
|
= 2∑ yi −∑a j xi |
xi . |
|||||
|
∂am |
||||||
|
i=1 |
j=0 |
и, таким образом, реализация выбранного критерия сводится к решению системы (n+1) линейных (это очень важно для последующего решения) уравнений с (n+1) неизвестными aj
|
i=k |
j=n |
|||||
|
m |
−∑a j xi |
j+m |
= 0, m = 0,1,2,…, n. |
(2.8) |
||
|
∑ yi xi |
||||||
|
i=1 |
j=0 |
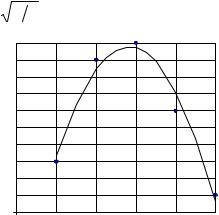
Пример 2.2. Найти аппроксимирующую функцию в виде f(x)=a0+a1x+a2x2, наилучшую по критерию наименьших квадратов, для результатов измерений, приведенных в табл.2.3.
Таблица 2.3
|
i |
1 |
2 |
3 |
4 |
5 |
|||
|
xi |
1 |
2 |
3 |
4 |
5 |
|||
|
yi |
3,0 |
9,0 |
10,0 |
6,0 |
1,0 |
|||
|
Запишем систему (2.10) |
для трех неизвестных a0 , a1 и a2. |
∑i=5 (yi −a0 −a1xi −a2 xi2 )= 0
i=1
∑i=5 (yi xi −a0 xi −a1xi2 −a2 xi3 )= 0
i=1
∑i=5 (yi xi2 −a0 xi2 −a1xi3 −a2 xi4 )= 0 i=1
и преобразуем ее к стандартному виду
|
i=5 |
i=5 |
i=5 |
||||||||||||
|
5a0 |
+ a1 ∑xi + a2 |
∑xi2 = |
∑yi |
|||||||||||
|
i=5 |
i=1 |
i=5 |
i=1 |
i=5 |
i=1 |
i=5 |
||||||||
|
0 |
1 |
∑ i |
2 |
∑ i |
∑ i |
i |
||||||||
|
∑ i |
||||||||||||||
|
a |
x |
+a |
x2 +a |
x3 = |
x y |
|||||||||
|
i=1 |
i=1 |
i=1 |
i=1 |
|||||||||||
|
a0 |
i=5 |
+a1 |
i=5 |
i=5 |
i=5 |
|||||||||
|
∑xi |
∑xi |
+ a2 ∑xi = |
∑xi yi . |
|||||||||||
|
2 |
3 |
4 |
2 |
|||||||||||
|
i=1 |
i=1 |
i=1 |
i=1 |
|||||||||||
|
Подставив значения xi и yi |
из табл.2.3, получим систему |
|||||||||||||
|
5a |
0 |
+15a +55a |
2 |
= 29 |
||||||||||
|
1 |
||||||||||||||
|
15a0 + |
+ 225a2 |
=80 |
||||||||||||
|
55a1 |
||||||||||||||
|
55a0 + |
||||||||||||||
|
225a1 + 979a2 = 250 , |
решение которой a0 ≈ –5,6 , a1 ≈ 10,9, a2 ≈ –1,93.
Таким образом, искомое приближение по методу наименьших квадратов есть f(x)= –5,6 + 10,9 x –1,93 x2. На рис. 2.4 изображены точки, отражающие исходные данные табл. 2.3, и график аппроксимирующей функции. Средний квадрат модуля отклонения аппроксимирующей функции от экспериментальных значений (среднеквадратическая ошибка) составляет
|
σ = |
V k = 0,61. |
||||||
|
y |
10 |
||||||
|
9 |
|||||||
|
8 |
|||||||
|
7 |
|||||||
|
6 |
|||||||
|
5 |
|||||||
|
4 |
|||||||
|
3 |
|||||||
|
2 |
|||||||
|
1 |
x |
||||||
|
0 |
|||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
||
|
Рис. 2.4 |
До сих пор в качестве аппроксимирующей функции рассматривался степенной многочлен, являющийся линейным относительно своих параметров – коэффициентов a0, a1,…, an. Поэтому удавалось решить аналитически линейную систему уравнений относительно этих параметров. Однако, на практике, исходя из имеющихся экспериментальных данных и априорной информации о физических законах, реализующихся в эксперименте, могут быть выбраны и другие аппроксимирующие функции, в которых параметры входят нелинейно.
Например, для результатов измерений, изображенных на рис. 2.5,а и б, целесообразно выбрать соответственно
|
f (x) = |
1 |
, |
a, b > 0 |
(2.9) |
|||
|
a + bx |
b < 0, |
c > 0. |
(2.10) |
||||
|
f (x) = c +aebx |
|||||||
|
y |
y |
• |
|||||
|
• |
|||||||
|
• |
|||||||
|
• |
a<0 |
||||||
|
• |
|||||||
|
• |
|||||||
|
• |
• |
||||||
|
• |
|||||||
|
• |
• |
||||||
|
• |
|||||||
|
• |
|||||||
|
• |
• |
• |
a>0 |
||||
|
• |
• |
||||||
|
0 |
x |
0 |
• |
x |
|||
|
а) |
б) |
||||||
|
Рис. 2.5 |
Подобные экспериментальные данные могут быть получены, соответственно при измерении частотной зависимости коэффициента передачи электронной схемы и при записи переходного теплового или электрического процессов.
Если непосредственно применить критерий наименьших квадратов для выбора параметров предложенных функций, то мы столкнемся с системой нелинейных уравнений, которая, возможно, не будет иметь аналитического решения. В принципе эта ситуация не является тупиковой – можно применить численные методы. Чтобы избежать этого, применяется метод линеаризации.
Суть метода состоит в переходе к новым переменным, которые входили бы в аппроксимирующую функцию линейно. Положив для функции (2.9) Y=1/y, A0 = a, A1 = b, X = x, получим линейную зависимость Y= F(X)= A0 +A1X, эквивалентную исходной. Экспериментальные данные должны быть пересчитаны по приведенным формулам (в данном случае только значения Yi=1/yi), и далее может быть применен критерий наименьших квадратов.
В случае (2.10) аналогичная линеаризация Y=F(X)= A0 + A1X достигается, если положить Y = ln(y-c), A0 = lna, A1 = b, X = x. Чтобы пересчитать экспериментальные данные по этим формулам необходимо предварительно определить значение c. Обычно на практике значение c может быть специально измерено. В противном случае это можно сделать, исходя из рассмотрения экспериментальных данных, нанесенных в виде точек на плоскость xoy, и, в дальнейшем уточнить значение c путем его вариаций.
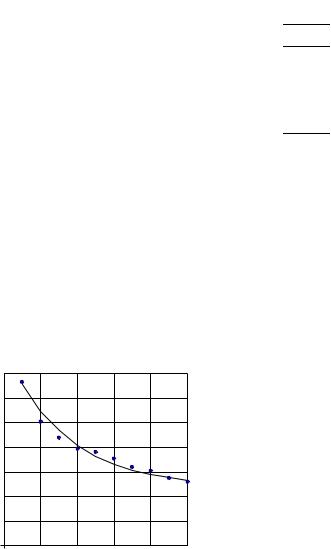
−0,036 x
Пример 2.3. Рассмотрим пример аппроксимации с использованием метода линеаризации и критерия наименьших квадратов для экспериментальных данных, заданных следующей таблицей (первые три строки табл. 2.4):
Таблица 2.4
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
xi |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
yi |
23, |
20, |
18, |
17, |
17, |
17, |
16, |
16, |
15,5 |
15,2 |
|
3 |
1 |
8 |
9 |
6 |
1 |
4 |
1 |
— |
||
|
Y |
2,1 |
1,6 |
1,3 |
1,0 |
0,9 |
0,7 |
0,3 |
0,1 |
— |
|
|
i |
7 |
3 |
4 |
6 |
6 |
4 |
4 |
0 |
0,69 |
1,61 |
Нанесем экспериментальные точки на плоскость xoy (рис.2.6). Ход экспериментальной зависимости определяет тип функции (2.10) –
|
экспонента. |
Выберем |
для |
начала |
значение |
|
c = 15,0. |
Пересчитываем экспериментальные значения по формуле Yi= ln (yi — c) и записываем результаты в табл. 2.4. Теперь для пар значений (xi,Yi), используя критерий наименьших квадратов, можно построить аппроксимирующую функцию в виде F(X)=A0+ A1X= = 2,57 – 0,036 x. Тогда аппроксимирующая функция для исходных данных будет иметь вид f (x) =15,0 +13,0e . Среднеквадратическая ошибка аппроксимации составит σ = 0,58 .
|
y 24 |
|||||
|
22 |
|||||
|
20 |
|||||
|
18 |
|||||
|
16 |
|||||
|
14 |
|||||
|
12 |
|||||
|
10 |
x |
||||
|
0 |
20 |
40 |
60 |
80 |
100 |
Рис. 2.6
Этот результат может быть улучшен путем небольших вариаций параметра c.
|
В частности, при c = |
14,8 получим аппроксимирующую функцию в |
|
виде f (x) =14,8 +11,2e−0,030 x и |
среднеквадратическую ошибку σ = 0,40 . График |
этой функции изображен на рис.2.6. Процесс уточнения параметра c может быть продолжен.
В заключение данного раздела для читателя, уже получившего некоторый опыт решения задач аппроксимации экспериментальных данных, сделаем следующее замечание. Данную задачу можно рассматривать как частный случай огромного класса так называемых обратных задач. В отличие от прямых задач, когда по известным формулам, отражающим физические законы, вычисляются значения физических величин, при решении обратных задач, наоборот, по известным значениям физических величин необходимо
восстановить параметры, входящие в формулы физических законов, а, возможно, и выбрать сами эти формулы.
Например, если задано положение в пространстве и величина электрического заряда одного или нескольких точечных источников электрического поля, мы сможем вычислить по формулам электростатики напряженность электрического поля в любой точке пространства (прямая задача). Обратная задача в этом случае состоит в определении местоположения и величины зарядов точечных источников по известной напряженности электрического поля, измеренной в произвольном числе точек пространства. При решении такой задачи необходимо сначала выбрать модель поля – число источников, а затем определить их параметры: местоположение и заряд. Здесь очевидна аналогия с задачей аппроксимации экспериментальных данных – сначала выбор типа аппроксимирующей функции, затем – определение ее параметров.
Общая теория обратных задач разработана академиком А.Н. Тихоновым [2,3]. При решении обратных задач основными вопросами являются наличие и единственность решения, а также его устойчивость к малым вариациям исходных данных (например, искажениям результатов измерений под действием помех).
По аналогии с обратными задачами и при аппроксимации экспериментальных данных методом наименьших квадратов существует проблема устойчивости. Эта проблема может проявиться при решении системы уравнений типа (2.8). Главный определитель этой системы под действием малых случайных ошибок измерения может оказаться близким к нулю, что приведет к большой среднеквадратической ошибке аппроксимации.
Впоследнее время в связи с бурным развитием вычислительной техники и повышением ее быстродействия стало возможным решение обратных задач методом случайных испытаний (методом Монте-Карло [6], см. раздел 4.1.), когда решение обратной задачи заменяется многократным решением прямой задачи при вариации значений искомых параметров. За решение обратной задачи принимается наилучшая из попыток по выбранному заранее критерию.
Впринципе такой метод может быть использован и при аппроксимации экспериментальных данных при выбранном критерии качества. Определив тип аппроксимирующей функции можно далее испытывать различные случайные наборы значений параметров этой функции с тем, чтобы выбрать из них наилучший.
2.3.Статистическая обработка экспериментальных
данных
При проведении измерений в рамках научных экспериментов исследователь получает некоторый результат, который носит случайный характер. Для характеристики этого факта используется термин «неопределенность результата измерения». Уменьшение неопределенности результата измерения
возможно путем многократного повторения эксперимента и дальнейшего анализа результатов – статистической обработки.
При наличии некоторого большого массива измерений может быть поставлена задача определения закона распределения случайной величины или проверки гипотезы о том или ином законе распределения [4]. При относительно небольшом числе измерений можно поставить задачу определить, хотя бы приближенно, важнейшие числовые характеристики случайной величины. Например, если заранее известно, что случайная величина X имеет нормальное распределение, необходимо определить его параметры: математическое ожидание mx и среднеквадратическое отклонение
σx.
Значение параметра, вычисленное на основе ограниченного числа опытов, всегда будет случайным. Поэтому следует говорить не об определении, а об оценке параметра. Ошибка в оценке в среднем тем больше, чем меньше значение n.
Оценка параметра закона распределения должна отвечать следующим требованиям:
состоятельность – при увеличении числа наблюдений (n → ∞) оценка параметра должна стремиться к его истинному значению; несмещенность – математическое ожидание оценки параметра должно быть равно его истинному значению (отсутствие систематической ошибки); эффективность – дисперсия оценки параметра должна быть минимальной. Различают генеральную и выборочную совокупности измерений. Генеральная совокупность – это множество результатов всех измерений, которые в принципе можно провести. Генеральная совокупность может быть конечной (например, при определении среднего роста студентов университета можно действительно измерить рост всех студентов без исключения) или бесконечной (например, при определении среднего значения шума можно сделать сколь угодно много измерений его мгновенных значений). Выборочная совокупность (выборка из генеральной совокупности) предполагает ограниченное, относительно небольшое число измерений (например, при изучении общественного мнения россиян в опросе обычно участвуют не более 0,01% населения).
|
Приведем формулы для оценок математического ожидания |
~ |
и дисперсии |
|
mx |
||
|
~ |
случайной величины X, полученных по результатам |
измерений xi из |
|
Dx |
выборки объемом n. (Символ «~» означает статистическую оценку, а не истинное значение параметра.)
|
~ |
1 |
n |
; |
~ |
1 |
n |
~ 2 |
. (2.11) |
|
mx = |
∑xi |
Dx = |
∑(xi − mx ) |
|||||
|
n i=1 |
n −1 i=1 |
Эти оценки удовлетворяют требованиям состоятельности и несмещенности, а при нормальном законе распределения случайной величины X – требованию эффективности. Далее мы ограничимся рассмотрением только нормально распределенных случайных величин.

|
Оценки в виде числа |
~ |
~ |
|
mx илиDx называются точечными. В ряде задач |
требуется не только найти подходящее численное значение параметра, но и оценить точность этого значения. Такая задача особенно актуальна при малом объеме выборки, когда точечная оценка параметра в значительной мере случайна.
Чтобы дать представление о точности и надежности оценки используются понятия доверительный интервал и доверительная вероятность.
Доверительный интервал Iβ – интервал значений исследуемого параметра, например среднего значения случайной величины,
|
~ |
~ |
~ |
~ |
(2.12) |
|
Iβ = (mx −tβσm~ |
, mx + tβσm~ ) , |
который с заданной надежностью (доверительной вероятностью β) накроет
|
истинное значение параметра mx. В (2.12) σ~m~ = |
~ |
n – среднеквадратическое |
|
Dx |
отклонение оценки m~x , определенное по результатам выборки (эта формула
справедлива для n > 30), tβ – гарантийный коэффициент, значения которого приведены в табл. 2.5 для различных значений доверительной вероятности. Можно сказать, что ширину доверительного интервала отсчитывают в «сигмах».
Таблица 2.5
|
β |
0,8 |
0,9 |
0,95 |
0,99 |
0,997 |
0,999 |
|
2,576 |
3 |
|||||
|
t |
1,282 |
1,645 |
1,960 |
3,00 |
3,291 |
При небольшом объеме выборки (n <30) для интервальной (вероятностной) оценки параметров используются формулы, аналогичные (2.11) и (2.12). Различие состоит в том, что сумма относительного небольшого числа случайных величин (результатов измерений xi) уже не является нормально распределенной случайной величиной. В результате границы доверительного интервала расширяются по сравнению с (2.12)
|
~ |
~ |
~ |
~ |
|
|
Dx |
Dx |
) . (2.13) |
||
|
Iβ = (mx −tβ |
n |
, mx +tβ |
n |
|
Расширение границ доверительного интервала связано, во-первых, с уменьшением n, и, во-вторых, с увеличением гарантийного коэффициента tβ . Значения tβ приведены в табл. 2.6 (t-распределение Стьюдента для K= n–1 степеней свободы).
Таблица 2.6
|
β K |
0,8 |
0,9 |
0,95 |
0,99 |
0,999 |
|
2 |
1,886 |
2,920 |
4,303 |
9,925 |
31,60 |
|
4 |
1,533 |
2,132 |
2,776 |
4,604 |
8,610 |
|
10 |
1,372 |
1,812 |
2,228 |
3,169 |
4,587 |
|
20 |
1,325 |
1,725 |
2,086 |
2,845 |
3,850 |
|
30 |
1,310 |
1,697 |
2,042 |
2,750 |
3,646 |
|
∞ |
1,282 |
1,645 |
1,960 |
2,576 |
3,291 |

Заметим, что при большом числе измерений (нижняя строка табл. 2.6) значения коэффициента tβ, взятые из t-распределения Стьюдента, совпадают со значениями из табл. 2.5.
В процессе обработки экспериментальных данных следует исключать грубые ошибки или промахи. Однако прежде, чем исключить результат того или иного измерения, необходимо убедиться, что это действительно промах, а не отклонение вследствие статистического разброса.
Простым способом исключения резко выделяющегося измерения является правило «трех сигма»: разброс случайных величин от среднего значения не должен превышать ±3σ~x . Более достоверными являются методы,
использующие доверительный интервал.
Пусть имеется ряд измерений малой выборки, подчиняющийся закону нормального распределения. Критические пороги появления грубых ошибок при n измерениях, среди которых определены наибольшее и наименьшее значения – xmax и xmin, определяются по формулам:
|
~ |
~ |
|||||
|
t1 = (xmax − mx ), |
t2 = (mx − xmin ), |
|||||
|
σ |
n −1 |
σ |
n −1 |
|||
|
n |
||||||
|
n |
||||||
В табл. 2.7 приведены в зависимости от доверительной вероятности β максимальные значения tmax, возникающие вследствие статистического разброса. Если t1 > tmax, то значение xmax необходимо исключить из ряда измерений как промах. При t2 > tmax исключается измерение xmin. После
исключения грубых ошибок определяются новые значения m~ и ~ . из
x Dx
оставшихся результатов измерений. Таблица 2.7
|
n |
tmax |
при β |
||
|
0,90 |
0,95 |
0,99 |
||
|
3 |
1,41 |
1,41 |
1,41 |
|
|
5 |
1,79 |
1,87 |
1,96 |
|
|
10 |
2,15 |
2,29 |
2,54 |
|
|
20 |
2,45 |
2,62 |
2,96 |
|
|
30 |
2,61 |
2,79 |
3,16 |
В ходе исследований часто возникает вопрос о достоверности опытных результатов. Предположим, например, что некоторое устройство обработки радиосигнала подверглось модернизации с целью увеличения отношения q сигнал/помеха на его выходе. Для сравнения качества старого и нового устройств были проведены многократные измерения величины q, по результатам которых были вычислены оценки математического ожидания и среднеквадратического отклонения q~1 = 5, σ~1 = 0,2 и q~2 = 6 , σ~2 = 0,2 . Возникает вопрос, действительно ли величина q увеличилась на 20%, или это увеличение можно объяснить разбросом опытных данных.
Проведем проверку достоверности экспериментальных данных по критерию «трех сигма». В данном случае на достоверность проверяется разность q~ = q~2 − q~1 =1. Как известно, дисперсия алгебраической суммы двух случайных
На самом деле обработка экспериментальных данных проходит несколько более сложно, но суть остаётся.
Один из обязательных компонентов профессиональной подготовки начинающего исследователя – освоение методов статистического анализа экспериментальных данных.
Доклад опирается на многочисленные экспериментальные данные, полученные сотрудниками обоих авторов, в частности, на многие харьковские исследования.
Иногда на основе новых экспериментальных данных мы находим границы применимости той или иной теории и мы снова и снова начинаем сомневаться в том, к чему привыкли.
На основе экспериментальных данных можно с уверенностью утверждать, что младенцы предпочитают именно музыкальную форму коммуникации.
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: отдушка — это что-то нейтральное, положительное или отрицательное?
Имеющиеся экспериментальные данные в той или иной мере подтверждают все основные теории агрессии.
Получены экспериментальные данные о том, что стратегии поведения человека различаются в зависимости от того, мешают ли его деятельности преднамеренно или же трудности возникли по объективным причинам.
Крайне самонадеянно думать, что в вопросах, где объём экспериментальных данных сильно уступает попыткам их осмысления, люди тысячелетиями ошибались и прозрели лишь в течение последнего полувека.
Это объяснение было тщательно проверено путём сопоставления экспериментальных данных, полученных в других специально проведённых для этого исследованиях.
Экспериментальные данные всегда оставляют возможность для модификации любого утверждения или даже теории в целом.
И я обещаю ей, что всё, о чём я расскажу в этой книге, будет убедительно доказано строгими экспериментальными данными.
И наконец, теоретическое обобщение, сведение воедино всех экспериментальных данных оказалось последней точкой приложения теоретического анализа к нашему исследованию.
Модель согласуется с известными экспериментальными данными, а также позволяет предсказать и проверить целый ряд неочевидных феноменов.
На втором этапе, в 1960–1970-е годы, под влиянием противоречивых экспериментальных данных начинает доминировать скептицизм в отношении универсальных закономерностей воздействия.
Получить прямые экспериментальные данные в этой области практически невозможно.
Рассмотрим некоторые важнейшие экспериментальные данные об устойчивости индивидуальных различий.
Полученные экспериментальные данные свидетельствуют о том, что начиная с самого раннего возраста у младенцев существует механизм, позволяющий им реагировать на ситуации с учётом сохранения объекта, даже когда он скрыт (когда, например, коробка преграждает путь машине, а прямоугольный экран скрывает мышку).
Мы имеем теорию, полную и вполне определённую теорию всех этих адронов, и у нас есть огромное количество экспериментальных данных с кучей подробностей – почему же мы не можем немедленно проверить теорию, обнаружить, правильна она или нет?
Многочисленные экспериментальные данные свидетельствуют о том, что страх перед наказанием или возмездием резко снижает возможность прямого проявления агрессивности в поведении – иными словами, ожидание негативных последствий агрессии является одним из наиболее значимых регуляторов торможения агрессии.
Экспериментальные данные позволяют утверждать, что существуют корреляционные плеяды способностей, обеспечивающие эффективность выполнения отдельных действий в структуре деятельности, определяющие производительность, качество и надёжность.
Более того, растущий объём теоретических и экспериментальных исследований показывал, что выводы, сделанные на основании статистического анализа больших наборов частиц – описаний того, как они летают по ёмкостям, наталкиваясь на стенки и оказывая таким образом давление на ту или иную поверхность, или приобретают такую-то плотность, или остывают до определённой температуры, – соответствовали экспериментальным данным с такой точностью, что не оставалось никакой возможности усомниться в объяснительной силе этого подхода.
Между тем, в последние десятилетия получен большой массив экспериментальных данных, убедительно показывающих динамизм отношений объект-образ и теснейшую взаимосвязь восприятия с другими психическими процессами, состояниями и свойствами личности.
Большая часть современных экспериментальных данных, характеризующих перцептивный процесс, получена на материале восприятия сверхкоротких экспозиций элементов среды и опирается на представления о сенсорных системах (Eysenck, Keane, 1995; Levitin, 2002; Palmer, 2002; Pylyshyn, 2003).
Сказанное подтверждают экспериментальные данные.
Заметим попутно: имеется множество экспериментальных данных, из которых следует, что научение посредством наблюдения оказывает на личность даже большее влияние, чем непосредственный деятельный опыт.
Неполная индукция предполагает, что вынесенные за скобки эксперимента аналогичные объекты обладают теми же свойствами, что и изученные, и это позволяет использовать экспериментальные данные для теоретического обоснования.
Однако после настоящего бума исследований мотивации, и прежде всего – мотивации достижения, в западноевропейской психологии под влиянием ряда экспериментальных данных начинает формироваться критическое осмысление постулата о том, что мотивационные процессы, основанные на оценке ожидания успеха и привлекательности цели, прямо определяют поведение.
Отмеченное следует относить к «совокупному» или «статистическому» 3, отразившему едва ли не первое в истории обобщение экспериментальных данных.
Проблема исследования заключается в ряде существенных противоречий, а именно: между инновационными процессами в экономической, производственной, социальной сферах и существующими традиционными установками образовательных стратегий; между социальной необходимостью в обновлении педагогических кадров и отсутствием экспериментальных данных о резервных возможностях личности учителя к эволюционированию в русле реформирования образования; между необходимостью развития ресурсных возможностей учителя и недостаточной разработанностью теоретико-методологических оснований для выделения личностных детерминант, предопределяющих преобразовательный эффект профессионального развития учителя; между необходимостью формирования у современного учителя готовности к риску в ситуациях неопределённости и недостаточной проработанностью психологических условий и средств развития личностных характеристик, позволяющих учителю прогнозировать и реализовывать развивающие возможности рисконесущих факторов; между задачами совершенствования образовательного процесса, стимулирующего прогрессивное поступательное личностно-профессиональное становление учителя, и отсутствием инновационных психологических технологий профессионального развития педагогов.
Существуют экспериментальные данные, свидетельствующие о том, что человеческое лицо столь же эмоционально значимо для такого ребёнка, как и для любого другого, но вот глазной контакт он выдерживает гораздо менее длительно, чем все остальные.
Таким образом, действие каждого фактора предсказывает определённую «элементарную последовательность» событий и задача факторного анализа состоит в том, чтобы представить исторический процесс в виде суммы, суперпозиции «элементарных последовательностей», подобно тому, как в регрессионном анализе пытаются приблизить последовательность наблюдаемых экспериментальных данных суммой последовательностей-факторов, а затем оценить «остаточную дисперсию» – долю тех событий, которые нельзя объяснить этим методом.
Таким образом, предсказатель имел бы те же основные достоинства и недостатки, что и любой другой источник экспериментальных данных, и был бы полезен только в тех случаях, когда обращение к нему оказывалось бы удобнее, чем к другим источникам.
В 1644 г. он писал коллеге: «Мы живём на самом дне океана, состоящего из воздуха, который, согласно неоспоримым экспериментальным данным, имеет вес».
Именно с началом использования математических методов физика стала быстро развиваться, ведь без этого точные экспериментальные данные до некоторой степени были не востребованы (разумеется, верно и обратное: приход математики отчасти стимулирован появлением точных измерений наблюдаемых параметров).
Экспериментальные данные особенно важны, потому что они могут дать информацию о контрфактуальности (DD-тип 6: данные, которые могли бы существовать), упомянутой в главе 1.
Как известно и доказано различными экспериментальными данными, мысли материализуются, поэтому этот способ является очень действенным.
Мы отделим научно-фантастический элемент популярных «графиков похудения» от собственно научного, спросим себя, можно ли иметь здоровый метаболизм и не быть худым, а также изучим свежие экспериментальные данные, подтверждающие благотворный эффект таких традиционных режимов питания, как, например, средиземноморская диета.
Устремления исследователя к накоплению экспериментальных данных, необходимых для решения в конечном итоге проблем устранения неблагоприятных проявлений стресса, могут потребовать создания таких проявлений у испытуемого.
Перечисленные науки подошли к рубежу, когда мало экспериментальных данных и физики предлагают теории, основанные на воображении и фантазии.
Научные теории отбираются и провераются по принципу соответствия экспериментальным данным, что определяет их количественный характер.
Интерпретация экспериментальных данных с целью создания теории.
На этапе обобщения и синтеза экспериментальных данных начинается воссоздание целостного представления об исследуемом объекте, но уже с точки зрения сущностных отношений и на этой основе экспериментально преобразованного.
У нас есть метод, которым можно уверенно пользоваться в заданных условиях, и этот метод даёт умопомрачительно точные прогнозы, триумфально подтверждённые экспериментальными данными.
Между тем шимпанзе чувствует и думает, а возможно – согласно новейшим экспериментальным данным – способен даже освоить некую форму человеческого языка.
Возникла необходимость в теоретическом обобщении накопленных экспериментальных данных, в разработке теории рабочего цикла и отдельных процессов.
Эта материально-специфическая гипотеза редко прямо формулируется, но часто упоминается мимоходом при обсуждении экспериментальных данных.
Нам уже были известны экспериментальные данные о резонансном захвате нейтронов промежуточных энергий.
С получением новых экспериментальных данных взгляд на мир может значительно измениться.
Статьи
Главная страница

видно, что существует вероятность, пусть и очень маленькая, что наше единичное
измерение покажет результат, сколь угодно далеко отстоящий от истинного
значения. Выходом из положения является проведение серии измерений. Если на
разброс данных действительно влияет случай, то в результате нескольких
измерений мы скорее всего получим следующее (рис 2):
Будет ли
рассчитанное среднее значение нескольких измерений совпадать с истинным? Как
правило – нет. Но по теории вероятности, чем больше сделано измерений, тем
ближе найденное среднее значение к истинному. На языке математики это можно
записать так:
Но с бесконечностью у всех дело обстоит неважно. Поэтому на практике мы имеем дело
не со всеми возможными результатами измерений, а с некоторой выборкой из этого
бесконечного множества. Сколько же реально следует делать измерений? Наверное,
до тех пор, пока полученное среднее значение не будет отличаться от истинного
меньше чем точность отдельного измерения.
Следовательно,
когда наше среднее значение (рис. 2) отличается от истинного меньше чем
погрешность измерений, дальнейшее увеличение числа опытов бессмысленно. Однако
на практике мы не знаем истинного значения! Значит, получив среднее по
результатам серии опытов, мы должны определить, какова вероятность того, что
истинное значение находится внутри заданного интервала ошибки. Или каков тот
доверительный интервал, в который с заданной надежностью попадет истинное
значение (рис 3).
Рассмотрим
некоторый условный эксперимент, где в серии измерений получены некоторые
значения величины Х (см. табл. 1). Рассчитаем среднее значение и, чтобы оценить
разброс данных найдем величины DХ = Х –
Хср
|
Таблица |
||||||
|
№ |
Х |
Х ср |
DХ |
DХ2 |
s2 |
s |
|
1 |
130 |
143,5 » 144 |
-13,5 |
182,3 |
420 |
20,5 |
|
2 |
162 |
18,5 |
342,3 |
|||
|
3 |
160 |
16,5 |
272,3 |
s2ср |
sср |
|
|
4 |
122 |
-21,5 |
462,3 |
105 |
10,2 |
Ясно, что
величины DХ как-то характеризуют
разброс данных. На практике для усредненной характеристики разброса серии измерений используется
дисперсия выборки:
и среднеквадратичное или стандартное отклонение выборки:
Последнее
показывает, что каждое измерение в данной серии (в данной выборке) отличается
от другого в среднем на ± s.
Понятно, что каждое отдельное
значение оказывает влияние на средний результат. Но это влияние тем меньше, чем
больше измерений в нашей выборке. Поэтому дисперсия и стандартное отклонение
среднего значения, будет определяться по формулам:
Можем ли мы теперь определить вероятность того, что
истинное значение попадет в указанный интервал среднего? Или наоборот,
рассчитать тот доверительный интервал в который истинное значение
попадет с заданной вероятностью (95%)? Поскольку кривая на наших графиках это
распределение вероятностей, то площадь под кривой, попадающая в указанный
интервал и будет равна этой вероятности (доля площади, в процентах). А площади
математики научились рассчитывать хорошо, знать бы только уравнение этой
кривой.
И здесь мы сталкиваемся еще с одной сложностью. Кривая, которая описывает распределение
вероятности для выборки, для ограниченного числа измерений, уже не будет кривой нормального
распределения. Ее форма будет зависеть
не только от дисперсии (разброса данных) но и от степени свободы для выборки
(от числа независимых измерений) (рис 4):
Уравнения этих кривых впервые были предложены в 1908
году английским математиком и химиком Госсетом, который опубликовал их под
псевдонимом Student (студент), откуда пошло хорошо известные термины
«коэффициент Стьюдента» и аналогичные. Коэффициенты Стьюдента получены на
основе обсчета этих кривых для разных степеней свободы (f = n-1) и уровней
надежности (Р) и сведены в специальные таблицы. Для получения доверительного интервала необходимо
умножить уже найденное стандартное отклонение среднего на соответствующий
коэффициент Стьюдента. ДИ = sср*tf, P
Проанализируем, как меняется доверительный интервал
при изменении требований к надежности результата и числа измерений в серии.
Данные в таблице 2 показывают, что чем больше требование к надежности, тем
больше будет коэффициент Стьюдента и, следовательно, доверительный интервал. В большинстве случаев, приемлемым считают значение Р=95%
|
Таблица |
||||
|
P |
0,9 |
0,95 |
0,99 |
0,999 |
|
t5, |
2,02 |
2,57 |
4,03 |
6,87 |
|
Таблица |
|||||||
|
f= |
1 |
2 |
3 |
4 |
5 |
16 |
30 |
|
tf, |
12,7 |
4,3 |
3,18 |
2,78 |
2,57 |
2,23 |
2,04 |
Из таблицы 3 и графика
видно, что чем больше число измерений, тем меньше коэффициент и доверительный
интервал для данного уровня надежности. Особенно значительное падение
происходит при переходе от степени свободы 1 (два измерения) к 2 (три
измерения). Отсюда следует, что имеет смысл ставить не менее трех параллельных
опытов, проводить не менее трех измерений.
Окончательно
для измеряемой величины Х получаем значение Хсред±sср*tf,P. В
нашем случае получаем: f=3; t=3,18;
ДИ = 3,18*10,2 = 32,6; X = 143,5 ±32,6
Как правило,
значение доверительного интервала округляется до одной значащей цифры, а
значение измеряемой величины – в соответствии с округлением доверительного
интервала. Поэтому для нашей серии окончательно имеем: X = 140 ±30
Найденная
нами погрешность является абсолютной погрешностью и ничего не говорит еще о
точности измерений. Она свидетельствует о точности измерений только в сравнении
с измеряемой величиной. Отсюда представление об относительной ошибке:
Косвенные определения.
Исследуемая величина рассчитывается в этом случае с помощью
математических формул по другим величинам, которые были измерены
непосредственно. В этом случае для расчета ошибок можно использовать
соотношения, приведенные в таблице 4.
|
Таблица |
||
|
Формула |
Абсолютная |
Относительная |
|
x = a ± b |
Dx = Da+Db |
e = |
|
x = a* b; x = a* k |
Dx = bDa+aDb; Dx = kDa |
e = Da/a+Db/b = ea + e b |
|
x = a / b |
Dx = (bDa+aDb) / b2 |
e = Da/a+Db/b = ea + e b |
|
x = a*k; (x = a / k) |
Dx = Da*k; (Dx = Da/k ) |
e = ea |
|
x = a2 |
Dx = 2aDa |
e = 2Da/a = 2ea |
|
x = Öa |
Dx = Da/(2Öa) |
e = Da/2a = ea/2 |
Из таблицы видно, что относительная ошибка и точность определения не изменяются при умножении (делении) на некоторый постоянный коэффициент. Особенно сильно относительная ошибка может возрасти при вычитании
близких величин, так как при этом абсолютные ошибки суммируются, а значение Х
может уменьшиться на порядки.
Пусть например, нам необходимо определить
объем проволочки.
Если диаметр проволочки измерен с погрешностью 0,01 мм (микрометром) и равен 4 мм, то относительная погрешность составит 0,25% (приборная). Если
длину проволочки (200 мм) мы измерим линейкой с погрешностью 0,5 мм, то относительная погрешность также составит 0,25%. Объем можно рассчитать по формуле: V=(pd2/4)*L. Посмотрим, как будут меняться ошибки
по мере проведения расчетов (табл. 5):
|
Таблица 5. Расчет абсолютных и относительных ошибок. |
|||
|
Величина |
Значение |
Абсолютная |
Относительная |
|
d2 |
16 |
Dx = 2*4*0,01=0,08 |
e = 0,5% |
|
pd2 *) |
50,27 |
Dx = 0,08*3,14+0,0016*16 |
e = 0,55% |
|
pd2/4 |
12,57 |
Dx = 0,28/4 = 0,07 |
e = 0,55% |
|
(pd2/4)*L |
2513 |
Dx = 12,57*0,5+200*0,07=20 |
e = 0,8% |
|
*) Если мы возьмем привычное p=3,14, то Dp=0,0016 |
Окончательный
результат V=2510±20 (мм3) e
=0,8%. Чтобы повысить точность косвенного определения, нужно в первую очередь
повышать точность измерения той величины, которая вносит больший вклад в ошибку
(в данном случае – точность измерения диаметра проволочки).
План проведения измерений:
[1]
1. Знакомство
с методикой, подготовка прибора, оценка приборной погрешности d. Оценка возможных причин
систематических ошибок, их исключение.
2.
Проведение серии измерений. Если получены совпадающие результаты, можно
считать что случайная ошибка равна 0, DХ
= d. Переходим к пункту 7.
3.
Исключение промахов – результатов значительно отличающихся по своей
величине от остальных.
4.
Расчет
среднего значения Хср, и стандартного отклонение среднего
значения scp
5.
Задание значения уровня надежности P,
определение коэффициента Стьюдента t и
нахождение доверительного интервала ДИ= t*scp
6.
Сравнение случайной и приборной погрешности, при этом возможны варианты:
—
ДИ << d, можно
считать, что DХ = d, повысить точность измерения
можно, применив более точный прибор
—
ДИ >> d, можно
считать, что DХ = ДИ,
повысить точность можно, уменьшая случайную ошибку, повышая число измерений в
серии, снижая требования к надежности.
—
ДИ » d, в этом
случае расчитываем ошибку по формуле DХ
=
7.
Записывается окончательный результат Х = Хср ± DХ.
Оценивается относительная ошибка
измерения e = DХ/Хср
Если
проводится несколько однотипных измерений (один прибор, исследователь, порядок
измеряемой величины, условия) то подобную работу можно проводить один раз. В
дальнейшем можно считать DХ
постоянной и ограничиться минимальным числом измерений (два-три измерения
должны отличаться не более, чем на DХ)
Для косвенных
измерений необходимо провести обработку данных измерения каждой величины. При
этом желательно использовать приборы, имеющие близкие относительные погрешности
и задавать одинаковую надежность для расчета доверительного интервала. На
основании полученных значений Da, Db, определяется DХ
для результирующей величины (см табл. 4). Для повышения точности надо
совершенствовать измерение той величины, вклад ошибки которой в DХ наиболее существенен.
Изучение зависимостей.
Частым вариантом экспериментальной работы является
измерение различных величин с целью установления зависимостей. Характер этих
зависимостей может быть различен: линейный, квадратичный, экспоненциальный,
логарифмический, гиперболический. Для выявления зависимостей широко
используется построение графиков.
При построении графиков вручную важно правильно
выбрать оси, величины, масштаб, шкалы. Следует предупредить школьников, что
шкалы должны иметь равномерный характер, нежелательна как слишком детальная,
так и слишком грубая их разметка. Точки должны заполнять всю площадь графика,
их расположение в одном углу, или «прижатыми» к одной из осей, говорит о
неправильно выбранном масштабе и затрудняет определение характера зависимости.
При проведении линии по точкам надо использовать теоретические представление о
характере зависимости: является она непрерывной или прерывистой, возможно ли ее
прохождение через начало координат, отрицательные значения, максимумы и
минимумы.
Наиболее легко проводится и анализируется прямая
линия. Поэтому часто при изучении более сложных зависимостей часто используется
линеаризация зависимостей, которая достигается подходящей заменой переменных.
Например:
Зависимость . Вводя новую переменную
, получаем уравнение
a = bx, которое
будет изображаться на графике прямой линией. Наклон этой прямой позволяет
рассчитать константу диссоциации.
Разумеется и в этом случае полученные в эксперименте данные включают в себя различные ошибки, и точки редко лежат строго на прямой. Возникает
вопрос, как с наибольшей точностью провести прямую по экспериментальным точкам, каковы ошибки в определении
параметров.
Математическая статистика показывает, что наилучшим
приближением будет такая линия, для которой дисперсия (разброс) точек
относительно ее будет минимальным. А дисперсия определяется как средний квадрат
отклонений наблюдаемого положения точки от расчитанного:
Отсюда название этого метода – метод наименьших
квадратов. Задавая условие, чтобы величина s2
принимала минимальное значение, получают формулы для коэффициентов а и b в уравнении прямой у = а + bx:

и формулы для расчета соответствующих ошибок
[2].
Если
делать расчеты, используя калькулятор, то лучше оформлять их в виде таблицы:
|
x |
x2 |
y |
y2 |
xy |
|
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
|
Sx = |
Sx2 |
Sy = |
Sy2 |
Sxy = |
Подводя
итог, следует сказать, что обработка данных эксперимента достаточно сложный
этап работы ученого. Необходимость проведения большого числа измерений требует
большой затраты времени и материальных ресурсов. Громоздкость формул, необходимость
использования большого числа значащих цифр затрудняют вычисления. Поэтому, возможно,
не все рекомендации этой статьи применимы в рамках школьного исследования. Но
понимать их сущность, значимость, необходимость, и в соответствии с этим
адекватно оценивать свои результаты, должен любой исследователь.
В настоящее время обработку экспериментальных данных
существенно облегчают современные компьютерные технологии, современное
программное обеспечение. Об том, как их можно использовать – в следующей
статье.
Литература:
[1]
Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений, М., «Наука»,
1970, 194 с.
[2]
Петерс Д., Хайес Дж., Хифтье Г. Химическое разделение и измерение – М.,: Химия,
1978, 816 с.
Проведение
эксперимента
Познакомимся с
вычислением ошибки опыта, или, как ее часто называют, ошибки воспроизводимости.
Ошибки параллельных
опытов
Каждый
эксперимент содержит элемент неопределенности вследствие ограниченности
экспериментального материала. Постановка повторных (или параллельных) опытов
не дает полностью совпадающих результатов, потому что всегда существует ошибка
опыта (ошибка воспроизводимости). Эту ошибку и нужно оценить по параллельным
опытам. Для этого опыт воспроизводится по возможности в одинаковых условиях
несколько раз и затем берется среднее арифметическое всех результатов. Среднее
арифметическое равно сумме всех п отдельных результатов, деленной на количество
параллельных опытов п
.
Отклонение
результата любого опыта от среднего арифметического можно представить как
разность где
– результат отдельного опыта. Наличие
отклонения свидетельствует об изменчивости, вариации значений повторных
опытов. Для измерения этой изменчивости чаще всего используют дисперсию.
Дисперсией называется среднее значение квадрата отклонений величины от ее
среднего значения. Дисперсия обозначается s2 и
выражается формулой
.
где (n – 1) – число
степеней свободы, равное количеству опытов минус единица. Одна степень свободы
использована для вычисления среднего.
Корень квадратный из
дисперсии, взятый с положительным знаком, называется средним квадратическим отклонением,
стандартом или квадратичной ошибкой
Стандарт имеет
размерность той величины, для которой он вычислен. Дисперсия и стандарт – это
меры рассеяния, изменчивости. Чем больше дисперсия и стандарт, тем больше
рассеяны значения параллельных опытов около среднего значения.
Ошибка опыта являемся
суммарной величиной, результатом многих ошибок: ошибок измерений факторов,
ошибок измерений параметра оптимизации и др. Каждую из этих ошибок можно, в свою
очередь, разделить на составляющие.
Вопрос о классификации ошибок
довольно сложный и вызывает много дискуссий. В качестве примера одной из
возможных схем классификации мы приведем схему из книги Ю. В. Кельница «Теория
ошибок измерений» (М., изд-во «Недра», 1967).
Все ошибки принято разделять
на два класса: систематические и случайные.
Систематические ошибки
порождаются причинами, действующими регулярно, в определенном направлении. Чаще
всего эти ошибки можно изучить и определить количественно.
Систематические ошибки
находят, калибруя измерительные приборы и сопоставляя опытные данные с изменяющимися
внешними условиями (например, при градуировке термопары по реперным точкам,
при сравнении с эталонным прибором).
Если систематические ошибки
вызываются внешними условиями (переменной температуры, сырья и т. д.), следует
компенсировать их влияние. Как это делать, будет показано ниже.
Случайными ошибками называются
те, которые появляются нерегулярно, причины возникновения которых неизвестны и
которые невозможно учесть заранее.
Систематические и случайные
ошибки состоят из множества элементарных ошибок. Для того, чтобы исключать инструментальные
ошибки, следует проверять приборы перед опытом, иногда в течение опыта и обязательно
после опыта. Ошибки при проведении самого опыта возникают вследствие неравномерного
нагрева реакционной среды, разного способа перемешивания и т.п. При повторении
опытов такие ошибки могут вызвать большой разброс экспериментальных
результатов.
Очень важно исключить из экспериментальных
данных грубые ошибки, так называемый брак при повторных опытах. Для отброса ошибочных
опытов существуют правила. Для определения брака используют, например, критерий
Стьюдента
.
Значение t берут из таблицы t-распределения Стьюдента. Опыт считается
бракованным, если экспериментальное значение критерия t по модулю больше табличного значения.
Дисперсия параметра
оптимизации
Дисперсия всего эксперимента
получается в результате усреднения дисперсий всех опытов. По терминологии,
принятой в планировании эксперимента, речь идет о подсчете дисперсии параметра
оптимизации или, что то же самое, дисперсии воспроизводимости эксперимента
При подсчете дисперсии
параметра оптимизации квадрат разности между значением yq в каждом опыте и средним значением из n повторных наблюдений y нужно просуммировать по числу опытов в
матрице N, а затем разделить на N(n — 1):
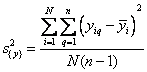
Где i = 1, 2, …, N; q = 1, 2, …, n.
Такой формулой можно
пользоваться в случаях, когда число повторных опытов одинаково во всей матрице.
Дисперсию воспроизводимости
проще всего рассчитывать, когда соблюдается равенство числа повторных опытов
во всех экспериментальных точках. На практике весьма часто приходится
сталкиваться со случаями, когда число повторных опытов различно. Это происходит
вследствие отброса грубых наблюдений, неуверенности экспериментатора в
правильности некоторых результатов (в таких случаях возникает желание еще и еще
раз повторить опыт) и т.п.
Тогда при усреднении
дисперсий приходится пользоваться средним взвешенным значением дисперсий,
взятым с учетом числа степеней свободы
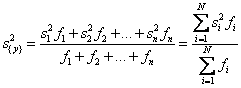
где
– дисперсия i-го опыта;
– число степеней свободы i-м опыте, равное числу параллельных опытов
ni минус 1.
Число степеней
свободы средней дисперсии принимается равным сумме чисел степеней свободы
дисперсий, из которых она вычислена.
Случай с неравным числом
наблюдений, который мы рассмотрели выше, связан с нарушением ортогональности
матрицы. Поэтому здесь нельзя использовать расчетные формулы для коэффициентов,
приведенные ранее. Этот вопрос будет рассмотрен ниже.
Экспериментатору не следует
забывать о проверке однородности дисперсий, неоднородные дисперсии усреднять
нельзя. Прежде чем пользоваться приведёнными выше формулами, нужно убедиться в
однородности суммируемых дисперсий.
Проверка
однородности дисперсий
Проверка однородности
дисперсий производится с помощью различных статистических критериев. Простейшим
из них является критерий Фишера, предназначенный для сравнения двух дисперсий.
Критерий Фишера (F—критерий)
представляет собою отношение большей дисперсии к меньшей. Полученная величина
сравнивается с табличной величиной F-критерия.
Если полученное значение
дисперсионного отношения больше приведенного в таблице для соответствующих
степеней свободы и выбранного уровня значимости, это означает, что дисперсии
значимо отличаются друг от друга, т. е. что они неоднородны.
Если сравниваемое количество
дисперсий больше двух и одна дисперсия значительно превышает остальные, можно воспользоваться
критерием Кохрена. Этот критерий пригоден для случаев, когда во всех точках
имеется одинаковое число повторных опытов. При этом подсчитывается дисперсия в
каждой горизонтальной строке матрицы
,
а затем из
всех дисперсий находится наибольшая которая делится на сумму всех дисперсий. Критерий Кохрена – это
отношение максимальной дисперсии к сумме всех дисперсий
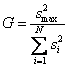
Гипотеза
об однородности дисперсий подтверждается, если экспериментальное значение
критерия Кохрена не превышает табличного значения. Тогда можно усреднять дисперсии
и пользоваться формулой
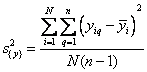
Если возникает предположение
о наличии неоднородности дисперсий для случая, когда число повторных опытов неодинаково
во всех точках, можно воспользоваться критерием Бартлета. По уже знакомой
формуле подсчитывается дисперсия воспроизводимости

Далее
находится величина
,
где
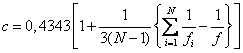
Здесь число
степеней свободы равно N–1, где N – число сравниваемых дисперсий. При планировании эксперимента типа
2k это число равно числу опытов в матрице.
Бартлет показал, что величина
приближенно подчиняется
– распределению с (N–1) степенями свободы. Значимость критерия
Бартлета проверяется обычным способом.
Критерий Бартлета базируется
на нормальном распределении. Если имеются отклонения от нормального распределения,
то проверка неоднородности дисперсий может привести к ошибочным результатам.
Можно предложить
использование F-критерия даже в тех случаях, когда число
дисперсий больше двух. Делается это следующим образом. Из всех дисперсий
выделяются наибольшая и наименьшая. По F-критерию производится проверка, значимо ли они различаются между
собой. Ясно, что если наибольшая и наименьшая дисперсии не отличаются значимо,
то дисперсии, имеющие промежуточные значения, также не могут значимо
отличаться друг от друга. Тогда всю группу дисперсий можно считать
принадлежащей к единой совокупности. В таких случаях нет надобности применять
критерий Бартлета.
Рандомизация
Чтобы исключить влияние
систематических ошибок, вызванных внешними условиями (переменой температуры,
сырья, лаборанта и т. д.), рекомендуется случайная последовательность при
постановке опытов, запланированных матрицей. Опыты необходимо рандомизировать
во времени. Термин «рандомизация» происходит от английского слова random – случайный.
Если экспериментатор
располагает сведениями о предстоящих изменениях внешней среды, сырья,
аппаратуры и т. п., то целесообразно планировать эксперимент таким образом,
чтобы эффект влияния внешних условий был смешан с определенным
взаимодействием, которое не жалко потерять. Так, при наличии двух партий сырья
матрицу 23 можно разбить на два блока таким образом, чтобы эффект
сырья сказался на величине трехфакторного взаимодействия. Тогда все линейные
коэффициенты и парные взаимодействия будут освобождены от влияния
неоднородности сырья.
|
№ блока |
x0 |
x1 |
x2 |
x3 |
x1x2 |
x1x3 |
x2x3 |
x1x2x3 |
y |
|
1 |
+ |
– |
– |
+ |
+ |
– |
– |
+ |
|
|
+ |
+ |
– |
– |
– |
– |
+ |
+ |
|
|
|
+ |
– |
+ |
– |
– |
+ |
– |
+ |
|
|
|
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
|
|
2 |
+ |
– |
– |
– |
+ |
+ |
+ |
– |
y5 |
|
+ |
+ |
– |
+ |
– |
+ |
– |
– |
y6 |
|
|
+ |
– |
+ |
+ |
– |
– |
+ |
– |
y7 |
|
|
+ |
+ |
+ |
– |
+ |
– |
– |
– |
y8 |
В этой матрице при
составлении блока 1 отобраны все строки, для которых , а при составления блока 2 – все строки,
для которых . Различие в сырье можно рассматривать как
новый фактор . Тогда матрица 23, разбитая на
два блока, представляет собой полуреплику 24-1 с определяющим
контрастом .
,
;
,
;
,
;
,
;
,
;
,
;
,
;
,
;
Эффект сырья
отразился на подсчете свободного члена b0 и
эффекта взаимодействия второго порядка b123.
Аналогично можно разбить на
два блока любой эксперимент типа 23. Главное – правильно выбрать
взаимодействие, которым можно безболезненно пожертвовать. При отсутствии
априорных сведений выбирают взаимодействие самого высокого порядка: x1x2x3 для 23, x1x2x3х4 для 24, x1x2x3x4x5 25 и т. д. Но если
экспериментатору известно, что одно из парных взаимодействий лишено, например,
физико-химического смысла, то можно пожертвовать парным взаимодействием.
Матрицу типа 2k можно разбить на количество блоков 2n (n – степень
двойки) при . Так, матрица 23
разбивается на два блока по четыре опыта в каждом и на четыре блока по
два опыта в каждом. Матрица 24 – на два блока по 8 опытов в каждом,
на четыре блока по четыре опыта и на восемь блоков по два опыта и т.д.
Синтаксические нормы простого предложения Нормы управления
1. Поставьте имена существительные в нужном падеже, правильно выбрав форму управления.
Оскорбиться (брошенная фраза) – обидеться (оскорбительные слова); отзыв (книга) – рецензия (дипломная работа); плата (проезд) – оплатить (покупка); поражаться (красота природы) – удивляться (неувядающая молодость); преимущество (новые технологии) – превосходство (соперник); скучать (мать) – скучать (мы), тосковать (муж); уверенность (победа) – вера (успех); удивляться (необычное решение) – удивлен (странный поступок); характерный (он) – свойственный (он).
2. Из предложенных пар словосочетаний выберите верную.
1) Свойственный для него – свойственный ему; 2) иммунитет на корь – иммунитет к кори; 3) заведующий складом – заведующий склада; 4) журить в равнодушии – журить за равнодушие; 5) уделять внимание учебе – уделять внимание на учебу; 6) преимущество над врагом – преимущество перед врагом; 7) приемлемый для использования – приемлемый к использованию; 
3. Раскройте скобки, составьте и запишите словосочетания с данными словами.
1. Восторгаться, удивляться (его смелость). 2. Усваивать, овладевать (язык). 3. Уделять внимание, обращать внимание (физическое воспитание). 4. Опираться, основываться (новые изыскания). 5. Поддержать уверенность, поддержать веру (благополучный исход дела). 6. Препятствовать, предотвращать (получение незаконных доходов).
4. Раскройте скобки, поставив существительное в нужном падеже с предлогом или без предлога.
Беспокоиться (ребенок), тормозить (развитие), пойти (школа, факультет, университет, фирма), потребность (знание), платить (проезд), удивляться (результаты), контроль (выполнение), сообщить (приезд).
5. Проанализируйте словосочетания с управлением. Найдите нарушение синтаксической нормы. Исправьте ошибки.
I. Оперировать факты, отчет о проделанной работе, дать ответы на все задания, считать за преступника, действовать согласно закона, управляющий банка, благодаря своевременному лечению, не имея свободного времени, базироваться на экспериментальные данные.
II. Наперекор здравого смысла, вопреки желания трудящихся, рецензия о новой книге, указать о проблемах, свойственный для него, взгляд по данной проблеме, высказывание по поводу, постановили о введении следующих мер, дискутировать вопрос об инвестициях.
6. Найдите предложения, в которых нарушены нормы управления, и исправьте их.
1. Все герои были поглощены в свои мысли. 2. Мцыри стал вслушиваться к неясным звукам. 3. Тарас Бульба не терпел предательство. 4. Любовь к людям помогла ему выжить. 5. Я от тебя заберу свою книгу. 6. Я делюсь со своей подругой обо всем. 7. Я прошу твой совет. 8. Пионеры ветеранам в магазин ходят. 9. Князь Андрей всегда особенно оживлялся, когда ему приходилось руководить молодого генерала и помогать ему.
7. В приведенных предложениях исправьте недочеты в выборе предлога, а также ошибочное употребление падежных форм.
I. 1. Согласно приказа директора предприятие перешло на круглосуточную работу. 2. Разрушения произошли за счёт плохой работы системы водоснабжения. 3. Благодаря тому что график нарушен, строителям приходится работать в очень тяжёлых условиях. 4. В силу недостаточности освещения многие растения гибнут.
II. 1. По окончанию работы все должны собраться в зале. 2. Вопреки указанных положений на заводе продолжается нарушение техники безопасности. 3. По истечению некоторого времени можно будет снова вернуться к этому вопросу. 4. Вследствие запланированной работы, некоторым придется работать сверхурочно. 5. Благодаря трудностей мы не успели выполнить задание в срок.
8. Исправьте ошибки в грамматической форме слов, примыкающих к устойчивым оборотам.
1. Оружие – это товар, на который страна не испытывала дефицита. 2. Мы не всегда отдаем отчёт тому, как важны праздники в нашей жизни. 3. Узнав о катастрофе военного самолёта, министр обороны выразил сожаление случившемся. 4. Чемпион мира заявил о своем согласии принять участие на этих соревнованиях.
9. Найдите и исправьте синтаксические ошибки в предложениях.
I. 1. Целых два часа преподаватель объяснял студентам, как работает новый прибор. 2. Последние два слова были написаны неразборчиво. 3. Четыре новенькие машины стояли на парковке. 4. Я почувствовал тонкий аромат: в вазе стояли три желтые тюльпана. 5. Два крайние здания были довоенной постройки. 6. Три тонкие стебелька растения пригнулись к земле. 7. Два новые спецкурса ввели в программу обучения.
II. 1. Мальчик был редкостной разиней. 2. По краям дороги виднелись чахлые тополя с посеревшей от пыли листьями. 3. Часто можно видеть картины, изображающих животных, птиц и людей.
10. Выберите правильные формы согласования подлежащего и сказуемого.
1. Отец с матерью (уехал, уехали) в Крым. 2. В спальне (стояло, стояла) кресло-кровать. 3. Анна Ахматова – (одна из лучших, один из лучших) поэтов XX века. 4. Врач Краснова (зашла, зашел) в палату. 5. Большинство учащихся (считало, считали) себя (подготовленными, подготовленным) к экзаменам. 6. Ряд ученых (участвовал, участвовали) в научной конференции. 7. Часть курса (сдала, сдали) экзамен по риторике. 8. Большинство (согласилось, согласились) с решением комиссии. 9. В цирке (дрессировалось, дрессировались) несколько медвежат. 10. Несколько абитуриентов (сдает, сдают) экзамен по белорусскому языку. 11. Много забот (выпало, выпали) на долю матери. 12. К 15 августа (убрано, убраны) 10 гектаров льна. 13. На представление (пришли, пришло) 80 человек. 14. Десять студентов (получило, получили) грамоты за активное участие в общественной жизни университета. 15. Группа запорожцев (хотела, хотели) написать письмо турецкому султану. 16. Стая птиц (летела, летели) в теплые края. 17. Вдруг перед ним (возникло, возникли) три человека. 18. В шкафу (стоят, стоит) много книг.
Нормы употребления конструкций с однородными членами предложения
11. Укажите предложения, в которых нарушены нормы построения предложений с однородными членами. Отредактируйте их.
I. 1. Ребята интересуются и любят историю своего родного края. 2. Надо, чтобы все заботились и берегли природу. 3. К зиме готовятся не только звери, а также птицы. 4. Мы подошли к домику, стоявшему на небольшой полянке и который был освещен яркими лучами солнца. 5. Причастия – это слова, обозначающие признаки предметов по действию и которые отвечают на вопрос какой? что делающий? 6. Это не только были годы одиночества, а также период, когда будущий писатель сформировался как личность. 7. Мы должны бережно относиться и обращаться с новыми учебниками. 8. Герои предпочитают смерть, чем рабство. 9. По дороге мы зашли в магазин, купили сладости, яблоки и фрукты.
II. 1. Надо не только выучить правило, но и выполнить упражнение. 2. В ходе обсуждения доклада были внесены предложения и замечания. 3. За год было прочитано около пятидесяти лекций, около ста докладов и более семидесяти бесед. 4. Народ и крестьяне приступили к посевной. 5. Он все делал прекрасно, чувствуя прилив сил. 6. Класс получил учебники по алгебре и геометрии. 7. Над землей в октябре тянутся воздушные мосты осенних переселенцев: уток, жаворонков, малиновок, дроздов. 8. В колхозном саду растут облепиха, рябина, разнообразные плодовые деревья и сливы.
Нормы употребления причастного оборота
12. Найдите предложения, в которых нарушена синтаксическая норма в употреблении причастных оборотов. Исправьте их.
I. 1. В поросших лугах буйной растительностью водилось множество птиц. 2. Созданный роман молодым автором вызывал оживленные споры. 3. Жителям пострадавшего села от наводнения была оказана своевременная помощь. 4. Отряд избежал опасности благодаря проявленной решительности командиром. 5. Подгоняемая лодка волнами и ветром быстро неслась по реке. 6. Издалека были видны плывущие бревна по воде.
II. 1. Приближающиеся машины остановились у подъезда высокого здания. 2. Пришедшие зрители на спектакль прохаживались по фойе и рассматривали портреты актеров театра. 3. С нами разговаривал преподаватель, занимающийся теми же научными проблемами, что и мы. 4. Прилетевшие скворцы из южных стран начали вить гнезда, готовясь к появлению птенцов. 5. Написанные стихи ровным красивым почерком лежали на столе. 6. На столе стояли предназначенные для гостей столовые приборы.
III. 1. Помещенная в вольер овчарка бегала и лаяла. 2. Написанный роман этим молодым писателем рассказывает о далеком прошлом нашей страны. 3. Увлеченные мальчики игрой в футбол не заметили автомобиля, мчавшегося на большой скорости. 4. Дует сильный, все сметающий ветер на своем пути. 5. Пассажирам, вошедшим в салон автобуса, сразу же следует оплатить проезд. 6. Вся деятельность ученого, направленная на уничтожение человеческих страданий, вызывает уважение.
Нормы употребления деепричастного оборота
13. Исправьте предложения, если это необходимо. Объясните причины нарушения синтаксической нормы в предложениях.
1. Открыв окно, я залюбовался видом города. 2. Открывая дверь, она громко скрипнула. 3. Мама сидела, откинувшись на спинку стула. 4. Заканчивая чертеж, у меня сломался карандаш. 5. Возвращаясь домой, шёл дождь. 6. Прочитав рассказ, он показался мне слишком грустным. 7. Разложив игрушки на диване, дети начали какую-то интересную игру. 8. Возвращаясь из школы, меня застала гроза. 9. Подъезжая к деревне, у машины спустилось колесо. 10. Познакомившись с произведениями А. Гайдара, мне больше всего понравилась повесть «Школа». 11. Читая эти строки, создается впечатление, что автор пишет о нас.
14. Устраните ошибку в следующих предложениях с деепричастными оборотами. Дайте свои варианты правки.
1. Повернув направо, будет видно здание художественной галереи. 2. Глядя на ваши сияющие глаза, радостно становится и мне. 3. Уезжая из Минска, мое настроение испортилось. 4. Листая старые альбомы, вспоминаются давно забытые друзья. 5. Анализируя эти статьи, учитывалось мнение авторитетных политиков. 6. Проснувшись рано утром, Ольге показалось, что день будет ясным. 7. Вернувшись домой с работы, маму ждал ужин, приготовленный дочерью. 8. Сергею нравилось глядеть в бездонное звездное небо, замирая от любви ко всему на свете.
На самом деле обработка экспериментальных данных проходит несколько более сложно, но суть остаётся.
Один из обязательных компонентов профессиональной подготовки начинающего исследователя – освоение методов статистического анализа экспериментальных данных.
Доклад опирается на многочисленные экспериментальные данные, полученные сотрудниками обоих авторов, в частности, на многие харьковские исследования.
Иногда на основе новых экспериментальных данных мы находим границы применимости той или иной теории и мы снова и снова начинаем сомневаться в том, к чему привыкли.
На основе экспериментальных данных можно с уверенностью утверждать, что младенцы предпочитают именно музыкальную форму коммуникации.
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: куда там — это что-то нейтральное, положительное или отрицательное?
Имеющиеся экспериментальные данные в той или иной мере подтверждают все основные теории агрессии.
Крайне самонадеянно думать, что в вопросах, где объём экспериментальных данных сильно уступает попыткам их осмысления, люди тысячелетиями ошибались и прозрели лишь в течение последнего полувека.
Это объяснение было тщательно проверено путём сопоставления экспериментальных данных, полученных в других специально проведённых для этого исследованиях.
Экспериментальные данные всегда оставляют возможность для модификации любого утверждения или даже теории в целом.
И я обещаю ей, что всё, о чём я расскажу в этой книге, будет убедительно доказано строгими экспериментальными данными.
И наконец, теоретическое обобщение, сведение воедино всех экспериментальных данных оказалось последней точкой приложения теоретического анализа к нашему исследованию.
Модель согласуется с известными экспериментальными данными, а также позволяет предсказать и проверить целый ряд неочевидных феноменов.
На втором этапе, в 1960–1970-е годы, под влиянием противоречивых экспериментальных данных начинает доминировать скептицизм в отношении универсальных закономерностей воздействия.
Получить прямые экспериментальные данные в этой области практически невозможно.
Рассмотрим некоторые важнейшие экспериментальные данные об устойчивости индивидуальных различий.
Полученные экспериментальные данные свидетельствуют о том, что начиная с самого раннего возраста у младенцев существует механизм, позволяющий им реагировать на ситуации с учётом сохранения объекта, даже когда он скрыт (когда, например, коробка преграждает путь машине, а прямоугольный экран скрывает мышку).
Мы имеем теорию, полную и вполне определённую теорию всех этих адронов, и у нас есть огромное количество экспериментальных данных с кучей подробностей – почему же мы не можем немедленно проверить теорию, обнаружить, правильна она или нет?
Многочисленные экспериментальные данные свидетельствуют о том, что страх перед наказанием или возмездием резко снижает возможность прямого проявления агрессивности в поведении – иными словами, ожидание негативных последствий агрессии является одним из наиболее значимых регуляторов торможения агрессии.
Более того, растущий объём теоретических и экспериментальных исследований показывал, что выводы, сделанные на основании статистического анализа больших наборов частиц – описаний того, как они летают по ёмкостям, наталкиваясь на стенки и оказывая таким образом давление на ту или иную поверхность, или приобретают такую-то плотность, или остывают до определённой температуры, – соответствовали экспериментальным данным с такой точностью, что не оставалось никакой возможности усомниться в объяснительной силе этого подхода.
Между тем, в последние десятилетия получен большой массив экспериментальных данных, убедительно показывающих динамизм отношений объект-образ и теснейшую взаимосвязь восприятия с другими психическими процессами, состояниями и свойствами личности.
Большая часть современных экспериментальных данных, характеризующих перцептивный процесс, получена на материале восприятия сверхкоротких экспозиций элементов среды и опирается на представления о сенсорных системах (Eysenck, Keane, 1995; Levitin, 2002; Palmer, 2002; Pylyshyn, 2003).
Сказанное подтверждают экспериментальные данные.
Заметим попутно: имеется множество экспериментальных данных, из которых следует, что научение посредством наблюдения оказывает на личность даже большее влияние, чем непосредственный деятельный опыт.
Неполная индукция предполагает, что вынесенные за скобки эксперимента аналогичные объекты обладают теми же свойствами, что и изученные, и это позволяет использовать экспериментальные данные для теоретического обоснования.
Однако после настоящего бума исследований мотивации, и прежде всего – мотивации достижения, в западноевропейской психологии под влиянием ряда экспериментальных данных начинает формироваться критическое осмысление постулата о том, что мотивационные процессы, основанные на оценке ожидания успеха и привлекательности цели, прямо определяют поведение.
Отмеченное следует относить к «совокупному» или «статистическому» 3, отразившему едва ли не первое в истории обобщение экспериментальных данных.
Проблема исследования заключается в ряде существенных противоречий, а именно: между инновационными процессами в экономической, производственной, социальной сферах и существующими традиционными установками образовательных стратегий; между социальной необходимостью в обновлении педагогических кадров и отсутствием экспериментальных данных о резервных возможностях личности учителя к эволюционированию в русле реформирования образования; между необходимостью развития ресурсных возможностей учителя и недостаточной разработанностью теоретико-методологических оснований для выделения личностных детерминант, предопределяющих преобразовательный эффект профессионального развития учителя; между необходимостью формирования у современного учителя готовности к риску в ситуациях неопределённости и недостаточной проработанностью психологических условий и средств развития личностных характеристик, позволяющих учителю прогнозировать и реализовывать развивающие возможности рисконесущих факторов; между задачами совершенствования образовательного процесса, стимулирующего прогрессивное поступательное личностно-профессиональное становление учителя, и отсутствием инновационных психологических технологий профессионального развития педагогов.
Существуют экспериментальные данные, свидетельствующие о том, что человеческое лицо столь же эмоционально значимо для такого ребёнка, как и для любого другого, но вот глазной контакт он выдерживает гораздо менее длительно, чем все остальные.
Таким образом, действие каждого фактора предсказывает определённую «элементарную последовательность» событий и задача факторного анализа состоит в том, чтобы представить исторический процесс в виде суммы, суперпозиции «элементарных последовательностей», подобно тому, как в регрессионном анализе пытаются приблизить последовательность наблюдаемых экспериментальных данных суммой последовательностей-факторов, а затем оценить «остаточную дисперсию» – долю тех событий, которые нельзя объяснить этим методом.
Таким образом, предсказатель имел бы те же основные достоинства и недостатки, что и любой другой источник экспериментальных данных, и был бы полезен только в тех случаях, когда обращение к нему оказывалось бы удобнее, чем к другим источникам.
В 1644 г. он писал коллеге: «Мы живём на самом дне океана, состоящего из воздуха, который, согласно неоспоримым экспериментальным данным, имеет вес».
Именно с началом использования математических методов физика стала быстро развиваться, ведь без этого точные экспериментальные данные до некоторой степени были не востребованы (разумеется, верно и обратное: приход математики отчасти стимулирован появлением точных измерений наблюдаемых параметров).
Экспериментальные данные особенно важны, потому что они могут дать информацию о контрфактуальности (DD-тип 6: данные, которые могли бы существовать), упомянутой в главе 1.
Как известно и доказано различными экспериментальными данными, мысли материализуются, поэтому этот способ является очень действенным.
Мы отделим научно-фантастический элемент популярных «графиков похудения» от собственно научного, спросим себя, можно ли иметь здоровый метаболизм и не быть худым, а также изучим свежие экспериментальные данные, подтверждающие благотворный эффект таких традиционных режимов питания, как, например, средиземноморская диета.
Устремления исследователя к накоплению экспериментальных данных, необходимых для решения в конечном итоге проблем устранения неблагоприятных проявлений стресса, могут потребовать создания таких проявлений у испытуемого.
Перечисленные науки подошли к рубежу, когда мало экспериментальных данных и физики предлагают теории, основанные на воображении и фантазии.
Научные теории отбираются и провераются по принципу соответствия экспериментальным данным, что определяет их количественный характер.
Интерпретация экспериментальных данных с целью создания теории.
На этапе обобщения и синтеза экспериментальных данных начинается воссоздание целостного представления об исследуемом объекте, но уже с точки зрения сущностных отношений и на этой основе экспериментально преобразованного.
У нас есть метод, которым можно уверенно пользоваться в заданных условиях, и этот метод даёт умопомрачительно точные прогнозы, триумфально подтверждённые экспериментальными данными.
Между тем шимпанзе чувствует и думает, а возможно – согласно новейшим экспериментальным данным – способен даже освоить некую форму человеческого языка.
Возникла необходимость в теоретическом обобщении накопленных экспериментальных данных, в разработке теории рабочего цикла и отдельных процессов.
Эта материально-специфическая гипотеза редко прямо формулируется, но часто упоминается мимоходом при обсуждении экспериментальных данных.
Нам уже были известны экспериментальные данные о резонансном захвате нейтронов промежуточных энергий.
С получением новых экспериментальных данных взгляд на мир может значительно измениться.
Статьи
Главная страница

видно, что существует вероятность, пусть и очень маленькая, что наше единичное
измерение покажет результат, сколь угодно далеко отстоящий от истинного
значения. Выходом из положения является проведение серии измерений. Если на
разброс данных действительно влияет случай, то в результате нескольких
измерений мы скорее всего получим следующее (рис 2):
Будет ли
рассчитанное среднее значение нескольких измерений совпадать с истинным? Как
правило – нет. Но по теории вероятности, чем больше сделано измерений, тем
ближе найденное среднее значение к истинному. На языке математики это можно
записать так:
Но с бесконечностью у всех дело обстоит неважно. Поэтому на практике мы имеем дело
не со всеми возможными результатами измерений, а с некоторой выборкой из этого
бесконечного множества. Сколько же реально следует делать измерений? Наверное,
до тех пор, пока полученное среднее значение не будет отличаться от истинного
меньше чем точность отдельного измерения.
Следовательно,
когда наше среднее значение (рис. 2) отличается от истинного меньше чем
погрешность измерений, дальнейшее увеличение числа опытов бессмысленно. Однако
на практике мы не знаем истинного значения! Значит, получив среднее по
результатам серии опытов, мы должны определить, какова вероятность того, что
истинное значение находится внутри заданного интервала ошибки. Или каков тот
доверительный интервал, в который с заданной надежностью попадет истинное
значение (рис 3).
Рассмотрим
некоторый условный эксперимент, где в серии измерений получены некоторые
значения величины Х (см. табл. 1). Рассчитаем среднее значение и, чтобы оценить
разброс данных найдем величины DХ = Х –
Хср
|
Таблица |
||||||
|
№ |
Х |
Х ср |
DХ |
DХ2 |
s2 |
s |
|
1 |
130 |
143,5 » 144 |
-13,5 |
182,3 |
420 |
20,5 |
|
2 |
162 |
18,5 |
342,3 |
|||
|
3 |
160 |
16,5 |
272,3 |
s2ср |
sср |
|
|
4 |
122 |
-21,5 |
462,3 |
105 |
10,2 |
Ясно, что
величины DХ как-то характеризуют
разброс данных. На практике для усредненной характеристики разброса серии измерений используется
дисперсия выборки:
и среднеквадратичное или стандартное отклонение выборки:
Последнее
показывает, что каждое измерение в данной серии (в данной выборке) отличается
от другого в среднем на ± s.
Понятно, что каждое отдельное
значение оказывает влияние на средний результат. Но это влияние тем меньше, чем
больше измерений в нашей выборке. Поэтому дисперсия и стандартное отклонение
среднего значения, будет определяться по формулам:
Можем ли мы теперь определить вероятность того, что
истинное значение попадет в указанный интервал среднего? Или наоборот,
рассчитать тот доверительный интервал в который истинное значение
попадет с заданной вероятностью (95%)? Поскольку кривая на наших графиках это
распределение вероятностей, то площадь под кривой, попадающая в указанный
интервал и будет равна этой вероятности (доля площади, в процентах). А площади
математики научились рассчитывать хорошо, знать бы только уравнение этой
кривой.
И здесь мы сталкиваемся еще с одной сложностью. Кривая, которая описывает распределение
вероятности для выборки, для ограниченного числа измерений, уже не будет кривой нормального
распределения. Ее форма будет зависеть
не только от дисперсии (разброса данных) но и от степени свободы для выборки
(от числа независимых измерений) (рис 4):
Уравнения этих кривых впервые были предложены в 1908
году английским математиком и химиком Госсетом, который опубликовал их под
псевдонимом Student (студент), откуда пошло хорошо известные термины
«коэффициент Стьюдента» и аналогичные. Коэффициенты Стьюдента получены на
основе обсчета этих кривых для разных степеней свободы (f = n-1) и уровней
надежности (Р) и сведены в специальные таблицы. Для получения доверительного интервала необходимо
умножить уже найденное стандартное отклонение среднего на соответствующий
коэффициент Стьюдента. ДИ = sср*tf, P
Проанализируем, как меняется доверительный интервал
при изменении требований к надежности результата и числа измерений в серии.
Данные в таблице 2 показывают, что чем больше требование к надежности, тем
больше будет коэффициент Стьюдента и, следовательно, доверительный интервал. В большинстве случаев, приемлемым считают значение Р=95%
|
Таблица |
||||
|
P |
0,9 |
0,95 |
0,99 |
0,999 |
|
t5, |
2,02 |
2,57 |
4,03 |
6,87 |
|
Таблица |
|||||||
|
f= |
1 |
2 |
3 |
4 |
5 |
16 |
30 |
|
tf, |
12,7 |
4,3 |
3,18 |
2,78 |
2,57 |
2,23 |
2,04 |
Из таблицы 3 и графика
видно, что чем больше число измерений, тем меньше коэффициент и доверительный
интервал для данного уровня надежности. Особенно значительное падение
происходит при переходе от степени свободы 1 (два измерения) к 2 (три
измерения). Отсюда следует, что имеет смысл ставить не менее трех параллельных
опытов, проводить не менее трех измерений.
Окончательно
для измеряемой величины Х получаем значение Хсред±sср*tf,P. В
нашем случае получаем: f=3; t=3,18;
ДИ = 3,18*10,2 = 32,6; X = 143,5 ±32,6
Как правило,
значение доверительного интервала округляется до одной значащей цифры, а
значение измеряемой величины – в соответствии с округлением доверительного
интервала. Поэтому для нашей серии окончательно имеем: X = 140 ±30
Найденная
нами погрешность является абсолютной погрешностью и ничего не говорит еще о
точности измерений. Она свидетельствует о точности измерений только в сравнении
с измеряемой величиной. Отсюда представление об относительной ошибке:
Косвенные определения.
Исследуемая величина рассчитывается в этом случае с помощью
математических формул по другим величинам, которые были измерены
непосредственно. В этом случае для расчета ошибок можно использовать
соотношения, приведенные в таблице 4.
|
Таблица |
||
|
Формула |
Абсолютная |
Относительная |
|
x = a ± b |
Dx = Da+Db |
e = |
|
x = a* b; x = a* k |
Dx = bDa+aDb; Dx = kDa |
e = Da/a+Db/b = ea + e b |
|
x = a / b |
Dx = (bDa+aDb) / b2 |
e = Da/a+Db/b = ea + e b |
|
x = a*k; (x = a / k) |
Dx = Da*k; (Dx = Da/k ) |
e = ea |
|
x = a2 |
Dx = 2aDa |
e = 2Da/a = 2ea |
|
x = Öa |
Dx = Da/(2Öa) |
e = Da/2a = ea/2 |
Из таблицы видно, что относительная ошибка и точность определения не изменяются при умножении (делении) на некоторый постоянный коэффициент. Особенно сильно относительная ошибка может возрасти при вычитании
близких величин, так как при этом абсолютные ошибки суммируются, а значение Х
может уменьшиться на порядки.
Пусть например, нам необходимо определить
объем проволочки.
Если диаметр проволочки измерен с погрешностью 0,01 мм (микрометром) и равен 4 мм, то относительная погрешность составит 0,25% (приборная). Если
длину проволочки (200 мм) мы измерим линейкой с погрешностью 0,5 мм, то относительная погрешность также составит 0,25%. Объем можно рассчитать по формуле: V=(pd2/4)*L. Посмотрим, как будут меняться ошибки
по мере проведения расчетов (табл. 5):
|
Таблица 5. Расчет абсолютных и относительных ошибок. |
|||
|
Величина |
Значение |
Абсолютная |
Относительная |
|
d2 |
16 |
Dx = 2*4*0,01=0,08 |
e = 0,5% |
|
pd2 *) |
50,27 |
Dx = 0,08*3,14+0,0016*16 |
e = 0,55% |
|
pd2/4 |
12,57 |
Dx = 0,28/4 = 0,07 |
e = 0,55% |
|
(pd2/4)*L |
2513 |
Dx = 12,57*0,5+200*0,07=20 |
e = 0,8% |
|
*) Если мы возьмем привычное p=3,14, то Dp=0,0016 |
Окончательный
результат V=2510±20 (мм3) e
=0,8%. Чтобы повысить точность косвенного определения, нужно в первую очередь
повышать точность измерения той величины, которая вносит больший вклад в ошибку
(в данном случае – точность измерения диаметра проволочки).
План проведения измерений:
[1]
1. Знакомство
с методикой, подготовка прибора, оценка приборной погрешности d. Оценка возможных причин
систематических ошибок, их исключение.
2.
Проведение серии измерений. Если получены совпадающие результаты, можно
считать что случайная ошибка равна 0, DХ
= d. Переходим к пункту 7.
3.
Исключение промахов – результатов значительно отличающихся по своей
величине от остальных.
4.
Расчет
среднего значения Хср, и стандартного отклонение среднего
значения scp
5.
Задание значения уровня надежности P,
определение коэффициента Стьюдента t и
нахождение доверительного интервала ДИ= t*scp
6.
Сравнение случайной и приборной погрешности, при этом возможны варианты:
—
ДИ << d, можно
считать, что DХ = d, повысить точность измерения
можно, применив более точный прибор
—
ДИ >> d, можно
считать, что DХ = ДИ,
повысить точность можно, уменьшая случайную ошибку, повышая число измерений в
серии, снижая требования к надежности.
—
ДИ » d, в этом
случае расчитываем ошибку по формуле DХ
=
7.
Записывается окончательный результат Х = Хср ± DХ.
Оценивается относительная ошибка
измерения e = DХ/Хср
Если
проводится несколько однотипных измерений (один прибор, исследователь, порядок
измеряемой величины, условия) то подобную работу можно проводить один раз. В
дальнейшем можно считать DХ
постоянной и ограничиться минимальным числом измерений (два-три измерения
должны отличаться не более, чем на DХ)
Для косвенных
измерений необходимо провести обработку данных измерения каждой величины. При
этом желательно использовать приборы, имеющие близкие относительные погрешности
и задавать одинаковую надежность для расчета доверительного интервала. На
основании полученных значений Da, Db, определяется DХ
для результирующей величины (см табл. 4). Для повышения точности надо
совершенствовать измерение той величины, вклад ошибки которой в DХ наиболее существенен.
Изучение зависимостей.
Частым вариантом экспериментальной работы является
измерение различных величин с целью установления зависимостей. Характер этих
зависимостей может быть различен: линейный, квадратичный, экспоненциальный,
логарифмический, гиперболический. Для выявления зависимостей широко
используется построение графиков.
При построении графиков вручную важно правильно
выбрать оси, величины, масштаб, шкалы. Следует предупредить школьников, что
шкалы должны иметь равномерный характер, нежелательна как слишком детальная,
так и слишком грубая их разметка. Точки должны заполнять всю площадь графика,
их расположение в одном углу, или «прижатыми» к одной из осей, говорит о
неправильно выбранном масштабе и затрудняет определение характера зависимости.
При проведении линии по точкам надо использовать теоретические представление о
характере зависимости: является она непрерывной или прерывистой, возможно ли ее
прохождение через начало координат, отрицательные значения, максимумы и
минимумы.
Наиболее легко проводится и анализируется прямая
линия. Поэтому часто при изучении более сложных зависимостей часто используется
линеаризация зависимостей, которая достигается подходящей заменой переменных.
Например:
Зависимость . Вводя новую переменную
, получаем уравнение
a = bx, которое
будет изображаться на графике прямой линией. Наклон этой прямой позволяет
рассчитать константу диссоциации.
Разумеется и в этом случае полученные в эксперименте данные включают в себя различные ошибки, и точки редко лежат строго на прямой. Возникает
вопрос, как с наибольшей точностью провести прямую по экспериментальным точкам, каковы ошибки в определении
параметров.
Математическая статистика показывает, что наилучшим
приближением будет такая линия, для которой дисперсия (разброс) точек
относительно ее будет минимальным. А дисперсия определяется как средний квадрат
отклонений наблюдаемого положения точки от расчитанного:
Отсюда название этого метода – метод наименьших
квадратов. Задавая условие, чтобы величина s2
принимала минимальное значение, получают формулы для коэффициентов а и b в уравнении прямой у = а + bx:

и формулы для расчета соответствующих ошибок
[2].
Если
делать расчеты, используя калькулятор, то лучше оформлять их в виде таблицы:
|
x |
x2 |
y |
y2 |
xy |
|
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
|
Sx = |
Sx2 |
Sy = |
Sy2 |
Sxy = |
Подводя
итог, следует сказать, что обработка данных эксперимента достаточно сложный
этап работы ученого. Необходимость проведения большого числа измерений требует
большой затраты времени и материальных ресурсов. Громоздкость формул, необходимость
использования большого числа значащих цифр затрудняют вычисления. Поэтому, возможно,
не все рекомендации этой статьи применимы в рамках школьного исследования. Но
понимать их сущность, значимость, необходимость, и в соответствии с этим
адекватно оценивать свои результаты, должен любой исследователь.
В настоящее время обработку экспериментальных данных
существенно облегчают современные компьютерные технологии, современное
программное обеспечение. Об том, как их можно использовать – в следующей
статье.
Литература:
[1]
Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений, М., «Наука»,
1970, 194 с.
[2]
Петерс Д., Хайес Дж., Хифтье Г. Химическое разделение и измерение – М.,: Химия,
1978, 816 с.
Характер приближений в информационных моделях
Специфичность информационных моделей проявляется не только в способах их синтеза, но и характере делаемых приближений (и связанных с ними ошибок). Отличия в поведении системы и ее информационной модели возникают вследствие свойств экспериментальных данных.
- Информационные модели ab initio являются неполными. Пространства входных и выходных переменных не могут, в общем случае, содержать все параметры, существенные для описания поведения системы. Это связано как с техническими ограничениями, так и с ограниченностью наших представлений о моделируемой системе. Кроме того, при увеличении числа переменных ужесточаются требования на объем необходимых экспериментальных данных для построения модели (об этом см. ниже). Эффект опущенных (скрытых) входных параметров может нарушать однозначность моделируемой системной функции F.
- База экспериментальных данных, на которых основывается модель G рассматривается, как внешняя данность. При этом, в данных всегда присутствуют ошибки разной природы, шум, а также противоречия отдельных измерений друг другу. За исключением простых случаев, искажения в данных не могут быть устранены полностью.
- Экспериментальные данные, как правило, имеют произвольное распределение в пространстве переменных задачи. Как следствие, получаемые модели будут обладать неодинаковой достоверностью и точностью в различных областях изменения параметров.
- Экспериментальные данные могут содержать пропущенные значения (например, вследствие потери информации, отказа измеряющих датчиков, невозможности проведения полного набора анализов и т.п.). Произвольность в интерпретации этих значений, опять-таки, ухудшает свойства модели.
Такие особенности в данных и в постановке задач требуют особого отношения к ошибкам информационных моделей.
Ошибка обучения и ошибка обобщения
Итак, при информационном подходе требуемая модель G системы F не может быть полностью основана на явных правилах и формальных законах. Процесс получения G из имеющихся отрывочных экспериментальных сведений о системе F может рассматриваться, как обучение модели G поведению F в соответствии с заданным критерием, настолько близко, насколько возможно. Алгоритмически, обучение означает подстройку внутренних параметров модели (весов синаптических связей в случае нейронной сети) с целью минимизации ошибки модели 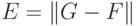
Прямое измерение указанной ошибки модели на практике не достижимо, поскольку системная функция F при произвольных значениях аргумента не известна. Однако возможно получение ее оценки:
где суммирование по X проводится по некоторому конечному набору параметров X, называемому обучающим множеством. При использовании базы данных наблюдений за системой, для обучения может отводиться некоторая ее часть, называемая в этом случае обучающей выборкой. Для обучающих примеров X отклики системы Y известны7С учетом описанных выше особенностей экспериментальных данных.
. Норма невязки модельной функции G и системной функции Y на множестве X играет важную роль в информационном моделировании и называется ошибкой обучения модели.
Для случая точных измерений (например, в некоторых задачах классификации, когда отношение образца к классу не вызывает сомнений) однозначность системной функции для достаточно широкого класса G моделей гарантирует возможность достижения произвольно малого значения ошибки обучения EL. Нарушение однозначности системной функции в присутствии экспериментальных ошибок и неполноты признаковых пространств приводит в общем случае к ненулевым ошибкам обучения. В этом случае предельная достижимая ошибка обучения может служить мерой корректности постановки задачи и качества класса моделей G.
В приложениях пользователя обычно интересуют предсказательные свойства модели. При этом главным является вопрос, каковым будет отклик системы на новое воздействие, пример которого отсутствует в базе данных наблюдений. Наиболее общий ответ на этот вопрос дает (по-прежнему недоступная) ошибка модели E. Неизвестная ошибка, допускаемая моделью G на данных, не использовавшихся при обучении, называется ошибкой обобщения модели EG.
Основной целью при построении информационной модели является уменьшение именно ошибки обобщения, поскольку малая ошибка обучения гарантирует адекватность модели лишь в заранее выбранных точках (а в них значения отклика системы известны и без всякой модели!). Проводя аналогии с обучением в биологии, можно сказать, что малая ошибка обучения соответствует прямому запоминанию обучающей информации, а малая ошибка обобщения — формированию понятий и навыков, позволяющих распространить ограниченный опыт обучения на новые условия. Последнее значительно более ценно при проектировании нейросетевых систем, так как для непосредственного запоминания информации лучше приспособлены не нейронные устройства компьютерной памяти.
Важно отметить, что малость ошибки обучения не гарантирует малость ошибки обобщения. Классическим примером является построение модели функции (аппроксимация функции) по нескольким заданным точкам полиномом высокого порядка. Значения полинома (модели) при достаточно высокой его степени являются точными в обучающих точках, т.е. ошибка обучения равна нулю. Однако значения в промежуточных точках могут значительно отличаться от аппроксимируемой функции, следовательно ошибка обобщения такой модели может быть неприемлемо большой.
Поскольку истинное значение ошибки обобщения не доступно, в практике используется ее оценка. Для ее получения анализируется часть примеров из имеющейся базы данных, для которых известны отклики системы, но которые не использовались при обучении. Эта выборка примеров называется тестовой выборкой. Ошибка обобщения оценивается, как норма уклонения модели на множестве примеров из тестовой выборки.
Оценка ошибки обобщения является принципиальным моментом при построении информационной модели. На первый взгляд может показаться, что сознательное не использование части примеров при обучении может только ухудшить итоговую модель. Однако без этапа тестирования единственной оценкой качества модели будет лишь ошибка обучения, которая, как уже отмечалось, мало связана с предсказательными способностями модели. В профессиональных исследованиях могут использоваться несколько независимых тестовых выборок, этапы обучения и тестирования повторяются многократно с вариацией начального распределения весов нейросети, ее топологии и параметров обучения. Окончательный выбор «наилучшей» нейросети выполняется с учетом имеющегося объема и качества данных, специфики задачи, с целью минимизации риска большой ошибки обобщения при эксплуатации модели.