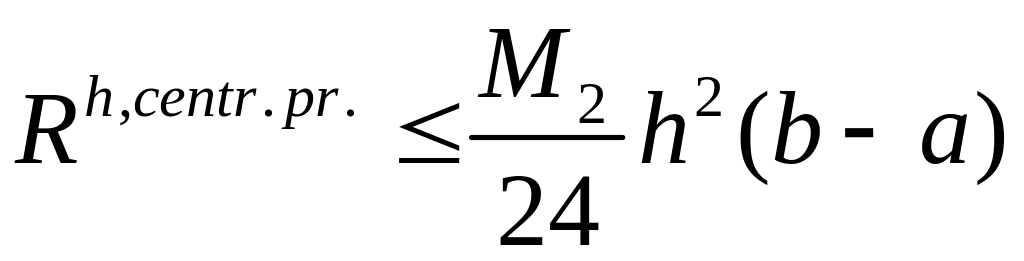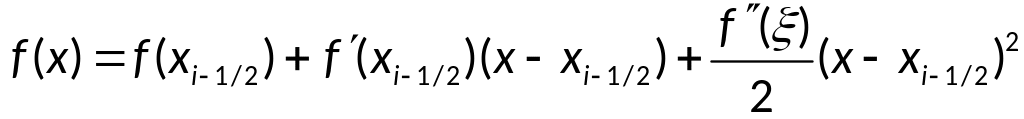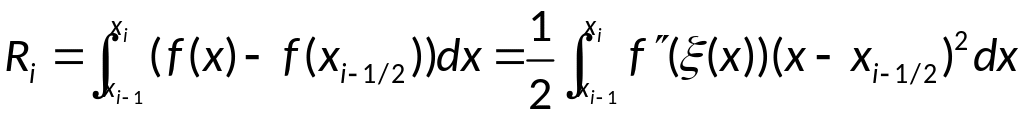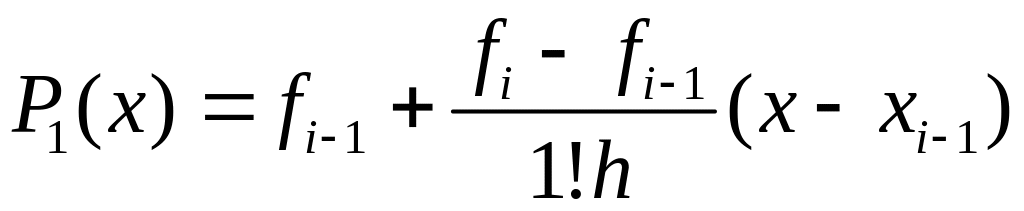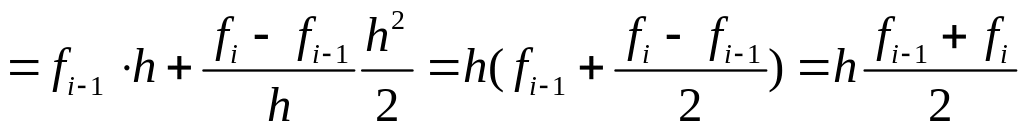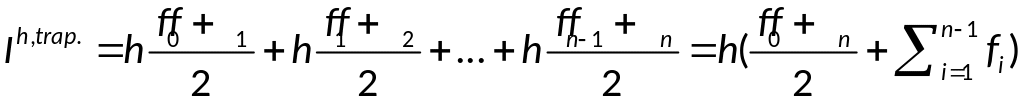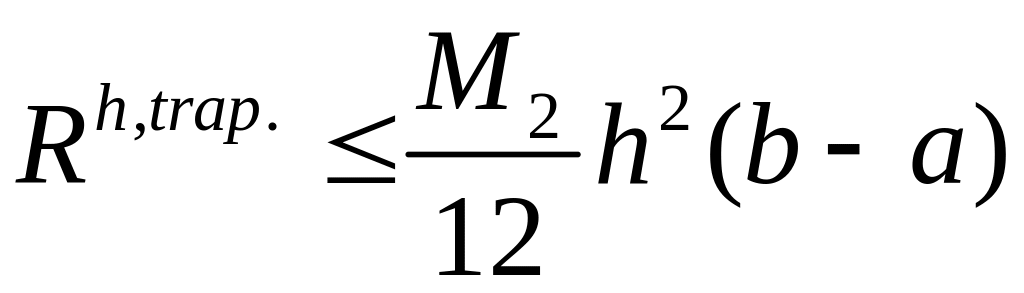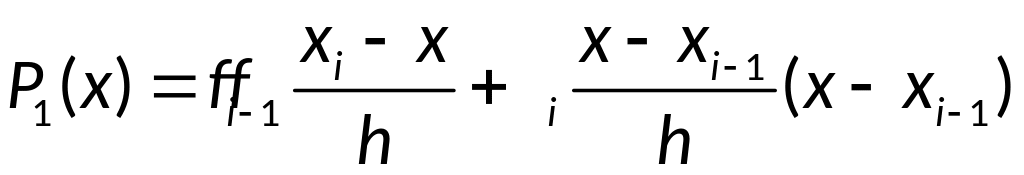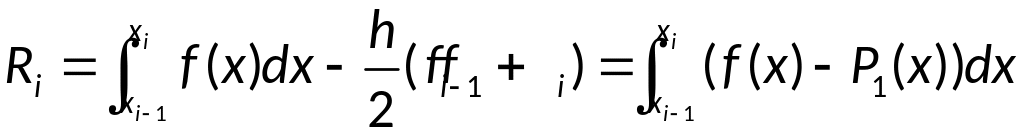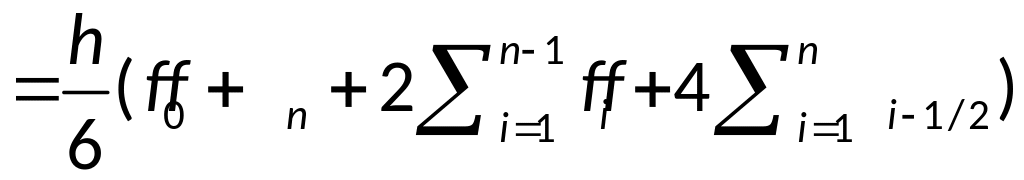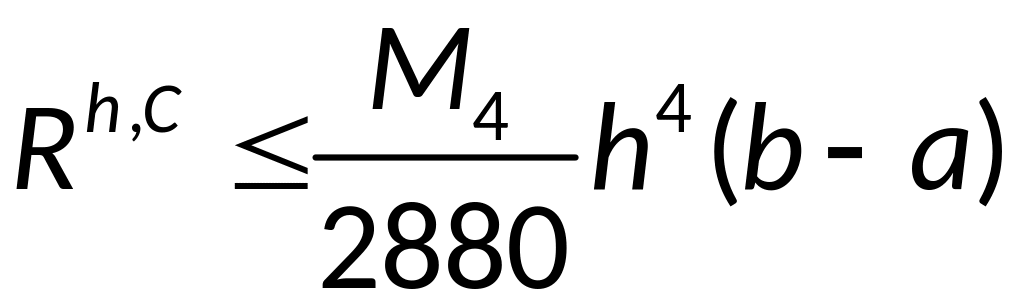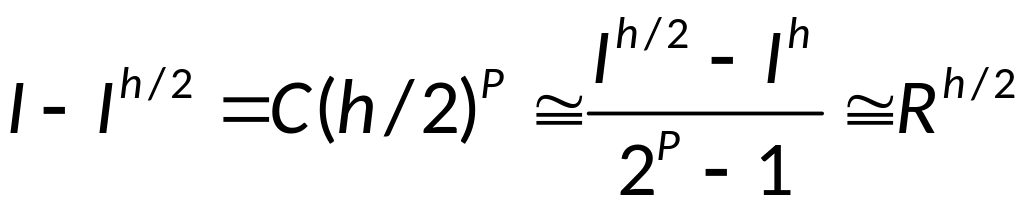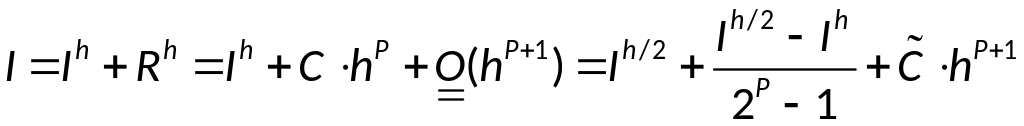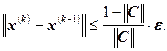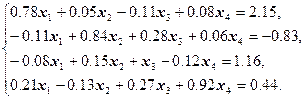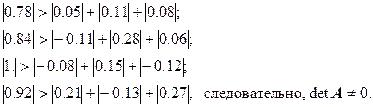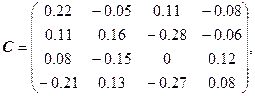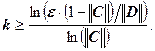-
Численное интегрирование: вывод формулы прямоугольников и оценки погрешности.
Постановка задачи:
дано
,
требуется
найти приближённое значение интеграла
:
,
— заданная точность.
Актуальность
задачи: — f(x)
вычисляется «сложно» из эксперимента
— f(x)
задана таблицей своих значений.
Задача интерполяции:
y(x)
– задана таблично
— глобальная
интерполяция
— m+1
узел,
— кусочно-полиномиальная
интерполяция
.
Основная идея
построения формул интерполяционного
типа:
,
— такова, что интеграл вычисляется,
.
Простейшие формулы
численного интегрирования:
;
— узлы квадратурной формулы,
;
— элементарный
отрезок интегрирования;
— составной отр. инт-я;
— числовые
коэффициенты – веса квадратурной
формулы.
— квадратурная
сумма (формула).
Величина
— называется погрешностью (или остаточным
членом) квадратурной формулы.
Будем говорить,
что квадратурная формула точна для
многочленов степени m,
если для любого многочлена степени не
выше m
эта формула даёт точное решение интеграла,
т.е.
Формула левых
прямоугольников:
— априорная оценка
погрешности,
.
Формула правых
прямоугольников:
;
;
.
Формула центральных
прямоугольников:
;
;
.
Вывод оценки
интерполяции: условие: f
– дважды непрерывно дифференцируема.
Представим
погрешность
формулы в виде:
Используя формулу
Тейлора:
,
где
,
имеем:
;
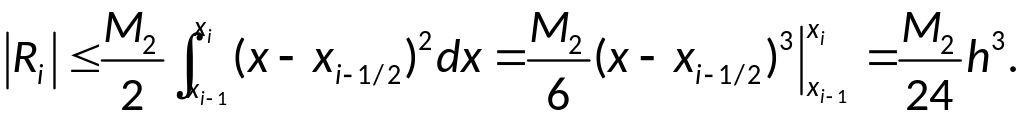
Так как
,
то
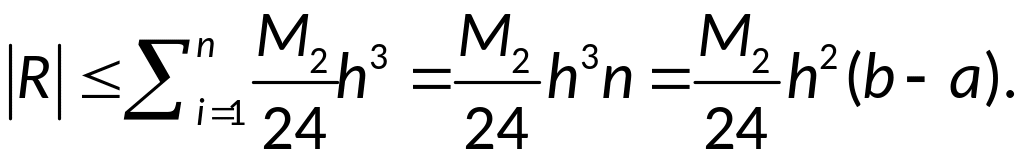
-
Численное интегрирование: вывод формулы трапеций и оценки погрешности.
;
— многочлен Ньютона.
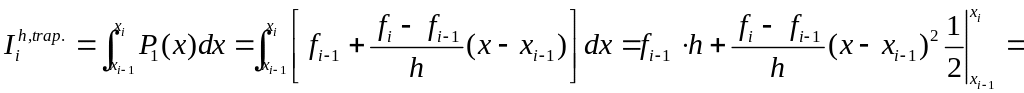
— элементарная
формула трап.
— составная ф-ла.
— априорная оценка.
Для вывода оценки
воспользуемся тем, что отрезок, соединяющий
две соседние точки, представляет собой
график интерполяционного многочлена
первой степени
.
Поэтому для элементарной формулы
трапеций верно равенство:
.
Используя оценку
погрешности линейной интерполяции,
имеем:
,
следовательно, для
справедлива оценка:
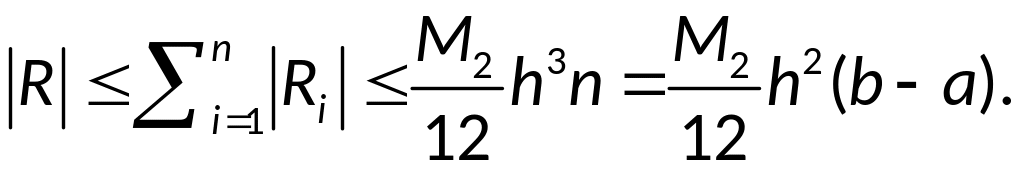
-
Численное интегрирование: формула Симпсона и оценка погрешности.
Если площадь
элементарной криволинейной трапеции
заменить площадью фигуры, расположенной
под параболой, проходящей через точки
,
то получим приближённое равенство
,
— интерполяционный многочлен второй
степени.
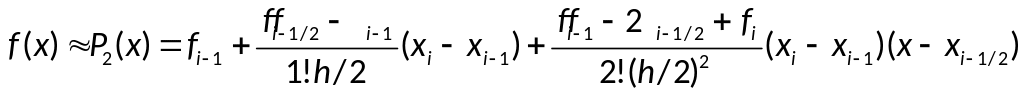
— элементарная
квадратурная формула Симпсона.
— составная формула
Симпсона.
— априорная оценка
погрешности формулы Симпсона, при
условии, что функция f
имеет на отрезке [a,b]
непрерывную производную четвёртого
порядка.
-
Правило Рунге оценки погрешностей. Уточнение по Рунге.
Дано
,
— квадратурная сумма (приближённое
значение интеграла).
.
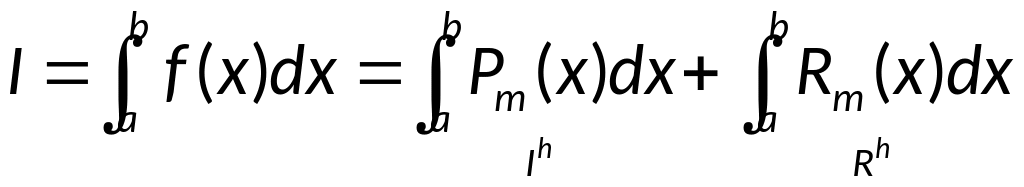
Опр.
Квадратурная формула имеет порядок
точности
.
Правило Рунге:
(правило двойного пересчёта) – для
практической оценки погрешности
(апостериорное правило).
Вычитая из второго
первое получаем:
Окончательно
получаем:
— правило Рунге.
Уточнение по Рунге:
главный член погрешности становится
точнее.
Для того, чтобы
сделать уточнение по Рунге для формулы
трапеции с шагом h,
нужно: записать формулу трапеции с
половинным шагом, в результате получим
формулу Симпсона при шаге интерполяции
h.
Опр.
Пусть квадратурная формула применяется
для многочленов степени m
и пусть значения интегралов для всех
многочленов степени
являются точными, а интеграл от многочлена
степени m+1
вычисляется приближённо, тогда:
квадратурная формула называется формулой
алгебраической степени точности m.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Advances in Adaptive Computational Methods in Mechanics
E. Stein, … M. Schmidt, in Studies in Applied Mechanics, 1998
4 A NUMERICAL EXAMPLE
We chose a ‘rectangular plate with a circular hole under plane strain constraint’ and unidirectional monotonous loading for numerical tests of the different error sources and their indicators, Fig. 1a.
Figure 1a:. Benchmark system: Stretched square plate with a hole in plane strain, h = 200, r = 10
Three material parameters describe linear isotropic elastic and perfect plastic deformations, while mixed linear and nonlinear isotropic hardening with saturation need additionally three parameters, Table 2.
Table 2. Material parameters
| 1. | Young’s modulus | E = 206900.00 N/mm2 |
| 2. | Poisson’s ratio | ν = 0.29 |
| 3. | Initial yield stress | y0 = 450.00 N/mm2 |
| 4. | Saturation stress | y∞ = 750.00 N/mm2 |
| 5. | Linear hardening modulus | h = 129.00 N/mm2 |
| 6. | Hardening exponent | ω = 16.93 |
From a priori error considerations the adaptive computation of the above example starts with a sequence of graded meshes, ranging from 64 bilinear elements with 25 nodes to 8192 bilinear elements with 8385 nodes, Figs. 2b. Additionally, a reference solution with 24200 bilinear elements, 24642 nodes and 49062 d.o.f. was computed. In order to obtain comparable results for all meshes and material equations, some selected points were chosen for data evaluation, Figs. 1a, 2b and Table 3. In the following sections, spatial distributions of the different error indicators are shown for a load factor of λ = 4.5 where the critical load for perfect plasticity is λcrit = 4.66 and λcrit = 7.89 for nonlinear hardening material. The load was applied in 18 load steps which renders the time discretization error negligible against the spatial discretization errors. All given results hold for hardening material, Table 2
Figure 2b:. Smallest mesh with 16 elements a = 61.953, b = 28.047, c = 131.421
Table 3. Selected points and data of system in Fig. 1a,1b
| Physical quantity | node No. | |
|---|---|---|
| Displacement | ux | 2 |
| Displacement | uy | 4 |
| Displacement | ux | 5 |
| Stress | σxx | 7 |
Figure 1b:. Upper left quarter, using symmetry conditions, with point numbers of computed data
Figure 2a:. v. Mises stresses at λ = 4.5 for hardening material
.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0922538298800068
INTRODUCTION
G.M. PHILLIPS, P.J. TAYLOR, in Theory and Applications of Numerical Analysis (Second Edition), 1996
Section 1.2
- 1.2
-
Show that an a priori error bound for the result of the bisection method for finding √a with 0 < a < 1 is
|x−√a| ≤ (1−a)/2N,
where N is the number of iterations completed.
- 1.3
-
In Algorithm 1.1 we have at each stage
|x−√a| ≤ x1−x02.
Show that if
(x1−x0)2<4aε2,
then the relative error in x as an approximation to √a satisfies
|x−√a√a|<ε.
Hence modify the algorithm so that the iterations stop when the relative error is less than ε.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780125535601500021
Computational Error and Complexity in Science and Engineering
V. Lakshmikantham, S.K. Sen, in Mathematics in Science and Engineering, 2005
2.4.1 A priori versus a posteriori error analysis
The main function of the a priori error analysis is to show if an algorithm is stable. If it is not then the job of the analysis is to determine the reasons for its instability. In this analysis, we do not assume that a solution has already been obtained.
Having obtained an approximate solution, we can obtain sharper backward error bounds in a posteriori error analysis. Let λ and x be the computed eigenvalue and the corresponding normalized eigenvector (||x|| = 1) of the n × n matrix A. If we write the residual r = Ax – λx as (A – rxH)x = λx then the computed λ and computed x are exact for the matrix A – rxH. The matrix A has an eigenvalue in the interval [λ – ||r||, λ + ||r||] if A is Hermitian.
When solving linear system Ax = b, we can compute the residual r = Ax — b, where x is the computed solution vector. An improved solution x – Δx of the system can then be obtained by solving the system AΔx = r. Further improvement (iterative refinement) can be achieved by replacing x by x – Δx and solving AΔx = r.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0076539205800530
Spline Adaptive Filters
Michele Scarpiniti, … Aurelio Uncini, in Adaptive Learning Methods for Nonlinear System Modeling, 2018
3.4.2 Steady-State MSE
The aim of this paragraph is to evaluate the mean square performance of some of the proposed architectures at steady state. In particular, we are interested in the derivation of the EMSE of the nonlinear adaptive filter [2]. For simplicity we limit our analysis to the case of the Wiener and Hammerstein systems. The steady-state analysis is performed in a separate manner, by considering first the case of the linear filter alone and then the nonlinear spline function alone. Note that, since we are interested only in the steady state, the fixed subsystem in each substep can be considered adapted. The analysis is conducted by using a model of the same type of the used one, as shown in Fig. 3.5 for the particular case of the WSAF. Similar schemes are valid for the other kinds of architectures.
Figure 3.5. Model used for statistical performance evaluation, in the particular case of the WSAF.
In the following we denote with ε[n] the a priori error of the whole system, with εw[n] the a priori error when only the linear filter is adapted while the spline control points are fixed and similarly with εq[n] the a priori error when only the control points are adapted while the linear filter is fixed. In order to make tractable the mathematical derivation, some assumption must be introduced:
- A1.
-
The noise sequence v[n] is independent and identically distributed with variance σv2 and zero mean.
- A2.
-
The noise sequence v[n] is independent of xn, sn, ε[n], εw[n] and εq[n].
- A3.
-
The input sequence x[n] is zero mean with variance σx2 and at steady state it is independent of wn.
- A4.
-
At steady state, the error sequence e[n] and the a priori error sequence ε[n] are independent of φi′(un), φi′2(un), ‖xn‖, ‖sn‖, ‖CTun‖ and ‖CTUi,nwn‖.
The EMSE ζ is defined at steady state as
(3.30)ζ≡limn→∞E{ε2[n]}.
Similar definitions hold for the EMSE ζw due to the linear filter component wn only and the EMSE ζq due to the spline nonlinearity qn only.
The MSE analysis has been performed by the energy conservation method [2]. Following the derivation presented in [41] and [44] we obtain an interesting property.
Proposition 1
The EMSE ζ of a Wiener and a Hammerstein spline adaptive filter satisfies the condition
(3.31)ζ≈ζw+ζq.
The values of ζw and ζq are dependent on the particular SAF architecture considered. Specifically, for the Wiener case, we have [44]
(3.32)ζw=μw[n]σv2E{φi′2(un)‖xn‖2}2Δx2E{φi′(un)c3qi,n}−μw[n]E{φi′2(un)‖xn‖2},
where c3 is the third row of the C matrix and
(3.33)ζq=μq[n]σv2E{‖CTun‖2}2−μq[n]E{‖CTun‖2}.
Other useful properties on the steady-state performances of the WSAF can be found in [44]. For the Hammerstein case, we have [41]
(3.34)ζw=μw[n]σv2E{‖sn‖2}2−μw[n]E{‖sn‖2}
and
(3.35)ζq=μq[n]σv2E{‖CTUi,nwn‖2}2−μq[n]E{‖CTUi,nwn‖2}.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978012812976000004X
Advances in Adaptive Computational Methods in Mechanics
T. Coupez, … J.L. Chenot, in Studies in Applied Mechanics, 1998
2 FINITE ELEMENT SOLVER AND ADAPTIVE ANALYSIS
Most of the adaptive schemes are based on the convergence properties and the associated a priori error estimate of the finite element method. It assumes that a mesh independent solution exists and that the numerical solutions approximate it. More precisely, it is expected that the error decreases along with the mesh size parameter. In this context, the behavior of finite element method is well known for linear elasticity problems and it has been extended to incompressible materials both in fluid and solid applications through the mixed finite element theory [5].
Both in metal and polymer forming, the viscoplastic behavior of the material can be modeled by a flow formulation, the viscosity being a function of the second invariant of the strain rate tensor ε(v):
(1)ηεv=K2|εv|m−1.
On a time depending domain Ω, inertia effects and volume forces being negligible, the velocity v and pressure p fields are solution of the following problem:
(2)∇⋅2ηεvεv−∇p=0∇⋅v=0inΩon∂Ω∩∂Ov−vO.n>0andτ=0orv−vO.n=0,andτ=αv−vOv−vO,
The inequality characterizes the unilateral contact boundary condition which plays a crucial role in the applications presented here. vO denotes the velocity of the contacting rigid bodies (the forming tools) described by the domain O, n being the outside normal of its boundary ∂Ο. The relationship which gives the tangent shear stress τ at the interface matter/tool as a function of the relative tangent velocity follows a power friction law. The viscoplasticity coefficient m usually ranges between 0 and 1. It is often around 0.1 in hot metal forming applications.
The solvers behind the applications presented in this paper are designed to be used with triangle elements in 2D and tetrahedral elements in 3D, making it possible to deal with general meshing techniques detailed after. In 2D the mixed finite element will be based on the Crouseix-Raviart element (P2 + /P1) and on the P2/P0 element [16]. In 3D, we use a first order element entering in the mini-element family [1]. The bubble is constructed with a pyramidal function which is condensed at the element level, without taking into account the nonlinear part of the behavior law [9]. This element enters in the equivalent class of stable/stabilized mixed formulation [20, 15, 27]. An important advantage of this formulation is to enable a fully parallel iterative solution [14].
Despite of the unilateral contact condition, this flow formulation can be analyzed in term of a generalized Stokes problem. From the numerical analysis standpoint, the convergence of the finite element method for the viscoplastic problem (quasi-Newtonian flow) has been analyzed in term of the a priori estimate in [3], using the W1,m + 1 norm, m being the viscoplastic power index. In term of the a posteriori estimate, the residual technique introduced for the Stokes equation [30] has been extended to the quasi-Newtonian flows [2]. In engineering, the error analysis is often based on an energy norm point of view. In this context, the simple Zienkiewicz-Zhu adaptive procedure [25] based on the smoothness of the stress tensor has been adopted in [18, 17, 19] from which several 2D examples are presented in this paper. From the mechanical point of view, a constitutive relation error analysis has been introduced by Ladeveze and specifically applied to elastoplastic materials [24].
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0922538298800214
FINITE ELEMENT METHODS
S.S. Rao, in Encyclopedia of Vibration, 2001
Error Estimation
The error estimation procedures can be grouped into two distinct types: a priori and a posteriori estimates. A priori error estimates are based upon the characteristics of the solution and provide qualitative information about the asymptotic rate of convergence. The classic a priori error estimate is given by:
[88]‖u−uh‖m≤chp,p=k+1−m>0
where k is the degree of the interpolation polynomial, h is the characteristic length of an element, p is the rate of convergence, and c is a constant. Eqn (88) gives not only the rate at which the FE solution approaches the exact solution, but also indicates how one can improve the solution. We can decrease the mesh size (called h-convergence) or increase the order of the interpolation polynomial (called p-convergence). Incorporating both h— and p-convergences produces the h − p convergence technique. For illustration, consider the differential equation:
[89]d2udx2+2=0;0<x<1
with:
[90]u(0)=u(1)=0
The exact solution of the problem is:
[91]u(x)=x(1−x)
and the FE solutions are given by, for different number of elements, N:
ForN=2:uh(x)={hx,0≤x≤hh2(2−xh),h≤x≤2h}
[93]ForN=3:uh(x)={2hx,0≤x≤h2h2,h≤x≤2h2h2(3−xh),2h≤x≤3h}
[94]ForN=4:uh(x)={3hx,0≤x≤h2h2+hx,h≤x≤2h6h2−hx,2h≤x≤3h3h2(4−xh),3h≤x≤4h}
The energy and L2 norms can be determined using N = 2(h = 0.5), N = 3(h = 0.333) and N = 4(h = 0.25) and the results are given in Table 3. These results are shown plotted in Figure 6 using a log–log scale. The slopes of the plots represent measures of the rates of convergence. The results indicate that the error in the energy and L2 norms have different rates of convergence; the error in the energy norm is of order one lower than the error in the L2 norm. Physically, this indicates that derivatives (stresses in structural problems) converge more slowly than the values themselves (displacements in structural problems). A priori estimates are adequate for determining the convergence rate of a particular FE element solution, but they lack the ability to give quantitative information about the local or global errors of the solution. If refinement of the solution is to be performed, quantitative estimates are clearly needed to determine whether refinement is needed in any given area of the computational domain. For this reason, a posteriori (after the solution of the problem) error estimates are developed. Many researchers have developed different estimates over the years and all the methods can be grouped into four categories: (i) dual analysis; (ii) Richardson’s extrapolation; (iii) residual type of estimator; and (iv) postprocessing type of estimator.
Table 3. A priori estimates of the error in the energy and L2 norms
| h | ∥e∥0 | ∥e∥1 |
|---|---|---|
| 0.5 | 0.04564 | 0.2923 |
| 0.333 | 0.02029 | 0.1935 |
| 0.25 | 0.01141 | 0.1443 |
Figure 6. Energy and L2 norms of error with mesh size.
In the dual analysis, the principles of complementary energy and potential energy are applied to obtain upper and lower bounds, respectively, on the energy of the exact solution. Since the potential and complementary energy principles are fundamentally different, two separate programs are to be used for this analysis. In addition, the solution based on complementary energy is very difficult and hence the dual analysis is not commonly used. The Richardson’s extrapolation is a numerical analysis technique for estimating the error in the solution by solving the problem with two different grid sizes, provided the functional form of the solution is known. In the context of the FE method, the a priori analysis provides the functional form. Similar to the dual analysis, the extrapolation technique is a classic method of error estimation that has proven to be computationally very expensive in order to compete with other more efficient methods and hence is not widely used.
The residual type of error estimation can be understood by considering the FE solution of the following boundary value problem, stated in operator form:
[95]Au+f=0
When the FE finite element solution uh, is used, eqn (95) leads to the residual R:
[96]Auh+f=R≠0
Eqn (96) shows that the residual effectively acts as a separate forcing function in the differential equation. This leads to the concept that the FE solution is the exact solution to a perturbed problem with a supplementary pseudo-force system. Subtracting eqn (96) from [95] produces:
[97]Ac+R=0
where e = u − uh is the error. Hence the estimation of the error in the problem amounts to finding the solution of this problem. The residual R is composed of residuals in the interior of the domain as well as residuals on the boundary. The domain residuals are determined by substituting the FE solution into the differential equation. The boundary residuals, however, are more complicated since the derivatives of uh, may not be continuous along the boundary.
For the postprocessing type of estimator, the error in the FE stress solution (obtained by differentiating the FE displacement solution) is defined as:
[98]eσ=σ−σh
Then the error in the energy norm is computed as:
[99]‖e‖=u−uh‖=(∫VeσTD−1eσdV)1/2
where D is the elasticity matrix. An estimator to eσ can be produced by replacing σ in eqn (98) by the recovered solution σ*:
[100]eσ≈eσ*=σ*−σh
where σ* is interpolated from the nodal values using the same basis functions N as those used for uh.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B0122270851000047
Partial-update adaptive filters
Kutluyıl Doğançay, in Partial-Update Adaptive Signal Processing, 2008
4.7.6 Set-membership partial-update APA
Set-membership filtering aims to maintain a bound on the output error magnitude of an adaptive filter. Adaptive filter coefficients are only updated when the a priori error magnitude exceeds a predetermined threshold γ. The resulting update mechanism is sparse in time and provides an important reduction in power consumption. The set-membership partial-update NLMS updates M out of N coefficients with largest regressor norm whenever |e(k)|>γ. The coefficient updates are constructed to achieve |ep(k)|=γ.
Extending the error magnitude bound over P≤M outputs y(k),y(k−1),…,y(k−P+1) and using selective partial updates to limit update complexity leads to the set-membership partial-update APA. At each coefficient update the set-membership partial-update APA solves the following constrained optimization problem:
(4.74a)minIM(k)minwM(k+1)‖wM(k+1)−wM(k)︸δwM(k+1)‖22
subject to:
(4.74b)ep(k)=γ(k)
where γ(k)=[γ1(k),…,γP(k)]T is an error constraint vector with |γi(k)|≤γ. Equation (4.74b) can be rewritten as:
(4.75)
e(k)−ep(k)=e(k)−γ(k)
XM(k)δwM(k+1)=e(k)−γ(k)
For fixed IM(k), (4.74) is equivalent to solving the following underdetermined minimum-norm least-squares problem for δwM(k+1):
(4.76)XM(k)δwM(k+1)=e(k)−γ(k),‖δwM(k+1)‖22 is minimum
with the unique solution given by:
(4.77)δwM(k+1)=XM†(k)(e(k)−γ(k))=XMT(k)(XM(k)XMT(k))−1(e(k)−γ(k))
where XM(k)XMT(k) is assumed to be invertible. Introducing a regularization parameter to avoid rank-deficient matrix inversion we finally obtain the set-membership partial-update APA recursion for fixed IM(k):
(4.78)wM(k+1)=wM(k)+μ(k)XMT(k)(ϵI+XM(k)XMT(k))−1(e(k)−γ(k))
where:
(4.79)μ(k)={1if |e(k)|>γ0otherwise
There are infinitely many possibilities for the error constraint vector γ(k). Two particular choices for γ(k) were proposed in (Werner and Diniz, 2001). The first one sets γ(k)=0 which leads to:
(4.80)w(k+1)=w(k)+μ(k)IM(k)XT(k)(ϵI+X(k)IM(k)XT(k))−1e(k)
This recursion, which we call the set-membership partial-update APA-1, uses the selective-partial-update APA whenever |e(k)|>γ and applies no update otherwise. The other possibility for γ(k) is defined by:
(4.81)γ(k)=[γe(k)|e(k)|e2(k)⋮eP(k)]
where e(k)=[e(k),e2(k),…,eP(k)]T with |ei(k)|≤γ for i=2,…,P. This results in:
w(k+1)=w(k)+μ(k)IM(k)XT(k)(ϵI+X(k)IM(k)XT(k))−1u(k),
(4.82)u(k)=[e(k)(1−γ|e(k)|)0⋮0]
which we shall refer to as the set-membership partial-update APA-2.
The optimum coefficient selection matrix IM(k) solving (4.74) is obtained from:
(4.83)
minIM(k)‖XMT(k)(XM(k)XMT(k))−1(e(k)−γ(k))‖22
minIM(k)(e(k)−γ(k))T(XM(k)XMT(k))−1(e(k)−γ(k))
which is similar to the minimization problem for the selective-partial-update APA in (4.70). Thus, a simplified approximate coefficient selection matrix for the set-membership partial-update APA is given by (4.64). Note that the full implementation of (4.83) would be computationally expensive and, therefore, we do not advocate its use.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123741967000106
Approaches to partial coefficient updates
Kutluyıl Doğançay, in Partial-Update Adaptive Signal Processing, 2008
2.6.1 Constrained optimization
Let us assume a linear adaptive filter with output signal y(k)=wT(k)x(k). Then we have:
(2.82)
e(k)=d(k)−y(k)a priori error
ep(k)=d(k)−wT(k+1)x(k)a posteriori error
The a posteriori error gives the error signal at the adaptive filter output when the current adaptive filter coefficients are replaced with the updated coefficients. Using the principle of minimum disturbance, a selective-partial-update adaptive filtering algorithm is derived from the solution of the following constrained optimization problem:
(2.83a)minIM(k)minwM(k+1)‖wM(k+1)−wM(k))‖22
subject to:
(2.83b)ep(k)−(1−μ‖xM(k)‖22ϵ+‖xM(k)‖22)e(k)=0
where ϵ is a small positive regularization constant which also serves the purpose of avoiding division by zero, wM(k) is an M×1 subvector of w(k) comprised of entries given by the set {wj(k):ij(k)=1}, and xM(k) is an M×1 subvector of x(k) defined similarly to wM(k). Here the ij(k) are the diagonal elements of the coefficient selection matrix IM(k). Note that wT(k)IM(k)w(k)=‖wM(k)‖22 and xT(k)IM(k)x(k)=‖xM(k)‖22. Thus wM(k) is the subset of adaptive filter coefficients selected for update according to IM(k). For example, if N=3 and M=2, IM(k) and wM(k) are related as follows:
IM(k)=diag(1,1,0),wM(k)=[w1(k),w2(k)]TIM(k)=diag(1,0,1),wM(k)=[w1(k),w3(k)]TIM(k)=diag(0,1,1),wM(k)=[w2(k),w3(k)]T.
Using this relationship between IM(k) and wM(k), we have ‖wM(k+1)−wM(k))‖22=‖IM(k)(w(k+1)−w(k))‖22 in (2.83). Since only the coefficients identified by IM(k) are updated, an implicit constraint of any partial-update technique, including (2.83), is that:
(2.84)w(k+1)−w(k)=IM(k)(w(k+1)−w(k))
We will have occasion to resort to this partial-update ‘constraint’ in the sequel.
The constrained optimization problem in (2.83) may be solved either by using the method of Lagrange multipliers as we shall see next or by formulating it as an underdetermined minimum-norm estimation problem. We will use the latter approach when we discuss the ℓ1 and ℓ∞-norm constrained optimization problems later in the section. Suppose that IM(k) is fixed for the time being. Then we have:
(2.85a)minwM(k+1)‖wM(k+1)−wM(k))‖22
subject to:
(2.85b)ep(k)−(1−μ‖xM(k)‖22ϵ+‖xM(k)‖22)e(k)=0.
The cost function to be minimized is:
(2.86)J(wM(k+1),λ)=‖wM(k+1)−wM(k))‖22+λ(ep(k)−(1−μ‖xM(k)‖22ϵ+‖xM(k)‖22)e(k))
where λ is a Lagrange multiplier. Setting:
(2.87)∂J(wM(k+1),λ)∂wM(k+1)=0and∂J(wM(k+1),λ)∂λ=0
yields:
(2.88a)wM(k+1)−wM(k)−λ2xM(k)=0
(2.88b)(w(k+1)−w(k))Tx(k)−μe(k)‖xM(k)‖22ϵ+‖xM(k)‖22=0
From (2.88a) we have:
(2.89a)(wM(k+1)−wM(k))TxM(k)=λ2xMT(k)xM(k)
(2.89b)=(w(k+1)−w(k))Tx(k)
since only the adaptive filter coefficients selected by IM(k) are updated [see (2.84)]. Substituting (2.89) into (2.88b) yields:
(2.90)λ=2μe(k)1ϵ+‖xM(k)‖22
Using this result in (2.88a) gives the desired adaptation equation for fixed IM(k):
(2.91)wM(k+1)=wM(k)+μϵ+‖xM(k)‖22e(k)xM(k)
What remains to be done is to find IM(k) that results in the minimum-norm coefficient update. This is done by solving:
(2.92)minIM(k)‖μϵ+‖xM(k)‖22e(k)xM(k)‖22
which is equivalent to:
(2.93)maxIM(k)‖xM(k)‖22+ϵ2‖xM(k)‖22
If any M entries of the regressor vector were zero, then the solution would be:
(2.94)minIM(k)‖xM(k)‖22
which would select the adaptive filter coefficients corresponding to the M zero input samples. For such an input (2.83) would yield the trivial solution wM(k+1)=wM(k). However, this solution is not what we wanted. We get zero update and therefore the adaptation process freezes while we could have selected some non-zero subset of the regressor vector yielding a non-zero update. This example highlights an important consideration when applying the principle of minimum disturbance, viz. the requirement to avoid the trivial solution by ruling out zero regressor subsets from consideration. Letting ϵ→0 does the trick by replacing (2.93) with:
(2.95)maxIM(k)‖xM(k)‖22
The solution to this selection criterion is identical to the coefficient selection matrix of the M-max LMS algorithm:
(2.96)IM(k)=[i1(k)0⋯00i2(k)⋱⋮⋮⋱⋱00⋯0iN(k)],ij(k)={1if |x(k−j+1)|∈max1≤l≤N(|x(k−l+1)|,M)0otherwise
If the step-size parameter μ in the optimization constraint obeys the inequality:
(2.97)|1−μ‖xM(k)‖22ϵ+‖xM(k)‖22|<1
then the a posteriori error magnitude is always smaller than the a priori error magnitude for non-zero e(k). This condition is readily met if 0<μ<2 with μ=1 yielding ep(k)≈0.
Combining (2.91) and (2.96) we obtain the solution to (2.83) as:
(2.98)w(k+1)=w(k)+μϵ+‖IM(k)x(k)‖22e(k)IM(k)x(k)
This algorithm is known as the selective-partial-update NLMS algorithm. When M=N (i.e. all coefficients are updated) it reduces to the conventional NLMS algorithm. The M-max NLMS algorithm is defined by:
(2.99)w(k+1)=w(k)+μϵ+‖x(k)‖22e(k)IM(k)x(k)
The selective-partial-update NLMS algorithm differs from the M-max NLMS algorithm in the way the step-size parameter μ is normalized. The following discussion will show that the selective-partial-update NLMS algorithm is a natural extension of Newton’s method.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123741967000088
Kurtosis-based, data-selective affine projection adaptive filtering algorithm for speech processing application
S. Radhika, A. Chandrasekar, in Applied Speech Processing, 2021
1.4.1 Steady-state mean square analysis
The update recursion of the proposed DS-APA is written as follows:
(1.16)wk+1=wk+μATkδI+AkATk−1ekifγminσn2≤ek2≤γmaxσn2wkotherwise
In order to obtain steady-state MSE, Eq. (1.7) is taken. Substituting for d(k) and y(k) in e(k) we get e(k) = woTx(k) + n(k) − wTx(k).The error consists of two terms, namely, a priori error and a posteriori error vectors as follows:
(1.17)eak=Akw~k
(1.18)epk=Akw~k+1
where w~k=woT−wTk is the weights error vector. In order to resolve the nonlinearity present in Eq. (1.16), the model introduced in Section 1.2 is used in Eq. (1.16) as
(1.19)wn+1=wk+μPupdateATkδI+AkATk−1ek
Eq. (1.19) is still more nonlinear due to the presence of Pupdate, which lies between 0 and 1 and is valid only for a certain range given by Eq. (1.10).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128238981000059
Elements of Computational Methods
Riccardo Sacco, … Aurelio Giancarlo Mauri, in A Comprehensive Physically Based Approach to Modeling in Bioengineering and Life Sciences, 2019
3.3.1.1 Error Analysis
In this section we consider the case of the interpolation of a given continuous function f:[a,b]→R. For any x∈R, the interpolation error is defined as
(3.29)Enf(x):=f(x)−Πnf(x).
The principal aim of the polynomial interpolation process is the uniform convergence of Πnf to f as a function of the polynomial degree n.
Definition 3.10
We say that Πnf converges uniformly to f if
(3.30)limn→∞Πnf(x)=f(x)∀x∈[a,b].
The following a priori error estimate can be proved.
Theorem 3.3
Given n+1 distinct nodes xi∈[a,b] and given a function f∈Cn+1([a,b]), we have
(3.31)‖Enf‖C0([a,b])⩽1(n+1)!‖f(n+1)‖C0([a,b])‖ωn+1‖C0([a,b]),
where ‖⋅‖C0([a,b]) denotes the norm for the space C0([a,b]) introduced in (2.120) and ωn+1∈Pn+1 is the nodal polynomial defined as
(3.32)ωn+1(x)=(x−x0)(x−x1)…(x−xn)=Πi=0n(x−xi).
Remark 3.6
The a priori error estimate (3.31) clearly indicates that a sufficient condition in order for (3.30) to be satisfied is
(3.33)limn→∞1(n+1)!‖f(n+1)‖C0([a,b])‖ωn+1‖C0([a,b])=0.
A glance at the three terms contributing to (3.33) shows that the first term becomes very small as n grows, the second term depends only on the given function f, whereas the third term depends on the distribution of the interpolation nodes xi, i=0,…,n. This issue plays a relevant role, as outlined in Example 3.4.
Example 3.3
We apply to the case of Example 3.2 the interpolating polynomial approximation on a set of n+1 equally spaced nodes. We show in Fig. 3.8 the logarithmic plot of the error as a function of n, for n∈[1,15]. We see that the interpolating polynomial approximation is uniformly converging because the maximum error continues to decrease as n becomes large. The Matlab commands to be run to obtain Fig. 3.8 are listed in the script 28.8.
Figure 3.8. Uniform convergence of polynomial interpolation on equally spaced nodes. Plot of the logarithm of the maximum error in absolute value for f(x)=sin(x) over [a,b]=[0,10]. The degree n varies between 1 and 15.
Example 3.4 Runge’s counterexample
Let f(x)=1/(1+x2) and [a,b]=[−5,5]. The function f is known as Runge’s function and it represents the example of a smooth function for which the uniform convergence condition (3.30) is not satisfied. The essence of the example is clarified by Fig. 3.9, which shows the result of having interpolated the function f with a polynomial Πnf of degree n on n+1 nodes equally distributed in [a,b], where n takes the values 1, 5, 10 and 15. We see that, as n increases, oscillations of increasing size occur throughout the interval [a,b], being much larger in the neighborhood of the endpoints of the interval. This trend gets even worse if larger values of the polynomial degree n are considered. Fig. 3.9 can be obtained by running the Matlab script 28.9.
Figure 3.9. Polynomial interpolation of Runge’s function over [−5,+5]. The interpolating nodes xi, i = 0,…,n are equally distributed on [a,b]. The degree n takes the values 1, 5, 10 and 15. A legend in the figure associates the linestyle of each interpolating polynomial with the corresponding value of n. The solid line in cyan color (light gray in the printed version) represents Runge’s function.
The negative conclusions that can be drawn from Example 3.4 suggest that a safer approach to polynomial interpolation should be taken in order to ensure that the uniform convergence condition (3.30) is verified for every continuous function f and for every choice of the distribution of the interpolation nodes. This objective can be achieved by resorting to piecewise polynomial interpolations, as described in the next section.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128125182000111
Пусть ищется решение системы линейных уравнений с невырожденной матрицей A (
).
Так как , следовательно, система линейных уравнений
имеет единственное решение.
Преобразуем систему линейных уравнений к виду:
, где
– квадратная матрица,
– вектор. Причем системы являются эквивалентными, то есть их решения совпадают. В дальнейшем мы будем рассматривать систему
.
Выбирается вектор начального приближения:
.
Строится итерационный процесс:
.
Итерационный процесс прекращается при выполнении условия:
,
где – точное решение системы линейных уравнений. В этом случае
– приближенное решение системы линейных уравнений с точностью
, полученное методом итераций.
Естественно, возникает ряд вопросов:
· При каких условиях последовательность сходится к точному решению системы линейных уравнений?
· Как выбирать начальное приближение ?
· Как сформулировать условия остановки итерационного процесса?
Последовательно будем отвечать на эти вопросы.
Теорема о сходимости
Пусть система линейных уравнений имеет единственное решение. Для сходимости последовательности приближений
к точному решению системы линейных уравнений
достаточно, чтобы
. При выполнении этого условия последовательность
сходится к точному решению при любом векторе начального приближения
.
Оценка погрешности. Для метода итераций удается получить две оценки погрешности: априорную и апостериорную.
Априорная оценка погрешности – это оценка погрешности , которую можно получить до начала вычислений, зная только
и
.
Апостериорная оценка погрешности – это оценка погрешности , которую получают, используя вычислительные приближения
и зная
.
Теорема (априорная оценка погрешности)
Пусть система линейных уравнений имеет единственное решение. Пусть
. Тогда имеет место неравенство:
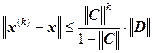
,
где – k-е приближение, полученное методом итераций;
– точное решение системы линейных уравнений
.
Отметим, что априорная оценка погрешности позволяет до вычислений оценить число шагов k, необходимых для достижения точности :
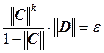

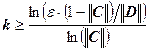
Следствие. Пусть система линейных уравнений имеет единственное решение. Пусть
, тогда для числа итераций k, необходимых для достижения точности e, справедливо следующее неравенство:
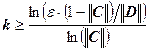
Отметим, что все нормы, входящие в это неравенство, должны быть согласованы. То есть если мы выбираем первую норму матрицы С, то должны взять и первую норму вектора D. Как правило, число шагов k, полученное из этой оценки, является заметно завышенным.
Теорема (апостериорная оценка погрешности)
Пусть система линейных уравнений имеет единственное решение. Пусть
, тогда имеет место неравенство:
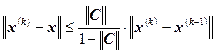
Следствие. Если выполняется условие 
. То есть, для того чтобы получить приближенное решение с точностью e, необходимо использовать следующее условие остановки итерационного процесса:
Сформулируем алгоритм метода итераций
1) Задана система линейных уравнений с невырожденной матрицей.
Преобразуем систему линейных уравнений к виду:
, где C – квадратная матрица, D – вектор. Причем системы являются эквивалентными и
.
2) Выбираем произвольный вектор начального приближения: .
3) Строим последовательность: .
4) Эта последовательность сходится к точному решению системы линейных уравнений . При выполнении условия остановки итерационного процесса вычисления прекращаются.
Пример 1
Построить и обосновать алгоритм решения системы линейных уравнений методом итераций с точностью
:
Решение
Прежде всего, необходимо обосновать, что , если это не заданно в условии задачи. В нашем случае можно воспользоваться следующей теоремой:
Теорема
Если для матрицы А выполняются n неравенств 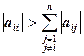
Это свойство называется диагональным преобладанием: модуль диагонального элемента больше, чем сумма модулей внедиагональных элементов строки.
Эту теорему можно сформулировать и в другом виде, используя перенумерацию строк (столбцов). Определитель матрицы А не равен нулю, если в каждой строке (столбце) А имеется преобладающий элемент и эти элементы расположены в различных столбцах (строках).
В нашем случае:
В общем случае, нахождение матрицы C – сложная задача. Но в нашем примере очень легко найти матрицу C, удовлетворяющую всем условиям. Достаточно взять , тогда
:
,
– эти системы эквивалентны.
.
Найдем С и докажем, что :
.
Вычислим первую норму С:
2. Выбираем вектор начального приближения:
Так как , то итерационный процесс:
сходится для любого начального приближения.
3. Формула метода: .
4. Условие остановки итерационного процесса:
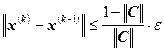
, следовательно,
.
При выполнении этого условия считается приближенным решением система линейных уравнений с точностью
, полученным методом итераций.
Пример 2
Оценить число шагов, необходимых для достижения точности , при решении системы линейных уравнений
методом итераций.
Решение
Рассмотрим ту же систему линейных уравнений. Воспользуемся следствием из априорной оценкой погрешности. Условие на матрицу C выполнено:
, следовательно, метод итераций сходится и справедливо неравенство:
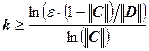
Мы вычисляли первую норму матрицы С, следовательно, и у вектора D также необходимо вычислять первую норму:
,
,
следовательно, .
Оценку сложности алгоритма метода итераций (по времени) мы получаем из априорной оценки погрешности
На каждом шаге итерационного процесса мы выполняем О(n2) арифметических действий, где n – порядок матрицы, следовательно, общее число арифметических действий: kО(n2).
Для реализации алгоритма метода итераций на каждом шаге необходимо хранить матрицу С, ,
и D, следовательно, требуется памяти О(n2).
Если ||C|| < 1, то алгоритм метода итераций для решения система линейных уравнений является устойчивым по отношению к вычислительной погрешности.
Недостатки метода итераций для решения систем линейных уравнений
1) Нет общего приема для перехода от матрицы А к матрице С таким образом, чтобы .
2) Метод итераций медленно сходится, если близка к 1.