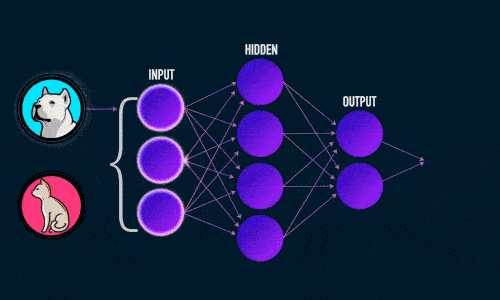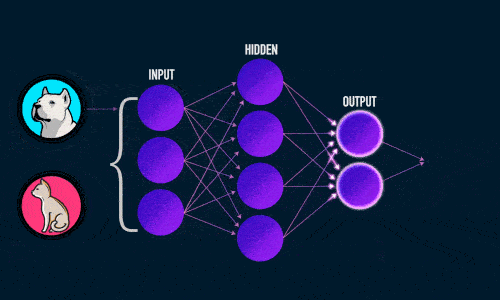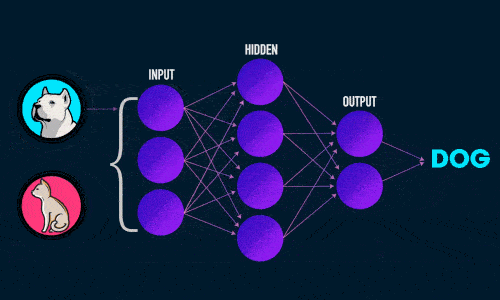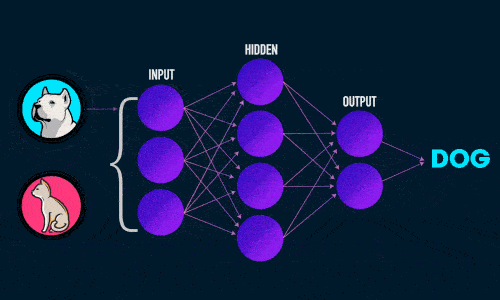
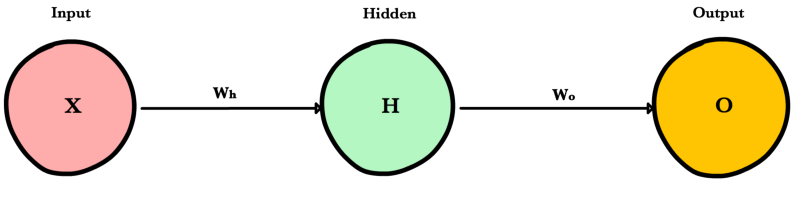
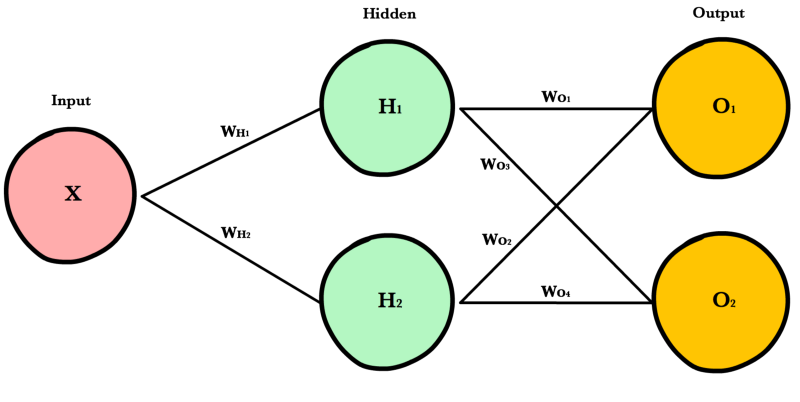
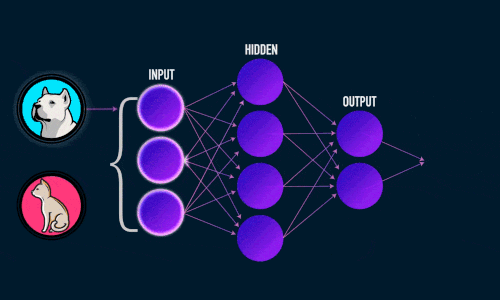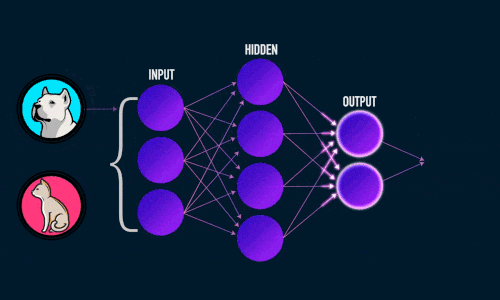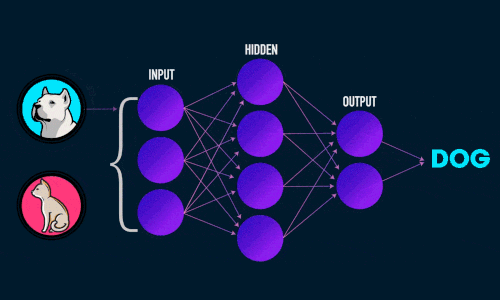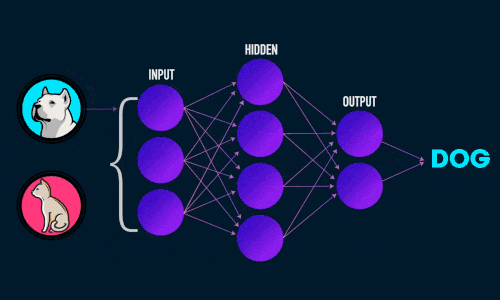
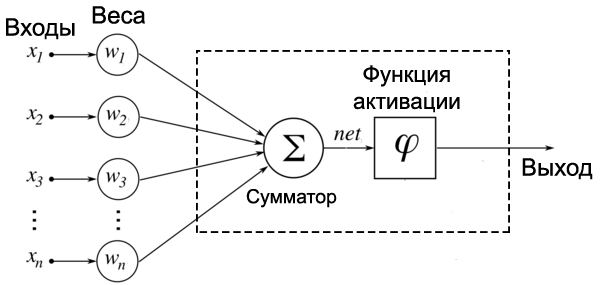
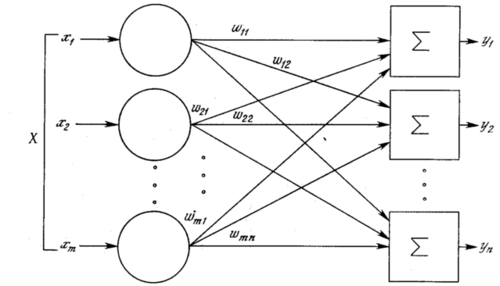
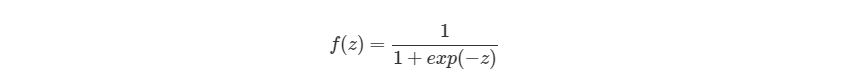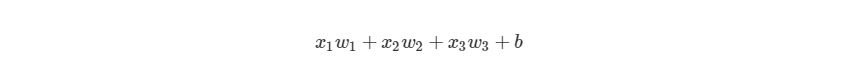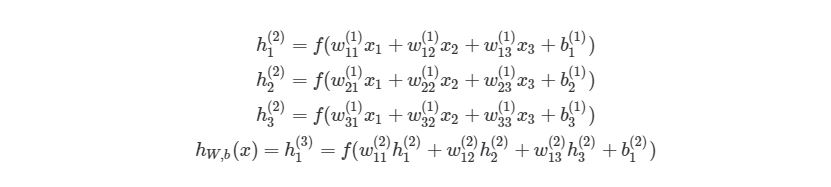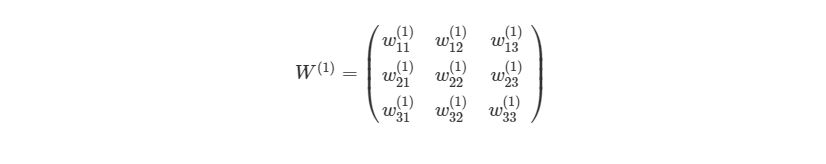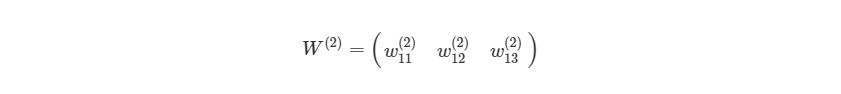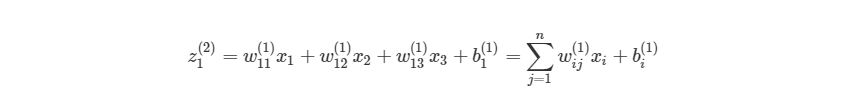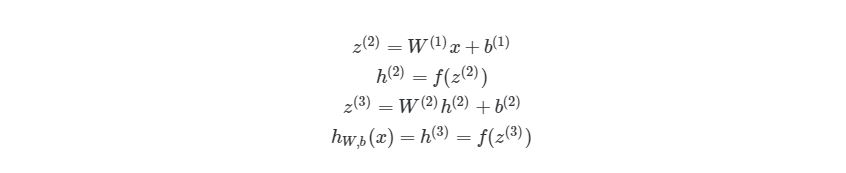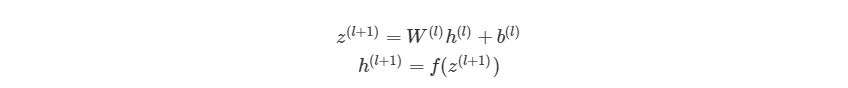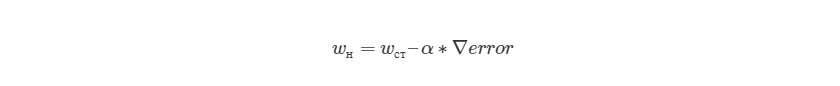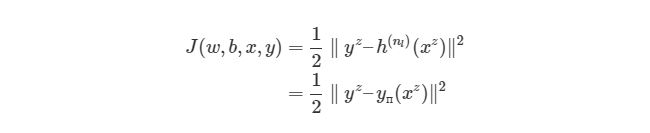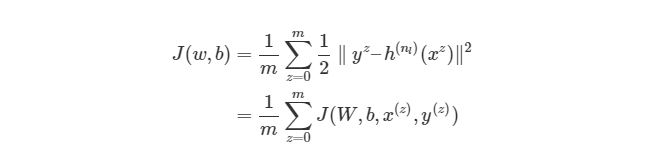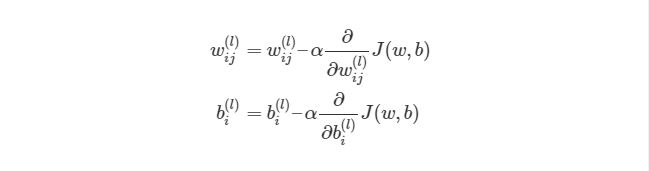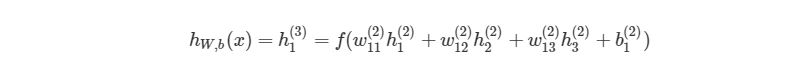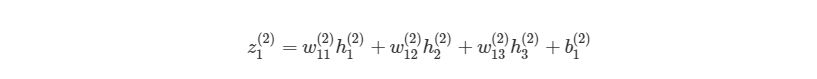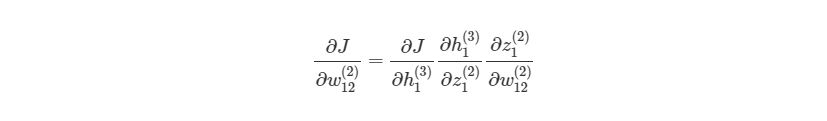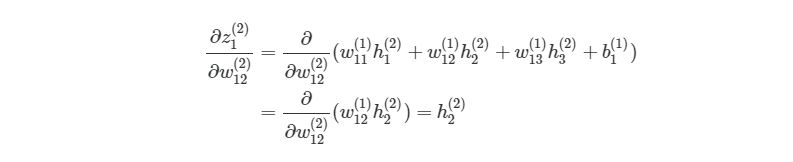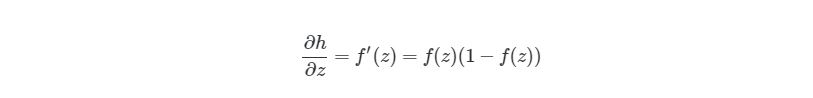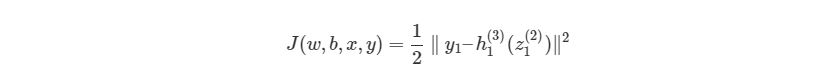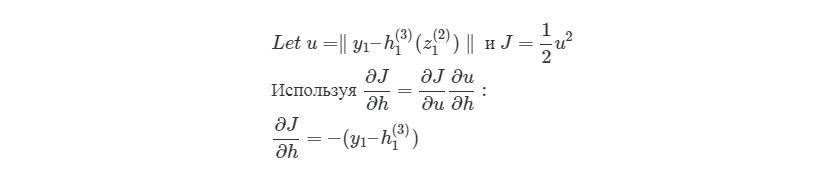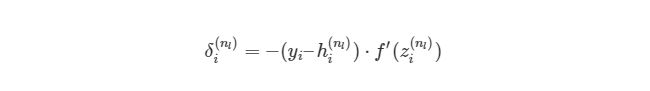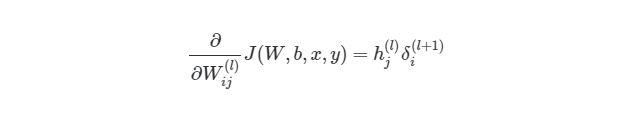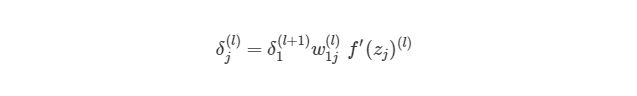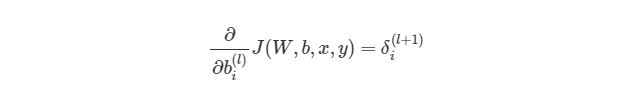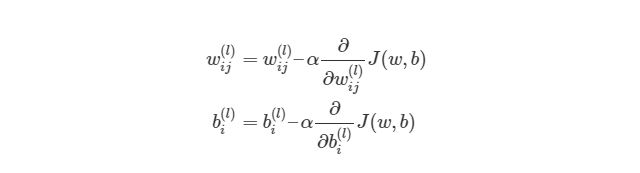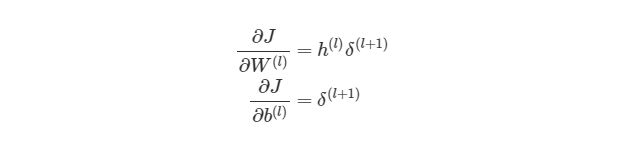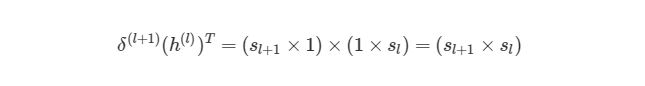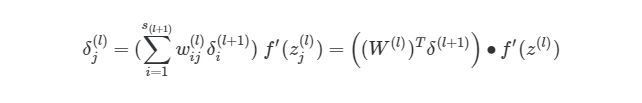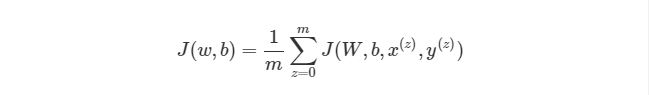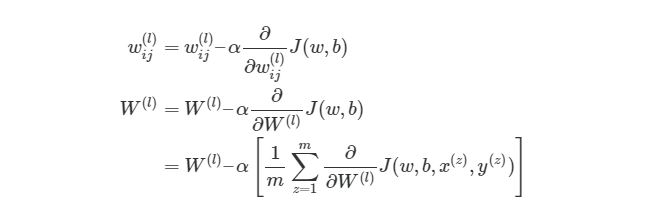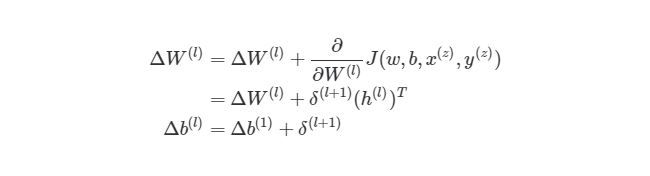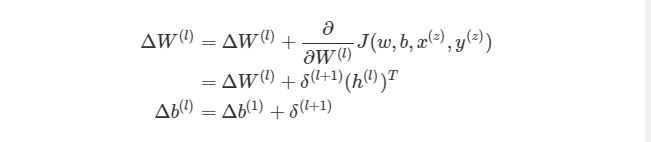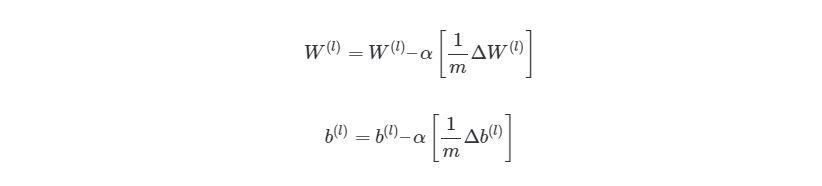Алгоритм прямого распространения ошибки - Решение и исправление самых разных ошибок на TopOshibok.ru

Нейронная сеть — попытка с помощью математических моделей воспроизвести работу человеческого мозга для создания машин, обладающих искусственным интеллектом.

Нейросеть обычно обучается с учителем. Это означает наличие обучающего набора данных (датасета), который содержит примеры с правильными результатами решений: ответами на вопросы, метками, сегментами, классами. Нейронная сеть пытается воспроизвести результат самостоятельно на новом наборе данных.

Неразмеченные наборы также используют для обучения нейронных сетей, но мы не будем здесь это рассматривать.

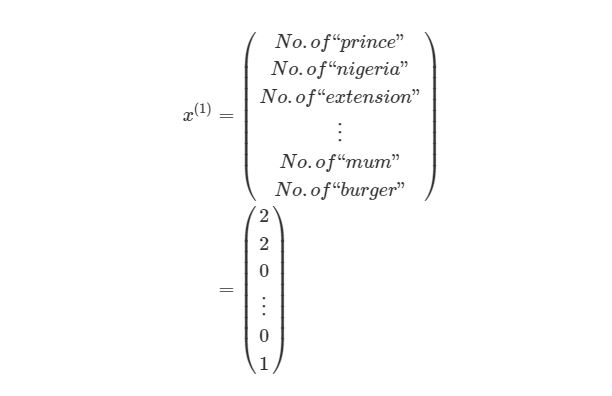
Например, если вы хотите создать нейросеть для оценки эмоциональную тональности текста, датасетом будет список предложений с соответствующими каждому эмоциональными оценками. Тональность текста определяют признаки (слова, фразы, структура предложения), которые придают негативную или позитивную окраску. Веса признаков в итоговой оценке тональности текста (позитивный, негативный, нейтральный) зависят от математической функции, которая вычисляется во время обучения нейронной сети.

Раньше люди генерировали признаки вручную. Чем больше признаков и точнее подобраны веса, тем точнее ответ. Нейронная сеть автоматизировала этот процесс.

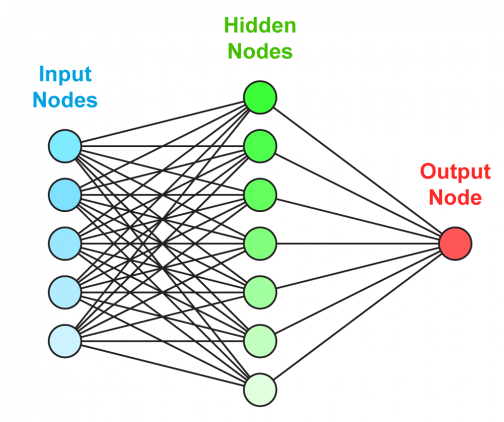
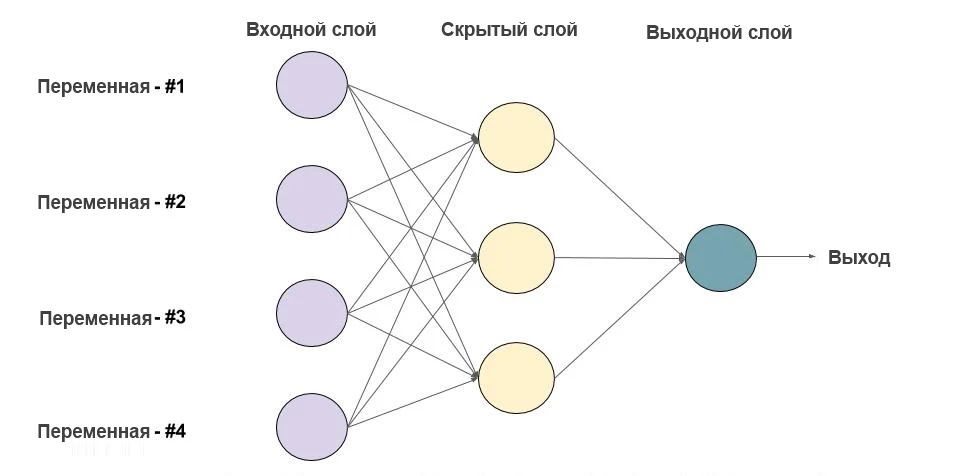
Из чего состоит нейронная сеть

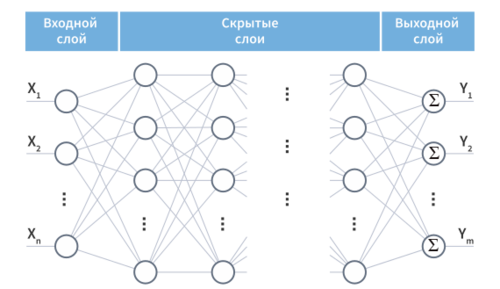
Искусственная нейронная сеть состоит из трех компонентов:

- Входной слой;
- Скрытые (вычислительные) слои;
- Выходной слой.

Обучение нейросети происходит в два этапа:

Прямое распространение ошибки;
Обратное распространение ошибки.

Во время прямого распространения ошибки делается предсказание ответа. При обратном распространении ошибка между фактическим ответом и предсказанным минимизируется.

Визуализация работы нейронной сети для классификации изображений:

Обучение: прямое распространение ошибки

Прямое распространение

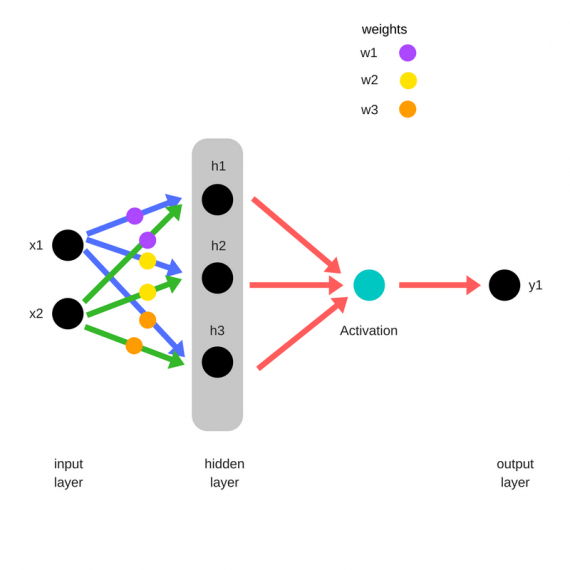
Зададим начальные веса случайным образом:

Умножим входные данные на веса для формирования скрытого слоя:

h1 = (x1 * w1) + (x2 * w1)
h2 = (x1 * w2) + (x2 * w2)
h3 = (x1 * w3) + (x2 * w3)

Выходные данные из скрытого слоя передается через нелинейную функцию (функцию активации), для получения выхода сети:

y_ = fn(h1 , h2, h3)

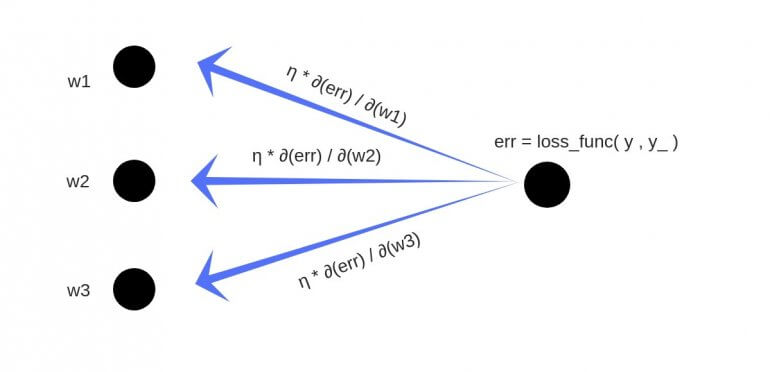
Обратное распространение

Суммарная ошибка (total_error) вычисляется как разность между ожидаемым значением «y» (из обучающего набора) и полученным значением «y_» (посчитанное на этапе прямого распространения ошибки), проходящих через функцию потерь (cost function).
Частная производная ошибки вычисляется по каждому весу (эти частные дифференциалы отражают вклад каждого веса в общую ошибку (total_loss)).
Затем эти дифференциалы умножаются на число, называемое скорость обучения или learning rate (η).

Полученный результат затем вычитается из соответствующих весов.

В результате получатся следующие обновленные веса:

w1 = w1 — (η * ∂(err) / ∂(w1))
w2 = w2 — (η * ∂(err) / ∂(w2))
w3 = w3 — (η * ∂(err) / ∂(w3))

То, что мы предполагаем и инициализируем веса случайным образом, и они будут давать точные ответы, звучит не вполне обоснованно, тем не менее, работает хорошо.

Популярный мем о том, как Карлсон стал Data Science разработчиком

bias Если вы знакомы с рядами Тейлора, обратное распространение ошибки имеет такой же конечный результат. Только вместо бесконечного ряда мы пытаемся оптимизировать только его первый член.

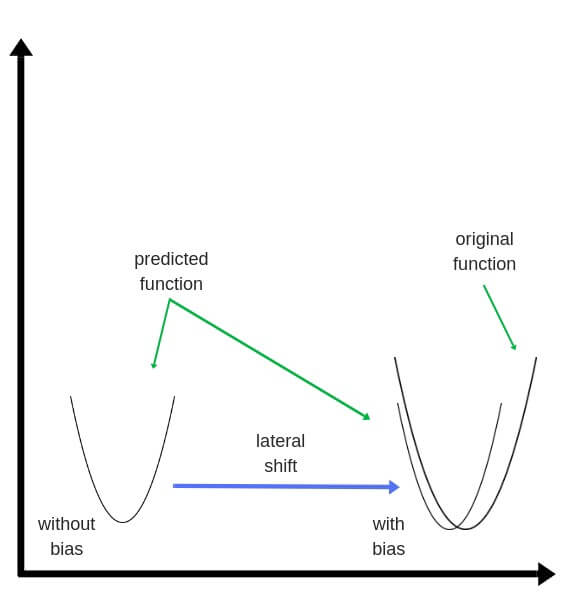
Смещения – это веса, добавленные к скрытым слоям. Они тоже случайным образом инициализируются и обновляются так же, как скрытый слой. Роль скрытого слоя заключается в том, чтобы определить форму базовой функции в данных, в то время как роль смещения – сдвинуть найденную функцию в сторону так, чтобы она частично совпала с исходной функцией.

Частные производные

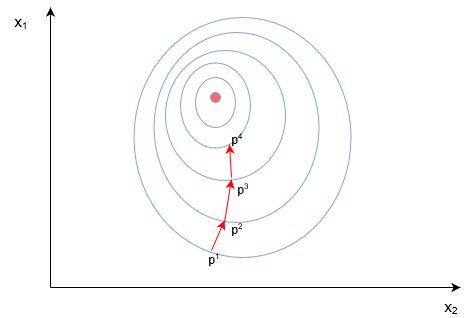
Частные производные можно вычислить, поэтому известно, какой был вклад в ошибку по каждому весу. Необходимость производных очевидна. Представьте нейронную сеть, пытающуюся найти оптимальную скорость беспилотного автомобиля. Eсли машина обнаружит, что она едет быстрее или медленнее требуемой скорости, нейронная сеть будет менять скорость, ускоряя или замедляя автомобиль. Что при этом ускоряется/замедляется? Производные скорости.

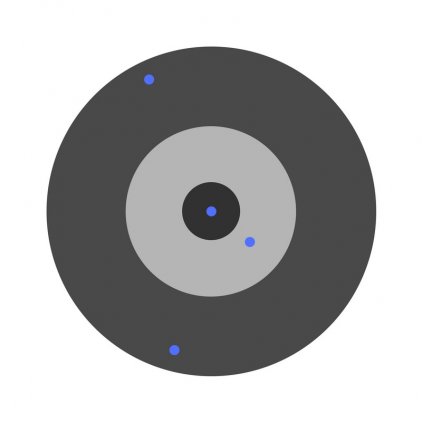
Разберем необходимость частных производных на примере.

Предположим, детей попросили бросить дротик в мишень, целясь в центр. Вот результаты:

Теперь, если мы найдем общую ошибку и просто вычтем ее из всех весов, мы обобщим ошибки, допущенные каждым. Итак, скажем, ребенок попал слишком низко, но мы просим всех детей стремиться попадать в цель, тогда это приведет к следующей картине:

Ошибка нескольких детей может уменьшиться, но общая ошибка все еще увеличивается.

Найдя частные производные, мы узнаем ошибки, соответствующие каждому весу в отдельности. Если выборочно исправить веса, можно получить следующее:

Гиперпараметры нейронной сети

Нейронная сеть используется для автоматизации отбора признаков, но некоторые параметры настраиваются вручную.

Скорость обучения (learning rate) нейросети

Скорость обучения является очень важным гиперпараметром. Если скорость обучения слишком мала, то даже после обучения нейронной сети в течение длительного времени она будет далека от оптимальных результатов. Результаты будут выглядеть примерно так:

С другой стороны, если скорость обучения слишком высока, то сеть очень быстро выдаст ответы. Получится следующее:

Функция активации (activation function) нейронной сети

Функция активации — это один из самых мощных инструментов, который влияет на силу, приписываемую нейронным сетям. Отчасти, она определяет, какие нейроны будут активированы, другими словами и какая информация будет передаваться последующим слоям.

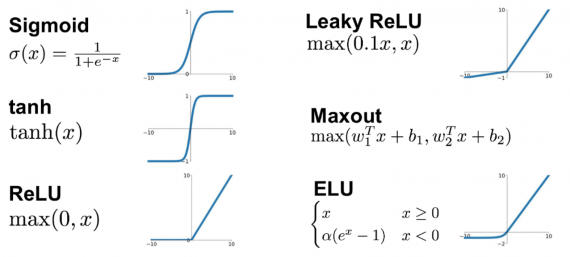
Без функций активации глубокие сети теряют значительную часть своей способности к обучению. Нелинейность этих функций отвечает за повышение степени свободы, что позволяет обобщать проблемы высокой размерности в более низких измерениях. Ниже приведены примеры распространенных функций активации:

Функция потери (loss function)

Функция потерь находится в центре нейронной сети. Она используется для расчета ошибки между реальными и полученными ответами. Наша глобальная цель — минимизировать эту ошибку. Таким образом, функция потерь эффективно приближает обучение нейронной сети к этой цели.

Функция потерь измеряет «насколько хороша» нейронная сеть в отношении данной обучающей выборки и ожидаемых ответов. Она также может зависеть от таких переменных, как веса и смещения.

Функция потерь одномерна и не является вектором, поскольку она оценивает, насколько хорошо нейронная сеть работает в целом.

Некоторые известные функции потерь:

Квадратичная (среднеквадратичное отклонение);
Кросс-энтропия;
Экспоненциальная (AdaBoost);
Расстояние Кульбака-Лейблера или прирост информации.

Cреднеквадратичное отклонение – самая простая функция потерь и наиболее часто используемая. Она задается следующим образом:

Функция потерь в нейронной сети должна удовлетворять двум условиям:

Функция потерь должна быть записана как среднее;
Функция потерь не должна зависеть от каких-либо активационных значений нейронной сети, кроме значений, выдаваемых на выходе.

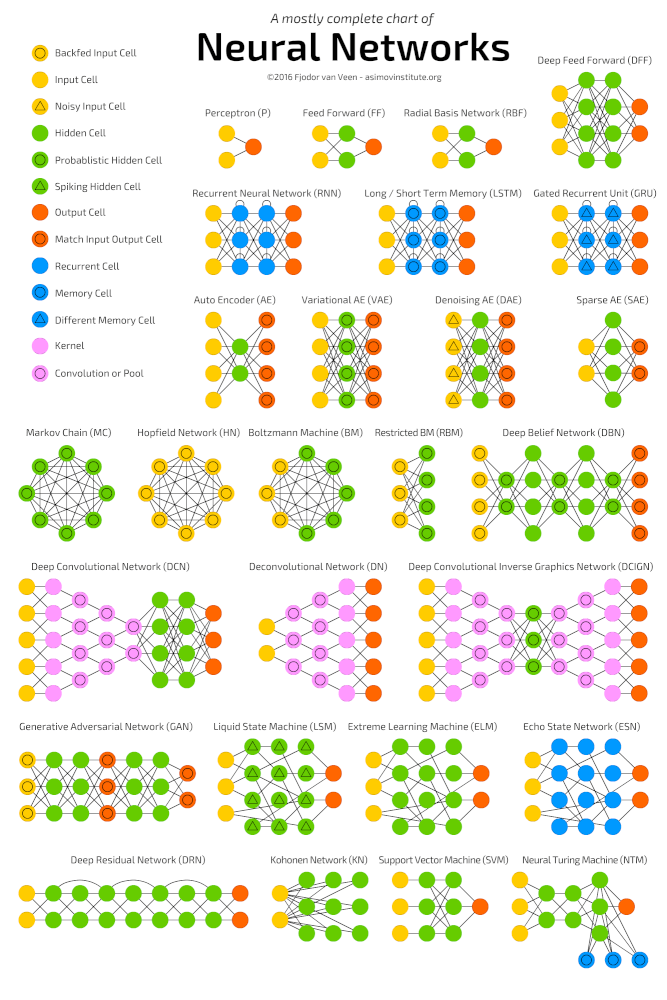
Глубокая нейронная сеть

Глубокое обучение (deep learning) – это класс алгоритмов машинного обучения, которые учатся глубже (более абстрактно) понимать данные. Популярные алгоритмы нейронных сетей глубокого обучения представлены на схеме ниже.

Популярные алгоритмы нейронных сетей (http://www.asimovinstitute.org/neural-network-zoo)

Более формально в deep learning:

Используется каскад (пайплайн, как последовательно передаваемый поток) из множества обрабатывающих слоев (нелинейных) для извлечения и преобразования признаков;
Основывается на изучении признаков (представлении информации) в данных без обучения с учителем. Функции более высокого уровня (которые находятся в последних слоях) получаются из функций нижнего уровня (которые находятся в слоях начальных слоях);
Изучает многоуровневые представления, которые соответствуют разным уровням абстракции; уровни образуют иерархию представления.

Пример простой нейронной сети

Рассмотрим однослойную нейронную сеть:

Здесь, обучается первый слой (зеленые нейроны), он просто передается на выход.

В то время как в случае двухслойной нейронной сети, независимо от того, как обучается зеленый скрытый слой, он затем передается на синий скрытый слой, где продолжает обучаться:

Следовательно, чем больше число скрытых слоев, тем больше возможности обучения сети.

Не следует путать с широкой нейронной сетью.

В этом случае большое число нейронов в одном слое не приводит к глубокому пониманию данных. Но это приводит к изучению большего числа признаков.

Пример:

Изучая английскую грамматику, требуется знать огромное число понятий. В этом случае однослойная широкая нейронная сеть работает намного лучше, чем глубокая нейронная сеть, которая значительно меньше.

Но

В случае изучения преобразования Фурье, ученик (нейронная сеть) должен быть глубоким, потому что не так много понятий, которые нужно знать, но каждое из них достаточно сложное и требует глубокого понимания.

Главное — баланс

Очень заманчиво использовать глубокие и широкие нейронные сети для каждой задачи. Но это может быть плохой идеей, потому что:

Обе требуют значительно большего количества данных для обучения, чтобы достичь минимальной желаемой точности;
Обе имеют экспоненциальную сложность;
Слишком глубокая нейронная сеть попытается сломать фундаментальные представления, но при этом она будет делать ошибочные предположения и пытаться найти псевдо-зависимости, которые не существуют;
Слишком широкая нейронная сеть будет пытаться найти больше признаков, чем есть. Таким образом, подобно предыдущей, она начнет делать неправильные предположения о данных.

Проклятье размерности нейросети

Проклятие размерности относится к различным явлениям, возникающим при анализе и организации данных в многомерных пространствах (часто с сотнями или тысячами измерений), и не встречается в ситуациях с низкой размерностью.

Грамматика английского языка имеет огромное количество аттрибутов, влияющих на нее. В машинном обучении мы должны представить их признаками в виде массива/матрицы конечной и существенно меньшей длины (чем количество существующих признаков). Для этого сети обобщают эти признаки. Это порождает две проблемы:

Из-за неправильных предположений появляется смещение. Высокое смещение может привести к тому, что алгоритм пропустит существенную взаимосвязь между признаками и целевыми переменными. Это явление называют недообучение.
От небольших отклонений в обучающем множестве из-за недостаточного изучения признаков увеличивается дисперсия. Высокая дисперсия ведет к переобучению, ошибки воспринимаются в качестве надежной информации.

Компромисс

На ранней стадии обучения смещение велико, потому что выход из сети далек от желаемого. А дисперсия очень мала, поскольку данные имеет пока малое влияние.

В конце обучения смещение невелико, потому что сеть выявила основную функцию в данных. Однако, если обучение слишком продолжительное, сеть также изучит шум, характерный для этого набора данных. Это приводит к большому разбросу результатов при тестировании на разных множествах, поскольку шум меняется от одного набора данных к другому.

Действительно,

алгоритмы с большим смещением обычно в основе более простых моделей, которые не склонны к переобучению, но могут недообучиться и не выявить важные закономерности или свойства признаков. Модели с маленьким смещением и большой дисперсией обычно более сложны с точки зрения их структуры, что позволяет им более точно представлять обучающий набор. Однако они могут отображать много шума из обучающего набора, что делает их прогнозы менее точными, несмотря на их дополнительную сложность.

Как правило, невозможно иметь маленькое смещение и маленькую дисперсию одновременно.

Есть множество инструментов, с помощью которых можно легко создать сложные модели машинного обучения, переобучение занимает центральное место. Поскольку смещение появляется, когда сеть не получает достаточно информации. Но чем больше примеров, тем больше появляется вариантов зависимостей и изменчивостей в этих корреляциях.

Источник

В этой статье мы узнаем о нейронных сетях прямого распространения, также известных как сети с глубокой прямой связью или многослойные персептроны. Они составляют основу многих важных нейронных сетей, используемых в последнее время, таких как сверточные нейронные сети^એ (широко используемые в приложениях компьютерного зрения), рекуррентные нейронные сети^એ (широко используемые для понимания естественного языка и последовательного обучения) и так далее. Мы постараемся понять важные концепции, используя интуитивно понятную игрушку и не будем вдаваясь в математику. Если вы хотите погрузиться в глубокое обучение, но не обладаете достаточным опытом в области статистики и машинного обучения, то эта статья станет идеальной отправной точкой.

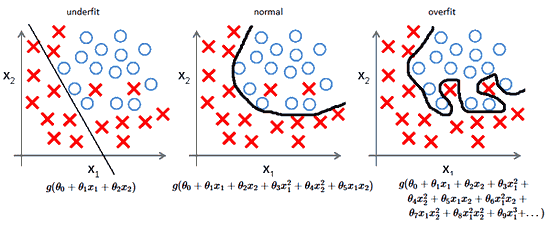
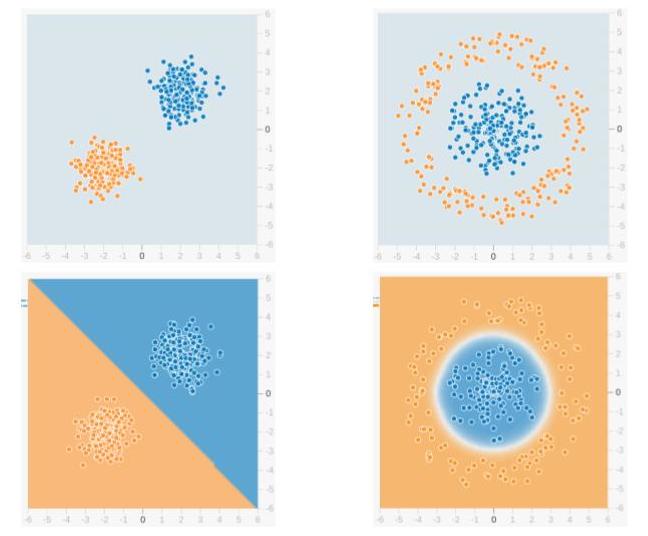
Мы будем использовать сеть прямого распространения для решения задачи двоичной классификации. В машинном обучении классификация — это тип метода контролируемого обучения, в котором задача состоит в том, чтобы разделить образцы данных на заранее определенные группы с помощью функции принятия решений. Когда есть только две группы, это называется двоичной классификацией. На приведенном ниже рисунке показан пример. Точки синего цвета принадлежат одной группе (или классу), а оранжевые точки — другой. Воображаемые линии, разделяющие группы, называются границами принятия решений. Функция принятия решения извлекается из набора помеченных образцов, который называется обучающими данными, а процесс обучения функции принятия решения называется обучением.

В приведенном примере верхняя строка показывает два разных распределения данных, а нижняя строка показывает границу решения. На левом изображении показан пример данных, которые можно разделить линейно. Это означает, что линейная граница (например, прямой линии) достаточно, чтобы разделить данные на группы. С другой стороны, изображение справа показывает пример данных, которые нельзя разделить линейно. Граница решения в этом случае должна быть круговой или многоугольной, как показано на рисунке.

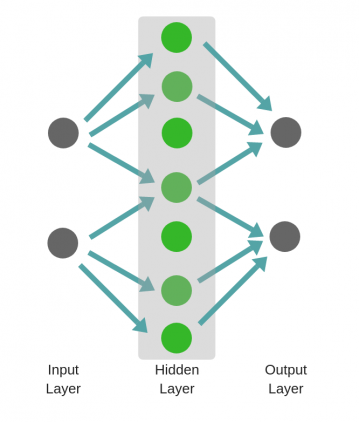
1. Что есть нейронная сеть?

Пример нейронной сети прямого распространения с одним скрытым слоем (3 нейрона)

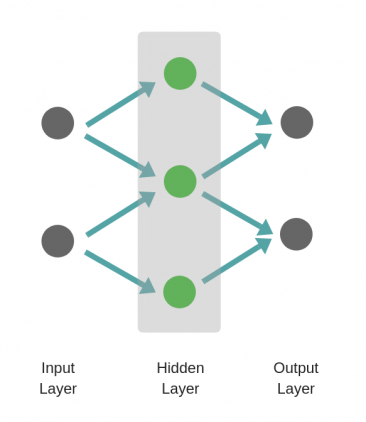
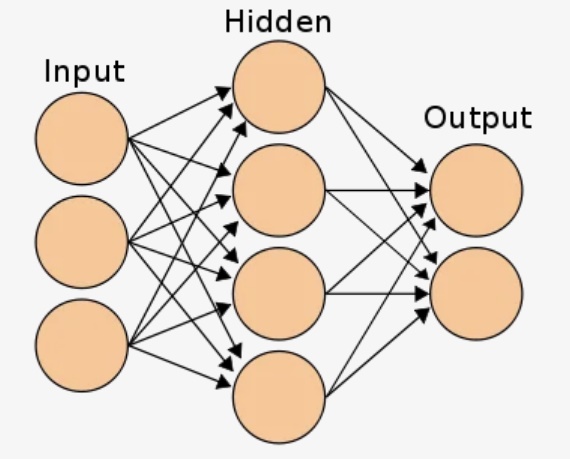
Ниже приведен пример нейронной сети прямого распространения. Это направленный ациклический граф, что означает, что в сети нет обратных связей или петель. У него есть входной слой, выходной слой и скрытый слой. Как правило, может быть несколько скрытых слоев. Каждый узел в слое — нейрон, который можно рассматривать как основной процессор нейронной сети.

1.1. Что есть нейрон?

Показан пример нейрона с входми (x_1, x_n), соответствующими весовыми коэффициентами (w_1, w_n), смещением (b) и функцией активации f, где выходом является сумма смещения со взвешенной суммой входов

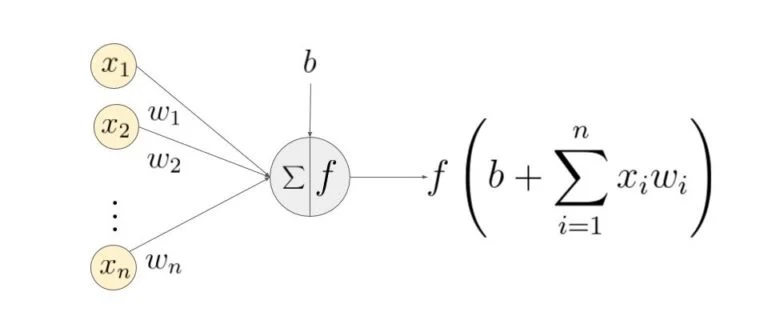
Искусственный нейрон — это основная единица нейронной сети. Принципиальная схема нейрона приведена ниже.

Как видно выше, он работает в два этапа: вычисляет взвешенную сумму своих входных данных, а затем применяет функцию активации для нормализации суммы. Функции активации могут быть линейными или нелинейными. Также, есть веса, связанные с каждым входом нейрона. Это параметры, которые сеть должна приобрести на этапе обучения.

1.2. Функции активации

Функция активации^એ используется как орган принятия решений на выходе нейрона. Нейрон изучает линейные или нелинейные границы принятия решений на основе функции активации. Он также оказывает нормализующее влияние на выход нейронов, что предотвращает выход нейронов после нескольких слоев, чтобы стать очень большим, за счет каскадного эффекта. Есть три наиболее часто используемых функции активации.

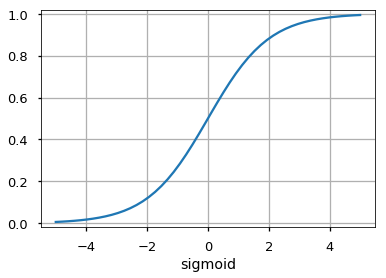
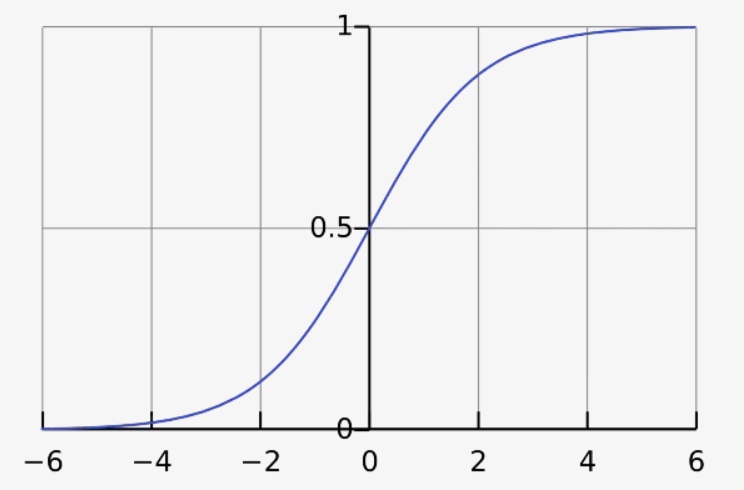
Сигмоида^એ
Он отображает входные данные (ось x) на значения от 0 до 1.

Сигмоида

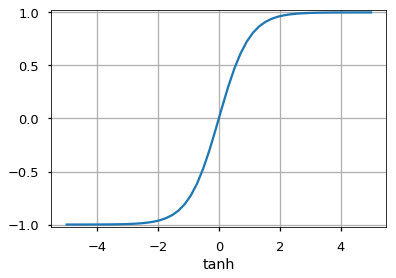
Tanh
Похожа на сигмовидную функцию, но отображает входные данные в значения от -1 до 1.

tanh

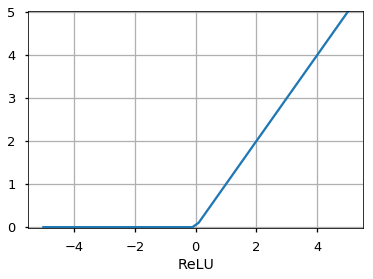
Rectified Linear Unit (ReLU)
Он позволяет проходить через него только положительным значениям. Отрицательные значения отображаются на ноль.

Функция активации^એ может быть другой, например, функция Unit Step, leaky ReLU, Noisy ReLU, Exponential LU и т.д., которые имеют свои плюсы и минусы.

1.3. Входной слой

Это первый слой нейронной сети. Он используется для передачи и приёма входных данных или функций в сеть.

1.4. Выходной слой

Это слой, который выдает прогнозы. Функция активации, используемая на этом уровне, различается для разных задач. Для задачи двоичной классификации мы хотим, чтобы на выходе было либо 0, либо 1. Таким образом, используется сигмовидная функция активации. Для задачи мультиклассовой классификации используется Softmax^એ (воспринимайте это как обобщение сигмоида на несколько классов). Для задачи регрессии, когда результат не является предопределенной категорией, мы можем просто использовать линейную единицу.

1.5. Скрытый слой

Сеть прямого распространения применяет к входу ряд функций. Имея несколько скрытых слоев, мы можем вычислять сложные функции, каскадируя более простые функции. Предположим, мы хотим вычислить седьмую степень числа, но хотим, чтобы вещи были простыми (поскольку их легко понять и реализовать). Вы можете использовать более простые степени, такие как квадрат и куб, для вычисления функций более высокого порядка. Точно так же вы можете вычислять очень сложные функции с помощью этого каскадного эффекта. Наиболее широко используемый скрытый блок — это тот, где функция активации^એ использует выпрямленный линейный блок (ReLU). Выбор скрытых слоёв — очень активная область исследований в машинном обучении. Тип скрытого слоя отличает разные типы нейронных сетей, такие как CNN^એ, RNN^એ и т.д. Количество скрытых слоев называется глубиной нейронной сети. Вы можете задать вопрос: сколько слоев в сети делают ее глубокой? На это нет правильного ответа. В общем случае, более глубокие сети могут научиться более сложным функциям.

1.6. Как сеть учится?

Обучающие образцы передаются по сети, и выходные данные, полученные от сети, сравниваются с фактическими выходными данными. Эта ошибка используется для изменения веса нейронов таким образом, чтобы ошибка постепенно уменьшалась. Это делается с помощью алгоритма обратного распространения ошибки, также называемого обратным распространением. Итеративная передача пакетов данных по сети и обновление весов для уменьшения ошибки называется стохастический градиентный спуск^એ (SGD). Величина, на которую изменяются веса, определяется параметром, называемым «Скорость обучения». Подробности SGD и backprop будут описаны в отдельном посте.

2.Зачем использовать скрытые слои?

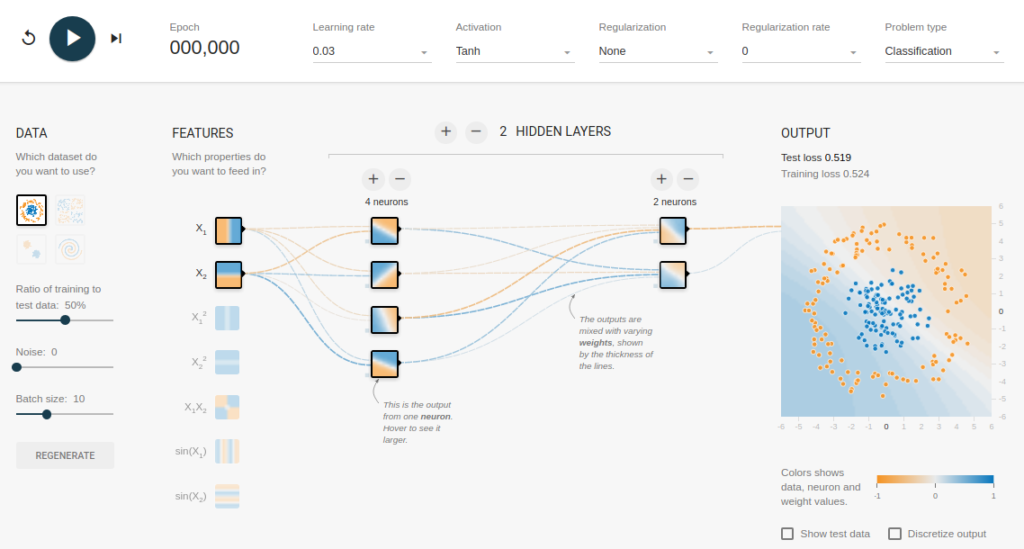
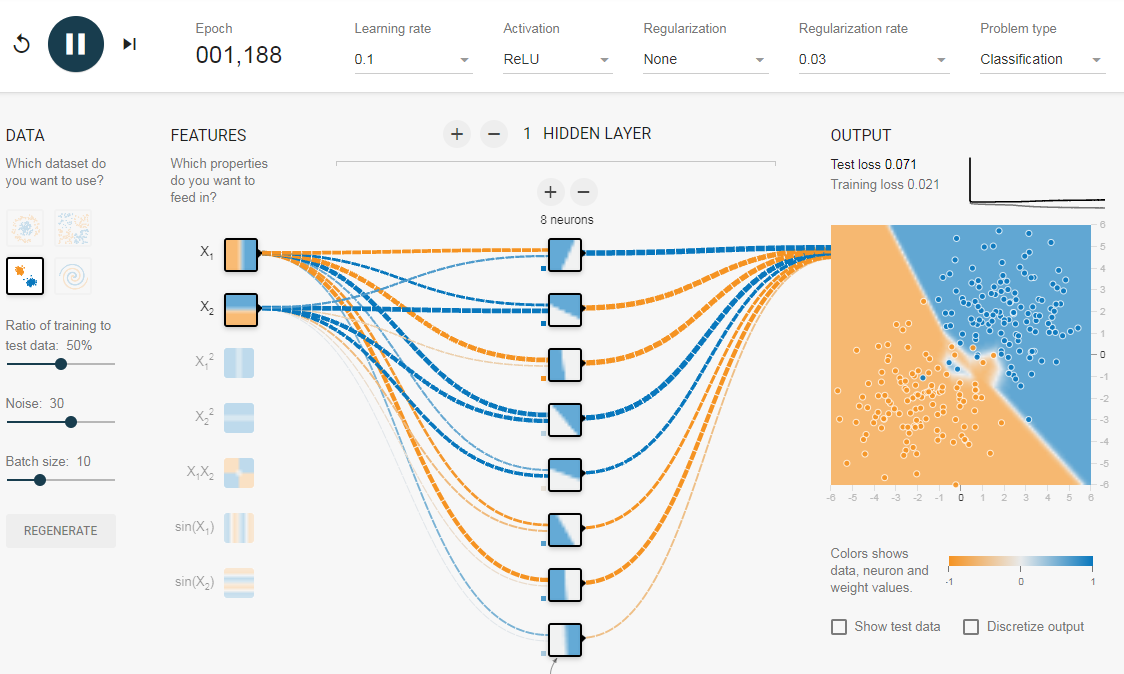
Снимок экрана веб-страницы plays.tensorflow.org

Чтобы понять значение скрытых слоев, мы попытаемся решить проблему двоичной классификации без скрытых слоев. Для этого мы будем использовать интерактивную платформу от Google, plays.tensorflow.org, которая представляет собой веб-приложение, где вы можете создавать простые нейронные сети с прямой связью и видеть эффекты обучения в реальном времени. Вы можете поиграть, изменив количество скрытых слоев, количество нейронов в скрытом слое, тип функции активации, тип данных, скорость обучения, параметры регуляризации и т.д. Выше приведен снимок экрана веб-страницы.

На приведенной выше странице вы можете выбрать данные и нажать кнопку воспроизведения, чтобы начать обучение.
Он покажет вам изученную границу решения и кривые потерь в правом верхнем углу.

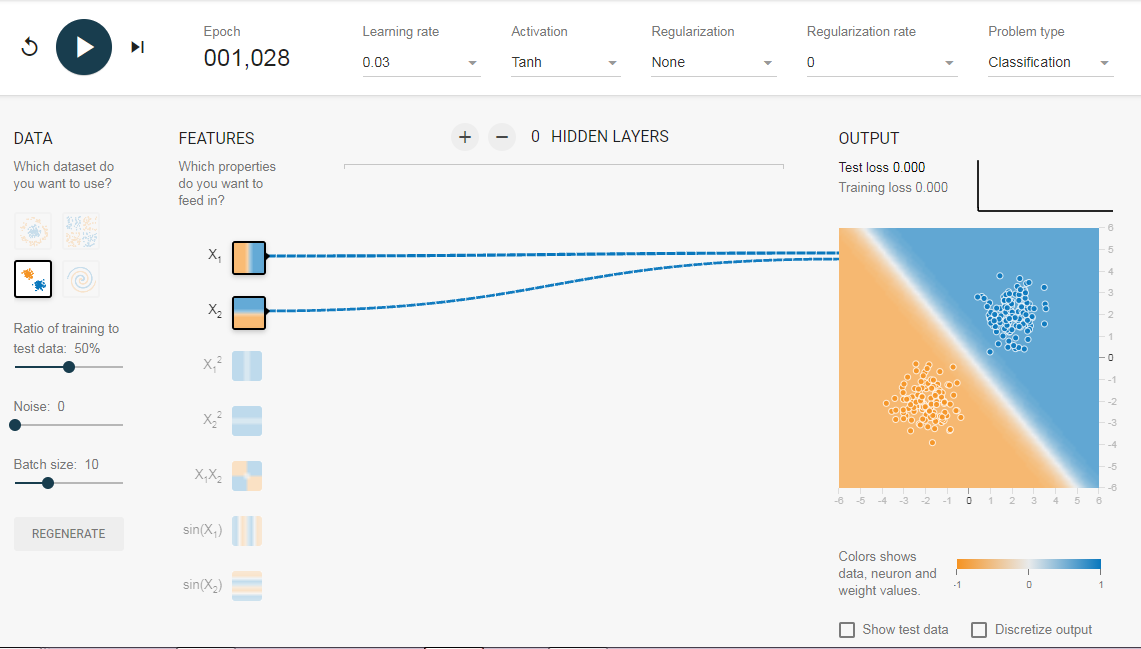
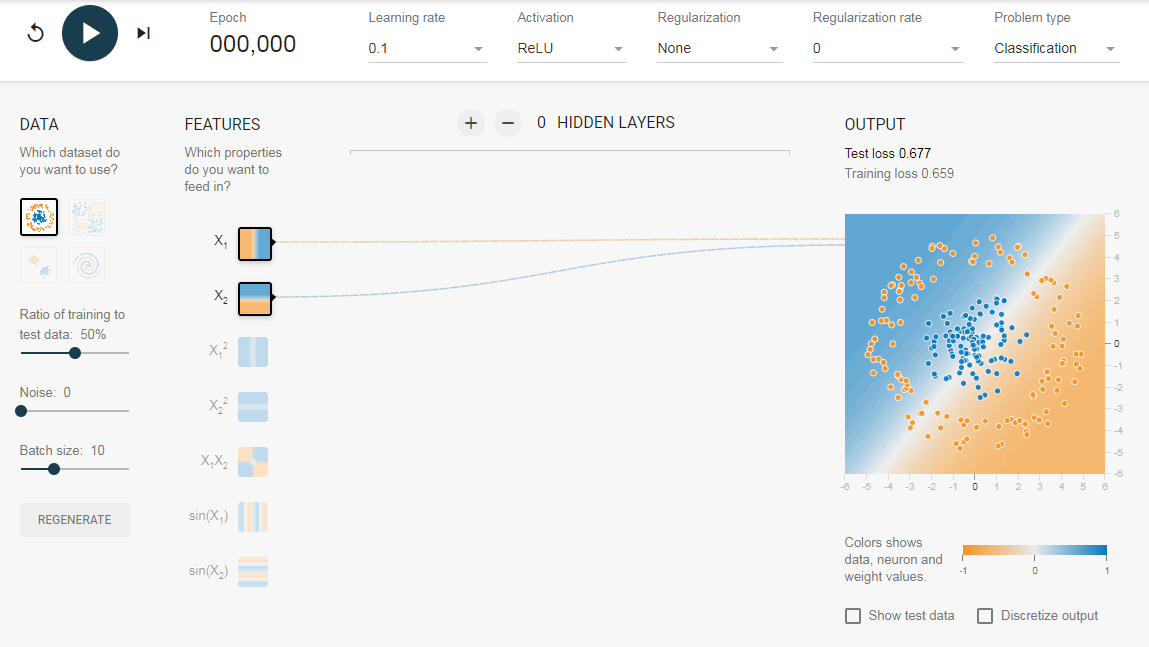
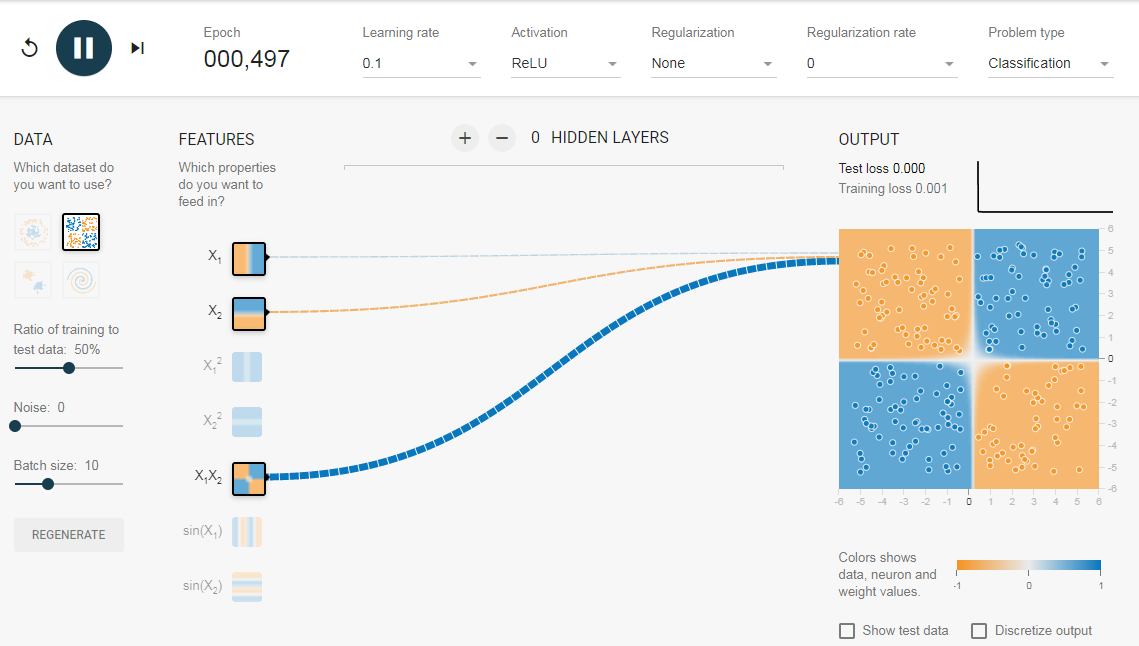
2.1. Без скрытого слоя

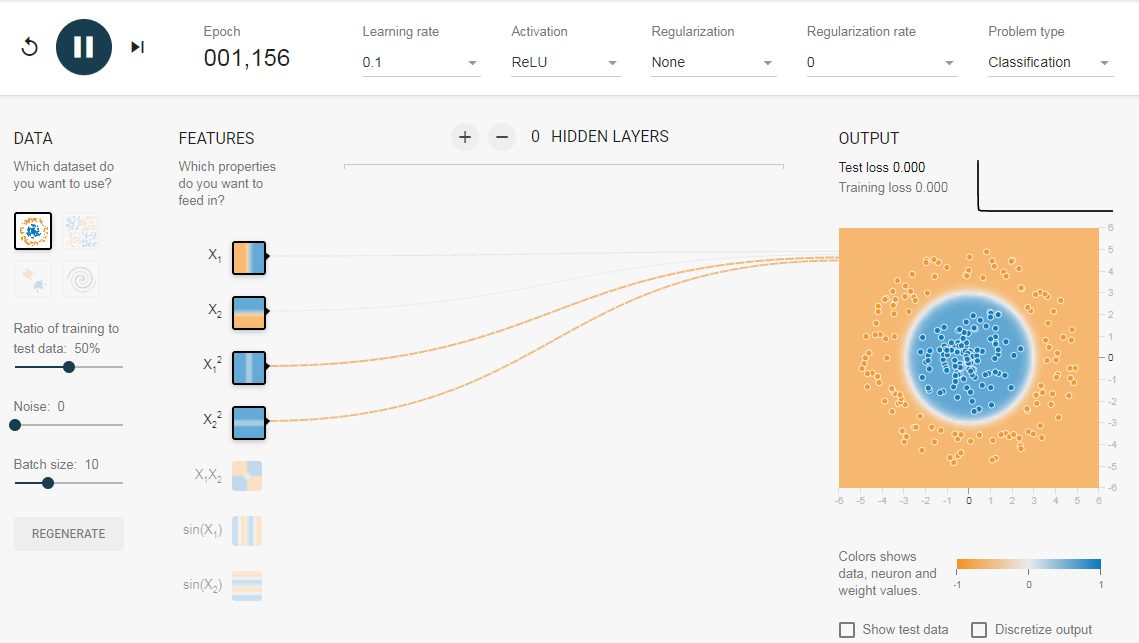
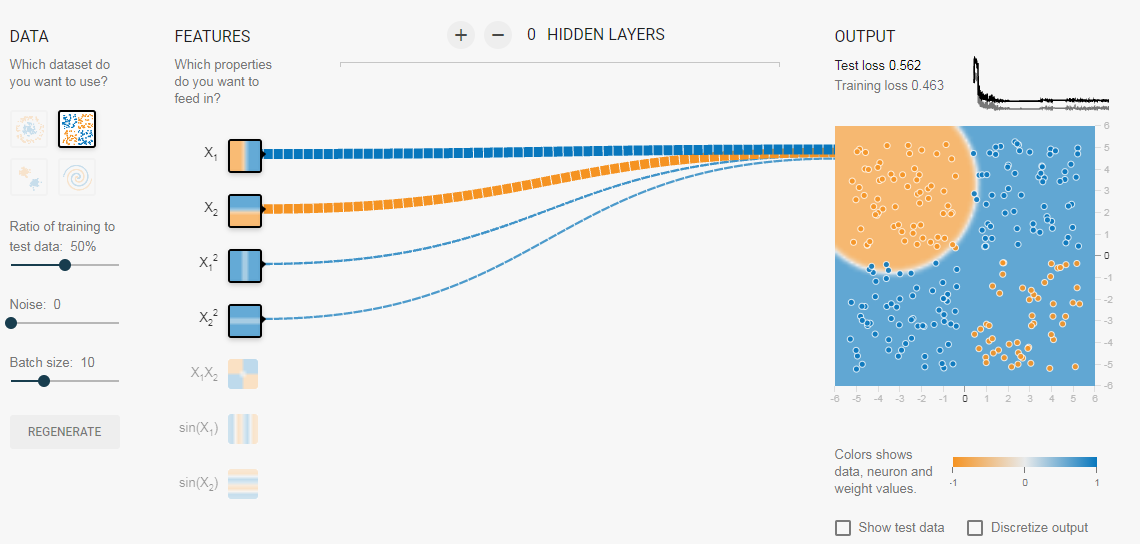
Нам нужна сеть без скрытого слоя, который я создал по этой ссылке. Здесь нет скрытых слоев, поэтому он становится простым нейроном, способным изучать линейную границу принятия решения. Мы можем выбрать тип данных в верхнем левом углу. В случае линейно разделяемых данных (3-й тип), он сможет получить (когда вы нажмете кнопку воспроизведения) линейную границу, как показано ниже.

Однако, если вы выберете первые данные, вы не сможете для них узнать границу кругового решения.

Поскольку данные находятся в круговой области, можно сказать, что использование квадратов значений функций в качестве входных данных может помочь. Оказывается, после обучения нейрон сможет найти круговую границу принятия решения.

Теперь, если вы выберете 2-е данные, та же конфигурация не сможет узнать соответствующую границу решения.

Опять же интуитивно кажется, что граница решения — это коническое сечение (например, парабола или гипербола). Итак, если мы включим продукт функции (например, X_1 X_2), нейрон сможет узнать желаемую границу принятия решения.

Описанные эксперименты показали:

Используя один нейрон, мы можем узнать только линейную границу решения.
Нам пришлось придумать преобразования функций (например, квадрат функций или продукт функций) путем визуализации данных. Этот шаг может быть сложным для данных, которые нелегко визуализировать.

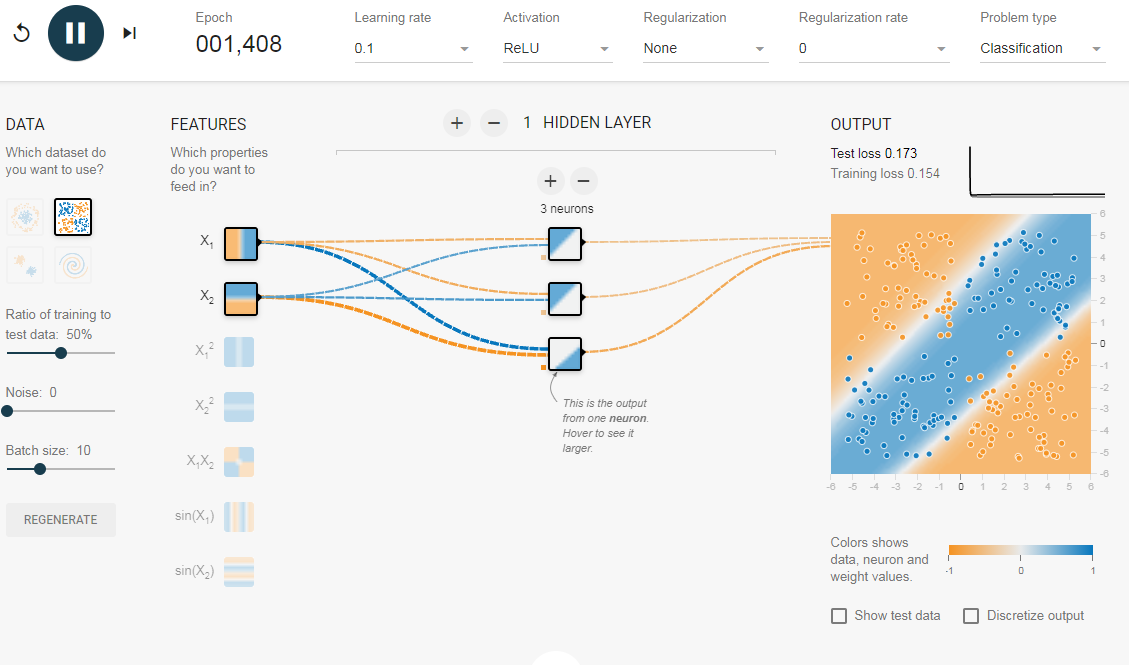
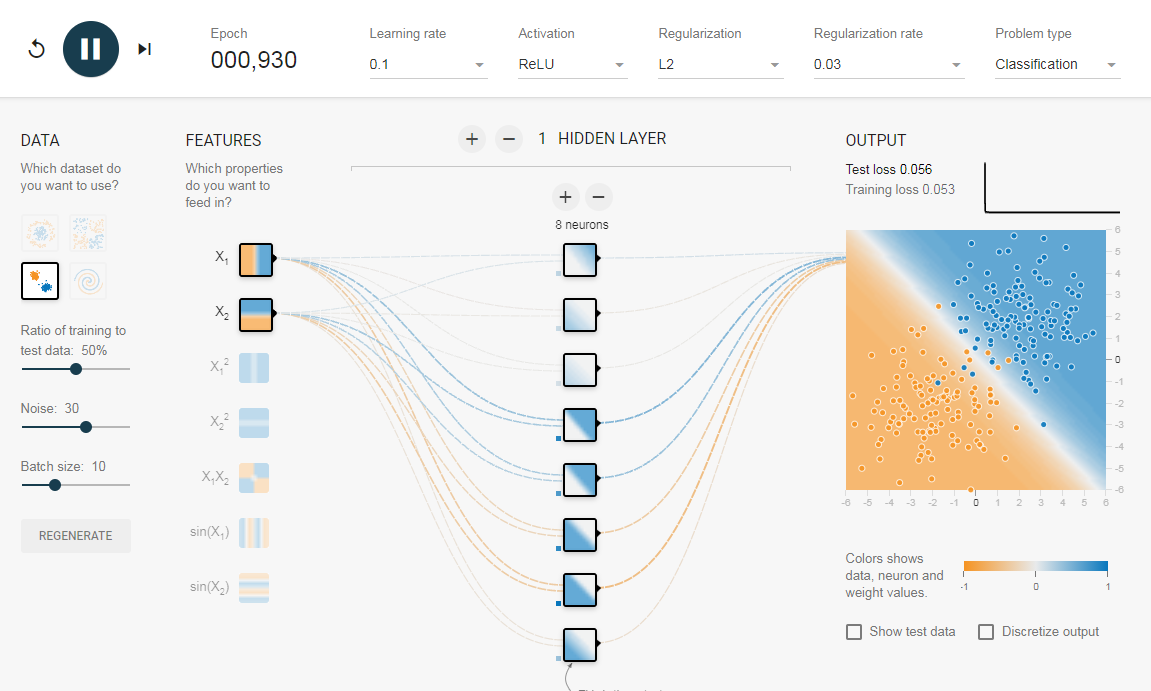
2.2. Добавление скрытого слоя

Добавив скрытый слой, как показано в этой ссылке, мы можем избавиться от этой функции проектирования и получить единую сеть, которая может изучить все три границы принятия решений. Нейронная сеть с одним скрытым слоем с нелинейными функциями активации считается универсальным аппроксиматором функций, теорема Цыбенко^એ (т.е. способной к обучению любой функции). Однако количество единиц в скрытом слое не фиксировано. Результат добавления скрытого слоя всего с 3 нейронами показан ниже:

3. Регуляризация

Как мы видели в предыдущем разделе, многослойная сеть может изучать нелинейные границы принятия решений. Однако, если в данных есть шум (что часто бывает), сеть может попытаться изучить нелинейность, вносимую шумом, пытаясь подогнать зашумленные выборки. В таких случаях зашумленные образцы следует рассматривать как выбросы. В этой ссылке я добавил немного шума к линейно разделяемым данным. Также, чтобы продемонстрировать идею, я увеличил количество скрытых нейронов.

На приведенном выше рисунке можно увидеть, что граница принятия решения очень старается приспособить зашумленные выборки, чтобы уменьшить ошибку. Но, как видите, это ошибочно из-за шумных сэмплов. Другими словами, сеть будет неустойчивой при наличии шума. Это явление называется переобучением. В таких случаях, ошибка обучающих данных может уменьшиться, но сеть плохо работает с невидимыми данными. Это видно по кривым потерь в правом верхнем углу.

Потери в обучении уменьшаются, но потери в тестах увеличиваются. Также, можно видеть, что некоторые веса стали очень большими (очень толстые соединения или вы можете увидеть веса, если наведете курсор на соединения). Это можно исправить, наложив некоторые ограничения на значения весов (например, не позволяя весам становиться очень высокими). Это называется регуляризацией. Мы накладываем ограничения на остальные параметры сети. В некотором смысле мы не полностью доверяем обучающим данным и хотим, чтобы сеть усвоила «хорошие» границы принятия решений. Я добавил регуляризацию L2 в приведенную выше конфигурацию по этой ссылке, и результат показан ниже.

После включения регуляризации L2 граница принятия решения, изученная сетью, становится более гладкой и аналогичной случаю, когда не было шума. Эффект регуляризации также можно увидеть из кривых потерь и значений весов.

В следующем посте, если он случится мы узнаем, как реализовать нейронную сеть прямого распространения в Keras для решения нескольких проблема классификации и узнайте ещё больше о сетях прямого распространения.

Использованы материалы Understanding Feedforward Neural Networks

Источник

Прямое распространение¶

Простая сеть
- Прямой проход по шагам
- Код
Более сложная сеть
- Архитектура
- Инициализация весов
- Bias Terms
- Working with Matrices
- Dynamic Resizing
- Refactoring Our Code
- Final Result

Простая сеть¶

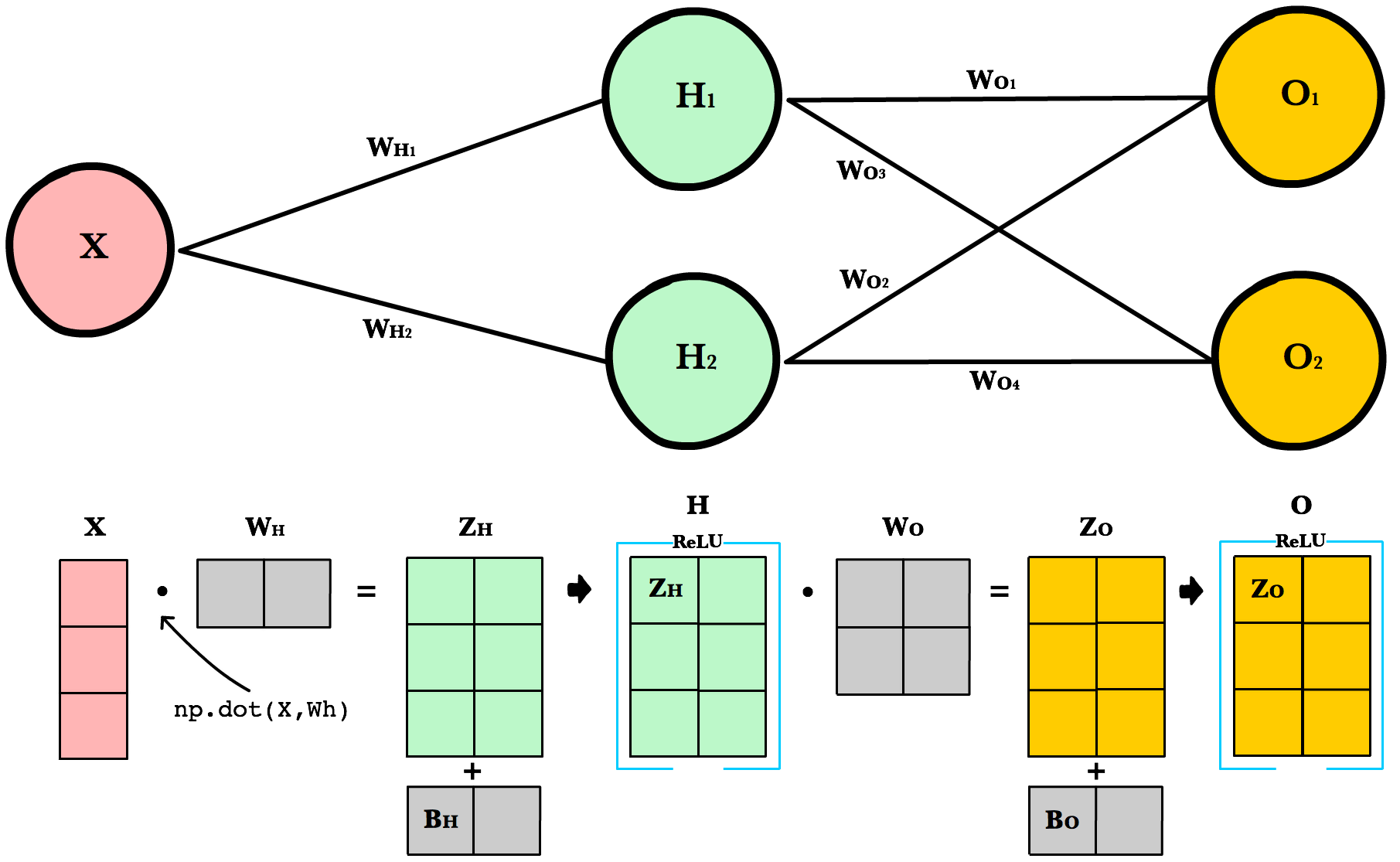
Прямое распространение — это процесс с помощью которого сеть делает предсказание (prediction). Также это основной режим работы обученной нейронной сети. Входные данные «распространяются» через каждый слой сети и выходной слой выдает финальный результат — предсказание. Для простой учебной нейронной сети один проход данных можно выразить математически как:

\[Prediction = A(\;A(\;X W_h\;)W_o\;)\]

Где $A$ это функция активации, например ReLU, $X$ это входные данные, $W_h$ и $W_o$ это веса слоев.

Прямой проход по шагам¶

Вычислить значения входов скрытого слоя умножениием $X$ на веса скрытого слоя $W_h$ и получить $Z_h$.
Применить функцию активации к $Z_h$ и передать результат $H$ в выходной слой.
Вычислить значения входов выходного слоя умножением значения $H$ на веса выходного слоя $W_o$ и получить $Z_o$
Применить функцию активации к $Z_o$. Результатом будет предсказание сети.

Код¶

Давайте напишем метод feed_forward() для распространения входных данных через нейронную сеть с 1-м скрытым слоем. Выход этого метода будет представлять собой предсказание модели.

def relu(z):
    return max(0,z)

def feed_forward(x, Wh, Wo):
    # Hidden layer
    Zh = x * Wh
    H = relu(Zh)

    # Output layer
    Zo = H * Wo
    output = relu(Zo)
    return output

x это вход сети, Zo и Zh это «взвешенный» вход слоев, a Wo и Wh это веса слоев.

Более сложная сеть¶

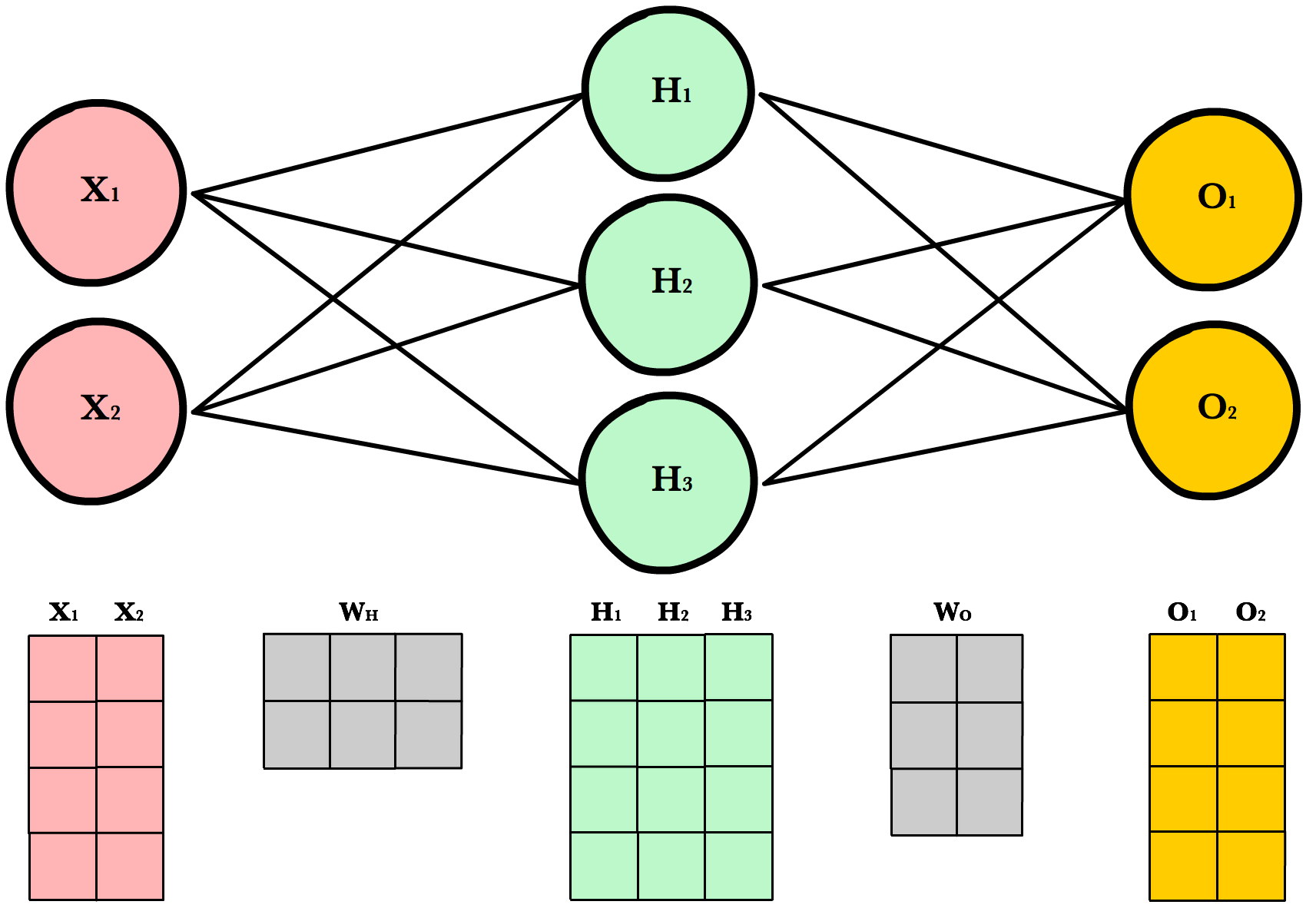
Простая сеть очень помогает в учебном процессе, но реальные сети намного больше и сложнее устроены. Современные нейронные сети имеют гораздо больше скрытых слоев, больше нейронов в каждом слое, больше входных переменных. Рассмотрим более крупную (но всё ещё простую) нейронную сеть, которая позволит нам показать универсальный подход, основанный на матричном умножении, используемом в больших, «промышленных» нейронных сетях.

Архитектура¶

Для произвольного изменения количества входов или выходов сети, мы должны сделать наш код более гибким с помощью добавления новых параметров в __init_ метод: inputLayerSize, hiddenLayerSize,outputLayerSize. Мы будем продолжать ограничивать себя в количестве скрытых слоев, но сейчас это не так важно, потому что мы можем менять ширину (количество нейронов) имеющихся слоев.

INPUT_LAYER_SIZE = 1
HIDDEN_LAYER_SIZE = 2
OUTPUT_LAYER_SIZE = 2

Инициализация весов¶

Unlike last time where Wh and Wo were scalar numbers, our new weight variables will be numpy arrays. Each array will hold all the weights for its own layer — one weight for each synapse. Below we initialize each array with the numpy’s np.random.randn(rows, cols) method, which returns a matrix of random numbers drawn from a normal distribution with mean 0 and variance 1.

def init_weights():
    Wh = np.random.randn(INPUT_LAYER_SIZE, HIDDEN_LAYER_SIZE) * \
                np.sqrt(2.0/INPUT_LAYER_SIZE)
    Wo = np.random.randn(HIDDEN_LAYER_SIZE, OUTPUT_LAYER_SIZE) * \
                np.sqrt(2.0/HIDDEN_LAYER_SIZE)

Here’s an example calling random.randn():

arr = np.random.randn(1, 2)

print(arr)
>> [[-0.36094661 -1.30447338]]

print(arr.shape)
>> (1,2)

As you’ll soon see, there are strict requirements on the dimensions of these weight matrices. The number of rows must equal the number of neurons in the previous layer. The number of columns must match the number of neurons in the next layer.

A good explanation of random weight initalization can be found in the Stanford CS231 course notes [1] chapter on neural networks.

Bias Terms¶

Смещение (Bias) terms allow us to shift our neuron’s activation outputs left and right. This helps us model datasets that do not necessarily pass through the origin.

Using the numpy method np.full() below, we create two 1-dimensional bias arrays filled with the default value 0.2. The first argument to np.full is a tuple of array dimensions. The second is the default value for cells in the array.

def init_bias():
    Bh = np.full((1, HIDDEN_LAYER_SIZE), 0.1)
    Bo = np.full((1, OUTPUT_LAYER_SIZE), 0.1)
    return Bh, Bo

Working with Matrices¶

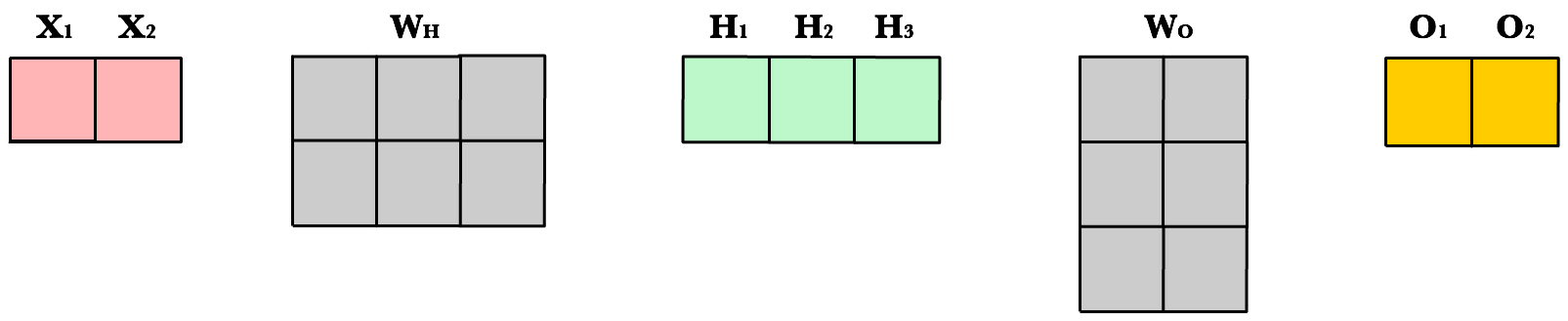
To take advantage of fast linear algebra techniques and GPUs, we need to store our inputs, weights, and biases in matrices. Here is our neural network diagram again with its underlying matrix representation.

What’s happening here? To better understand, let’s walk through each of the matrices in the diagram with an emphasis on their dimensions and why the dimensions are what they are. The matrix dimensions above flow naturally from the architecture of our network and the number of samples in our training set.

Matrix dimensions

Var	Name	Dimensions	Explanation
`X`	Input	(3, 1)	Includes 3 rows of training data, and each row has 1 attribute (height, price, etc.)
`Wh`	Hidden weights	(1, 2)	These dimensions are based on number of rows equals the number of attributes for the observations in our training set. The number columns equals the number of neurons in the hidden layer. The dimensions of the weights matrix between two layers is determined by the sizes of the two layers it connects. There is one weight for every input-to-neuron connection between the layers.
`Bh`	Hidden bias	(1, 2)	Each neuron in the hidden layer has is own bias constant. This bias matrix is added to the weighted input matrix before the hidden layer applies ReLU.
`Zh`	Hidden weighted input	(1, 2)	Computed by taking the dot product of X and Wh. The dimensions (1,2) are required by the rules of matrix multiplication. Zh takes the rows of in the inputs matrix and the columns of weights matrix. We then add the hidden layer bias matrix Bh.
`H`	Hidden activations	(3, 2)	Computed by applying the Relu function to Zh. The dimensions are (3,2) — the number of rows matches the number of training samples and the number of columns equals the number of neurons. Each column holds all the activations for a specific neuron.
`Wo`	Output weights	(2, 2)	The number of rows matches the number of hidden layer neurons and the number of columns equals the number of output layer neurons. There is one weight for every hidden-neuron-to-output-neuron connection between the layers.
`Bo`	Output bias	(1, 2)	There is one column for every neuron in the output layer.
`Zo`	Output weighted input	(3, 2)	Computed by taking the dot product of H and Wo and then adding the output layer bias Bo. The dimensions are (3,2) representing the rows of in the hidden layer matrix and the columns of output layer weights matrix.
`O`	Output activations	(3, 2)	Each row represents a prediction for a single observation in our training set. Each column is a unique attribute we want to predict. Examples of two-column output predictions could be a company’s sales and units sold, or a person’s height and weight.

Dynamic Resizing¶

Before we continue I want to point out how the matrix dimensions change with changes to the network architecture or size of the training set. For example, let’s build a network with 2 input neurons, 3 hidden neurons, 2 output neurons, and 4 observations in our training set.

Now let’s use same number of layers and neurons but reduce the number of observations in our dataset to 1 instance:

As you can see, the number of columns in all matrices remains the same. The only thing that changes is the number of rows the layer matrices, which fluctuate with the size of the training set. The dimensions of the weight matrices remain unchanged. This shows us we can use the same network, the same lines of code, to process any number of observations.

Refactoring Our Code¶

Here is our new feed forward code which accepts matrices instead of scalar inputs.

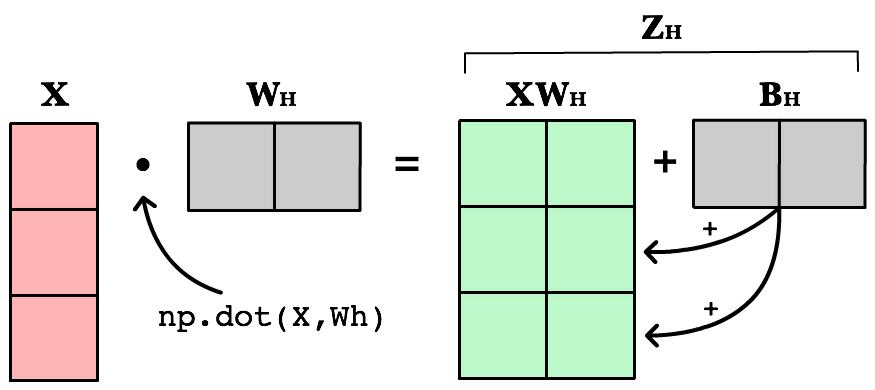
def feed_forward(X):
    '''
    X    - input matrix
    Zh   - hidden layer weighted input
    Zo   - output layer weighted input
    H    - hidden layer activation
    y    - output layer
    yHat - output layer predictions
    '''

    # Hidden layer
    Zh = np.dot(X, Wh) + Bh
    H = relu(Zh)

    # Output layer
    Zo = np.dot(H, Wo) + Bo
    yHat = relu(Zo)
    return yHat

Weighted input

The first change is to update our weighted input calculation to handle matrices. Using dot product, we multiply the input matrix by the weights connecting them to the neurons in the next layer. Next we add the bias vector using matrix addition.

The first column in Bh is added to all the rows in the first column of resulting dot product of X and Wh. The second value in Bh is added to all the elements in the second column. The result is a new matrix, Zh which has a column for every neuron in the hidden layer and a row for every observation in our dataset. Given all the layers in our network are fully-connected, there is one weight for every neuron-to-neuron connection between the layers.

The same process is repeated for the output layer, except the input is now the hidden layer activation H and the weights Wo.

ReLU activation

The second change is to refactor ReLU to use elementwise multiplication on matrices. It’s only a small change, but its necessary if we want to work with matrices. np.maximum() is actually extensible and can handle both scalar and array inputs.

def relu(Z):
    return np.maximum(0, Z)

In the hidden layer activation step, we apply the ReLU activation function np.maximum(0,Z) to every cell in the new matrix. The result is a matrix where all negative values have been replaced by 0. The same process is repeated for the output layer, except the input is Zo.

Final Result¶

Putting it all together we have the following code for forward propagation with matrices.

INPUT_LAYER_SIZE = 1
HIDDEN_LAYER_SIZE = 2
OUTPUT_LAYER_SIZE = 2

def init_weights():
    Wh = np.random.randn(INPUT_LAYER_SIZE, HIDDEN_LAYER_SIZE) * \
                np.sqrt(2.0/INPUT_LAYER_SIZE)
    Wo = np.random.randn(HIDDEN_LAYER_SIZE, OUTPUT_LAYER_SIZE) * \
                np.sqrt(2.0/HIDDEN_LAYER_SIZE)


def init_bias():
    Bh = np.full((1, HIDDEN_LAYER_SIZE), 0.1)
    Bo = np.full((1, OUTPUT_LAYER_SIZE), 0.1)
    return Bh, Bo

def relu(Z):
    return np.maximum(0, Z)

def relu_prime(Z):
    '''
    Z - weighted input matrix

    Returns gradient of Z where all
    negative values are set to 0 and
    all positive values set to 1
    '''
    Z[Z < 0] = 0
    Z[Z > 0] = 1
    return Z

def cost(yHat, y):
    cost = np.sum((yHat - y)**2) / 2.0
    return cost

def cost_prime(yHat, y):
    return yHat - y

def feed_forward(X):
    '''
    X    - input matrix
    Zh   - hidden layer weighted input
    Zo   - output layer weighted input
    H    - hidden layer activation
    y    - output layer
    yHat - output layer predictions
    '''

    # Hidden layer
    Zh = np.dot(X, Wh) + Bh
    H = relu(Zh)

    # Output layer
    Zo = np.dot(H, Wo) + Bo
    yHat = relu(Zo)

References

[1]	http://cs231n.github.io/neural-networks-2/#init

Источник

Подробно рассматриваем обратное распространение ошибки для простой нейронной сети. Численный пример

Уровень сложности
Средний

Время на прочтение
6 мин

Количество просмотров 5.4K

В данной статье мы рассмотрим прямое распространение сигнала и обратное распространение ошибки в полносвязной нейронной сети прямого распространения. В результате получим весь набор формул, необходимых для программной реализации нейронной сети. В завершении статьи рассмотрим численный пример.

«Полносвязная» (fully connected) — означает, что каждый нейрон предыдущего слоя соединён с каждым нейроном следующего слоя. «Прямого распространения» (feedforward) — означает, что сигнал проходит через нейронную сеть в одном направлении от входного к выходному слою.

Полносвязная нейронная сеть прямого распространения («перцептрон») — это простейший и наиболее типичный пример искусственной нейронной сети.

Содержание

Нейронная сеть как функция
Дизайн нейронной сети
Прямое распространение сигнала
Обратное распространение ошибки и обновление

4.1. Вычисление новых весов матрицы W^3

4.2. Вычисление новых смещений вектора b^3

4.3. Вычисление новых весов матрицы W^2

4.4. Вычисление новых смещений вектора b^2
Численный пример
Обобщение для произвольного числа слоёв

Нейронная сеть как функция

Искусственная нейронная сеть является математической функцией, а точнее — композицией (суперпозицией) функций.

Было доказано (George Cybenko, 1989), что полносвязная нейронная сеть прямого распространения с хотя бы одним скрытым слоем и достаточным количеством нейронов потенциально может аппроксимировать любую непрерывную функцию, т.е. по своей сути она — универсальный аппроксиматор.

«Свойства универсальной аппроксимации встречаются в математике чаще, чем можно было бы ожидать. Например, теорема Вейерштрасса — Стоуна доказывает, что любая непрерывная функция на замкнутом интервале может быть приближена многочленной функцией. Если ослабить наши критерии далее, можно использовать ряды Тейлора и ряды Фурье, предлагающие некоторые возможности универсальной аппроксимации (в пределах их областей схождения). Тот факт, что универсальная сходимость — довольно обычное явление в математике, дает частичное обоснование эмпирического наблюдения, что существует много малых вариантов полносвязных сетей, которые, судя по всему, дают свойство универсальной аппроксимации».

— Рамсундар Б., Заде Р.Б. TensorFlow для глубокого обучения. Спб., 2019. С. 101.

Запишем нейронную сеть, которую мы будем рассматривать в данной статье, в виде функции:

$\mathbf{a}^3=\mathbf{a}^3(\mathbf{x}^3),\\\mathbf{x}^3=\mathbf{W}^3\times\mathbf{a}^2(\mathbf{x}^2)+\mathbf{b}^3,\\\mathbf{x}^2=\mathbf{W}^2\times\mathbf{x}^1+\mathbf{b}^2,$

где $\mathbf{x}^1$ — вектор входных значений — первый слой, $\mathbf{x}^2$ — второй, скрытый и $\mathbf{x}^3$ — третий слои нейронной сети, $\mathbf{b}^2$ , $\mathbf{b}^3$ — векторы смещений и $\mathbf{W}^2$ , $\mathbf{W}^3$ — матрицы весов второго и третьего слоёв соответственно, $\mathbf{a}^2$ — вектор-функция активации второго слоя, $\mathbf{a}^3$ — вектор-функция активации третьего, последнего слоя и, соответственно, вектор выходных значений нейронной сети.

Мы будем использовать принятую в литературе по нейронам сетям запись ${\mathbf{W}}\times{\mathbf{x}}$ , где $\mathbf{x}$ — вектор-столбец (в литературе по математике под вектором стандартно (по умолчанию) понимается вектор-столбец). Произведение матриц ${\mathbf{A}}\times{\mathbf{B}}$ определено, если число столбцов $\mathbf{A}$ равно числу строк $\mathbf{B}$ . Таким образом число столбцов матрицы $\mathbf{W}_{ij}$ равно числу строк векторов $\mathbf{x}$ и $\mathbf{a}$ .

Для комфортного чтения статьи необходимо обладать некоторым знанием линейной алгебры (обязательный минимум — операции над матрицами), производной сложной функции и частных производных.

Дизайн нейронной сети

Нейронная сеть имеет три слоя с тремя нейронами в каждом из них. Нелинейное изменение проходящего через сеть сигнала обеспечивает функция активации сигмоид (sigmoid) на скрытом и выходном слоях:

$f(x)=\frac{1}{1+e^{-x}}.$

Поскольку на практике большинство реальных данных имеют нелинейный характер, используются нелинейные функции активации, позволяющие извлекать нелинейные зависимости в данных.

Архитектура нейронной сети

Перепишем уравнение рассматриваемой сети для заданных параметров:

$\mathbf{a}^3=\mathbf{f}(\mathbf{x}^3)=\mathbf{f}\left(\left[\begin{matrix}w_{11}^3&w_{12}^3&w_{13}^3\\w_{21}^3&w_{22}^3&w_{23}^3\\w_{31}^3&w_{32}^3&w_{33}^3\\\end{matrix}\right]\times\mathbf{a}^2+\left[\begin{matrix}b_1^3\\b_2^3\\b_3^3\\\end{matrix}\right]\right),$ $\mathbf{a}^2=\mathbf{f}(\mathbf{x}^2)=\mathbf{f}\left(\left[\begin{matrix}w_{11}^2&w_{12}^2&w_{13}^2\\w_{21}^2&w_{22}^2&w_{23}^2\\w_{31}^2&w_{32}^2&w_{33}^2\\\end{matrix}\right]\times\left[\begin{matrix}x_1^1\\x_2^1\\x_3^1\\\end{matrix}\right]+\left[\begin{matrix}b_1^2\\b_2^2\\b_3^2\\\end{matrix}\right]\right).$

Функция активации поэлементно применяется к каждому элементу соответствующего вектора $\mathbf{x}$ .

Прямое распространение сигнала

Запишем уравнения для прямого прохождения сигнала через нейронную сеть:

$a_1^2=\ f(x_1^2)\ =\ f(w_{11}^2x_1^1+w_{12}^2x_2^1+w_{13}^2x_3^1+b_1^2),\\a_2^2=\ f(x_2^2)\ =f(w_{21}^2x_1^1+w_{22}^2x_2^1+w_{23}^2x_3^1+b_2^2),\\a_3^2=\ \ f(x_3^2)\ =f(w_{31}^2x_1^1+w_{32}^2x_2^1+w_{33}^2x_3^1+b_3^2);\\a_1^3=\ f(x_1^3)\ =\ f(w_{11}^3a_1^2+w_{12}^3a_2^2+w_{13}^3a_3^2+b_1^3),\\a_2^3=\ f(x_2^3)\ =f(w_{21}^3a_1^2+w_{22}^3a_2^2+w_{23}^3a_3^2+b_2^3),\\a_3^3=\ \ f(x_3^3)\ =f(w_{31}^3a_1^2+w_{32}^3a_2^2+w_{33}^3a_3^2+b_3^3);$

и функцию стоимости (cost function)

$Cost=\frac{1}{n}\sum_{i=1}^{n}{\left(y_i-a_i^3\right)^2{\rightarrow}min},$

где — номер соответствующего целевого (вектора $\mathbf{y}$ ) и выходного значений, — число выходных значений.

Таким образом, функция стоимости для нашей нейронной сети в развёрнутом виде:

$C=\frac{1}{3}(\left(y_1-a_1^3\right)^2+\left(y_2-a_2^3\right)^2+\left(y_3-a_3^3\right)^2).$

Функция стоимости показывает нам насколько сильно отличаются текущие значения нейронной сети от целевых.

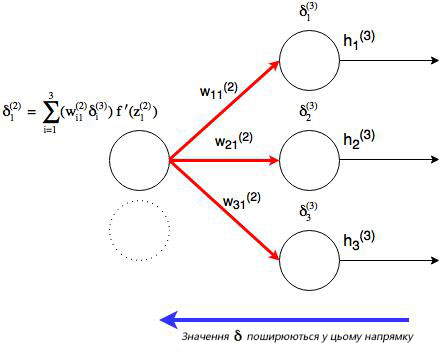
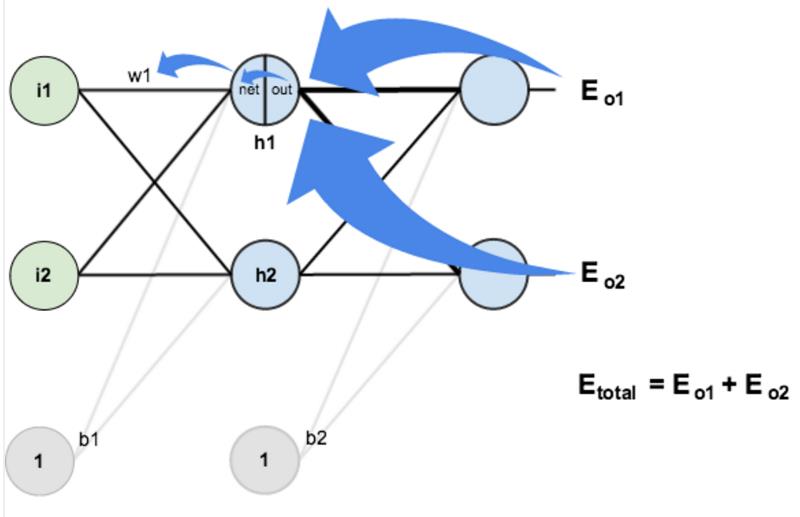
Обратное распространение ошибки и обновление

В сущности, для реализации алгоритма обратного распространения ошибки используется довольно простая идея.

Градиент (в общем случае) — вектор, определяющий направление наискорейшего роста функции нескольких переменных. Вычитая из текущих значений весов и смещений соответствующие значения частных производных как элементов градиента функции стоимости $\nabla{C}$ , мы будем приближаться к одному из ближайших (относительно начальной точки) минимумов функции стоимости и, таким образом, уменьшать величину ошибки. Согласно необходимому условию экстремума, в точках экстремума функции многих переменных её градиент равен нулю, $\nabla{C}=0$ .

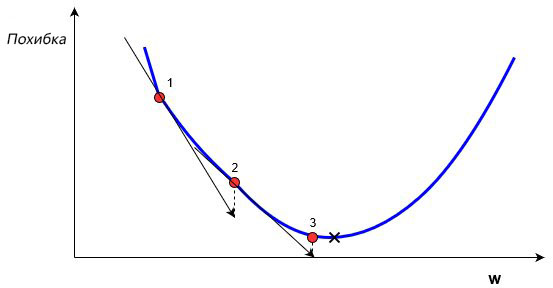
Этот подход называется алгоритмом градиентного спуска. Иногда может возникать путаница или отождествление этих двух алгоритмов, поскольку они тесно взаимосвязаны и один используется для реализации другого.

Несмотря на простоту и эффективность, алгоритм градиентного спуска в общем случае имеет свои ограничения, например, седловая точка, локальный минимум, перетренировка (overtraining) (попадание в глобальный минимум).

Найдём частные производные по всем элементам матрицы $\mathbf{W}^3$ :

$\frac{\partial C}{\partial\mathbf{W}^3}=\frac{1}{3}\sum_{i=1}^{3}\frac{\partial\left(y_i-a_i^3\right)^2}{\partial\mathbf{W}^3},\\\frac{\partial C}{\partial\mathbf{W}^3}=\frac{2}{3}\sum_{i=1}^{3}{\left(y_i-a_i^3\right)\frac{\partial\left(y_i-a_i^3\right)}{\partial\mathbf{W}^3}},\\\frac{\partial C}{\partial\mathbf{W}^3}=\frac{2}{3}\sum_{i=1}^{3}\left(y_i-a_i^3\right)\left(\frac{\partial y_i}{\partial\mathbf{W}^3}-\frac{\partial a_i^3}{\partial\mathbf{W}^3}\right),$

поскольку — константа, то $\frac{\partial y_i}{\partial\mathbf{W}^3}=0$ ,

$\frac{\partial C}{\partial\mathbf{W}^3}=-\frac{2}{3}\sum_{i=1}^{3}{\left(y_i-a_i^3\right)\frac{\partial a_i^3}{\partial\mathbf{W}^3}},\\\frac{\partial C}{\partial\mathbf{W}^3}=-\frac{2}{3}\sum_{i=1}^{3}{\left(y_i-a_i^3\right)\frac{\partial a_i^3}{\partial x_i^3}}\frac{\partial x_i^3}{\partial\mathbf{W}^3}.$

Преобразуем функцию активации сигмоид и найдём её производную:

$\frac{\partial C}{\partial\mathbf{W}^3}=-\frac{2}{3}\sum_{i=1}^{3}{\left(y_i-a_i^3\right)\frac{e^{x_i^3}}{\left(1+e^{x_i^3}\right)^2}}\frac{\partial x_i^3}{\partial\mathbf{W}^3}.$

В производной по матрице мы находим производную по каждому из её элементов.

Раскроем сумму для переменной $w_{11}^3$ матрицы $\mathbf{W}^3$ :

$\scriptsize\frac{\partial C}{\partial w_{11}^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial w_{11}^3}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial w_{11}^3}+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial w_{11}^3}).$

Найдём частную производную по переменной $w_{11}^3$ . Поскольку

$x_1^3=w_{11}^3a_1^2+w_{12}^3a_2^2+w_{13}^3a_3^2+b_1^3,\\x_2^3=w_{21}^3a_1^2+w_{22}^3a_2^2+w_{23}^3a_3^2+b_2^3,\\x_3^3=w_{31}^3a_1^2+w_{32}^3a_2^2+w_{33}^3a_3^2+b_3^3,$ $тогда \frac{\partial C}{\partial w_{11}^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}a_1^2+0+0).$

Преобразуем сигмоид и получим окончательную форму выражения для $\frac{\partial C}{\partial w_{11}^3}$ :

$\frac{\partial C}{\partial w_{11}^3}=-\frac{2}{3}\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)}{\left(1-\frac{e^{x_1^3}}{1+e^{x_1^3}}\right)}a_1^2\\или \frac{\partial C}{\partial w_{11}^3}=-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)a_1^2.$

Обратное распространение ошибки является частным случаем автоматического дифференцирования, для реализации которого нам и необходимо привести все вычислительные выражения к определённому виду.

Таким же образом для переменных $w_{12}^3$ и $w_{13}^3$ получим:

$\frac{\partial C}{\partial w_{12}^3}=-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)a_2^2,\\\frac{\partial C}{\partial w_{13}^3}=-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)a_3^2.$

Найдём новые значения (обновлённые веса) для переменных $w_{11}^3$ , $w_{12}^3$ и $w_{13}^3$ :

$^*w_{11}^3=\ w_{11}^3-\eta(-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)a_1^2),\\^*w_{12}^3=\ w_{12}^3-\eta(-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)a_2^2),\\^*w_{13}^3=\ w_{13}^3-\eta(-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)a_3^2),$

где $\eta$ (и́та) — буква греческого алфавита, обычно используемая для обозначения скорости обучения (learning rate), её значение должно быть установлено на промежутке от 0 до 1; * — новое значение переменной.

Найдём остальные частные производные для матрицы $\mathbf{W}^3$ . Раскроем сумму для $w_{21}^3$ :

$\scriptsize\frac{\partial C}{\partial w_{21}^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial w_{21}^3}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial w_{21}^3}+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial w_{21}^3}).$

Найдём частную производную по переменной $w_{21}^3$ :

$\frac{\partial C}{\partial w_{21}^3}=-\frac{2}{3}(0+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}a_1^2+0).$

Преобразуем сигмоид и получим окончательную форму выражения для $\frac{\partial C}{\partial w_{21}^3}$ :

$\frac{\partial C}{\partial w_{21}^3}=-\frac{2}{3}\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)}{\left(1-\frac{e^{x_2^3}}{1+e^{x_2^3}}\right)a_1^2}\\или \frac{\partial C}{\partial w_{21}^3}=-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)a_1^2.$

Таким же образом для переменных $w_{22}^3$ и $w_{23}^3$ получим:

$\frac{\partial C}{\partial w_{22}^3}=-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)a_2^2,\\\frac{\partial C}{\partial w_{23}^3}=-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)a_3^2.$

Найдём новые значения (обновлённые веса) для переменных $w_{21}^3$ , $w_{22}^3$ и $w_{23}^3$ :

$^*w_{21}^3=\ w_{21}^3-\eta(-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)a_1^2),\\^*w_{22}^3=\ w_{22}^3-\eta(-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)a_2^2),\\^*w_{23}^3=\ w_{23}^3-\eta(-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)a_3^2).$

Раскроем сумму для $w_{31}^3$ :

$\scriptsize\frac{\partial C}{\partial w_{31}^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial w_{31}^3}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial w_{31}^3}+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial w_{31}^3}).$

Найдём частную производную по переменной $w_{31}^3$ :

$\frac{\partial C}{\partial w_{31}^3}=-\frac{2}{3}(0+0+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}a_1^2).$

Преобразуем сигмоид и получим окончательную форму выражения для $\frac{\partial C}{\partial w_{31}^3}$ :

$\frac{\partial C}{\partial w_{31}^3}=-\frac{2}{3}\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)}{\left(1-\frac{e^{x_3^3}}{1+e^{x_3^3}}\right)a_1^2}\\или \frac{\partial C}{\partial w_{31}^3}=-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)a_1^2.$

Таким же образом для переменных $w_{32}^3$ и $w_{33}^3$ получим:

$\frac{\partial C}{\partial w_{32}^3}=-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)a_2^2,\\\frac{\partial C}{\partial w_{33}^3}=-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)a_3^2.$

Найдём новые значения (обновлённые веса) для переменных $w_{31}^3$ , $w_{32}^3$ и $w_{33}^3$ :

$^*w_{31}^3=\ w_{31}^3-\eta(-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)a_1^2),\\^*w_{32}^3=\ w_{32}^3-\eta(-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)a_2^2),\\^*w_{33}^3=\ w_{33}^3-\eta(-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)a_3^2).$

Теперь найдём частные производные по всем элементам вектора $\mathbf{b}^3$ :

$\frac{\partial C}{\partial\mathbf{b}^3}=-\frac{2}{3}\sum_{i=1}^{3}{\left(y_i-a_i^3\right)\frac{e^{x_i^3}}{\left(1+e^{x_i^3}\right)^2}}\frac{\partial x_i^3}{\partial\mathbf{b}^3}.$

Найдём частную производную по :

$\scriptsize\frac{\partial C}{\partial b_1^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial b_1^3}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial b_1^3}+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial b_1^3}),$ $\frac{\partial C}{\partial b_1^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}1+0+0).$

Преобразуем сигмоид и получим окончательную форму выражения для $\frac{\partial C}{\partial b_1^3}$ :

$\frac{\partial C}{\partial b_1^3}=-\frac{2}{3}\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)}\left(1-\frac{e^{x_1^3}}{1+e^{x_1^3}}\right)\\или \frac{\partial C}{\partial b_1^3}=-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right).$

Найдём новое значение для смещения :

$^*b_1^3=\ b_1^3-\eta(-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)).$

Вычислим частные производные по и :

$\scriptsize\frac{\partial C}{\partial b_2^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial b_2^3}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial b_2^3}+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial b_2^3}),$ $\frac{\partial C}{\partial b_2^3}=-\frac{2}{3}(0+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial b_2^2}+0),\\\frac{\partial C}{\partial b_2^3}=-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right).$ $\scriptsize\frac{\partial C}{\partial b_3^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial b_3^3}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial b_3^3}+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial b_3^3}),$ $\frac{\partial C}{\partial b_3^3}=-\frac{2}{3}(0+0+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial b_3^2}),\\\frac{\partial C}{\partial b_3^3}=-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right).$

Найдём новые значения для и:

$^*b_2^3=\ b_2^3-\eta(-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)),\\^*b_3^3=\ b_3^3-\eta(-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)).$

Найдём частные производные по всем элементам матрицы $\mathbf{W}^2$ . Раскроем сумму для переменной $w_{11}^2$ матрицы $\mathbf{W}^2$ . Поскольку

$x_1^3=w_{11}^3a_1^2+w_{12}^3a_2^2+w_{13}^3a_3^2+b_1^3,\\x_2^3=w_{21}^3a_1^2+w_{22}^3a_2^2+w_{23}^3a_3^2+b_2^3,\\x_3^3=w_{31}^3a_1^2+w_{32}^3a_2^2+w_{33}^3a_3^2+b_3^3,$

в свою очередь,

тогда сумма для переменной $w_{11}^2$ матрицы $\mathbf{W}^2$ :

$\frac{\partial C}{\partial w_{11}^2}=-\frac{2}{3}\sum_{i=1}^{3}{\left(y_i-a_i^3\right)\frac{e^{x_i^3}}{\left(1+e^{x_i^3}\right)^2}}\frac{\partial x_i^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial w_{11}^2},$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{11}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial w_{11}^2}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial w_{11}^2}\\+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial w_{11}^2}),\\\frac{\partial C}{\partial w_{11}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}w_{11}^3\frac{e^{x_1^2}}{\left(1+e^{x_1^2}\right)}\left(1-\frac{e^{x_1^2}}{1+e^{x_1^2}}\right)x_1^1\\+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}w_{21}^3\frac{e^{x_1^2}}{\left(1+e^{x_1^2}\right)}\left(1-\frac{e^{x_1^2}}{1+e^{x_1^2}}\right)x_1^1\\+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}w_{31}^3\frac{e^{x_1^2}}{\left(1+e^{x_1^2}\right)}\left(1-\frac{e^{x_1^2}}{1+e^{x_1^2}}\right)x_1^1),\\\frac{\partial C}{\partial w_{11}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{11}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_1^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{21}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_1^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{31}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_1^1).\end{gather}}$

Найдём новое значение (обновлённый вес) для переменной $w_{11}^2$ :

$^*w_{11}^2=\ w_{11}^2-\eta\frac{\partial C}{\partial w_{11}^2}.$

Найдём остальные частные производные и их новые значения для матрицы $\mathbf{W}^2$ .

$\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{12}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{11}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_2^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{21}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_2^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{31}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_2^1).\end{gather}}$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{13}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{11}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_3^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{21}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_3^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{31}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_3^1).\end{gather}}$ $^*w_{12}^2=\ w_{12}^2-\eta\frac{\partial C}{\partial w_{12}^2}, ^*w_{13}^2=\ w_{13}^2-\eta\frac{\partial C}{\partial w_{13}^2}.$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{21}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{12}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_1^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{22}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_1^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{32}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_1^1).\end{gather}}$ $\scriptsize{\begin{gather} \frac{\partial C}{\partial w_{22}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{12}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_2^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{22}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_2^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{32}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_2^1).\end{gather}}$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{23}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{12}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_3^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{22}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_3^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{32}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_3^1).\end{gather}}$ $^*w_{21}^2=\ w_{21}^2-\eta\frac{\partial C}{\partial w_{21}^2}, ^*w_{22}^2=\ w_{22}^2-\eta\frac{\partial C}{\partial w_{22}^2},\\^*w_{23}^2=\ w_{23}^2-\eta\frac{\partial C}{\partial w_{23}^2}.$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{31}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{13}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_1^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{23}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_1^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{33}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_1^1).\end{gather}}$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{32}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{13}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_2^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{23}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_2^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{33}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_2^1).\end{gather}}$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{33}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{13}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_3^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{23}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_3^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{33}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_3^1).\end{gather}}$ $^*w_{31}^2=\ w_{31}^2-\eta\frac{\partial C}{\partial w_{31}^2}, ^*w_{32}^2=\ w_{32}^2-\eta\frac{\partial C}{\partial w_{32}^2},\\^*w_{33}^2=\ w_{33}^2-\eta\frac{\partial C}{\partial w_{33}^2}.$

Теперь найдём частные производные по всем элементам вектора $\mathbf{b}^2$ . Раскроем сумму для переменной :

$\frac{\partial C}{\partial b_1^2}=-\frac{2}{3}\sum_{i=1}^{3}{\left(y_i-a_i^3\right)\frac{e^{x_i^3}}{\left(1+e^{x_i^3}\right)^2}}\frac{\partial x_i^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial b_1^2},$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial b_1^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial b_1^2}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial b_1^2}\\+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial b_1^2}),\\\frac{\partial C}{\partial b_1^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}w_{11}^3\frac{e^{x_1^2}}{\left(1+e^{x_1^2}\right)}\left(1-\frac{e^{x_1^2}}{1+e^{x_1^2}}\right)\\+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}w_{21}^3\frac{e^{x_1^2}}{\left(1+e^{x_1^2}\right)}\left(1-\frac{e^{x_1^2}}{1+e^{x_1^2}}\right)\\+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}w_{31}^3\frac{e^{x_1^2}}{\left(1+e^{x_1^2}\right)}\left(1-\frac{e^{x_1^2}}{1+e^{x_1^2}}\right)),\\\frac{\partial C}{\partial b_1^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{11}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{21}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{31}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)).\end{gather}}$

Найдём новое значение для :

$^*b_1^2=\ b_1^2-\eta\frac{\partial C}{\partial b_1^2}.$

Найдём остальные частные производные для вектора $\mathbf{b}^2$ :

$\scriptsize{\begin{gather}\frac{\partial C}{\partial b_2^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{12}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{22}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{32}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)).\end{gather}}$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial b_3^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{13}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{23}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{33}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)).\end{gather}}$

Найдём новые значения для переменных и :

$^*b_2^2=\ b_2^2-\eta\frac{\partial C}{\partial b_2^2}, ^*b_3^2=\ b_3^2-\eta\frac{\partial C}{\partial b_3^2}.$

Численный пример

Задача обучения нейронной сети состоит в аппроксимации некоторой неизвестной функции, которая отображает $\mathbf{x}^1$ в $\mathbf{y}$ .

Другими словами, существует некоторая неизвестная нам функция $\mathbf{y}=\mathbf{f}(\mathbf{x}^1)$ , которая для набора значений независимых переменных выдаёт результат, соответствующий набору значений зависимых переменных . Задача нейронной сети в результате обучения «заменить», приблизить, т.е. аппроксимировать неизвестную функцию $\mathbf{y}=\mathbf{f}(\mathbf{x}^1)$ . В случае успешного решения задачи, значения нашей нейронной сети на выходном слое $\mathbf{a}^3$ будут приблизительно равны значениям вектора $\mathbf{y}$ аппроксимируемой функции.

Выберем случайным образом следующие начальные значения для нашей нейронной сети:

$\mathbf{W}^2=\left[\begin{matrix}0.88&0.39&0.9\\0.37&0.14&0.41\\0.96&0.5&0.6\\\end{matrix}\right],\mathbf{W}^3=\left[\begin{matrix}0.29&0.57&0.36\\0.73&0.53&0.68\\0.01&0.02&0.58\\\end{matrix}\right],\\\mathbf{b}^2=\left[\begin{matrix}0.23\\0.89\\0.08\\\end{matrix}\right], \mathbf{b}^3=\left[\begin{matrix}0.78\\0.83\\0.8\\\end{matrix}\right].$

А также входные и целевые значения: $\mathbf{x}^1=\left[\begin{matrix}0.03\\0.72\\0.49\\\end{matrix}\right], \mathbf{y}=\left[\begin{matrix}0.93\\0.74\\0.17\\\end{matrix}\right].$

После первого прямого прохождения сигнала значения скрытого и выходного слоёв:

$\mathbf{a}^2=\left[\begin{matrix}0.726750911\\0.769022513\\0.681961335\\\end{matrix}\right], \mathbf{a}^3=\left[\begin{matrix}0.842189045\\0.903072871\\0.771744079\\\end{matrix}\right].$

Для скорости обучения установим значение $\eta=0.01$ .

Вычислим для первой эпохи (epoch) обучения нейронной сети обновлённые значения весов $w_{11}^3$ и $w_{11}^2$ :

$\scriptsize{\begin{gather}^*w_{11}^3=0.29+0.01\cdot \frac{2}{3}\cdot (0.93-0.842189045)\cdot 0.842189045\cdot (1-0.842189045)\cdot 0.726750911=0.290056544,\\^*w_{11}^2=0.88+0.01\cdot \frac{2}{3}\cdot (\left(0.93-0.842189045\right)\cdot 0.842189045\cdot \left(1-0.842189045\right)\cdot 0.29\cdot 0.726750911\cdot\\ \left(1-0.726750911\right)\cdot 0.03+\left(0.74-0.903072871\right)\cdot \:0.903072871\cdot \left(1-0.903072871\right)\cdot \:0.73\cdot \:0.769022513\cdot\\ \left(1-0.769022513\right)\cdot \:0.03+\left(0.17-0.771744079\right)\cdot \:0.771744079\cdot \left(1-0.771744079\right)\cdot \:0.01\cdot \:0.681961335\cdot\\ \left(1-0.681961335\right)\cdot \:0.03)=0.879999678.\end{gather}}$

Новые значения других весов и смещений находятся аналогичным образом, в соответствии с полученными ранее формулами.

После 10 000 эпох обучения матрицы весов и выходной слой имеют следующие значения:

$\mathbf{W}^2=\left[\begin{matrix}0.881449843&0.424796239&0.923680774\\0.372218081&0.193233937&0.446228651\\0.957567842&0.441628217&0.560274759\\\end{matrix}\right],\\\mathbf{W}^3=\left[\begin{matrix}0.480573892&0.772236752&0.529654336\\0.394700365&0.174298746&0.381672097\\-0.771753134&-0.808346904&-0.127425218\\\end{matrix}\right],\\\mathbf{a}^3=\left[\begin{matrix}0.913047169\\0.741592957\\0.173072228\\\end{matrix}\right].$

Обобщение для произвольного числа слоёв

Мы рассмотрели частный случай алгоритма обратного распространения ошибки для нейронной сети с одним скрытым слоем. Запишем формулы для реализации нейронной сети с произвольным числом скрытых слоёв.

$\delta_i^L=\left(y_i-a_i^L\right)a_i^L\left(x_i^L\right)\left(1-a_i^L\left(x_i^L\right)\right),\\\delta_i^l=\sum_{k=1}^{n}{\delta_k^{l+1}w_{ki}^{l+1}\frac{\partial a_i^l}{\partial x_i^l}},\\\frac{\partial C}{\partial w_{ij}^l}=\frac{1}{n}\delta_i^l\frac{\partial x_i^l}{\partial w_{ij}^l},\\\frac{\partial C}{\partial b_i^l}=\delta_i^l,$

где — номер выходного слоя, — индекс строки матрицы весов, — число выходных значений.

$\delta$ — обобщённое дельта-правило (delta rule).

Надеемся, что статья будет интересной и полезной для всех, кто приступает к изучению глубинного обучения и нейронных сетей!

Источник

Искусственная нейронная сеть обычно обучается с учителем. Это означает наличие обучающего набора (датасета), который содержит примеры с истинными значениями: тегами, классами, показателями.

Неразмеченные наборы также используют для обучения нейронных сетей, но мы не будем здесь это рассматривать.

Например, если вы хотите создать нейросеть для оценки тональности текста, датасетом будет список предложений с соответствующими каждому эмоциональными оценками. Тональность текста определяют признаки (слова, фразы, структура предложения), которые придают негативную или позитивную окраску. Веса признаков в итоговой оценке тональности текста (позитивный, негативный, нейтральный) зависят от математической функции, которая вычисляется во время обучения нейронной сети.

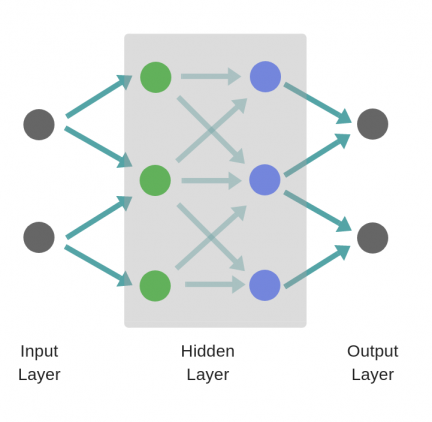
Искусственная нейронная сеть состоит из трех компонентов:

Входной слой;
Скрытые (вычислительные) слои;
Выходной слой.

Обучение нейросетей происходит в два этапа:

Прямое распространение ошибки;
Обратное распространение ошибки.

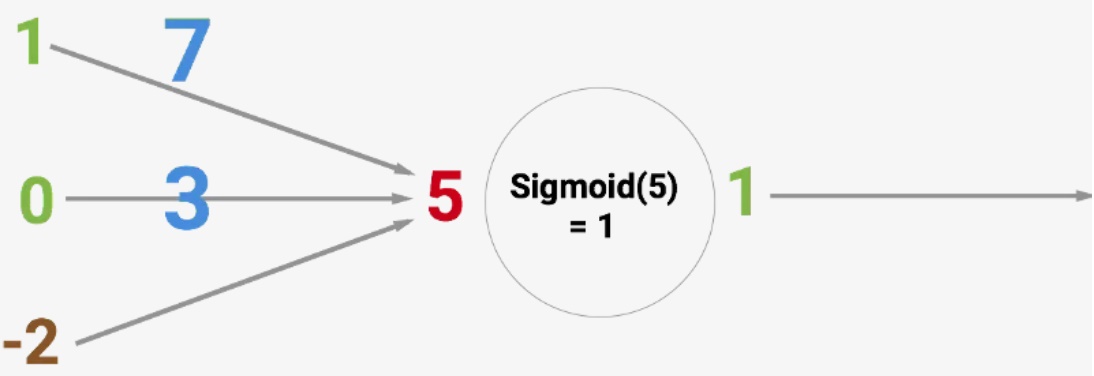
Прямое распространение ошибки

Прямое распространение

Зададим начальные веса случайным образом:

Умножим входные данные на веса для формирования скрытого слоя:

h1 = (x1 * w1) + (x2 * w1)
h2 = (x1 * w2) + (x2 * w2)
h3 = (x1 * w3) + (x2 * w3)

y_ = fn(h1 , h2, h3)

Обратное распространение

Суммарная ошибка (total_error) вычисляется как разность между ожидаемым значением «y» (из обучающего набора) и полученным значением «y_» (посчитанное на этапе прямого распространения ошибки), проходящих через функцию потерь (cost function).
Частная производная ошибки вычисляется по каждому весу (эти частные дифференциалы отражают вклад каждого веса в общую ошибку (total_loss)).
Затем эти дифференциалы умножаются на число, называемое скорость обучения или learning rate (η).

Полученный результат затем вычитается из соответствующих весов.

В результате получатся следующие обновленные веса:

w1 = w1 — (η * ∂(err) / ∂(w1))
w2 = w2 — (η * ∂(err) / ∂(w2))
w3 = w3 — (η * ∂(err) / ∂(w3))

Популярный мем о том, как Карлсон стал Data Science разработчиком

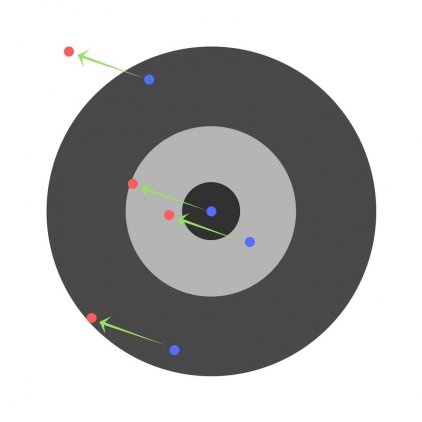
Частные производные

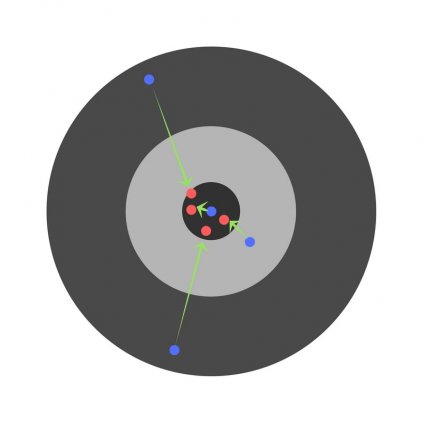
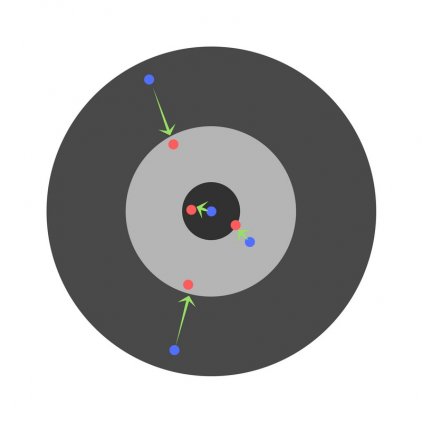
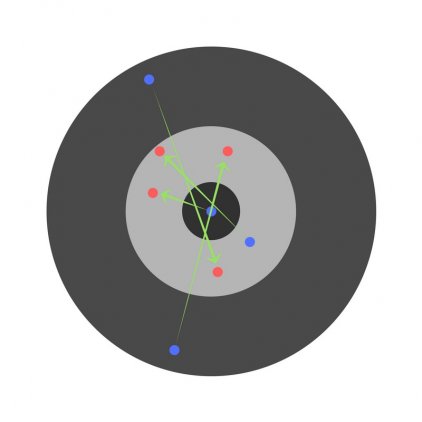
Разберем необходимость частных производных на примере.

Предположим, детей попросили бросить дротик в мишень, целясь в центр. Вот результаты:

Ошибка нескольких детей может уменьшиться, но общая ошибка все еще увеличивается.

Гиперпараметры

Скорость обучения (learning rate)

Функция активации (activation function)

Функция потери (loss function)

Некоторые известные функции потерь:

Квадратичная (среднеквадратичное отклонение);
Кросс-энтропия;
Экспоненциальная (AdaBoost);
Расстояние Кульбака — Лейблера или прирост информации.

Cреднеквадратичное отклонение – самая простая фукция потерь и наиболее часто используемая. Она задается следующим образом:

Функция потерь в нейронной сети должна удовлетворять двум условиям:

Функция потерь должна быть записана как среднее;
Функция потерь не должна зависеть от каких-либо активационных значений нейронной сети, кроме значений, выдаваемых на выходе.

Глубокие нейронные сети

Популярные алгоритмы нейронных сетей (http://www.asimovinstitute.org/neural-network-zoo)

Более формально в deep learning:

Используется каскад (пайплайн, как последовательно передаваемый поток) из множества обрабатывающих слоев (нелинейных) для извлечения и преобразования признаков;
Основывается на изучении признаков (представлении информации) в данных без обучения с учителем. Функции более высокого уровня (которые находятся в последних слоях) получаются из функций нижнего уровня (которые находятся в слоях начальных слоях);
Изучает многоуровневые представления, которые соответствуют разным уровням абстракции; уровни образуют иерархию представления.

Пример

Рассмотрим однослойную нейронную сеть:

Здесь, обучается первый слой (зеленые нейроны), он просто передается на выход.

Следовательно, чем больше число скрытых слоев, тем больше возможности обучения сети.

Не следует путать с широкой нейронной сетью.

Пример:

Но

Главное — баланс

Обе требуют значительно большего количества данных для обучения, чтобы достичь минимальной желаемой точности;
Обе имеют экспоненциальную сложность;
Слишком глубокая нейронная сеть попытается сломать фундаментальные представления, но при этом она будет делать ошибочные предположения и пытаться найти псевдо-зависимости, которые не существуют;
Слишком широкая нейронная сеть будет пытаться найти больше признаков, чем есть. Таким образом, подобно предыдущей, она начнет делать неправильные предположения о данных.

Проклятье размерности

Из-за неправильных предположений появляется смещение. Высокое смещение может привести к тому, что алгоритм пропустит существенную взаимосвязь между признаками и целевыми переменными. Это явление называют недообучение.
От небольших отклонений в обучающем множестве из-за недостаточного изучения признаков увеличивается дисперсия. Высокая дисперсия ведет к переобучению, ошибки воспринимаются в качестве надежной информации.

Компромисс

Действительно,

Следовательно, как правило, невозможно иметь маленькое смещение и маленькую дисперсию одновременно.

Сейчас есть множество инструментов, с помощью которых можно легко создать сложные модели машинного обучения, переобучение занимает центральное место. Поскольку смещение появляется, когда сеть не получает достаточно информации. Но чем больше примеров, тем больше появляется вариантов зависимостей и изменчивостей в этих корреляциях.

Подробно рассматриваем обратное распространение ошибки для простой нейронной сети. Численный пример

Уровень сложности
Средний

Время на прочтение
6 мин

Количество просмотров 3.7K

Содержание

Нейронная сеть как функция
Дизайн нейронной сети
Прямое распространение сигнала
Обратное распространение ошибки и обновление

4.1. Вычисление новых весов матрицы W^3

4.2. Вычисление новых смещений вектора b^3

4.3. Вычисление новых весов матрицы W^2

4.4. Вычисление новых смещений вектора b^2
Численный пример
Обобщение для произвольного числа слоёв

Нейронная сеть как функция

«Свойства универсальной аппроксимации встречаются в математике чаще, чем можно было бы ожидать. Например, теорема Вейерштрасса — Стоуна доказывает, что любая непрерывная функция на замкнутом интервале может быть приближена многочленной функцией. Если ослабить наши критерии далее, можно использовать ряды Тейлора и ряды Фурье, предлагающие некоторые возможности универсальной аппроксимации (в пределах их областей схождения). Тот факт, что универсальная сходимость — довольно обычное явление в математике, дает частичное обоснование эмпирического наблюдения, что существует много малых вариантов полносвязных сетей, которые, судя по всему, дают свойство универсальной аппроксимации».

— Рамсундар Б., Заде Р.Б. TensorFlow для глубокого обучения. Спб., 2019. С. 101.

Запишем нейронную сеть, которую мы будем рассматривать в данной статье, в виде функции:

$mathbf{a}^3=mathbf{a}^3(mathbf{x}^3),\mathbf{x}^3=mathbf{W}^3timesmathbf{a}^2(mathbf{x}^2)+mathbf{b}^3,\mathbf{x}^2=mathbf{W}^2timesmathbf{x}^1+mathbf{b}^2,$

где $mathbf{x}^1$ — вектор входных значений — первый слой, $mathbf{x}^2$ — второй, скрытый и $mathbf{x}^3$ — третий слои нейронной сети, $mathbf{b}^2$ , $mathbf{b}^3$ — векторы смещений и $mathbf{W}^2$ , $mathbf{W}^3$ — матрицы весов второго и третьего слоёв соответственно, $mathbf{a}^2$ — вектор-функция активации второго слоя, $mathbf{a}^3$ — вектор-функция активации третьего, последнего слоя и, соответственно, вектор выходных значений нейронной сети.

Мы будем использовать принятую в литературе по нейронам сетям запись , где — вектор-столбец (в литературе по математике под вектором стандартно (по умолчанию) понимается вектор-столбец). Произведение матриц определено, если число столбцов равно числу строк . Таким образом число столбцов матрицы $mathbf{W}_{ij}$ равно числу строк векторов и .

Дизайн нейронной сети

$f(x)=frac{1}{1+e^{-x}}.$

Архитектура нейронной сети

Перепишем уравнение рассматриваемой сети для заданных параметров:

$mathbf{a}^3=mathbf{f}(mathbf{x}^3)=mathbf{f}left(left[begin{matrix}w_{11}^3&w_{12}^3&w_{13}^3\w_{21}^3&w_{22}^3&w_{23}^3\w_{31}^3&w_{32}^3&w_{33}^3\end{matrix}right]timesmathbf{a}^2+left[begin{matrix}b_1^3\b_2^3\b_3^3\end{matrix}right]right),$ $mathbf{a}^2=mathbf{f}(mathbf{x}^2)=mathbf{f}left(left[begin{matrix}w_{11}^2&w_{12}^2&w_{13}^2\w_{21}^2&w_{22}^2&w_{23}^2\w_{31}^2&w_{32}^2&w_{33}^2\end{matrix}right]timesleft[begin{matrix}x_1^1\x_2^1\x_3^1\end{matrix}right]+left[begin{matrix}b_1^2\b_2^2\b_3^2\end{matrix}right]right).$

Функция активации поэлементно применяется к каждому элементу соответствующего вектора .

Прямое распространение сигнала

Запишем уравнения для прямого прохождения сигнала через нейронную сеть:

$a_1^2= f(x_1^2) = f(w_{11}^2x_1^1+w_{12}^2x_2^1+w_{13}^2x_3^1+b_1^2),\a_2^2= f(x_2^2) =f(w_{21}^2x_1^1+w_{22}^2x_2^1+w_{23}^2x_3^1+b_2^2),\a_3^2= f(x_3^2) =f(w_{31}^2x_1^1+w_{32}^2x_2^1+w_{33}^2x_3^1+b_3^2);\a_1^3= f(x_1^3) = f(w_{11}^3a_1^2+w_{12}^3a_2^2+w_{13}^3a_3^2+b_1^3),\a_2^3= f(x_2^3) =f(w_{21}^3a_1^2+w_{22}^3a_2^2+w_{23}^3a_3^2+b_2^3),\a_3^3= f(x_3^3) =f(w_{31}^3a_1^2+w_{32}^3a_2^2+w_{33}^3a_3^2+b_3^3);$

и функцию стоимости (cost function)

$Cost=frac{1}{n}sum_{i=1}^{n}{left(y_i-a_i^3right)^2{rightarrow}min},$

где — номер соответствующего целевого (вектора ) и выходного значений, — число выходных значений.

Таким образом, функция стоимости для нашей нейронной сети в развёрнутом виде:

$C=frac{1}{3}(left(y_1-a_1^3right)^2+left(y_2-a_2^3right)^2+left(y_3-a_3^3right)^2).$

Функция стоимости показывает нам насколько сильно отличаются текущие значения нейронной сети от целевых.

Обратное распространение ошибки и обновление

В сущности, для реализации алгоритма обратного распространения ошибки используется довольно простая идея.

Градиент (в общем случае) — вектор, определяющий направление наискорейшего роста функции нескольких переменных. Вычитая из текущих значений весов и смещений соответствующие значения частных производных как элементов градиента функции стоимости , мы будем приближаться к одному из ближайших (относительно начальной точки) минимумов функции стоимости и, таким образом, уменьшать величину ошибки. Согласно необходимому условию экстремума, в точках экстремума функции многих переменных её градиент равен нулю, .

Найдём частные производные по всем элементам матрицы $mathbf{W}^3$ :

$frac{partial C}{partialmathbf{W}^3}=frac{1}{3}sum_{i=1}^{3}frac{partialleft(y_i-a_i^3right)^2}{partialmathbf{W}^3},\frac{partial C}{partialmathbf{W}^3}=frac{2}{3}sum_{i=1}^{3}{left(y_i-a_i^3right)frac{partialleft(y_i-a_i^3right)}{partialmathbf{W}^3}},\frac{partial C}{partialmathbf{W}^3}=frac{2}{3}sum_{i=1}^{3}left(y_i-a_i^3right)left(frac{partial y_i}{partialmathbf{W}^3}-frac{partial a_i^3}{partialmathbf{W}^3}right),$

поскольку — константа, то $frac{partial y_i}{partialmathbf{W}^3}=0$ ,

$frac{partial C}{partialmathbf{W}^3}=-frac{2}{3}sum_{i=1}^{3}{left(y_i-a_i^3right)frac{partial a_i^3}{partialmathbf{W}^3}},\frac{partial C}{partialmathbf{W}^3}=-frac{2}{3}sum_{i=1}^{3}{left(y_i-a_i^3right)frac{partial a_i^3}{partial x_i^3}}frac{partial x_i^3}{partialmathbf{W}^3}.$

Преобразуем функцию активации сигмоид и найдём её производную:

$frac{partial C}{partialmathbf{W}^3}=-frac{2}{3}sum_{i=1}^{3}{left(y_i-a_i^3right)frac{e^{x_i^3}}{left(1+e^{x_i^3}right)^2}}frac{partial x_i^3}{partialmathbf{W}^3}.$

В производной по матрице мы находим производную по каждому из её элементов.

Раскроем сумму для переменной $w_{11}^3$ матрицы $mathbf{W}^3$ :

$scriptsizefrac{partial C}{partial w_{11}^3}=-frac{2}{3}(left(y_1-a_1^3right)frac{e^{x_1^3}}{left(1+e^{x_1^3}right)^2}frac{partial x_1^3}{partial w_{11}^3}+left(y_2-a_2^3right)frac{e^{x_2^3}}{left(1+e^{x_2^3}right)^2}frac{partial x_2^3}{partial w_{11}^3}+left(y_3-a_3^3right)frac{e^{x_3^3}}{left(1+e^{x_3^3}right)^2}frac{partial x_3^3}{partial w_{11}^3}).$

Найдём частную производную по переменной $w_{11}^3$ . Поскольку

$x_1^3=w_{11}^3a_1^2+w_{12}^3a_2^2+w_{13}^3a_3^2+b_1^3,\x_2^3=w_{21}^3a_1^2+w_{22}^3a_2^2+w_{23}^3a_3^2+b_2^3,\x_3^3=w_{31}^3a_1^2+w_{32}^3a_2^2+w_{33}^3a_3^2+b_3^3,$ $тогда frac{partial C}{partial w_{11}^3}=-frac{2}{3}(left(y_1-a_1^3right)frac{e^{x_1^3}}{left(1+e^{x_1^3}right)^2}a_1^2+0+0).$

Преобразуем сигмоид и получим окончательную форму выражения для $frac{partial C}{partial w_{11}^3}$ :

$frac{partial C}{partial w_{11}^3}=-frac{2}{3}left(y_1-a_1^3right)frac{e^{x_1^3}}{left(1+e^{x_1^3}right)}{left(1-frac{e^{x_1^3}}{1+e^{x_1^3}}right)}a_1^2\или frac{partial C}{partial w_{11}^3}=-frac{2}{3}left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)a_1^2.$

Таким же образом для переменных $w_{12}^3$ и $w_{13}^3$ получим:

$frac{partial C}{partial w_{12}^3}=-frac{2}{3}left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)a_2^2,\frac{partial C}{partial w_{13}^3}=-frac{2}{3}left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)a_3^2.$

Найдём новые значения (обновлённые веса) для переменных $w_{11}^3$ , $w_{12}^3$ и $w_{13}^3$ :

$^*w_{11}^3= w_{11}^3-eta(-frac{2}{3}left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)a_1^2),\^*w_{12}^3= w_{12}^3-eta(-frac{2}{3}left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)a_2^2),\^*w_{13}^3= w_{13}^3-eta(-frac{2}{3}left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)a_3^2),$

где (и́та) — буква греческого алфавита, обычно используемая для обозначения скорости обучения (learning rate), её значение должно быть установлено на промежутке от 0 до 1; * — новое значение переменной.

Найдём остальные частные производные для матрицы $mathbf{W}^3$ . Раскроем сумму для $w_{21}^3$ :

$scriptsizefrac{partial C}{partial w_{21}^3}=-frac{2}{3}(left(y_1-a_1^3right)frac{e^{x_1^3}}{left(1+e^{x_1^3}right)^2}frac{partial x_1^3}{partial w_{21}^3}+left(y_2-a_2^3right)frac{e^{x_2^3}}{left(1+e^{x_2^3}right)^2}frac{partial x_2^3}{partial w_{21}^3}+left(y_3-a_3^3right)frac{e^{x_3^3}}{left(1+e^{x_3^3}right)^2}frac{partial x_3^3}{partial w_{21}^3}).$

Найдём частную производную по переменной $w_{21}^3$ :

$frac{partial C}{partial w_{21}^3}=-frac{2}{3}(0+left(y_2-a_2^3right)frac{e^{x_2^3}}{left(1+e^{x_2^3}right)^2}a_1^2+0).$

Преобразуем сигмоид и получим окончательную форму выражения для $frac{partial C}{partial w_{21}^3}$ :

$frac{partial C}{partial w_{21}^3}=-frac{2}{3}left(y_2-a_2^3right)frac{e^{x_2^3}}{left(1+e^{x_2^3}right)}{left(1-frac{e^{x_2^3}}{1+e^{x_2^3}}right)a_1^2}\или frac{partial C}{partial w_{21}^3}=-frac{2}{3}left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)a_1^2.$

Таким же образом для переменных $w_{22}^3$ и $w_{23}^3$ получим:

$frac{partial C}{partial w_{22}^3}=-frac{2}{3}left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)a_2^2,\frac{partial C}{partial w_{23}^3}=-frac{2}{3}left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)a_3^2.$

Найдём новые значения (обновлённые веса) для переменных $w_{21}^3$ , $w_{22}^3$ и $w_{23}^3$ :

$^*w_{21}^3= w_{21}^3-eta(-frac{2}{3}left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)a_1^2),\^*w_{22}^3= w_{22}^3-eta(-frac{2}{3}left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)a_2^2),\^*w_{23}^3= w_{23}^3-eta(-frac{2}{3}left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)a_3^2).$

Раскроем сумму для $w_{31}^3$ :

$scriptsizefrac{partial C}{partial w_{31}^3}=-frac{2}{3}(left(y_1-a_1^3right)frac{e^{x_1^3}}{left(1+e^{x_1^3}right)^2}frac{partial x_1^3}{partial w_{31}^3}+left(y_2-a_2^3right)frac{e^{x_2^3}}{left(1+e^{x_2^3}right)^2}frac{partial x_2^3}{partial w_{31}^3}+left(y_3-a_3^3right)frac{e^{x_3^3}}{left(1+e^{x_3^3}right)^2}frac{partial x_3^3}{partial w_{31}^3}).$

Найдём частную производную по переменной $w_{31}^3$ :

$frac{partial C}{partial w_{31}^3}=-frac{2}{3}(0+0+left(y_3-a_3^3right)frac{e^{x_3^3}}{left(1+e^{x_3^3}right)^2}a_1^2).$

Преобразуем сигмоид и получим окончательную форму выражения для $frac{partial C}{partial w_{31}^3}$ :

$frac{partial C}{partial w_{31}^3}=-frac{2}{3}left(y_3-a_3^3right)frac{e^{x_3^3}}{left(1+e^{x_3^3}right)}{left(1-frac{e^{x_3^3}}{1+e^{x_3^3}}right)a_1^2}\или frac{partial C}{partial w_{31}^3}=-frac{2}{3}left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)a_1^2.$

Таким же образом для переменных $w_{32}^3$ и $w_{33}^3$ получим:

$frac{partial C}{partial w_{32}^3}=-frac{2}{3}left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)a_2^2,\frac{partial C}{partial w_{33}^3}=-frac{2}{3}left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)a_3^2.$

Найдём новые значения (обновлённые веса) для переменных $w_{31}^3$ , $w_{32}^3$ и $w_{33}^3$ :

$^*w_{31}^3= w_{31}^3-eta(-frac{2}{3}left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)a_1^2),\^*w_{32}^3= w_{32}^3-eta(-frac{2}{3}left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)a_2^2),\^*w_{33}^3= w_{33}^3-eta(-frac{2}{3}left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)a_3^2).$

Теперь найдём частные производные по всем элементам вектора $mathbf{b}^3$ :

$frac{partial C}{partialmathbf{b}^3}=-frac{2}{3}sum_{i=1}^{3}{left(y_i-a_i^3right)frac{e^{x_i^3}}{left(1+e^{x_i^3}right)^2}}frac{partial x_i^3}{partialmathbf{b}^3}.$

Найдём частную производную по :

$scriptsizefrac{partial C}{partial b_1^3}=-frac{2}{3}(left(y_1-a_1^3right)frac{e^{x_1^3}}{left(1+e^{x_1^3}right)^2}frac{partial x_1^3}{partial b_1^3}+left(y_2-a_2^3right)frac{e^{x_2^3}}{left(1+e^{x_2^3}right)^2}frac{partial x_2^3}{partial b_1^3}+left(y_3-a_3^3right)frac{e^{x_3^3}}{left(1+e^{x_3^3}right)^2}frac{partial x_3^3}{partial b_1^3}),$ $frac{partial C}{partial b_1^3}=-frac{2}{3}(left(y_1-a_1^3right)frac{e^{x_1^3}}{left(1+e^{x_1^3}right)^2}1+0+0).$

Преобразуем сигмоид и получим окончательную форму выражения для $frac{partial C}{partial b_1^3}$ :

$frac{partial C}{partial b_1^3}=-frac{2}{3}left(y_1-a_1^3right)frac{e^{x_1^3}}{left(1+e^{x_1^3}right)}left(1-frac{e^{x_1^3}}{1+e^{x_1^3}}right)\или frac{partial C}{partial b_1^3}=-frac{2}{3}left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right).$

Найдём новое значение для смещения :

$^*b_1^3= b_1^3-eta(-frac{2}{3}left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)).$

Вычислим частные производные по и :

$scriptsizefrac{partial C}{partial b_2^3}=-frac{2}{3}(left(y_1-a_1^3right)frac{e^{x_1^3}}{left(1+e^{x_1^3}right)^2}frac{partial x_1^3}{partial b_2^3}+left(y_2-a_2^3right)frac{e^{x_2^3}}{left(1+e^{x_2^3}right)^2}frac{partial x_2^3}{partial b_2^3}+left(y_3-a_3^3right)frac{e^{x_3^3}}{left(1+e^{x_3^3}right)^2}frac{partial x_3^3}{partial b_2^3}),$ $frac{partial C}{partial b_2^3}=-frac{2}{3}(0+left(y_2-a_2^3right)frac{e^{x_2^3}}{left(1+e^{x_2^3}right)^2}frac{partial x_2^3}{partial b_2^2}+0),\frac{partial C}{partial b_2^3}=-frac{2}{3}left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right).$ $scriptsizefrac{partial C}{partial b_3^3}=-frac{2}{3}(left(y_1-a_1^3right)frac{e^{x_1^3}}{left(1+e^{x_1^3}right)^2}frac{partial x_1^3}{partial b_3^3}+left(y_2-a_2^3right)frac{e^{x_2^3}}{left(1+e^{x_2^3}right)^2}frac{partial x_2^3}{partial b_3^3}+left(y_3-a_3^3right)frac{e^{x_3^3}}{left(1+e^{x_3^3}right)^2}frac{partial x_3^3}{partial b_3^3}),$ $frac{partial C}{partial b_3^3}=-frac{2}{3}(0+0+left(y_3-a_3^3right)frac{e^{x_3^3}}{left(1+e^{x_3^3}right)^2}frac{partial x_3^3}{partial b_3^2}),\frac{partial C}{partial b_3^3}=-frac{2}{3}left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right).$

Найдём новые значения для и:

$^*b_2^3= b_2^3-eta(-frac{2}{3}left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)),\^*b_3^3= b_3^3-eta(-frac{2}{3}left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)).$

Найдём частные производные по всем элементам матрицы $mathbf{W}^2$ . Раскроем сумму для переменной $w_{11}^2$ матрицы $mathbf{W}^2$ . Поскольку

$x_1^3=w_{11}^3a_1^2+w_{12}^3a_2^2+w_{13}^3a_3^2+b_1^3,\x_2^3=w_{21}^3a_1^2+w_{22}^3a_2^2+w_{23}^3a_3^2+b_2^3,\x_3^3=w_{31}^3a_1^2+w_{32}^3a_2^2+w_{33}^3a_3^2+b_3^3,$

в свою очередь,

тогда сумма для переменной $w_{11}^2$ матрицы $mathbf{W}^2$ :

$frac{partial C}{partial w_{11}^2}=-frac{2}{3}sum_{i=1}^{3}{left(y_i-a_i^3right)frac{e^{x_i^3}}{left(1+e^{x_i^3}right)^2}}frac{partial x_i^3}{partial a_1^2}frac{partial a_1^2}{partial x_1^2}frac{partial x_1^2}{partial w_{11}^2},$ $scriptsize{begin{gather}frac{partial C}{partial w_{11}^2}=-frac{2}{3}(left(y_1-a_1^3right)frac{e^{x_1^3}}{left(1+e^{x_1^3}right)^2}frac{partial x_1^3}{partial a_1^2}frac{partial a_1^2}{partial x_1^2}frac{partial x_1^2}{partial w_{11}^2}+left(y_2-a_2^3right)frac{e^{x_2^3}}{left(1+e^{x_2^3}right)^2}frac{partial x_2^3}{partial a_1^2}frac{partial a_1^2}{partial x_1^2}frac{partial x_1^2}{partial w_{11}^2}\+left(y_3-a_3^3right)frac{e^{x_3^3}}{left(1+e^{x_3^3}right)^2}frac{partial x_3^3}{partial a_1^2}frac{partial a_1^2}{partial x_1^2}frac{partial x_1^2}{partial w_{11}^2}),\frac{partial C}{partial w_{11}^2}=-frac{2}{3}(left(y_1-a_1^3right)frac{e^{x_1^3}}{left(1+e^{x_1^3}right)^2}w_{11}^3frac{e^{x_1^2}}{left(1+e^{x_1^2}right)}left(1-frac{e^{x_1^2}}{1+e^{x_1^2}}right)x_1^1\+left(y_2-a_2^3right)frac{e^{x_2^3}}{left(1+e^{x_2^3}right)^2}w_{21}^3frac{e^{x_1^2}}{left(1+e^{x_1^2}right)}left(1-frac{e^{x_1^2}}{1+e^{x_1^2}}right)x_1^1\+left(y_3-a_3^3right)frac{e^{x_3^3}}{left(1+e^{x_3^3}right)^2}w_{31}^3frac{e^{x_1^2}}{left(1+e^{x_1^2}right)}left(1-frac{e^{x_1^2}}{1+e^{x_1^2}}right)x_1^1),\frac{partial C}{partial w_{11}^2}=-frac{2}{3}(left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)w_{11}^3a_1^2left(x_1^2right)left(1-a_1^2left(x_1^2right)right)x_1^1\+left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)w_{21}^3a_1^2left(x_1^2right)left(1-a_1^2left(x_1^2right)right)x_1^1\+left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)w_{31}^3a_1^2left(x_1^2right)left(1-a_1^2left(x_1^2right)right)x_1^1).end{gather}}$

Найдём новое значение (обновлённый вес) для переменной $w_{11}^2$ :

$^*w_{11}^2= w_{11}^2-etafrac{partial C}{partial w_{11}^2}.$

Найдём остальные частные производные и их новые значения для матрицы $mathbf{W}^2$ .

$scriptsize{begin{gather}frac{partial C}{partial w_{12}^2}=-frac{2}{3}(left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)w_{11}^3a_1^2left(x_1^2right)left(1-a_1^2left(x_1^2right)right)x_2^1\+left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)w_{21}^3a_1^2left(x_1^2right)left(1-a_1^2left(x_1^2right)right)x_2^1\+left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)w_{31}^3a_1^2left(x_1^2right)left(1-a_1^2left(x_1^2right)right)x_2^1).end{gather}}$ $scriptsize{begin{gather}frac{partial C}{partial w_{13}^2}=-frac{2}{3}(left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)w_{11}^3a_1^2left(x_1^2right)left(1-a_1^2left(x_1^2right)right)x_3^1\+left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)w_{21}^3a_1^2left(x_1^2right)left(1-a_1^2left(x_1^2right)right)x_3^1\+left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)w_{31}^3a_1^2left(x_1^2right)left(1-a_1^2left(x_1^2right)right)x_3^1).end{gather}}$ $^*w_{12}^2= w_{12}^2-etafrac{partial C}{partial w_{12}^2}, ^*w_{13}^2= w_{13}^2-etafrac{partial C}{partial w_{13}^2}.$ $scriptsize{begin{gather}frac{partial C}{partial w_{21}^2}=-frac{2}{3}(left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)w_{12}^3a_2^2left(x_2^2right)left(1-a_2^2left(x_2^2right)right)x_1^1\+left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)w_{22}^3a_2^2left(x_2^2right)left(1-a_2^2left(x_2^2right)right)x_1^1\+left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)w_{32}^3a_2^2left(x_2^2right)left(1-a_2^2left(x_2^2right)right)x_1^1).end{gather}}$ $scriptsize{begin{gather} frac{partial C}{partial w_{22}^2}=-frac{2}{3}(left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)w_{12}^3a_2^2left(x_2^2right)left(1-a_2^2left(x_2^2right)right)x_2^1\+left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)w_{22}^3a_2^2left(x_2^2right)left(1-a_2^2left(x_2^2right)right)x_2^1\+left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)w_{32}^3a_2^2left(x_2^2right)left(1-a_2^2left(x_2^2right)right)x_2^1).end{gather}}$ $scriptsize{begin{gather}frac{partial C}{partial w_{23}^2}=-frac{2}{3}(left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)w_{12}^3a_2^2left(x_2^2right)left(1-a_2^2left(x_2^2right)right)x_3^1\+left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)w_{22}^3a_2^2left(x_2^2right)left(1-a_2^2left(x_2^2right)right)x_3^1\+left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)w_{32}^3a_2^2left(x_2^2right)left(1-a_2^2left(x_2^2right)right)x_3^1).end{gather}}$ $^*w_{21}^2= w_{21}^2-etafrac{partial C}{partial w_{21}^2}, ^*w_{22}^2= w_{22}^2-etafrac{partial C}{partial w_{22}^2},\^*w_{23}^2= w_{23}^2-etafrac{partial C}{partial w_{23}^2}.$ $scriptsize{begin{gather}frac{partial C}{partial w_{31}^2}=-frac{2}{3}(left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)w_{13}^3a_3^2left(x_3^2right)left(1-a_3^2left(x_3^2right)right)x_1^1\+left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)w_{23}^3a_3^2left(x_3^2right)left(1-a_3^2left(x_3^2right)right)x_1^1\+left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)w_{33}^3a_3^2left(x_3^2right)left(1-a_3^2left(x_3^2right)right)x_1^1).end{gather}}$ $scriptsize{begin{gather}frac{partial C}{partial w_{32}^2}=-frac{2}{3}(left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)w_{13}^3a_3^2left(x_3^2right)left(1-a_3^2left(x_3^2right)right)x_2^1\+left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)w_{23}^3a_3^2left(x_3^2right)left(1-a_3^2left(x_3^2right)right)x_2^1\+left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)w_{33}^3a_3^2left(x_3^2right)left(1-a_3^2left(x_3^2right)right)x_2^1).end{gather}}$ $scriptsize{begin{gather}frac{partial C}{partial w_{33}^2}=-frac{2}{3}(left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)w_{13}^3a_3^2left(x_3^2right)left(1-a_3^2left(x_3^2right)right)x_3^1\+left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)w_{23}^3a_3^2left(x_3^2right)left(1-a_3^2left(x_3^2right)right)x_3^1\+left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)w_{33}^3a_3^2left(x_3^2right)left(1-a_3^2left(x_3^2right)right)x_3^1).end{gather}}$ $^*w_{31}^2= w_{31}^2-etafrac{partial C}{partial w_{31}^2}, ^*w_{32}^2= w_{32}^2-etafrac{partial C}{partial w_{32}^2},\^*w_{33}^2= w_{33}^2-etafrac{partial C}{partial w_{33}^2}.$

Теперь найдём частные производные по всем элементам вектора $mathbf{b}^2$ . Раскроем сумму для переменной :

$frac{partial C}{partial b_1^2}=-frac{2}{3}sum_{i=1}^{3}{left(y_i-a_i^3right)frac{e^{x_i^3}}{left(1+e^{x_i^3}right)^2}}frac{partial x_i^3}{partial a_1^2}frac{partial a_1^2}{partial x_1^2}frac{partial x_1^2}{partial b_1^2},$ $scriptsize{begin{gather}frac{partial C}{partial b_1^2}=-frac{2}{3}(left(y_1-a_1^3right)frac{e^{x_1^3}}{left(1+e^{x_1^3}right)^2}frac{partial x_1^3}{partial a_1^2}frac{partial a_1^2}{partial x_1^2}frac{partial x_1^2}{partial b_1^2}+left(y_2-a_2^3right)frac{e^{x_2^3}}{left(1+e^{x_2^3}right)^2}frac{partial x_2^3}{partial a_1^2}frac{partial a_1^2}{partial x_1^2}frac{partial x_1^2}{partial b_1^2}\+left(y_3-a_3^3right)frac{e^{x_3^3}}{left(1+e^{x_3^3}right)^2}frac{partial x_3^3}{partial a_1^2}frac{partial a_1^2}{partial x_1^2}frac{partial x_1^2}{partial b_1^2}),\frac{partial C}{partial b_1^2}=-frac{2}{3}(left(y_1-a_1^3right)frac{e^{x_1^3}}{left(1+e^{x_1^3}right)^2}w_{11}^3frac{e^{x_1^2}}{left(1+e^{x_1^2}right)}left(1-frac{e^{x_1^2}}{1+e^{x_1^2}}right)\+left(y_2-a_2^3right)frac{e^{x_2^3}}{left(1+e^{x_2^3}right)^2}w_{21}^3frac{e^{x_1^2}}{left(1+e^{x_1^2}right)}left(1-frac{e^{x_1^2}}{1+e^{x_1^2}}right)\+left(y_3-a_3^3right)frac{e^{x_3^3}}{left(1+e^{x_3^3}right)^2}w_{31}^3frac{e^{x_1^2}}{left(1+e^{x_1^2}right)}left(1-frac{e^{x_1^2}}{1+e^{x_1^2}}right)),\frac{partial C}{partial b_1^2}=-frac{2}{3}(left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)w_{11}^3a_1^2left(x_1^2right)left(1-a_1^2left(x_1^2right)right)\+left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)w_{21}^3a_1^2left(x_1^2right)left(1-a_1^2left(x_1^2right)right)\+left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)w_{31}^3a_1^2left(x_1^2right)left(1-a_1^2left(x_1^2right)right)).end{gather}}$

Найдём новое значение для :

$^*b_1^2= b_1^2-etafrac{partial C}{partial b_1^2}.$

Найдём остальные частные производные для вектора $mathbf{b}^2$ :

$scriptsize{begin{gather}frac{partial C}{partial b_2^2}=-frac{2}{3}(left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)w_{12}^3a_2^2left(x_2^2right)left(1-a_2^2left(x_2^2right)right)\+left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)w_{22}^3a_2^2left(x_2^2right)left(1-a_2^2left(x_2^2right)right)\+left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)w_{32}^3a_2^2left(x_2^2right)left(1-a_2^2left(x_2^2right)right)).end{gather}}$ $scriptsize{begin{gather}frac{partial C}{partial b_3^2}=-frac{2}{3}(left(y_1-a_1^3right)a_1^3left(x_1^3right)left(1-a_1^3left(x_1^3right)right)w_{13}^3a_3^2left(x_3^2right)left(1-a_3^2left(x_3^2right)right)\+left(y_2-a_2^3right)a_2^3left(x_2^3right)left(1-a_2^3left(x_2^3right)right)w_{23}^3a_3^2left(x_3^2right)left(1-a_3^2left(x_3^2right)right)\+left(y_3-a_3^3right)a_3^3left(x_3^3right)left(1-a_3^3left(x_3^3right)right)w_{33}^3a_3^2left(x_3^2right)left(1-a_3^2left(x_3^2right)right)).end{gather}}$

Найдём новые значения для переменных и :

$^*b_2^2= b_2^2-etafrac{partial C}{partial b_2^2}, ^*b_3^2= b_3^2-etafrac{partial C}{partial b_3^2}.$

Численный пример

Задача обучения нейронной сети состоит в аппроксимации некоторой неизвестной функции, которая отображает $mathbf{x}^1$ в .

Другими словами, существует некоторая неизвестная нам функция $mathbf{y}=mathbf{f}(mathbf{x}^1)$ , которая для набора значений независимых переменных выдаёт результат, соответствующий набору значений зависимых переменных . Задача нейронной сети в результате обучения «заменить», приблизить, т.е. аппроксимировать неизвестную функцию $mathbf{y}=mathbf{f}(mathbf{x}^1)$ . В случае успешного решения задачи, значения нашей нейронной сети на выходном слое $mathbf{a}^3$ будут приблизительно равны значениям вектора аппроксимируемой функции.

Выберем случайным образом следующие начальные значения для нашей нейронной сети:

$mathbf{W}^2=left[begin{matrix}0.88&0.39&0.9\0.37&0.14&0.41\0.96&0.5&0.6\end{matrix}right],mathbf{W}^3=left[begin{matrix}0.29&0.57&0.36\0.73&0.53&0.68\0.01&0.02&0.58\end{matrix}right],\mathbf{b}^2=left[begin{matrix}0.23\0.89\0.08\end{matrix}right], mathbf{b}^3=left[begin{matrix}0.78\0.83\0.8\end{matrix}right].$

А также входные и целевые значения: $mathbf{x}^1=left[begin{matrix}0.03\0.72\0.49\end{matrix}right], mathbf{y}=left[begin{matrix}0.93\0.74\0.17\end{matrix}right].$

После первого прямого прохождения сигнала значения скрытого и выходного слоёв:

$mathbf{a}^2=left[begin{matrix}0.726750911\0.769022513\0.681961335\end{matrix}right], mathbf{a}^3=left[begin{matrix}0.842189045\0.903072871\0.771744079\end{matrix}right].$

Для скорости обучения установим значение .

Вычислим для первой эпохи (epoch) обучения нейронной сети обновлённые значения весов $w_{11}^3$ и $w_{11}^2$ :

$scriptsize{begin{gather}^*w_{11}^3=0.29+0.01cdot frac{2}{3}cdot (0.93-0.842189045)cdot 0.842189045cdot (1-0.842189045)cdot 0.726750911=0.290056544,\^*w_{11}^2=0.88+0.01cdot frac{2}{3}cdot (left(0.93-0.842189045right)cdot 0.842189045cdot left(1-0.842189045right)cdot 0.29cdot 0.726750911cdot\ left(1-0.726750911right)cdot 0.03+left(0.74-0.903072871right)cdot :0.903072871cdot left(1-0.903072871right)cdot :0.73cdot :0.769022513cdot\ left(1-0.769022513right)cdot :0.03+left(0.17-0.771744079right)cdot :0.771744079cdot left(1-0.771744079right)cdot :0.01cdot :0.681961335cdot\ left(1-0.681961335right)cdot :0.03)=0.879999678.end{gather}}$

После 10 000 эпох обучения матрицы весов и выходной слой имеют следующие значения:

$mathbf{W}^2=left[begin{matrix}0.881449843&0.424796239&0.923680774\0.372218081&0.193233937&0.446228651\0.957567842&0.441628217&0.560274759\end{matrix}right],\mathbf{W}^3=left[begin{matrix}0.480573892&0.772236752&0.529654336\0.394700365&0.174298746&0.381672097\-0.771753134&-0.808346904&-0.127425218\end{matrix}right],\mathbf{a}^3=left[begin{matrix}0.913047169\0.741592957\0.173072228\end{matrix}right].$

Обобщение для произвольного числа слоёв

$delta_i^L=left(y_i-a_i^Lright)a_i^Lleft(x_i^Lright)left(1-a_i^Lleft(x_i^Lright)right),\delta_i^l=sum_{k=1}^{n}{delta_k^{l+1}w_{ki}^{l+1}frac{partial a_i^l}{partial x_i^l}},\frac{partial C}{partial w_{ij}^l}=frac{1}{n}delta_i^lfrac{partial x_i^l}{partial w_{ij}^l},\frac{partial C}{partial b_i^l}=delta_i^l,$

где — номер выходного слоя, — индекс строки матрицы весов, — число выходных значений.

— обобщённое дельта-правило (delta rule).

Отличный гайд про нейросеть от теории к практике. Вы узнаете из каких элементов состоит ИНС, как она работает и как ее создать самому.

Если вы в поисках пособия по искусственным нейронным сетям (ИНС), то, возможно, у вас уже имеются некоторые предположения относительно того, что это такое. Но знали ли вы, что нейронные сети — основа новой и интересной области глубинного обучения? Глубинное обучение — область машинного обучения, в наше время помогло сделать большой прорыв во многих областях, начиная с игры в Го и Покер с живыми игроками, и заканчивая беспилотными автомобилями. Но, прежде всего, глубинное обучение требует знаний о работе нейронных сетей.

В этой статье будут представлены некоторые понятия, а также немного кода и математики, с помощью которых вы сможете построить и понять простые нейронные сети. Для ознакомления с материалом нужно иметь базовые знания о матрицах и дифференциалах. Код будет написан на языке программирования Python с использованием библиотеки numpy. Вы построите ИНС, используя Python, которая с высокой точностью классифицировать числа на картинках.

1 Что такое искусственная нейросеть?

Искусственные нейросеть (ИНС) — это программная реализация нейронных структур нашего мозга. Мы не будем обсуждать сложную биологию нашей головы, достаточно знать, что мозг содержит нейроны, которые являются своего рода органическими переключателями. Они могут изменять тип передаваемых сигналов в зависимости от электрических или химических сигналов, которые в них передаются. Нейросеть в человеческом мозге — огромная взаимосвязанная система нейронов, где сигнал, передаваемый одним нейроном, может передаваться в тысячи других нейронов. Обучение происходит через повторную активацию некоторых нейронных соединений. Из-за этого увеличивается вероятность вывода нужного результата при соответствующей входной информации (сигналах). Такой вид обучения использует обратную связь — при правильном результате нейронные связи, которые выводят его, становятся более плотными.

Искусственные нейронные сети имитируют поведение мозга в простом виде. Они могут быть обучены контролируемым и неконтролируемым путями. В контролируемой ИНС, сеть обучается путем передачи соответствующей входной информации и примеров исходной информации. Например, спам-фильтр в электронном почтовом ящике: входной информацией может быть список слов, которые обычно содержатся в спам-сообщениях, а исходной информацией — классификация для уведомления (спам, не спам). Такой вид обучения добавляет веса связям ИНС, но это будет рассмотрено позже.

Неконтролируемое обучение в ИНС пытается «заставить» ИНС «понять» структуру передаваемой входной информации «самостоятельно». Мы не будем рассматривать это в данном посте.

2 Структура ИНС

2.1 Искусственный нейрон

Биологический нейрон имитируется в ИНС через активационную функцию. В задачах классификации (например определение спам-сообщений) активационная функция должна иметь характеристику «включателя». Иными словами, если вход больше, чем некоторое значение, то выход должен изменять состояние, например с 0 на 1 или -1 на 1 Это имитирует «включение» биологического нейрона. В качестве активационной функции обычно используют сигмоидальную функцию:

Которая выглядит следующим образом:


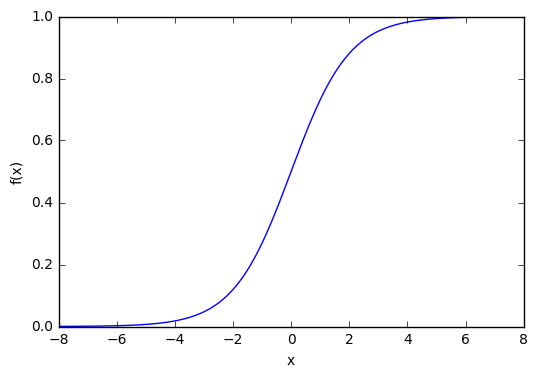
import matplotlib.pylab as plt
import numpy as np
x = np.arange(-8, 8, 0.1)
f = 1 / (1 + np.exp(-x))
plt.plot(x, f)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.show()

Из графика можно увидеть, что функция «активационная» — она растет с 0 до 1 с каждым увеличением значения х. Сигмоидальная функция является гладкой и непрерывной. Это означает, что функция имеет производную, что в свою очередь является очень важным фактором для обучения алгоритма.

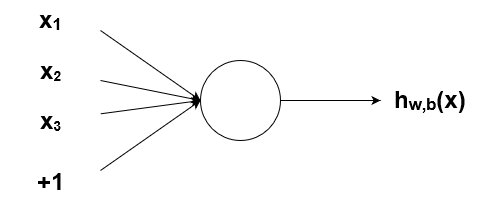
2.2 Узлы

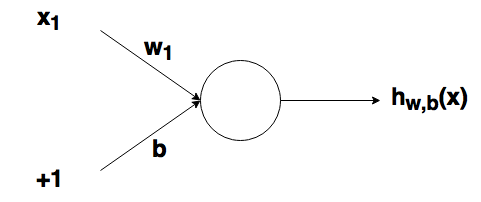
Как было упомянуто ранее, биологические нейроны иерархически соединены в сети, где выход одних нейронов является входом для других нейронов. Мы можем представить такие сети в виде соединенных слоев с узлами. Каждый узел принимает взвешенный вход, активирует активационную функцию для суммы входов и генерирует выход.

Круг на картинке изображает узел. Узел является «местоположением» активационной функции, он принимает взвешенные входы, складывает их, а затем вводит их в активационную функцию. Вывод активационной функции представлен через h. Примечание: в некоторых источниках узел также называют перцептроном.

Что такое «вес»? По весу берутся числа (не бинарные), которые затем умножаются на входе и суммируются в узле. Иными словами, взвешенный вход в узел имеет вид:

где w_i— числовые значения веса ( b мы будем обсудим позже). Весы нам нужны, они являются значениями, которые будут меняться в течение процесса обучения. b является весом элемента смещения на 1, включение веса b делает узел гибким. Проще это понять на примере.

2.3 Смещение

Рассмотрим простой узел, в котором есть по одному входу и выходу:

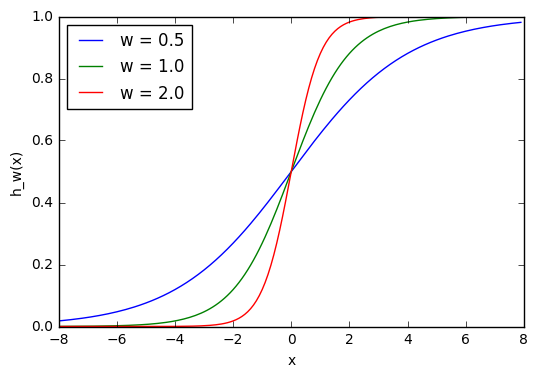
Ввод для активационной функции в этом узле просто x₁w₁. На что влияет изменение в w₁ в этой простой сети?


w1 = 0.5
w2 = 1.0
w3 = 2.0
l1 = 'w = 0.5'
l2 = 'w = 1.0'
l3 = 'w = 2.0'
for w, l in [(w1, l1), (w2, l2), (w3, l3)]:
  f = 1 / (1 + np.exp(-x * w))
plt.plot(x, f, label = l)
plt.xlabel('x')
plt.ylabel('h_w(x)')
plt.legend(loc = 2)
plt.show()

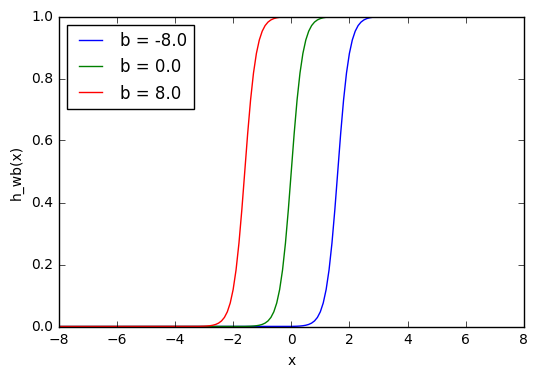
Здесь мы можем видеть, что при изменении веса изменяется также уровень наклона графика активационной функции. Это полезно, если мы моделируем различные плотности взаимосвязей между входами и выходами. Но что делать, если мы хотим, чтобы выход изменялся только при х более 1? Для этого нам нужно смещение. Рассмотрим такую сеть со смещением на входе:


w = 5.0
b1 = -8.0
b2 = 0.0
b3 = 8.0
l1 = 'b = -8.0'
l2 = 'b = 0.0'
l3 = 'b = 8.0'
for b, l in [(b1, l1), (b2, l2), (b3, l3)]:
  f = 1 / (1 + np.exp(-(x * w + b)))
plt.plot(x, f, label = l)
plt.xlabel('x')
plt.ylabel('h_wb(x)')
plt.legend(loc = 2)
plt.show()

Из графика можно увидеть, что меняя «вес» смещения b, мы можем изменять время запуска узла. Смещение очень важно в случаях, когда нужно имитировать условные отношения.

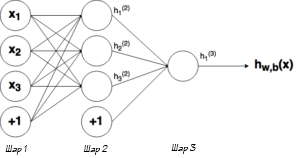
2.4 Составленная структура

Выше было объяснено, как работает соответствующий узел / нейрон / перцептрон. Но, как вы знаете, в полной нейронной сети находится много таких взаимосвязанных между собой узлов. Структуры таких сетей могут принимать мириады различных форм, но самая распространенная состоит из входного слоя, скрытого слоя и выходного слоя. Пример такой структуры приведены ниже:

Ну рисунке выше можно увидеть три слоя сети — Слой 1 является входным слоем, где сеть принимает внешние входные данные. Слой 2 называют скрытым слоем, этот слой не является частью ни входа, ни выхода. Примечание: нейронные сети могут иметь несколько скрытых слоев, в данном примере для примера был показан лишь один. И наконец, Слой 3 является исходным слоем. Вы можете заметить, что между Шаром 1 (Ш1) и Шаром 2 (Ш2) существует много связей. Каждый узел в Ш1 имеет связь со всеми узлами в Ш2, при этом от каждого узла в Ш2 идет по одной связи к единому выходному узлу в Ш3. Каждая из этих связей должна иметь соответствующий вес.

2.5 Обозначение

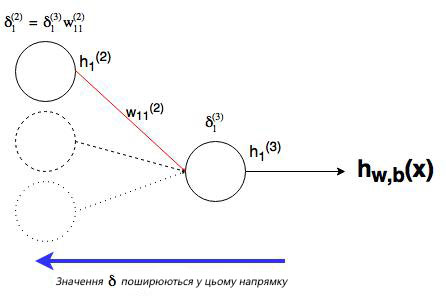
Вся математика, приведенная выше, требует очень точной нотации. Нотация, которая используется здесь, используется и в руководстве по глубинному обучению от Стэнфордского Университета. В следующих уравнениях вес соответствующего связи будет обозначаться как w _ij^(l), где i — номер узла в слое l+1, а j- номер узла в слое l. Например, вес связи между узлом 1 в слое 1 и узлом 2 в слое 2 будет обозначаться как w ₂₁^(l). Непонятно, почему индексы 2-1 означают связь 1-2? Такая нотация более понятна, если добавить смещения.

Из графика выше видно, что смещение 1 связано со всеми узлами в соседнем слое. Смещение в Ш1 имеет связь со всеми узлами в Ш2. Так как смещение не является настоящим узлом с активационной функцией, оно не имеет и входов (его входное значение всегда равно константе). Вес связи между смещением и узлом будем обозначать через b_i^(l), где i- номер узла в слое l+1, так же, как в w _ij^(l). К примеру с w ₂₁^(l) вес между смещением в Ш1 и вторым узлом в Ш2 будет иметь обозначение b₂⁽¹⁾.

Помните, что эти значения -w _ij^(l)и b_i^(l) — будут меняться в течение процесса обучения ИНС.
Обозначение связи с исходным узлом будет выглядеть следующим образом: h_j^l, где j- номер узла в слое l. Тогда в предыдущем примере, связью с исходным узлом является h₁⁽²⁾.
Теперь давайте рассмотрим, как рассчитывать выход сети, когда нам известны вес и вход. Процесс нахождения выхода в нейронной сети называется процессом прямого распространения.

3 Процесс прямого распространения

Чтобы продемонстрировать, как находить выход, имея уже известный вход, в нейронных сетях, начнем с предыдущего примера с тремя слоями. Ниже такая система представлена в виде системы уравнений:

, где f(∙) — активационная функция узла, в нашем случае сигмоидальная функция. В первой строке h₁⁽²⁾— выход первого узла во втором слое, его входами соответственно являются w₁₁⁽¹⁾x₁(1), w₁₂⁽¹⁾x₂(1),w₁₃⁽¹⁾x₃(1) и b₁⁽¹⁾. Эти входы было сложены, а затем переданы в активационную функцию для расчета выхода первого узла. С двумя следующими узлами аналогично.

Последняя строка рассчитывает выход единого узла в последнем третьем слое, он является конечной исходной точкой в нейронной сети. В нем вместо взвешенных входных переменных (x₁,x₂,x₃)берутся взвешенные выходы узлов с другой слоя (h₁⁽²⁾,h₂⁽²⁾,h₃⁽²⁾)и смещения. Такая система уравнений также хорошо показывает иерархическую структуру нейронной сети.

3.1 Пример прямого распространения

Приведем простой пример первого вывода нейронной сети языке Python . Обратите внимание, веса w₁₁⁽¹⁾,w₁₂⁽¹⁾,… между Ш1 и Ш2 идеально могут быть представлены в матрице:

Представим эту матрицу через массивы библиотеки numpy.


import numpy as np
w1 = np.array([
  [0.2, 0.2, 0.2],
  [0.4, 0.4, 0.4],
  [0.6, 0.6, 0.6]
])

Мы просто присвоили некоторые рандомные числовые значения весу каждой связи с Ш1. Аналогично можно сделать и с Ш2:


	w2 = np.zeros((1, 3))
	w2[0, : ] = np.array([0.5, 0.5, 0.5])

Мы можем присвоить некоторые значения весу смещения в Ш1 и Ш2:


b1 = np.array([0.8, 0.8, 0.8])
b2 = np.array([0.2])

Наконец, перед написанием основной программы для расчета выхода нейронной сети, напишем отдельную функцию для активационной функции:


	def f(x):
	  return 1 / (1 + np.exp(-x))

3.2 Первая попытка реализовать процесс прямого распространения

Приведем простой способ расчета выхода нейронной сети, используя вложенные циклы в Python. Позже мы быстро рассмотрим более эффективные способы.


def simple_looped_nn_calc(n_layers, x, w, b):
  for l in range(n_layers - 1): #Формируется входной массив - перемножения весов в каждом слое# Если первый слой, то входной массив равен вектору х# Если слой не первый, вход для текущего слоя равен# выходу предыдущего
if l == 0:
  node_in = x
else :
  node_in = h #формирует выходной массив для узлов в слое l + 1
h = np.zeros((w[l].shape[0], ))#проходит по строкам массива весов
for i in range(w[l].shape[0]): #считает сумму внутри активационной функции
f_sum = 0 #проходит по столбцам массива весов
for j in range(w[l].shape[1]):
  f_sum += w[l][i][j] * node_in[j] #добавляет смещение
f_sum += b[l][i]

#использует активационную функцию для расчета
#i - того выхода, в данном случае h1, h2, h3
h[i] = f(f_sum)
return h

Данная функция принимает в качестве входа номер слоя в нейронной сети, х — входной массив / вектор:


w = [w1, w2]
b = [b1, b2] #Рандомный входной вектор x
x = [1.5, 2.0, 3.0]

Функция сначала проверяет, чем является входной массив для соответствующего слоя с узлами / весами. Если рассматривается первый слой, то входом для второго слоя является входной массив xx, Умноженный на соответствующие веса. Если слой не первый, то входом для последующего будет выход предыдущего.
Вызов функции:


	simple_looped_nn_calc(3, x, w, b)

возвращает результат 0.8354. Можно проверить правильность, вставив те же значения в систему уравнений:

3.3 Более эффективная реализация

Использование циклов — не самый эффективный способ расчета прямого распространения на языке Python , потому что циклы в этом языке программирования работают довольно медленно. Мы кратко рассмотрим лучшие решения. Также можно будет сравнить работу алгоритмов, используя функцию в IPython:


	%timeit simple_looped_nn_calc(3, x, w, b)

В данном случае процесс прямого распространения с циклами занимает около 40 микросекунд. Это довольно быстро, но не для больших нейронных сетей с > 100 узлами на каждом слое, особенно при их обучении. Если мы запустим этот алгоритм на нейронной сети с четырьмя слоями, то получим результат 70 микросекунд. Эта разница является достаточно значительной.

3.4 Векторизация в нейронных сетях

Можно более компактно написать предыдущие уравнения, тем самым найти результат эффективнее. Сначала добавим еще одну переменную z_i^(l), которая является суммой входа в узел i слоя l, Включая смещение. Тогда для первого узла в Ш2, z будет равна:

, где n- количество узлов в Ш1. Используя это обозначение, систему уравнений можно сократить:

Обратите внимание на W, что означает матричную форму представления весов. Помните, что теперь все элементы в уравнении сверху являются матрицами / векторами. Но на этом упрощение не заканчивается. Данные уравнения можно свести к еще более краткому виду:

Так выглядит общая форма процесса прямого распространения, выход слоя l становится входом в слой l+1. Мы знаем, что h⁽¹⁾ является входным слоем x, а h^(nl)(где nl- номер слоя в сети) является исходным слоем. Мы также не стали использовать индексы i и j-за того, что можно просто перемножить матрицы — это даст нам тот же результат. Поэтому данный процесс и называется «векторизацией». Этот метод имеет ряд плюсов. Во-первых, код его реализации выглядит менее запутанным. Во-вторых, используются свойства по линейной алгебре вместо циклов, что делает работу программы быстрее. С numpy можно легко сделать такие подсчеты. В следующей части быстро повторим операции над матрицами, для тех, кто их немного подзабыл.

3.5 Умножение матриц

Распишем z^(l+1)=W^(l)h^(l)+b^(l) на выражение из матрицы и векторов входного слоя ( h^(l)=x):

Для тех, кто не знает или забыл, как перемножаются матрицы. Когда матрица весов умножается на вектор, каждый элемент в строке матрицы весов умножается на каждый элемент в столбце вектора, после этого все произведения суммируются и создается новый вектор (3х1). После перемножения матрицы на вектор, добавляются элементы из вектора смещения и получается конечный результат.

Каждая строка полученного вектора соответствует аргументу активационной функции в оригинальной НЕ матричной системе уравнений выше. Это означает, что в Python мы можем реализовать все, не используя медленные циклы. К счастью, библиотека numpy дает возможность сделать это достаточно быстро, благодаря функциям-операторам над матрицами. Рассмотрим код простой и быстрой версии функции simple_looped_nn_calc:


def matrix_feed_forward_calc(n_layers, x, w, b):
  for l in range(n_layers - 1):
  if l == 0:
  node_in = x
else :
  node_in = h
z = w[l].dot(node_in) + b[l]
h = f(z)
return h

Обратите внимание на строку 7, в которой происходит перемножение матрицы и вектора. Если вместо функции умножения a.dot (b) вы используете символ *, то получится нечто похожее на поэлементное умножение вместо настоящего произведения матриц.

Если сравнить время работы этой функции с предыдущей на простой сети с четырьмя слоями, то мы получим результат лишь на 24 микросекунды меньше. Но если увеличить количество узлов в каждом слое до 100-100-50-10, то мы получим гораздо большую разницу. Функция с циклами в этом случае дает результат 41 миллисекунду, когда у функции с векторизацией это занимает лишь 84 микросекунды. Также существуют еще более эффективные реализации операций над матрицами, которые используют пакеты глубинного обучения, такие как TensorFlow и Theano.

На этом все о процессе прямого распространения в нейронных сетях. В следующих разделах мы поговорим о способах обучения нейронных сетей, используя градиентный спуск и обратное распространение.

4 Градиентный спуск и оптимизация

Расчеты значений весов, которые соединяют слои в сети, это как раз то, что мы называем обучением системы. В контролируемом обучении идея заключается в том, чтобы уменьшить погрешность между входом и нужным выходом. Если у нас есть нейросеть с одним выходным слоем и некоторой вход xx и мы хотим, чтобы на выходе было число 2, но сеть выдает 5, то нахождение погрешности выглядит как abs(2-5)=3. Говоря языком математики, мы нашли норму ошибки L¹(Это будет рассмотрено позже).

Смысл контролируемого обучения в том, что предоставляется много пар вход-выход уже известных данных и нужно менять значения весов, основываясь на этих примерах, чтобы значение ошибки стало минимальным. Эти пары входа-выхода обозначаются как (x⁽¹⁾,y⁽¹⁾),…,(x^(m),y^(m)), где m является количеством экземпляров для обучения. Каждое значение входа или выхода может представлять собой вектор значений, например x⁽¹⁾ не обязательно только одно значение, оно может содержать N-размерный набор значений. Предположим, что мы обучаем нейронную сеть выявлению спам-сообщений — в таком случае x⁽¹⁾ может представлять собой количество соответствующих слов, которые встречаются в сообщении:

y⁽¹⁾ в этом случае может представлять собой единое скалярное значение, например, 1 или 0, обозначающий, было сообщение спамом или нет. В других приложениях это также может быть вектор с K измерениями. Например, мы имеем вход xx, Который является вектором черно-белых пикселей, считанных с фотографии. При этом y может быть вектором с 26 элементами со значениями 1 или 0, обозначающие, какая буква была изображена на фото, например (1,0,…,0)для буквы а, (0,1,…,0) для буквы б и т. д.

В обучении сети, используя (x,y), целью является улучшение нахождения правильного y при известном x. Это делается через изменение значений весов, чтобы минимизировать погрешность. Как тогда менять их значение? Для этого нам и понадобится градиентный спуск. Рассмотрим следующий график:

На этом графике изображено погрешность, зависящую от скалярного значения веса, w. Минимально возможная погрешность обозначена черным крестиком, но мы не знаем какое именно значение w дает нам это минимальное значение. Подсчет начинается с рандомного значения переменной w, которая дает погрешность, обозначенную красной точкой под номером «1» на кривой. Нам нужно изменить w таким образом, чтобы достичь минимальной погрешности, черного крестика. Одним из самых распространенных способов является градиентный спуск.

Сначала находится градиент погрешности на «1» по отношению к w. Градиент является уровнем наклона кривой в соответствующей точке. Он изображен на графике в виде черных стрелок. Градиент также дает некоторую информацию о направлении — если он положителен при увеличении w, то в этом направлении погрешность будет увеличиваться, если отрицательный — уменьшаться (см. График). Как вы уже поняли, мы пытаемся сделать, чтобы погрешность с каждым шагом уменьшалась. Величина градиента показывает, как быстро кривая погрешности или функция меняется в соответствующей точке. Чем больше значение, тем быстрее меняется погрешность в соответствующей точке в зависимости от w.

Метод градиентного спуска использует градиент, чтобы принимать решение о следующей смены в w для того, чтобы достичь минимального значения кривой. Он итеративным методом, каждый раз обновляет значение w через:

, где w_н означает новое значение w, w_ст— текущее или «старое» значение w, ∇error является градиентом погрешности на w_ст и α является шагом. Шаг α также будет означать, как быстро ответ приближается к минимальной погрешности. При каждой итерации в таком алгоритме градиент должен уменьшаться. Из графика выше можно заметить, что с каждым шагом градиент «стихает». Как только ответ достигнет минимального значения, мы уходим из итеративного процесса. Выход можно реализовать способом условия «если погрешность меньше некоторого числа». Это число называют точностью.

4.1 Простой пример на коде

Рассмотрим пример простой имплементации градиентного спуска для нахождения минимума функции f(x)=x⁴-3x³+2 на языке Python . Градиент этой функции можно найти аналитически через производную f»(x)=4x³-9x². Это означает, что для любого xx мы можем найти градиент по этой простой формуле. Мы можем найти минимум через производную — x=2.25.

x_old = 0 # Нет разницы, какое значение, главное abs(x_new - x_old) > точность
x_new = 6 # Алгоритм начинается с x = 6
gamma = 0.01 # Размер шага
precision = 0.00001 # Точность

def df(x):
   y = 4 * x * * 3 - 9 * x * * 2
   return y

while abs(x_new - x_old) > precision:
   x_old = x_new
   x_new += -gamma * df(x_old)

print("Локальный минимум находится на %f"  % x_new)

Вывод этой функции: «Локальный минимум находится на 2.249965», что удовлетворяет правильному ответу с некоторой точностью. Этот код реализует алгоритм изменения веса, о котором рассказывалось выше, и может находить минимум функции с соответствующей точностью. Это был очень простой пример градиентного спуска, нахождение градиента при обучении нейронной сети выглядит несколько иначе, хотя и главная идея остается той же — мы находим градиент нейронной сети и меняем веса на каждом шагу, чтобы приблизиться к минимальной погрешности, которую мы пытаемся найти. Но в случае ИНС нам нужно будет реализовать градиентный спуск с многомерным вектором весов.

Мы будем находить градиент нейронной сети, используя достаточно популярный метод обратного распространения ошибки, о котором будет написано позже. Но сначала нам нужно рассмотреть функцию погрешности более детально.

4.2 Функция оценки

Существует более общий способ изобразить выражения, которые дают нам возможность уменьшить погрешность. Такое общее представление называется функция оценки. Например, функция оценки для пары вход-выход (x^z, y^z) в нейронной сети будет выглядеть следующим образом:

Выражение является функцией оценки учебного экземпляра z_th, где h^(nl)является выходом последнего слоя, то есть выход нейронной сети. h^(nl) можно представить как yпyп, Что означает полученный результат, когда нам известен вход xz. Две вертикальные линии означают норму L² погрешности или сумму квадратов ошибок. Сумма квадратов погрешностей является довольно распространенным способом представления погрешностей в системе машинного обучения. Вместо того, чтобы брать абсолютную погрешность abs(ypred(x^z)-y^z), мы берем квадрат погрешности. Мы не будем обсуждать причину этого в данной статье. 1/2 в начале просто константой, которая нормализует ответ после того, как мы продифференцируем функцию оценки во время обратного распространения.

Обратите внимание, что приведенная ранее функция оценки работает только с одной парой (x,y). Мы хотим минимизировать функцию оценки со всеми mm парами вход-выход:

Тогда как же мы будем использовать функцию J для обучения наших сетей? Конечно, используя градиентный спуск и обратное распространение ошибок. Сначала рассмотрим градиентный спуск в нейронных сетях более детально.

4.3 Градиентный спуск в нейронных сетях

Градиентный спуск для каждого веса w_(ij)^(l) и смещение bi(l) в нейронной сети выглядит следующим образом:

Выражение выше фактически аналогично представлению градиентного спуска:
w_new=w_old-α*∇error. Нет лишь некоторых обозначений, но достаточно понимать, что слева расположены новые значения, а справа — старые. Опять же задействован итерационный метод для расчета весов на каждой итерации, но на этот раз основываясь на функции оценки J(w,b).

Значения ∂/∂w_ij^(l)и ∂/∂b_i^(l) являются частными производными функции оценки, основываясь на значениях веса. Что это значит? Вспомните простой пример градиентного спуска ранее, каждый шаг зависит от наклона погрешности / оценки по отношению к весу. Производная также имеет значение наклона / градиента. Конечно, производная обозначается как d/dx. x в нашем случае является вектором, а это значит, что наша производная тоже будет вектором, который является градиент каждого измерения x.

4.4 Пример двумерного градиентного спуска

Рассмотрим пример стандартного двумерного градиентного спуска. Ниже представлены диаграмму работы двух итеративных двумерных градиентных спусков:

Синим обозначены контуры функции оценки, они обозначают области, в которых значение погрешности примерно одинаковы. Каждый шаг (p1→p2→p3) В градиентном спуске используют градиент или производную, которые обозначаются стрелкой / вектором. Этот вектор проходит через два пространства [x1, x2][x1,x2]и показывает направление, в котором находится минимум. Например, производная, исчисленная в p1 может быть d/dx=[2.1,0.7], Где производная является вектором с двумя значениями. Частичная производная ∂/∂x₁ в этом случае равна скаляру →[2.1]- иными словами, это значение градиента только в одном измерении поискового пространства (x1).

В нейронных сетях не существует простой полной функции оценки, с которой можно легко посчитать градиент, похожей на функцию, которую мы ранее рассматривали f(x)=x⁴-3x³+2). Мы можем сравнить выход нейронной сети с нашим ожидаемым значением y^(z), После чего функция оценки будет меняться из-за изменения в значениях веса, но как мы это сделаем со всеми скрытыми слоями в сети?

Поэтому нам нужен метод обратного распространения. Этот метод дает нам возможность «делить» функцию оценки или ошибку со всеми весами в сети. Другими словами, мы можем выяснить, как каждый вес влияет на погрешность.

4.5 Углубляемся в обратное распространение

Если математика вам не очень хорошо дается, то вы можете пропустить этот раздел. В следующем разделе вы узнаете, как реализовать обратное распространение языке программирования. Но если вы не против немного больше поговорить о математике, то продолжайте читать, вы получите более глубокие знания по обучению нейронных сетей.

Сначала, давайте вспомним базовые уравнения для нейронной сети с тремя слоями из предыдущих разделов:

Выход этой нейронной сети находится по формуле:

Мы можем упростить это уравнение к h₁(3)=f(z₁⁽²⁾), добавив новое значение z₁⁽²⁾, которое означает:

Предположим, что мы хотим узнать, как влияет изменение в весе w₁₂⁽²⁾ на функцию оценки. Это означает, что нам нужно вычислить ∂J/∂w₁₂⁽²⁾. Чтобы сделать это, нужно использовать правило дифференцирования сложной функции:

Если присмотреться, то правая часть полностью сокращается (по принципу 2552=22=1). ∂J∂w12(2) были разбиты на три множителя, два из которых можно прекрасно заменить. Начнем с ∂z₁⁽²⁾/∂w₁₂⁽²⁾:

Частичная производная z₁⁽²⁾ по w₁₂⁽²⁾ зависит только от одного произведения в скобках, w12(1)h2(2), Так как все элементы в скобках, кроме w₁₂⁽²⁾, не изменяются. Производная от константы всегда равна 1, а ∂/∂w₁₂⁽²⁾)сокращается до просто h₂⁽²⁾, Что является обычным выходом второго узла из слоя 2.

Следующая частичная производная сложной функции ∂h₁⁽³⁾/∂z₁⁽²⁾ является частичной производной активационной функции выходного узла h₁₍₃₎. Так что нам нужно брать производные активационной функции, следует условие ее включения в нейронные сети — функция должна быть дифференцированной. Для сигмоидальной активационной функции производная будет выглядеть так:

, где f(z)является самой активационной функцией. Теперь нам нужно разобраться, что делать с ∂J∂h₁⁽³⁾. Вспомните, что J(w,b,x,y) есть функция квадрата погрешности, выглядит так:

здесь y1 является ожидаемым выходом для выходного узла. Опять используем правило дифференцирования сложной функции:

Мы выяснили, как находить ∂J/∂w₁₂⁽²⁾по крайней мере для весов связей с исходным слоем. Перед тем, как перейти к одному из скрытых слоев, введем некоторые новые значения δ, чтобы немного сократить наши выражения:

, где i является номером узла в выходном слое. В нашем примере есть только один узел, поэтому i=1. Напишем полный вид производной функции оценки:

, где выходной слой, в нашем случае, l=2, а i соответствует номеру узла.

4.6 Распространение в скрытых слоях

Что делать с весами в скрытых слоях (в нашем случае в слое 2)? Для весов, которые соединены с выходным слоем, производная ∂J/∂h=-(y_i-h_i^(nl))имела смысл, т.к. функция оценки может быть сразу найдена через сравнение выходного слоя с существующими данными. Но выходы скрытых узлов не имеют подобных уже существующих данных для проверки, они связаны с функцией оценки только через другие слои узлов. Как мы можем найти изменения в функции оценки из-за изменений весов, которые находятся глубоко в нейронной сети? Как уже было сказано, мы используем метод обратного распространения.

Мы уже сделали тяжелую работу по правилу дифференцирования сложных функций, теперь рассмотрим все более графически. Значение, которое будет обратно распространяться, — δ_i^(nl), т.к. оно в ближайшей связи с функцией оценки. А что с узлом j во втором слое (скрытом слое)? Как он влияет на δ_i^(nl) в нашей сети? Он меняет другие значения из-за веса w_ij⁽²⁾(см. диаграмму ниже, где j=1 i=1).

Как можно понять из рисунка, выходной слой соединяется со скрытым узлом из-за веса. В случае, когда в исходном слое есть только один узел, общее выражение скрытого слоя будет выглядеть так:

, где j номер узла в слое l. Но что будет, если в исходном слое находится много выходных узлов? В этом случае δ_j^(l) находится по взвешенной сумме всех связанных между собой погрешностей, как показано на диаграмме ниже:

На рисунке показано, что каждое значение δ из исходного слоя суммируется для нахождения δ₁⁽²⁾, Но каждый выход δ должен быть взвешенным соответствующими значению w_i1⁽²⁾. Другими словами, узел 1 в слое 2 способствует изменениям погрешностей в трех выходных узлах, при этом полученная погрешность (или значение функции оценки) в каждом из этих узлов должна быть «передана назад» значению δ этого узла. Сформируем общее выражение значение δ для узлов в скрытом слое:
, где j является номером узла в слое l, i- номер узла в слое l+1(что аналогично обозначениям, которое мы использовали ранее). s_(l+1)— это количество узлов в слое l+1.
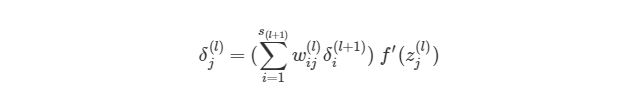
Теперь мы знаем, как находить:
Но что делать с весами смещения? Принцип работы с ними аналогичный обычным весам, используя правила дифференцирования сложных функций:

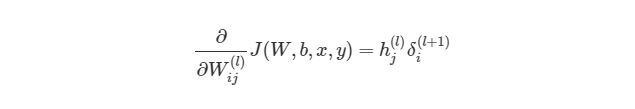
Отлично, теперь мы знаем, как реализовать градиентный спуск в нейронных сетях:

Однако, для такой реализации, нам нужно будет снова применить циклы. Как мы уже знаем из предыдущих разделов, циклы в языке программирования Python работают довольно медленно. Нам нужно будет понять, как можно векторизовать такие подсчеты.

4.7 Векторизация обратного распространения

Для того, чтобы понять, как векторизовать процесс градиентного спуска в нейронных сетях, рассмотрим сначала упрощенную векторизованную версию градиента функции оценки (внимание: это пока неправильная версия!):

Что представляет собой h^(l)? Все просто, вектор (s_l×1), где s_l является количеством узлов в слое l. Как тогда выглядит произведение h^(l)δ^(l+1)? Мы знаем, что α×∂J/∂W^(l) должно быть того же размера, что и матрица весов W(l), Мы также знаем, что результат h_(l)δ^(l+1) должен быть того же размера, что и матрица весов для слоя l. Иными словами, произведение должно быть размера (s_{l + 1}× s_l).

Мы знаем, что δ_(l+1) имеет размер (s_l+1×1), а h ^(l)— размер (s_l×1). По правилу умножения матриц, если матрицу (n×m)умножить на матрицу (o×p), То мы получим матрицу размера (n×p). Если мы просто перемножим h_(l) на δ_(l+1), то количество столбцов в первом векторе (один столбец) не будет равно количеству строк во втором векторе (3 строки). Поэтому, для того, чтобы можно было умножить эти матрицы и получить результат размера (s_l+1× s_l), Нужно сделать трансформирование. Оно меняет в матрице столбцы на строки и наоборот (например матрицу вида (s_l×1)на (1×s_l)). Трансформирование обозначается как буква T над матрицей. Мы можем сделать следующее:

Используя операцию трансформирования, мы можем достичь результата, который нам нужен.

Еще одно трансформирование нужно сделать с суммой погрешностей в обратном распространении:

символ (∙) в предыдущем выражении означает поэлементное умножение (произведение Адамара), не является умножением матриц. Обратите внимание, что произведение матриц (((W^(l))^Tδ_(l+1))требует еще одного сложения весов и значений δ.

4.8 Реализация этапа градиентного спуска

Как тогда интегрировать векторизацию в этапы градиентного спуска нашего алгоритма? Во-первых, вспомним полный вид нашей функции оценки, который нам нужно сократить:

Из формулы видно, что полная функция оценки состоит из суммы поэтапных расчетов функции оценки. Также следует вспомнить, как находится градиентный спуск (поэлементная и векторизованная версии):

Это означает, что по прохождению через экземпляры обучения нам нужно иметь отдельную переменную, которая равна сумме частных производных функции оценки каждого экземпляра. Такая переменная соберет в себе все значения для «глобального» подсчета. Назовем такую «суммированную» переменную ΔW^(l). Соответствующая переменная для смещения будет обозначаться как Δb^(l). Следовательно, при каждой итерации в процессе обучения сети нам нужно будет сделать следующие шаги:

Выполняя эти операции на каждой итерации, мы подсчитываем упомянутую ранее сумму Σ^m_{z= 1}∂/∂W^(l)J( w , b , x^(z), y^(z))(и аналогичная формула для b). После того, как будут проитерированы все экземпляры и получены все значения δ, мы обновляем значения параметров веса:

4.9 Конечный алгоритм градиентного спуска

И, наконец, мы пришли к определению метода обратного распространения через градиентный спуск для обучения наших нейронных сетей. Финальный алгоритм обратного распространения выглядит следующим образом:
Рандомная инициализация веса для каждого слоя W^(l). Когда итерация < границы итерации:

01. Зададим ΔW и Δb начальное значение ноль.
02. Для экземпляров от 1 до m: а. Запустите процесс прямого распространения через все n_l слоев. Храните вывод активационной функции в h^(l)б. Найдите значение δ^{( nl)} выходного слоя. Обновите ΔW^(l)и Δb^{( l )} для каждого слоя.
03. Запустите процесс градиентного спуска, используя:

Из этого алгоритма следует, что мы будем повторять градиентный спуск, пока функция оценки не достигнет минимума. На этом этапе нейросеть считается обученной и готовой к использованию.

Далее мы попробуем реализовать этот алгоритм на языке программирования для обучения нейронной сети распознаванию чисел, написанных от руки.

5 Имплементация нейросети языке Python

В предыдущем разделе мы рассмотрели теорию по обучению нейронной сети через градиентный спуск и метод обратного распространения. В этом разделе мы используем полученные знания на практике — напишем код, который прогнозирует, основываясь на данных MNIST. База данных MNIST — это набор примеров в нейронных сетях и глубинном обучении. Она включает в себя изображения цифр, написанных от руки, с соответствующими ярлыками, которые объясняют, что это за число. Каждое изображение размером 8х8 пикселей. В этом примере мы используем сети данных MNIST для библиотеки машинного обучения scikit learn в языке программирования Python . Пример такого изображения можно увидеть под кодом:


	from sklearn.datasets
	import load_digits
	digits = load_digits()
	print(digits.data.shape)
	import matplotlib.pyplot as plt
	plt.gray()
	plt.matshow(digits.images[1])
	plt.show()

Код, который мы собираемся написать в нашей нейронной сети, будет анализировать цифры, которые изображают пиксели на изображении. Для начала, нам нужно отсортировать входные данные. Для этого мы сделаем две следующие вещи:

01. Масштабировать данные.
02. Разделить данные на тесты и учебные тесты.

5.1 Масштабирование данных

Почему нам нужно масштабировать данные? Во-первых, рассмотрим представление пикселей одного из сетов данных:


digits.data[0, : ]
Out[2]:
   array([0., 0., 5., 13., 9., 1., 0., 0., 0., 0., 13.,
      15., 10., 15., 5., 0., 0., 3., 15., 2., 0., 11.,
      8., 0., 0., 4., 12., 0., 0., 8., 8., 0., 0.,
      5., 8., 0., 0., 9., 8., 0., 0., 4., 11., 0.,
      1., 12., 7., 0., 0., 2., 14., 5., 10., 12., 0.,
      0., 0., 0., 6., 13., 10., 0., 0., 0.
   ])

Заметили ли вы, что входные данные меняются в интервале от 0 до 15? Достаточно распространенной практикой является масштабирование входных данных так, чтобы они были только в интервале от [0, 1], или [1, 1]. Это делается для более легкого сравнения различных типов данных в нейронной сети. Масштабирование данных можно легко сделать через библиотеку машинного обучения scikit learn:


from sklearn.preprocessing import StandardScaler
X_scale = StandardScaler()
X = X_scale.fit_transform(digits.data)
X[0,:]
Out[3]:
array([ 0.        , -0.33501649, -0.04308102,  0.27407152, -0.66447751,
       -0.84412939, -0.40972392, -0.12502292, -0.05907756, -0.62400926,
        0.4829745 ,  0.75962245, -0.05842586,  1.12772113,  0.87958306,
       -0.13043338, -0.04462507,  0.11144272,  0.89588044, -0.86066632,
       -1.14964846,  0.51547187,  1.90596347, -0.11422184, -0.03337973,
        0.48648928,  0.46988512, -1.49990136, -1.61406277,  0.07639777,
        1.54181413, -0.04723238,  0.        ,  0.76465553,  0.05263019,
       -1.44763006, -1.73666443,  0.04361588,  1.43955804,  0.        ,
       -0.06134367,  0.8105536 ,  0.63011714, -1.12245711, -1.06623158,
        0.66096475,  0.81845076, -0.08874162, -0.03543326,  0.74211893,
        1.15065212, -0.86867056,  0.11012973,  0.53761116, -0.75743581,
       -0.20978513, -0.02359646, -0.29908135,  0.08671869,  0.20829258,
       -0.36677122, -1.14664746, -0.5056698 , -0.19600752])

Стандартный инструмент масштабирования в scikit learn нормализует данные через вычитание и деление. Вы можете видеть, что теперь все данные находятся в интервале от -2 до 2. По же на счет выходных данных yy, то обычно нет необходимости их масштабировать.

5.2 Создание тестов и учебных наборов данных

В машинном обучении появляется такой феномен, который называется «переобучением». Это происходит, когда модели, во время учебы, становятся слишком запутанными — они достаточно хорошо обучены, но когда им передаются новые данные, которые они никогда на «видели», то результат, который они выдают, становится плохим. Иными словами, модели генерируются не очень хорошо. Чтобы убедиться, что мы не создаем слишком сложные модели, обычно набор данных разбивают на учебные наборы и тестовые наборы. Учебный набором данных, на которых модель будет учиться, а тестовый набор — это данные, на которых модель будет тестироваться после завершения обучения. Количество учебных данных должно быть всегда больше тестовых данных. Обычно они занимают 60-80% от набора данных.

Опять же, scikit learn легко разбивает данные на учебные и тестовые наборы:


from sklearn.model_selection import train_test_split
y = digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)

В этом случае мы выделили 40% данных на тестовые наборы и 60% соответственно на обучение. Функция train_test_split в scikit learn добавляет данные рандомно в различные базы данных — то есть, функция не берет первые 60% строк для учебного набора, а то, что осталось, использует как тестовый.

5.3 Настройка выходного слоя

Для того, чтобы получать результат — числа от 0 до 9, нам нужен выходной слой. Более-менее точная нейросеть, как правило, имеет выходной слой с 10 узлами, каждый из которых выдает число от 0 до 9. Мы хотим научить сеть так, чтобы, например, при цифре 5 на изображении, узел с цифрой 5 в исходном слое имел наибольшее значение. В идеале, мы бы хотели иметь следующий вывод: [0, 0, 0, 0, 0, 1, 0, 0, 0, 0]. Но на самом деле мы можем получить что-то похожее на это: [0.01, 0.1, 0.2, 0.05, 0.3, 0.8, 0.4, 0.03, 0.25, 0.02]. В таком случае мы можем взять крупнейших индекс в исходном массиве и считать это нашим полученным числом.

В данных MNIST нужны результаты от изображений записаны как отдельное число. Нам нужно конвертировать это единственное число в вектор, чтобы его можно было сравнивать с исходным слоем с 10 узлами. Иными словами, если результат в MNIST обозначается как «1», то нам нужно его конвертировать в вектор: [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]. Такую конвертацию осуществляет следующий код:


import numpy as np
def convert_y_to_vect(y):
    y_vect = np.zeros((len(y), 10))
    for i in range(len(y)):
        y_vect[i, y[i]] = 1
    return y_vect


y_v_train = convert_y_to_vect(y_train)
y_v_test = convert_y_to_vect(y_test)
y_train[0], y_v_train[0]
Out[8]:
(1, array([ 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.]))

Этот код конвертирует «1» в вектор [0, 1, 0, 0, 0, 0, 0, 0, 0, 0].

5.4 Создаем нейросеть

Следующим шагом является создание структуры нейронной сети. Для входного слоя, мы знаем, что нам нужно 64 узла, чтобы покрыть 64 пикселей изображения. Как было сказано ранее, нам нужен выходной слой с 10 узлами. Нам также потребуется скрытый слой в нашей сети. Обычно, количество узлов в скрытых слоях не менее и не больше количества узлов во входном и выходном слоях. Объявим простой список на языке Python , который определяет структуру нашей сети:


nn_structure = [64, 30, 10]

Мы снова используем сигмоидальную активационную функцию, так что сначала нужно объявить эту функцию и ее производную:


	def f(x):
	  return 1 / (1 + np.exp(-x))


def f_deriv(x):
    return f(x) * (1 - f(x))

Сейчас мы не имеем никакого представления, как выглядит наша нейросеть. Как мы будем ее учить? Вспомним наш алгоритм из предыдущих разделов:
Рандомно инициализируем веса для каждого слоя W^(l) Когда итерация <границы итерации:

Значит первым этапом является инициализация весов для каждого слоя. Для этого мы используем словари в языке программирования Python (обозначается через {}). Рандомные значения предоставляются весам для того, чтобы убедиться, что нейросеть будет работать правильно во время обучения. Для рандомизации мы используем random_sample из библиотеки numpy. Код выглядит следующим образом:


import numpy.random as r
def setup_and_init_weights(nn_structure):
    W = {}
    b = {}
    for l in range(1, len(nn_structure)):
        W[l] = r.random_sample((nn_structure[l], nn_structure[l-1]))
        b[l] = r.random_sample((nn_structure[l],))
    return W, b

Следующим шагом является присвоение двум переменным ΔW и Δb нулевых начальных значений (они должны иметь такой же размер, что и матрицы весов и смещений)


def init_tri_values(nn_structure):
    tri_W = {}
    tri_b = {}
    for l in range(1, len(nn_structure)):
        tri_W[l] = np.zeros((nn_structure[l], nn_structure[l-1]))
        tri_b[l] = np.zeros((nn_structure[l],))
    return tri_W, tri_b

Далее запустим процесс прямого распространения через нейронную сеть:


def feed_forward(x, W, b):
    h = {1: x}
    z = {}
    for l in range(1, len(W) + 1):
    #Если первый слой, то весами является x, в противном случае
    #Это выход из последнего слоя
 if l == 1:
            node_in = x
        else:
            node_in = h[l]
        z[l+1] = W[l].dot(node_in) + b[l] # z^(l+1) = W^(l)*h^(l) + b^(l)  
        h[l+1] = f(z[l+1]) # h^(l) = f(z^(l)) 
    return h, z

И наконец, найдем выходной слой δ ^(nl) и значение δ^(l) в скрытых слоях для запуска обратного распространения:


def calculate_out_layer_delta(y, h_out, z_out):
    # delta^(nl) = -(y_i - h_i^(nl)) * f'(z_i^(nl))
    return -(y-h_out) * f_deriv(z_out)


def calculate_hidden_delta(delta_plus_1, w_l, z_l):
    # delta^(l) = (transpose(W^(l)) * delta^(l+1)) * f'(z^(l))
    return np.dot(np.transpose(w_l), delta_plus_1) * f_deriv(z_l)

Теперь мы можем соединить все этапы в одну функцию:



def train_nn(nn_structure, X, y, iter_num=3000, alpha=0.25):
    W, b = setup_and_init_weights(nn_structure)
    cnt = 0
    m = len(y)
    avg_cost_func = []
    print('Начало градиентного спуска для {} итераций'.format(iter_num))
    while cnt  1:
                        delta[l] = calculate_hidden_delta(delta[l+1], W[l], z[l])
                    # triW^(l) = triW^(l) + delta^(l+1) * transpose(h^(l))
                    tri_W[l] += np.dot(delta[l+1][:,np.newaxis], np.transpose(h[l][:,np.newaxis])) 
                    # trib^(l) = trib^(l) + delta^(l+1)
                    tri_b[l] += delta[l+1]
        # запускает градиентный спуск для весов в каждом слое
        for l in range(len(nn_structure) - 1, 0, -1):
            W[l] += -alpha * (1.0/m * tri_W[l])
            b[l] += -alpha * (1.0/m * tri_b[l])
        # завершает расчеты общей оценки
        avg_cost = 1.0/m * avg_cost
        avg_cost_func.append(avg_cost)
        cnt += 1
    return W, b, avg_cost_func

Функция сверху должна быть немного объяснена. Во-первых, мы не задаем лимит работы градиентного спуска, основываясь на изменениях или точности функции оценки. Вместо этого, мы просто запускаем её с фиксированным числом итераций (3000 в нашем случае), а затем наблюдаем, как меняется общая функция оценки с прогрессом в обучении. В каждой итерации градиентного спуска, мы перебираем каждый учебный экземпляр (range (len (y)) и запускаем процесс прямого распространения, а после него и обратное распространение. Этап обратного распространения является итерацией через слои, начиная с выходного слоя к началу — range (len (nn_structure), 0, 1). Мы находим среднюю оценку на исходном слое (l == len (nn_structure)). Мы также обновляем значение ΔW и Δb с пометкой tri_W и tri_b, для каждого слоя, кроме исходного (исходный слой не имеет никакого связи, который связывает его со следующим слоем).

И наконец, после того, как мы прошлись по всем учебным экземплярам, накапливая значение tri_W и tri_b, мы запускаем градиентный спуск и меняем значения весов и смещений:

После окончания процесса, мы возвращаем полученные вес и смещение со средней оценкой для каждой итерации. Теперь время вызвать функцию. Ее работа может занять несколько минут, в зависимости от компьютера.


W, b, avg_cost_func = train_nn(nn_structure, X_train, y_v_train)

Мы можем увидеть, как функция средней оценки уменьшилась после итерационной работы градиентного спуска:


plt.plot(avg_cost_func)
plt.ylabel('Средняя J')
plt.xlabel('Количество итераций')
plt.show()

Выше изображен график, где показано, как за 3000 итераций нашего градиентного спуска функция средней оценки снизилась и маловероятно, что подобная итерация изменит результат.

5.5 Оценка точности модели

Теперь, после того, как мы научили нашу нейросеть MNIST, мы хотим увидеть, как хорошо она работает на тестах. Дан входной тест (64 пикселя), нам нужно получить вывод нейронной сети — это делается через запуск процесса прямого распространения через сеть, используя наши полученные значения веса и смещения. Как было сказано ранее, мы выбираем результат выходного слоя через выбор узла с максимальным выводом. Для этого можно использовать функцию numpy.argmax, она возвращает индекс элемента массива с наибольшим значением:


def predict_y(W, b, X, n_layers):
    m = X.shape[0]
    y = np.zeros((m,))
    for i in range(m):
        h, z = feed_forward(X[i, :], W, b)
        y[i] = np.argmax(h[n_layers])
    return y

Теперь, наконец, мы можем оценить точность результата (процент раз, когда сеть выдала правильный результат), используя функцию accuracy_score из библиотеки scikit learn:


from sklearn.metrics import accuracy_score
y_pred = predict_y(W, b, X_test, 3)
accuracy_score(y_test, y_pred)*100

Мы получили результат 86% точности. Звучит довольно неплохо? На самом деле, нет, это довольно низкая точностью. В наше время точность алгоритмов глубинного обучения достигает 99.7%, мы немного отстали.

Предлагаем также посмотреть:

Лучший видеокурс по нейронным сетям на русском
Подборка материалов по нейронным сетям
Введение в глубинное обучение

Нейросети кажутся людям чем-то очень сложным и запутанным, однако это вовсе не так. Простую нейросеть можно написать менее чем за час с нуля. В нашей статье мы создадим нейронную сеть прямого распространения (также называемую многослойным перцептроном), используя лишь массивы, циклы и условные операторы, а значит этот код легко можно будет перенести на любой язык программирования, предоставляющий эти возможности. А если язык предоставляет библиотеку для матричных и векторных вычислений (как, например, numpy в языке Python, то написание займёт ещё меньше времени).

Что такое нейросеть?

Согласно Википедии, искусственная нейронная сеть (ИНС) — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма.

Более простыми словами, это некий чёрный ящик, который превращает входные данные в выходные, или, говоря более математическим языком, является отображением пространства входных признаков X в пространство выходных признаков Y: X → Y. То есть мы хотим найти какую-то функцию F, которая сможет выполнять это преобразование. Для начала этой информации нам будет достаточно. Для более подробного ознакомления рекомендуем ознакомиться с этой статьёй на хабре.

Коротко об искусственном нейроне

Чаще всего в подобных статьях начинают расписывать про устройство биологического нейрона, связь с его искусственной моделью и прочую лирику. Мы же этого делать не будем, а сразу перейдём к сути. Искусственный нейрон — это всего лишь взвешенная сумма значений входного вектора элементов, которая передаётся на нелинейную функцию активации f: z = f(y), где y = w₀·x₀ + w₁·x₁ + ... + w_{m - 1}·x_{m - 1}. Здесь w₀, ..., w_{m - 1} — коэффициенты, веса каждого элемента вектора, x₀, ..., x_{m - 1} — значения входного вектора X, y — взвешенная сумма элементов X, а z — результат применения функции активации. Мы вернёмся к функции активации немного позднее, а пока давайте придумаем, как вместо одного выходного значения получить n.

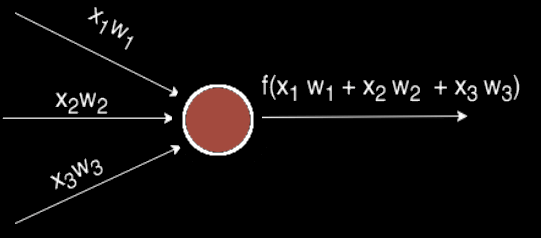
Искусственный нейрон с тремя входами

Нейронный слой

Один нейрон способен входной вектор превратить в одну точку, однако по условию мы хотим получить несколько точек, так как выходной вектор Y может иметь произвольную размерность, определяемую лишь конкретной ситуацией (один выход для XOR, 10 выходов для определения принадлежности к одному из 10 классов и т.д.). Как же нам получить n точек, преобразуя элементы входного вектора X? Оказывается, всё довольно просто: для того, чтобы получить n выходных значений, необходимо использовать не один нейрон, а n. Тогда для каждого из элементов выходного вектора Y будет использовано ровно n различных взвешенных сумм от вектора X. То есть мы получаем, что z_i = f(y_i) = f(w_i0·x₀ + w_i1·x₁ + ... + w_{im - 1}·x_{m - 1})

Если внимательно посмотреть, то оказывается, что написанная выше формула является определением умножения матрицы на вектор. И действительно, если взять матрицу W размера n на m и умножить её на вектор X размерности m, то получится другой вектор размерности n, то есть ровно то, что нам и нужно. Таким образом, получение выходного вектора по входному для n нейронов можно записать в более удобной матричной форме: Y = W·X, где W — матрица весовых коэффициентов, X — входной вектор и Y — выходной вектор. Однако полученный вектор является неактивированным состоянием (промежуточным, невыходным) всех нейронов, а чтобы получить выходное значение,, необходимо каждое неактивированное значение подать на вход функции активации. Результат её применения и будет выходным значением слоя.

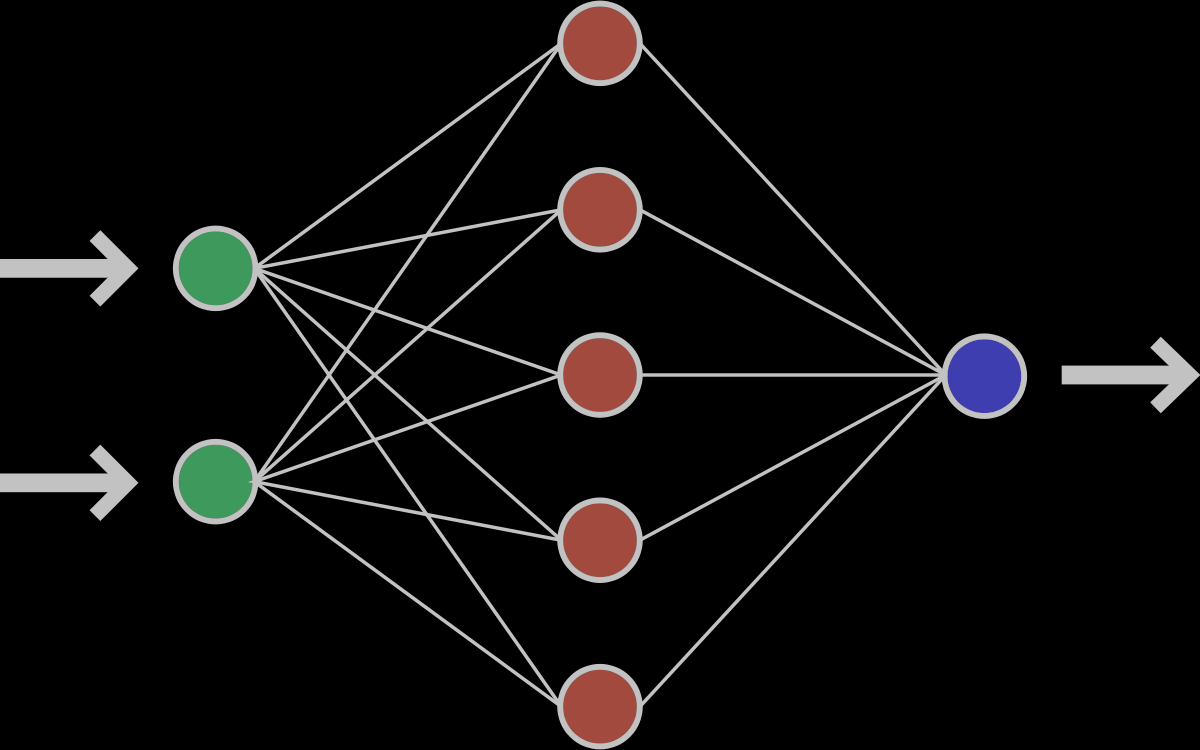
Пример нейронной сети с двумя входами, пятью нейронами в скрытом слое и одним выходом

Забегая вперёд скажем о том, что нередко используют последовательность нейронных слоёв для более глубокого обучения сети и большей формализации данных. Поэтому для получения итогового выходного вектора необходимо проделать описанную выше операцию несколько раз подряд от одного слоя к другому. Тогда для первого слоя входным вектором будет X, а для всех последующих входом будет являться выход предыдущего слоя. К примеру, сеть с 3 скрытыми слоями может выглядеть так:

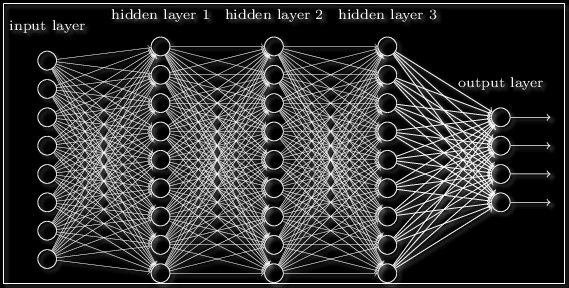
Пример многослойной нейронной сети

Функция активации

Функция активации — это функция, которая добавляет в сеть нелинейность, благодаря чему нейроны могут довольно точно имитировать любую функцию. Наиболее распространёнными функциями активации являются:

Сигмоида: f(x) = 1 / (1 + e^-x)
Гиперболический тангенс: f(x) = tanh(x)
ReLU: f(x) = max(x,0)

У каждой из них есть свои особенности, но об этом лучше почитать в другой статье.

Хватит бла бла, давайте писать код

Теперь нам достаточно знаний, чтобы написать код получения результата нейронной сети. Мы будем писать код на языке C#, однако, уверяем, код будет практически идентичным для других языков программирования. Давайте разберёмся, что нам потребуется для реализации сети прямого распространения:

Вектор (входные, выходные);
Матрица (каждый слой содержит матрицу весовых коэффициентов);
Нейросеть.

1. Вектор:

Вектор можно создавать из количества элементов (длины);
Вектор можно создавать из перечисления вещественных чисел;
Можно получать значения по индексу i.
Можно изменять значения по индексу i.

Напишем же это:

class Vector {
    public double[] v; // значения вектора
    public int n; // длина вектора

	// конструктор из длины
    public Vector(int n) {
        this.n = n; // копируем длину
        v = new double[n]; // создаём массив
    }

	// создание вектора из вещественных значений
    public Vector(params double[] values) {
        n = values.Length;
        v = new double[n];

        for (int i = 0; i < n; i++)
            v[i] = values[i];
    }

	// обращение по индексу
    public double this[int i] {
        get { return v[i]; } // получение значение
        set { v[i] = value; } // изменение значения
    }
}

2. Матрица:

Матрицу можно создавать из числа строк, столбцов и генератора случайных чисел для заполнения случайными значениями;
Можно получать значения по индексам i и j;
Можно изменять значения по индексам i и j;

Напишем же это:

class Matrix {
    double[][] v; // значения матрицы
    public int n, m; // количество строк и столбцов

	// создание матрицы заданного размера и заполнение случайными числами из интервала (-0.5, 0.5)
    public Matrix(int n, int m, Random random) {
        this.n = n;
        this.m = m;

        v = new double[n][];

        for (int i = 0; i < n; i++) {
            v[i] = new double[m];

            for (int j = 0; j < m; j++)
                v[i][j] = random.NextDouble() - 0.5; // заполняем случайными числами
        }
    }

	// обращение по индексу
    public double this[int i, int j] {
        get { return v[i][j]; } // получение значения
        set { v[i][j] = value; } // изменение значения
    }
}

3. Сама нейросеть:

class Network {
    Matrix[] weights; // матрицы весов слоя

    int layersN; // число слоёв

	// создание сети из массива количества нейронов в каждом слое
    public Network(int[] sizes) {
        Random random = new Random(DateTime.Now.Millisecond); // создаём генератор случайных чисел

        layersN = sizes.Length - 1; // запоминаем число слоёв

        weights = new Matrix[layersN]; // создаём массив матриц

		// для каждого слоя создаём матрицы весовых коэффициентов
        for (int k = 1; k < sizes.Length; k++) {
            weights[k - 1] = new Matrix(sizes[k], sizes[k - 1], random);
        }
    }

	// получение выхода сети (прямое распространение)
    Vector Forward(Vector input) {
    	Vector output; // будущий выходной вектор

        for (int k = 0; k < layersN; k++) {
        	output = new Vector(weights[k].n); // создаём новый выходной вектор для каждого слоя

            for (int i = 0; i < weights[k].n; i++) {
                double y = 0; // неактивированный выход нейрона

                for (int j = 0; j < weights[k].m; j++)
                    y += weights[k][i, j] * input[j];

				// выполняем активацию с помощью сигмоидальной функции
                output[i] = 1 / (1 + Math.Exp(-y));

                // выполняем активацию с помощью гиперболического тангенса
                // output[i] = Math.Tanh(y);

                // выполняем активацию с помощью ReLU
                // output[i] = Math.Max(0, y);
            }
        }

        return output;
    }
}

Сеть есть, но её ответы случайны. Как обучать?

На данный момент мы имеем случайную (необученную) нейронную сеть, которая может по входному вектору input выдать случайный ответ, однако нам требуется ответы, удовлетворяющие конкретной задаче. Чтобы добиться этого нашу сеть необходимо обучить. Для этого нам необходима база тренировочных примеров, то есть множество пар векторов X — Y, на которых будет обучаться сеть. Обучать нейросеть мы будем с помощью алгоритма обратного распространения ошибки. Если кратко, то он работает следующим образом:

Подать на вход сети обучающий пример (один входной вектор)
Распространить сигнал по сети вперёд (получить выход сети)
Вычислить ошибку (разница получившегося и ожидаемого векторов)
Распространить ошибку на предыдущие слои
Обновить весовые коэффициенты для уменьшения ошибки

Сам же алгоритм обучения выглядит так:

error = 0
epoch = 1

повторять:
	Для каждого обучающего примера:
		Найти ошибку e = f - d
		Прибавить к error сумму квадратов значений e
		Распространенить ошибку к первому слою
		Обновить веса

	если error < eps
		выйти

	если epoch > maxEpoch
		выйти из-за ограничения на число эпох

	epoch = epoch + 1

Обучаем нейронную сеть

Для обратного распространения ошибки нам потребуется знать значения входов, выходов и значения производных функции активации сети на каждом из слоёв, поэтому создадим структуру LayerT, в которой будет 3 вектора: x — вход слоя, z — выход слоя, df — производная функции активации. Также для каждого слоя потребуются векторы дельт, поэтому добавим в наш класс ещё и их. С учётом вышесказанного наш класс станет выглядеть так:

class Network {
    struct LayerT {
        public Vector x; // вход слоя
        public Vector z; // активированный выход слоя
        public Vector df; // производная функции активации слоя
    }

    Matrix[] weights; // матрицы весов слоя
    LayerT[] L; // значения на каждом слое
    Vector[] deltas; // дельты ошибки на каждом слое

    int layersN; // число слоёв

    public Network(int[] sizes) {
        Random random = new Random(DateTime.Now.Millisecond); // создаём генератор случайных чисел

        layersN = sizes.Length - 1; // запоминаем число слоёв

        weights = new Matrix[layersN]; // создаём массив матриц весовых коэффициентов
        L = new LayerT[layersN]; // создаём массив значений на каждом слое
        deltas = new Vector[layersN]; // создаём массив для дельт

        for (int k = 1; k < sizes.Length; k++) {
            weights[k - 1] = new Matrix(sizes[k], sizes[k - 1], random); // создаём матрицу весовых коэффициентов
	
            L[k - 1].x = new Vector(sizes[k - 1]); // создаём вектор для входа слоя
            L[k - 1].z = new Vector(sizes[k]); // создаём вектор для выхода слоя
            L[k - 1].df = new Vector(sizes[k]); // создаём вектор для производной слоя

            deltas[k - 1] = new Vector(sizes[k]); // создаём вектор для дельт
        }
    }

	// прямое распространение
    public Vector Forward(Vector input) {
        for (int k = 0; k < layersN; k++) {
            if (k == 0) {
                for (int i = 0; i < input.n; i++)
                    L[k].x[i] = input[i];
            }
            else {
                for (int i = 0; i < L[k - 1].z.n; i++)
                    L[k].x[i] = L[k - 1].z[i];
            }

            for (int i = 0; i < weights[k].n; i++) {
                double y = 0;

                for (int j = 0; j < weights[k].m; j++)
                    y += weights[k][i, j] * L[k].x[j];

				// активация с помощью сигмоидальной функции
                L[k].z[i] = 1 / (1 + Math.Exp(-y));
                L[k].df[i] = L[k].z[i] * (1 - L[k].z[i]);

				// активация с помощью гиперболического тангенса
                //L[k].z[i] = Math.Tanh(y);
                //L[k].df[i] = 1 - L[k].z[i] * L[k].z[i];
				
				// активация с помощью ReLU
                //L[k].z[i] = y > 0 ? y : 0;
                //L[k].df[i] = y > 0 ? 1 : 0;
            }
        }

        return L[layersN - 1].z; // возвращаем результат
    }
}

Обратное распространение ошибки

Перейдём к обратному распространению ошибки. В качестве функции оценки сети E(W) возьмём среднее квадратичное отклонение: E = 0.5 · Σ(y_1i - y_2i)². Чтобы найти значение ошибки E, нам нужно найти сумму квадратов разности значений вектора, который выдала сеть в качестве ответа, и вектора, который мы ожидаем увидеть при обучении. Также нам потребуется найти дельту для каждого слоя, причём для последнего слоя она будет равна вектору разности полученного и ожидаемого векторов, умноженному (покомпонентно) на вектор значений производных последнего слоя: δ_last = (z_last - d)·f'_last, где z_last — выход последнего слоя сети, d — ожидаемый вектор сети, f'_last — вектор значений производной функции активации последнего слоя.

Теперь, зная дельту последнего слоя, мы можем найти дельты всех предыдущих слоёв. Для этого нужно умножить транспонированную матрицы текущего слоя на дельту текущего слоя и затем умножить полученный вектор на вектор производных функции активации предыдущего слоя: δ_k-1 = W^T_k·δ_k·f'_k.

Что ж, давайте реализуем это в коде:

// обратное распространение
void Backward(Vector output, ref double error) {
    int last = layersN - 1;

    error = 0; // обнуляем ошибку

    for (int i = 0; i < output.n; i++) {
        double e = L[last].z[i] - output[i]; // находим разность значений векторов

        deltas[last][i] = e * L[last].df[i]; // запоминаем дельту
        error += e * e / 2; // прибавляем к ошибке половину квадрата значения
    }

	// вычисляем каждую предудущю дельту на основе текущей с помощью умножения на транспонированную матрицу
    for (int k = last; k > 0; k--) {
        for (int i = 0; i < weights[k].m; i++) {
            deltas[k - 1][i] = 0;

            for (int j = 0; j < weights[k].n; j++)
                deltas[k - 1][i] += weights[k][j, i] * deltas[k][j];

            deltas[k - 1][i] *= L[k - 1].df[i]; // умножаем получаемое значение на производную предыдущего слоя
        }
    }
}

Изменение весов

Для того, чтобы уменьшить ошибку сети нужно изменить весовые коэффициенты каждого слоя. Как же именно нужно менять весовые коэффициенты матриц на каждом слое? Оказывается, всё довольно просто. Для этого используется метод градиентного спуска, а значит нам необходимо вычислить градиент по весам и сделать шаг в отрицательную сторону от этого градиента. На этапе прямого распространения мы зачем-то запоминали входные сигналы, а при обратном распространении ошибки мы вычисляли дельты в каждом слое. Именно их мы и будем сейчас использовать для нахождения градиента! Градиент по весам равен перемножению входного вектора и вектора дельт (не покомпонентно). Поэтому, чтобы обновить весовые коэффициенты и уменьшить тем самым ошибку сети нужно всего лишь вычесть из матрицы весов результат перемножения дельт и входных векторов, умноженный на скорость обучения. Это можно записать в таком виде: W_t+1 = W_t - η·δ·X, где W_t+1 — новая матрица весов, W_t — текущая матрица весов, X — входное значение слоя, δ — дельта этого слоя. Почему именно так с математической точки зрения хорошо описано в этой статье.

// обновление весовых коэффициентов, alpha - скорость обучения
void UpdateWeights(double alpha) {
    for (int k = 0; k < layersN; k++) {
        for (int i = 0; i < weights[k].n; i++) {
            for (int j = 0; j < weights[k].m; j++) {
                weights[k][i, j] -= alpha * deltas[k][i] * L[k].x[j];
            }
        }
    }
}

Обучение сети

Теперь, имея методы прямого распространения сигнала, обратного распространения ошибки и изменения весовых коэффициентов, нам остаётся лишь соединить всё вместе в один метод обучения.

public void Train(Vector[] X, Vector[] Y, double alpha, double eps, int epochs) {
	int epoch = 1; // номер эпохи
        
    double error; // ошибка эпохи

    do {
        error = 0; // обнуляем ошибку

		// проходимся по всем элементам обучающего множества
        for (int i = 0; i < X.Length; i++) {
            Forward(X[i]); // прямое распространение сигнала
            Backward(Y[i], ref error); // обратное распространение ошибки
            UpdateWeights(alpha); // обновление весовых коэффициентов
        }

        Console.WriteLine("epoch: {0}, error: {1}", epoch, error); // выводим в консоль номер эпохи и величину ошибку
        
        epoch++; // увеличиваем номер эпохи
    } while (epoch <= epochs && error > eps);
}

Сеть готова. Давайте же её чему-нибудь научим!

Тренируем нейросеть на функции XOR

Почему функция XOR так интересна? Просто потому, что её невозможно получить одним нейроном: 0 ^ 0 = 0, 0 ^ 1 = 1, 1 ^ 0 = 1, 1 ^ 1 = 0. Однако она легко получается увеличением числа нейронов. Мы же попробуем выполнить обучение сети с 3 нейронами в скрытом слое и 1 выходным (так как выход у нас всего один). Для этого нам необходимо создать массив векторов X и Y с обучающими данными и саму нейросеть:

// массив входных обучающих векторов
Vector[] X = {
    new Vector(0, 0),
    new Vector(0, 1),
    new Vector(1, 0),
    new Vector(1, 1)
};

// массив выходных обучающих векторов
Vector[] Y = {
    new Vector(0.0), // 0 ^ 0 = 0
    new Vector(1.0), // 0 ^ 1 = 1
    new Vector(1.0), // 1 ^ 0 = 1
    new Vector(0.0) // 1 ^ 1 = 0
};

Network network = new Network(new int[]{2, 3, 1}); // создаём сеть с двумя входами, тремя нейронами в скрытом слое и одним выходом

После чего запустим обучение со следующими параметрами: скорость обучения — 0.5, число эпох — 100000, величина ошибки — 1e-7:

network.Train(X, Y, 0.5, 1e-7, 100000); // запускаем обучение сети

После обучения посмотрим на результаты выполнив прямой проход для всех элементов:

for (int i = 0; i < 4; i++) {
	Vector output = network.Forward(X[i]);
	Console.WriteLine("X: {0} {1}, Y: {2}, output: {3}", X[i][0], X[i][1], Y[i][0], output[0]);
}

В результате вывод может быть таким:

X: 0 0, Y: 0, output: 0,00503439463431083
X: 0 1, Y: 1, output: 0,996036009216668
X: 1 0, Y: 1, output: 0,996036033202241
X: 1 1, Y: 0, output: 0,00550270947767007

Проверять результаты на тренировочной же выборке довольно скучно, ведь как никак на ней мы сеть обучали, но, увы, для XOR проблемы ничего другого не остаётся. В качестве более серьёзного примера рекомендуем выполнить задачу распознавания картинок с рукописными цифрами MNIST. Это база содержит 60000 картинок написанных от руки цифр размером 28 на 28 пикселей и используется как один из основных датасетов для начала изучения машинного обучения. Не смотря на простоту нашей сети, при грамотном выборе параметров (число нейронов, число слоёв, скорость обучения, число эпох…) можно получить точность распознавания до 98%! Проверить свою сеть вы можете, поучаствовав в соревновании на сайте Kaggle. Нашей команде удалось достичь точности в 98.171%! А вы сможете больше?

В заключение

Мы написали с вами нейронную сеть прямого распространения и даже обучили её функции XOR. При этом мы позаботились об универсальности, благодаря чему нейросеть может быть обучена на любых данных, главное только подготовить два массива обучающих векторов X и Y, подобрать параметры обучения и запустить само обучение, после чего наблюдать за процессом. Важно помнить, что при использовании сигмоидальной функции активации, выходные значения сети не будут превышать 1, а значит, для обучения данным, которые значительно больше 1 необходимо отнормировать их, то есть привести к отрезку [0, 1].

Возможно, будет интересно: Свёрточная нейронная сеть с нуля. Часть 0. Введение.

Введение

ИИ уже успел достаточно нашуметь — о нейросетях сейчас знают и в научной среде, и в бизнесе. Вам наверняка случалось читать, что совсем скоро ваши рабочие процессы уже не будут прежними из-за какой-нибудь формы ИИ или нейросети. И вы, я уверен, слышали (пусть и не всё) о глубоких нейронных сетях и глубоком обучении.

В этой статье я приведу самые короткие, но эффективные способы понять, что такое глубокие нейронные сети, а также расскажу о том, как внедрить их с помощью библиотеки PyTorch.

История создания нейронных сетей

Какова же история развития нейронных сетей в науке и технике? Она берет свое начало с появлением первых компьютеров или ЭВМ (электронно-вычислительная машина) как их называли в те времена. Так еще в конце 1940-х годов некто Дональд Хебб разработал механизм нейронной сети, чем заложил правила обучения ЭВМ, этих «протокомпьютеров».

Дальнейшая хронология событий была следующей:

В 1954 году происходит первое практическое использование нейронных сетей в работе ЭВМ.
В 1958 году Франком Розенблатом разработан алгоритм распознавания образов и математическая аннотация к нему.
В 1960-х годах интерес к разработке нейронных сетей несколько угас из-за слабых мощностей компьютеров того времени.
И снова возродился уже в 1980-х годах, именно в этот период появляется система с механизмом обратной связи, разрабатываются алгоритмы самообучения.
К 2000 году мощности компьютеров выросли настолько, что смогли воплотить самые смелые мечты ученых прошлого. В это время появляются программы распознавания голоса, компьютерного зрения и многое другое.

GeekUniversity совместно с Mail.ru Group открыли первый в России факультет Искусственного интеллекта преподающий нейронные сети. Для учебы достаточно школьных знаний. Программа включает в себя все необходимые ресурсы и инструменты + целая программа по высшей математике. Не абстрактная, как в обычных вузах, а построенная на практике. Обучение познакомит вас с технологиями машинного обучения и нейронными сетями, научит решать настоящие бизнес-задачи.

Нейросети для чайников

Сегодняшняя статья будет посвящена достаточно сложной теме — что такое искусственные нейронные сети и зачем они нужны. Я расскажу вам историю создания нейронных сетей, как развивалась эта наука о сетях и что сейчас она может предложить человечеству. Тема сложная для понимания и сразу вникнуть в тему вряд ли получится, однако я постараюсь изложить информацию как можно проще.

Тема нейронных сетей актуальна сейчас, как никогда — то и дело в сети встречается масса сайтов, на которых эти самые сети забавно совмещают картинки, разукрашивают ч/б фотографии, распознают рукописный текст, речь и т.д. Это лишь малая часть того, что на самом деле умеет ИНС (искусственная нейронная сеть). В теории, возможности ИНС безграничны, однако сейчас они существенно уступают тому, что умеет человеческий мозг. По сравнению с нейронными сетями, мы спокойно можем разобрать речь собеседника в шумном помещении, узнать человека среди сотен других людей и т.д.

ИНС умеет все то же самое, но работает намного медленнее и сравнивая нейросеть с живым существом, ее мощность пока находится на уровне мухи. Все же наш мозг добился отличной работоспособности спустя 50 000 лет эволюции (если мы говорим о Homo sapiens), а нейросети существуют не более 65 лет. Современные технологии сильно шагнули вперед и нет никаких сомнений, что через 10-15 лет нейрокомпьютеры вплотную приблизятся по своим возможностям к человеческому мозгу благодаря стремительному развитию нейросетей и искусственного интеллекта в целом.

Нейросеть — в целом об ИНС

Как я уже говорил, в этой статье все будет упрощено. Важно, чтобы каждый хотя бы в общих чертах понимал, что такое нейронные сети.

Итак, что же такое ИНС? Вспомните уроки биологии — каждое существо в нашем мире имеет нервную систему, а более продвинутые жители Земли еще и мозг. Биологические нейронные сети и есть наши с вами мозги. Органы чувств передают информацию о раздражителе нейронным сетям, а те в свою очередь обрабатывают ее, благодаря чему мы чувствуем тепло и холод, ветер, влагу, можем распознать образы, запомнить информацию и т.д.

Вот так выглядит наш с вами нейрон — очень сложная биологическая система.

Искусственный нейрон — это тот же биологический нейрон, но только сильно упрощенный. Нам ведь не нужны оболочки, мембраны, ядра, рибосомы и прочее, чтобы математический нейрон смог жить. Требуется лишь алгоритм работы биологического нейрона, чтобы осуществлять задуманное — самообучение компьютеров и их систем. Вот как выглядит упрощённый биологический нейрон в математическом виде.

Какие бывают нейронные сети?

Пока что мы будем рассматривать примеры на самом базовом типе нейронных сетей — это сеть прямого распространения (далее СПР). Также в последующих статьях я введу больше понятий и расскажу вам о рекуррентных нейронных сетях. СПР как вытекает из названия это сеть с последовательным соединением нейронных слоев, в ней информация всегда идет только в одном направлении.

Виды нейронных сетей

В общих чертах мы определились с тем, что же такое нейронная сеть. Теперь пришло время поговорить об их разновидностях и типах, то есть о классификации. Но тут потребуется небольшое уточнение. Каждая нейронная сеть включает в себя первый слой нейронов, называемый входным. Этот слой не выполняет каких-либо преобразований и вычислений, его задача в другом: принимать и распределять входные сигналы по остальным нейронам. И этот слой единственный, являющийся общим для всех типов нейросетей, а критерием для деления является уже дальнейшая структура:
1. Однослойная структура нейронной сети. Представляет собой структуру взаимодействия нейронов, в которой сигналы со входного слоя сразу направляются на выходной слой, который, собственно говоря, не только преобразует сигнал, но и сразу же выдаёт ответ. Как уже было сказано, 1-й входной слой только принимает и распределяет сигналы, а нужные вычисления происходят уже во втором слое. Входные нейроны являются объединёнными с основным слоем с помощью синапсов с разными весами, обеспечивающими качество связей.
2. Многослойная нейронная сеть. Здесь, помимо выходного и входного слоёв, имеются ещё несколько скрытых промежуточных слоёв. Число этих слоёв зависит от степени сложности нейронной сети. Она в большей степени напоминает структуру биологической нейронной сети. Такие виды были разработаны совсем недавно, до этого все процессы были реализованы с помощью однослойных нейронных сетей. Соответствующие решения обладают большими возможностями, если сравнивать с однослойными, ведь в процессе обработки данных каждый промежуточный слой — это промежуточный этап, на котором осуществляется обработка и распределение информации.

Кроме количества слоёв, нейронные сети можно классифицировать по направлению распределения информации по синапсам между нейронами:
1. Нейросети прямого распространения (однонаправленные). В этой структуре сигнал перемещается строго по направлению от входного слоя к выходному. Движение сигнала в обратном направлении не осуществляется и в принципе невозможно. Сегодня разработки этого плана распространены широко и на сегодняшний день успешно решают задачи распознавания образов, прогнозирования и кластеризации.
2. Рекуррентные нейронные сети (с обратными связями). Здесь сигнал двигается и в прямом, и в обратном направлении. В итоге результат выхода способен возвращаться на вход. Выход нейрона определяется весовыми характеристиками и входными сигналами, плюс дополняется предыдущими выходами, снова вернувшимися на вход. Этим нейросетям присуща функция кратковременной памяти, на основании чего сигналы восстанавливаются и дополняются во время их обработки.
3. Радиально-базисные функции.
4. Самоорганизующиеся карты.

Но это далеко не все варианты классификации и виды нейронных сетей. Также их делят:
1. В зависимости от типов нейронов:
— однородные;
— гибридные.
2. В зависимости от метода нейронных сетей по обучению:
— обучение с учителем;
— без учителя;
— с подкреплением.
3. По типу входной информации нейронные сети бывают:
— аналоговые;
— двоичные;
— образные.
4. По характеру настройки синапсов:
— с фиксированными связями;
— с динамическими связями.

Ещё существуют понятия гетероассоциативные или автоассоциативные нейросети.

Схема и концепция работы

Представить принцип работы нейросети можно, не имея конкретных навыков. Общая схема или алгоритм следующий:
— на входной слой нейронов происходит поступление определённых данных;
— информация передаётся с помощью синапсов следующему слою, причём каждый синапс имеет собственный коэффициент веса, а любой следующий нейрон способен иметь несколько входящих синапсов;
— данные, полученные следующим нейроном, — это сумма всех данных для нейронных сетей, которые перемножены на коэффициенты весов (каждый на свой);
— полученное в итоге значение подставляется в функцию активации, в результате чего происходит формирование выходной информации;
— информация передаётся дальше до тех пор, пока не дойдёт до конечного выхода.

Как мы знаем, 1-й запуск нейросети не даст верных результатов, ведь она ещё не натренирована. Если мы говорим о понятии функции активации, то эта функция используется в целях нормализации входных данных. Этих функций бывает много, но хотелось бы выделить основные, имеющие самое широкое распространение. Главное отличие — диапазон значений, где они функционируют:
— линейная функция f(x) = x. Является наиболее простой из всех, должна применяться лишь для тестирования созданной нейросети либо передачи данных в исходной форме;
— сигмоид — более распространённая функция активации. Диапазон значений — от нуля до единицы. Также её называю логистической функцией;
— гиперболический тангенс. Метод нужен для охвата также и отрицательных значений. Когда их применение не предусмотрено, гиперболический тангенс не нужен.

Остаётся сказать, что для задания нейросети данных для дальнейшего оперирования ими, потребуются тренировочные сеты.

Как работают нейронные сети?

Искусственная нейронная сеть — совокупность нейронов, взаимодействующих друг с другом. Они способны принимать, обрабатывать и создавать данные. Это настолько же сложно представить, как и работу человеческого мозга. Нейронная сеть в нашем мозгу работает для того, чтобы вы сейчас могли это прочитать: наши нейроны распознают буквы и складывают их в слова.

Нейронная сеть включает в себя несколько слоёв нейронов, каждый из которых отвечает за распознавание конкретного критерия: формы, цвета, размера, текстуры, звука, громкости и т.д.

Год от года в результате миллионов экспериментов и тонн вычислений к простейшей сети добавлялись новые и новые слои нейронов. Они работают по очереди. Например, первый определяет, квадрат или не квадрат, второй понимает, квадрат красный или нет, третий вычисляет размер квадрата и так далее. Не квадраты, не красные и неподходящего размера фигуры попадают в новые группы нейронов и исследуются уже ими.

Для чего нужны нейросети?

Нейронные сети используются для решения сложных задач, которые требуют аналитических вычислений подобных тем, что делает человеческий мозг. Самыми распространенными применениями нейронных сетей является:

Классификация — распределение данных по параметрам. Например, на вход дается набор людей и нужно решить, кому из них давать кредит, а кому нет. Эту работу может сделать нейронная сеть, анализируя такую информацию как: возраст, платежеспособность, кредитная история и тд.
Предсказание — возможность предсказывать следующий шаг. Например, рост или падение акций, основываясь на ситуации на фондовом рынке.
Распознавание — в настоящее время, самое широкое применение нейронных сетей. Используется в Google, когда вы ищете фото или в камерах телефонов, когда оно определяет положение вашего лица и выделяет его и многое другое.

Область применения искусственных нейронных сетей с каждым годом все более расширяется, на сегодняшний день они используются в таких сферах как:

Машинное обучение (machine learning), представляющее собой разновидность искусственного интеллекта. В основе его лежит обучение ИИ на примере миллионов однотипных задач. В наше время машинное обучение активно внедряют поисковые системы Гугл, Яндекс, Бинг, Байду. Так на основе миллионов поисковых запросов, которые все мы каждый день вводим в Гугле, их алгоритмы учатся показывать нам наиболее релевантную выдачу, чтобы мы могли найти именно то, что ищем.
В роботехнике нейронные сети используются в выработке многочисленных алгоритмов для железных «мозгов» роботов.
Архитекторы компьютерных систем пользуются нейронными сетями для решения проблемы параллельных вычислений.
С помощью нейронных сетей математики могут разрешать разные сложные математические задачи.

Теперь, чтобы понять, как же работают нейронные сети, давайте взглянем на ее составляющие и их параметры.

Что такое нейрон?

Нейрон — это вычислительная единица, которая получает информацию, производит над ней простые вычисления и передает ее дальше. Они делятся на три основных типа: входной (синий), скрытый (красный) и выходной (зеленый):

Также есть нейрон смещения и контекстный нейрон. В том случае, когда нейросеть состоит из большого количества нейронов, вводят термин слоя. Соответственно, есть входной слой, который получает информацию, n скрытых слоев (обычно их не больше 3), которые ее обрабатывают и выходной слой, который выводит результат.

У каждого из нейронов есть 2 основных параметра:

входные данные (input data),
выходные данные (output data).

В случае входного нейрона: input=output. В остальных, в поле input попадает суммарная информация всех нейронов с предыдущего слоя, после чего, она нормализуется, с помощью функции активации (пока что просто представим ее f(x)) и попадает в поле output.

Что такое синапс?

Синапс это связь между двумя нейронами. У синапсов есть 1 параметр — вес. Благодаря ему, входная информация изменяется, когда передается от одного нейрона к другому. Допустим, есть 3 нейрона, которые передают информацию следующему. Тогда у нас есть 3 веса, соответствующие каждому из этих нейронов. У того нейрона, у которого вес будет больше, та информация и будет доминирующей в следующем нейроне (пример — смешение цветов).

На самом деле, совокупность весов нейронной сети или матрица весов — это своеобразный мозг всей системы. Именно благодаря этим весам, входная информация обрабатывается и превращается в результат.

Важно помнить, что во время инициализации нейронной сети, веса расставляются в случайном порядке.

Биологическая основа нейросвязей

В нашем мозге есть нейроны. Их около 86 миллиардов. Нейрон это клетка, соединенная с другими такими клетками. Клетки соединены друг с другом отростками. Всё это вместе напоминает своего рода сеть. Вот вам и нейронная сеть. Каждая клетка получает сигналы от других клеток. Далее обрабатывает их и сама отправляет сигнал другим клеткам.

Проще говоря нейрон получает сигнал (информацию), обрабатывает его (что то там решает, думает) и отправляет свой ответ дальше. Стрелки изображают связи-отростки по которым передается информация:

Вот так передавая друг другу сигналы, нейронная сеть приходит к какому либо решению. А мы то думали, что мы единолично все решаем! Нет, наше решение — это результат коллективной работы миллиарда нейронов.

На моей картинке стрелки обозначают связи нейронов. Связи бывают разные. Например стрелка внизу между нейроном 2 и 5 длинная. И значит сигнал от нейрона 2 до нейрона 5 будет дольше идти, чем например сигнал от нейрона 3 где стрелка вдвое короче. Да и вообще сигнал может затухнуть и прийти слабым. В биологии много всего интересного.

Но рассматривать всё это — как там думает нейрон, затухнет ли сигнал, когда он придет или не придет в IT не стали. А что голову морочить? И просто построили упрощенную модель.

В этой модели можно выделить две основные составляющие:

Алгоритм. В биологии нейрон думает. В программировании «думанье» заменяется алгоритмом — то есть набором команд. Например — если на вход пришла 1 отправь 0. Вот и все «мозги» нашего нейрона.
Вес решения. Все связи, затухания и т.д. решили заменить «весом». Вес это как сила решения, его важность. Это просто величина, чаще число. Нашему нейрону приходит решение с определенным весом, нашему нейрону приходит число. И если оно больше другого пришедшего числа то оно важнее. Это как пример.

Итого: есть алгоритм и есть вес решения. Это всё что нужно для построения простейшей нейросети.

Тренировочный сет

Тренировочный сет — это последовательность данных, которыми оперирует нейронная сеть. В нашем случае исключающего или (xor) у нас всего 4 разных исхода то есть у нас будет 4 тренировочных сета: 0xor0=0, 0xor1=1, 1xor0=1,1xor1=0.

Итерация

Это своеобразный счетчик, который увеличивается каждый раз, когда нейронная сеть проходит один тренировочный сет. Другими словами, это общее количество тренировочных сетов пройденных нейронной сетью.

Искусственные нейронные сети

Под искусственными нейронными сетями принято понимать вычислительные системы, имеющие способности к самообучению, постепенному повышению своей производительности. Основными элементами структуры нейронной сети являются:

Искусственные нейроны, представляющие собой элементарные, связанные между собой единицы.
Синапс – это соединение, которые используется для отправки-получения информации между нейронами.
Сигнал – собственно информация, подлежащая передаче.

Применение нейронных сетей

Машинное обучение (machine learning), представляющее собой разновидность искусственного интеллекта. В основе его лежит обучение ИИ на примере миллионов однотипных задач. В наше время машинное обучение активно внедряют поисковые системы Гугл, Яндекс, Бинг, Байду. Так на основе миллионов поисковых запросов, которые все мы каждый день вводим в Гугле, их алгоритмы учатся показывать нам наиболее релевантную выдачу, чтобы мы могли найти именно то, что ищем.
В роботехнике нейронные сети используются в выработке многочисленных алгоритмов для железных «мозгов» роботов.
Архитекторы компьютерных систем пользуются нейронными сетями для решения проблемы параллельных вычислений.
С помощью нейронных сетей математики могут разрешать разные сложные математические задачи.

Типы нейронных сетей

В целом для разных задач применяются различные виды и типы нейронных сетей, среди которых можно выделить:

сверточные нейронные сети,
реккурентные нейронные сети,
нейронную сеть Хопфилда.

Далее мы детально остановимся на некоторых из них.

Сверточные нейронные сети

Сверточные сети являются одними из самых популярных типов искусственных нейронных сетей. Так они доказали свою эффективность в распознавании визуальных образов (видео и изображения), рекомендательных системах и обработке языка.

Сверточные нейронные сети отлично масштабируются и могут использоваться для распознавания образов, какого угодно большого разрешения.
В этих сетях используются объемные трехмерные нейроны. Внутри одного слоя нейроны связаны лишь небольшим полем, названые рецептивным слоем.
Нейроны соседних слоев связаны посредством механизма пространственной локализации. Работу множества таких слоев обеспечивают особые нелинейные фильтры, реагирующие на все большее число пикселей.

Рекуррентные нейронные сети

Рекуррентными называют такие нейронные сети, соединения между нейронами которых, образуют ориентировочный цикл. Имеет такие характеристики:

У каждого соединения есть свой вес, он же приоритет.
Узлы делятся на два типа, вводные узлы и узлы скрытые.
Информация в рекуррентной нейронной сети передается не только по прямой, слой за слоем, но и между самими нейронами.
Важной отличительной особенностью рекуррентной нейронной сети является наличие так званой «области внимания», когда машине можно задать определенные фрагменты данных, требующие усиленной обработки.

Рекуррентные нейронные сети применяются в распознавании и обработке текстовых данных (в частотности на их основе работает Гугл переводчик, алгоритм Яндекс «Палех», голосовой помощник Apple Siri).

Где применяют нейронные сети?

Нейронные сети применяются для решения множества разных задач. Если мы говорим о простых проектах, то с ними справляется обычная компьютерная программа, если говорить об усложнённых задачах, требующих решения уравнений и прогнозирования, применяется компьютерная программа, поддерживающая статические методы обработки. Есть и совсем сложные задачи, то же распознавание образов. Здесь нужен другой подход, ведь в голове человека все эти процессы проходят неосознанно (при распознавании и запоминании образов человек делает это, если можно так сказать, сам по себе, то есть он не управляет соответствующими процессами в мозгу).

Собственно говоря, нейронные сети как раз для этого и созданы, чтобы помогать людям решать задачи со сложными и не до конца исследованными алгоритмами. Имеет значение и качество нейронных сетей.

Схема нейронной сети:

Сегодня нейронные сети применяются в следующих сферах: — распознавание образов (по этому направлению работают наиболее широко); — предсказание следующего шага (повышает эффективность и качество торговли на тех же фондовых рынках); — классификация входной информации по параметрам (с этой работой легко справляются кредитные роботы, способные быстро принять решение об одобрении или отказе по поводу кредита, используя для этого входные наборы разнообразных параметров).

Так как современные нейронные сети имеют очень большие способности и разные варианты использования, их популярность растёт, а развитие отрасли тоже идёт семимильными шагами. Их учат играть в компьютерные игры, узнавать голоса и т. д. По сути, искусственные сети создаются по принципу биологических, а значит, мы можем обучить их выполнению тех процессов, которые человек выполняет не вполне осознанно.

P. S. Одно дело читать, другое дело — практиковаться. Если вас интересует развитие навыков работы с современными нейронными сетями (neural networks) и вы хотели изучить различные связанные технологии из категории «нейро», ждём вас на наших курсах. Все занятия проходят онлайн, потребуется только компьютер и интернет. Специалистом может стать каждый

Обратное распространение

Суммарная ошибка (total_error) вычисляется как разность между ожидаемым значением «y» (из обучающего набора) и полученным значением «y_» (посчитанное на этапе прямого распространения ошибки), проходящих через функцию потерь (cost function).
Частная производная ошибки вычисляется по каждому весу (эти частные дифференциалы отражают вклад каждого веса в общую ошибку (total_loss)).
Затем эти дифференциалы умножаются на число, называемое скорость обучения или learning rate (η).

Полученный результат затем вычитается из соответствующих весов.

В результате получатся следующие обновленные веса:

w1 = w1 — (η * ∂(err) / ∂(w1))
w2 = w2 — (η * ∂(err) / ∂(w2))
w3 = w3 — (η * ∂(err) / ∂(w3))

Популярный мем о том, как Карлсон стал Data Science разработчиком

bias
Если вы знакомы с рядами Тейлора, обратное распространение ошибки имеет такой же конечный результат. Только вместо бесконечного ряда мы пытаемся оптимизировать только его первый член.

Частные производные

Разберем необходимость частных производных на примере.

Предположим, детей попросили бросить дротик в мишень, целясь в центр. Вот результаты:

Ошибка нескольких детей может уменьшиться, но общая ошибка все еще увеличивается.

Прямое распространение ошибки

Прямое распространение

Зададим начальные веса случайным образом:

Умножим входные данные на веса для формирования скрытого слоя:

h1 = (x1 * w1) + (x2 * w1)
h2 = (x1 * w2) + (x2 * w2)
h3 = (x1 * w3) + (x2 * w3)

y_ = fn(h1 , h2, h3)

Гиперпараметры

Глубокие нейронные сети

Более формально в deep learning:

Используется каскад (пайплайн, как последовательно передаваемый поток) из множества обрабатывающих слоев (нелинейных) для извлечения и преобразования признаков;
Основывается на изучении признаков (представлении информации) в данных без обучения с учителем. Функции более высокого уровня (которые находятся в последних слоях) получаются из функций нижнего уровня (которые находятся в слоях начальных слоях);
Изучает многоуровневые представления, которые соответствуют разным уровням абстракции; уровни образуют иерархию представления.

Пример

Рассмотрим однослойную нейронную сеть:

Здесь, обучается первый слой (зеленые нейроны), он просто передается на выход.

Следовательно, чем больше число скрытых слоев, тем больше возможности обучения сети.

Не следует путать с широкой нейронной сетью.

Пример:

Но

Главное — баланс

Обе требуют значительно большего количества данных для обучения, чтобы достичь минимальной желаемой точности;
Обе имеют экспоненциальную сложность;
Слишком глубокая нейронная сеть попытается сломать фундаментальные представления, но при этом она будет делать ошибочные предположения и пытаться найти псевдо-зависимости, которые не существуют;
Слишком широкая нейронная сеть будет пытаться найти больше признаков, чем есть. Таким образом, подобно предыдущей, она начнет делать неправильные предположения о данных.

Проклятье размерности

Из-за неправильных предположений появляется смещение. Высокое смещение может привести к тому, что алгоритм пропустит существенную взаимосвязь между признаками и целевыми переменными. Это явление называют недообучение.
От небольших отклонений в обучающем множестве из-за недостаточного изучения признаков увеличивается дисперсия. Высокая дисперсия ведет к переобучению, ошибки воспринимаются в качестве надежной информации.

Компромисс

Действительно,

Следовательно, как правило, невозможно иметь маленькое смещение и маленькую дисперсию одновременно.

Обучение нейронной сети

Один из главных и самый важный критерий – возможность обучения нейросети. В целом, нейросеть – это совокупность нейронов, через которые проходит сигнал. Если подать его на вход, то пройдя через тысячи нейронов, на выходе получится неизвестно что. Для преобразования нужно менять параметры сети, чтобы на выходе получились нужные результаты.

Входной сигнал изменить нельзя, сумматор выполняет функцию суммирования и изменить что-то в нем или вывести из системы не выйдет, так как это перестанет быть нейросетью. Остается одно – использовать коэффициенты или коррелирующие функции и применять их на веса связей. В этом случае можно дать определение обучения нейронной сети – это поиск набора весовых коэффициентов, которые при прохождении через сумматор позволят получить на выходе нужный сигнал.

Такую концепцию применяет и наш мозг. Вместо весов в нем используются синопсы, позволяющие усиливать или делать затухание входного сигнала. Человек обучается, благодаря изменению синапсов при прохождении электрохимического импульса в нейросети головного мозга.

Но есть один нюанс. Если же задать вручную коэффициенты весов, то нейросеть запомнит правильный выходной сигнал. При этом вывод информации будет мгновенным и может показаться, что нейросеть смогла быстро обучиться. И стоит немного изменить входной сигнал, как на выходе появятся неправильные, не логические ответы.

Поэтому, вместо указания конкретных коэффициентов для одного входного сигнала, можно создать обобщающие параметры с помощью выборки.

С помощью такой выборки можно обучать сеть, чтобы она выдавала корректные результаты. В этом моменте, можно поделить обучение нейросети на обучение с учителем и без учителя.

Обучение с учителем

Обучение таким способом подразумевает концепцию: даете выборку входных сигналов нейросети, получаете выходные и сравниваете с готовым решением.

Как готовить такие выборки:

Для опознавания лиц создать выборку из 5000-10000 фотографий (вход) и самостоятельно указать, какие содержат лица людей (выход, правильный сигнал).
Для прогнозирования роста или падения акций, выборка делается с помощью анализа данных прошлых десятилетий. Входными сигналами могут быть как состояние рынка в целом, так и конкретные дни.

Учителем не обязательно выступает человек. Сеть нужно тренировать сотнями и тысячами часов, поэтому в 99% случаев тренировкой занимается компьютерная программа.

Обучение без учителя

Концепция состоит в том, что делается выборка входных сигналов, но правильных ответов на выходе вы знать не можете.

Как происходит обучение? В теории и на практике, нейросеть начинает кластеризацию, то есть определяет классы подаваемых входных сигналов. Затем, она выдает сигналы различных типов, отвечающие за входные объекты.

Заключение

Целью этой статьи было вкратце познакомить новичков с глубокими нейросетями, объяснив тему простым языком. Упрощение математических расчётов и полное сосредоточение на функциональности позволит максимально эффективно использовать глубокое обучение для современных бизнес-проектов.

Источники

https://nuancesprog.ru/p/8421/
https://Mining-CryptoCurrency.ru/nejronnye-seti/
https://zen.yandex.ru/media/iteasy/chto-takoe-neiroseti-ins-i-kak-oni-rabotaiut-5ee3585169fe895ccbaa226b
https://habr.com/ru/post/312450/
https://otus.ru/nest/post/1263/
https://www.poznavayka.org/nauka-i-tehnika/neyronnyie-seti-ih-primenenie-rabota/
https://neurohive.io/ru/osnovy-data-science/osnovy-nejronnyh-setej-algoritmy-obuchenie-funkcii-aktivacii-i-poteri/

[свернуть]

Искусственная нейронная сеть (ИНС) (англ. Artificial neural network (ANN)) — упрощенная модель биологической нейронной сети, представляющая собой совокупность искусственных нейронов, взаимодействующих между собой.

Основные принципы работы нейронных сетей были описаны еще в 1943 году Уорреном Мак-Каллоком и Уолтером Питтсом^[1]. В 1957 году нейрофизиолог Фрэнк Розенблатт разработал первую нейронную сеть^[2], а в 2010 году большие объемы данных для обучения открыли возможность использовать нейронные сети для машинного обучения.

На данный момент нейронные сети используются в многочисленных областях машинного обучения и решают проблемы различной сложности.

Содержание

1 Структура нейронной сети
2 Виды нейронных сетей
- 2.1 Однослойные нейронные сети
- 2.2 Многослойные нейронные сети
- 2.3 Сети прямого распространения
- 2.4 Сети с обратными связями
3 Обучение нейронной сети
4 Перцептрон
- 4.1 История
- 4.2 Описание
- 4.3 Классификация перцептронов
- 4.4 Обучение перцептрона
- 4.5 Применение
- 4.6 Примеры кода
  - 4.6.1 Пример использования с помощью scikit-learn^[4]
  - 4.6.2 Пример использования с помощью tensorflow^[6]
  - 4.6.3 Пример на языке Java
5 См. также
6 Примечания
7 Источники информации

Структура нейронной сети

Хорошим примером биологической нейронной сети является человеческий мозг. Наш мозг — сложнейшая биологическая нейронная сеть, которая принимает информацию от органов чувств и каким-то образом ее обрабатывает (узнавание лиц, возникновение ощущений и т.д.). Мозг же, в свою очередь, состоит из нейронов, взаимодействующих между собой.

Для построения искусственной нейронной сети будем использовать ту же структуру. Как и биологическая нейронная сеть, искусственная состоит из нейронов, взаимодействующих между собой, однако представляет собой упрощенную модель. Так, например, искусственный нейрон, из которых состоит ИНС, имеет намного более простую структуру: у него есть несколько входов, на которых он принимает различные сигналы, преобразует их и передает другим нейронам. Другими словами, искусственный нейрон — это такая функция , которая преобразует несколько входных параметров в один выходной.

Как видно на рисунке справа, у нейрона есть входов , у каждого из которого есть вес , на который умножается сигнал, проходящий по связи. После этого взвешенные сигналы направляются в сумматор, который аггрегирует все сигналы во взвешенную сумму. Эту сумму также называют . Таким образом, .

Просто так передавать взвешенную сумму на выход достаточно бессмысленно — нейрон должен ее как-то обработать и сформировать адекватный выходной сигнал. Для этих целей используют функцию активации, которая преобразует взвешенную сумму в какое-то число, которое и будет являться выходом нейрона. Функция активации обозначается . Таким образом, выходов искусственного нейрона является .

Для разных типов нейронов используют самые разные функции активации, но одними из самых популярных являются:

Функция единичного скачка. Если , , а иначе ;
Сигмоидальная функция. , где параметр характеризует степень крутизны функции;
Гиперболический тангенс. , где параметр также определяет степень крутизны графика функции;
Rectified linear units (ReLU). .

Виды нейронных сетей

Разобравшись с тем, как устроен нейрон в нейронной сети, осталось понять, как их в этой сети располагать и соединять.

Как правило, в большинстве нейронных сетей есть так называемый входной слой, который выполняет только одну задачу — распределение входных сигналов остальным нейронам. Нейроны этого слоя не производят никаких вычислений. В остальном нейронные сети делятся на основные категории, представленные ниже.

Однослойные нейронные сети

Однослойная нейронная сеть (англ. Single-layer neural network) — сеть, в которой сигналы от входного слоя сразу подаются на выходной слой, который и преобразует сигнал и сразу же выдает ответ.

Как видно из схемы однослойной нейронной сети, представленной справа, сигналы поступают на входной слой (который не считается за слой нейронной сети), а затем сигналы распределяются на выходной слой обычных нейронов. На каждом ребре от нейрона входного слоя к нейрону выходного слоя написано число — вес соответствующей связи.

Многослойные нейронные сети

Многослойная нейронная сеть (англ. Multilayer neural network) — нейронная сеть, состоящая из входного, выходного и расположенного(ых) между ними одного (нескольких) скрытых слоев нейронов.

Помимо входного и выходного слоев эти нейронные сети содержат промежуточные, скрытые слои. Такие сети обладают гораздо большими возможностями, чем однослойные нейронные сети, однако методы обучения нейронов скрытого слоя были разработаны относительно недавно.

Работу скрытых слоев нейронов можно сравнить с работой большого завода. Продукт (выходной сигнал) на заводе собирается по стадиям на станках. После каждого станка получается какой-то промежуточный результат. Скрытые слои тоже преобразуют входные сигналы в некоторые промежуточные результаты.

Сети прямого распространения

Сети прямого распространения (англ. Feedforward neural network) (feedforward сети) — искусственные нейронные сети, в которых сигнал распространяется строго от входного слоя к выходному. В обратном направлении сигнал не распространяется.

Все сети, описанные выше, являлись сетями прямого распространения, как следует из определения. Такие сети широко используются и вполне успешно решают определенный класс задач: прогнозирование, кластеризация и распознавание.

Однако сигнал в нейронных сетях может идти и в обратную сторону.

Сети с обратными связями

Сети с обратными связями (англ. Recurrent neural network) — искусственные нейронные сети, в которых выход нейрона может вновь подаваться на его вход. В более общем случае это означает возможность распространения сигнала от выходов к входам.

В сетях прямого распространения выход сети определяется входным сигналом и весовыми коэффициентами при искусственных нейронах. В сетях с обратными связями выходы нейронов могут возвращаться на входы. Это означает, что выход какого-нибудь нейрона определяется не только его весами и входным сигналом, но еще и предыдущими выходами (так как они снова вернулись на входы).

Обучение нейронной сети

Обучение нейронной сети — поиск такого набора весовых коэффициентов, при котором входной сигнал после прохода по сети преобразуется в нужный нам выходной.

Это определение «обучения нейронной сети» соответствует и биологическим нейросетям. Наш мозг состоит из огромного количества связанных друг с другом нейросетей, каждая из которых в отдельности состоит из нейронов одного типа (с одинаковой функцией активации). Наш мозг обучается благодаря изменению синапсов — элементов, которые усиливают или ослабляют входной сигнал.

Если обучать сеть, используя только один входной сигнал, то сеть просто «запомнит правильный ответ», а как только мы подадим немного измененный сигнал, вместо правильного ответа получим бессмыслицу. Мы ждем от сети способности обобщать какие-то признаки и решать задачу на различных входных данных. Именно с этой целью и создаются обучающие выборки.

Обучающая выборка — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит обучение сети.

После обучения сети, то есть когда сеть выдает корректные результаты для всех входных сигналов из обучающей выборки, ее можно использовать на практике. Однако прежде чем сразу использовать нейронную сеть, обычно производят оценку качества ее работы на так называемой тестовой выборке.

Тестовая выборка — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит оценка качества работы сети.

Само обучение нейронной сети можно разделить на два подхода: обучение с учителем^{[на 28.01.19 не создан]} и обучение без учителя^{[на 28.01.19 не создан]}. В первом случае веса меняются так, чтобы ответы сети минимально отличались от уже готовых правильных ответов, а во втором случае сеть самостоятельно классифицирует входные сигналы.

Перцептрон

Перцептрон (англ. Perceptron) — простейший вид нейронных сетей. В основе лежит математическая модель восприятия информации мозгом, состоящая из сенсоров, ассоциативных и реагирующих элементов.

История

Идею перцептрона предложил нейрофизиолог Фрэнк Розенблатт. Он предложил схему устройства, моделирующего процесс человеческого восприятия, и назвал его «перцептроном» (от латинского perceptio — восприятие). В 1960 году Розенблатт представил первый нейрокомпьютер — «Марк-1», который был способен распознавать некоторые буквы английского алфавита.

Таким образом перцептрон является одной из первых моделей нейросетей, а «Марк-1» — первым в мире нейрокомпьютером.

Описание

В основе перцептрона лежит математическая модель восприятия информации мозгом. Разные исследователи по-разному его определяют. В самом общем своем виде (как его описывал Розенблатт) он представляет систему из элементов трех разных типов: сенсоров, ассоциативных элементов и реагирующих элементов.

Принцип работы перцептрона следующий:

Первыми в работу включаются S-элементы. Они могут находиться либо в состоянии покоя (сигнал равен 0), либо в состоянии возбуждения (сигнал равен 1);
Далее сигналы от S-элементов передаются A-элементам по так называемым S-A связям. Эти связи могут иметь веса, равные только -1, 0 или 1;
Затем сигналы от сенсорных элементов, прошедших по S-A связям, попадают в A-элементы, которые еще называют ассоциативными элементами;
- Одному A-элементу может соответствовать несколько S-элементов;
- Если сигналы, поступившие на A-элемент, в совокупности превышают некоторый его порог , то этот A-элемент возбуждается и выдает сигнал, равный 1;
- В противном случае (сигнал от S-элементов не превысил порога A-элемента), генерируется нулевой сигнал;
Далее сигналы, которые произвели возбужденные A-элементы, направляются к сумматору (R-элемент), действие которого нам уже известно. Однако, чтобы добраться до R-элемента, они проходят по A-R связям, у которых тоже есть веса (которые уже могут принимать любые значения, в отличие от S-A связей);
R-элемент складывает друг с другом взвешенные сигналы от A-элементов, а затем
- если превышен определенный порог, генерирует выходной сигнал, равный 1;
- eсли порог не превышен, то выход перцептрона равен -1.

Для элементов перцептрона используют следующие названия:

S-элементы называют сенсорами;
A-элементы называют ассоциативными;
R-элементы называют реагирующими.

Классификация перцептронов

Перцептрон с одним скрытым слоем (элементарный перцептрон, англ. elementary perceptron) — перцептрон, у которого имеется только по одному слою S, A и R элементов.

Однослойный персептрон (англ. Single-layer perceptron) — перцептрон, каждый S-элемент которого однозначно соответствует одному А-элементу, S-A связи всегда имеют вес 1, а порог любого А-элемента равен 1. Часть однослойного персептрона соответствует модели искусственного нейрона.

Его ключевая особенность состоит в том, что каждый S-элемент однозначно соответствует одному A-элементу, все S-A связи имеют вес, равный +1, а порог A элементов равен 1. Часть однослойного перцептрона, не содержащая входы, соответствует искусственному нейрону, как показано на картинке. Таким образом, однослойный перцептрон — это искусственный нейрон, который на вход принимает только 0 и 1.

Однослойный персептрон также может быть и элементарным персептроном, у которого только по одному слою S,A,R-элементов.

Многослойный перцептрон по Розенблатту (англ. Rosenblatt multilayer perceptron) — перцептрон, который содержит более 1 слоя А-элементов.

Многослойный перцептрон по Румельхарту (англ. Rumelhart multilater perceptron) — частный случай многослойного персептрона по Розенблатту, с двумя особенностями:

S-A связи могут иметь произвольные веса и обучаться наравне с A-R связями;
Обучение производится по специальному алгоритму, который называется обучением по методу обратного распространения ошибки.

Обучение перцептрона

Задача обучения перцептрона — подобрать такие , чтобы как можно чаще совпадал с — значением в обучающей выборке (здесь — функция активации). Для удобства, чтобы не тащить за собой свободный член , добавим в вектор $x$ лишнюю «виртуальную размерность» и будем считать, что . Тогда можно заменить на .

Чтобы обучать эту функцию, сначала надо выбрать функцию ошибки, которую потом можно оптимизировать градиентным спуском. Число неверно классифицированных примеров не подходит на эту кандидатуру, потому что эта функция кусочно-гладкая, с массой разрывов: она будет принимать только целые значения и резко меняться при переходе от одного числа неверно классифицированных примеров к другому. Поэтому использовать будем другую функцию, так называемый критерий перцептрона: , где — множество примеров, которые перцептрон с весами классифицирует неправильно.

Иначе говоря, мы минимизируем суммарное отклонение наших ответов от правильных, но только в неправильную сторону; верный ответ ничего не вносит в функцию ошибки. Умножение на здесь нужно для того, чтобы знак произведения всегда получался отрицательным: если правильный ответ −1, значит, перцептрон выдал положительное число (иначе бы ответ был верным), и наоборот. В результате у нас получилась кусочно-линейная функция, дифференцируемая почти везде, а этого вполне достаточно.

Теперь можно оптимизировать градиентным спуском. На очередном шаге получаем: .

Алгоритм такой — мы последовательно проходим примеры из обучающего множества, и для каждого :

если он классифицирован правильно, не меняем ничего;
а если неправильно, прибавляем .

Ошибка на примере при этом, очевидно, уменьшается, но, конечно, совершенно никто не гарантирует, что вместе с тем не увеличится ошибка от других примеров. Это правило обновления весов так и называется — правило обучения перцептрона, и это было основной математической идеей работы Розенблатта.

Применение

Решение задач классификации, если объекты классификации обладают свойством линейной разделимости;
Прогнозирование и распознавание образов;
Управление агентами^[3].

Примеры кода

Пример использования с помощью scikit-learn^[4]

Будем классифицировать с помощью перцептрона датасет MNIST^[5].

 # Load required libraries
 from sklearn import datasets
 from sklearn.preprocessing import StandardScaler
 from sklearn.linear_model import Perceptron      #Single-layer perceptron
 from sklearn.neural_network import MLPClassifier #Multilayer perceptron 
 from sklearn.model_selection import train_test_split
 from sklearn.metrics import accuracy_score
 import numpy as np

 # Load the mnist dataset
 mnist = datasets.load_digits()

 # Create our X and y data
 n_samples = len(mnist.images)
 X = mnist.images.reshape((n_samples, -1))
 y = mnist.target

 # Split the data into 70% training data and 30% test data
 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

 # Train the scaler, which standarizes all the features to have mean=0 and unit variance
 sc = StandardScaler()
 sc.fit(X_train)

 # Apply the scaler to the X training data
 X_train_std = sc.transform(X_train)

 # Apply the SAME scaler to the X test data
 X_test_std = sc.transform(X_test)

 # Create a single-layer perceptron object with the parameters: 40 iterations (epochs) over the data, and a learning rate of 0.1
 ppn = Perceptron(n_iter=40, eta0=0.1, random_state=0)
 # Create a multilayer perceptron object
 mppn = MLPClassifier(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=(256, 512, 128), random_state=1)

 # Train the perceptrons
 ppn.fit(X_train_std, y_train)
 mppn.fit(X_train_std, y_train)

 # Apply the trained perceptrons on the X data to make predicts for the y test data
 y_pred = ppn.predict(X_test_std)
 multi_y_pred = mppn.predict(X_test_std)

 # View the accuracies of the model, which is: 1 - (observations predicted wrong / total observations)
 print('Single-layer perceptron accuracy: %.4f' % accuracy_score(y_test, y_pred))
 print('Multilayer perceptron accuracy: %.4f' % accuracy_score(y_test, multi_y_pred))

Вывод:

 Single-layer perceptron accuracy: 0.9574
 Multilayer perceptron accuracy: 0.9759

Пример использования с помощью tensorflow^[6]

Будем классифицировать цифры из того же датасета MNIST.

 # Load required libraries
 import tensorflow as tf
 from tensorflow.examples.tutorials.mnist import input_data

 #Load MNIST dataset
 mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

 #placeholder for test data
 x = tf.placeholder(tf.float32, [None, 784])
 #placeholder for weights and bias
 W = tf.Variable(tf.zeros([784, 10]))
 b = tf.Variable(tf.zeros([10]))
 #tensorflow model
 y = tf.nn.softmax(tf.matmul(x, W) + b)
 
 #loss function
 y_ = tf.placeholder(tf.float32, [None, 10])
 cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))

 #gradient descent step
 train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

 init = tf.initialize_all_variables()
 sess = tf.Session()
 sess.run(init)
 for i in range(1000):
   batch_xs, batch_ys = mnist.train.next_batch(100)
   sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
 correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
 accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
 print("Accuracy: %s" % sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

Рисунок 8.
Правильные метки — 5, 4, 9, 7.
Результат классификации — 6, 6, 4, 4.

Вывод:

 Accuracy: 0.9164

На рисунке справа показаны четыре типичных изображения, на которых классификаторы ошибаются. Согласитесь, случаи действительно тяжелые.

Пример на языке Java

Пример классификации с применением weka.classifiers.functions.MultilayerPerceptron^[7]

Maven зависимость:

 <dependency>
   <groupId>nz.ac.waikato.cms.weka</groupId>
   <artifactId>weka-stable</artifactId>
   <version>3.8.0</version>
 </dependency>

 import weka.classifiers.functions.MultilayerPerceptron;
 import weka.core.converters.CSVLoader;
 import java.io.File;

 // read train & test datasets and build MLP classifier
 var trainds = new DataSource("etc/train.csv");
 var train   = trainds.getDataSet();
 train.setClassIndex(train.numAttributes() - 1);
 var testds = new DataSource("etc/test.csv");
 var test   = testds.getDataSet();
 test.setClassIndex(test.numAttributes() - 1);
 var mlp = new MultilayerPerceptron();
 mlp.buildClassifier(train);
 // Test the model
 var eTest = new Evaluation(train);
 eTest.evaluateModel(mlp, test);
 // Print the result à la Weka explorer:
 var strSummary = eTest.toSummaryString();
 System.out.println(strSummary);

См. также

Сверточные нейронные сети
Рекуррентные нейронные сети
Рекурсивные нейронные сети^{[на 28.01.19 не создан]}

Примечания

↑ Artificial neuron, Wikipedia
↑ Perceptron, Wikipedia
↑ Применения перцептрона, Wikipedia
↑ Библиотека scikit-learn для Python
↑ Датасет MNIST
↑ Библиотека tensorflow для Python
↑ Weka, MLP

Источники информации

Сергей Николенко, Артур Кадурин, Екатерина Архангельская. Глубокое обучение. Погружение в мир нейронных сетей. — «Питер», 2018. — С. 93-123.
Нейронные сети — учебник

В этой статье вы получите ряд разъяснений и рекомендаций, которые пригодятся вам при создании нейронной сети. Также будут предоставлены полезные ссылки для самостоятельного изучения. Материал предназначен для начинающих. Что же, не будем терять времени!

Шаг 1. Поговорим о нейронах и методах прямого распространения

Прежде чем начать разговор о нейросетях и о том, как создать и обучить нейросеть, нужно сначала немного разобраться с тем, что такое один нейрон. Здесь всё достаточно просто: нейрон принимает несколько значений, а возвращает только одно, что значит, что он похож на функцию.

Теперь для наилучшего понимания давайте посмотрим на картинку ниже. Там показан круг — это искусственный нейрон. Что он делает? Он получает 5, а возвращает 1. Под вводом понимается сумма трёх синапсов, соединённых с нейроном (это три стрелки слева).

В левой части у нас находятся два входных значения (выделены зелёным цветом) и одно смещение (выделено коричневым цветом).

Входные данные могут быть численными представлениями 2-х различных свойств. К примеру, когда создаёшь спам-фильтр, они могут означать наличие больше чем одного слова, написанного прописными буквами, и наличие слова «Виагра».

Также следует понимать, что входные значения умножаются на собственные так называемые «веса» — в нашем случае это 7 и 3 (выделены синим).

Позже полученные значения складываются со смещением, и получается число 5, которое у нас выделено красным. Именно так и выглядит ввод искусственного нейрона.

Идём далее. Нейрон выполняет вычисление, выдавая выходное значение. Мы получили 1, так как именно единице равно округлённое значение сигмоиды в точке 5. Если, опять же, вспомнить про спам-фильтр, то факт вывода единицы означал бы, что текст был помечен нейроном в качестве спама.

Объединив эти нейроны, вы получите в итоге прямо распространяющуюся нейросеть. В ней процесс идёт от ввода к выводу и через нейроны, которые соединены синапсами.

Для наилучшего понимания этого процесса посмотрите серию видео на английском, от Welch Labs.

Шаг 2. Сигмоида

Прежде чем приступить к следующему шагу, было бы неплохо ознакомиться с 4-й неделей курса по Machine Learning от Coursera — она как раз посвящена нейросетям и помогла бы вам разобраться в особенностях и принципах их работы. Да, этот курс слишком сильно углубляется в математику, плюс основан на Octave, хотя многие предпочитают язык программирования Python. Но все же там можно почерпнуть много полезных знаний.

Вернёмся к нашей сигмоиде. Дело в том, что она фигурирует во многих аспектах нейронных сетей. Её описание вы можете посмотреть, к примеру, здесь. Но на одной теории, сами понимаете, далеко не уедешь. Именно поэтому для наилучшего понимания следует создавать её самостоятельно. Чтобы это сделать, необходимо написать реализацию алгоритма логистической регрессии, использующего сигмоиду.

Если честно, это может занять целый день, причём результат будет далёк от идеального. Вот, к примеру, как с этим справился Per Harald Borgen, англоязычная статья которого стала основой материала, который вы сейчас читаете. Но главное здесь не в том, чтобы сделать всё идеально, а в том, чтобы разобраться, как всё работает. И понять, как устроена сигмоида.

Шаг 3. О методе обратного распространения ошибки

Понимание принципа работы нейронной сети, начиная от ввода, заканчивая выводом, вряд ли вызовет у вас затруднения. Намного тяжелее понять, каким образом нейронная сеть обучается, используя для этого наборы данных. Один из применяемых принципов называют методом обратного распространения ошибки.

Если говорить коротко, то вы оцениваете, насколько сильно ошиблась нейросеть, а потом изменяете вес входных значений (на первой картинке это синие числа).

Собственно говоря, процесс движется от конца к началу, ведь мы начинаем с конца сети и смотрим, как сильно догадка сети отклоняется от истины. Затем мы двигаемся назад, изменяя веса, и так до тех пор, пока не дойдём до ввода. А для вычисления всего этого вручную вам потребуется знание математического анализа. Однако вы можете на заморачиваться и использовать библиотеки, которые всё посчитают за вас.

Если вас интересуют англоязычные источники, которые помогут разобраться в данном методе, то хорошо известны следующие:
• A Step by Step Backpropagation Example;
• Hacker’s guide to Neural Networks;
• Using neural nets to recognize handwritten digits.

Однако учтите, что читая первые 2 статьи, вам обязательно придётся кодить самому, что поможет в дальнейшем. Избегать этого не рекомендуется, ведь в нейронных сетях невозможно разобраться, не практикуя. В 3-й статье находится материал размером с книгу, больше напоминающую энциклопедию. Зато в ней даны подробные разъяснения важнейших принципов работы нейронных сетей. К примеру, вы изучите такие определения, как функция стоимости, градиентный спуск, функция активации, скрытые слои, выходные и входные слои и т. д. После освоения такого материала вы достигнете более высокого уровня понимания.

Шаг 4. Создание своей нейросети. Как написать нейронную сеть? Пишем и обучаем

Читая разные статьи и руководства, вы так или иначе будете создавать небольшие нейросети. Сегодня сказано и рассказано много о соответствующих моделях, задачах и способах их решения. Некоторые статьи являются сложными, а некоторые простыми, понятными для любого человека. И все это очень эффективно для процесса обучения.

Пример очень полезной информации можно найти здесь. В этом материале удивительное количество знаний сжато до 11 строк кода.

Прочитав вышеупомянутую статью и реализовав приведённые в ней примеры самостоятельно, вы закроете много пробелов в знаниях, а когда всё получится, почувствуете себя суперчеловеком)).

Что ещё? Ну, при реализации многих примеров используются векторные вычисления, поэтому понимание линейной алгебры тоже потребуется. Если же интересуют нейронные сети посложнее, то вот вам новое руководство.

С его помощью вы сможете как написать свою нейросеть, так и поэкспериментировать с уже созданными. Довольно забавным бывает найти нужный набор данных, а потом проверить разные предположения с помощью нескольких нейросетей.

Кстати, если интересуют хорошие наборы данных, вы можете посетить этот сайт.

Чем раньше вы начнёте свои эксперименты, тем лучше. Будет кстати и изучение Python-библиотек для программирования нейронных сетей: Theano, Lasagne, Nolearn. А ещё лучше — попробовать записаться на курс «Нейронные сети на Python» в OTUS. С его помощью вы освоите архитектуру нейронных сетей, узнаете методы их обучения и общие особенности реализации. Остается лишь решиться и приняться за дело.

По материалам статьи «Learning How To Code Neural Networks».

Источник