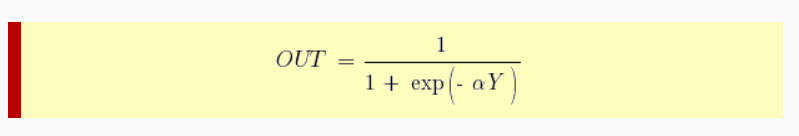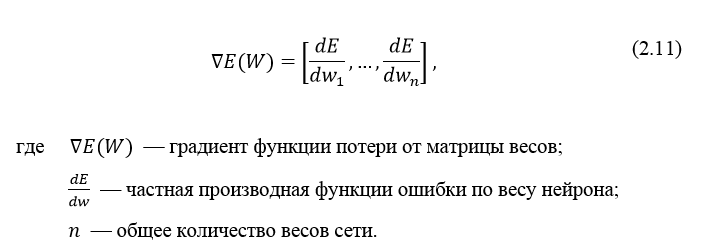Алгоритм обратного распространения ошибки используется

Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.

Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.

Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(\ldots (g_1(x)) \ldots))$, то $\frac{\partial f}{\partial x} = \frac{\partial g_m}{\partial g_{m-1}}\frac{\partial g_{m-1}}{\partial g_{m-2}}\ldots \frac{\partial g_2}{\partial g_1}\frac{\partial g_1}{\partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $\frac{\partial g_m}{\partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.

Backpropagation в одномерном случае

В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид

$$f(w_0) = g_m(g_{m-1}(\ldots g_1(w_0)\ldots)),$$

где все $g_i$ скалярные. Тогда

$$f'(w_0) = g_m'(g_{m-1}(\ldots g_1(w_0)\ldots))\cdot g’_{m-1}(g_{m-2}(\ldots g_1(w_0)\ldots))\cdot\ldots \cdot g’_1(w_0)$$

Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем

$$g_1(w_0), g_2(g_1(w_0)),\ldots,g_{m-1}(\ldots g_1(w_0)\ldots),$$

то мы действуем следующим образом:

• берём производную $g_m$ в точке $g_{m-1}(\ldots g_1(w_0)\ldots)$;

• умножаем на производную $g_{m-1}$ в точке $g_{m-2}(\ldots g_1(w_0)\ldots)$;

• и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.

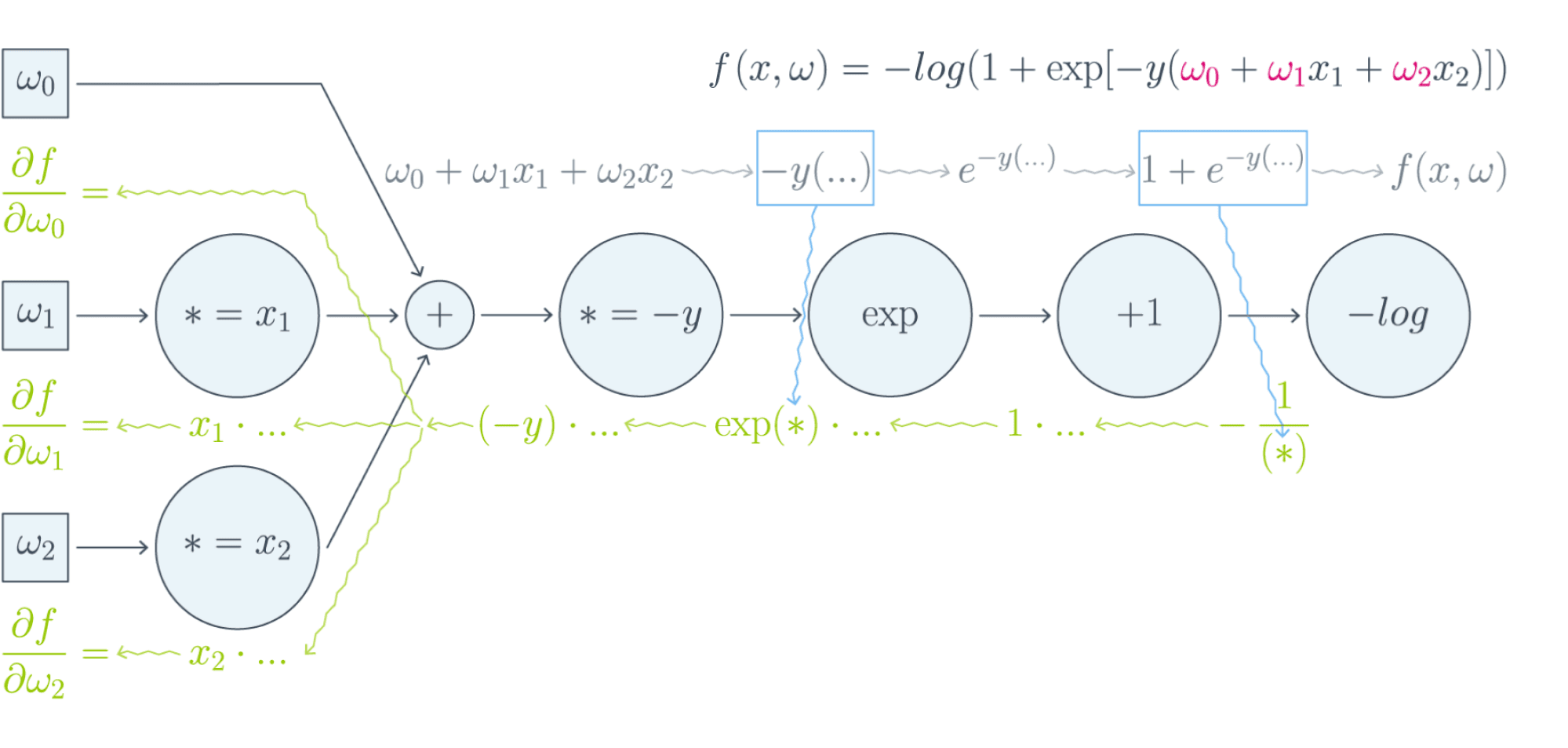
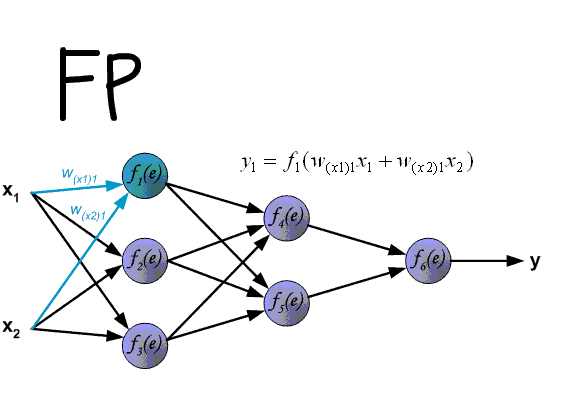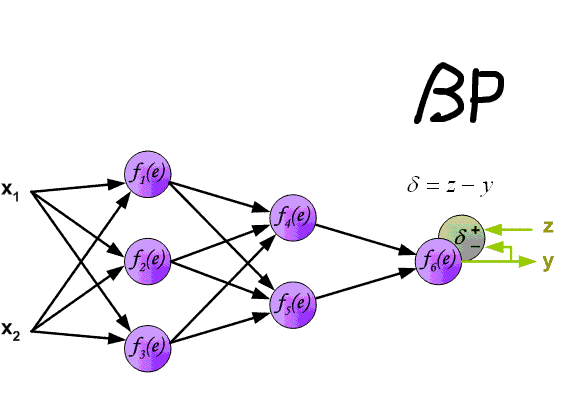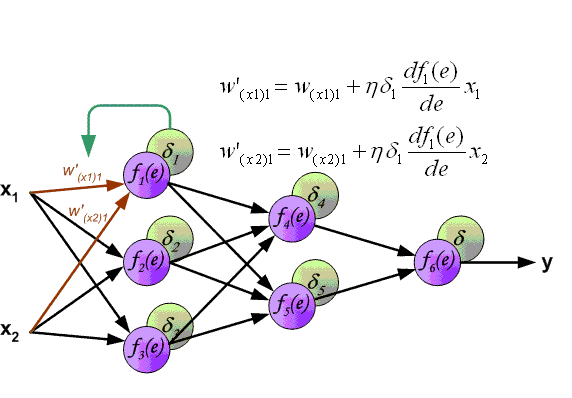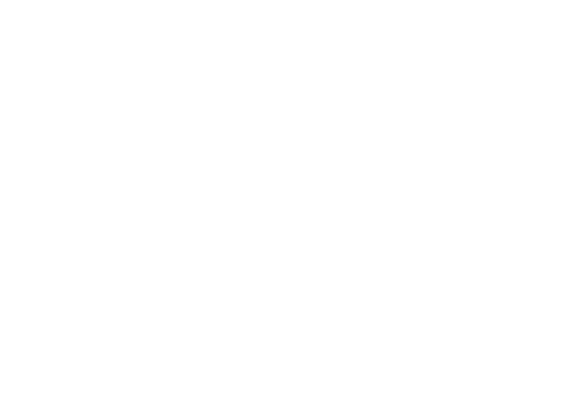
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):

Собирая все множители вместе, получаем:

$$\frac{\partial f}{\partial w_0} = (-y)\cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}\cdot\frac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$

$$\frac{\partial f}{\partial w_1} = x_1\cdot(-y)\cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}\cdot\frac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$

$$\frac{\partial f}{\partial w_2} = x_2\cdot(-y)\cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}\cdot\frac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$

Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.

Почему же нельзя просто пойти и начать везде вычислять производные?

В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $N\times M$ и $N\times K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $\frac{\partial\mathcal{L}}{\partial X^{r+1}_{ij}}$ функции потерь $\mathcal{L}$, тогда

$$\frac{\partial\mathcal{L}}{\partial X^{r}_{st}} = \sum_{i,j}\frac{\partial f^{r+1}_{ij}}{\partial X^{r}_{st}}\frac{\partial\mathcal{L}}{\partial X^{r+1}_{ij}}$$

И мы видим, что, хотя оба градиента $\frac{\partial\mathcal{L}}{\partial X_{ij}^{r+1}}$ и $\frac{\partial\mathcal{L}}{\partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $\frac{\partial f_{ij}^{r+1}}{\partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $\frac{\partial f^{r+1}}{\partial X^{r}}$ рассматривать не как вычисляемые объекты $\frac{\partial f_{ij}^{r+1}}{\partial X_{st}^{r}}$, а как преобразования, которые превращают $\frac{\partial\mathcal{L}}{\partial X_{ij}^{r+1}}$ в $\frac{\partial\mathcal{L}}{\partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.

  Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?

Встречный вопрос. Найдите производную функции по вектору $x$:

$$f(x) = x^TAx,\ A\in Mat_{n}{\mathbb{R}}\text{ — матрица размера }n\times n$$

А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.

Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.

Градиент сложной функции

Напомним, что формула производной сложной функции выглядит следующим образом:

$$\left[D_{x_0} (\color{#5002A7}{u} \circ \color{#4CB9C0}{v}) \right](h) = \color{#5002A7}{\left[D_{v(x_0)} u \right]} \left( \color{#4CB9C0}{\left[D_{x_0} v\right]} (h)\right)$$

Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда

$$\left[D_{x_0} f \right] (x-x_0) = \langle\nabla_{x_0} f, x-x_0\rangle.$$

С другой стороны,

$$\left[D_{h(x_0)} g \right] \left(\left[D_{x_0}h \right] (x-x_0)\right) = \langle\nabla_{h_{x_0}} g, \left[D_{x_0} h\right] (x-x_0)\rangle = \langle\left[D_{x_0} h\right]^* \nabla_{h(x_0)} g, x-x_0\rangle.$$

То есть $\color{#FFC100}{\nabla_{x_0} f} = \color{#348FEA}{\left[D_{x_0} h \right]}^* \color{#FFC100}{\nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $\nabla_{h(x_0)} g$.

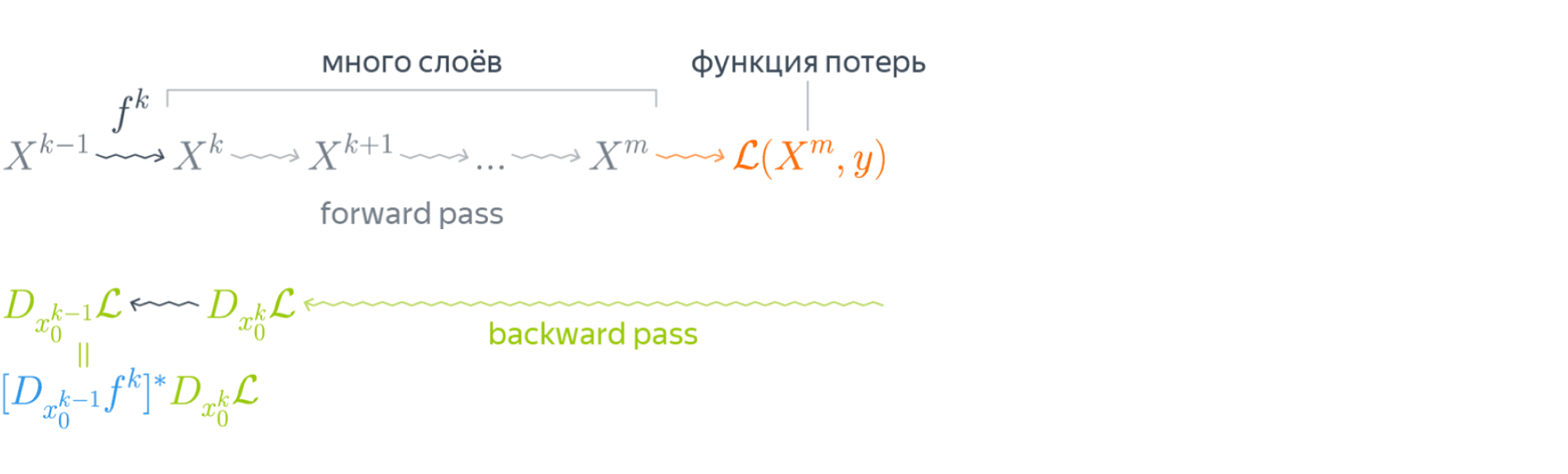
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:

Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.

Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.

Градиенты для типичных слоёв

Рассмотрим несколько важных примеров.

Примеры

1. $f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:

   $$v\begin{pmatrix}
   x_1 \\
   \vdots\\
   x_N
   \end{pmatrix}
   = \begin{pmatrix}
   v(x_1)\\
   \vdots\\
   v(x_N)
   \end{pmatrix}$$

   Тогда, как мы знаем,

   $$\left[D_{x_0} f\right] (h) = \langle\nabla_{x_0} f, h\rangle = \left[\nabla_{x_0} f\right]^T h.$$

   Следовательно,

   $$
   \left[D_{v(x_0)} u\right] \left( \left[ D_{x_0} v\right] (h)\right) = \left[\nabla_{v(x_0)} u\right]^T \left(v'(x_0) \odot h\right) =\\
   $$

   $$
   = \sum\limits_i \left[\nabla_{v(x_0)} u\right]_i v'(x_{0i})h_i
   = \langle\left[\nabla_{v(x_0)} u\right] \odot v'(x_0), h\rangle.
   ,$$

   где $\odot$ означает поэлементное перемножение. Окончательно получаем

   $$\color{#348FEA}{\nabla_{x_0} f = \left[\nabla_{v(x_0)}u\right] \odot v'(x_0) = v'(x_0) \odot \left[\nabla_{v(x_0)} u\right]}$$

   Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $\frac{\partial f}{\partial x_i} = \sum_j\big(\frac{\partial z_j}{\partial x_i}\big)\cdot\big(\frac{\partial h}{\partial z_j}\big)$. В этом случае матрица $\big(\frac{\partial z_j}{\partial x_i}\big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $\big(\frac{\partial z_j}{\partial x_i}\big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.

2. $f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,

   $$\left[D_{X_0} f \right] (X-X_0) = \text{tr}, \left(\left[\nabla_{X_0} f\right]^T (X-X_0)\right).$$

   Тогда

   $$
   \left[ D_{X_0W} g \right] \left(\left[D_{X_0} \left( \ast W\right)\right] (H)\right) =
   \left[ D_{X_0W} g \right] \left(HW\right)=\\
   $$ $$
   = \text{tr}\, \left( \left[\nabla_{X_0W} g \right]^T \cdot (H) W \right) =\\
   $$ $$
   =
   \text{tr} \, \left(W \left[\nabla_{X_0W} (g) \right]^T \cdot (H)\right) = \text{tr} \, \left( \left[\left[\nabla_{X_0W} g\right] W^T\right]^T (H)\right)
   $$

   Здесь через $\ast W$ мы обозначили отображение $Y \hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:

   $$
   \text{tr} , (A B C) = \text{tr} , (C A B),
   $$

   где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем

   $$\color{#348FEA}{\nabla_{X_0} f = \left[\nabla_{X_0W} (g) \right] \cdot W^T}$$

3. $f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем

   $$
   \left[D_{W_0} f \right] (H) = \text{tr} , \left( \left[\nabla_{W_0} f \right]^T (H)\right)
   $$

   Тогда

   $$
   \left[D_{XW_0} g \right] \left( \left[D_{W_0} \left(X \ast\right) \right] (H)\right) = \left[D_{XW_0} g \right] \left( XH \right) = \
   $$ $$
   = \text{tr} , \left( \left[\nabla_{XW_0} g \right]^T \cdot X (H)\right) =
   \text{tr}, \left(\left[X^T \left[\nabla_{XW_0} g \right] \right]^T (H)\right)
   $$

   Здесь через $X \ast$ обозначено отображение $Y \hookrightarrow XY$. Значит,

   $$\color{#348FEA}{\nabla_{X_0} f = X^T \cdot \left[\nabla_{XW_0} (g)\right]}$$

4. $f(X) = g(softmax(X))$, где $X$ — матрица $N\times K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$

   $$softmax(x) = \left(\frac{e^{x_1}}{\sum_te^{x_t}},\ldots,\frac{e^{x_K}}{\sum_te^{x_t}}\right)$$

   В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $\frac{\partial s_l}{\partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = \frac{e^{x_l}} {\sum_te^{x_t}}$. Нетрудно проверить, что

   $$\frac{\partial s_l}{\partial x_j} = \begin{cases}
   s_j(1 — s_j),\ & j = l,\
   -s_ls_j,\ & j\ne l
   \end{cases}$$

   Так как softmax вычисляется независимо от каждой строчки, то

   $$\frac{\partial s_{rl}}{\partial x_{ij}} = \begin{cases}
   s_{ij}(1 — s_{ij}),\ & r=i, j = l,\
   -s_{il}s_{ij},\ & r = i, j\ne l,\
   0,\ & r\ne i
   \end{cases},$$

   где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.

   Теперь пусть $\nabla_{rl} = \nabla g = \frac{\partial\mathcal{L}}{\partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда

   $$\frac{\partial\mathcal{L}}{\partial x_{ij}} = \sum_{r,l}\frac{\partial s_{rl}}{\partial x_{ij}} \nabla_{rl}$$

   Так как $\frac{\partial s_{rl}}{\partial x_{ij}} = 0$ при $r\ne i$, мы можем убрать суммирование по $r$:

   $$\ldots = \sum_{l}\frac{\partial s_{il}}{\partial x_{ij}} \nabla_{il} = -s_{i1}s_{ij}\nabla_{i1} — \ldots + s_{ij}(1 — s_{ij})\nabla_{ij}-\ldots — s_{iK}s_{ij}\nabla_{iK} =$$

   $$= -s_{ij}\sum_t s_{it}\nabla_{it} + s_{ij}\nabla_{ij}$$

   Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:

   $$\begin{multline*}
   \color{#348FEA}{\nabla_{X_0}f =}\\
   \color{#348FEA}{= -softmax(X_0) \odot \text{sum}\left(
   softmax(X_0)\odot\nabla_{softmax(X_0)}g, \text{ axis = 1}
   \right) +}\\
   \color{#348FEA}{softmax(X_0)\odot \nabla_{softmax(X_0)}g}
   \end{multline*}
   $$

Backpropagation в общем виде

Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:

1. Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, \ldots, X^m = \widehat{y}$.
2. Вычислить все градиенты с помощью backward pass.
3. С помощью полученных градиентов совершить шаг SGD.

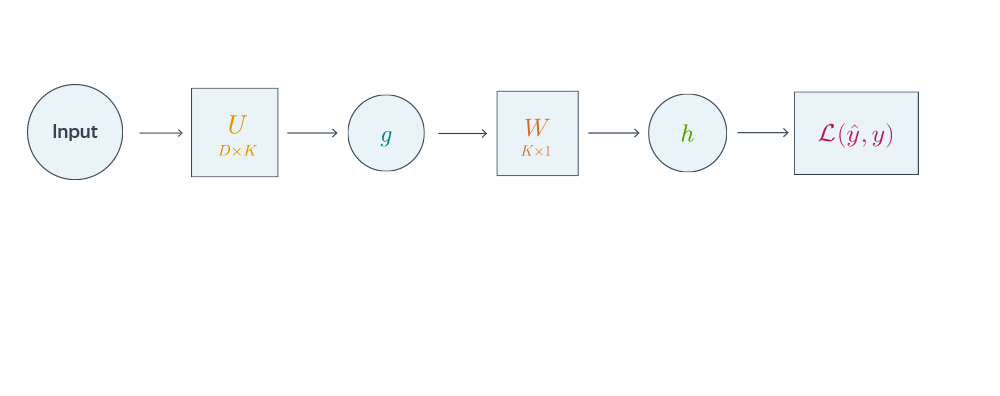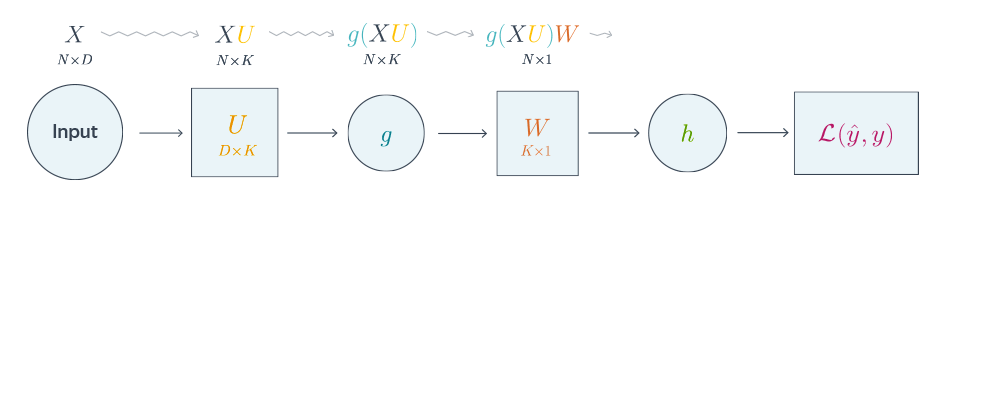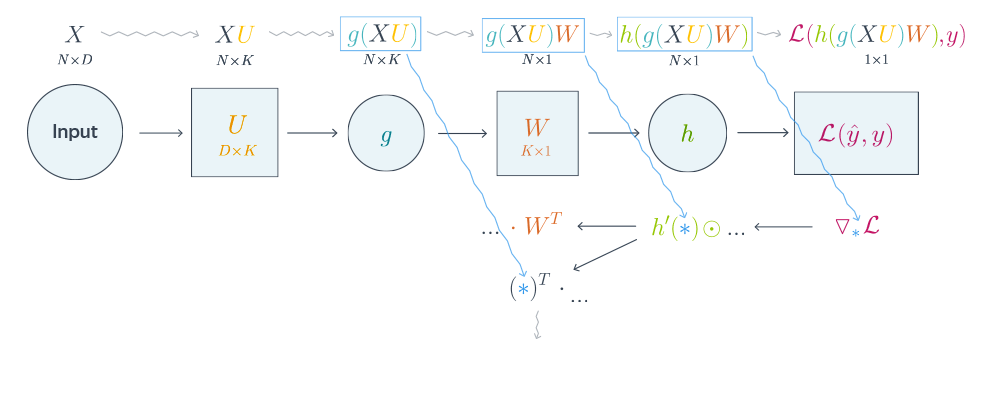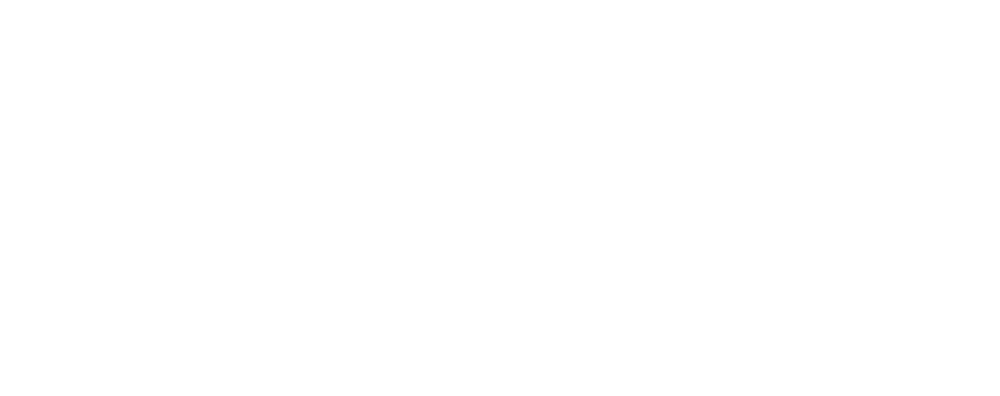
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.

Обучаемые параметры – матрицы $U$ и $W$. Как найти градиенты по ним в точке $U_0, W_0$?

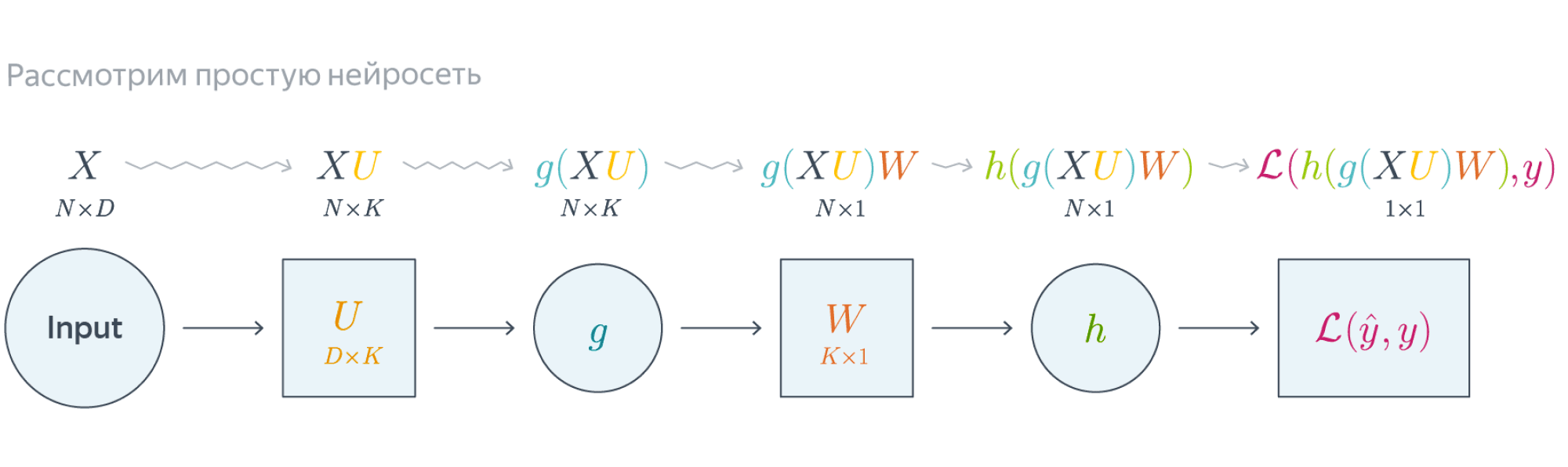
$$\nabla_{W_0}\mathcal{L} = \nabla_{W_0}{\left({\vphantom{\frac12}\mathcal{L}\circ h\circ\left[W\mapsto g(XU_0)W\right]}\right)}=$$

$$=g(XU_0)^T\nabla_{g(XU_0)W_0}(\mathcal{L}\circ h) = \underbrace{g(XU_0)^T}_{k\times N}\cdot
\left[\vphantom{\frac12}\underbrace{h’\left(\vphantom{\int_0^1}g(XU_0)W_0\right)}_{N\times 1}\odot
\underbrace{\nabla_{h\left(\vphantom{\int_0^1}g(XU_0)W_0\right)}\mathcal{L}}_{N\times 1}\right]$$

Итого матрица $k\times 1$, как и $W_0$

$$\nabla_{U_0}\mathcal{L} = \nabla_{U_0}\left(\vphantom{\frac12}
\mathcal{L}\circ h\circ\left[Y\mapsto YW_0\right]\circ g\circ\left[ U\mapsto XU\right]
\right)=$$

$$=X^T\cdot\nabla_{XU^0}\left(\vphantom{\frac12}\mathcal{L}\circ h\circ [Y\mapsto YW_0]\circ g\right) =$$

$$=X^T\cdot\left(\vphantom{\frac12}g'(XU_0)\odot
\nabla_{g(XU_0)}\left[\vphantom{\in_0^1}\mathcal{L}\circ h\circ[Y\mapsto YW_0\right]
\right)$$

$$=\ldots = \underset{D\times N}{X^T}\cdot\left(\vphantom{\frac12}
\underbrace{g'(XU_0)}_{N\times K}\odot
\underbrace{\left[\vphantom{\int_0^1}\left(
\underbrace{h’\left(\vphantom{\int_0^1}g(XU_0)W_0\right)}_{N\times1}\odot\underbrace{\nabla_{h(\vphantom{\int_0^1}g\left(XU_0\right)W_0)}\mathcal{L}}_{N\times 1}
\right)\cdot \underbrace{W^T}_{1\times K}\right]}_{N\times K}
\right)$$

Итого $D\times K$, как и $U_0$

Схематически это можно представить следующим образом:

Backpropagation для двуслойной нейронной сети

Подробнее о предыдущих вычисленияхЕсли вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = \sigma$).

Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:

$$
\widehat{y} = \sigma(X^1 W^2) = \sigma\Big(\big(\sigma(X^0 W^1 )\big) W^2 \Big).
$$

Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.

Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = \sigma(X^0 W^1_0)$, $X^3 = \sigma(X^0 W^1_0) W^2_0$, $X^4 = \sigma(\sigma(X^0 W^1_0) W^2_0) = \widehat{y}$. Они понадобятся нам дальше.

Для полученных предсказаний вычисляется значение функции потерь:

$$
l = \mathcal{L}(y, \widehat{y}) = y \log(\widehat{y}) + (1-y) \log(1-\widehat{y}).
$$

Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.

1. Градиент $\mathcal{L}$ по предсказаниям имеет вид

   $$
   \nabla_{\widehat{y}}l = \frac{y}{\widehat{y}} — \frac{1 — y}{1 — \widehat{y}} = \frac{y — \widehat{y}}{\widehat{y} (1 — \widehat{y})},
   $$

   где, напомним, $ \widehat{y} = \sigma(X^3) = \sigma\Big(\big(\sigma(X^0 W^1_0 )\big) W^2_0 \Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).

2. Следующий слой — поэлементное взятие $\sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $\sigma$, в которую подставлено предыдущее промежуточное представление:

   $$
   \nabla_{X^3}l = \sigma'(X^3)\odot\nabla_{\widehat{y}}l = \sigma(X^3)\left( 1 — \sigma(X^3) \right) \odot \frac{y — \widehat{y}}{\widehat{y} (1 — \widehat{y})} =
   $$

   $$
   = \sigma(X^3)\left( 1 — \sigma(X^3) \right) \odot \frac{y — \sigma(X^3)}{\sigma(X^3) (1 — \sigma(X^3))} =
   y — \sigma(X^3)
   $$

3. Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:

   $$
   \color{blue}{\nabla_{W^2_0}l} = (X^2)^T\cdot \nabla_{X^3}l = (X^2)^T\cdot(y — \sigma(X^3)) =
   $$

   $$
   = \color{blue}{\left( \sigma(X^0W^1_0) \right)^T \cdot (y — \sigma(\sigma(X^0W^1_0)W^2_0))}
   $$

   Аналогичным образом

   $$
   \nabla_{X^2}l = \nabla_{X^3}l\cdot (W^2_0)^T = (y — \sigma(X^3))\cdot (W^2_0)^T =
   $$

   $$
   = (y — \sigma(X^2W_0^2))\cdot (W^2_0)^T
   $$

4. Следующий слой — снова взятие $\sigma$.

   $$
   \nabla_{X^1}l = \sigma'(X^1)\odot\nabla_{X^2}l = \sigma(X^1)\left( 1 — \sigma(X^1) \right) \odot \left( (y — \sigma(X^2W_0^2))\cdot (W^2_0)^T \right) =
   $$

   $$
   = \sigma(X^1)\left( 1 — \sigma(X^1) \right) \odot\left( (y — \sigma(\sigma(X^1)W_0^2))\cdot (W^2_0)^T \right)
   $$

5. Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:

   $$
   \color{blue}{\nabla_{W^1_0}l} = (X^0)^T\cdot \nabla_{X^1}l = (X^0)^T\cdot \big( \sigma(X^1) \left( 1 — \sigma(X^1) \right) \odot (y — \sigma(\sigma(X^1)W_0^2))\cdot (W^2_0)^T\big) =
   $$

   $$
   = \color{blue}{(X^0)^T\cdot\big(\sigma(X^0W^1_0)\left( 1 — \sigma(X^0W^1_0) \right) \odot (y — \sigma(\sigma(X^0W^1_0)W_0^2))\cdot (W^2_0)^T\big) }
   $$

Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.

Автоматизация и autograd

Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}\mapsto X^k$ с параметрами $W^k$ уметь:

• превращать $\nabla_{X^k_0}\mathcal{L}$ в $\nabla_{X^{k-1}_0}\mathcal{L}$ (градиент по выходу в градиент по входу);
• считать градиент по его параметрам $\nabla_{W^k_0}\mathcal{L}$.

При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.

Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).

Но это лишь начало

Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.

Применение алгоритма обратного распространения ошибки — один из известных методов, используемых для глубокого обучения нейронных сетей прямого распространения (такие сети ещё называют многослойными персептронами). Этот метод относят к методу обучения с учителем, поэтому требуется задавать в обучающих примерах целевые значения. В этой статье мы рассмотрим, что собой представляет метод обратного распространения ошибки, как он реализуется, каковы его плюсы и минусы.

Сегодня нейронные сети прямого распространения используются для решения множества сложных задач. Если говорить об обучении нейронных сетей методом обратного распространения, то тут пользуются двумя проходами по всем слоям нейросети: прямым и обратным. При выполнении прямого прохода осуществляется подача входного вектора на входной слой сети, после чего происходит распространение по нейронной сети от слоя к слою. В итоге должна осуществляться генерация набора выходных сигналов — именно он, по сути, является реакцией нейронной сети на этот входной образ. При прямом проходе все синаптические веса нейросети фиксированы. При обратном проходе все синаптические веса настраиваются согласно правил коррекции ошибок, когда фактический выход нейронной сети вычитается из желаемого, что приводит к формированию сигнала ошибки. Такой сигнал в дальнейшем распространяется по сети, причём направление распространения обратно направлению синаптических связей. Именно поэтому соответствующий метод и называют алгоритмом с обратно распространённой ошибкой. Синаптические веса настраивают с целью наибольшего приближения выходного сигнала нейронной сети к желаемому.

Общее описание алгоритма обратного распространения ошибки

К примеру, нам надо обучить нейронную сеть по аналогии с той, что представлена на картинке ниже. Естественно, задачу следует выполнить, применяя алгоритм обратного распространения ошибки:

В многослойных персептронах в роли активационной функции обычно применяют сигмоидальную активационную функция, в нашем случае — логистическую. Формула:

Причём «альфа» здесь означает параметр наклона сигмоидальной функции. Меняя его, мы получаем возможность строить функции с разной крутизной.

Сигмоид может сужать диапазон изменения таким образом, чтобы значение OUT лежало между нулем и единицей. Нейронные многослойные сети характеризуются более высокой представляющей мощностью, если сравнивать их с однослойными, но это утверждение справедливо лишь в случае нелинейности. Нужную нелинейность и обеспечивает сжимающая функция. Но на практике существует много функций, которые можно использовать. Говоря о работе алгоритма обратного распространения ошибки, скажем, что для этого нужно лишь, чтобы функция была везде дифференцируема, а данному требованию как раз и удовлетворяет сигмоид. У него есть и дополнительное преимущество — автоматический контроль усиления. Если речь идёт о слабых сигналах (OUT близко к нулю), то кривая «вход-выход» характеризуется сильным наклоном, дающим большое усиление. При увеличении сигнала усиление падает. В результате большие сигналы будут восприниматься сетью без насыщения, а слабые сигналы будут проходить по сети без чрезмерного ослабления.

Цель обучения сети

Цель обучения нейросети при использовании алгоритма обратного распространения ошибки — это такая подстройка весов нейросети, которая позволит при приложении некоторого множества входов получить требуемое множество выходов нейронов (выходных нейронов). Можно назвать эти множества входов и выходов векторами. В процессе обучения предполагается, что для любого входного вектора существует целевой вектор, парный входному и задающий требуемый выход. Эту пару называют обучающей. Работая с нейросетями, мы обучаем их на многих парах.

Также можно сказать, что алгоритм использует стохастический градиентный спуск и продвигается в многомерном пространстве весов в направлении антиградиента, причём цель — это достижение минимума функции ошибки.

При практическом применении метода обучение продолжают не до максимально точной настройки нейросети на минимум функции ошибки, а пока не будет достигнуто довольно точное его приближение. С одной стороны, это даёт возможность уменьшить количество итераций обучения, с другой — избежать переобучения нейронной сети.

Пошаговая реализация метода обратного распространения ошибки

Необходимо выполнить следующие действия:
1. Инициализировать синаптические веса случайными маленькими значениями.
2. Выбрать из обучающего множества очередную обучающую пару; подать на вход сети входной вектор.
3. Выполнить вычисление выходных значений нейронной сети.
4. Посчитать разность между выходом нейросети и требуемым выходом (речь идёт о целевом векторе обучающей пары).
5. Скорректировать веса сети в целях минимизации ошибки.
6. Повторять для каждого вектора обучающего множества шаги 2-5, пока ошибка обучения нейронной сети на всём множестве не достигнет уровня, который является приемлемым.

Виды обучения сети по методу обратного распространения

Сегодня существует много модификаций алгоритма обратного распространения ошибки. Возможно обучение не «по шагам» (выходная ошибка вычисляется, веса корректируются на каждом примере), а «по эпохам» в offline-режиме (изменения весовых коэффициентов происходит после подачи на вход нейросети всех примеров обучающего множества, а ошибка обучения neural сети усредняется по всем примерам).

Обучение «по эпохам» более устойчиво к выбросам и аномальным значениям целевой переменной благодаря усреднению ошибки по многим примерам. Зато в данном случае увеличивается вероятность «застревания» в локальных минимумах. При обучении «по шагам» такая вероятность меньше, ведь применение отдельных примеров создаёт «шум», «выталкивающий» алгоритм обратного распространения из ям градиентного рельефа.

Преимущества и недостатки метода

К плюсам можно отнести простоту в реализации и устойчивость к выбросам и аномалиям в данных, и это основные преимущества. Но есть и минусы:
• неопределенно долгий процесс обучения;
• вероятность «паралича сети» (при больших значениях рабочая точка функции активации попадает в область насыщения сигмоиды, а производная величина приближается к 0, в результате чего коррекции весов почти не происходят, а процесс обучения «замирает»;
• алгоритм уязвим к попаданию в локальные минимумы функции ошибки.

Значение метода обратного распространения

Появление алгоритма стало знаковым событием и положительно отразилось на развитии нейросетей, ведь он реализует эффективный с точки зрения вычислительных процессов способ обучения многослойного персептрона. В то же самое время, было бы неправильным сказать, что алгоритм предлагает наиболее оптимальное решение всех потенциальных проблем. Зато он действительно развеял пессимизм относительно машинного обучения многослойных машин, который воцарился после публикации в 1969 году работы американского учёного с фамилией Минский.

Источники:
— «Алгоритм обратного распространения ошибки»;
— «Back propagation algorithm».

Метод обратного распространения ошибки — метод обучения многослойного перцептрона. Впервые метод был описан в 1974 г. Полем Дж. Вербосом^[1], а также независимо и одновременно А. И. Галушкиным^[2]. Далее существенно развит в 1986 г. Дэвидом И. Румельхартом, Дж. Е. Хинтоном и Рональдом Дж. Вильямсом^[3] и независимо и одновременно С. И. Барцевым и В. А. Охониным (Красноярская группа)^[4]. Это итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойного перцептрона и получения желаемого выхода.

Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к её входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Барцев и Охонин предложили сразу общий метод («принцип двойственности»), приложимый к более широкому классу систем, включая системы с запаздыванием, распределённые системы, и т. п.^[5]

Для возможноcти применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема.

Cигмоидальные функции активации[]

Наиболее часто в качестве функций активации используются следующие виды сигмоид:

Функция Ферми (экспоненциальная сигмоида):

Рациональная сигмоида:

Гиперболический тангенс:

где s — выход сумматора нейрона,  — произвольная константа.

Менее всего, сравнительно с другими сигмоидами, процессорного времени требует расчет рациональной сигмоиды. Для вычисления гиперболического тангенса требуется больше всего тактов работы процессора. Если же сравнивать с пороговыми функциями активациями, то сигмоиды расчитываются очень медленно. Если после суммирования в пороговой функции сразу можно начинать сравнение с определенной величиной (порогом), то в случае сигмоидальной функции активации — нужно расчитать сигмоид (затратить время в лучшем случае на три операции: взятие модуля, сложение и деление), и только потом сравнивать с пороговой величиной (например, нулем). Если считать, что все простейшие операции расчитываются процессором за примерно одинаковое время, то работа сигмоидальной функции активации после произведенного суммирования (которое займет одинаковое время) будет медленее пороговой функции активации как 1:4.

Функция оценки работы сети[]

В тех случаях, когда удается оценить работу сети обучение нейронных сетей можно представить как задачу оптимизации. Оценить — означает указать количественно хорошо или плохо сеть решает поставленные ей задачи. Для этого строится функция оценки. Она, как правило, явно зависит от выходных сигналов сети и неявно (через функционирование) — от всех ее параметров. Простейший и самый распространенный пример оценки — сумма квадратов расстояний от выходных сигналов сети до их требуемых значений:
,
где  — требуемое значение выходного сигнала.

Метод наименьших квадратов далеко не всегда является лучшим выбором оценки. Тщательное конструирование функции оценки позволяет на порядок поысить эффективность обучения сети, а также получать дополнительную информацию — «уровень уверенности» сети в даваемом ответе^[6].

Описание алгоритма[]

Файл:Neuro.PNG

Алгоритм обратного распространения ошибки применяется для многослойного перцептрона. У сети есть входы , выходы Outputs и внутренние узлы. Перенумеруем все узлы (включая входы и выходы) числами от 1 до N. Обозначим через вес, стоящий на ребре, соединяющем i-ый и j-ый узлы, а через  — выход i-го узла. Если у нас m тестовых примеров с целевыми значениями выходов , , то функция ошибки, полученная по методу наименьших квадратов, выглядит так:

Как модифицировать веса? Мы будем реализовывать стохастический градиентный спуск, то есть будем подправлять веса после каждого тестового примера. Нам нужно двигаться в сторону, противоположную градиенту, то есть добавлять к каждому весу

где

Производная считается следующим образом. Пусть сначала , то есть интересующий нас вес входит в перцептрон последнего уровня. Сначала отметим, что влияет на выход перцептрона только как часть суммы , где сумма берется по входам j-го узла. Поэтому

Аналогично, влияет на общую ошибку только в рамках выхода j-го узла (напоминаем, что это выход всей сети). Поэтому

Если же j-й узел — не на последнем уровне, то у него есть выходы; обозначим их через Children(j). В этом случае

,

и

.

Ну а  — это в точности аналогичная поправка, но вычисленная для узла следующего уровня (будем обозначать ее через  — от она отличается отсутствием множителя . Поскольку мы научились вычислять поправку для узлов последнего уровня и выражать поправку для узла более низкого уровня через поправки более высокого, можно уже писать алгоритм. Именно из-за этой особенности вычисления
поправок алгоритм называется алгоритмом обратного распространения ошибки (backpropagation). Краткое резюме проделанной работы:

• для узла последнего уровня

• для внутреннего узла сети

• для всех узлов

Получающийся алгоритм представлен ниже. На вход алгоритму, кроме указанных параметров, нужно также подавать в каком-нибудь формате структуру сети. На практике очень хорошие результаты показывают сети достаточно простой структуры, состоящие из двух уровней нейронов — скрытого уровня (hidden units) и нейронов-выходов (output units); каждый вход сети соединен со всеми скрытыми нейронами, а результат работы каждого скрытого нейрона подается на вход каждому из нейронов-выходов. В таком случае достаточно подавать на вход количество нейронов скрытого уровня.

Алгоритм[]

Алгоритм:
BackPropagation

1. Инициализировать маленькими случайными значениями.
2. Повторить NUMBER_OF_STEPS раз:

   Для всех d от 1 до m:

   1. Подать на вход сети и подсчитать выходы каждого узла.
   2. Для всех

      .

   3. Для каждого уровня l, начиная с предпоследнего:

      Для каждого узла j уровня l вычислить

      .

   4. Для каждого ребра сети {i, j}

      .

3. Выдать значения .

Математическая интерпретация обучения нейронной сети[]

На каждой итерации алгоритма обратного распространения весовые коэффициенты нейронной сети модифицируются так, чтобы улучшить решение одного примера. Таким образом, в процессе обучения циклически решаются однокритериальные задачи оптимизации.

Обучение нейронной сети характеризуется четырьмя специфическими ограничениями, выделяющих обучение нейросетей из общих задач оптимизации: астрономическое число параметров, необходимость высокого параллелизма при обучении, многокритериальность решаемых задач, необходимость найти достаточно широкую область, в которой значения всех минимизируемых функций близки к минимальным. В остальном проблему обучения можно, как правило, сформулировать как задачу минимизации оценки. Осторожность предыдущей фразы («как правило») связана с тем, что на самом деле нам неизвестны и никогда не будут известны все возможные задачи для нейронных сетей, и, быть может, где-то в неизвестности есть задачи, которые несводимы к минимизации оценки. Минимизация оценки — сложная проблема: параметров астрономически много (для стандартных примеров, реализуемых на РС — от 100 до 1000000), адаптивный рельеф (график оценки как функции от подстраиваемых параметров) сложен, может содержать много локальных минимумов.

Недостатки алгоритма[]

Несмотря на многочисленные успешные применения обратного распространения, оно не является панацеей. Больше всего неприятностей приносит неопределенно долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.

Паралич сети[]

В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях OUT, в области, где производная сжимающей функции очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть. В теоретическом отношении эта проблема плохо изучена. Обычно этого избегают уменьшением размера шага η, но это увеличивает время обучения. Различные эвристики использовались для предохранения от паралича или для восстановления после него, но пока что они могут рассматриваться лишь как экспериментальные.

Локальные минимумы[]

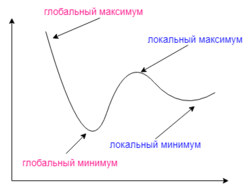
Обратное распространение использует разновидность градиентного спуска, то есть осуществляет спуск вниз по поверхности ошибки, непрерывно подстраивая веса в направлении к минимуму. Поверхность ошибки сложной сети сильно изрезана и состоит из холмов, долин, складок и оврагов в пространстве высокой размерности. Сеть может попасть в локальный минимум (неглубокую долину), когда рядом имеется гораздо более глубокий минимум. В точке локального минимума все направления ведут вверх, и сеть неспособна из него выбраться. Статистические методы обучения могут помочь избежать этой ловушки, но они медленны.

Размер шага[]

Внимательный разбор доказательства сходимости^[3] показывает, что коррекции весов предполагаются бесконечно малыми. Ясно, что это неосуществимо на практике, так как ведет к бесконечному времени обучения. Размер шага должен браться конечным, и в этом вопросе приходится опираться только на опыт. Если размер шага очень мал, то сходимость слишком медленная, если же очень велик, то может возникнуть паралич или постоянная неустойчивость. П. Д. Вассерман^[7] описал адаптивный алгоритм выбора шага, автоматически корректирующий размер шага в процессе обучения. В книге А. Н. Горбаня^[8] предложена разветвлённая технология оптимизации обучения.

См. также[]

• Сигмоид
• Многослойный перцептрон

Литература[]

1. Уоссермен Ф. Нейрокомпьютерная техника: Теория и практика. — М.: «Мир», 1992.

1. Хайкин С. Нейронные сети: Полный курс. Пер. с англ. Н. Н. Куссуль, А. Ю. Шелестова. 2-е изд., испр. — М.: Издательский дом Вильямс, 2008, 1103 с.

Внешние ссылки[]

1. Копосов А.И., Щербаков И.Б., Кисленко Н.А., Кисленко О.П., Варивода Ю.В. и др. Отчет по научно-исследовательской работе «Создание аналитического обзора информационных источников по применению нейронных сетей для задач газовой технологии». — Москва: ВНИИГАЗ, 1995.

1. Миркес Е. М., Нейроинформатика: Учеб. пособие для студентов с программами для выполнения лабораторных работ. Красноярск: ИПЦ КГТУ, 2002, 347 с. Рис. 58, табл. 59, библиогр. 379 наименований. ISBN 5-7636-0477-6

Примечания[]

Время на прочтение
5 мин

Количество просмотров 83K

В первой части были рассмотрены: структура, топология, функции активации и обучающее множество. В этой части попробую объяснить как происходит обучение сверточной нейронной сети.

Обучение сверточной нейронной сети

На начальном этапе нейронная сеть является необученной (ненастроенной). В общем смысле под обучением понимают последовательное предъявление образа на вход нейросети, из обучающего набора, затем полученный ответ сравнивается с желаемым выходом, в нашем случае это 1 – образ представляет лицо, минус 1 – образ представляет фон (не лицо), полученная разница между ожидаемым ответом и полученным является результат функции ошибки (дельта ошибки). Затем эту дельту ошибки необходимо распространить на все связанные нейроны сети.

Таким образом обучение нейронной сети сводится к минимизации функции ошибки, путем корректировки весовых коэффициентов синаптических связей между нейронами. Под функцией ошибки понимается разность между полученным ответом и желаемым. Например, на вход был подан образ лица, предположим, что выход нейросети был 0.73, а желаемый результат 1 (т.к. образ лица), получим, что ошибка сети является разницей, то есть 0.27. Затем веса выходного слоя нейронов корректируются в соответствии с ошибкой. Для нейронов выходного слоя известны их фактические и желаемые значения выходов. Поэтому настройка весов связей для таких нейронов является относительно простой. Однако для нейронов предыдущих слоев настройка не столь очевидна. Долгое время не было известно алгоритма распространения ошибки по скрытым слоям.

Алгоритм обратного распространения ошибки

Для обучения описанной нейронной сети был использован алгоритм обратного распространения ошибки (backpropagation). Этот метод обучения многослойной нейронной сети называется обобщенным дельта-правилом. Метод был предложен в 1986 г. Румельхартом, Макклеландом и Вильямсом. Это ознаменовало возрождение интереса к нейронным сетям, который стал угасать в начале 70-х годов. Данный алгоритм является первым и основным практически применимым для обучения многослойных нейронных сетей.

Для выходного слоя корректировка весов интуитивна понятна, но для скрытых слоев долгое время не было известно алгоритма. Веса скрытого нейрона должны изменяться прямо пропорционально ошибке тех нейронов, с которыми данный нейрон связан. Вот почему обратное распространение этих ошибок через сеть позволяет корректно настраивать веса связей между всеми слоями. В этом случае величина функции ошибки уменьшается и сеть обучается.

Основные соотношения метода обратного распространения ошибки получены при следующих обозначениях:

Величина ошибки определяется по формуле 2.8 среднеквадратичная ошибка:

Неактивированное состояние каждого нейрона j для образа p записывается в виде взвешенной суммы по формуле 2.9:

Выход каждого нейрона j является значением активационной функции

, которая переводит нейрон в активированное состояние. В качестве функции активации может использоваться любая непрерывно дифференцируемая монотонная функция. Активированное состояние нейрона вычисляется по формуле 2.10:

В качестве метода минимизации ошибки используется метод градиентного спуска, суть этого метода сводится к поиску минимума (или максимума) функции за счет движения вдоль вектора градиента. Для поиска минимума движение должно быть осуществляться в направлении антиградиента. Метод градиентного спуска в соответствии с рисунком 2.7.

Градиент функции потери представляет из себя вектор частных производных, вычисляющийся по формуле 2.11:

Производную функции ошибки по конкретному образу можно записать по правилу цепочки, формула 2.12:

Ошибка нейрона обычно записывается в виде символа δ (дельта). Для выходного слоя ошибка определена в явном виде, если взять производную от формулы 2.8, то получим t минус y, то есть разницу между желаемым и полученным выходом. Но как рассчитать ошибку для скрытых слоев? Для решения этой задачи, как раз и был придуман алгоритм обратного распространения ошибки. Суть его заключается в последовательном вычислении ошибок скрытых слоев с помощью значений ошибки выходного слоя, т.е. значения ошибки распространяются по сети в обратном направлении от выхода к входу.

Ошибка δ для скрытого слоя рассчитывается по формуле 2.13:

Алгоритм распространения ошибки сводится к следующим этапам:

• прямое распространение сигнала по сети, вычисления состояния нейронов;
• вычисление значения ошибки δ для выходного слоя;
• обратное распространение: последовательно от конца к началу для всех скрытых слоев вычисляем δ по формуле 2.13;
• обновление весов сети на вычисленную ранее δ ошибки.

Алгоритм обратного распространения ошибки в многослойном персептроне продемонстрирован ниже:

До этого момента были рассмотрены случаи распространения ошибки по слоям персептрона, то есть по выходному и скрытому, но помимо них, в сверточной нейросети имеются подвыборочный и сверточный.

Расчет ошибки на подвыборочном слое

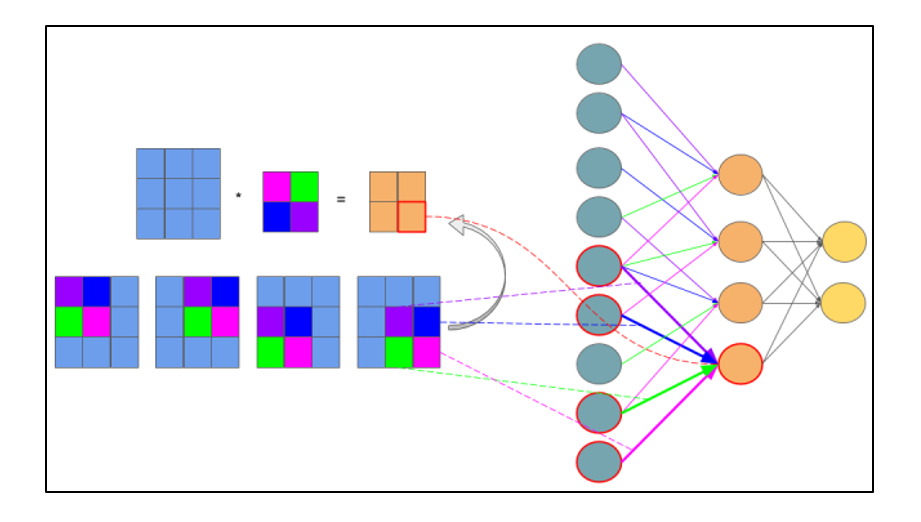
Расчет ошибки на подвыборочном слое представляется в нескольких вариантах. Первый случай, когда подвыборочный слой находится перед полносвязным, тогда он имеет нейроны и связи такого же типа, как в полносвязном слое, соответственно вычисление δ ошибки ничем не отличается от вычисления δ скрытого слоя. Второй случай, когда подвыборочный слой находится перед сверточным, вычисление δ происходит путем обратной свертки. Для понимания обратно свертки, необходимо сперва понять обычную свертку и то, что скользящее окно по карте признаков (во время прямого распространения сигнала) можно интерпретировать, как обычный скрытый слой со связями между нейронами, но главное отличие — это то, что эти связи разделяемы, то есть одна связь с конкретным значением веса может быть у нескольких пар нейронов, а не только одной. Интерпретация операции свертки в привычном многослойном виде в соответствии с рисунком 2.8.

Рисунок 2.8 — Интерпретация операции свертки в многослойный вид, где связи с одинаковым цветом имеют один и тот же вес. Синим цветом обозначена подвыборочная карта, разноцветным – синаптическое ядро, оранжевым – получившаяся свертка

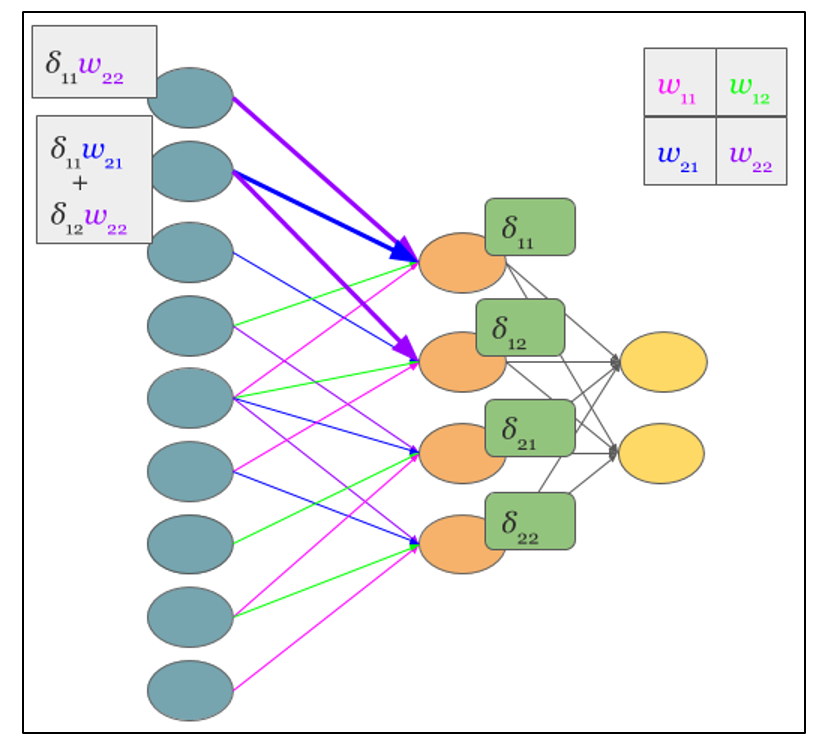
Теперь, когда операция свертки представлена в привычном многослойном виде, можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети. Соответственно имея вычисленные ранее дельты сверточного слоя можно вычислить дельты подвыборочного, в соответствии с рисунком 2.9.

Рисунок 2.9 — Вычисление δ подвыборочного слоя за счет δ сверточного слоя и ядра

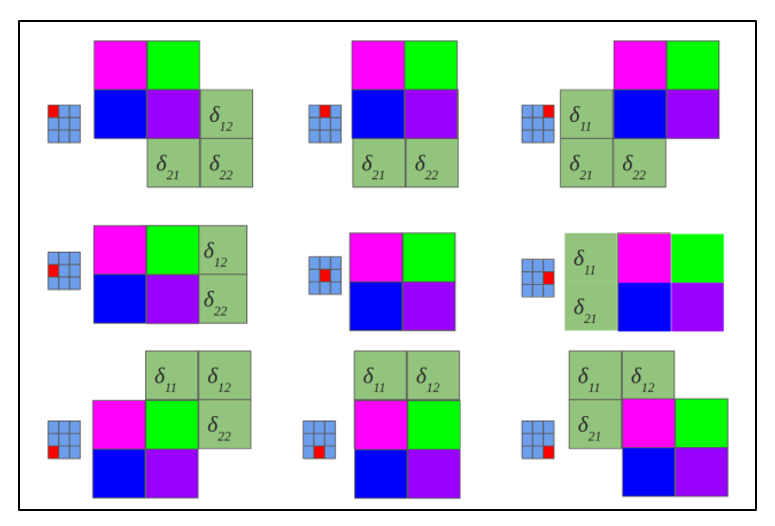
Обратная свертка – это тот же самый способ вычисления дельт, только немного хитрым способом, заключающийся в повороте ядра на 180 градусов и скользящем процессе сканирования сверточной карты дельт с измененными краевыми эффектами. Простыми словами, нам необходимо взять ядро сверточной карты (следующего за подвыборочным слоем) повернуть его на 180 градусов и сделать обычную свертку по вычисленным ранее дельтам сверточной карты, но так чтобы окно сканирования выходило за пределы карты. Результат операции обратной свертки в соответствии с рисунком 2.10, цикл прохода обратной свертки в соответствии с рисунком 2.11.

Рисунок 2.10 — Результат операции обратной свертки

Рисунок 2.11 — Повернутое ядро на 180 градусов сканирует сверточную карту

Расчет ошибки на сверточном слое

Обычно впередиидущий слой после сверточного это подвыборочный, соответственно наша задача вычислить дельты текущего слоя (сверточного) за счет знаний о дельтах подвыборочного слоя. На самом деле дельта ошибка не вычисляется, а копируется. При прямом распространении сигнала нейроны подвыборочного слоя формировались за счет неперекрывающегося окна сканирования по сверточному слою, в процессе которого выбирались нейроны с максимальным значением, при обратном распространении, мы возвращаем дельту ошибки тому ранее выбранному максимальному нейрону, остальные же получают нулевую дельту ошибки.

Заключение

Представив операцию свертки в привычном многослойном виде (рисунок 2.8), можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети.

Источники

Алгоритм обратного распространения ошибки для сверточной нейронной сети

Обратное распространение ошибки в сверточных слоях
раз и два

Обратное распространение ошибки в персептроне

Еще можно почитать в РГБ диссертацию Макаренко: АЛГОРИТМЫ И ПРОГРАММНАЯ СИСТЕМА КЛАССИФИКАЦИИ

Метод обратного распространения ошибок (англ. backpropagation) — метод вычисления градиента, который используется при обновлении весов в нейронной сети.

Обучение как задача оптимизации

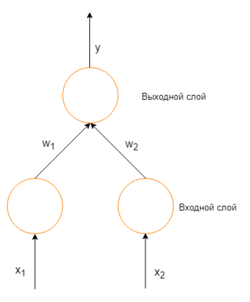
Рассмотрим простую нейронную сеть без скрытых слоев, с двумя входными вершинами и одной выходной, в которых каждый нейрон использует линейную функцию активации, (обычно, многослойные нейронные сети используют нелинейные функции активации, линейные функции используются для упрощения понимания) которая является взвешенной суммой входных данных.

Изначально веса задаются случайно. Затем, нейрон обучается с помощью тренировочного множества, которое в этом случае состоит из множества троек где и — это входные данные сети и — правильный ответ. Начальная сеть, приняв на вход и , вычислит ответ , который вероятно отличается от . Общепринятый метод вычисления несоответствия между ожидаемым и получившимся ответом — квадратичная функция потерь:

где ошибка.

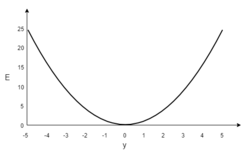
В качестве примера, обучим сеть на объекте , таким образом, значения и равны 1, а равно 0. Построим график зависимости ошибки от действительного ответа , его результатом будет парабола. Минимум параболы соответствует ответу , минимизирующему . Если тренировочный объект один, минимум касается горизонтальной оси, следовательно ошибка будет нулевая и сеть может выдать ответ равный ожидаемому ответу . Следовательно, задача преобразования входных значений в выходные может быть сведена к задаче оптимизации, заключающейся в поиске функции, которая даст минимальную ошибку.

В таком случае, выходное значение нейрона — взвешенная сумма всех его входных значений:

где и — веса на ребрах, соединяющих входные вершины с выходной. Следовательно, ошибка зависит от весов ребер, входящих в нейрон. И именно это нужно менять в процессе обучения. Распространенный алгоритм для поиска набора весов, минимизирующего ошибку — градиентный спуск. Метод обратного распространения ошибки используется для вычисления самого «крутого» направления для спуска.

Дифференцирование для однослойной сети

Метод градиентного спуска включает в себя вычисление дифференциала квадратичной функции ошибки относительно весов сети. Обычно это делается с помощью метода обратного распространения ошибки. Предположим, что выходной нейрон один, (их может быть несколько, тогда ошибка — это квадратичная норма вектора разницы) тогда квадратичная функция ошибки:

где — квадратичная ошибка, — требуемый ответ для обучающего образца, — действительный ответ сети.

Множитель добавлен чтобы предотвратить возникновение экспоненты во время дифференцирования. На результат это не повлияет, потому что позже выражение будет умножено на произвольную величину скорости обучения (англ. learning rate).

Для каждого нейрона , его выходное значение определено как

Входные значения нейрона — это взвешенная сумма выходных значений предыдущих нейронов. Если нейрон в первом слое после входного, то входного слоя — это просто входные значения сети. Количество входных значений нейрона . Переменная обозначает вес на ребре между нейроном предыдущего слоя и нейроном текущего слоя.

Функция активации нелинейна и дифференцируема. Одна из распространенных функций активации — сигмоида:

у нее удобная производная:

Находим производную ошибки

Вычисление частной производной ошибки по весам выполняется с помощью цепного правила:

Только одно слагаемое в зависит от , так что

Если нейрон в первом слое после входного, то — это просто .

Производная выходного значения нейрона по его входному значению — это просто частная производная функции активации (предполагается что в качестве функции активации используется сигмоида):

По этой причине данный метод требует дифференцируемой функции активации. (Тем не менее, функция ReLU стала достаточно популярной в последнее время, хоть и не дифференцируема в 0)

Первый множитель легко вычислим, если нейрон находится в выходном слое, ведь в таком случае и

Тем не менее, если произвольный внутренний слой сети, нахождение производной по менее очевидно.

Если рассмотреть как функцию, берущую на вход все нейроны получающие на вход значение нейрона ,

и взять полную производную по , то получим рекурсивное выражение для производной:

Следовательно, производная по может быть вычислена если все производные по выходным значениям следующего слоя известны.

Если собрать все месте:

и

Чтобы обновить вес используя градиентный спуск, нужно выбрать скорость обучения, . Изменение в весах должно отражать влияние на увеличение или уменьшение в . Если , увеличение увеличивает ; наоборот, если , увеличение уменьшает . Новый добавлен к старым весам, и произведение скорости обучения на градиент, умноженный на , гарантирует, что изменения будут всегда уменьшать . Другими словами, в следующем уравнении, всегда изменяет в такую сторону, что уменьшается:

Алгоритм

• — скорость обучения
• — коэффициент инерциальности для сглаживания резких скачков при перемещении по поверхности целевой функции
• — обучающее множество
• — количество повторений
• — функция, подающая x на вход сети и возвращающая выходные значения всех ее узлов
• — количество слоев в сети
• — множество нейронов в слое i
• — множество нейронов в выходном слое

fun BackPropagation:
   init 
   repeat :
       for  =  to :
            =  
           for :
                = 
           for  =  to :
               for :
                    = 
           for :
                = 
                = 
   return 

Недостатки алгоритма

Несмотря на многочисленные успешные применения обратного распространения, оно не является универсальным решением. Больше всего неприятностей приносит неопределённо долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.

Паралич сети

В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших выходных значениях, а производная активирующей функции будет очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть.

Локальные минимумы

Градиентный спуск с обратным распространением ошибок гарантирует нахождение только локального минимума функции; также, возникают проблемы с пересечением плато на поверхности функции ошибки.

Примечания

• Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
• Neural Nets
• Understanding backpropagation

См. также

• Нейронные сети, перцептрон
• Стохастический градиентный спуск
• Настройка глубокой сети
• Практики реализации нейронных сетей

Источники информации

• https://en.wikipedia.org/wiki/Backpropagation
• https://ru.wikipedia.org/wiki/Метод_обратного_распространения_ошибки