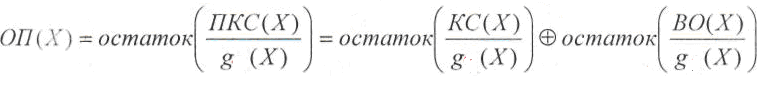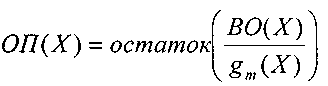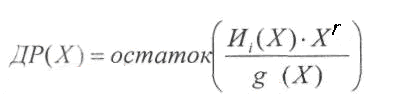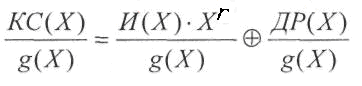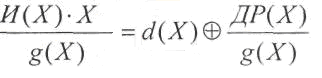Код Хэмминга. Пример работы алгоритма
Время на прочтение
4 мин
Количество просмотров 525K
Вступление.
Прежде всего стоит сказать, что такое Код Хэмминга и для чего он, собственно, нужен. На Википедии даётся следующее определение:
Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.
Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение. Сегодня, я опишу самый простой алгоритм Хемминга, который может исправлять лишь одну ошибку.
Также стоит отметить, что существуют более совершенные модификации данного алгоритма, которые позволяют обнаруживать (и если возможно исправлять) большее количество ошибок.
Сразу стоит сказать, что Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.
Как это работает.
Для того, чтобы понять работу данного алгоритма, рассмотрим пример.
Подготовка
Допустим, у нас есть сообщение «habr», которое необходимо передать без ошибок. Для этого сначала нужно наше сообщение закодировать при помощи Кода Хэмминга. Нам необходимо представить его в бинарном виде.
На этом этапе стоит определиться с, так называемой, длиной информационного слова, то есть длиной строки из нулей и единиц, которые мы будем кодировать. Допустим, у нас длина слова будет равна 16. Таким образом, нам необходимо разделить наше исходное сообщение («habr») на блоки по 16 бит, которые мы будем потом кодировать отдельно друг от друга. Так как один символ занимает в памяти 8 бит, то в одно кодируемое слово помещается ровно два ASCII символа. Итак, мы получили две бинарные строки по 16 бит:

После этого процесс кодирования распараллеливается, и две части сообщения («ha» и «br») кодируются независимо друг от друга. Рассмотрим, как это делается на примере первой части.
Прежде всего, необходимо вставить контрольные биты. Они вставляются в строго определённых местах — это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно, у нас получилось 5 контрольных бит (выделены красным цветом):
Было:
Стало:
Таким образом, длина всего сообщения увеличилась на 5 бит. До вычисления самих контрольных бит, мы присвоили им значение «0».
Вычисление контрольных бит.
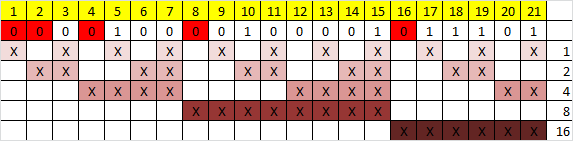
Теперь необходимо вычислить значение каждого контрольного бита. Значение каждого контрольного бита зависит от значений информационных бит (как неожиданно), но не от всех, а только от тех, которые этот контрольных бит контролирует. Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N. Не очень понятно, но по картинке, думаю, станет яснее:
Здесь знаком «X» обозначены те биты, которые контролирует контрольный бит, номер которого справа. То есть, к примеру, бит номер 12 контролируется битами с номерами 4 и 8. Ясно, что чтобы узнать какими битами контролируется бит с номером N надо просто разложить N по степеням двойки.
Но как же вычислить значение каждого контрольного бита? Делается это очень просто: берём каждый контрольный бит и смотрим сколько среди контролируемых им битов единиц, получаем некоторое целое число и, если оно чётное, то ставим ноль, в противном случае ставим единицу. Вот и всё! Можно конечно и наоборот, если число чётное, то ставим единицу, в противном случае, ставим 0. Главное, чтобы в «кодирующей» и «декодирующей» частях алгоритм был одинаков. (Мы будем применять первый вариант).
Высчитав контрольные биты для нашего информационного слова получаем следующее:
и для второй части:
Вот и всё! Первая часть алгоритма завершена.
Декодирование и исправление ошибок.
Теперь, допустим, мы получили закодированное первой частью алгоритма сообщение, но оно пришло к нас с ошибкой. К примеру мы получили такое (11-ый бит передался неправильно):
Вся вторая часть алгоритма заключается в том, что необходимо заново вычислить все контрольные биты (так же как и в первой части) и сравнить их с контрольными битами, которые мы получили. Так, посчитав контрольные биты с неправильным 11-ым битом мы получим такую картину:
Как мы видим, контрольные биты под номерами: 1, 2, 8 не совпадают с такими же контрольными битами, которые мы получили. Теперь просто сложив номера позиций неправильных контрольных бит (1 + 2 + 8 = 11) мы получаем позицию ошибочного бита. Теперь просто инвертировав его и отбросив контрольные биты, мы получим исходное сообщение в первозданном виде! Абсолютно аналогично поступаем со второй частью сообщения.
Заключение.
В данном примере, я взял длину информационного сообщения именно 16 бит, так как мне кажется, что она наиболее оптимальная для рассмотрения примера (не слишком длинная и не слишком короткая), но конечно же длину можно взять любую. Только стоит учитывать, что в данной простой версии алгоритма на одно информационное слово можно исправить только одну ошибку.
Примечание.
На написание этого топика меня подвигло то, что в поиске я не нашёл на Хабре статей на эту тему (чему я был крайне удивлён). Поэтому я решил отчасти исправить эту ситуацию и максимально подробно показать как этот алгоритм работает. Я намеренно не приводил ни одной формулы, дабы попытаться своими словами донести процесс работы алгоритма на примере.
Источники.
1. Википедия
2. Calculating the Hamming Code
Hamming code is a block code that is capable of detecting up to two simultaneous bit errors and correcting single-bit errors. It was developed by R.W. Hamming for error correction.
In this coding method, the source encodes the message by inserting redundant bits within the message. These redundant bits are extra bits that are generated and inserted at specific positions in the message itself to enable error detection and correction. When the destination receives this message, it performs recalculations to detect errors and find the bit position that has error.
Hamming Code for Single Error Correction
The procedure for single error correction by Hamming Code includes two parts, encoding at the sender’s end and decoding at receiver’s end.
Encoding a message by Hamming Code
The procedure used by the sender to encode the message encompasses the following steps −
-
Step 1 − Calculation of the number of redundant bits.
-
Step 2 − Positioning the redundant bits.
-
Step 3 − Calculating the values of each redundant bit.
Once the redundant bits are embedded within the message, this is sent to the destination.
Step 1 − Calculation of the number of redundant bits.
If the message contains m number of data bits, r number of redundant bits are added to it so that is able to indicate at least (m + r + 1) different states. Here, (m + r) indicates location of an error in each of bit positions and one additional state indicates no error. Since, r bits can indicate 2r states, 2r must be at least equal to (m + r + 1). Thus the following equation should hold −
2r ≥ 𝑚 + 𝑟 + 1
Example 1 − If the data is of 7 bits, i.e. m = 7, the minimum value of r that will satisfy the above equation is 4, (24 ≥ 7 + 4 + 1). The total number of bits in the encoded message, (m + r) = 11. This is referred as (11,4) code.
Step 2 − Positioning the redundant bits.
The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc. They are referred in the rest of this text as r1 (at position 1), r2 (at position 2), r3 (at position 4), r4 (at position 
Example 2 − If, m = 7 comes to 4, the positions of the redundant bits are as follows −
Step 3 − Calculating the values of each redundant bit.
The redundant bits are parity bits. A parity bit is an extra bit that makes the number of 1s either even or odd. The two types of parity are −
-
Even Parity − Here the total number of bits in the message is made even.
-
Odd Parity − Here the total number of bits in the message is made odd.
Each redundant bit, ri, is calculated as the parity, generally even parity, based upon its bit position. It covers all bit positions whose binary representation includes a 1 in the ith position except the position of ri. Thus −
-
r1 is the parity bit for all data bits in positions whose binary representation includes a 1 in the least significant position excluding 1 (3, 5, 7, 9, 11 and so on)
-
r2 is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 2 from right except 2 (3, 6, 7, 10, 11 and so on)
-
r3 is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 3 from right except 4 (5-7, 12-15, 20-23 and so on)
Example 3 − Suppose that the message 1100101 needs to be encoded using even parity Hamming code. Here, m = 7 and r comes to 4. The values of redundant bits will be as follows −
Hence, the message sent will be 11000101100.
Decoding a message in Hamming Code
Once the receiver gets an incoming message, it performs recalculations to detect errors and correct them. The steps for recalculation are −
-
Step 1 − Calculation of the number of redundant bits.
-
Step 2 − Positioning the redundant bits.
-
Step 3 − Parity checking.
-
Step 4 − Error detection and correction
Step 1) Calculation of the number of redundant bits
Using the same formula as in encoding, the number of redundant bits are ascertained.
2r ≥ 𝑚 + 𝑟 + 1
where m is the number of data bits and r is the number of redundant bits.
Step 2) Positioning the redundant bits
The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc.
Step 3) Parity checking
Parity bits are calculated based upon the data bits and the redundant bits using the same rule as during generation of c1, c2, c3, c4 etc. Thus
c1 = parity(1, 3, 5, 7, 9, 11 and so on)
c2 = parity(2, 3, 6, 7, 10, 11 and so on)
c3 = parity(4-7, 12-15, 20-23 and so on)
Step 4) Error detection and correction
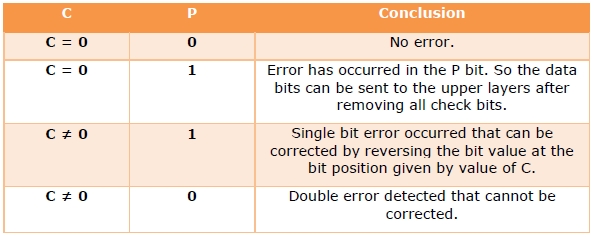
The decimal equivalent of the parity bits binary values is calculated. If it is 0, there is no error. Otherwise, the decimal value gives the bit position which has error. For example, if c1c2c3c4 = 1001, it implies that the data bit at position 9, decimal equivalent of 1001, has error. The bit is flipped (converted from 0 to 1 or vice versa) to get the correct message.
Example 4 − Suppose that an incoming message 11110101101 is received.
Step 1 − At first the number of redundant bits are calculated using the formula 2r ≥ m + r + 1. Here, m + r + 1 = 11 + 1 = 12. The minimum value of r such that 2r ≥ 12 is 4.
Step 2 − The redundant bits are positioned as below −
Step 3 − Even parity checking is done −
c1 = even_parity(1, 3, 5, 7, 9, 11) = 0
c2 = even_parity(2, 3, 6, 7, 10, 11) = 0
c3 = even_parity (4, 5, 6, 7) = 0
c4 = even_parity (8, 9, 10, 11) = 0
Step 4 — Since the value of the check bits c1c2c3c4 = 0000 = 0, there are no errors in this message.
Hamming Code for double error detection
The Hamming code can be modified to correct a single error and detect double errors by adding a parity bit as the MSB, which is the XOR of all other bits.
Example 5 − If we consider the codeword, 11000101100, sent as in example 3, after adding P = XOR(1,1,0,0,0,1,0,1,1,0,0) = 0, the new codeword to be sent will be 011000101100.
At the receiver’s end, error detection is done as shown in the following table −
- Related Articles
- Explain the Hamming Codes in Error Correction
- Error Detection Code-Checksum
- Error Detection and Correction in Data link Layer
- Forward Error Correction (FEC)
- What is Error Correction?
- Error Correcting Codes — Hamming codes
- What is Error Detection?
- Forward Error Correction in Computer Networks
- Bit Stuffing error detection technique using Java
- Unreachable Code Error in Java
- Error Correcting Codes — Binary Convolutional Code
- Sending HTTP error code using Express.js
- What is the effect of errors in Error Detection?
- Error detection at its best: Implementing Checksum using Python
- Hamming Code in Computer Networks
Kickstart Your Career
Get certified by completing the course
Get Started

Пример
. Предположим, в канале связи под действием
помех произошло искажение и вместо
0100101 было принято 01001(1)1.
Решение:
Для обнаружения ошибки производят уже
знакомые нам проверки на четность.
Первая
проверка:
сумма П1+П3+П5+П7
= 0+0+1+1 четна.
В младший разряд номера ошибочной
позиции запишем 0.
Вторая
проверка:
сумма П2+П3+П6+П7
= 1+0+1+1 нечетна.
Во второй разряд номера ошибочной
позиции запишем 1
Третья
проверка:
сумма П4+П5+П6+П7
= 0+1+1+1 нечетна.
В третий разряд номера ошибочной позиции
запишем 1. Номер ошибочной позиции 110=
6. Следовательно,
символ шестой позиции следует изменить
на обратный, и получим правильную кодовую
комбинацию.
Код, исправляющий
одиночную и обнаруживающий двойную
ошибки
Если по изложенным
выше правилам строить корректирующий
код с обнаружением и исправлением
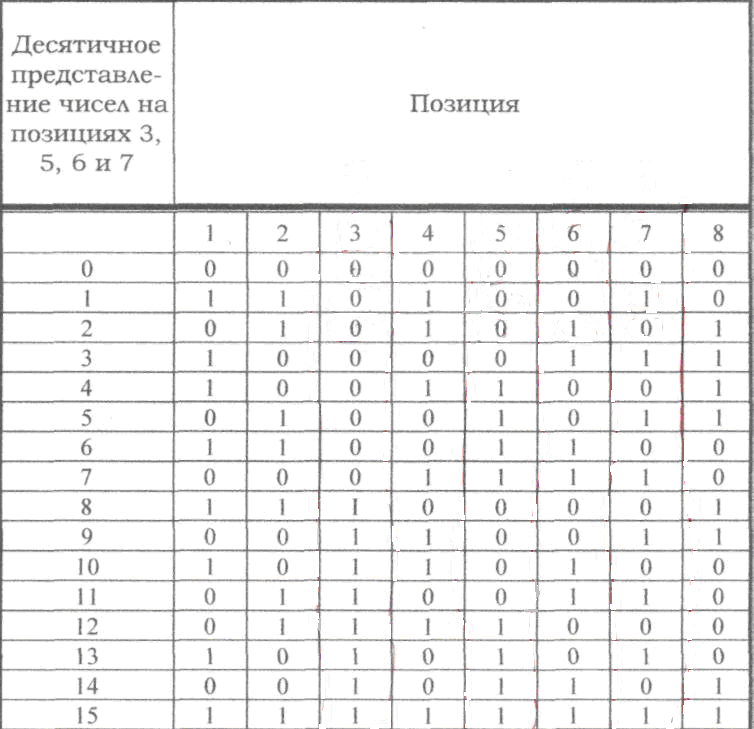
одиночной ошибки для равномерного
двоичного кода, то первые 16 кодовых
комбинаций будут иметь вид, показанный
в таблице. Такой код может быть использован
для построения кода с исправлением
одиночной ошибки и обнаружением двойной.
Для
этого, кроме указанных выше проверок
по контрольным позициям, следует провести
еще одну проверку на четность для всей
строки в целом. Чтобы осуществить такую
проверку, следует к каждой строке кода
добавить контрольные символы, записанные
в дополнительной колонке (таблица,
колонка 8). Тогда в случае одной ошибки
проверки по позициям укажут номер
ошибочной позиции, а проверка на четность
— на наличие ошибки. Если проверки позиций
укажут на наличие ошибки, а проверка на
четность не фиксирует ее, значит в
кодовой комбинации две ошибки.
Лекция 8
8.1 Двоичные циклические коды
Вышеприведенная
процедура построения линейного кода
матричным методом имеет ряд недостатков.
Она неоднозначна (МДР можно задать
различным образом) и неудобна
в реализации в виде технических устройств.
Этих недостатков лишены
линейные корректирующие коды, принадлежащие
к классу циклических.
Циклическими
называют
линейные (n,k)-коды,
обладающие
следующим свойством:
для любого кодового слова:
существует другое
кодовое слово:
полученное
циклическим сдвигом элементов исходного
кодового слова ||КС||
вправо
или влево, которое также принадлежит
этому коду.
Для
описания циклических кодов используют
полиномы с фиктивной переменной
X.
Например,
пусть кодовое слово ||КС||
=
||011010||.
Его
можно описать полиномом
Таким
образом, разряды кодового слова в
описывающем его полиноме используются
в качестве коэффициентов при степенях
фиктивной переменной
X.
Наибольшая
степень фиктивной переменной X
в
слагаемом с ненулевым
коэффициентом называется степенью
полинома. В вышеприведенном примере
получился полином 4-й степени.
Теперь
действия над кодовыми словами сводятся
к действиям над полиномами.
Вместо алгебры матриц здесь используется
алгебра полиномов.
Рассмотрим
алгебраические действия над полиномами,
используемые в теории
циклических кодов. Суммирование
полиномов разберем на примере
С(Х)=А(Х)+В(Х).
Пусть
||A||
= ||011010||,
||В|| =
||110111|.
Тогда
—————————————————————
Таким
образом, при суммировании коэффициентов
при X
в одинаковой степени
результат берется по модулю 2. При таком
правиле вычитание эквивалентно
суммированию.
Умножение
выполняется как обычно, но с использованием
суммирования
по модулю 2.
Рассмотрим
умножение на примере умножения полинома
(X3+X1+X0)
на
полином X1+X0
X3
+ 0*X2+X1+X0
*
X1+X0
—————————————————
X3+
0*X2+X1+Х0
X4+0*Х3+
X2+Х1
____________________________________
Х4+
X3+
X2+0*X1+X0
Операция
— обратная умножению -деление. Деление
полиномов выполняется как обычно, за
исключением того, что вычитание
выполняется по модулю 2. Вспомним, что
вычитание по модулю 2 эквивалентно
сложению по модулю 2
Пример
деления полинома X6+X4+X3
на полином
X3+X2+1
X6+0*X5+X4
+ X3+0*X2+0*X1+0
| X3+X2+1
X6+X5+0*X4+X3 результат== |X3+X2
————————————
X5
+X4
+ 0*X3+0*X2
X5
+X4
+ 0*X3+
X2
—————————————-
остаток==
X2
=
100
Циклический
сдвиг влево на одну позицию коэффициентов
полинома степени n-1
получается
путем его умножения на X
с
последующим вычитанием из
результата полинома Xn+1,
если его порядок >
п.
Проверим это на
примере.
Пусть требуется
выполнить циклический сдвиг влево на
одну позицию
коэффициентов
полинома
C(X)=X5+Х3+X2+1
→ (101101)
В результате должен
получиться полином
C1(X)=X4+Х3+X1+1
→ (011011)
Это легко
доказывается:
C1(X)=C(X)*X-(X6+1)=(X6+Х4+X3+X)+(
X6+1)=X4+Х3+X1+1
В
основе циклического кода лежит образующий
полином r-го
порядка
(напомним, что r—
число дополнительных разрядов). Будем
обозначать
его gr(X).
Образование
кодовых слов (кодирование) КС
выполняется
путем умножения
информационного полинома с коэффициентами,
являющимися информационной
последовательностью
И(Х)
порядка
i<k
на
образующий полином gr(X)
КСr+k(Х)=gr(X)+ИСk(Х).
Принятое кодовое
слово может отличаться от переданного
искаженными разрядами в результате
воздействия помех.
ПКС(Х)=КС(Х)+ВО(Х).
где
ВО(Х)
— полином
вектора ошибки, а суммирование, как
обычно, ведется
по модулю 2.
Декодирование,
как и раньше начинается с нахождения
опознавателя,
в данном случае в виде полинома ОП(Х).
Этот
полином вычисляется как
остаток от деления полинома принятого
кодового слова ПКС(Х)
на
образующий
полином g(Х):
Первое
слагаемое остатка не имеет, т.к. кодовое
слово было образовано путем умножения
полинома информационной последовательности
на
образующий полином. Следовательно, и в
данном случае опознаватель
полностью зависит от вектора ошибки.
Образующий
полином выбирается таким, чтобы при
данном r
как
можно
большее число отношений ВО(Х)/g(Х)
давало
различные остатки.
Такому
требованию отвечают так называемые
неприводимые
полиномы,
которые
не делятся без остатка ни на один полином
степени r
и ниже, а
делятся только сами на себя и на 1.
Приведенная
здесь процедура образования кодового
слова неудобна тем,
что такой код получается несистематическим,
т.е. таким, в кодовых словах
которого нельзя выделить информационные
и дополнительные разряды.
Этот недостаток
был устранен следующим образом.
Способ
кодирования, приводящий к получению
систематического линейного циклического
кода, состоит в приписывании к
информационной
последовательности И
дополнительных разрядов ДР.
Эти
дополнительные разряды предлагается
находить по следующей формуле:
Порядок
полинома ДР(Х)
гарантировано
меньше r
(поскольку
это остаток).
Приписывание
дополнительных разрядов к информационной
последовательности,
используя алгебру полиномов, можно
описать формулой:
Одним
из свойств циклических линейных кодов
является то, что результат
деления любого разрешенного кодового
слова КС
на
образующий полином также, является
разрешенным кодовым словом.
Покажем,
что получаемые по вышеприведенному
алгоритму кодовые
слова являются кодовыми словами
циклического линейного кода. Для
этого нужно убедиться в том, что
произвольное разрешенное кодовое
слово делится на образующий полином
g(X)
без остатка:
Рассмотрим первое
слагаемое:
где
d(Х)
— целая
часть результата деления.
Подставим полученную
сумму на место первого слагаемого:
Суммирование
последних двух слагаемых дает нулевой
результат (напомним,
что суммирование выполняется по модулю
2).
Значит
—
целая часть деления. Остатка нет. Это
означает,
что описанный выше способ кодирования
соответствует циклическому
коду.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Hamming-Code (a systematic coding)
The Hamming code is self-checking and self-correcting code. Built in relation to the binary number system. Allows you to fix a single error and find a double one. Written in python 3 using the Numpy library.
In this work, a systematic coding is considered, where a systematic code is a code for which the first k characters of a word correspond to message i.
The pictures below show the following: x1, x2, x3, x4 — message, a1, a2, a3 — control bits.
Блок-схема к программной реализации кодера
Блок-схема к программной реализации декодера
Coding algorithm
The input receives 4 bits of the original text, then we multiply this vector of the original message by the generating matrix G. As a result of multiplication, we get the encoded text with three control bits at the end.
Decoding algorithm
We have received a message from the sender on a communication channel in which there may be interference. There is a possibility that the transmitted text was distorted as a result of interference. In order to determine if there is an error, multiply F ‘by the matrix H and get the syndrome.
Syndrome zero (000) indicates that there are no or no reception errors.
Otherwise, a certain configuration of errors corresponds to any syndrome; they are corrected using a matrix of single errors E. As a result, we get the original text.
Кодирование
Коды Хэмминга позволяют исправлять одиночную ошибку в блоке.
Построение кодов Хэмминга основано на принципе проверки на четность числа единичных символов: к последовательности добавляется такой элемент, чтобы число единичных символов в получившейся последовательности было четным.
Рассмотрим классический код Хемминга (7, 4 ).
Составим матрицу преобразования, состоящую из 7 столбцов и 3-х строк.
Где количество столбцов — это кол-во битов в закодированном слове, а кол-во строк показывает количество проверочных битов.
Хэмминг предложил построить матрицу следующим образом, где каждый столбец проверочной матрицы будет соответствовать битовому представлению номера разряда числа, которому он соответствует.
Так выглядит данная матрица:
Эта матрица должна иметь систематический вид, поэтому приведем ее к каноническому виду. Мы переставим в конец столбцы с одной единицей. Тогда матрица H примет вид:
Теперь нам нужно построить порождающую матрицу G из матрицы Н.
Проверочная матрица H в каноническом виде имеет вид: H=(An−k,k | En−k), а порождающая матрица G: G = (Ek | A⊤n−k, k). Матрице E принадлежат столбцы с одной единицей => возьмем матрицу А из матрицы H:
Тогда транспонированная матрица А будет иметь вид:
Ek — матрица со столбцами с одной единицей, где k = числу информационных битов:
Теперь составим порождающую матрицу G:
Правило формирования проверочных символов составим по вышеупомянутой матрице:
Теперь можно произвести алгоритм кодирования:
(i1 i2 i3 i4) — информационные биты, то есть, кодируемый текст, а ( r1 r2 r3 ) — контрольные биты. ( i1 i2 i3 i4 r1 r2 r3 ) — кодовое слово.
Декодирование
Транспонированная матрица H будет иметь вид:
Предположим, что на вход декодера для (7,4)-кода Хэмминга поступает кодовое слово
Штрих означает, что любой символ слова может быть искажен помехой в канале связи и возникает ошибка E
В декодере в режиме исправления ошибок строится последовательность синдромов:
S = (S1, S2, S3) называется синдромом последовательности.
Получение синдрома происходит по такому выражению:
И выглядит следующим образом:
В данном случае синдром S представляет собой сочетание результатов проверки на четность соответствующих символов кодовой группы и характеризует определенную конфигурацию ошибок(вектор ошибок).
Число возможных синдромов определяется выражением 2^3=8
При числе проверочных символов имеется восемь возможных синдромов (2^3 = 8).
Для определения и исправления искаженного разряда можно использовать матрицу E одиночных ошибок (а можно пользоваться и просто матрицей H
Данная матрица одиночных ошибок выглядит так:
При определении синдрома в проверочной матрице находится комбинация синдрома. Искаженный разряд – это разряд в данной строке, в которой стоит «1». Искаженный разряд исправляем посредством сложения строки в матрице ошибок полученной комбинации
Аннотация: Контроль по четности, CRC, алгоритм Хэмминга. Введение в коды Рида-Соломона: принципы, архитектура и реализация. Метод коррекции ошибок FEC (Forward Error Correction).
Каналы передачи данных ненадежны (шумы, наводки и т.д.), да и само оборудование обработки информации работает со сбоями. По этой причине важную роль приобретают механизмы детектирования ошибок. Ведь если ошибка обнаружена, можно осуществить повторную передачу данных и решить проблему. Если исходный код по своей длине равен полученному коду, обнаружить ошибку передачи не предоставляется возможным. Можно, конечно, передать код дважды и сравнить, но это уже двойная избыточность.
Простейшим способом обнаружения ошибок является контроль по четности. Обычно контролируется передача блока данных ( М бит). Этому блоку ставится в соответствие кодовое слово длиной N бит, причем N>M. Избыточность кода характеризуется величиной 1-M/N. Вероятность обнаружения ошибки определяется отношением M/N (чем меньше это отношение, тем выше вероятность обнаружения ошибки, но и выше избыточность).
При передаче информации она кодируется таким образом, чтобы с одной стороны характеризовать ее минимальным числом символов, а с другой – минимизировать вероятность ошибки при декодировании получателем. Для выбора типа кодирования важную роль играет так называемое расстояние Хэмминга.
Пусть А и Б — две двоичные кодовые последовательности равной длины. Расстояние Хэмминга между двумя этими кодовыми последовательностями равно числу символов, которыми они отличаются. Например, расстояние Хэмминга между кодами 00111 и 10101 равно 2.
Можно показать, что для детектирования ошибок в n битах схема кодирования требует применения кодовых слов с расстоянием Хэмминга не менее N + 1. Можно также показать, что для исправления ошибок в N битах необходима схема кодирования с расстоянием Хэмминга между кодами не менее 2N + 1. Таким образом, конструируя код, мы пытаемся обеспечить расстояние Хэмминга между возможными кодовыми последовательностями большее, чем оно может возникнуть из-за ошибок.
Широко распространены коды с одиночным битом четности. В этих кодах к каждым М бит добавляется 1 бит, значение которого определяется четностью (или нечетностью) суммы этих М бит. Так, например, для двухбитовых кодов 00, 01, 10, 11 кодами с контролем четности будут 000, 011, 101 и 110. Если в процессе передачи один бит будет передан неверно, четность кода из М+1 бита изменится.
Предположим, что частота ошибок ( BER – Bit Error Rate) равна р = 10-4. В этом случае вероятность передачи 8 бит с ошибкой составит 1 – (1 – p)8 = 7,9 х 10-4. Добавление бита четности позволяет детектировать любую ошибку в одном из переданных битах. Здесь вероятность ошибки в одном из 9 битов равна 9p(1 – p)8. Вероятность же реализации необнаруженной ошибки составит 1 – (1 – p)9 – 9p(1 – p)8 = 3,6 x 10-7. Таким образом, добавление бита четности уменьшает вероятность необнаруженной ошибки почти в 1000 раз. Использование одного бита четности типично для асинхронного метода передачи. В синхронных каналах чаще используется вычисление и передача битов четности как
для строк, так и для столбцов передаваемого массива данных. Такая схема позволяет не только регистрировать, но и исправлять ошибки в одном из битов переданного блока.
Контроль по четности достаточно эффективен для выявления одиночных и множественных ошибок в условиях, когда они являются независимыми. При возникновении ошибок в кластерах бит метод контроля четности неэффективен, и тогда предпочтительнее метод вычисления циклических сумм ( CRC — Cyclic Redundancy Check). В этом методе передаваемый кадр делится на специально подобранный образующий полином. Дополнение остатка от деления и является контрольной суммой.
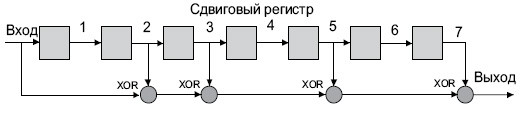
В Ethernet вычисление CRC производится аппаратно. На
рис.
4.1 показан пример реализации аппаратного расчета CRC для образующего полинома R(x) = 1 + x2 + x3 + x5 + x7. В этой схеме входной код приходит слева.
Рис.
4.1.
Схема реализации расчета CRC
Эффективность CRC для обнаружения ошибок на многие порядки выше простого контроля четности. В настоящее время стандартизовано несколько типов образующих полиномов. Для оценочных целей можно считать, что вероятность невыявления ошибки в случае использования CRC, если ошибка на самом деле имеет место, равна (1/2)r, где r — степень образующего полинома.
| CRC -12 | x12 + x11 + x3 + x2 + x1 + 1 |
| CRC -16 | x16 + x15 + x2 + 1 |
| CRC -CCITT | x16 + x12 + x5 + 1 |
4.1. Алгоритмы коррекции ошибок
Исправлять ошибки труднее, чем их детектировать или предотвращать. Процедура коррекции ошибок предполагает два совмещеных процесса: обнаружение ошибки и определение места (идентификации сообщения и позиции в сообщении). После решения этих двух задач исправление тривиально — надо инвертировать значение ошибочного бита. В наземных каналах связи, где вероятность ошибки невелика, обычно используется метод детектирования ошибок и повторной пересылки фрагмента, содержащего дефект. Для спутниковых каналов с типичными для них большими задержками системы коррекции ошибок становятся привлекательными. Здесь используют коды Хэмминга или коды свертки.
Код Хэмминга представляет собой блочный код, который позволяет выявить и исправить ошибочно переданный бит в пределах переданного блока. Обычно код Хэмминга характеризуется двумя целыми числами, например, (11,7), используемыми при передаче 7-битных ASCII-кодов. Такая запись говорит, что при передаче 7-битного кода используется 4 контрольных бита (7 + 4 = 11). При этом предполагается, что имела место ошибка в одном бите и что ошибка в двух или более битах существенно менее вероятна. С учетом этого исправление ошибки осуществляется с определенной вероятностью. Например, пусть возможны следующие правильные коды (все они, кроме первого и последнего, отстоят друг от друга на расстояние Хэмминга 4):
00000000
11110000
00001111
11111111
При получении кода 00000111 нетрудно предположить, что правильное значение полученного кода равно 00001111. Другие коды отстоят от полученного на большее расстояние Хэмминга.
Рассмотрим пример передачи кода буквы s = 0x073 = 1110011 с использованием кода Хэмминга (11,7). Таблица 4.2.
| Позиция бита | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение бита | 1 | 1 | 1 | * | 0 | 0 | 1 | * | 1 | * | * |
Символами * помечены четыре позиции, где должны размещаться контрольные биты. Эти позиции определяются целой степенью 2 (1, 2, 4, 8 и т.д.). Контрольная сумма формируется путем выполнения операции XoR (исключающее ИЛИ) над кодами позиций ненулевых битов. В данном случае это 11, 10, 9, 5 и 3. Вычислим контрольную сумму:
| 11= | 1011 |
| 10= | 1010 |
| 09= | 1001 |
| 05= | 0101 |
| 03= | 0011 |
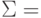 |
1110 |
Таким образом, приемник получит код
| Позиция бита | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение бита | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
Просуммируем снова коды позиций ненулевых битов и получим нуль;
| 11= | 1011 |
| 10= | 1010 |
| 09= | 1001 |
| 08= | 1000 |
| 05= | 0101 |
| 04= | 0100 |
| 03= | 0011 |
| 02= | 0010 |
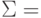 |
0000 |
Ну а теперь рассмотрим два случая ошибок в одном из битов посылки, например в бите 7 (1 вместо 0) и в бите 5 (0 вместо 1). Просуммируем коды позиций ненулевых битов еще раз:
|
|
В обоих случаях контрольная сумма равна позиции бита, переданного с ошибкой. Теперь для исправления ошибки достаточно инвертировать бит, номер которого указан в контрольной сумме. Понятно, что если ошибка произойдет при передаче более чем одного бита, код Хэмминга при данной избыточности окажется бесполезен.
В общем случае код имеет N = M + C бит и предполагается, что не более чем один бит в коде может иметь ошибку. Тогда возможно N+1 состояние кода (правильное состояние и n ошибочных). Пусть М = 4, а N = 7, тогда слово-сообщение будет иметь вид: M4, M3, M2, C3, M1, C2, C1. Теперь попытаемся вычислить значения С1, С2, С3. Для этого используются уравнения, где все операции представляют собой сложение по модулю 2:
С1 = М1 + М2 + М4 С2 = М1 + М3 + М4 С3 = М2 + М3 + М4
Для определения того, доставлено ли сообщение без ошибок, вычисляем следующие выражения (сложение по модулю 2):
С11 = С1 + М4 + М2 + М1 С12 = С2 + М4 + М3 + М1 С13 = С3 + М4 + М3 + М2
Результат вычисления интерпретируется следующим образом:
| C11 | C12 | C13 | Значение |
|---|---|---|---|
| 1 | 2 | 4 | Позиция бит |
| 0 | 0 | 0 | Ошибок нет |
| 0 | 0 | 1 | Бит С3 неверен |
| 0 | 1 | 0 | Бит С2 неверен |
| 0 | 1 | 1 | Бит M3 неверен |
| 1 | 0 | 0 | Бит С1 неверен |
| 1 | 0 | 1 | Бит M2 неверен |
| 1 | 1 | 0 | Бит M1 неверен |
| 1 | 1 | 1 | Бит M4 неверен |
Описанная схема легко переносится на любое число n и М.
Число возможных кодовых комбинаций М помехоустойчивого кода делится на n классов, где N — число разрешенных кодов. Разделение на классы осуществляется так, чтобы в каждый класс вошел один разрешенный код и ближайшие к нему (по расстоянию Хэмминга ) запрещенные коды. В процессе приема данных определяется, к какому классу принадлежит пришедший код. Если код принят с ошибкой, он заменяется ближайшим разрешенным кодом. При этом предполагается, что кратность ошибки не более qm.
В теории кодирования существуют следующие оценки максимального числа N n -разрядных кодов с расстоянием D.
| d=1 | n=2n |
| d=2 | n=2n-1 |
| d=3 | N 2n/(1 + n) |
| d = 2q + 1 | (для кода Хэмминга это неравенство превращается в равенство) |
В случае кода Хэмминга первые k разрядов используются в качестве информационных, причем
K = n – log(n + 1), откуда следует (логарифм по основанию 2), что k может принимать значения 0, 1, 4, 11, 26, 57 и т.д., это и определяет соответствующие коды Хэмминга (3,1); (7,4); (15,11); (31,26); (63,57) и т.д.
Обобщением кодов Хэмминга являются циклические коды BCH (Bose-Chadhuri-hocquenghem). Эти коды имеют широкий выбор длин и возможностей исправления ошибок.
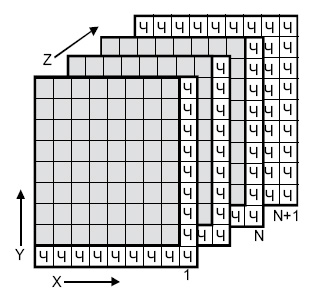
Одной из старейших схем коррекции ошибок является двух-и трехмерная позиционная схема (
рис.
4.2). Для каждого байта вычисляется бит четности (бит <Ч>, направление Х). Для каждого столбца также вычисляется бит четности (направление Y. Производится вычисление битов четности для комбинаций битов с координатами (X,Y) (направление Z, слои с 1 до N ). Если при транспортировке будет искажен один бит, он может быть найден и исправлен по неверным битам четности X и Y. Если же произошло две ошибки в одной из плоскостей, битов четности данной плоскости недостаточно. Здесь поможет плоскость битов четности N+1.
Таким образом, на 512 передаваемых байтов данных пересылается около 200 бит четности.
Рис.
4.2.
Позиционная схема коррекции ошибок