Абсолютная ошибка опыта - Решение и исправление самых разных ошибок на TopOshibok.ru

где
— абсолютное значение разности между
величинойх_i,
полученной вi– том измерении и
средним значением <х>. Абсолютная
погрешность опыта характеризует таким
образом качество проведённых измерений,
т. е. указывает, на сколько истинное
значение измеряемой величины может
отличаться от значения, измеренного в
опыте.

3. Для оценки точности, с которой
определена измеряемая величина,
используется понятие относительной
погрешности:

Таким образом, относительная погрешность
показывает, какая часть абсолютной
погрешности приходится на каждую единицу
измеряемой величины.

Пример. При измерении толщиныh
стеклянной пластинки с помощью
микрометра было сделано четыре измерения,
результаты которых занесены в табл. 1:

Таблица 1.

Результаты измерений толщины стеклянной
пластинки

№ измерения	h, мм	< h>, мм	Δ h_i, мм	Δ h, мм	ε_h, %
1	3,82	3,84	— 0,02	0,03	0,8
2	3,85	+ 0,01
3	3,89	+ 0,05
4	3,80	— 0,04

По данным таблицы рассчитываем среднее
значение толщины:

Определяем абсолютную погрешность
опыта (серии измерений):

Определяем относительную погрешность:

При косвенных измеренияхискомую
величину вычисляют по результатам
прямого измерения других величин,
связанных с искомой определённой
функциональной зависимостьюy = f
(x₁,х₂,…,х_n).

Абсолютная и относительная погрешности
некоторых простейших функций приведены
в табл.2.

Таблица 2

Погрешности при косвенных измерениях
в простейших случаях

Вид функции	Абсолютная погрешность Δy	Относительная погрешность ε_y
1	2	3
x₁ + x₂	Δ x₁ + Δ x₂
1	2	3
x₁ — x₂	Δ x₁ + Δ x₂
x₁ x₂	x₁ Δ x₂ + x₂ Δ x₁	ε_x₁ + ε_x₂
x₁ / x₂		ε_x₁ + ε_x₂
xⁿ	nx^n-¹ Δ x	nε_x

e^x	e^x Δ x	Δx

Когда функция y = f (x₁,х₂,…,х_n)удобна для логарифмирования, то вначале
лучше рассчитать относительную
погрешность ε_yфункции (в %) и затем её абсолютную
погрешность

Пример. Ускорение свободного паденияgопределяется по результатам
измерений периодов колебанийТ₁иТ₂двух математических
маятников с длинамиl₁иl₂соответственно (l₁>l₂)
по формуле

где a= l₁—l₂.
Логарифмирование даёт lng=ln(4π²)
+lna–ln.
После дифференцирования lngс заменамиdaна ΔaиdТна ΔТполучим:

(предполагается, что погрешности
независимых измерений Δa,ΔТ₁и ΔТ₂усиливают
друг друга, и поэтому их влияние
учитывается в формуле со знаком плюс).
Затем найдём абсолютную погрешность

,
где.

Окончательный результат вычислений
– среднее арифметическое измеряемой
величины записывают в виде числа из
нескольких разрядов. Цифры в этом числе
делятся на значащие и незначащие. К
значащим цифрам относятся все верные
и сомнительные цифры. К незначащим
относятся: а) нули в начале числа,
определяющие разряды десятичных дробей
в числах меньших единицы; б) нули в конце
числа, заменившие цифры после округления;
в) неверные цифры, если они не были
отброшены.

Для определения значащих цифр в
результате измерения необходимо
вычислить абсолютную погрешность опыта,
числовое значение которой тоже может
содержать несколько разрядов. Но
абсолютная погрешность показывает, в
каком разряде полученного результата
содержится неточность. Поэтому её
числовое значение всегда округляется
до одной значащей цифры, кроме того, в
случае когда эта цифра представляет
единицу – в этом случае округление
производится до цифры первого младшего
разряда. Тогда сохранение цифр меньших
разрядов в среднем арифметическом
измеряемой величины теряет смысл.

Пример. В нескольких опытах по
результатам измерений периода колебаний
математического маятника было проведено
с различной погрешностью определение
ускорения свободного падения:

неправильная запись результата
правильная запись результата

g= (10,1835±0,433) м/с²g=
(10,2±0,4) м/с²

g= (9,8167±0,053) м/с²g=
(9,82±0,05) м/с²

g= (9,9423±0,132) м/с²g=
(9,94 ±0,13) м/с²

g= (10,8261±2,026) м/с²g=
(11±2) м/с²

При записи измеренного значения х
последней, таким образом, должна
указываться цифра того десятичного
разряда, который был использован при
указании погрешности. Это правило должно
соблюдаться и в тех случаях, когда
некоторые из цифр являются нулями.
Пусть, например, при вычислении gв
предыдущем опыте было получено значение
9,88 м/с²(точно), а погрешность
составила ± 0,004 м/с², то окончательный
результат следует представить в таком
виде:

g= 9,880± 0,004 м/с².

При записи окончательного результата
измерения наряду с основными единицами
СИ и производными от них допускаются к
применению кратные единицы (например,
см, МПа, мВ и т.д.) в тех случаях, когда
это упрощает запись. Полученные в ходе
эксперимента результаты часто изображают
в виде графика.

При построении графика чаще всего
пользуются прямоугольной системой
координат, причем значения аргумента
откладывают по горизонтальной оси, а
значения функции по вертикальной оси.
Начало координат не обязательно должно
совпадать с нулевыми значениями функции
и аргумента. При выборе масштаба величин,
откладываемых на осях координат, исходят
из того, чтобы получить примерно равные
отрезки, которые соответствуют
установленным в опыте интервалам
численных значений функции и аргумента.
Например, по результатам измерения
показателя преломления п водного
раствора глюкозы был построен графикп= п(с), гдес — концентрация
глюкозы (рис.1). На рис.1а график удовлетворяет
необходимым требованиям. На рис. 1б
из-за неудачного выбора масштаба и
начала отсчета дляпзависимостьп(с)почти незаметна, и такой график
бесполезен для практического применения.

Рис. 1

Использование гpафических методов
облегчается в тех случаях, когда гpафик
представляет собой прямую линию. С целью
«спрямления» гpафика исследуемой
зависимости, имеющей сложный характер,
целесообразно использовать нелинейные
шкалы, например, логарифмическую,
квадратичную и т.д. или откладывать не
сами величины аргумента и функции, а их
логарифмы, степени, обратные значения.
Например, в работе «Исследование
теплового излучения чёрного тела» с
целью экспериментальной проверки закона
Стефана – Больцмана

R_э=σТ⁴,

где R_э–
энергетическая светимость тела, аТ– его абсолютная температура, по оси
абсцисс откладывают Т, а по оси ординат
—.

Выбрав рациональные масштаб и размеры
гpафика, на координатные оси наносят
деления через 10-20 мм и обозначают их.
Затем наносят экспериментальные точки,
с которыми совмещают прямоугольные
крестики, размеры которых вдоль осей
координат ОхиОуравны удвоенным
погрешностям соответственно 2Δхи
2Δув выбранном масштабе. По отмеченным
точкам проводят линию так, чтобы она
прошла как можно ближе к экспериментальным
точкам, и чтобы равное количество их
оказалось по обе стороны от этой линии.

Для построения графиков, как правило,
используют масштабно-координатную
(миллиметровую) бумагу.

Если в лабораторной работе по графику
определяется какая-либо константа,
например, как угловой коэффициент
экспериментальной прямой y = x₀+kx,
то в этом случае тангенс угла α наклона
прямой к оси абсцисс может быть определён
только с учётом соответствующих масштабов
и единиц измерения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Таблица 1.

Результаты измерений толщины стеклянной
пластинки

№ измерения	h, мм	< h>, мм	Δ h_i, мм	Δ h, мм	ε_h, %
1	3,82	3,84	— 0,02	0,03	0,8
2	3,85	+ 0,01
3	3,89	+ 0,05
4	3,80	— 0,04

По данным таблицы рассчитываем среднее
значение толщины:

Определяем абсолютную погрешность
опыта (серии измерений):

Определяем относительную погрешность:

Абсолютная и относительная погрешности
некоторых простейших функций приведены
в табл.2.

Таблица 2

Погрешности при косвенных измерениях
в простейших случаях

Вид функции	Абсолютная погрешность Δy	Относительная погрешность ε_y
1	2	3
x₁ + x₂	Δ x₁ + Δ x₂
1	2	3
x₁ — x₂	Δ x₁ + Δ x₂
x₁ x₂	x₁ Δ x₂ + x₂ Δ x₁	ε_x₁ + ε_x₂
x₁ / x₂		ε_x₁ + ε_x₂
xⁿ	nx^n-¹ Δ x	nε_x

e^x	e^x Δ x	Δx

где a= l₁—l₂.
Логарифмирование даёт lng=ln(4π²)
+lna–ln.
После дифференцирования lngс заменамиdaна ΔaиdТна ΔТполучим:

,
где.

неправильная запись результата
правильная запись результата

g= (10,1835±0,433) м/с²g=
(10,2±0,4) м/с²

g= (9,8167±0,053) м/с²g=
(9,82±0,05) м/с²

g= (9,9423±0,132) м/с²g=
(9,94 ±0,13) м/с²

g= (10,8261±2,026) м/с²g=
(11±2) м/с²

g= 9,880± 0,004 м/с².

Рис. 1

R_э=σТ⁴,

Для построения графиков, как правило,
используют масштабно-координатную
(миллиметровую) бумагу.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Подборка по базе: Исправьте ошибки в построении сложных предложений.docx, тест 1 теория и методика основы физического воспитания.docx, Найдите и исправьте ошибки в словоупотреблении.docx, тест 1 теория и методика основы физического воспитания.docx, № Правильно ли сформулированы следующие вопросы. Найдите ошибки., Памятка для родителей Как помочь ребенку победить ошибки 1.doc, Конспект урока по алгебре в 9 классе на тему _Абсолютная и относ, математика — Какие ошибки допускают младшие школьники при делени, Речевые ошибки.docx, Инструкция по устранению ошибки со входом в phpMyAdmin (1).docx

Ч а с т ь I

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК

Абсолютная и относительная ошибки

Никакую физическую величину невозможно измерить абсолютно точно: как бы тщательно ни был поставлен опыт, измеренное значение величины х будет отличаться от ее истинного значения Х. Разница между этими значениями представляет собой абсолютную ошибку (или абсолютную погрешность^{^*}) измерения х:

х = х – Х. (1)

Абсолютная погрешность является размерной величиной: она выражается в тех же единицах, что и сама измеряемая величина (например, абсолютная погрешность измерения длины выражается в метрах, силы тока – в амперах и т.д.). Как следует из выражения (1), х может быть как положительной, так и отрицательной величиной.

Хотя величина х показывает, насколько измеренное значение отличается от истинного, одной лишь абсолютной ошибкой нельзя полностью характеризовать точность проделанного измерения. Пусть, например, известно, что абсолютная погрешность измерения расстояния равна 1 м. Если измерялось расстояние между географическими пунктами (порядка нескольких километров), то точность такого измерения следует признать весьма высокой; если же измерялись размеры помещения (не превышающие десятка метров), то измерение является грубым. Для характеристики точности существует понятие относительной ошибки (или относительной погрешности) Е, представляющей собой отношение модуля абсолютной ошибки к измеряемой величине:

. (2)

Очевидно, что относительная погрешность – величина безразмерная, чаще всего ее выражают в процентах.

При определении ошибок измерений важно иметь в виду следующее. Выражения (1) и (2) содержат истинное значение измеряемой величины Х, которое точно знать невозможно: поэтому значения х и Е в принципе не могут быть рассчитаны точно. Можно лишь оценить эти значения, т.е. найти их приближенно с той или иной степенью достоверности. Поэтому все расчеты, связанные с определением погрешностей, должны носить приближенный (оценочный) характер.

Случайная и приборная погрешности

Разнообразные ошибки, возникающие при измерениях, можно классифицировать как по их происхождению, так и по характеру их проявления.

По происхождению ошибки делятся на инструментальные и методические.

Инструментальные погрешности обусловлены несовершенством применяемых измерительных приборов и приспособлений. Эти погрешности могут быть уменьшены за счет применения более точных приборов. Так, размер детали можно измерить линейкой или штанген-циркулем. Очевидно, что во втором случае ошибка измерения меньше, чем в первом.

Методические погрешности возникают из-за того, что реальные физические процессы всегда в той или иной степени отличаются от их теоретических моделей. Например, формула для периода колебаний математического маятника в точности верна лишь при бесконечно малой амплитуде колебаний; формула Стокса, определяющая силу трения при движении шарика в вязкой жидкости, справедлива только в случае идеально сферической формы и т.д. Обнаружить и учесть методическую погрешность можно путем измерения той же величины совершенно иным независимым методом.

По характеру проявления ошибки бывают систематические и случайные.

Систематическая погрешность может быть обусловлена как приборами, так и методикой измерения. Она имеет две характерные особенности. Во-первых, систематическая погрешность всегда либо положительна, либо отрицательна и не меняет своего знака от опыта к опыту. Во-вторых, систематическую погрешность нельзя уменьшить за счет увеличения числа измерений. Например, если при отсутствии внешних воздействий стрелка измерительного прибора показывает величину х₀, отличную от нуля, то во всех дальнейших измерениях будет присутствовать систематическая ошибка, равная х₀.

Случайная ошибка также может быть как инструментальной, так и методической. Причину ее появления установить трудно, а чаще всего – невозможно (это могут быть различные помехи, случайные толчки, вибрации, неверно взятый отсчет по прибору и т.д.). Случайная погрешность бывает и положительной и отрицательной, причем непредсказуемо изменяет свой знак от опыта к опыту. Значение ее можно уменьшить путем увеличения числа измерений.

Детальный анализ погрешностей измерения представляет собой сложную задачу, для решения которой не существует единого рецепта. Поэтому в каждом конкретном случае этот анализ проводят по-разному. Однако, в первом приближении, если исключена систематическая ошибка, то остальные можно условно свести к следующим двум видам: приборная и случайная.

Приборной погрешностью в дальнейшем будем называть случайную ошибку, обусловленную измерительными приборами и приспособлениями, а случайной – ошибку, причина появления которой неизвестна. Приборную погрешность измерения величины х будем обозначать как х, случайную – как _sx.

Оценка случайной погрешности. Доверительный интервал

Методика оценки случайной погрешности основана на положениях теории вероятностей и математической статистики. Оценить случайную ошибку можно только в том случае, когда проведено неоднократное измерение одной и той же величины.

Пусть в результате проделанных измерений получено п значений величины х: х₁, х₂, …, х_п. Обозначим через среднеарифметическое значение

. (3)

В теории вероятностей доказано, что при увеличении числа измерений п среднеарифметическое значение измеряемой величины приближается к истинному:

При небольшом числе измерений (п  10) среднее значение может существенно отличаться от истинного. Для того, чтобы знать, насколько точно значение характеризует измеряемую величину, необходимо определить так называемый доверительный интервал полученного результата.

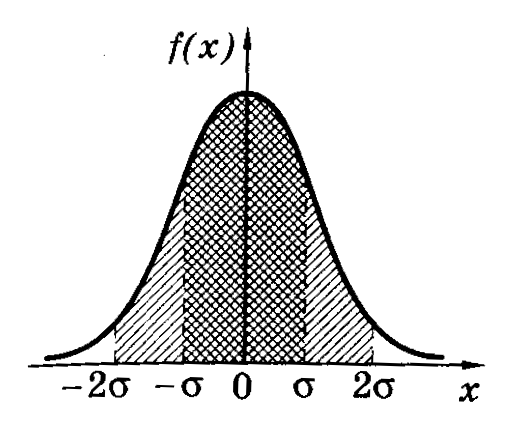
Поскольку абсолютно точное измерение невозможно, то вероятность правильности утверждения «величина х имеет значение, в точности равное » равна нулю. Вероятность же утверждения «величина х имеет какое-либо значение» равна единице (100%). Таким образом, вероятность правильности любого промежуточного утверждения лежит в пределах от 0 до 1. Цель измерения – найти такой интервал, в котором с наперед заданной вероятностью (0 <  < 1) находится истинное значение измеряемой величины. Этот интервал называется доверительным интервалом, а неразрывно связанная с ним величина  – доверительной вероятностью (или коэффициентом надежности). За середину интервала принимается среднее значение, рассчитанное по формуле (3). Половина ширины доверительного интервала представляет собой случайную погрешность _sx (рис. 1).

Рис.1
Очевидно, что ширина доверительного интервала (а следовательно, и ошибка _sx) зависит от того, насколько сильно отличаются отдельные измерения величины х_i от среднего значения . «Разброс» результатов измерений относительно среднего характеризуется среднеквадратичной ошибкой , которую находят по формуле

, (4)

где .

Ширина искомого доверительного интервала прямо пропорциональна среднеквадратичной ошибке:

. (5)

Коэффициент пропорциональности t_n,_ называется коэффициентом Стьюдента; он зависит от числа опытов п и доверительной вероятности .

На рис. 1, а, б наглядно показано, что при прочих равных условиях для увеличения вероятности попадания истинного значения в доверительный интервал необходимо увеличить ширину последнего (вероятность «накрывания» значения Х более широким интервалом выше). Следовательно, величина t_n,_ должна быть тем больше, чем выше доверительная вероятность .

С увеличением количества опытов среднее значение приближается к истинному; поэтому при той же вероятности  доверительный интервал можно взять более узким (см. рис. 1, а,в). Таким образом, с ростом п коэффициент Сьюдента должен уменьшаться. Таблица значений коэффи-циента Стьюдента в зависимости от п и  дана в приложениях к настоящему пособию.

Следует отметить, что доверительная вероятность никак не связана с точностью результата измерений. Величиной  задаются заранее, исходя из требований к их надежности. В большинстве технических экспериментов и в лабораторном практикуме значение  принимается равным 0,95.

Расчет случайной погрешности измерения величины х проводится в следующем порядке:

1) вычисляется сумма измеренных значений, а затем – среднее значение величины по формуле (3);

2) для каждого i-го опыта рассчитываются разность между измеренным и средним значениями , а также квадрат этой разности (отклонения) (х_i)²;

3) находится сумма квадратов отклонений, а затем – средне-квадратичная ошибка  по формуле (4);

4) по заданной доверительной вероятности  и числу проведенных опытов п из таблицы на с. 149 приложений выбирается соответствующее значение коэффициента Стьюдента t_n,_ и определяется случайная погрешность _sx по формуле (5).

Для удобства расчетов и проверки промежуточных результатов данные заносятся в таблицу, три последних столбца которой заполняются по образцу табл.1.

Таблица 1

Номер опыта	…	х	х	(х)²
1	…
2	…
…	…
п	…
	 =		 =

В каждом конкретном случае величина х имеет определенный физический смысл и соответствующие единицы измерения. Это может быть, например, ускорение свободного падения g (м/с²), коэффициент вязкости жидкости  (Пас) и т.д. Пропущенные столбцы табл. 1 могут содержать промежуточные измеряемые величины, необходимые для расчета соответствующих значений х.
Пример 1. Для определения ускорения а движения тела измерялось время t прохождения им пути S без начальной скорости. Используя известное соотношение , получим расчетную формулу

. (6)

Результаты измерений пути S и времени t приведены во втором и третьем столбцах табл. 2. Проведя вычисления по формуле (6), заполним

четвертый столбец значениями ускорения a_i и найдем их сумму, которую запишем под этим столбцом в ячейку «  = ». Затем рассчитаем среднее значение по формуле (3)

Таблица 2

Номер опыта	S, м	t, c	а, м/с²	а, м/с²	(а)², (м/с²)²
1	5	2,20	2,07	0,04	0,0016
2	7	2,68	1,95	-0,08	0,0064
3	9	2,91	2,13	0,10	0,0100
4	11	3,35	1,96	-0,07	0,0049
		 =	8,11	 =	0,0229

Вычитая из каждого значения a_i среднее, найдем разности a_i и занесем их в пятый столбец таблицы. Возводя эти разности в квадрат, заполним последний столбец. Затем рассчитаем сумму квадратов отклонений и запишем ее во вторую ячейку «  = ». По формуле (4) определим среднеквадратичную погрешность:

Задавшись величиной доверительной вероятности  = 0,95, для числа опытов п = 4 из таблицы в приложениях (с. 149) выбираем значение коэффициента Стьюдента t_n,_ = 3,18; с помощью формулы (5) оценим случайную погрешность измерения ускорения

_sа = 3,180,0437  0,139 (м/с²) .

Способы определения приборных ошибок

Основными характеристиками измерительных приборов являются предел измерения и цена деления, а также – главным образом для электро-измерительных приборов – класс точности.

Предел измерения П – это максимальное значение величины, которое может быть измерено с помощью данной шкалы прибора. Если предел измерения не указан отдельно, то его определяют по оцифровке шкалы. Так, если рис. 2 изображает шкалу миллиамперметра, то его предел измерения равен 100 мА.

Р
ис.2

Цена деления Ц – значение измеряемой величины, соответствующее самому малому делению шкалы. Если шкала начинается с нуля, то

где N – общее количество делений (например, на рис. 2 N = 50). Если эта шкала принадлежит амперметру с пределом измерения 5 А, то цена деления равна 5/50 = 0,1 (А). Если шкала принадлежит термометру и проградуирована в С, то цена деления Ц = 100/50 = 2 (С). Многие электроизмерительные приборы имеют несколько пределов измерения. При переключении их с одного предела на другой изменяется и цена деления шкалы.

Класс точности К представляет собой отношение абсолютной приборной погрешности к пределу измерения шкалы, выраженное в процентах:

. (7)

Значение класса точности (без символа «%») указывается, как правило, на электроизмерительных приборах.

В зависимости от вида измерительного устройства абсолютная приборная погрешность определяется одним из нижеперечисленных способов.

1. Погрешность указана непосредственно на приборе. Так, на микрометре есть надпись «0,01 мм». Если с помощью этого прибора измеряется, например, диаметр шарика D (лабораторная работа 1.2), то погрешность его измерения D = 0,01 мм. Абсолютная ошибка указывается обычно на жидкостных (ртутных, спиртовых) термометрах, штангенциркулях и др.

2. На приборе указан класс точности. Согласно определению этой величины, из формулы (7) имеем

. (8)

Например, для вольтметра с классом точности 2,5 и пределом измерения 600 В абсолютная приборная ошибка измерения напряжения

3. Если на приборе не указаны ни абсолютная погрешность, ни класс точности, то в зависимости от характера работы прибора возможны два способа определения величины х:

а) указатель значения измеряемой величины может занимать только определенные (дискретные) положения, соответствующие делениям шкалы (например, электронные часы, секундомеры, счетчики импульсов и т.п.). Такие приборы являются приборами дискретного действия, и их абсолютная погрешность равна цене деления шкалы: х = Ц. Так, при измерении промежутка времени t секундомером с ценой деления 0,2 с погрешность t = 0,2 с;

б) указатель значения измеряемой величины может занимать любое положение на шкале (линейки, рулетки, стрелочные весы, термометры и т.п.). В этом случае абсолютная приборная погрешность равна половине цены деления: х = Ц/2. Точность снимаемых показаний прибора не должна превышать его возможностей. Например, при показанном на рис. 3 положении стрелки прибора следует записать либо 62,5 либо 63,0 – в обоих случаях ошибка не превысит половины цены деления. Записи же типа 62,7 или 62,8 не имеют смысла.

Рис.3
4. Если какая-либо величина не измеряется в данном оыте, а была измерена независимо и известно лишь ее значение, то она является заданным параметром. Так, в работе 2.1 по определению коэффициента вязкости воздуха такими параметрами являются размеры капилляра, в опыте Юнга по интерференции света (работа 5.1) – расстояние между щелями и т.д. Погрешность заданного параметра принимается равной половине единицы последнего разряда числа, которым задано значение этого параметра. Например, если радиус капилляра r задан с точностью до сотых долей миллиметра, то его погрешность r = 0,005 мм.

Погрешности косвенных измерений
В большинстве физических экспериментов искомая величина и не измеряется непосредственно каким-либо одним прибором, а рассчитывается на основе измерения ряда промежуточных величин x, y, z,… Расчет проводится по определенной формуле, которую в общем виде можно записать как

и = и(x, y, z,…). (9)

В этом случае говорят, что величина и представляет собой результат косвенного измерения в отличие от x, y, z,…, являющихся результатами прямых измерений. Например, в работе 1.2 коэффициент вязкости жидкости  рассчитывается по формуле

, (10)

где _ш – плотность материала шарика; _ж – плотность жидкости; g – ускорение свободного падения; D – диаметр шарика; t – время его падения в жидкости; l – расстояние между метками на сосуде. В данном случае результатами прямых измерений являются величины l, D и t, а коэффициент вязкости  – результат косвенного измерения. Величины _ш, _ж и g представляют собой заданные параметры.

Абсолютная погрешность косвенного измерения и зависит от погрешностей прямых измерений x, y, z…и от вида функции (9). Как правило, величину и можно оценить по формуле вида

, (11)

где коэффициенты k_x, k_y, k_z,… определяются видом зависимостей величины и от x, y, z,… Приведенная ниже табл. 3 позволяет найти эти коэффициенты для наиболее распространенных элементарных функций (a, b, c, n – заданные константы).

Таблица 3

и(х)	k_x

На практике зависимость (9) чаще всего имеет вид степенной функции

показатели степеней которой k, m, n,… – вещественные (положительные или отрицательные, целые или дробные) числа; С – постоянный коэффициент. В этом случае абсолютная приборная погрешность и оценивается по формуле

, (12)

где – среднее значение величины и; – относительные приборные погрешности прямых измерений величин x, y, z,… Для подстановки в формулу (12) выбираются наиболее представительные, т.е. близкие к средним значения x, y, z,…

При расчетах по формулам типа (12) необходимо помнить следующее.

1. Измеряемые величины и их абсолютные погрешности (например, х и х) должны быть выражены в одних и тех же единицах.

2. Расчеты не требуют высокой точности вычислений и должны иметь оценочный характер. Так, входящие в подкоренное выражение и возводимые в квадрат величины (kE_x, mE_y, nE_z,…) обычно округляются с точностью до двух значащих цифр (напомним, что ноль является значащей цифрой только тогда, когда перед ним слева есть хотя бы одна цифра, отличная от нуля). Далее, если одна из этих величин (например, |kE_x|)по модулю превышает наибольшую из остальных (|mE_y|, |nE_z|,…) более чем в три раза, то можно, не прибегая к вычислениям по формуле (12), принять абсолютную ошибку равной . Если же одна из них более чем в три раза меньше наименьшей из остальных, то при расчете по формуле (12) ею можно пренебречь.
Пример 2. Пусть при определении ускорения тела (см. пример 1) путь S измерялся рулеткой с ценой деления 1 мм, а время t – электронным секундомером. Тогда, в соответствии с изложенными в п.3, а, б (с. 13) правилами, погрешности прямых измерений будут равны

S = 0,5 мм = 0,0005 м;

t = 0,01 с.

Расчетную формулу (6) можно записать в виде степенной функции

a(S, t) = 2S¹t^– 2;

тогда на основании (12) погрешность косвенного измерения ускорения а определится выражением

В качестве наиболее представительных значений измеренных величин возьмем (см. табл. 2) S  8 м; t  3 с и оценим по модулю относительные приборные ошибки прямых измерений с учетом их весовых коэффициентов:

;

Очевидно, что в данном случае величиной E_S можно пренебречь и принять погрешность а равной

Пример 3. Вернемся к определению коэффициента вязкости жидкости (работа 1.2). Расчетную формулу (10) можно представить в виде

где . Тогда для оценки приборной погрешности , согласно (12), получим выражение

, (13)

где .

Пусть расстояние между метками l измерено сантиметровой лентой с ценой деления 0,5 см, диаметр шарика – микрометром, время его падения – электронным секундомером. Тогда l = 0,25 см; D = 0,01 мм; t = 0,01 с. Предположим, что измеренные значения равны: l  80 cм; D  4 мм; t  10 с; Пас. Оценим величины, входящие в формулу (13):

Пренебрегая величиной Е_t, проведем расчет по формуле (13):

.
Полная ошибка. Окончательный результат измерений
В результате оценки случайной и приборной ошибок измерения величины х получено два доверительных интервала, характеризуемые значениями _sx и х. Результирующий доверительный интервал характеризуется полной абсолютной ошибкой , которая, в зависимости от соотношения между величинами _sx и х, находится следующим образом.

Если одна из погрешностей более чем в три раза превышает другую (например, _sx > 3х), то полная ошибка  принимается равной этой большей величине (в приведенном примере   _sx). Если же величины _sx и х близки между собой, то полная ошибка вычисляется как

. (14)
Запись окончательного результата измерений должна включать в себя следующие обязательные элементы.

1) Доверительный интервал вида

с указанием значения доверительной вероятности . Величины и  выражаются в одних и тех же единицах измерения, которые выносятся за скобку.

2) Значение полной относительной погрешности

выраженное в процентах и округленное до десятых долей.
Полная ошибка  округляется до двух значащих цифр. Если полученное после округления число оканчивается цифрами 4, 5 или 6, то дальнейшее округление не производится; если же вторая значащая цифра 1, 2, 3, 7, 8 или 9, то значение  округляется до одной значащей цифры (примеры: а) 0,2642  0,26; б) 3,177  3,2  3; в) 7,8310^– 7  810^– 7 и т.д.). После этого среднее значение округляется с той же точностью.
Пример 4. В результате определения ускорения движения тела (примеры 1 и 2) получено среднее значение ускорения = 2,03 м/с², случайная ошибка _sа = 0,139 м/с² с доверительной вероятностью  = 0,95 и приборная ошибка а = 0,0136 м/с². Так как а более чем в десять раз меньше _sа, то ею можно пренебречь и принять округленную полную абсолютную погрешность равной   _sа  0,14 м/с². Оценим относительную ошибку:

и запишем окончательный результат измерений:

Пример 5. Пусть при определении скорости звука и (лабораторная работа 4.2) получены следующие результаты: среднее значение = 343,3 м/с; случайная погрешность _sи = 8,27 м/с при  = 0,90; абсолютная приборная погрешность и = 1,52 м/с. Очевидно, что и в данном случае величиной и можно пренебречь по сравнению с _sи, и расчет по формуле (14) не требуется. Полная ошибка после округления равна   _sи  8 м/с; округленное среднее значение  343 м/с. Полная относительная погрешность

Окончательный результат измерений имеет вид

Пример 6. При определении длины волны  лазерного излучения (работа 5.1) получено: при  = 0,95;  = 1,8610^— 5 мм. В данном случае значения приборной и случайной погрешностей близки между собой, поэтому полную ошибку найдем по формуле (14):

Округленное среднее будет равно мм. Оценим полную относительную ошибку

и запишем окончательный результат:

Е = 4,4%.

* Термины «ошибка» и «погрешность» применительно к измерениям имеют один и тот же смысл.

Статьи
Главная страница

Из графика
видно, что существует вероятность, пусть и очень маленькая, что наше единичное
измерение покажет результат, сколь угодно далеко отстоящий от истинного
значения. Выходом из положения является проведение серии измерений. Если на
разброс данных действительно влияет случай, то в результате нескольких
измерений мы скорее всего получим следующее (рис 2):

Будет ли
рассчитанное среднее значение нескольких измерений совпадать с истинным? Как
правило – нет. Но по теории вероятности, чем больше сделано измерений, тем
ближе найденное среднее значение к истинному. На языке математики это можно
записать так:

Но с бесконечностью у всех дело обстоит неважно. Поэтому на практике мы имеем дело
не со всеми возможными результатами измерений, а с некоторой выборкой из этого
бесконечного множества. Сколько же реально следует делать измерений? Наверное,
до тех пор, пока полученное среднее значение не будет отличаться от истинного
меньше чем точность отдельного измерения.

Следовательно,
когда наше среднее значение (рис. 2) отличается от истинного меньше чем
погрешность измерений, дальнейшее увеличение числа опытов бессмысленно. Однако
на практике мы не знаем истинного значения! Значит, получив среднее по
результатам серии опытов, мы должны определить, какова вероятность того, что
истинное значение находится внутри заданного интервала ошибки. Или каков тот
доверительный интервал, в который с заданной надежностью попадет истинное
значение (рис 3).

Рассмотрим
некоторый условный эксперимент, где в серии измерений получены некоторые
значения величины Х (см. табл. 1). Рассчитаем среднее значение и, чтобы оценить
разброс данных найдем величины DХ = Х –
Х_ср

Таблица 1. Данные измерений и их обработка
№	Х	Х ср	DХ	DХ²	s²	s
1	130	143,5 » 144	-13,5	182,3	420	20,5
2	162	18,5	342,3
3	160	16,5	272,3	*s²_ср*	*s_ср*
4	122	-21,5	462,3	105	10,2

Ясно, что
величины DХ как-то характеризуют
разброс данных. На практике для усредненной характеристики разброса серии измерений используется
дисперсия выборки:

и среднеквадратичное или стандартное отклонение выборки:

Последнее
показывает, что каждое измерение в данной серии (в данной выборке) отличается
от другого в среднем на ± s.

Понятно, что каждое отдельное
значение оказывает влияние на средний результат. Но это влияние тем меньше, чем
больше измерений в нашей выборке. Поэтому дисперсия и стандартное отклонение
среднего значения, будет определяться по формулам:

Можем ли мы теперь определить вероятность того, что
истинное значение попадет в указанный интервал среднего? Или наоборот,
рассчитать тот доверительный интервал в который истинное значение
попадет с заданной вероятностью (95%)? Поскольку кривая на наших графиках это
распределение вероятностей, то площадь под кривой, попадающая в указанный
интервал и будет равна этой вероятности (доля площади, в процентах). А площади
математики научились рассчитывать хорошо, знать бы только уравнение этой
кривой.

И здесь мы сталкиваемся еще с одной сложностью. Кривая, которая описывает распределение
вероятности для выборки, для ограниченного числа измерений, уже не будет кривой нормального
распределения. Ее форма будет зависеть
не только от дисперсии (разброса данных) но и от степени свободы для выборки
(от числа независимых измерений) (рис 4):

Уравнения этих кривых впервые были предложены в 1908
году английским математиком и химиком Госсетом, который опубликовал их под
псевдонимом Student (студент), откуда пошло хорошо известные термины
«коэффициент Стьюдента» и аналогичные. Коэффициенты Стьюдента получены на
основе обсчета этих кривых для разных степеней свободы (f = n-1) и уровней
надежности (Р) и сведены в специальные таблицы. Для получения доверительного интервала необходимо
умножить уже найденное стандартное отклонение среднего на соответствующий
коэффициент Стьюдента. ДИ = s_ср*t_{f, P}

Проанализируем, как меняется доверительный интервал
при изменении требований к надежности результата и числа измерений в серии.
Данные в таблице 2 показывают, что чем больше требование к надежности, тем
больше будет коэффициент Стьюдента и, следовательно, доверительный интервал. В большинстве случаев, приемлемым считают значение Р=95%

Таблица 2. Коэффициент Стьюдента для различных уровней надежности.
P	0,9	0,95	0,99	0,999
t_5,_P	2,02	2,57	4,03	6,87

Таблица 3. Коэффициент Стьюдента для различных степеней свободы.
f= n-1	1	2	3	4	5	16	30
t_f, 0,95	12,7	4,3	3,18	2,78	2,57	2,23	2,04

Из таблицы 3 и графика
видно, что чем больше число измерений, тем меньше коэффициент и доверительный
интервал для данного уровня надежности. Особенно значительное падение
происходит при переходе от степени свободы 1 (два измерения) к 2 (три
измерения). Отсюда следует, что имеет смысл ставить не менее трех параллельных
опытов, проводить не менее трех измерений.

Окончательно
для измеряемой величины Х получаем значение Х_сред±s_ср*t_f,P. В
нашем случае получаем: f=3; t=3,18;
ДИ = 3,18*10,2 = 32,6; X = 143,5 ±32,6

Как правило,
значение доверительного интервала округляется до одной значащей цифры, а
значение измеряемой величины – в соответствии с округлением доверительного
интервала. Поэтому для нашей серии окончательно имеем: X = 140 ±30

Найденная
нами погрешность является абсолютной погрешностью и ничего не говорит еще о
точности измерений. Она свидетельствует о точности измерений только в сравнении
с измеряемой величиной. Отсюда представление об относительной ошибке:

Косвенные определения.

Исследуемая величина рассчитывается в этом случае с помощью
математических формул по другим величинам, которые были измерены
непосредственно. В этом случае для расчета ошибок можно использовать
соотношения, приведенные в таблице 4.

Таблица 4. Формулы для расчета абсолютных и относительных ошибок.
Формула	Абсолютная	Относительная
x = a ± b	Dx = Da+Db	e = (Da+Db) /(a±b )
x = a* b; x = a* k	Dx = bDa+aDb; Dx = kDa	e = Da/a+Db/b = e_a + e_b
x = a / b	Dx = (bDa+aDb) / b²	e = Da/a+Db/b = e_a + e_b
x = a*k; (x = a / k)	Dx = Da*k; (Dx = Da/k )	e = e_a
x = a²	Dx = 2aDa	e = 2Da/a = 2e_a
x = Öa	Dx = Da/(2Öa)	e = Da/2a = e_a/2

Из таблицы видно, что относительная ошибка и точность определения не изменяются при умножении (делении) на некоторый постоянный коэффициент. Особенно сильно относительная ошибка может возрасти при вычитании
близких величин, так как при этом абсолютные ошибки суммируются, а значение Х
может уменьшиться на порядки.

Пусть например, нам необходимо определить
объем проволочки.
Если диаметр проволочки измерен с погрешностью 0,01 мм (микрометром) и равен 4 мм, то относительная погрешность составит 0,25% (приборная). Если
длину проволочки (200 мм) мы измерим линейкой с погрешностью 0,5 мм, то относительная погрешность также составит 0,25%. Объем можно рассчитать по формуле: V=(pd²/4)*L. Посмотрим, как будут меняться ошибки
по мере проведения расчетов (табл. 5):

Таблица 5. Расчет абсолютных и относительных ошибок.
Величина	Значение	Абсолютная	Относительная
d²	16	Dx = 240,01=0,08	e = 0,5%
pd² *)	50,27	Dx = 0,083,14+0,001616 =0,28	e = 0,55%
pd²/4	12,57	Dx = 0,28/4 = 0,07	e = 0,55%
(pd²/4)*L	2513	Dx = 12,570,5+2000,07=20	e = 0,8%
*) Если мы возьмем привычное p=3,14, то Dp=0,0016 то e_p = 0,05%, но если используем более точное значение, то Dp и e_p можно будет пренебречь

Окончательный
результат V=2510±20 (мм³) e
=0,8%. Чтобы повысить точность косвенного определения, нужно в первую очередь
повышать точность измерения той величины, которая вносит больший вклад в ошибку
(в данном случае – точность измерения диаметра проволочки).

План проведения измерений:

[1]

1. Знакомство
с методикой, подготовка прибора, оценка приборной погрешности d. Оценка возможных причин
систематических ошибок, их исключение.

2.
Проведение серии измерений. Если получены совпадающие результаты, можно
считать что случайная ошибка равна 0, DХ
= d. Переходим к пункту 7.

3.
Исключение промахов – результатов значительно отличающихся по своей
величине от остальных.

4.
Расчет
среднего значения Х_ср, и стандартного отклонение среднего
значения s_cp

5.
Задание значения уровня надежности P,
определение коэффициента Стьюдента t и
нахождение доверительного интервала ДИ= t*s_cp

6.
Сравнение случайной и приборной погрешности, при этом возможны варианты:

—
ДИ << d, можно
считать, что DХ = d, повысить точность измерения
можно, применив более точный прибор

—
ДИ >> d, можно
считать, что DХ = ДИ,
повысить точность можно, уменьшая случайную ошибку, повышая число измерений в
серии, снижая требования к надежности.

—
ДИ » d, в этом
случае расчитываем ошибку по формуле DХ
=

7.
Записывается окончательный результат Х = Х_ср ± DХ.
Оценивается относительная ошибка
измерения e = DХ/Х_ср

Если
проводится несколько однотипных измерений (один прибор, исследователь, порядок
измеряемой величины, условия) то подобную работу можно проводить один раз. В
дальнейшем можно считать DХ
постоянной и ограничиться минимальным числом измерений (два-три измерения
должны отличаться не более, чем на DХ)

Для косвенных
измерений необходимо провести обработку данных измерения каждой величины. При
этом желательно использовать приборы, имеющие близкие относительные погрешности
и задавать одинаковую надежность для расчета доверительного интервала. На
основании полученных значений Da, Db, определяется DХ
для результирующей величины (см табл. 4). Для повышения точности надо
совершенствовать измерение той величины, вклад ошибки которой в DХ наиболее существенен.

Изучение зависимостей.

Частым вариантом экспериментальной работы является
измерение различных величин с целью установления зависимостей. Характер этих
зависимостей может быть различен: линейный, квадратичный, экспоненциальный,
логарифмический, гиперболический. Для выявления зависимостей широко
используется построение графиков.

При построении графиков вручную важно правильно
выбрать оси, величины, масштаб, шкалы. Следует предупредить школьников, что
шкалы должны иметь равномерный характер, нежелательна как слишком детальная,
так и слишком грубая их разметка. Точки должны заполнять всю площадь графика,
их расположение в одном углу, или «прижатыми» к одной из осей, говорит о
неправильно выбранном масштабе и затрудняет определение характера зависимости.
При проведении линии по точкам надо использовать теоретические представление о
характере зависимости: является она непрерывной или прерывистой, возможно ли ее
прохождение через начало координат, отрицательные значения, максимумы и
минимумы.

Наиболее легко проводится и анализируется прямая
линия. Поэтому часто при изучении более сложных зависимостей часто используется
линеаризация зависимостей, которая достигается подходящей заменой переменных.
Например:

Зависимость . Вводя новую переменную
, получаем уравнение
a = bx, которое
будет изображаться на графике прямой линией. Наклон этой прямой позволяет
рассчитать константу диссоциации.

Разумеется и в этом случае полученные в эксперименте данные включают в себя различные ошибки, и точки редко лежат строго на прямой. Возникает
вопрос, как с наибольшей точностью провести прямую по экспериментальным точкам, каковы ошибки в определении
параметров.

Математическая статистика показывает, что наилучшим
приближением будет такая линия, для которой дисперсия (разброс) точек
относительно ее будет минимальным. А дисперсия определяется как средний квадрат
отклонений наблюдаемого положения точки от расчитанного:

Отсюда название этого метода – метод наименьших
квадратов. Задавая условие, чтобы величина s²
принимала минимальное значение, получают формулы для коэффициентов а и b в уравнении прямой у = а + bx:

и формулы для расчета соответствующих ошибок
^[2].

Если
делать расчеты, используя калькулятор, то лучше оформлять их в виде таблицы:

x	x²	y	y²	xy
…	…	…	…	…
…	…	…	…	…
Sx =	Sx² =	Sy =	Sy² =	Sxy =

Подводя
итог, следует сказать, что обработка данных эксперимента достаточно сложный
этап работы ученого. Необходимость проведения большого числа измерений требует
большой затраты времени и материальных ресурсов. Громоздкость формул, необходимость
использования большого числа значащих цифр затрудняют вычисления. Поэтому, возможно,
не все рекомендации этой статьи применимы в рамках школьного исследования. Но
понимать их сущность, значимость, необходимость, и в соответствии с этим
адекватно оценивать свои результаты, должен любой исследователь.

В настоящее время обработку экспериментальных данных
существенно облегчают современные компьютерные технологии, современное
программное обеспечение. Об том, как их можно использовать – в следующей
статье.

Литература:

[1]
Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений, М., «Наука»,
1970, 194 с.

[2]
Петерс Д., Хайес Дж., Хифтье Г. Химическое разделение и измерение – М.,: Химия,
1978, 816 с.

Источник

Загрузить PDF

Абсолютная ошибка – это разность между измеренным значением и фактическим значением.^[1] Эта ошибка характеризует точность измерений. Если вам известны фактическое и измеренное значения, можно с легкостью вычислить абсолютную ошибку. Но иногда фактическое значение не дано, поэтому в качестве абсолютной ошибки пользуются максимально возможной ошибкой.^[2] Если даны фактическое значение и относительная ошибка, можно вычислить абсолютную ошибку.

1

Запишите формулу для вычисления абсолютной ошибки. Формула: $\Delta x=x_{{0}}-x$ , где $\Delta x$ – абсолютная ошибка (разность между измеренным и фактическим значениями), $x_{{0}}$ – измеренное значение, – фактическое значение.^[3]
2
Подставьте в формулу фактическое значение. Фактическое значение должно быть дано; в противном случае используйте принятое опорное значение. Фактическое значение подставьте вместо .
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м: $\Delta x=x_{{0}}-105$ .
3
Подставьте в формулу измеренное значение. Оно будет дано; в противном случае измерьте величину (длину или ширину и так далее). Измеренное значение подставьте вместо $x_{0}$ .
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м: $\Delta x=104-105$ .
4
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[4] Так вы вычислите абсолютную ошибку.
- В нашем примере: $\Delta x=104-105=-1$ , то есть абсолютная ошибка измерения равна 1 м.
Реклама

1

Запишите формулу для вычисления относительной ошибки. Формула: $\delta x={\frac {x_{{0}}-x}{x}}$ , где $\delta x$ – относительная ошибка (отношение абсолютной ошибки к фактическому значению), $x_{{0}}$ – измеренное значение, – фактическое значение.^[5]
2
Подставьте в формулу относительную ошибку. Скорее всего, она будет дана в виде десятичной дроби. Относительную ошибку подставьте вместо $\delta x$ .
- Например, если относительная ошибка равна 0,02, формула запишется так: $0,02={\frac {x_{{0}}-x}{x}}$ .
3
Подставьте в формулу фактическое значение. Оно будет дано. Фактическое значение подставьте вместо .
- Например, если фактическое значение равно 105 м, формула запишется так: $0,02={\frac {x_{{0}}-105}{105}}$ .
4

Умножьте обе стороны уравнения на фактическое значение. Так вы избавитесь от дроби.
5

Прибавьте фактическое значение к каждой стороне уравнения. Так вы найдете $x_{{0}}$ , то есть измеренное значение.
6
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[6] Так вы вычислите абсолютную ошибку.
- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так: . Таким образом, абсолютная ошибка равна 2,1 м.
Реклама

1
Определите единицу измерения. То есть выясните, было ли значение измерено с точностью до сантиметра, метра и так далее. Возможно, эта информация будет дана (например, «длина поля измерена с точностью до метра»). Чтобы определить единицу измерения, посмотрите на то, как округлено данное значение.^[7]
- Например, если измеренная длина поля равна 106 м, значение было округлено до метров. Таким образом, единица измерения равна 1 м.
2
3
Используйте максимально возможную ошибку в качестве абсолютной ошибки.^[9] Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[10] Так вы вычислите абсолютную ошибку.
- Например, если измеренная длина поля равна $106\pm 0,5$ м, то есть абсолютная ошибка равна 0,5 м.
Реклама

Советы

Если фактическое значение не указано, найдите принятое опорное или теоретическое значение.

Об этой статье

Эту страницу просматривали 26 271 раз.

Была ли эта статья полезной?

Источник

Таблица 1.

Результаты измерений толщины стеклянной
пластинки

№ измерения	h, мм	< h>, мм	Δ h_i, мм	Δ h, мм	ε_h, %
1	3,82	3,84	— 0,02	0,03	0,8
2	3,85	+ 0,01
3	3,89	+ 0,05
4	3,80	— 0,04

По данным таблицы рассчитываем среднее
значение толщины:

Определяем абсолютную погрешность
опыта (серии измерений):

Определяем относительную погрешность:

Абсолютная и относительная погрешности
некоторых простейших функций приведены
в табл.2.

Таблица 2

Погрешности при косвенных измерениях
в простейших случаях

Вид функции	Абсолютная погрешность Δy	Относительная погрешность ε_y
1	2	3
x₁ + x₂	Δ x₁ + Δ x₂
1	2	3
x₁ — x₂	Δ x₁ + Δ x₂
x₁ x₂	x₁ Δ x₂ + x₂ Δ x₁	ε_x₁ + ε_x₂
x₁ / x₂		ε_x₁ + ε_x₂
xⁿ	nx^n-¹ Δ x	nε_x

e^x	e^x Δ x	Δx

где a= l₁—l₂.
Логарифмирование даёт lng=ln(4π²)
+lna–ln.
После дифференцирования lngс заменамиdaна ΔaиdТна ΔТполучим:

,
где.

неправильная запись результата
правильная запись результата

g= (10,1835±0,433) м/с²g=
(10,2±0,4) м/с²

g= (9,8167±0,053) м/с²g=
(9,82±0,05) м/с²

g= (9,9423±0,132) м/с²g=
(9,94 ±0,13) м/с²

g= (10,8261±2,026) м/с²g=
(11±2) м/с²

g= 9,880± 0,004 м/с².

Рис. 1

R_э=σТ⁴,

Для построения графиков, как правило,
используют масштабно-координатную
(миллиметровую) бумагу.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Подборка по базе: конспект к № 1 теория.docx, отчет Морозова (проверка на ошибки).docx, 3 ошибки, из-за которых тебя отправят служить.pdf, 2.Эконометрика для ИМИТ_ Теоретический материал 5_ Стандартные о, РЕЧЕВЫЕ ОШИБКИ ИИХ ПРЕДУПРЕЖДЕНИЕ.docx, Письменная работа 1 теория управления реферат.docx, Найдите ошибки.docx, Негрубые ошибки.doc, Исправь ошибки (1).docx, рк 1 теория вероятности 19 вариант.pdf

Ч а с т ь I

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК

Абсолютная и относительная ошибки

х = х – Х. (1)

. (2)

Очевидно, что относительная погрешность – величина безразмерная, чаще всего ее выражают в процентах.

Случайная и приборная погрешности

Разнообразные ошибки, возникающие при измерениях, можно классифицировать как по их происхождению, так и по характеру их проявления.

По происхождению ошибки делятся на инструментальные и методические.

Инструментальные погрешности обусловлены несовершенством применяемых измерительных приборов и приспособлений. Эти погрешности могут быть уменьшены за счет применения более точных приборов. Так, размер детали можно измерить линейкой или штанген-циркулем. Очевидно, что во втором случае ошибка измерения меньше, чем в первом.

Методические погрешности возникают из-за того, что реальные физические процессы всегда в той или иной степени отличаются от их теоретических моделей. Например, формула для периода колебаний математического маятника в точности верна лишь при бесконечно малой амплитуде колебаний; формула Стокса, определяющая силу трения при движении шарика в вязкой жидкости, справедлива только в случае идеально сферической формы и т.д. Обнаружить и учесть методическую погрешность можно путем измерения той же величины совершенно иным независимым методом.

По характеру проявления ошибки бывают систематические и случайные.

Систематическая погрешность может быть обусловлена как приборами, так и методикой измерения. Она имеет две характерные особенности. Во-первых, систематическая погрешность всегда либо положительна, либо отрицательна и не меняет своего знака от опыта к опыту. Во-вторых, систематическую погрешность нельзя уменьшить за счет увеличения числа измерений. Например, если при отсутствии внешних воздействий стрелка измерительного прибора показывает величину х₀, отличную от нуля, то во всех дальнейших измерениях будет присутствовать систематическая ошибка, равная х₀.

Случайная ошибка также может быть как инструментальной, так и методической. Причину ее появления установить трудно, а чаще всего – невозможно (это могут быть различные помехи, случайные толчки, вибрации, неверно взятый отсчет по прибору и т.д.). Случайная погрешность бывает и положительной и отрицательной, причем непредсказуемо изменяет свой знак от опыта к опыту. Значение ее можно уменьшить путем увеличения числа измерений.

Детальный анализ погрешностей измерения представляет собой сложную задачу, для решения которой не существует единого рецепта. Поэтому в каждом конкретном случае этот анализ проводят по-разному. Однако, в первом приближении, если исключена систематическая ошибка, то остальные можно условно свести к следующим двум видам: приборная и случайная.

Приборной погрешностью в дальнейшем будем называть случайную ошибку, обусловленную измерительными приборами и приспособлениями, а случайной – ошибку, причина появления которой неизвестна. Приборную погрешность измерения величины х будем обозначать как х, случайную – как _sx.

Оценка случайной погрешности. Доверительный интервал

. (3)

, (4)

где .

Ширина искомого доверительного интервала прямо пропорциональна среднеквадратичной ошибке:

. (5)

Расчет случайной погрешности измерения величины х проводится в следующем порядке:

1) вычисляется сумма измеренных значений, а затем – среднее значение величины по формуле (3);

3) находится сумма квадратов отклонений, а затем – средне-квадратичная ошибка  по формуле (4);

Таблица 1

Номер опыта	…	х	х	(х)²
1	…
2	…
…	…
п	…
	 =		 =

. (6)

Таблица 2

Номер опыта	S, м	t, c	а, м/с²	а, м/с²	(а)², (м/с²)²
1	5	2,20	2,07	0,04	0,0016
2	7	2,68	1,95	-0,08	0,0064
3	9	2,91	2,13	0,10	0,0100
4	11	3,35	1,96	-0,07	0,0049
		 =	8,11	 =	0,0229

_sа = 3,180,0437  0,139 (м/с²) .

Способы определения приборных ошибок

Р
ис.2

. (7)

Значение класса точности (без символа «%») указывается, как правило, на электроизмерительных приборах.

2. На приборе указан класс точности. Согласно определению этой величины, из формулы (7) имеем

. (8)

и = и(x, y, z,…). (9)

, (10)

, (11)

Таблица 3

и(х)	k_x

На практике зависимость (9) чаще всего имеет вид степенной функции

, (12)

При расчетах по формулам типа (12) необходимо помнить следующее.

S = 0,5 мм = 0,0005 м;

t = 0,01 с.

Расчетную формулу (6) можно записать в виде степенной функции

a(S, t) = 2S¹t^– 2;

тогда на основании (12) погрешность косвенного измерения ускорения а определится выражением

;

Очевидно, что в данном случае величиной E_S можно пренебречь и принять погрешность а равной

где . Тогда для оценки приборной погрешности , согласно (12), получим выражение

, (13)

где .

Пренебрегая величиной Е_t, проведем расчет по формуле (13):

. (14)
Запись окончательного результата измерений должна включать в себя следующие обязательные элементы.

1) Доверительный интервал вида

2) Значение полной относительной погрешности

и запишем окончательный результат измерений:

Окончательный результат измерений имеет вид

Округленное среднее будет равно мм. Оценим полную относительную ошибку

и запишем окончательный результат:

Е = 4,4%.

* Термины «ошибка» и «погрешность» применительно к измерениям имеют один и тот же смысл.

Источник

Загрузить PDF

1

Запишите формулу для вычисления абсолютной ошибки. Формула: $Delta x=x_{{0}}-x$ , где – абсолютная ошибка (разность между измеренным и фактическим значениями), $x_{{0}}$ – измеренное значение, – фактическое значение.^[3]
2
Подставьте в формулу фактическое значение. Фактическое значение должно быть дано; в противном случае используйте принятое опорное значение. Фактическое значение подставьте вместо .
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м: $Delta x=x_{{0}}-105$ .
3
Подставьте в формулу измеренное значение. Оно будет дано; в противном случае измерьте величину (длину или ширину и так далее). Измеренное значение подставьте вместо $x_{0}$ .
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м: .
4
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[4] Так вы вычислите абсолютную ошибку.
- В нашем примере: , то есть абсолютная ошибка измерения равна 1 м.
Реклама

1

Запишите формулу для вычисления относительной ошибки. Формула: $delta x={frac {x_{{0}}-x}{x}}$ , где – относительная ошибка (отношение абсолютной ошибки к фактическому значению), $x_{{0}}$ – измеренное значение, – фактическое значение.^[5]
2
Подставьте в формулу относительную ошибку. Скорее всего, она будет дана в виде десятичной дроби. Относительную ошибку подставьте вместо .
- Например, если относительная ошибка равна 0,02, формула запишется так: $0,02={frac {x_{{0}}-x}{x}}$ .
3
Подставьте в формулу фактическое значение. Оно будет дано. Фактическое значение подставьте вместо .
- Например, если фактическое значение равно 105 м, формула запишется так: $0,02={frac {x_{{0}}-105}{105}}$ .
4

Умножьте обе стороны уравнения на фактическое значение. Так вы избавитесь от дроби.
5

Прибавьте фактическое значение к каждой стороне уравнения. Так вы найдете $x_{{0}}$ , то есть измеренное значение.
6
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[6] Так вы вычислите абсолютную ошибку.
- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так: . Таким образом, абсолютная ошибка равна 2,1 м.
Реклама

1
Определите единицу измерения. То есть выясните, было ли значение измерено с точностью до сантиметра, метра и так далее. Возможно, эта информация будет дана (например, «длина поля измерена с точностью до метра»). Чтобы определить единицу измерения, посмотрите на то, как округлено данное значение.^[7]
- Например, если измеренная длина поля равна 106 м, значение было округлено до метров. Таким образом, единица измерения равна 1 м.
2
3
Используйте максимально возможную ошибку в качестве абсолютной ошибки.^[9] Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[10] Так вы вычислите абсолютную ошибку.
- Например, если измеренная длина поля равна м, то есть абсолютная ошибка равна 0,5 м.
Реклама

Советы

Если фактическое значение не указано, найдите принятое опорное или теоретическое значение.

Об этой статье

Эту страницу просматривали 24 549 раз.

Была ли эта статья полезной?

Абсолютная и относительная погрешность

4.2

Средняя оценка: 4.2

Всего получено оценок: 2108.

4.2

Средняя оценка: 4.2

Всего получено оценок: 2108.

Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.

Опыт работы учителем математики — более 33 лет.

Абсолютная погрешность

Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.

Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.

Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:

Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.

На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.

Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.

Относительная погрешность

Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.

Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.

Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.

Правила подсчета погрешностей

Для номинальной оценки погрешностей существует несколько правил:

при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
при делении и умножении чисел требуется сложить относительные погрешности;
при возведении в степень относительную погрешность умножают на показатель степени.

Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.

Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.

Что мы узнали?

Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Светлана Лобанова-Асямолова

10/10
Валерий Соломин

10/10
Анастасия Юшкова

10/10
Ксюша Пономарева

7/10
Паша Кривов

10/10
Евгений Холопик

9/10
Guzel Murtazina

10/10
Максим Аполонов

10/10
Olga Bimbirene

9/10
Света Колодий

10/10

Оценка статьи

4.2

Средняя оценка: 4.2

Всего получено оценок: 2108.

А какая ваша оценка?

Абсолютная погрешность

Причины возникновения погрешности измерения
Систематическая и случайная погрешности
Определение абсолютной погрешности
Алгоритм оценки абсолютной погрешности в серии прямых измерений
Значащие цифры и правила округления результатов измерений
Примеры

Причины возникновения погрешности измерения

Погрешность измерения – это отклонение измеренного значения величины от её истинного (действительного) значения.

Обычно «истинное» значение неизвестно, и можно только оценить погрешность, приняв в качестве «истинного» среднее значение, полученное в серии измерений. Таким образом, процесс оценки проводится статистическими методами.

Виды погрешности измерений

Причины

Инструментальная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Погрешность метода

Определяется несовершенством методов и допущениями в методике.

Теоретическая погрешность

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Погрешность оператора

Определяется субъективным фактором, ошибками экспериментатора.

Систематическая и случайная погрешности

Систематической погрешностью называют погрешность, которая остаётся постоянной или изменяется закономерно во времени при повторных измерениях одной и той же величины.

Систематическая погрешность всегда имеет знак «+» или «-», т.е. говорят о систематическом завышении или занижении результатов измерений.

Систематическую погрешность можно легко определить, если известно эталонное (табличное) значение измеряемой величины. Для других случаев разработаны эффективные статистические методы выявления систематических погрешностей. Причиной систематической погрешности может быть неправильная настройка приборов или неправильная оценка параметров (завышенная или заниженная) в расчётных формулах.

Случайной погрешностью называют погрешность, которая не имеет постоянного значения при повторных измерениях одной и той же величины.

Случайные погрешности неизбежны и всегда присутствуют при измерениях.

Определение абсолютной погрешности

Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины:

$$ Delta x = |x_{изм}-x_{ист} | $$

Например:

При пяти взвешиваниях гири с маркировкой 100 г были получены различные значения массы. Если принять маркировку за истинное значение, то получаем следующие значения абсолютной погрешности:

$m_i,г$

98,4

99,2

98,1

100,3

98,5

$Delta m_i, г$

1,6

0,8

1,9

0,3

1,5

Граница абсолютной погрешности – это величина h: $ |x-x_{ист}| le h $

Для оценки границы абсолютной погрешности на практике используются статистические методы.

Алгоритм оценки абсолютной погрешности в серии прямых измерений

Шаг 1. Проводим серию из N измерений, в каждом из которых получаем значение измеряемой величины $x_i, i = overline{1, N}$.

Шаг 2. Находим оценку истинного значения x как среднее арифметическое данной серии измерений:

$$ a = x_{cp} = frac{x_1+x_2+ cdots +x_N}{N} = frac{1}{N} sum_{i = 1}^N x_i $$

Шаг 3. Рассчитываем абсолютные погрешности для каждого измерения:

$$ Delta x_i = |x_i-a| $$

Шаг 4. Находим среднее арифметическое абсолютных погрешностей:

$$ Delta x_{cp} = frac{Delta x_1+ Delta x_2+ cdots + Delta x_N}{N} = frac{1}{N} sum_{i = 1}^N Delta x_i $$

Шаг 5. Определяем инструментальную погрешность при измерении как цену деления прибора (инструмента) d.

Шаг 6. Проводим оценку границы абсолютной погрешности серии измерений, выбирая большую из двух величин:

$$ h = max {d; Delta x_{cp} } $$

Шаг 7. Округляем и записываем результаты измерений в виде:

$$ a-h le x le a+h или x = a pm h $$

Значащие цифры и правила округления результатов измерений

Значащими цифрами – называют все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.

Например:

0,00501 — три значащие цифры 5,0 и 1.

5,01 — три значащие цифры.

5,0100 – пять значащих цифр; такая запись означает, что величина измерена с точностью 0,0001.

Внимание!

Правила округления.

Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу (округление по избытку, “ceiling”).

Округлять результаты измерений и вычислений нужно так, чтобы последняя значащая цифра находилась в том же десятичном разряде, что и абсолютная погрешность измеряемой величины.

Например: если при расчетах по результатам серии измерений получена оценка истинного значения a=1,725, а оценка абсолютной погрешности h = 0,11, то результат записывается так:

$$ a approx 1,7; h approx ↑0,2; 1,5 le x le 1,9 или x = 1,7 pm 0,2 $$

Примеры

Пример 1. При измерении температура воды оказалась в пределах от 11,55 ℃ до 11,63 ℃. Какова абсолютная погрешность этих измерений?

По условию $11,55 le t le 11,63$. Получаем систему уравнений:

$$ {left{ begin{array}{c} a-h = 11,55 \ a+h = 11,63 end{array} right.} Rightarrow {left{ begin{array}{c} 2a = 11,55+11,63 = 23,18 \ 2h = 11,63-11,55 = 0,08 end{array} right.} Rightarrow {left{ begin{array}{c} a = 11,59 \ h = 0,04end{array} right.} $$

$$ t = 11,59 pm 0,04 ℃ $$

Ответ: 0,04 ℃

Пример 2. По результатам измерений найдите границы измеряемой величины. Инструментальная погрешность d = 0,1.

$x_i$

15,3

16,4

15,3

15,8

15,7

16,2

15,9

Находим среднее арифметическое:

$$ a = x_{ср} = frac{15,3+16,4+ cdots +15,9}{7} = 15,8 $$

Находим абсолютные погрешности:

$$ Delta x_i = |x_i-a| $$

$ Delta x_i$

0,5

0,6

0,5

0,1

0,4

0,1

Находим среднее арифметическое:

$$ Delta x_{ср} = frac{0,5+0,6+ cdots + 0,1}{7} approx 0,31 gt d $$

Выбираем большую величину:

$$ h = max {d; Delta x_{ср} } = max⁡ {0,1; 0,31} = 0,31 $$

Округляем по правилам округления по избытку: $h approx ↑0,4$.

Получаем: x = 15, $8 pm 0,4$

Границы: $15,4 le x le 16,2$

Ответ: $15,4 le x le 16,2$

Пример 3*. В первой серии экспериментов было получено значение $x = a pm 0,3$. Во второй серии экспериментов было получено более точное значение $x = 5,631 pm 0,001$. Найдите оценку средней a согласно полученным значениям x.

Более точное значение определяет более узкий интервал для x. По условию:

$$ {left{ begin{array}{c} a-0,3 le x le a+0,3 \ 5,630 le x le 5,632 end{array} right.} Rightarrow a-0,3 le 5,630 le x le 5,632 le a+0,3 Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} a-0,3 le 5,630 \ 5,632 le a+0,3 end{array} right.} Rightarrow {left{ begin{array}{c} a le 5,930 \ 5,332 le a end{array} right.} Rightarrow 5,332 le a le 5,930 $$

Т.к. a получено в серии экспериментов с погрешностью h=0,3, следует округлить полученные границы до десятых:

$$ 5,3 le a le 5,9 $$

Ответ: $ 5,3 le a le 5,9 $

Абсолютная и относительная погрешности (ошибки).

Пусть некоторая
величина x
измерена n
раз. В результате получен ряд значений
этой величины: x₁,
x₂,
x₃,
…, x_n

Величиной, наиболее
близкой к действительному значению,
является среднее арифметическое этих
результатов:

Отсюда следует,
что каждое физическое измерение должно
быть повторено несколько раз.

Разность между
средним значением
измеряемой
величины и значением отдельного измерения
называется абсолютной
погрешностью отдельного измерения:

(13)

Абсолютная
погрешность может быть как положительной,
так и отрицательной и измеряется в тех
же единицах, что и измеряемая величина.

Средняя абсолютная
ошибка результата — это среднее
арифметическое значений абсолютных
погрешностей отдельных измерений,
взятых по абсолютной величине (модулю):

(14)

Отношения

называются относительными погрешностями
(ошибками) отдельных измерений.

Отношение средней
абсолютной погрешности результата

к среднему арифметическому значению

измеряемой величины называют относительной
ошибкой результата и выражают в процентах:

Относительная
ошибка характеризует точность измерения.

Законы распределения случайных величин.

Результат измерения
физической величины зависит от многих
факторов, влияние которых заранее учесть
невозможно. Поэтому значения, полученные
в результате прямых измерений какого
— либо параметра, являются случайными,
обычно не совпадающие между собой.
Следовательно, случайные
величины —
это такие величины, которые в зависимости
от обстоятельств могут принимать те
или иные значения. Если случайная
величина принимает только определенные
числовые значения, то она называется
дискретной.

Например,
количество заболеваний в данном регионе
за год, оценка, полученная студентом на
экзамене, энергия электрона в атоме и
т.д.

Непрерывная
случайная величина принимает любые
значения в данном интервале.

Например: температура
тела человека, мгновенные скорости
теплового движения молекул, содержание
кислорода в воздухе и т.д.

Под событием
понимается всякий результат или исход
испытания. В теории вероятностей
рассматриваются события, которые при
выполнение некоторых условий могут
произойти, а могут не произойти. Такие
события называются
случайными.
Например, событие, состоящее в появлении
цифры 1 при выполнении условия — бросания
игральной кости, может произойти, а
может не произойти.

Если событие
неизбежно происходит в результате
каждого испытания, то оно называется
достоверным.
Событие называется невозможным,
если оно вообще не происходит ни при
каких условиях.

Два события,
одновременное появление которых
невозможно, называются несовместными.

Пусть случайное
событие А в серии из n
независимых испытаний произошло m
раз, тогда отношение:

называется
относительной частотой события А. Для
каждой относительной частоты выполняется
неравенство:

При небольшом
числе опытов относительная частота
событий в значительной мере имеет
случайный характер и может заметно
изменяться от одной группы опытов к
другой. Однако при увеличении числа
опытов частота событий все более теряет
свой случайный характер и приближается
к некоторому постоянному положительному
числу, которое является количественной
мерой возможности реализации случайного
события А. Предел, к которому стремится
относительная частота событий при
неограниченном увеличении числа
испытаний, называется статистической
вероятностью события:

Например, при
многократном бросании монеты частота
выпадения герба будет лишь незначительно
отличаться от ½. Для достоверного события
вероятность Р(А) равна единице. Если
Р=0, то событие невозможно.

Математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений х_i
на вероятность этих значений р_i:

Статистическим
аналогом математического ожидания
является среднее арифметическое значений
:

где m_i
— число дискретных случайных величин,
имеющих значение х_i.

Для непрерывной
случайной величины математическим
ожиданием служит интеграл:

где р(х) — плотность
вероятности.

Отдельные значения
случайной величины группируются около
математического ожидания. Отклонение
случайной величины от ее математического
ожидания (среднего значения) характеризуется
дисперсией,
которая для дискретной случайной
величины определяется формулой:

(15)

(16)

Дисперсия имеет
размерность случайной величины. Для
того, чтобы оценивать рассеяние
(отклонение) случайной величины в
единицах той же размерности, введено
понятие среднего
квадратичного отклонения
σ(Х), которое
равно корню квадратному из дисперсии:

(17)

Вместо среднего
квадратичного отклонения иногда
используется термин «стандартное
отклонение».

Всякое отношение,
устанавливающее связь между всеми
возможными значениями случайной величины
и соответствующими им вероятностями,
называется законом
распределения случайной величины.
Формы задания закона распределения
могут быть разными:

а) ряд распределения
(для дискретных величин);

б) функция
распределения;

в) кривая распределения
(для непрерывных величин).

Существует
относительно много законов распределения
случайных величин.

Нормальный
закон распределения случайных
величин (закон
Гаусса).
Случайная величина

распределена по
нормальному закону, если ее плотность
вероятности f(x)
определяется формулой:

(18),

где <x>
— математическое ожидание (среднее
значение) случайной величины <x>
= M
(X);

—
среднее квадратичное отклонение;

—
основание натурального логарифма
(неперово число);

f
(x)
– плотность вероятности (функция
распределения вероятностей).

Многие случайные
величины (в том числе все случайные
погрешности) подчиняются нормальному
закону распределения (закону Гаусса).
Для этого распределения наиболее
вероятным значением
измеряемой
величины
является
её среднее
арифметическое
значение.

График нормального
закона распределения изображен на
рисунке (колоколообразная кривая).

Кривая симметрична
относительно прямой х=<x>=α,
следовательно, отклонения случайной
величины вправо и влево от <x>=α
равновероятны. При х=<x>±
кривая асимптотически приближается к
оси абсцисс. Если х=<x>,
то функция распределения вероятностей
f(x)
максимальна и принимает вид:

(19)

Таким образом,
максимальное значение функции f_max(x)
зависит от величины среднего квадратичного
отклонения. На рисунке изображены 3
кривые распределения. Для кривых 1 и 2
<x>
= α = 0 соответствующие значения среднего
квадратичного отклонения различны, при
этом ₂>₁.
(При увеличении 
кривая распределения становится более
пологой, а при уменьшении 
– вытягивается вверх). Для кривой 3 <x>
= α ≠ 0 и ₃
= ₂.

Закон
распределения
молекул в газах по скоростям называется
распределением
Максвелла.
Функция плотности вероятности попадания
скоростей молекул в определенный
интервал

теоретически была определена в 1860 году
английским физиком Максвеллом

. На рисунке
распределение Максвелла представлено
графически. Распределение движется
вправо или влево в зависимости от
температуры газа (на рисунке Т₁
< Т₂).
Закон распределения Максвелла определяется
формулой:

(20),

где m_о
– масса молекулы, k
– постоянная Больцмана, Т – абсолютная
температура газа,
—
скорость молекулы.

Распределение
концентрации молекул газа в атмосфере
Земли (т.е.
в силовом поле) в зависимости от высоты
было дано австрийским физиком Больцманом
и называется
распределением
Больцмана:

(21)

Где n(h)
– концентрация молекул газа на высоте
h,
n₀
– концентрация у поверхности Земли, g
– ускорение свободного падения, m
– масса молекулы.

Распределение
Больцмана.

Совокупность всех
значений случайной величины называется
простым
статистическим рядом.
Так как простой статистический ряд
оказывается большим, то его преобразуют
в вариационный
статистический
ряд или интервальный
статистический ряд. По интервальному

статистическому ряду для оценки вида
функции распределения вероятностей по
экспериментальным данным строят
гистограмму
– столбчатую
диаграмму. (Гистограмма – от греческих
слов “histos”–
столб и “gramma”–
запись).

Гистограмма
распределения Больцмана.

Для построения
гистограммы интервал, содержащий
полученные значения случайной величины
делят на несколько интервалов x_i
одинаковой ширины. Для каждого интервала
подсчитывают число m_i
значений случайной величины, попавших
в этот интервал. После этого вычисляют
плотность частоты случайной величины

для каждого интервала x_i
и среднее значение случайной величины
<x_i
> в каждом интервале.

Затем по оси абсцисс
откладывают интервалы x_i,
являющиеся основаниями прямоугольников,
высота которых равна
(или
высотой

– плотностью относительной частоты
).

Расчетами показано,
что вероятность попадания нормально
распределенной случайной величины в
интервале значений от <x>–
до <x>+
в среднем равна 68%. В границах вдвое
более широких (<x>–2;
<x>+2)
размещается в среднем 95% всех значений
измерений, а в интервале (<x>–3;<x>+3)
– уже 99,7%. Таким образом, вероятность
того, что отклонение значений нормально
распределенной случайной величины
превысит 3
(
– среднее квадратичное отклонение)
чрезвычайно мала (~0,003). Такое событие
можно считать практически невозможным.
Поэтому границы <x>–3
и <x>+3
принимаются за границы практически
возможных значений нормально распределенной
случайной величины («правило трех
сигм»).

Если число измерений
(объем выборки) невелико (n<30),
дисперсия вычисляется по формуле:

(22)

Уточненное среднее
квадратичное отклонение отдельного
измерения вычисляется по формуле:

(23)

Напомним, что для
эмпирического распределения по выборке
аналогом математического ожидания
является среднее арифметическое значение
<x>
измеряемой величины.

Чтобы дать
представление о точности и надежности
оценки измеряемой величины, используют
понятия доверительного интервала и
доверительной вероятности.

Доверительным
интервалом
называется интервал (<x>–x,
<x>+x),
в который по определению попадает с
заданной вероятностью действительное
(истинное) значение измеряемой величины.
Доверительный интервал характеризует
точность полученного результата: чем
уже доверительный интервал, тем меньше
погрешность.

Доверительной
вероятностью
(надежностью)

результата серии измерений называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал (<x>±x).
Чем больше величина доверительного
интервала, т.е. чем больше x,
тем с большей надежностью величина <x>
попадает в этот интервал. Надежность 
выбирается самим исследователем
самостоятельно, например, =0,95;
0,98. В медицинских и биологических
исследованиях, как правило, доверительную
вероятность (надежность) принимают
равной 0,95.

Если величина х
подчиняется нормальному закону
распределения Гаусса, а <x>
и <>
оцениваются по выборке (числу измерений)
и если объем выборки невелик (n<30),
то интервал (<x>
– t__,_n<>,
<x>
+ t__,_n<>)
будет доверительным интервалом для
известного параметра х с доверительной
вероятностью .

Коэффициент t__,_n
называется коэффициентом
Стьюдента
(этот коэффициент был предложен в 1908 г.
английским математиком и химиком В.С.
Госсетом, публиковавшим свои работы
под псевдонимом «Стьюдент» – студент).

Значении коэффициента
Стьюдента t__,_n
зависит от доверительной вероятности

и числа измерений n
(объема выборки). Некоторые значения
коэффициента Стьюдента приведены в
таблице 1.

Таблица 1

n	
0,6	0,7	0,8	0,9	0,95	0,98	0,99
2	1,38	2,0	3,1	6,3	12,7	31,8	63,7
3	1,06	1,3	1,9	2,9	4,3	7,0	9,9
4	0,98	1,3	1,6	2,4	3,2	4,5	5,8
5	0,94	1,2	1,5	2,1	2,8	3,7	4,6
6	0,92	1,2	1,5	2,0	2,6	3,4	4,0
7	0,90	1,1	1,4	1,9	2,4	3,1	3,7
8	0,90	1,1	1,4	1,9	2,4	3,0	3,5
9	0,90	1,1	1,4	1,9	2,3	2,9	3,4
10	0,88	1,1	1,4	1,9	2,3	2,8	3,3

В таблице 1 в верхней
строке заданы значения доверительной
вероятности 
от 0,6 до 0,99, в левом столбце – значение
n.
Коэффициент Стьюдента следует искать
на пересечении соответствующих строки
и столбца.

Окончательный
результат измерений записывается в
виде:

(25)

Где

– полуширина доверительного интервала.

Результат серии
измерений оценивается относительной
погрешностью:

(26)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Download Article

Absolute error is the difference between the measured value and the actual value.^[1] It is one way to consider error when measuring the accuracy of values. If you know the actual and measured values, calculating the absolute error is a simple matter of subtraction. Sometimes, however, you may be missing the actual value, in which case you should use the maximum possible error as the absolute error.^[2] If you know the actual value and the relative error, you can work backwards to find the absolute error.

1

Set up the formula for calculating the absolute error. The formula is $Delta x=x_{{0}}-x$ , where equals the absolute error (the difference, or change, in the measured and actual value), $x_{{0}}$ equals the measured value, and equals the actual value.^[3]
2
Plug the actual value into the formula. The actual value should be given to you. If not, use a standardly accepted value. Substitute this value for .^[4]
- For example, you might be measuring the length of a football field. You know that the actual, or accepted length of a professional American football field is 360 feet (including both end zones). So, you would use 360 as the actual value: $Delta x=x_{{0}}-360$ .
Advertisement
3
Find the measured value. This will be given to you, or you should make the measurement yourself. Substitute this value for $x_{{0}}$ .
- For example, if you measure the football field and find that it is 357 feet long, you would use 357 as the measured value:.
4
Subtract the actual value from the measured value. Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.^[5]
- For example, since , the absolute error of your measurement is 3 feet.

1

Set up the formula for relative error. The formula is $delta x={frac {x_{{0}}-x}{x}}$ , where equals the relative error (the ratio of the absolute error to the actual value), $x_{{0}}$ equals the measured value, and equals the actual value.^[6]
2
Plug in the value for the relative error. This will likely be a decimal. Make sure you substitute it for .
- For example, if you know that the relative error is .025, your formula will look like this: $.025={frac {x_{{0}}-x}{x}}$ .
3
Plug in the value for the actual value. This information should be given to you. Make sure you substitute this value for .
- For example, if you know that the actual value is 360 ft, your formula will look like this: $.025={frac {x_{{0}}-360}{360}}$ .
4

Multiply each side of the equation by the actual value. This will cancel out the fraction.
5

Add the actual value to each side of the equation. This will give you the value of $x_{{0}}$ , giving you the measured value.
6
Subtract the actual value from the measured value. Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.^[7]
- For example, if the measured value is 369 ft, and the actual value is 360 feet, you would subtract . So, the absolute error is 9 feet.

1
Determine the measuring unit. This is the “to the nearest” value. This might be explicitly stated (for example, “The building was measured to the nearest foot.”), but it doesn’t have to be. To determine the measuring unit, just look at what place value the measurement is rounded to.
- For example, if the measured length of a building is stated as 357 feet, you know that the building was measured to the nearest foot. So, the measuring unit is 1 foot.
2
3
Use the maximum possible error as the absolute error.^[9] Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.
- For example, if you find the measurement of a building to be , the absolute error is .5 ft.

Add New Question

Question

How do I find absolute error of any equation?

An equation does not contain an «absolute error.» Re-read the introduction above.
Question

How do I find the root value of a 6-digit number?
Question

What is the absolute error in 2.11?

As explained above, the concept of «absolute error» involves both a measured value and an «actual» value.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

If the actual value is not given, you can look for the accepted or theoretical value.

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To calculate the absolute error, use the formula, “Absolute Error = Measured Value — Actual Value.” Begin by plugging the actual value into the formula, which will either be given to you or is the standardly accepted value. Then, make a measurement and put the measured value into the formula. Finally, subtract the actual value from the measure value to calculate the absolute error. If there are any negative signs, ignore them when you record your answer. To learn how to find the absolute error if you don’t have the measured value, keep reading.

Did this summary help you?

Thanks to all authors for creating a page that has been read 193,656 times.

Did this article help you?

Download Article

1

Set up the formula for calculating the absolute error. The formula is $Delta x=x_{{0}}-x$ , where equals the absolute error (the difference, or change, in the measured and actual value), $x_{{0}}$ equals the measured value, and equals the actual value.^[3]
2
Plug the actual value into the formula. The actual value should be given to you. If not, use a standardly accepted value. Substitute this value for .^[4]
- For example, you might be measuring the length of a football field. You know that the actual, or accepted length of a professional American football field is 360 feet (including both end zones). So, you would use 360 as the actual value: $Delta x=x_{{0}}-360$ .
Advertisement
3
Find the measured value. This will be given to you, or you should make the measurement yourself. Substitute this value for $x_{{0}}$ .
- For example, if you measure the football field and find that it is 357 feet long, you would use 357 as the measured value:.
4
Subtract the actual value from the measured value. Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.^[5]
- For example, since , the absolute error of your measurement is 3 feet.

1

Set up the formula for relative error. The formula is $delta x={frac {x_{{0}}-x}{x}}$ , where equals the relative error (the ratio of the absolute error to the actual value), $x_{{0}}$ equals the measured value, and equals the actual value.^[6]
2
Plug in the value for the relative error. This will likely be a decimal. Make sure you substitute it for .
- For example, if you know that the relative error is .025, your formula will look like this: $.025={frac {x_{{0}}-x}{x}}$ .
3
Plug in the value for the actual value. This information should be given to you. Make sure you substitute this value for .
- For example, if you know that the actual value is 360 ft, your formula will look like this: $.025={frac {x_{{0}}-360}{360}}$ .
4

Multiply each side of the equation by the actual value. This will cancel out the fraction.
5

Add the actual value to each side of the equation. This will give you the value of $x_{{0}}$ , giving you the measured value.
6
Subtract the actual value from the measured value. Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.^[7]
- For example, if the measured value is 369 ft, and the actual value is 360 feet, you would subtract . So, the absolute error is 9 feet.

1
Determine the measuring unit. This is the “to the nearest” value. This might be explicitly stated (for example, “The building was measured to the nearest foot.”), but it doesn’t have to be. To determine the measuring unit, just look at what place value the measurement is rounded to.
- For example, if the measured length of a building is stated as 357 feet, you know that the building was measured to the nearest foot. So, the measuring unit is 1 foot.
2
3
Use the maximum possible error as the absolute error.^[9] Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.
- For example, if you find the measurement of a building to be , the absolute error is .5 ft.

Add New Question

Question

How do I find absolute error of any equation?

An equation does not contain an «absolute error.» Re-read the introduction above.
Question

How do I find the root value of a 6-digit number?
Question

What is the absolute error in 2.11?

As explained above, the concept of «absolute error» involves both a measured value and an «actual» value.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

If the actual value is not given, you can look for the accepted or theoretical value.

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

Did this summary help you?

Thanks to all authors for creating a page that has been read 193,656 times.

Did this article help you?

ВИДЕО УРОК

Абсолютная погрешность.

Разность между истинным значением измеряемой величины
и её приближённым значением называется абсолютной погрешностью.

Для подсчёта
абсолютной погрешности необходимо из большего числа вычесть меньшее число.

Существует формула
абсолютной погрешности. Обозначим точное число буквой А, а буквой а –
приближение к точному числу. Приближённое число – это число, которое
незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда
формула будет выглядеть следующим образом:

∆а = А – а.

ПРИМЕР:

В школе учится 374 ученика. Если округлить это число до 400,
то абсолютная погрешность измерения равна:

400 – 374 = 26.

ПРИМЕР:

На предприятии 1284 рабочих и
служащих. При округлении этого числа до 1300 абсолютная
погрешность составляет

1300 – 1284 = 16.

При округлении до 1280 абсолютная
погрешность составляет

1284 – 1280 = 4.

Редко когда можно
точно знать значение измеряемой величины, чтобы рассчитать абсолютную
погрешность. Но при выполнении различных измерений мы обычно представляем себе
границы абсолютной погрешности и всегда можем сказать, какого определённого
числа она не превосходит.

ПРИМЕР:

Торговые весы могут дать абсолютную погрешность, не
превышающую 5 г, а аптекарские – не превышающую одной сотой грамма.

Записывают
абсолютную погрешность числа, используя знак
±.

ПРИМЕР:

Длина рулона обоев составляет.

30 м ± 3
см.

Границу абсолютной
погрешности называют предельной абсолютной погрешностью.

Но абсолютная
погрешность не даёт нам представление о качестве измерения, то есть о том,
насколько тщательно это измерение выполнено. Чтобы понять эту мысль, достаточно
разобраться в таком примере.

ПРИМЕР:

Допустим, что при измерении коридора длиной в 20
м мы допустили абсолютную погрешность
всего только в 1 см. Теперь представим себе, что, измеряя корешок книги,
имеющий 18
см длины, мы тоже допустили абсолютную
погрешность в 1 см. Тогда понятно, что первое измерение нужно признать
превосходным, но зато второе – совершенно неудовлетворительным. Это значит, что
на 20
м ошибка в 1
см вполне допустима и неизбежна, но
на 18
см такая ошибка является очень грубой.

Отсюда ясно, что для оценки качества измерения
существенна не сама абсолютная погрешность, а та доля, какую она составляет от
измеряемой величины. При измерении коридора длиной в 20 м погрешность в 1 см
составляет

долю
измеряемой величины, а при измерении корешка книги погрешность в 1 см составляет

долю
измеряемой величины.

Делаем вывод, что измеряя корешок книги, имеющий 18
см длины и допустив погрешность в 1
см, можно считать измерение с большой ошибкой. Но если погрешность в 1
см была допущена при измерении коридора
длиной в 20
м, то это измерение можно считать максимально точным.

Если ошибка,
возникающая при измерении линейкой или каким либо другим измерительным
инструментом, значительно меньше, чем деления шкалы этой линейки, то в качестве
абсолютной погрешности измерения обычно берут половину деления. Если деления на
линейке нанесены достаточно точно, то ошибка при измерении близка к нулю.

Тогда
значение измеряемой длины предмета будет значение ближайшей метки линейки.
Поэтому, если измерение выполнено аккуратно, то истинная длина предмета может
отличаться от измеренной длины не более чем на половину деления шкалы, то есть 0,5 мм.

ПРИМЕР:

Для измерения длины болта использованы метровая линейка с
делениями 0,5 см и линейка с
делениями 1 мм. В обоих случаях получен результат 3,5
см. Ясно, что в первом случае отклонение найденной длины 3,5
см от истинной, не
должно по модулю превышать 0,5 см, во втором случае
0,1 см.

Если этот же результат получится при измерении
штангенциркулем, то

p(l; 3,5) = |l – 3,5 ≤ 0,01|.

Данный пример показывает зависимость абсолютной
погрешности и границ, в которых находится точный результат, от точности
измерительных приборов. В одном случае ∆l = 0,5 и, следовательно,

3
≤ l ≤ 4,

в другом – ∆l = 0,1 и

3,4
≤ l ≤ 3,6.

ПРИМЕР:

Длина листа бумаги формата А4 равна (29,7 ± 0,1)
см. А расстояние от Санкт-Петербурга до Москвы равно (650 ± 1) км. Абсолютная погрешность в первом случае
не превосходит одного миллиметра, а во втором – одного километра. Необходимо
сравнить точность этих измерений.

РЕШЕНИЕ:

Если вы думаете, что длина листа измерена точнее потому,
что величина абсолютной погрешности не
превышает 1 мм, то вы ошибаетесь.
Напрямую сравнить эти величины нельзя. Проведём некоторые рассуждения.

При измерении длины листа абсолютная погрешность не
превышает 0,1 см на 29,7 см, то есть в процентном отношении это составляет

0,1
: 29,7 ∙ 100% ≈ 0,33%

измеряемой величины.

Когда мы измеряем расстояние от Санкт-Петербурга до
Москвы, то абсолютная погрешность не превышает
1 км
на 650 км, что в процентном соотношении составляет

1
: 650 ∙ 100% ≈ 0,15%

измеряемой величины.

Видим, что расстояние между городами измерено точнее, чем
длинна листа формата А4.

Истинное значение
измеряемой величины известно бывает лишь в очень редких случаях, а поэтому и
действительная величина абсолютной погрешности почти никогда не может быть вычислена.
На практике абсолютной погрешности недостаточно для точной оценки измерения.
Поэтому на практике более важное значение имеет определение относительной
погрешности измерения.

Относительная погрешность.

Абсолютная
погрешность, как мы убедились, не даёт возможности судить о качестве измерения.
Поэтому для оценки качества приближения вводится новое понятие – относительная
погрешность. Относительная погрешность позволяет судить о качестве измерения.

Относительная погрешность –
это частное от деления абсолютной погрешности на модуль приближённого значения
измеряемой величины, выраженная в долях или процентах.

Относительная
погрешность величина всегда положительная. Это следует из того, что абсолютная погрешность
всегда положительная величина, и мы делим её на модуль приближённого значения
измеряемой величины, а модуль тоже всегда положителен.

ПРИМЕР:

Округлим дробь 14,7 до целых и найдём относительную погрешность приближённого
значения:

14,7 ≈ 15,

Для вычисления
относительной погрешности, кроме приближённого значения, нужно знать ещё и
абсолютную погрешность. Обычно абсолютная погрешность неизвестна, поэтому
вычислить относительную погрешность нельзя. В таких случаях ограничиваются
оценкой относительной погрешности.

ПРИМЕР:

При измерении в (сантиметрах) толщины
b
стекла и длины l книжной полки
получили следующие результаты:

b ≈ 0,4 с
точностью до 0,1,

l ≈ 100 с
точностью до 0,1.

Абсолютная погрешность каждого из этих измерений не
превосходит 0,1. Однако 0,1 составляет
существенную часть числа 0,4 и
ничтожную часть числа 100. Это показывает, что качество второго
измерения намного выше, чем первого.

В результате измерения нашли,
что b ≈ 0,4 с точностью до 0,1, то
есть абсолютная погрешность измерения не превосходит 0,1.
Значит, отношение абсолютной погрешности к приближённому значению меньше или равно

то есть относительная погрешность приближения не превосходит 25%.

Аналогично найдём, что
относительная погрешность приближения, полученного при измерении длины полки,
не превосходит

Говорят, что в первом случае измерение выполнено с
относительной точностью до 25%,
а во втором – с относительной точностью до 0,1%.

ПРИМЕР:

Если взять абсолютную погрешность в 1
см, при измерении длины отрезков 10
см и 10
м, то относительные погрешности будут соответственно равны 10% и 0,1%. Для
отрезка длиной в 10 см погрешность
в 1
см очень велика, это ошибка в 10%. А для десятиметрового отрезка 1 см не имеет значения, эта ошибка всего в 0,1%.

Чем меньше относительная погрешность
измерения, тем оно точнее.

Различают
систематические и случайные погрешности.

Систематической погрешностью называют ту погрешность, которая остаётся неизменной при
повторных измерениях.

Случайной погрешностью называют ту погрешность, которая возникает в результате
воздействия на процесс измерения внешних факторов и может изменять своё
значение.

В большинстве
случаев невозможно узнать точное значение приближённого числа, а значит, и
точную величину погрешности. Однако почти всегда можно установить, что
погрешность (абсолютная или относительная) не превосходит некоторого числа.

ПРИМЕР:

Продавец взвешивает арбуз на чашечных весах. В наборе
наименьшая гиря – 50
г. Взвешивание показало 3600 г. Это число – приближённое. Точный вес арбуза
неизвестен. Но абсолютная погрешность не превышает 50
г. Относительная погрешность не превосходит

⁵⁰/₃₆₀₀ ≈
1,4%.

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной
погрешностью.

Число, заведомо превышающее относительную погрешность (или в худшем случае равное ей), называется предельной относительной
погрешностью.

В предыдущем примере
за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность 1,4%.

Величина предельной
погрешности не является вполне определённой. Так в предыдущем примере можно
принять за предельную абсолютную погрешность
100 г, 150 г и вообще всякое
число, большее чем 50 г.
На практике берётся по возможности меньшее значение предельной погрешности. В
тех случаях, когда известна точная величина погрешности, эта величина служит
одновременно предельной погрешностью. Для каждого приближённого числа должна
быть известна его предельная погрешность (абсолютная или относительная). Когда
она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено
приближённое число 4,78 без указания предельной погрешности, то подразумевается,
что предельная абсолютная погрешность составляет 0,005. В следствии этого соглашения всегда можно обойтись без указания
предельной погрешности числа.

Предельная
абсолютная погрешность обозначается греческой буквой ∆ (<<дельта>>),
предельная относительная погрешность – греческой буквой δ
(<<дельта малая>>). Если приближённое число обозначить буквой а,

Правила округления.

На практике
относительную погрешность округляют до двух значащих цифр, выполняя округление
с избытком, то есть, всегда увеличивая последнюю значащую цифру на единицу.

ПРИМЕР:

Для х = 1,7 ± 0,2 относительная погрешность измерений равна:

ПРИМЕР:

Длина карандаша измерена линейкой с миллиметровым
делением. Измерение показало 17,9 см. Какова предельная относительная погрешность этого
измерения ?

РЕШЕНИЕ:

Здесь а =
17,9 см. Можно принять ∆ = 0,1 см, так как с точностью
до 1 мм
измерить карандаш нетрудно, а значительно уменьшить предельную
погрешность не удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но
у самого карандаша рёбра могут отличаться на большую величину). Относительная погрешность равна

Округляя, находим

ПРИМЕР:

Цилиндрический поршень имеет около 35
мм в диаметре. С какой точностью нужно
его измерить микрометром, чтобы предельная относительная погрешность составляла 0,05% ?

РЕШЕНИЕ:

По условию, предельная относительная
погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная абсолютная
погрешность равна

или, усиливая, 0,02
мм.

Можно воспользоваться
формулой

Подставляя в формулу

а = 35,

𝛿 = 0,0005,

имеем

Значит,

∆
= 35 × 0,0005 = 0,0175 мм.

Действия над приближёнными числами.

Сложение и вычитание приближённых чисел.

Абсолютная погрешность суммы двух величин равна сумме
абсолютных погрешностей отдельных слагаемых.

ПРИМЕР:

Складываются приближённые числа

265 и 32.

РЕШЕНИЕ:

Пусть предельная погрешность первого есть 5,
а второго 1. Тогда предельная погрешность суммы равна

5
+ 1 = 6.

Так, если истинное значение первого есть 270,
а второго 33, то приближённая сумма

265
+ 32 = 297

на 6 меньше истинной

270
+ 33 = 303.

ПРИМЕР:

Найти сумму приближённых чисел:

0,0909
+ 0,0833 + 0,0769 + 0,0714 + 0,0667

+ 0,0625 + 0,0588 + 0,0556 + 0,0526.

РЕШЕНИЕ:

Сложение даёт следующий результат – 0,6187.

Предельная погрешность каждого слагаемого

0,00005.

Предельная погрешность суммы:

0,00005
∙ 9 = 0,00045.

Значит, в последнем (четвёртом) знаке суммы возможна ошибка до 5
единиц. Поэтому округляем сумму до третьего знака, то есть до тысячных.
Получаем 0,619,
здесь все знаки верные.

При значительном
числе слагаемых обычно происходит взаимная компенсация погрешностей, поэтому
истинная погрешность суммы лишь в исключительных случаях совпадает с предельной
погрешностью или близка к ней. Насколько редки эти случаи, видно из предыдущего
примера, где 9 слагаемых. Истинная величина каждого из них может
отличаться в пятом знаке от взятого приближённого значения на 1, 2, 3, 4 или даже на 5 единиц в ту и в другую сторону.

Например, первое
слагаемое может быть больше своего истинного значения на 4 единицы пятого знака, второе – на две, третье – меньше
истинного на одну единицу и так далее.

Расчёт показывает,
что число всех возможных случаев распределения погрешностей составляет около
одного миллиарда. Между тем лишь в двух случаях погрешность суммы может
достигнуть предельной погрешности 0,00045,
это произойдёт:

– когда истинная величина каждого слагаемого больше
приближённой величины на 0,00005;

– когда истинная величина каждого слагаемого меньше
приближённой величины на 0,00005.

Значит, случаи,
когда погрешность суммы совпадает с предельной, составляют только 0,0000002% всех возможных случаев.

Дальнейший расчёт
показывает, что случаи, когда погрешность суммы девяти слагаемых может
превысить три единицы последнего знака, тоже очень редки. Они составляют
лишь 0,07%
из числа всех
возможных. Две единицы последнего знака погрешность может превысить 2% всех возможных случаев, а одну единицу –
примерно в 25%.
В остальных 75% случаев погрешность девяти слагаемых не
превышает одной единицы последнего знака.

ПРИМЕР:

Найти сумму точных чисел:

0,0909
+ 0,0833 + 0,0769 + 0,0714 + 0,0667

+ 0,0625 + 0,0588 + 0,0556 + 0,0526.

РЕШЕНИЕ:

Сложение даёт следующий результат – 0,6187.

Округлим их до тысячных и сложим:

0,091
+ 0,083 + 0,077 + 0,071 + 0,067

+ 0,062 + 0,059 + 0,056 + 0,053 = 0,619.

Предельная погрешность суммы:

0,0005
∙ 9 = 0,0045.

Приближённая сумма отличается от истинной на 0,0003,
то есть на треть единицы последнего знака приближённых чисел. Все три знака
приближённой суммы верны, хотя теоретически последняя цифра могла быть грубо
неверной.

Произведём в наших слагаемых округление до сотых. Теперь
предельная погрешность суммы будет:

0,005
∙ 9 = 0,045.

Между тем получим:

0,09
+ 0,08 + 0,08 + 0,07 + 0,07

+ 0,06 + 0,06 + 0,06 + 0,05 = 0,62.

Истинная погрешность составляет только 0,0013.

Предельная абсолютная погрешность разности двух величин
равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого.

ПРИМЕР:

Пусть предельная погрешность приближённого
уменьшаемого 85 равна 2,
а предельная погрешность вычитаемого 32 равна 3.
Предельная погрешность разности

85
– 32 = 53

есть

2
+ 3 = 5.

В самом деле, истинное значение уменьшаемого и
вычитаемого могут равняться

85
+ 2 = 87 и

32
– 3 = 29.

Тогда истинная разность есть

87
– 29 = 58.

Она на 5 отличается от
приближённой разности 53.

Относительная погрешность суммы и разности.

Предельную
относительную погрешность суммы и разности легко найти, вычислив сначала
предельную абсолютную погрешность.

Предельная
относительная погрешность суммы (но не разности!) лежит между наименьшей и
наибольшей из относительных погрешностей слагаемых. Если все слагаемые имеют
одну и ту же (или примерно одну и ту же) предельную относительную погрешность,
то и сумма имеет ту же (или примерно ту же) предельную относительную
погрешность. Другими словами, в этом случае точность суммы (в процентном
выражении) не уступает точности слагаемых. При значительном же числе слагаемых
сумма, как правило, гораздо точнее слагаемых.

ПРИМЕР:

Найти предельную абсолютную и предельную относительную
погрешность суммы чисел:

24,4
+ 25,2 + 24,7.

РЕШЕНИЕ:

В каждом слагаемом суммы

24,4
+ 25,2 + 24,7 = 74,3

предельная относительная погрешность примерно одна и та
же, а именно:

0,05
: 25 = 0,2%.

Такова же она и для суммы.

Здесь предельная абсолютная погрешность равна 0,15,
а относительная

0,15
: 74,3 ≈ 0,15 : 75 = 0,2%.

В противоположность
сумме разность приближённых чисел может быть менее точной, чем уменьшаемое и
вычитаемое. <<Потеря точности>> особенно велика в том случае, когда
уменьшаемое и вычитаемое мало отличаются друг от друга.

Относительные погрешности при сложении и вычитании
складывать нельзя.

Умножение и деление приближённых чисел.

При делении и умножении чисел требуется сложить
относительные погрешности.

ПРИМЕР:

Пусть перемножаются приближённые числа 50 и 20, и пусть предельная относительная погрешность первого
сомножителя есть 0,4%, а второго
0,5%.

Тогда предельная относительная погрешность произведения

50
× 20 = 1000

приближённо равна 0,9%.
В самом деле предельная абсолютная погрешность первого сомножителя есть

50
× 0,004 = 0,2,

а второго

20
× 0,005 = 0,1.

Поэтому истинная величина произведения не больше чем

(50
+ 0,2)(20 + 0,1) = 1009,02,

и не меньше, чем

(50
– 0,2)(20 – 0,1) = 991,022.

Если истинная величина произведения есть 1009,2,
то погрешность произведения равна

1009,2
– 1000 = 9,02,

а если 991,02, то погрешность произведения равна

1000
– 991,02 = 8,98.

Рассмотренные два случая – самые неблагоприятные. Значит,
предельная абсолютная погрешность произведения есть 9,02.
Предельная относительная погрешность равна

9,02
: 1000 = 0,902%,

то есть приближённо 0,9%.

Задания к уроку 16

Задание 1

Задание 2

Задание 3

Урок 1. Числовые неравенства
Урок 2. Свойства числовых неравенств
Урок 3. Сложение и умножение числовых неравенств
Урок 4. Числовые промежутки
Урок 5. Линейные неравенства
Урок 6. Системы линейных неравенств
Урок 7. Нелинейные неравенства
Урок 8. Системы нелинейных неравенств
Урок 9. Дробно-рациональные неравенства
Урок 10. Решение неравенств с помощью графиков
Урок 11. Неравенства с модулем
Урок 12. Иррациональные неравенства
Урок 13. Неравенства с двумя переменными
Урок 14. Системы неравенств с двумя переменными
Урок 15. Приближённые вычисления

Статья обновлена 10.07.2022

Что такое погрешность измерения

Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.

Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.

Математическая погрешность: формула для каждого типа

Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?

Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.

Формулы погрешностей вычисляются следующим образом.

Абсолютная погрешность измерений: формула

Формула дает разницу между измеренным и реальным значением.

Формула абсолютной погрешности

Относительная погрешность: формула

Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому значению.

Формула относительной погрешности

Приведенная погрешность: формула

Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.

Формула приведенной погрешности

Классификация оценочной погрешности

Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.

Классификация оценочной погрешности

Что такое случайная погрешность

Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.

Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.

Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.

Что такое систематическая погрешность

Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.

В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения.

Погрешность выборки

Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.

Погрешность структуры

Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.

Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.

Погрешность аудитории

Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.

Погрешность отбора

Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.

Как минимизировать погрешность выборки

Знайте свою аудиторию.
Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам.
Разделите аудиторию на группы.
Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию.
Увеличьте размер выборки.
Больший размер выборки приводит к более точному результату.

Погрешность измерения

Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.

К погрешностям измерения приводят следующие виды ошибок.

Ошибка цели

Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.

Предвзятость ответов

Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.

Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть или хотят казаться лучше, чем есть на самом деле.

Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.

Предвзятость интервьюера

Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.

Ошибка обработки

Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.

Ошибка ввода

Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.

Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.

Как минимизировать погрешность измерения

Предварительно протестируйте.
Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью.
Проводите выборку случайным образом.
Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка.
Тренируйте команду интервьюеров и наблюдателей.
Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования.
Всегда выполняйте проверку сделанных записей.
Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.

Мир без ошибок не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.

Источник

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Абсолютная и относительная ошибки

Случайная и приборная погрешности

Разнообразные ошибки, возникающие при измерениях, можно классифицировать как по их происхождению, так и по характеру их проявления.

По происхождению ошибки делятся на инструментальные и методические.

По характеру проявления ошибки бывают систематические и случайные.

Оценка случайной погрешности. Доверительный интервал

Номер опыта

Способы определения приборных ошибок

Р<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://topuch.com/absolyutnaya-i-otnositelenaya-oshibki/740283_html_f4c954ec9b5801fb.png" width="389" height="55" /> ис.2

Советы

Об этой статье

Была ли эта статья полезной?

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Абсолютная и относительная ошибки

Случайная и приборная погрешности

Разнообразные ошибки, возникающие при измерениях, можно классифицировать как по их происхождению, так и по характеру их проявления.

По происхождению ошибки делятся на инструментальные и методические.

По характеру проявления ошибки бывают систематические и случайные.

Оценка случайной погрешности. Доверительный интервал

Номер опыта

Способы определения приборных ошибок

Р<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://topuch.com/absolyutnaya-i-otnositelenaya-oshibki/740283_html_f4c954ec9b5801fb.png" width="389" height="55" /> ис.2

Советы

Об этой статье

Была ли эта статья полезной?

Абсолютная и относительная погрешность

Абсолютная погрешность

Относительная погрешность

Правила подсчета погрешностей

Что мы узнали?

Тест по теме

Оценка статьи

Абсолютная погрешность

Причины возникновения погрешности измерения

Систематическая и случайная погрешности

Определение абсолютной погрешности

Алгоритм оценки абсолютной погрешности в серии прямых измерений

Значащие цифры и правила округления результатов измерений

Примеры

Абсолютная и относительная погрешности (ошибки).

Законы распределения случайных величин.

Video

References

About This Article

Did this article help you?

Video

References

About This Article

Did this article help you?

Что такое погрешность измерения

Математическая погрешность: формула для каждого типа

Абсолютная погрешность измерений: формула

Относительная погрешность: формула

Приведенная погрешность: формула

Классификация оценочной погрешности

Что такое случайная погрешность

Что такое систематическая погрешность

Погрешность выборки

Как минимизировать погрешность выборки

Погрешность измерения

Как минимизировать погрешность измерения

Р
ис.2

Р
ис.2