2 распространение ошибок графы вычислительных процессов

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Введение
2 Распространение ошибок
- 2.1 Абсолютная ошибка
- 2.2 Относительная ошибка
3 Графы вычислительных процессов
- 3.1 Примеры
4 Памятка программисту
5 Список литературы
6 См. также

Введение

Одним из наиболее важных вопросов в численном анализе является вопрос о том, как ошибка, возникшая в определенном месте в ходе вычислений, распространяется дальше, то есть становится ли ее влияние больше или меньше по мере того, как производятся последующие операции. Крайним случаем является вычитание двух почти равных чисел: даже при очень маленьких ошибках обоих этих чисел относительная ошибка разности может оказаться очень большой. Такая относительная ошибка будет распространяться дальше при выполнении всех последующих арифметических операций.

Одним из источников вычислительных погрешностей (ошибок) является приближенное представление вещественных чисел в ЭВМ, обусловленное конечностью разрядной сетки. Хотя исходные данные представляются в ЭВМ с большой точностью накопление погрешностей округления в процессе счета может привести к значительной результирующей погрешности, а некоторые алгоритмы могут оказаться и вовсе непригодными для реального счета на ЭВМ. Подробнее о представлении вещественных чисел в ЭВМ можно узнать здесь.

Распространение ошибок

В качестве первого шага при рассмотрении такого вопроса, как распространение ошибок, необходимо найти выражения для абсолютной и относительной ошибок результата каждого из четырех арифметических действий как функции величин, участвющих в операции, и их ошибок.

Абсолютная ошибка

Сложение

Имеются два приближения $\bar{x}$ и $\bar{y}$ к двум величинам и , а также соответствующие абсолютные ошибки e_x и e_y . Тогда в результате сложения имеем

$x+y=\bar{x}+e_x+\bar{y}+e_y=(\bar{x}+\bar{y})+(e_x+e_y)$

Ошибка суммы, которую мы обозначим через $e_{x+y}$ , будет равна

$e_{x+y}=e_x+e_y$

Вычитание

Тем же путем получаем

$e_{x-y}=e_x-e_y$

Умножение

При умножении мы имеем

$x\cdot y=(\bar{x}+e_x)\cdot (\bar{y}+e_y)=\bar{x}\bar{y}+\bar{x}e_y+\bar{y}e_x+e_xe_y$

Поскольку ошибки обычно гораздо меньше самих величин, пренебрегаем произведением ошибок:

$x\cdot y\approx \bar{x}\bar{y}+\bar{x}e_y+\bar{y}e_x$

Ошибка произведения будет равна

$e_{xy}\approx \bar{x}e_y+\bar{y}e_x$

Деление

Имеем

$\frac{x}{y}=\frac{\bar{x}+e_x}{\bar{y}+e_y}$

Преобразовываем это выражение к виду

$\frac{x}{y}=\frac{\bar{x}+e_x}{\bar{y}}\cdot \left(\frac{1}{1+\frac{e_y}{\bar{y}}}\right)$

Множитель, стоящий в скобках, при $\left| \frac{e_y}{\bar{y}}\right|<<1$ можно разложить в ряд

$\frac{x}{y}=\frac{\bar{x}+e_x}{\bar{y}}\cdot \left(1-\frac{e_y}{\bar{y}}+\left(\frac{e_y}{\bar{y}}\right)^2-\ldots \right)$

Перемножая и пренебрегая всеми членами, которые содержат произведения ошибок или степени ошибок выше первой, имеем

$\frac{x}{y}\approx \frac{\bar{x}}{\bar{y}}+\frac{e_x}{\bar{y}}-\frac{\bar{x}}{\bar{y}^2}e_y$

Следовательно,

$e_{x/y}\approx \frac{1}{\bar{y}}e_x-\frac{\bar{x}}{\bar{y}^2}e_y$

Необходимо четко понимать, что знак ошибки бывает известен только в очень редких случаях. Не факт, например, что ошибка увеличивается при сложении и уменьшается при вычитании потому, что в формуле для сложения стоит плюс, а для вычитания — минус. Если, например, ошибки двух чисел имеют противоположные знаки, то дело будет обстоять как раз наоборот, то есть ошибка уменьшится при сложении и увеличится при вычитании этих чисел.

Относительная ошибка

После того, как мы вывели формулы для распространения абсолютных ошибок при четырех арифметических действиях, довольно просто вывести соответствующие формулы для относительных ошибок. Для сложения и вычитания формулы были преобразованы с тем, чтобы в них входила в явном виде относительная ошибка каждого исходного числа.

Сложение

$\frac{e_{x+y}}{\bar{x}+\bar{y}}=\frac{\bar{x}}{\bar{x}+\bar{y}}(\frac{e_x}{\bar{x}})+\frac{\bar{y}}{\bar{x}+\bar{y}}(\frac{e_y}{\bar{y}})$

Вычитание

$\frac{e_{x-y}}{\bar{x}-\bar{y}}=\frac{\bar{x}}{\bar{x}-\bar{y}}(\frac{e_x}{\bar{x}})-\frac{\bar{y}}{\bar{x}-\bar{y}}(\frac{e_y}{\bar{y}})$

Умножение

$\frac{e_{x\cdot y}}{\bar{x}\cdot \bar{y}}=\frac{e_x}{\bar{x}}+\frac{e_y}{\bar{y}}$

Деление

$\frac{e_{x/y}}{\bar{x}/\bar{y}}=\frac{e_x}{\bar{x}}-\frac{e_y}{\bar{y}}$

Мы начинаем арифметическую операцию, имея в своем распоряжении два приближенных значения $\bar{x}$ и $\bar{y}$ с соответствующими ошибками e_x и e_y . Ошибки эти могут быть любого происхождения. Величины $\bar{x}$ и $\bar{y}$ могут быть экспериментальными результатами, содержащими ошибки; они могут быть результатами предварительного вычисления согласно какому-либо бесконечному процессу и поэтому могут содержать ошибки ограничения; они могут быть результатами предшествующих арифметических операций и могут содержать ошибки округления. Естественно, они могут также содержать в различных комбинациях и все три вида ошибок.

Вышеприведенные формулы дают выражение ошибки результата каждого из четырех арифметических действий как функции от $\bar{x},\bar{y},e_x, e_y$ ; ошибка округления в данном арифметическом действии при этом не учитывается. Если же в дальнейшем необходимо будет подсчитать, как распространяется в последующих арифметических операциях ошибка этого результата, то необходимо к вычисленной по одной из четырех формул ошибке результата прибавить отдельно ошибку округления.

Графы вычислительных процессов

Теперь рассмотрим удобный способ подсчета распространения ошибки в каком-либо арифметическом вычислении. С этой целью мы будем изображать последовательность операций в вычислении с помощью графа и будем писать около стрелок графа коэффициенты, которые позволят нам сравнительно легко определить общую ошибку окончательного результата. Метод этот удобен еще и тем, что позволяет легко определить вклад любой ошибки, возникшей в процессе вычислений, в общую ошибку.

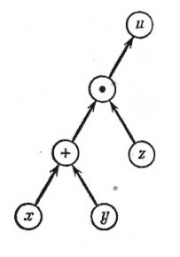
Рис.1. Граф вычислительного процесса $u=(x+y)\cdot z$

На рис.1 изображен граф вычислительного процесса $u=(x+y)\cdot z$ . Граф следует читать снизу вверх, следуя стрелкам. Сначала выполняются операции, расположенные на каком-либо горизонтальном уровне, после этого — операции, расположенные на более высоком уровне, и т. д. Из рис.1, например, ясно, что x и y сначала складываются, а потом умножаются на z. Граф, изображенный на рис.1, является только изображением самого вычислительного процесса. Для подсчета общей ошибки результата необходимо дополнить этот граф коэффициентами, которые пишутся около стрелок согласно следующим правилам.

Сложение

Пусть две стрелки, которые входят в кружок сложения, выходят из двух кружков с величинами a_1 и a_2 . Эти величины могут быть как исходными, так и результатами предыдущих вычислений. Тогда стрелка, ведущая от a_1 к знаку + в кружке, получает коэффициент , стрелка же, ведущая от a_2 к знаку + в кружке, получает коэффициент .

Вычитание

Если выполняется операция a_1-a_2 , то соответствующие стрелки получают коэффициенты и .

Умножение

Обе стрелки, входящие в кружок умножения, получают коэффициент +1.

Деление

Если выполняется деление a_1/a_2 , то стрелка от a_1 к косой черте в кружке получает коэффициент +1, а стрелка от a_2 к косой черте в кружке получает коэффициент −1.

Смысл всех этих коэффициентов следующий: относительная ошибка результата любой операции (кружка) входит в результат следующей операции, умножаясь на коэффициенты у стрелки, соединяющей эти две операции.

Примеры

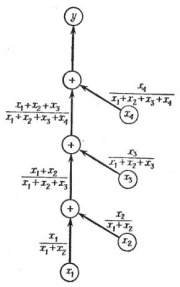
Рис.2. Граф вычислительного процесса для сложения , причем

Применим теперь методику графов к примерам и проиллюстрируем, что означает распространение ошибки в практических вычислениях.

Пример 1

Рассмотрим задачу сложения четырех положительных чисел:

где

Граф этого процесса изображен на рис.2. Предположим, что все исходные величины заданы точно и не имеют ошибок, и пусть r_1 , r_2 и r_3 являются относительными ошибками округления после каждой следующей операции сложения. Последовательное применение правила для подсчета полной ошибки окончательного результата приводит к формуле

$\frac{e_y}{y}=r_1\frac{x_1+x_2}{x_1+x_2+x_3}\cdot \frac{x_1+x_2+x_3}{x_1+x_2+x_3+x_4}+r_2\frac{x_1+x_2+x_3}{x_1+x_2+x_3+x_4}+r_3$

Сокращая сумму в первом члене и умножая все выражение на , получаем

e_y=r_1(x_1+x_2)+r_2(x_1+x_2+x_3)+r_3(x_1+x_2+x_3+x_4)

Учитывая, что ошибка округления равна $5\cdot 10^{-t}$ (в данном случае предполагается, что действительное число в ЭВМ представляется в виде десятичной дроби с t значищими цифрами), окончательно имеем

$|e_y|\leq (3x_1+3x_2+2x_3+x_4)\cdot 5\cdot 10^{-t}$

Из этой формулы ясно, что максимально возможная ошибка (абсолютная или относительная), обусловленная округлением, становится меньше, если сначала складывать меньшие числа. Результат довольно удивительный, так как вся классическая математика основана на предположении, что при перемене мест слагаемых или их группировке сумма не изменяется. Разница заключается в том, что ЭВМ не может производить вычисления с бесконечно большой точностью, а именно такие вычисления рассматриваются в классической математике.

Пример 2

Вычитание двух почти равных чисел. Предположим, что необходимо вычислить z=x-y . Тогда из формулы распространения ошибки при вычитании имеем

$\frac{e_z}{z}=\frac{x}{x-y}\left(\frac{e_x}{x}\right)-\frac{y}{x-y}\left(\frac{e_y}{y}\right)$

Предположим, кроме того, что x и y являются соответствующим образом округленными положительными числами, так что

$\left|\frac{e_x}{x}\right|\leq 5\cdot 10^{-t}$

и $\left|\frac{e_y}{y}\right|\leq 5\cdot 10^{-t}$

Если разность x-y мала, то относительная ошибка z может стать большой, даже если абсолютная ошибка мала. Так как в дальнейших вычислениях эта большая относительная ошибка будет распространяться, то она может поставить под сомнение точность окончательного результата вычислений.

Рассмотрим простой пример:

$x=0.5628\cdot 10^4$

$y=0.5631\cdot 10^4$

Тогда

$z=-0.0003\cdot 10^4$

Зная x и y, мы можем написать

$\left|\frac{e_x}{x}\right|\leq \frac{0.5}{0.5628}\cdot 10^{-4}<0.01%$

$\left|\frac{e_y}{y}\right|\leq \frac{0.5}{0.5631}\cdot 10^{-4}<0.01%$

Как видим, относительные ошибки x и y малы. Однако

$\left|\frac{e_z}{z}\right|\leq \frac{1}{0.0003}\cdot 10^{-4}\approx 33%$

Эта относительная ошибка очень велика, и, что важнее всего, она будет распространяться в ходе последующих вычислений.

Памятка программисту

Выводы, полученные выше, можно свести в краткий перечень рекомендаций для практической организации вычислений.

Если необходимо произвести сложение-вычитание длинной последовательности чисел, работайте сначала с наименьшими числами.
Если возможно, избегайте вычитания двух почти равных чисел. Формулы, содержащие такое вычитание, часто можно преобразовать так, чтобы избежать подобной операции.
Выражение вида можно написать в виде , а выражение вида можно написать в виде . Если числа в разности почти равны друг другу, производите вычитание до умножения или деления. При этом задача не будет осложнена дополнительными ошибками округления.
В любом случае сводите к минимуму число необходимых арифметических операций.

Список литературы

Д.Мак-Кракен, У.Дорн. Численные методы и программирование на Фортране. Москва «Мир», 1977
А. А. Самарский, А. В. Гулин. Численные методы. Москва «Наука», 1989.

См. также

Практикум ММП ВМК, 4й курс, осень 2008

Источник

Для оценки общей
(итоговой) погрешности (ошибки) выполнения
некоторой последовательности
арифметических операций существует
достаточно удобный способ, основанный
на использовании
графов вычислительных процессов. Граф
вычислительного процесса позволяет
наглядно изобразить последовательность
арифметических операций и легко
определить вклад любой ошибки, возникшей
в процессе вычислений, в общую ошибку.
Пусть вершинами графа являются значения
переменных или результатов арифметических
операций, а его дуги указывают направление
вычислений и нагружены коэффициентами,
оценивающими распространение ошибок.
Граф вычислительного процесса строится
для анализа процесса распространения
относительных ошибок в арифметических
выражениях, его следует читать в
направлении дуг. Сначала выполняются
операции, расположенные на каком-либо
горизонтальном уровне, затем операции
расположенные на более высоком уровне
и т.д. На рис.1.3. представлены графы
вычислительных процессов арифметических
операций.

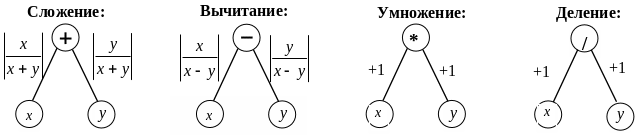
Рис. 1.3. Графы вычислительных процессов
основных арифметических операций.

Правило подсчета
общей ошибки с использованием графа
вычислительного процесса можно
сформулировать следующим образом:
относительная ошибка результата любой
операции (вершины) входит в результат
следующей операции, умножаясь на
коэффициент у дуги, соединяющей эти две
операции.

В качестве примера
рассмотрим выражение

и задачу оценки общей погрешности
результата его вычисления с учетом
ошибок округления результатов выполнения
арифметических операций. Предположим,
что

,

– относительные погрешности округления
чисел

при представлении их в памяти ЭВМ, а

– относительные ошибки округления
соответственно результатов операций
сложения и умножения. Учитывая
последовательность операций, для
рассматриваемого выражения граф
вычислительного процесса будет иметь
вид, представленный на рис. 1.4.

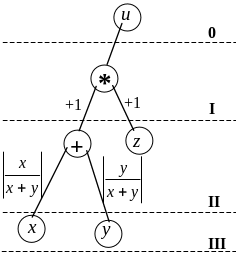
Рис. 1.4. Граф вычислительного процесса
для выражения

Исследуем граф,
представленный на рис. 1.4. Рассмотрим
операцию сложения (уровень II), использующую
числа

,
заданные с относительными погрешностями

и

.
Каждая из погрешностей входит в результат
выполнения операции, умноженной на
соответствующий коэффициент

и

.
Тогда ошибку операции сложения можно
оценить величиной

,
к которой следует прибавить ошибку
округления. В результате формула расчета
относительной ошибки операции сложения
будет выглядеть следующим образом:

Результат выполнения
операции сложения используется в
операции умножения (уровень I),
при этом погрешности передаются в
результат выполнения операции умноженными
на соответствующие коэффициенты

.
Тогда, с учетом погрешности округления,
общая относительная погрешность
вычисления значения

может быть рассчитана следующим образом:

Поскольку причина
ошибок округления и представления чисел
в памяти ЭВМ одна – ограниченность ее
разрядной сетки, – то для относительных
ошибок можно положить

.
Тогда формулу расчета общей погрешности
вычисления значения

можно упростить:

Полученная формула
позволяет дать верхнюю оценку общей
погрешности:

.
Вывод формулы оценки итоговой ошибки
выполнения ряда арифметических операций
с помощью графа вычислительного процесса
для произвольного алгоритма может
являться сложной задачей. Кроме того,
в процессе вычислений в алгоритмах
могут использоваться стандартные или
специальные подпрограммы, для которых
не известны значения и оценки погрешностей
вычисления. В то же время, оценить
погрешность арифметических операций
можно в результате проведения
вычислительного эксперимента.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

From Wikipedia, the free encyclopedia

Error diffusion is a type of halftoning in which the quantization residual is distributed to neighboring pixels that have not yet been processed. Its main use is to convert a multi-level image into a binary image, though it has other applications.

Unlike many other halftoning methods, error diffusion is classified as an area operation, because what the algorithm does at one location influences what happens at other locations. This means buffering is required, and complicates parallel processing. Point operations, such as ordered dither, do not have these complications.

Error diffusion has the tendency to enhance edges in an image. This can make text in images more readable than in other halftoning techniques.

An error-diffused image

Early history[edit]

Richard Howland Ranger received United States patent 1790723 for his invention, «Facsimile system». The patent, which issued in 1931, describes a system for transmitting images over telephone or telegraph lines, or by radio.^[1] Ranger’s invention permitted continuous-tone photographs to be converted first into black and white, then transmitted to remote locations, which had a pen moving over a piece of paper. To render black, the pen was lowered to the paper; to produce white, the pen was raised. Shades of gray were rendered by intermittently raising and lowering the pen, depending upon the luminance of the gray desired.

Ranger’s invention used capacitors to store charges, and vacuum tube comparators to determine when the present luminance, plus any accumulated error, was above a threshold (causing the pen to be raised) or below (causing the pen to be lowered). In this sense, it was an analog version of error diffusion.

Digital era[edit]

Floyd and Steinberg described a system for performing error diffusion on digital images based on a simple kernel^[2]

${\frac {1}{16}}{\begin{bmatrix}-&\#&7\\3&5&1\end{bmatrix}},$

where «» denotes a pixel in the current row which has already been processed (hence diffusing error to it would be pointless), and «#» denotes the pixel currently being processed.

Nearly concurrently, J. F. Jarvis, C. N. Judice, and W. H. Ninke of Bell Labs disclosed a similar method, which they termed «minimized average error» using a larger kernel^[3]

${\frac {1}{48}}{\begin{bmatrix}-&-&\#&7&5\\3&5&7&5&3\\1&3&5&3&1\end{bmatrix}}.$

Algorithm description[edit]

Error diffusion takes a monochrome or color image and reduces the number of quantization levels.^[4] A popular application of error diffusion involves reducing the number of quantization states to just two per channel. This makes the image suitable for printing on binary printers such as black and white laser printers.

In the discussion which follows, it is assumed that the number of quantization states in the error diffused image is two per channel, unless otherwise stated.

One-dimensional error diffusion[edit]

The simplest form of the algorithm scans the image one row at a time and one pixel at a time. The current pixel is compared to a half-gray value. If it is above the value a white pixel is generated in the resulting image. If the pixel is below the half way brightness, a black pixel is generated. Different methods may be used if the target palette is not monochrome, such as thresholding with two values if the target palette is black, gray and white. The generated pixel is either full bright, or full black, so there is an error in the image. The error is then added to the next pixel in the image and the process repeats.

Two-dimensional error diffusion[edit]

One-dimensional error diffusion tends to have severe image artifacts that show up as distinct vertical lines. Two-dimensional error diffusion reduces the visual artifacts. The simplest algorithm is exactly like one-dimensional error diffusion, except that half the error is added to the next pixel, and half of the error is added to the pixel on the next line below.

The kernel is

${\frac {1}{2}}{\begin{bmatrix}\#&1\\1&0\end{bmatrix}},$

where «#» denotes the pixel currently being processed.

Further refinement can be had by dispersing the error further away from the current pixel, as in the matrices given above in Digital era. The sample image at the start of this article is an example of two-dimensional error diffusion.

Color error diffusion[edit]

The same algorithms may be applied to each of the red, green, and blue (or cyan, magenta, yellow, black) channels of a color image to achieve a color effect on printers such as color laser printers that can only print single color values.

However, better visual results may be obtained by first converting the color channels into a perceptive color model that will separate lightness, hue and saturation channels, so that a higher weight for error diffusion will be given to the lightness channel, than to the hue channel. The motivation for this conversion is that human vision better perceives small differences of lightness in small local areas, than similar differences of hue in the same area, and even more than similar differences of saturation on the same area.

For example, if there is a small error in the green channel that cannot be represented, and another small error in the red channel in the same case, the properly weighted sum of these two errors may be used to adjust a perceptible lightness error, that can be represented in a balanced way between all three color channels (according to their respective statistical contribution to the lightness), even if this produces a larger error for the hue when converting the green channel. This error will be diffused in the neighboring pixels.

In addition, gamma correction may be needed on each of these perceptive channels, if they don’t scale linearly with the human vision, so that error diffusion can be accumulated linearly to these gamma-corrected linear channels, before computing the final color channels of the rounded pixel colors, using a reverse conversion to the native non gamma-corrected image format and from which the new residual error will be computed and converted again to be distributed to the next pixels.

Error diffusion with several gray levels[edit]

Error Diffusion may also be used to produce output images with more than two levels (per channel, in the case of color images). This has application in displays and printers which can produce 4, 8, or 16 levels in each image plane, such as electrostatic printers and displays in compact mobile telephones. Rather than use a single threshold to produce binary output, the closest permitted level is determined, and the error, if any, is diffused as described above.

Printer considerations[edit]

Most printers overlap the black dots slightly, so there is not an exact one-to-one relationship to dot frequency (in dots per unit area) and lightness. Tone scale linearization may be applied to the source image to get the printed image to look correct.

Edge enhancement versus lightness preservation[edit]

When an image has a transition from light to dark, the error-diffusion algorithm tends to
make the next generated pixel be black. Dark-to-light transitions tend to result in the next
generated pixel being white. This causes an edge-enhancement effect at the expense of gray-level reproduction accuracy. This results in error diffusion having a higher apparent resolution than other halftone methods. This is especially beneficial with images with text in them, such as the typical facsimile.

This effect shows fairly well in the picture at the top of this article. The grass detail and the text on the sign is well preserved,
and the lightness in the sky, containing little detail. A cluster-dot halftone image of the same resolution would be much less sharp.

References[edit]

^ Richard Howland Ranger, «Facsimile system». United States Patent 1790723, issued 3 February 1931.
^ Floyd, Robert W.; Steinberg, Louis (1976). «An Adaptive Algorithm for Spatial Grayscale». Proceedings of the Society for Information Display. 17 (2): 75–77.
^ J. F. Jarvis, C. N. Judice, and W. H. Ninke, «A survey of techniques for the display of continuous tone pictures on bilevel displays». Computer Graphics and Image Processing, 5:1:13–40 (1976).
^ «Error Diffusion — an overview | ScienceDirect Topics». www.sciencedirect.com. Retrieved 2022-05-09.

External links[edit]

Error diffusion in Matlab

Источник

Что такое распространение ошибок? (Определение и пример)

17 авг. 2022 г.
читать 2 мин

Распространение ошибки происходит, когда вы измеряете некоторые величины a , b , c , … с неопределенностями δ a , δ b , δc …, а затем хотите вычислить какую-то другую величину Q , используя измерения a , b , c и т. д.

Получается, что неопределенности δa , δb , δc будут распространяться (т.е. «растягиваться») на неопределенность Q.

Для вычисления неопределенности Q , обозначаемой δ Q , мы можем использовать следующие формулы.

Примечание. Для каждой из приведенных ниже формул предполагается, что величины a , b , c и т. д. имеют случайные и некоррелированные ошибки.

Сложение или вычитание

Если Q = a + b + … + c – (x + y + … + z)

Тогда δ Q = √ (δa) 2 + (δb) 2 + … + (δc) 2 + (δx) 2 + (δy) 2 + … + (δz) 2

Пример. Предположим, вы измеряете длину человека от земли до талии как 40 дюймов ± 0,18 дюйма. Затем вы измеряете длину человека от талии до макушки как 30 дюймов ± 0,06 дюйма.

Предположим, вы затем используете эти два измерения для расчета общего роста человека. Высота будет рассчитана как 40 дюймов + 30 дюймов = 70 дюймов. Неопределенность в этой оценке будет рассчитываться как:

δ Q = √ (δa) 2 + (δb) 2 + … + (δc) 2 + (δx) 2 + (δy) 2 + … + (δz) 2
δ Q = √ (.18) 2 + (.06) 2
δ Q = 0,1897

Это дает нам окончательное измерение 70 ± 0,1897 дюйма.

Умножение или деление

Если Q = (ab…c) / (xy…z)

Тогда δ Q = |Q| * √ (δa/a) 2 + (δb/b) 2 + … + (δc/c) 2 + (δx/x) 2 + (δy/y) 2 + … + (δz/z) 2

Пример: Предположим, вы хотите измерить отношение длины элемента a к элементу b.Вы измеряете длину a как 20 дюймов ± 0,34 дюйма, а длину b как 15 дюймов ± 0,21 дюйма.

Отношение, определенное как Q = a/b , будет рассчитано как 20/15 = 1,333.Неопределенность в этой оценке будет рассчитываться как:

δQ = | Q | * √ (δa/a) 2 + (δb/b) 2 + … + (δc/c) 2 + (δx/x) 2 + (δy/y) 2 + … + (δz/z) 2
δ Q = |1,333| * √ (0,34/20) 2 + (0,21/15) 2
δ Q = 0,0294

Это дает нам окончательное соотношение 1,333 ± 0,0294 дюйма.

Измеренное количество, умноженное на точное число

Если A точно известно и Q = A x

Тогда δ Q = |A|δx

Пример: предположим, что вы измеряете диаметр круга как 5 метров ± 0,3 метра. Затем вы используете это значение для вычисления длины окружности c = πd .

Длина окружности будет рассчитана как c = πd = π*5 = 15,708.Неопределенность в этой оценке будет рассчитываться как:

δ Q = |A|δx
δ = | π | * 0,3
δ Q = 0,942

Таким образом, длина окружности равна 15,708 ± 0,942 метра.

Неуверенность в силе

Если n — точное число и Q = x n

Тогда δ Q = | Вопрос | * | н | * (δ х/х )

Пример: предположим, что вы измеряете сторону куба как s = 2 дюйма ± 0,02 дюйма. Затем вы используете это значение для вычисления объема куба v = s 3 .

Объем будет рассчитан как v = s 3 = 2 3 = 8 дюймов 3.Неопределенность в этой оценке будет рассчитываться как:

δ = | Вопрос | * | н | * (δ х/х )
δ Q = |8| * |3| * (.02/2)
δ Q = 0,24

Таким образом, объем куба равен 8 ± 0,24 дюйма 3 .

Общая формула распространения ошибок

Если Q = Q(x) является любой функцией от x , то общая формула распространения ошибок может быть определена как:

δ Q = |dQ / dX |δx

Обратите внимание, что вам редко придется выводить эти формулы с нуля, но может быть полезно знать общую формулу, используемую для их вывода.

Источник

Материал из MachineLearning.

Содержание

Введение

Распространение ошибок

Абсолютная ошибка

Относительная ошибка

Графы вычислительных процессов

Примеры

Памятка программисту

Список литературы

См. также

Early history[edit]

Digital era[edit]

Algorithm description[edit]

One-dimensional error diffusion[edit]

Two-dimensional error diffusion[edit]

Color error diffusion[edit]

Error diffusion with several gray levels[edit]

Printer considerations[edit]

Edge enhancement versus lightness preservation[edit]

See also[edit]

References[edit]

External links[edit]

Что такое распространение ошибок? (Определение и пример)

Сложение или вычитание

Умножение или деление

Измеренное количество, умноженное на точное число

Неуверенность в силе

Общая формула распространения ошибок

Интересное по теме: